Número catalán

Los números Catalan son una secuencia de números naturales que aparecen en diversos problemas de conteo , a menudo relacionados con objetos definidos de forma recursiva . Reciben su nombre de Eugène Catalan , aunque Minggatu los descubrió en la década de 1730 .

El n -ésimo número catalán se puede expresar directamente en términos de los coeficientes binomiales centrales mediante

${\displaystyle C_{n}={\frac {1}{n+1}}{2n \choose n}={\frac {(2n)!}{(n+1)!\,n!}}\qquad {\text{para }}n\geq 0.}$

Los primeros números catalanes para n = 0, 1, 2, 3, ... son

1, 1, 2, 5, 14, 42, 132, 429, 1430, 4862, 16796, 58786, ... (secuencia A000108 en la OEIS ).

Una expresión alternativa para C _n es

${\displaystyle C_{n}={2n \elija n}-{2n \elija n+1}}$para${\displaystyle n\geq 0\,,}$

que es equivalente a la expresión dada anteriormente porque . Esta expresión muestra que C _n es un entero , lo cual no es inmediatamente obvio a partir de la primera fórmula dada. Esta expresión forma la base para una prueba de la exactitud de la fórmula.${\displaystyle {\tbinom {2n}{n+1}}={\tfrac {n}{n+1}}{\tbinom {2n}{n}}}$

Otra expresión alternativa es

${\displaystyle C_{n}={\frac {1}{2n+1}}{2n+1 \elegir n}\,,}$

que puede interpretarse directamente en términos del lema del ciclo ; ver más abajo.

Los números catalanes satisfacen las relaciones de recurrencia

${\displaystyle C_{0}=1\quad {\text{y}}\quad C_{n}=\sum _{i=1}^{n}C_{i-1}C_{ni}\quad {\text{para }}n>0}$

y

${\displaystyle C_{0}=1\quad {\text{y}}\quad C_{n}={\frac {2(2n-1)}{n+1}}C_{n-1}\quad {\text{para }}n>0.}$

Asintóticamente, los números catalanes crecen en el sentido de que el cociente del n -ésimo número catalán y la expresión de la derecha tiende a 1 cuando n tiende a infinito.$${\displaystyle C_{n}\sim {\frac {4^{n}}{n^{3/2}{\sqrt {\pi }}}}\,,}$$

Esto se puede demostrar utilizando el crecimiento asintótico de los coeficientes binomiales centrales , mediante la aproximación de Stirling para , o mediante funciones generadoras .${\estilo de visualización n!}$

Los únicos números catalanes C _n que son impares son aquellos para los que n = 2 ^k − 1 ; todos los demás son pares. Los únicos números primos catalanes son C ₂ = 2 y C ₃ = 5 . ^[1] De manera más general, la multiplicidad con la que un primo p divide a C _n se puede determinar expresando primero n + 1 en base p . Para p = 2 , la multiplicidad es el número de 1 bits, menos 1. Para p un primo impar, cuente todos los dígitos mayores que ( p + 1) / 2 ; también cuente los dígitos iguales a ( p + 1) / 2 a menos que sean finales; y cuente los dígitos iguales a ( p − 1) / 2 si no son finales y se cuenta el siguiente dígito. ^[2]

Los números catalanes tienen representaciones integrales ^{[3] [4]}

${\displaystyle C_{n}={\frac {1}{2\pi}}\int _{0}^{4}x^{n}{\sqrt {\frac {4-x}{x}}}\,dx\,={\frac {2}{\pi}}4^{n}\int _{-1}^{1}t^{2n}{\sqrt {1-t^{2}}}\,dt.}$

Lo cual produce inmediatamente .${\displaystyle \sum_{n=0}^{\infty}}{\frac {C_{n}}{4^{n}}}=2}$

Esto tiene una interpretación probabilística simple. Consideremos un paseo aleatorio en la línea de números enteros, comenzando en 0. Sea -1 un estado de "trampa", de modo que si el caminante llega a -1, permanecerá allí. El caminante puede llegar al estado de trampa en los momentos 1, 3, 5, 7..., y el número de formas en que el caminante puede llegar al estado de trampa en el momento es . Dado que el paseo aleatorio unidimensional es recurrente, la probabilidad de que el caminante llegue finalmente a -1 es .${\estilo de visualización 2k+1}$$Estilo de visualización C_{k}}$${\displaystyle \sum_{n=0}^{\infty}}{\frac {C_{n}}{2^{2n+1}}}=1}$

Existen muchos problemas de conteo en combinatoria cuya solución viene dada por los números de Catalan. El libro Enumerative Combinatorics: Volume 2 del combinatorio Richard P. Stanley contiene un conjunto de ejercicios que describen 66 interpretaciones diferentes de los números de Catalan. A continuación se presentan algunos ejemplos, con ilustraciones de los casos C ₃ = 5 y C ₄ = 14 .

• C _n es el número de palabras de Dyck ^[5] de longitud 2 n . Una palabra de Dyck es una cadena que consta de n X y n Y de manera que ningún segmento inicial de la cadena tiene más Y que X. Por ejemplo, las siguientes son las palabras de Dyck hasta una longitud de 6:

• Reinterpretando el símbolo X como paréntesis de apertura e Y como paréntesis de cierre, C _n cuenta el número de expresiones que contienen n pares de paréntesis que coinciden correctamente:

• C _n es el número de formas diferentes en que n + 1 factores pueden ser completamente paréntesis (o el número de formas de asociar n aplicaciones de un operador binario , como en el problema de multiplicación de cadenas de matrices ). Para n = 3 , por ejemplo, tenemos las siguientes cinco paréntesis diferentes de cuatro factores:

• Las aplicaciones sucesivas de un operador binario pueden representarse en términos de un árbol binario completo , etiquetando cada hoja como a , b , c , d . De ello se deduce que C _n es el número de árboles binarios completos con n + 1 hojas o, equivalentemente, con un total de n nodos internos:

• C _n es el número de árboles ordenados (o planos) no isomorfoscon n + 1 vértices. ^[6] Véase codificación de árboles generales como árboles binarios . Por ejemplo, C _n es el número de árboles de análisis posibles para una oración (suponiendo ramificación binaria), en el procesamiento del lenguaje natural.
• C _n es el número de caminos de red monótonos a lo largo de los bordes de una cuadrícula con n × n celdas cuadradas, que no pasan por encima de la diagonal. Un camino monótono es aquel que comienza en la esquina inferior izquierda, termina en la esquina superior derecha y consiste enteramente en bordes que apuntan hacia la derecha o hacia arriba. Contar estos caminos es equivalente a contar palabras de Dyck: X significa "mover a la derecha" e Y significa "mover hacia arriba".

Los siguientes diagramas muestran el caso n = 4 :

Esto se puede representar enumerando los elementos catalanes por altura de columna: ^[7]

• Un polígono convexo de n + 2 lados se puede dividir en triángulos conectando los vértices con segmentos de línea que no se cruzan (una forma de triangulación de polígonos ). El número de triángulos formados es n y el número de formas diferentes en que esto se puede lograr es C _n . Los siguientes hexágonos ilustran el caso n = 4 :

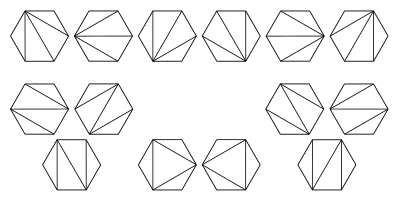
• C _n es el número de permutaciones ordenables en pila de {1, ..., n } . Una permutación w se llama ordenable en pila si S ( w ) = (1, ..., n ) , donde S ( w ) se define recursivamente de la siguiente manera: escriba w = unv donde n es el elemento más grande en w y u y v son secuencias más cortas, y establezca S ( w ) = S ( u ) S ( v ) n , con S siendo la identidad para secuencias de un elemento.
• C _n es el número de permutaciones de {1, ..., n } que evitan el patrón de permutación  123 (o, alternativamente, cualquiera de los otros patrones de longitud 3); es decir, el número de permutaciones sin subsecuencia creciente de tres términos. Para n = 3 , estas permutaciones son 132, 213, 231, 312 y 321. Para n = 4 , son 1432, 2143, 2413, 2431, 3142, 3214, 3241, 3412, 3421, 4132, 4213, 4231, 4312 y 4321.
• C _n es el número de particiones no cruzadas del conjunto {1, ..., n } . A fortiori , C _n nunca excede el n -ésimo número de Bell . C _n es también el número de particiones no cruzadas del conjunto {1, ..., 2 n } en el que cada bloque es de tamaño 2.
• C _n es la cantidad de formas de formar una escalera de altura n con n rectángulos. Si cortamos por la antidiagonal y observamos solo los bordes, obtenemos árboles binarios completos. La siguiente figura ilustra el caso n = 4 :

• C _n es el número de formas de formar una "cadena montañosa" con n trazos ascendentes y n trazos descendentes que se mantengan todos por encima de una línea horizontal. La interpretación de la cadena montañosa es que las montañas nunca bajarán del horizonte.

Cadenas montañosas

${\estilo de visualización n=0:}$	*	1 vía
${\estilo de visualización n=1:}$	/\	1 vía
${\estilo de visualización n=2:}$	0 0 0 0 0 0 0 /\ /\/\, 0 / 0 0 \	2 maneras
${\estilo de visualización n=3:}$	0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 /\ 0 0 0 0 0 0 0 0 0 0 0 0 / \ 0 0 0 0 /\ 0 0 0 0 0 0 /\/\ 0 0 0 0 / 0 0 \ /\/\/\, 0 /\/ 0 0 \, 0 / 0 0 \/\, 0 / 0 0 0 0 \ , 0/0 0 0 0 \ ​	5 maneras

• C _n es el número de cuadros de Young estándar cuyo diagrama es un rectángulo de 2 por n . En otras palabras, es el número de formas en que los números 1, 2, ..., 2 n se pueden organizar en un rectángulo de 2 por n de modo que cada fila y cada columna sean crecientes. Como tal, la fórmula se puede derivar como un caso especial de la fórmula de longitud de gancho .

123 124 125 134 135456 356 346 256 246

• $Estilo de visualización C_{n}$es el número de secuencias de longitud n que comienzan con , y pueden aumentar en o , o disminuir en cualquier número (hasta al menos ). Para estos son . Desde una ruta de Dyck, comience un contador en 0 . Una X aumenta el contador en 1 y una Y lo disminuye en 1 . Registre los valores solo en las X. En comparación con la representación similar de los números de Bell , solo falta .${\estilo de visualización 1}$${\estilo de visualización 0}$${\estilo de visualización 1}$${\estilo de visualización 1}$${\estilo de visualización n=4}$${\displaystyle 1234,1233,1232,1231,1223,1222,1221,1212,1211,1123,1122,1121,1112,1111}$${\estilo de visualización 1213}$

Hay varias formas de explicar por qué la fórmula

${\displaystyle C_{n}={\frac {1}{n+1}}{2n \elegir n}}$

Resuelve los problemas combinatorios enumerados anteriormente. La primera prueba a continuación utiliza una función generadora . Las otras pruebas son ejemplos de pruebas biyectivas ; implican contar literalmente una colección de algún tipo de objeto para llegar a la fórmula correcta.

Primero observamos que todos los problemas combinatorios enumerados anteriormente satisfacen la relación de recurrencia de Segner ^[8].

${\displaystyle C_{0}=1\quad {\text{y}}\quad C_{n+1}=\sum _{i=0}^{n}C_{i}\,C_{ni}\quad {\text{para }}n\geq 0.}$

Por ejemplo, cada palabra de Dyck w de longitud ≥ 2 se puede escribir de manera única en la forma

y = X y ₁ Y y ₂

con las palabras Dyck (posiblemente vacías) w ₁ y w ₂ .

La función generadora de los números catalanes está definida por

${\displaystyle c(x)=\sum _{n=0}^{\infty }C_{n}x^{n}.}$

La relación de recurrencia dada anteriormente se puede resumir en forma de función generadora mediante la relación

${\displaystyle c(x)=1+xc(x)^{2};}$

En otras palabras, esta ecuación se deduce de la relación de recurrencia al expandir ambos lados en series de potencias . Por un lado, la relación de recurrencia determina de manera única los números de Catalan; por otro lado, interpretando xc ² − c + 1 = 0 como una ecuación cuadrática de c y utilizando la fórmula cuadrática , la relación de función generadora se puede resolver algebraicamente para obtener dos posibilidades de solución.

${\displaystyle c(x)={\frac {1+{\sqrt {1-4x}}}{2x}}}$  o  .${\displaystyle c(x)={\frac {1-{\sqrt {1-4x}}}{2x}}}$

De las dos posibilidades, se debe elegir la segunda porque sólo la segunda da

${\displaystyle C_{0}=\lim _{x\to 0}c(x)=1}$.

El término de raíz cuadrada se puede expandir como una serie de potencias utilizando la serie binomial

$${\displaystyle {\begin{aligned}1-{\sqrt {1-4x}}&=-\sum _{n=1}^{\infty }{\binom {1/2}{n}}(-4x)^{n}=-\sum _{n=1}^{\infty }{\frac {(-1)^{n-1}(2n-3)!!}{2^{n}n!}}(-4x)^{n}\\&=-\sum _{n=0}^{\infty }{\frac {(-1)^{n}(2n-1)!!}{2^{n+1}(n+1)!}}(-4x)^{n+1}=\sum _{n=0}^{\infty }{\frac {2^{n+1}(2n-1)!!}{(n+1)!}}x^{n+1}\\&=\sum _{n=0}^{\infty }{\frac {2(2n)!}{(n+1)!n!}}x^{n+1}=\sum _{n=0}^{\infty }{\frac {2}{n+1}}{\binom {2n}{n}}x^{n+1}\,.\end{aligned}}}$$De este modo,$${\displaystyle c(x)={\frac {1-{\sqrt {1-4x}}}{2x}}=\sum _{n=0}^{\infty }{\frac {1}{n+1}}{\binom {2n}{n}}x^{n}\,.}$$

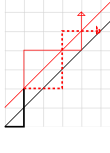
Contamos el número de caminos que comienzan y terminan en la diagonal de una cuadrícula de n × n . Todos estos caminos tienen n pasos hacia la derecha y n hacia arriba. Como podemos elegir cuál de los 2 n pasos es hacia arriba o hacia la derecha, en total hay caminos monótonos de este tipo. Un mal camino cruza la diagonal principal y toca la diagonal inmediatamente superior (en rojo en la ilustración).${\displaystyle {\tbinom {2n}{n}}}$

La parte del camino que se encuentra después de la diagonal superior se invierte sobre esa diagonal, como se ilustra con la línea de puntos roja. Esto cambia todos los pasos correctos por pasos hacia arriba y viceversa. En la sección del camino que no se refleja, hay un paso hacia arriba más que pasos hacia la derecha, por lo que la sección restante del camino incorrecto tiene un paso hacia la derecha más que pasos hacia arriba. Cuando se refleja esta parte del camino, tendrá un paso hacia arriba más que pasos hacia la derecha.

Como todavía hay 2 n pasos, ahora hay n + 1 pasos hacia arriba y n − 1 pasos hacia la derecha. Por lo tanto, en lugar de llegar a ( n , n ) , todos los caminos malos después de la reflexión terminan en ( n − 1, n + 1) . Debido a que cada camino monótono en la cuadrícula ( n − 1) × ( n + 1) se encuentra con la diagonal superior, y debido a que el proceso de reflexión es reversible, la reflexión es, por lo tanto, una biyección entre los caminos malos en la cuadrícula original y los caminos monótonos en la nueva cuadrícula.

El número de caminos malos es por tanto:

${\displaystyle {n-1+n+1 \choose n-1}={2n \choose n-1}={2n \choose n+1}}$

y el número de caminos catalanes (es decir, buenos caminos) se obtiene quitando el número de caminos malos del número total de caminos monótonos de la cuadrícula original,

${\displaystyle C_{n}={2n \choose n}-{2n \choose n+1}={\frac {1}{n+1}}{2n \choose n}.}$

En términos de palabras de Dyck, comenzamos con una secuencia (no de Dyck) de n X y n Y e intercambiamos todas las X e Y después de la primera Y que viola la condición de Dyck. Después de esta Y, observe que hay exactamente una Y más que X.

Esta prueba biyectiva proporciona una explicación natural del término n + 1 que aparece en el denominador de la fórmula para  C _n . Una versión generalizada de esta prueba se puede encontrar en un artículo de Rukavicka Josef (2011). ^[9]

Dado un camino monótono, la excedencia del camino se define como el número de aristas verticales por encima de la diagonal. Por ejemplo, en la Figura 2, las aristas por encima de la diagonal están marcadas en rojo, por lo que la excedencia de este camino es 5.

Dado un camino monótono cuya excedencia no es cero, aplicamos el siguiente algoritmo para construir un nuevo camino cuya excedencia sea 1 menos que el que iniciamos.

• Empezando desde la parte inferior izquierda, sigue el camino hasta que pase por encima de la diagonal.
• Continúe siguiendo el camino hasta que toque nuevamente la diagonal. Marque con X la primera arista de este tipo que alcance.
• Intercambie la parte de la ruta que ocurre antes de X con la parte que ocurre después de X.

En la Figura 3, el punto negro indica el punto donde el camino cruza por primera vez la diagonal. El borde negro es X y colocamos el último punto de la red de la porción roja en la esquina superior derecha y el primer punto de la red de la porción verde en la esquina inferior izquierda y colocamos X en consecuencia para crear un nuevo camino, como se muestra en el segundo diagrama.

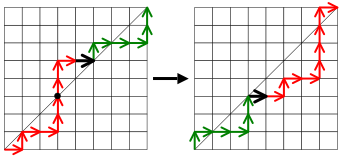
La excedencia ha bajado de 3 a 2. De hecho, el algoritmo hace que la excedencia disminuya en 1 para cualquier camino que le alimentemos, porque el primer paso vertical que comienza en la diagonal (en el punto marcado con un punto negro) es el único borde vertical que cambia de estar por encima de la diagonal a estar por debajo de ella cuando aplicamos el algoritmo; todos los demás bordes verticales permanecen en el mismo lado de la diagonal.

Se puede observar que este proceso es reversible : dado cualquier camino P cuya excedencia sea menor que n , hay exactamente un camino que produce P cuando se le aplica el algoritmo. De hecho, el borde (negro) X , que originalmente era el primer paso horizontal que terminaba en la diagonal, se ha convertido en el último paso horizontal que comenzaba en la diagonal. Alternativamente, invierta el algoritmo original para buscar el primer borde que pasa por debajo de la diagonal.

Esto implica que el número de caminos de excedencia n es igual al número de caminos de excedencia n − 1 , que es igual al número de caminos de excedencia n − 2 , y así sucesivamente, hasta cero. En otras palabras, hemos dividido el conjunto de todos los caminos monótonos en n + 1 clases de igual tamaño, correspondientes a las posibles excedencias entre 0 y n . Como hay caminos monótonos, obtenemos la fórmula deseada${\displaystyle \textstyle {2n \choose n}}$${\displaystyle \textstyle C_{n}={\frac {1}{n+1}}{2n \choose n}.}$

La figura 4 ilustra la situación para  n = 3. Cada una de las 20 posibles rutas monótonas aparece en algún lugar de la tabla. La primera columna muestra todas las rutas de excedencia tres, que se encuentran completamente por encima de la diagonal. Las columnas de la derecha muestran el resultado de aplicaciones sucesivas del algoritmo, con la excedencia disminuyendo una unidad a la vez. Hay cinco filas, es decir  C ₃ = 5 , y la última columna muestra todas las rutas no más altas que la diagonal.

Utilizando palabras de Dyck, comience con una secuencia de . Sea la primera X que iguala a una subsecuencia inicial y configure la secuencia como . La nueva secuencia es .${\displaystyle \textstyle {\binom {2n}{n}}}$${\displaystyle X_{d}}$${\displaystyle (F)X_{d}(L)}$${\displaystyle LXF}$

Esta prueba utiliza la definición de triangulación de los números Catalan para establecer una relación entre C _n y C _{n +1} .

Dado un polígono P con n + 2 lados y una triangulación, marque uno de sus lados como base y oriente también una de sus 2 n + 1 aristas totales. Existen (4 n + 2) C _n triangulaciones marcadas para una base dada.

Dado un polígono Q con n + 3 lados y una triangulación (diferente), marque nuevamente uno de sus lados como la base. Marque uno de los lados que no sea el lado de la base (y no una arista interna del triángulo). Hay ( n + 2) C _{n + 1} triangulaciones marcadas de este tipo para una base dada.

Hay una biyección simple entre estas dos triangulaciones marcadas: podemos colapsar el triángulo en Q cuyo lado está marcado (de dos maneras, y restar las dos que no pueden colapsar la base), o, a la inversa, expandir la arista orientada en P a un triángulo y marcar su nuevo lado.

De este modo

${\displaystyle (4n+2)C_{n}=(n+2)C_{n+1}}$.

Escribir${\displaystyle \textstyle {\frac {4n-2}{n+1}}C_{n-1}=C_{n}.}$

Porque

${\displaystyle (2n)!=(2n)!!(2n-1)!!=2^{n}n!(2n-1)!!}$

tenemos

${\displaystyle {\frac {(2n)!}{n!}}=2^{n}(2n-1)!!=(4n-2)!!!!.}$

Aplicando la recursión con se obtiene el resultado.${\displaystyle C_{0}=1}$

Esta prueba se basa en la interpretación de las palabras de Dyck de los números catalanes, por lo que también lo es el número de formas de hacer coincidir correctamente n pares de corchetes. Denotamos una cadena correcta (posiblemente vacía) con c y su inversa con c' . Dado que cualquier c se puede descomponer de forma única en , la suma de las longitudes posibles de da inmediatamente la definición recursiva${\displaystyle C_{n}}$${\displaystyle c=(c_{1})c_{2}}$${\displaystyle c_{1}}$

${\displaystyle C_{0}=1\quad {\text{and}}\quad C_{n+1}=\sum _{i=0}^{n}C_{i}\,C_{n-i}\quad {\text{for }}n\geq 0}$.

Sea b una cadena balanceada de longitud 2 n , es decir, b contiene un número igual de y , por lo que . Una cadena balanceada también se puede descomponer de forma única en o , por lo que${\displaystyle (}$${\displaystyle )}$${\displaystyle \textstyle B_{n}={2n \choose n}}$${\displaystyle (c)b}$${\displaystyle )c'(b}$

${\displaystyle B_{n+1}=2\sum _{i=0}^{n}B_{i}C_{n-i}.}$

Cualquier cadena balanceada incorrecta (no catalana) comienza con , y la cadena restante tiene uno más que , por lo que${\displaystyle c)}$${\displaystyle (}$${\displaystyle )}$

${\displaystyle B_{n+1}-C_{n+1}=\sum _{i=0}^{n}{2i+1 \choose i}C_{n-i}}$

Además, de las definiciones, tenemos:

${\displaystyle B_{n+1}-C_{n+1}=2\sum _{i=0}^{n}B_{i}C_{n-i}-\sum _{i=0}^{n}C_{i}\,C_{n-i}=\sum _{i=0}^{n}(2B_{i}-C_{i})C_{n-i}.}$

Por lo tanto, como esto es cierto para todos los n ,

${\displaystyle 2B_{i}-C_{i}={\binom {2i+1}{i}}}$

${\displaystyle C_{i}=2B_{i}-{\binom {2i+1}{i}}}$

${\displaystyle C_{i}=2{\binom {2i}{i}}-{\binom {2i+1}{i}}}$

${\displaystyle C_{i}={\frac {1}{i+1}}{\binom {2i}{i}}}$

Esta demostración se basa en la interpretación de las palabras de Dyck de los números catalanes y utiliza el lema del ciclo de Dvoretzky y Motzkin. ^{[10] [11]}

Llamamos dominante a una secuencia de X e Y si, leyendo de izquierda a derecha, el número de X es siempre estrictamente mayor que el número de Y. El lema del ciclo ^[12] establece que cualquier secuencia de X e Y, donde , tiene desplazamientos circulares dominantes precisos . Para ver esto, ordene la secuencia dada de X e Y en un círculo. Eliminar repetidamente pares XY deja exactamente X. Cada una de estas X fue el comienzo de un desplazamiento circular dominante antes de que se eliminara algo. Por ejemplo, considere . Esta secuencia es dominante, pero ninguno de sus desplazamientos circulares , , y lo son.${\displaystyle m}$${\displaystyle n}$${\displaystyle m>n}$${\displaystyle m-n}$${\displaystyle m+n}$${\displaystyle m-n}$${\displaystyle {\mathit {XXYXY}}}$${\displaystyle {\mathit {XYXYX}}}$${\displaystyle {\mathit {YXYXX}}}$${\displaystyle {\mathit {XYXXY}}}$${\displaystyle {\mathit {YXXYX}}}$

Una cadena es una palabra Dyck de X e Y si y solo si anteponer una X a la palabra Dyck da una secuencia dominante con X e Y, de modo que podemos contar las primeras contando en lugar de las segundas. En particular, cuando , hay exactamente un desplazamiento circular dominante. Hay secuencias con exactamente X e Y. Para cada una de ellas, solo uno de los desplazamientos circulares es dominante. Por lo tanto, hay secuencias distintas de X e Y que son dominantes, cada una de las cuales corresponde exactamente a una palabra Dyck.${\displaystyle n}$${\displaystyle n}$${\displaystyle n+1}$${\displaystyle n}$${\displaystyle m=n+1}$${\displaystyle \textstyle {2n+1 \choose n}}$${\displaystyle n+1}$${\displaystyle n}$${\displaystyle 2n+1}$${\displaystyle \textstyle {\frac {1}{2n+1}}{2n+1 \choose n}=C_{n}}$${\displaystyle n+1}$${\displaystyle n}$

La matriz de Hankel n × n cuya entrada ( i , j ) es el número de Catalan C _{i + j −2} tiene determinante 1, independientemente del valor de n . Por ejemplo, para n = 4 tenemos

${\displaystyle \det {\begin{bmatrix}1&1&2&5\\1&2&5&14\\2&5&14&42\\5&14&42&132\end{bmatrix}}=1.}$

Además, si la indexación se "desplaza" de modo que la entrada ( i , j ) se llene con el número Catalan C _{i + j −1} entonces el determinante sigue siendo 1, independientemente del valor de n . Por ejemplo, para n = 4 tenemos

${\displaystyle \det {\begin{bmatrix}1&2&5&14\\2&5&14&42\\5&14&42&132\\14&42&132&429\end{bmatrix}}=1.}$

En conjunto, estas dos condiciones definen de forma única los números catalanes.

Otra característica única de la matriz Catalan-Hankel es que la submatriz n × n que comienza en 2 tiene determinante n + 1 .

${\displaystyle \det {\begin{bmatrix}2\end{bmatrix}}=2}$

${\displaystyle \det {\begin{bmatrix}2&5\\5&14\end{bmatrix}}=3}$

${\displaystyle \det {\begin{bmatrix}2&5&14\\5&14&42\\14&42&132\end{bmatrix}}=4}$

${\displaystyle \det {\begin{bmatrix}2&5&14&42\\5&14&42&132\\14&42&132&429\\42&132&429&1430\end{bmatrix}}=5}$

etcétera.

La sucesión Catalan fue descrita en el siglo XVIII por Leonhard Euler , que estaba interesado en la cantidad de formas diferentes de dividir un polígono en triángulos. La sucesión recibe su nombre de Eugène Charles Catalan , quien descubrió la conexión con las expresiones entre paréntesis durante su exploración del rompecabezas de las Torres de Hanoi . El truco del conteo reflexivo (segunda prueba) para las palabras de Dyck fue descubierto por Désiré André en 1887.

El nombre “números catalanes” tiene su origen en John Riordan . ^[13]

En 1988, salió a la luz que la secuencia numérica catalana había sido utilizada en China por el matemático mongol Mingantu en 1730. ^{[14] [15]} Fue entonces cuando comenzó a escribir su libro Ge Yuan Mi Lu Jie Fa [El método rápido para obtener la razón precisa de la división de un círculo] , que fue completado por su estudiante Chen Jixin en 1774, pero publicado sesenta años después. Peter J. Larcombe (1999) esbozó algunas de las características del trabajo de Mingantu, incluido el estímulo de Pierre Jartoux, quien trajo tres series infinitas a China a principios del siglo XVIII.

Por ejemplo, Ming utilizó la secuencia Catalana para expresar expansiones de series de y en términos de .${\displaystyle \sin(2\alpha )}$${\displaystyle \sin(4\alpha )}$${\displaystyle \sin(\alpha )}$

Los números de Catalan pueden interpretarse como un caso especial del teorema de votación de Bertrand . En concreto, es el número de formas en que un candidato A con n + 1 votos puede superar al candidato B con n votos.${\displaystyle C_{n}}$

La sucesión de dos parámetros de números enteros no negativos es una generalización de los números catalanes. Estos se denominan números supercatalanes , según Ira Gessel . No deben confundirse con los números de Schröder-Hipparchus , que a veces también se denominan números supercatalanes.${\displaystyle {\frac {(2m)!(2n)!}{(m+n)!m!n!}}}$

Para , esto es sólo dos veces los números catalanes ordinarios, y para , los números tienen una descripción combinatoria fácil. Sin embargo, sólo se conocen otras descripciones combinatorias ^[16] para y , ^[17] y es un problema abierto encontrar una interpretación combinatoria general.${\displaystyle m=1}$${\displaystyle m=n}$${\displaystyle m=2,3}$${\displaystyle 4}$

Sergey Fomin y Nathan Reading han dado un número Catalan generalizado asociado a cualquier grupo de Coxeter cristalográfico finito , a saber, el número de elementos completamente conmutativos del grupo; en términos del sistema raíz asociado , es el número de anticadenas (o ideales de orden) en el conjunto de raíces positivas. El número Catalan clásico corresponde al sistema raíz de tipo . La relación de recurrencia clásica se generaliza: el número Catalan de un diagrama de Coxeter es igual a la suma de los números Catalan de todos sus subdiagramas propios máximos. ^[18]${\displaystyle C_{n}}$${\displaystyle A_{n}}$

Los números de Catalan son una solución de una versión del problema del momento de Hausdorff . ^[19]

La convolución k -fold de Catalan, donde k = m , es: ^[20]

${\displaystyle \sum _{i_{1}+\cdots +i_{m}=n \atop i_{1},\ldots ,i_{m}\geq 0}C_{i_{1}}\cdots C_{i_{m}}={\begin{cases}{\dfrac {m(n+1)(n+2)\cdots (n+m/2-1)}{2(n+m/2+2)(n+m/2+3)\cdots (n+m)}}C_{n+m/2},&m{\text{ even,}}\\[5pt]{\dfrac {m(n+1)(n+2)\cdots (n+(m-1)/2)}{(n+(m+3)/2)(n+(m+3)/2+1)\cdots (n+m)}}C_{n+(m-1)/2},&m{\text{ odd.}}\end{cases}}}$

• Stanley, Richard P. (2015), Los números catalanes . Cambridge University Press, ISBN 978-1-107-42774-7 . 
• Conway y Guy (1996) El libro de los números . Nueva York: Copernicus, págs. 96-106.
• Gardner, Martin (1988), Viajes en el tiempo y otros desconciertos matemáticos, Nueva York: WH Freeman and Company, págs. 253–266 (cap. 20), Bibcode :1988ttom.book.....G, ISBN 0-7167-1924-X
• Koshy, Thomas (2008), Números en catalán con aplicaciones, Oxford University Press, ISBN 978-0-19-533454-8
• Koshy, Thomas y Zhenguang Gao (2011) "Algunas propiedades de divisibilidad de los números catalanes", Mathematical Gazette 95:96–102.
• Larcombe, PJ (1999). "El descubrimiento chino del siglo XVIII de los números catalanes" (PDF) . Mathematical Spectrum . 32 : 5–7.
• Stanley, Richard P. (1999), Combinatoria enumerativa. Vol. 2, Cambridge Studies in Advanced Mathematics, vol. 62, Cambridge University Press , ISBN 978-0-521-56069-6, Sr.  1676282
• Egecioglu, Omer (2009), Una evaluación determinante de Catalan-Hankel (PDF)
• Gheorghiciuc, Irina; Orelowitz, Gidon (2020), Números supercatalanes de tercer y cuarto tipo , arXiv : 2008.00133

• Stanley, Richard P. (1998), Adenda catalana a Combinatoria Enumerativa, Volumen 2 (PDF)
• Weisstein, Eric W. "Número catalán". MathWorld .
• Davis, Tom: Números catalanes. Más ejemplos.
• "Equivalencia de tres interpretaciones de números catalanes" del Proyecto de Demostraciones Wolfram [1]
• Materiales de aprendizaje relacionados con Particiones relacionadas con triángulos numéricos en Wikiversidad