Conjunto contable

Conjunto matemático que puede enumerarse

En matemáticas , un conjunto es contable si es finito o puede hacerse una correspondencia biunívoca con el conjunto de números naturales . ^[a] De manera equivalente, un conjunto es contable si existe una función inyectiva de él en los números naturales; esto significa que cada elemento del conjunto puede estar asociado a un número natural único, o que los elementos del conjunto pueden contarse uno a uno, aunque el conteo puede no terminar nunca debido a un número infinito de elementos.

En términos más técnicos, asumiendo el axioma de elección contable , un conjunto es contable si su cardinalidad (el número de elementos del conjunto) no es mayor que la de los números naturales. Un conjunto contable que no es finito se dice que es contablemente infinito .

El concepto se atribuye a Georg Cantor , quien demostró la existencia de conjuntos incontables , es decir, conjuntos que no son contables; por ejemplo el conjunto de los números reales .

Una nota sobre la terminología

Aunque los términos "contable" y "contablemente infinito" como se definen aquí son bastante comunes, la terminología no es universal. ^[1] Un estilo alternativo utiliza contable para significar lo que aquí se llama contablemente infinito, y como máximo contable para significar lo que aquí se llama contable. ^[2]^[3]

Los términos enumerable ^[4] y numerable ^[5]^[6] también pueden usarse, por ejemplo, refiriéndose a contable y numerablemente infinito respectivamente, ^[7] las definiciones varían y se debe tener cuidado con respecto a la diferencia con recursivamente enumerable . ^[8]

Definición

Un conjunto es contable si: ${\estilo de visualización S}$

Su cardinalidad es menor o igual a ( aleph-null ), la cardinalidad del conjunto de los números naturales . ^[9] ${\estilo de visualización |S|}$ $estilo de visualización {\aleph _{0}}$ $\mathbb {N}$
Existe una función inyectiva de a . ^[10]^[11] ${\estilo de visualización S}$ $\mathbb {N}$
${\estilo de visualización S}$ está vacío o existe una función sobreyectiva de a . ^[11] $\mathbb {N}$ ${\estilo de visualización S}$
Existe una aplicación biyectiva entre y un subconjunto de . ^[12] ${\estilo de visualización S}$ $\mathbb {N}$
${\estilo de visualización S}$ es finito ( ) o contablemente infinito. ^[5] $|S|<\aleph _{0}$

Todas estas definiciones son equivalentes.

Un conjunto es infinito contablemente si: ${\estilo de visualización S}$

Su cardinalidad es exactamente . ^[9] ${\estilo de visualización |S|}$ $estilo de visualización {\aleph _{0}}$
Existe una aplicación inyectiva y sobreyectiva (y por lo tanto biyectiva ) entre y . ${\estilo de visualización S}$ $\mathbb {N}$
${\estilo de visualización S}$ tiene una correspondencia biunívoca con . ^[13] $\mathbb {N}$
Los elementos de se pueden organizar en una secuencia infinita , donde es distinto de para y cada elemento de está enumerado. ^[14]^[15] ${\estilo de visualización S}$ $a_{0},a_{1},a_{2},\ldots$ $Estilo de visualización ai$ $estilo de visualización a_ {j}}$ $i\neq j$ ${\estilo de visualización S}$

Un conjunto es incontable si no es contable, es decir, su cardinalidad es mayor que . ^[9] $estilo de visualización {\aleph _{0}}$

Historia

En 1874, en su primer artículo de teoría de conjuntos , Cantor demostró que el conjunto de números reales es incontable, mostrando así que no todos los conjuntos infinitos son contables. ^[16] En 1878, utilizó correspondencias uno a uno para definir y comparar cardinalidades. ^[17] En 1883, extendió los números naturales con sus ordinales infinitos y utilizó conjuntos de ordinales para producir una infinidad de conjuntos que tienen diferentes cardinalidades infinitas. ^[18]

Introducción

Un conjunto es una colección de elementos y puede describirse de muchas maneras. Una forma es simplemente enumerar todos sus elementos; por ejemplo, el conjunto que consta de los números enteros 3, 4 y 5 puede denotarse como , llamada forma de lista. ^[19] Sin embargo, esto solo es efectivo para conjuntos pequeños; para conjuntos más grandes, esto consumiría mucho tiempo y sería propenso a errores. En lugar de enumerar cada elemento individual, a veces se usa una elipsis ("...") para representar muchos elementos entre el elemento inicial y el elemento final en un conjunto, si el escritor cree que el lector puede adivinar fácilmente qué representa ...; por ejemplo, presumiblemente denota el conjunto de números enteros del 1 al 100. Sin embargo, incluso en este caso, todavía es posible enumerar todos los elementos, porque el número de elementos en el conjunto es finito. Si numeramos los elementos del conjunto 1, 2, y así sucesivamente, hasta , esto nos da la definición habitual de "conjuntos de tamaño ". ${\estilo de visualización \{3,4,5\}}$ $\{1,2,3,\puntos ,100\}$ ${\estilo de visualización n}$ ${\estilo de visualización n}$

Algunos conjuntos son infinitos ; estos conjuntos tienen más de elementos donde es cualquier entero que se pueda especificar. (No importa cuán grande sea el entero especificado , como , los conjuntos infinitos tienen más de elementos). Por ejemplo, el conjunto de números naturales, denotable por , ^[a] tiene infinitos elementos, y no podemos usar ningún número natural para dar su tamaño. Puede parecer natural dividir los conjuntos en diferentes clases: poner todos los conjuntos que contienen un elemento juntos; todos los conjuntos que contienen dos elementos juntos; ...; finalmente, poner juntos todos los conjuntos infinitos y considerarlos como si tuvieran el mismo tamaño. Esta visión funciona bien para conjuntos infinitos contables y era la suposición predominante antes del trabajo de Georg Cantor. Por ejemplo, hay infinitos números enteros impares, infinitos números enteros pares y también infinitos números enteros en general. Podemos considerar que todos estos conjuntos tienen el mismo "tamaño" porque podemos organizar las cosas de manera que, para cada número entero, haya un número entero par distinto: o, de manera más general, (ver imagen). Lo que hemos hecho aquí es organizar los números enteros y los números pares en una correspondencia biyectiva (o biyección ), que es una función que se aplica entre dos conjuntos de modo que cada elemento de cada conjunto corresponde a un único elemento del otro conjunto. Esta noción matemática de "tamaño", cardinalidad, es que dos conjuntos son del mismo tamaño si y solo si hay una biyección entre ellos. Llamamos a todos los conjuntos que están en correspondencia biyectiva con los números enteros infinitos contables y decimos que tienen cardinalidad . ${\estilo de visualización n}$ ${\estilo de visualización n}$ ${\estilo de visualización n}$ $n=10^{1000}$ ${\estilo de visualización n}$ $\{0,1,2,3,4,5,\puntos \}$ $\ldots \,-\!2\!\rightarrow \!-\!4,\,-\!1\!\rightarrow \!-\!2,\,0\!\rightarrow \!0,\,1\!\rightarrow \!2,\,2\!\rightarrow \!4\,\cdots$ $n\flecha derecha 2n$ $estilo de visualización {\aleph _{0}}$

Georg Cantor demostró que no todos los conjuntos infinitos son numerables. Por ejemplo, los números reales no pueden ponerse en correspondencia biunívoca con los números naturales (enteros no negativos). El conjunto de los números reales tiene una cardinalidad mayor que el conjunto de los números naturales y se dice que es incontable.

Descripción formal

Por definición, un conjunto es numerable si existe una biyección entre y un subconjunto de los números naturales . Por ejemplo, defina la correspondencia Dado que cada elemento de está emparejado con precisamente un elemento de , y viceversa, esto define una biyección y muestra que es numerable. De manera similar, podemos demostrar que todos los conjuntos finitos son numerables. ${\estilo de visualización S}$ ${\estilo de visualización S}$ $\mathbb {N} =\{0,1,2,\puntos \}$ $a\leftrightarrow 1,\ b\leftrightarrow 2,\ c\leftrightarrow 3$ $S=\{a,b,c\}$ ${\estilo de visualización \{1,2,3\}}$ ${\estilo de visualización S}$

En el caso de los conjuntos infinitos, un conjunto es numerablemente infinito si existe una biyección entre y todos los . Como ejemplos, considere los conjuntos , el conjunto de los números enteros positivos , y , el conjunto de los números enteros pares. Podemos demostrar que estos conjuntos son numerablemente infinitos al exhibir una biyección a los números naturales. Esto se puede lograr utilizando las asignaciones y , de modo que Todo conjunto numerablemente infinito es numerable, y todo conjunto numerable infinito es numerablemente infinito. Además, cualquier subconjunto de los números naturales es numerable, y de manera más general: ${\estilo de visualización S}$ ${\estilo de visualización S}$ $\mathbb {N}$ $A=\{1,2,3,\puntos \}$ $B=\{0,2,4,6,\puntos \}$ $n\flecha izquierda derecha n+1$ $n\flecha izquierda derecha 2n$ ${\begin{matrix}0\leftrightarrow 1,&1\leftrightarrow 2,&2\leftrightarrow 3,&3\leftrightarrow 4,&4\leftrightarrow 5,&\ldots \\[6pt]0\leftrightarrow 0,&1\leftrightarrow 2,&2\leftrightarrow 4,&3\leftrightarrow 6,&4\leftrightarrow 8,&\ldots \end{matrix}}$

Teorema : Un subconjunto de un conjunto contable es contable. ^[20]

El conjunto de todos los pares ordenados de números naturales (el producto cartesiano de dos conjuntos de números naturales, es numerablemente infinito, como se puede ver siguiendo un camino como el de la imagen: $\mathbb {N} \times \mathbb {N}$

El mapeo resultante procede de la siguiente manera:

$0\leftrightarrow (0,0),1\leftrightarrow (1,0),2\leftrightarrow (0,1),3\leftrightarrow (2,0),4\leftrightarrow (1,1),5\leftrightarrow (0,2),6\leftrightarrow (3,0),\ldots$ Este mapeo cubre todos estos pares ordenados.

Esta forma de mapeo triangular se generaliza recursivamente a - tuplas de números naturales, es decir, donde y son números naturales, al mapear repetidamente los primeros dos elementos de una - tupla a un número natural. Por ejemplo, se puede escribir como . Luego se mapea a 5 por lo que se mapea a , luego se mapea a 39. Dado que una 2-tupla diferente, es decir, un par como , se mapea a un número natural diferente, una diferencia entre dos n-tuplas por un solo elemento es suficiente para asegurar que las n-tuplas se mapeen a diferentes números naturales. Entonces, se prueba una inyección del conjunto de - tuplas al conjunto de números naturales . Para el conjunto de - tuplas hecho por el producto cartesiano de un número finito de conjuntos diferentes, cada elemento en cada tupla tiene la correspondencia con un número natural, por lo que cada tupla se puede escribir en números naturales luego se aplica la misma lógica para probar el teorema. $n$ $(a_{1},a_{2},a_{3},\dots ,a_{n})$ $a_{i}$ $n$ $n$ $(0,2,3)$ $((0,2),3)$ $(0,2)$ $((0,2),3)$ $(5,3)$ $(5,3)$ $(a,b)$ $n$ $\mathbb {N}$ $n$

Teorema : El producto cartesiano de un número finito de conjuntos numerables es numerable. ^[21]^[b]

El conjunto de todos los números enteros y el conjunto de todos los números racionales pueden parecer intuitivamente mucho mayores que . Pero las apariencias engañan. Si un par se trata como numerador y denominador de una fracción vulgar (una fracción en la forma de donde y son números enteros), entonces para cada fracción positiva, podemos obtener un número natural distinto que le corresponde. Esta representación también incluye los números naturales, ya que cada número natural es también una fracción . Por lo tanto, podemos concluir que hay exactamente tantos números racionales positivos como enteros positivos. Esto también es cierto para todos los números racionales, como se puede ver a continuación. $\mathbb {Z}$ $\mathbb {Q}$ $\mathbb {N}$ $a/b$ $a$ $b\neq 0$ $n$ $n/1$

Teorema — (el conjunto de todos los números enteros) y (el conjunto de todos los números racionales) son contables. ^[c] $\mathbb {Z}$ $\mathbb {Q}$

De manera similar, el conjunto de números algebraicos es contable. ^[23]^[d]

A veces es útil más de una aplicación: un conjunto que se va a mostrar como contable se asigna uno a uno (inyección) a otro conjunto , luego se demuestra que es contable si se asigna uno a uno al conjunto de números naturales. Por ejemplo, el conjunto de números racionales positivos se puede asignar fácilmente uno a uno al conjunto de pares de números naturales (2-tuplas) porque se asigna a . Dado que el conjunto de pares de números naturales se asigna uno a uno (en realidad, correspondencia uno a uno o biyección) al conjunto de números naturales como se muestra arriba, el conjunto de números racionales positivos se demuestra que es contable. $A$ $B$ $A$ $B$ $p/q$ $(p,q)$

Teorema — Toda unión finita de conjuntos numerables es numerable. ^[24]^[25]^[e]

Con la previsión de saber que hay conjuntos incontables, podemos preguntarnos si este último resultado puede llevarse más lejos. La respuesta es "sí" y "no", podemos extenderlo, pero para ello necesitamos suponer un nuevo axioma.

Teorema — (Suponiendo el axioma de elección contable ) La unión de un número contable de conjuntos contables es contable. ^[f]

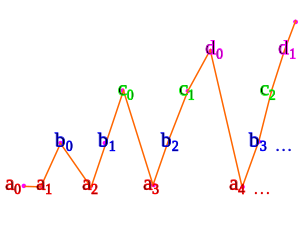
Enumeración para un número contable de conjuntos contables

Por ejemplo, dados conjuntos contables , primero asignamos a cada elemento de cada conjunto una tupla, luego asignamos a cada tupla un índice usando una variante de la enumeración triangular que vimos arriba: ${\textbf {a}},{\textbf {b}},{\textbf {c}},\dots$ ${\begin{array}{c|c|c }{\text{Index}}&{\text{Tuple}}&{\text{Element}}\\\hline 0&(0,0)&{\textbf {a}}_{0}\\1&(0,1)&{\textbf {a}}_{1}\\2&(1,0)&{\textbf {b}}_{0}\\3&(0,2)&{\textbf {a}}_{2}\\4&(1,1)&{\textbf {b}}_{1}\\5&(2,0)&{\textbf {c}}_{0}\\6&(0,3)&{\textbf {a}}_{3}\\7&(1,2)&{\textbf {b}}_{2}\\8&(2,1)&{\textbf {c}}_{1}\\9&(3,0)&{\textbf {d}}_{0}\\10&(0,4)&{\textbf {a}}_{4}\\\vdots &&\end{array}}$

Necesitamos el axioma de elección contable para indexar todos los conjuntos simultáneamente. ${\textbf {a}},{\textbf {b}},{\textbf {c}},\dots$

Teorema — El conjunto de todas las secuencias de números naturales de longitud finita es contable.

Este conjunto es la unión de las secuencias de longitud 1, de longitud 2 y de longitud 3, cada una de las cuales es un conjunto numerable (producto cartesiano finito). Por lo tanto, estamos hablando de una unión numerable de conjuntos numerables, que es numerable según el teorema anterior.

Teorema — El conjunto de todos los subconjuntos finitos de los números naturales es contable.

Los elementos de cualquier subconjunto finito se pueden ordenar en una secuencia finita. Solo hay una cantidad contable de secuencias finitas, por lo que también hay una cantidad contable de subconjuntos finitos.

Teorema — Sean y conjuntos. $S$ $T$

Si la función es inyectiva y es contable entonces es contable. $f:S\to T$ $T$ $S$
Si la función es sobreyectiva y es contable entonces es contable. $g:S\to T$ $S$ $T$

Estos se desprenden de las definiciones de conjunto contable como funciones inyectivas/sobreyectivas. ^[g]

El teorema de Cantor afirma que sies un conjunto yes su conjunto potencia , es decir, el conjunto de todos los subconjuntos de, entonces no existe ninguna función sobreyectiva dea. Se ofrece una prueba en el artículo Teorema de Cantor . Como consecuencia inmediata de esto y del Teorema Básico anterior tenemos: $A$ ${\mathcal {P}}(A)$ $A$ $A$ ${\mathcal {P}}(A)$

Proposición — El conjunto no es contable; es decir, es incontable . ${\mathcal {P}}(\mathbb {N} )$

Para una elaboración de este resultado véase el argumento diagonal de Cantor .

El conjunto de números reales es incontable, ^{[h] y también lo es el conjunto de todas}las secuencias infinitas de números naturales.

El modelo mínimo de la teoría de conjuntos es contable

Si existe un conjunto que es un modelo estándar (ver modelo interno ) de la teoría de conjuntos ZFC, entonces existe un modelo estándar mínimo (ver Universo construible ). El teorema de Löwenheim-Skolem se puede utilizar para demostrar que este modelo mínimo es numerable. El hecho de que la noción de "incontabilidad" tenga sentido incluso en este modelo, y en particular que este modelo M contenga elementos que son:

subconjuntos de M , por lo tanto contables,
pero incontable desde el punto de vista de M ,

Fue visto como paradójico en los primeros días de la teoría de conjuntos; véase la paradoja de Skolem para más información.

El modelo estándar mínimo incluye todos los números algebraicos y todos los números trascendentales efectivamente computables , así como muchos otros tipos de números.

Pedidos totales

Los conjuntos contables se pueden ordenar totalmente de varias maneras, por ejemplo:

Órdenes buenas (ver también número ordinal ):
- El orden habitual de los números naturales (0, 1, 2, 3, 4, 5, ...)
- Los números enteros en el orden (0, 1, 2, 3, ...; −1, −2, −3, ...)
Otros ( no muy bien pedidos):
- El orden habitual de los números enteros (..., −3, −2, −1, 0, 1, 2, 3, ...)
- El orden habitual de los números racionales (¡No se puede escribir explícitamente como una lista ordenada!)

En ambos ejemplos de órdenes bien definidos, cualquier subconjunto tiene un elemento mínimo ; y en ambos ejemplos de órdenes no bien definidos, algunos subconjuntos no tienen un elemento mínimo . Esta es la definición clave que determina si un orden total también es un orden bien definido.

Véase también

Notas

^ ab Dado que existe una biyección obvia entre y , no hay diferencia si se considera que 0 es un número natural o no. En cualquier caso, este artículo sigue la norma ISO 31-11 y la convención estándar en lógica matemática , que considera que 0 es un número natural. $\mathbb {N}$ $\mathbb {N} ^{*}=\{1,2,3,\dots \}$
^ Prueba: Obsérvese que es contable como consecuencia de la definición porque la función dada por es inyectiva. ^[22] Entonces se sigue que el producto cartesiano de dos conjuntos contables cualesquiera es contable, porque si y son dos conjuntos contables hay sobreyecciones y . Por lo tanto es una sobreyección del conjunto contable al conjunto y el Corolario implica que es contable. Este resultado se generaliza al producto cartesiano de cualquier colección finita de conjuntos contables y la prueba se sigue por inducción sobre el número de conjuntos en la colección. $\mathbb {N} \times \mathbb {N}$ $f:\mathbb {N} \times \mathbb {N} \to \mathbb {N}$ $f(m,n)=2^{m}\cdot 3^{n}$ $A$ $B$ $f:\mathbb {N} \to A$ $g:\mathbb {N} \to B$ $f\times g:\mathbb {N} \times \mathbb {N} \to A\times B$ $\mathbb {N} \times \mathbb {N}$ $A\times B$ $A\times B$
^ Demostración: Los números enteros son contables porque la función dada por si es no negativa y si es negativa, es una función inyectiva. Los números racionales son contables porque la función dada por es una sobreyección del conjunto contable a los racionales . $\mathbb {Z}$ $f:\mathbb {Z} \to \mathbb {N}$ $f(n)=2^{n}$ $n$ $f(n)=3^{-n}$ $n$ $\mathbb {Q}$ $g:\mathbb {Z} \times \mathbb {N} \to \mathbb {Q}$ $g(m,n)=m/(n+1)$ $\mathbb {Z} \times \mathbb {N}$ $\mathbb {Q}$
^ Demostración: Por definición, cada número algebraico (incluidos los números complejos) es una raíz de un polinomio con coeficientes enteros. Dado un número algebraico , sea un polinomio con coeficientes enteros tal que es la raíz -ésima del polinomio, donde las raíces se ordenan por valor absoluto de menor a mayor, luego se ordenan por argumento de menor a mayor. Podemos definir una función de inyección (es decir, uno a uno) dada por , donde es el primo -ésimo . $\alpha$ $a_{0}x^{0}+a_{1}x^{1}+a_{2}x^{2}+\cdots +a_{n}x^{n}$ $\alpha$ $k$ $f:\mathbb {A} \to \mathbb {Q}$ $f(\alpha )=2^{k-1}\cdot 3^{a_{0}}\cdot 5^{a_{1}}\cdot 7^{a_{2}}\cdots {p_{n+2}}^{a_{n}}$ $p_{n}$ $n$
^ Demostración: Si es un conjunto numerable para cada uno de , entonces para cada uno existe una función sobreyectiva y, por lo tanto, la función dada por es una sobreyección. Como es numerable, la unión es numerable. $A_{i}$ $i$ $I=\{1,\dots ,n\}$ $i$ $g_{i}:\mathbb {N} \to A_{i}$ $G:I\times \mathbf {N} \to \bigcup _{i\in I}A_{i},$ $G(i,m)=g_{i}(m)$ $I\times \mathbb {N}$ ${\textstyle \bigcup _{i\in I}A_{i}}$
^ Prueba : Como en el caso finito, pero y usamos el axioma de elección contable para elegir para cada uno en una sobreyección de la colección no vacía de sobreyecciones de a . ^[26] Nótese que dado que estamos considerando la sobreyección , en lugar de una inyección, no hay ningún requisito de que los conjuntos sean disjuntos. $I=\mathbb {N}$ $i$ $\mathbb {N}$ $g_{i}$ $\mathbb {N}$ $A_{i}$ $G:\mathbf {N} \times \mathbf {N} \to \bigcup _{i\in I}A_{i}$
^ Demostración : Para (1) observe que si es contable existe una función inyectiva . Entonces, si es inyectiva la composición es inyectiva, por lo que es contable. Para (2) observe que si es contable, o bien está vacía o existe una función sobreyectiva . Entonces, si es sobreyectiva, o bien y están vacías, o bien la composición es sobreyectiva. En cualquier caso es contable. $T$ $h:T\to \mathbb {N}$ $f:S\to T$ $h\circ f:S\to \mathbb {N}$ $S$ $S$ $S$ $h:\mathbb {N} \to S$ $g:S\to T$ $S$ $T$ $g\circ h:\mathbb {N} \to T$ $T$
^ Véase la primera prueba de incontabilidad de Cantor y también la Propiedad de intersección finita#Aplicaciones para una prueba topológica.

Citas

^ Manetti, Marco (19 de junio de 2015). Topología. Saltador. pag. 26.ISBN 978-3-319-16958-3.
^ Rudin 1976, Capítulo 2
^ Tao 2016, pág. 181
^ Kamke 1950, pág. 2
^ ab Lang 1993, §2 del Capítulo I
^ Apostol 1969, p. 23, Capítulo 1.14
^ Thierry, Vialar (4 de abril de 2017). Manual de matemáticas. BoD - Libros a pedido. p. 24. ISBN 978-2-9551990-1-5.
^ Mukherjee, Subir Kumar (2009). Primer curso de análisis real. Academic Publishers. pág. 22. ISBN 978-81-89781-90-3.
^ abc Yaqub, Aladdin M. (24 de octubre de 2014). Introducción a la metalógica. Broadview Press. ISBN 978-1-4604-0244-3.
^ Singh, Tej Bahadur (17 de mayo de 2019). Introducción a la topología. Springer. pág. 422. ISBN 978-981-13-6954-4.
^ ab Katzourakis, Nikolaos; Varvaruca, Eugen (2 de enero de 2018). Una introducción ilustrativa al análisis moderno. CRC Press. ISBN 978-1-351-76532-9.
^ Halmos 1960, pág. 91
^ Kamke 1950, pág. 2
^ Dlab, Vlastimil; Williams, Kenneth S. (9 de junio de 2020). Invitación al álgebra: un compendio de recursos para profesores, estudiantes universitarios avanzados y estudiantes de posgrado en matemáticas. World Scientific. pág. 8. ISBN 978-981-12-1999-3.
^ Tao 2016, pág. 182
^ Stillwell, John C. (2010), Caminos hacia el infinito: las matemáticas de la verdad y la prueba, CRC Press, pág. 10, ISBN 9781439865507El descubrimiento de los conjuntos incontables por parte de Cantor en 1874 fue uno de los acontecimientos más inesperados en la historia de las matemáticas. Antes de 1874, la mayoría de la gente ni siquiera consideraba el infinito un tema matemático legítimo, por lo que ni siquiera se podía imaginar la necesidad de distinguir entre infinitos contables e incontables.
^ Cantor 1878, pág. 242.
^ Ferreirós 2007, págs. 268, 272-273.
^ "¿Qué son los sets y la forma de la plantilla?". expii . 2021-05-09. Archivado desde el original el 2020-09-18.
^ Halmos 1960, pág. 91
^ Halmos 1960, pág. 92
^ Avelsgaard 1990, pág. 182
^ Kamke 1950, págs. 3-4
^ Avelsgaard 1990, pág. 180
^ Fletcher y Patty 1988, pág. 187
^ Hrbacek, Karel; Jech, Thomas (22 de junio de 1999). Introducción a la teoría de conjuntos, tercera edición, revisada y ampliada. CRC Press. pág. 141. ISBN 978-0-8247-7915-3.

Referencias

Apostol, Tom M. (junio de 1969), Cálculo multivariable y álgebra lineal con aplicaciones , Cálculo, vol. 2 (2.ª ed.), Nueva York: John Wiley + Sons, ISBN 978-0-471-00007-5
Avelsgaard, Carol (1990), Fundamentos de matemáticas avanzadas , Scott, Foresman and Company, ISBN 0-673-38152-8
Cantor, Georg (1878), "Ein Beitrag zur Mannigfaltigkeitslehre", Journal für die Reine und Angewandte Mathematik , 1878 (84): 242–248, doi :10.1515/crelle-1878-18788413, S2CID 123695365
Ferreirós, José (2007), Laberinto del pensamiento: Una historia de la teoría de conjuntos y su papel en el pensamiento matemático (2.ª edición revisada), Birkhäuser, ISBN 978-3-7643-8349-7
Fletcher, Peter; Patty, C. Wayne (1988), Fundamentos de las matemáticas superiores , Boston: PWS-KENT Publishing Company, ISBN 0-87150-164-3
Halmos, Paul R. (1960), Teoría ingenua de conjuntos , D. Van Nostrand Company, IncReimpreso por Springer-Verlag, Nueva York, 1974. ISBN 0-387-90092-6 (edición de Springer-Verlag). Reimpreso por Martino Fine Books, 2011. ISBN 978-1-61427-131-4 (edición de bolsillo).
Kamke, Erich (1950), Teoría de conjuntos , Serie Dover en matemáticas y física, Nueva York: Dover, ISBN 978-0486601410
Lang, Serge (1993), Análisis real y funcional , Berlín, Nueva York: Springer-Verlag, ISBN 0-387-94001-4
Rudin, Walter (1976), Principios del análisis matemático , Nueva York: McGraw-Hill, ISBN 0-07-054235-X
Tao, Terence (2016). "Conjuntos infinitos". Análisis I. Textos y lecturas en matemáticas. Vol. 37 (tercera edición). Singapur: Springer. págs. 181–210. doi :10.1007/978-981-10-1789-6_8. ISBN . 978-981-10-1789-6.

[ZeroN-1] Dado que existe una biyección obvia entre y , no hay diferencia si se considera que 0 es un número natural o no. En cualquier caso, este artículo sigue la norma ISO 31-11 y la convención estándar en lógica matemática , que considera que 0 es un número natural. $\mathbb {N}$ $\mathbb {N} ^{*}=\{1,2,3,\dots \}$

[24] Prueba: Obsérvese que es contable como consecuencia de la definición porque la función dada por es inyectiva. ^[22] Entonces se sigue que el producto cartesiano de dos conjuntos contables cualesquiera es contable, porque si y son dos conjuntos contables hay sobreyecciones y . Por lo tanto es una sobreyección del conjunto contable al conjunto y el Corolario implica que es contable. Este resultado se generaliza al producto cartesiano de cualquier colección finita de conjuntos contables y la prueba se sigue por inducción sobre el número de conjuntos en la colección. $\mathbb {N} \times \mathbb {N}$ $f:\mathbb {N} \times \mathbb {N} \to \mathbb {N}$ $f(m,n)=2^{m}\cdot 3^{n}$ $A$ $B$ $f:\mathbb {N} \to A$ $g:\mathbb {N} \to B$ $f\times g:\mathbb {N} \times \mathbb {N} \to A\times B$ $\mathbb {N} \times \mathbb {N}$ $A\times B$ $A\times B$

[25] Demostración: Los números enteros son contables porque la función dada por si es no negativa y si es negativa, es una función inyectiva. Los números racionales son contables porque la función dada por es una sobreyección del conjunto contable a los racionales . $\mathbb {Z}$ $f:\mathbb {Z} \to \mathbb {N}$ $f(n)=2^{n}$ $n$ $f(n)=3^{-n}$ $n$ $\mathbb {Q}$ $g:\mathbb {Z} \times \mathbb {N} \to \mathbb {Q}$ $g(m,n)=m/(n+1)$ $\mathbb {Z} \times \mathbb {N}$ $\mathbb {Q}$

[27] Demostración: Por definición, cada número algebraico (incluidos los números complejos) es una raíz de un polinomio con coeficientes enteros. Dado un número algebraico , sea un polinomio con coeficientes enteros tal que es la raíz -ésima del polinomio, donde las raíces se ordenan por valor absoluto de menor a mayor, luego se ordenan por argumento de menor a mayor. Podemos definir una función de inyección (es decir, uno a uno) dada por , donde es el primo -ésimo . $\alpha$ $a_{0}x^{0}+a_{1}x^{1}+a_{2}x^{2}+\cdots +a_{n}x^{n}$ $\alpha$ $k$ $f:\mathbb {A} \to \mathbb {Q}$ $f(\alpha )=2^{k-1}\cdot 3^{a_{0}}\cdot 5^{a_{1}}\cdot 7^{a_{2}}\cdots {p_{n+2}}^{a_{n}}$ $p_{n}$ $n$

[30] Demostración: Si es un conjunto numerable para cada uno de , entonces para cada uno existe una función sobreyectiva y, por lo tanto, la función dada por es una sobreyección. Como es numerable, la unión es numerable. $A_{i}$ $i$ $I=\{1,\dots ,n\}$ $i$ $g_{i}:\mathbb {N} \to A_{i}$ $G:I\times \mathbf {N} \to \bigcup _{i\in I}A_{i},$ $G(i,m)=g_{i}(m)$ $I\times \mathbb {N}$ ${\textstyle \bigcup _{i\in I}A_{i}}$

[32] Prueba : Como en el caso finito, pero y usamos el axioma de elección contable para elegir para cada uno en una sobreyección de la colección no vacía de sobreyecciones de a . ^[26] Nótese que dado que estamos considerando la sobreyección , en lugar de una inyección, no hay ningún requisito de que los conjuntos sean disjuntos. $I=\mathbb {N}$ $i$ $\mathbb {N}$ $g_{i}$ $\mathbb {N}$ $A_{i}$ $G:\mathbf {N} \times \mathbf {N} \to \bigcup _{i\in I}A_{i}$

[33] Demostración : Para (1) observe que si es contable existe una función inyectiva . Entonces, si es inyectiva la composición es inyectiva, por lo que es contable. Para (2) observe que si es contable, o bien está vacía o existe una función sobreyectiva . Entonces, si es sobreyectiva, o bien y están vacías, o bien la composición es sobreyectiva. En cualquier caso es contable. $T$ $h:T\to \mathbb {N}$ $f:S\to T$ $h\circ f:S\to \mathbb {N}$ $S$ $S$ $S$ $h:\mathbb {N} \to S$ $g:S\to T$ $S$ $T$ $g\circ h:\mathbb {N} \to T$ $T$

[34] Véase la primera prueba de incontabilidad de Cantor y también la Propiedad de intersección finita#Aplicaciones para una prueba topológica.

[2] Manetti, Marco (19 de junio de 2015). Topología. Saltador. pag. 26.ISBN 978-3-319-16958-3.

[Rudin-3] Rudin 1976, Capítulo 2

[4] Tao 2016, pág. 181

[5] Kamke 1950, pág. 2

[Lang-6] Lang 1993, §2 del Capítulo I

[Apostol-7] Apostol 1969, p. 23, Capítulo 1.14

[8] Thierry, Vialar (4 de abril de 2017). Manual de matemáticas. BoD - Libros a pedido. p. 24. ISBN 978-2-9551990-1-5.

[9] Mukherjee, Subir Kumar (2009). Primer curso de análisis real. Academic Publishers. pág. 22. ISBN 978-81-89781-90-3.

[Yaqub-10] Yaqub, Aladdin M. (24 de octubre de 2014). Introducción a la metalógica. Broadview Press. ISBN 978-1-4604-0244-3.

[Singh-11] Singh, Tej Bahadur (17 de mayo de 2019). Introducción a la topología. Springer. pág. 422. ISBN 978-981-13-6954-4.

[Katzourakis-12] Katzourakis, Nikolaos; Varvaruca, Eugen (2 de enero de 2018). Una introducción ilustrativa al análisis moderno. CRC Press. ISBN 978-1-351-76532-9.

[13] Halmos 1960, pág. 91

[14] Kamke 1950, pág. 2

[15] Dlab, Vlastimil; Williams, Kenneth S. (9 de junio de 2020). Invitación al álgebra: un compendio de recursos para profesores, estudiantes universitarios avanzados y estudiantes de posgrado en matemáticas. World Scientific. pág. 8. ISBN 978-981-12-1999-3.

[16] Tao 2016, pág. 182

[17] Stillwell, John C. (2010), Caminos hacia el infinito: las matemáticas de la verdad y la prueba, CRC Press, pág. 10, ISBN 9781439865507El descubrimiento de los conjuntos incontables por parte de Cantor en 1874 fue uno de los acontecimientos más inesperados en la historia de las matemáticas. Antes de 1874, la mayoría de la gente ni siquiera consideraba el infinito un tema matemático legítimo, por lo que ni siquiera se podía imaginar la necesidad de distinguir entre infinitos contables e incontables.

[18] Cantor 1878, pág. 242.

[19] Ferreirós 2007, págs. 268, 272-273.

[20] "¿Qué son los sets y la forma de la plantilla?". expii . 2021-05-09. Archivado desde el original el 2020-09-18.

[21] Halmos 1960, pág. 91

[22] Halmos 1960, pág. 92

[23] Avelsgaard 1990, pág. 182

[26] Kamke 1950, págs. 3-4

[28] Avelsgaard 1990, pág. 180

[29] Fletcher y Patty 1988, pág. 187

[31] Hrbacek, Karel; Jech, Thomas (22 de junio de 1999). Introducción a la teoría de conjuntos, tercera edición, revisada y ampliada. CRC Press. pág. 141. ISBN 978-0-8247-7915-3.