Modelos compartimentados en epidemiología

Los modelos compartimentados son una técnica de modelado muy general. A menudo se aplican al modelado matemático de enfermedades infecciosas . La población se asigna a compartimentos con etiquetas, por ejemplo, S , I o R ( susceptible , infeccioso o recuperado ) . Las personas pueden progresar entre compartimentos. El orden de las etiquetas generalmente muestra los patrones de flujo entre los compartimentos; por ejemplo, SEIS significa susceptible, expuesto, infeccioso y luego susceptible nuevamente.

El origen de estos modelos se remonta a principios del siglo XX, con trabajos importantes como los de Ross ^[1] en 1916, Ross y Hudson en 1917, ^{[2] [3]} Kermack y McKendrick en 1927, ^[4] y Kendall en 1956. ^[5] El modelo Reed-Frost también fue un antecesor significativo y ampliamente pasado por alto de los enfoques modernos de modelado epidemiológico. ^[6]

Los modelos se ejecutan con mayor frecuencia con ecuaciones diferenciales ordinarias (que son deterministas), pero también se pueden utilizar con un marco estocástico (aleatorio), que es más realista pero mucho más complicado de analizar.

Estos modelos se utilizan para analizar la dinámica de la enfermedad y estimar el número total de personas infectadas, el número total de personas recuperadas y para estimar parámetros epidemiológicos como el número básico de reproducción o el número efectivo de reproducción . Estos modelos pueden mostrar cómo diferentes intervenciones de salud pública pueden afectar el resultado de la epidemia.

El modelo SIR ^{[7] [8] [9] [10]} es uno de los modelos compartimentados más simples, y muchos modelos son derivados de esta forma básica. El modelo consta de tres compartimentos:

S : Número de individuos susceptibles . Cuando un individuo susceptible y un individuo infeccioso entran en "contacto infeccioso", el individuo susceptible contrae la enfermedad y pasa al compartimento infeccioso.

I : Número de individuos infecciosos . Son aquellos individuos que han sido infectados y son capaces de infectar a individuos susceptibles.

R es el número de individuos eliminados (e inmunes) o fallecidos. Se trata de individuos que han sido infectados y se han recuperado de la enfermedad y han entrado en el compartimento eliminado, o han muerto. Se supone que el número de muertes es insignificante con respecto a la población total. Este compartimento también puede denominarse " recuperado " o " resistente ".

Este modelo es razonablemente predictivo ^[11] para enfermedades infecciosas que se transmiten de persona a persona y donde la recuperación confiere resistencia duradera, como el sarampión , las paperas y la rubéola .

Estas variables ( S , I y R ) representan el número de personas en cada compartimento en un momento determinado. Para representar que el número de individuos susceptibles, infecciosos y eliminados puede variar con el tiempo (incluso si el tamaño total de la población permanece constante), hacemos que los números precisos sean una función de t (tiempo): S ( t ), I ( t ) y R ( t ). Para una enfermedad específica en una población específica, estas funciones se pueden calcular para predecir posibles brotes y controlarlos. ^[11] Nótese que en el modelo SIR, y son cantidades diferentes: la primera describe el número de recuperados en t = 0, mientras que la segunda describe la relación entre la frecuencia de contactos y la frecuencia de recuperación.${\estilo de visualización R(0)}$${\estilo de visualización R_{0}}$

Como lo implica la función variable de t , el modelo es dinámico en el sentido de que los números en cada compartimento pueden fluctuar con el tiempo. La importancia de este aspecto dinámico es más obvia en una enfermedad endémica con un período infeccioso corto, como el sarampión en el Reino Unido antes de la introducción de una vacuna en 1968. Tales enfermedades tienden a ocurrir en ciclos de brotes debido a la variación en el número de susceptibles (S( t )) a lo largo del tiempo. Durante una epidemia , el número de individuos susceptibles cae rápidamente a medida que más de ellos se infectan y, por lo tanto, ingresan a los compartimentos infecciosos y eliminados. La enfermedad no puede volver a estallar hasta que el número de susceptibles se haya recuperado, por ejemplo, como resultado del nacimiento de crías en el compartimento susceptible. ^{[ cita requerida ]}

Cada miembro de la población suele pasar de ser susceptible a infectivo y luego a recuperarse. Esto se puede representar mediante un diagrama de flujo en el que los recuadros representan los diferentes compartimentos y las flechas la transición entre ellos (véase el diagrama).

Para la especificación completa del modelo, las flechas deben estar etiquetadas con las tasas de transición entre compartimentos. Entre S e I , se supone que la tasa de transición es , donde es la población total, es el número promedio de contactos por persona por tiempo, multiplicado por la probabilidad de transmisión de la enfermedad en un contacto entre un sujeto susceptible y uno infeccioso, y es la fracción de esos contactos entre un individuo infeccioso y uno susceptible que resultan en que la persona susceptible se infecte. (Esto es matemáticamente similar a la ley de acción de masas en química en la que las colisiones aleatorias entre moléculas dan como resultado una reacción química y la tasa fraccionaria es proporcional a la concentración de los dos reactivos. ^[12] )${\displaystyle d(S/N)/dt=-\beta SI/N^{2}}$${\estilo de visualización N}$${\estilo de visualización \beta}$$Estilo de visualización SI/N^{2}}$

Entre I y R , se supone que la tasa de transición es proporcional al número de individuos infecciosos, que es . Si un individuo es infeccioso durante un período de tiempo promedio , entonces . Esto también es equivalente a la suposición de que el tiempo que pasa un individuo en estado infeccioso es una variable aleatoria con una distribución exponencial . El modelo SIR "clásico" puede modificarse utilizando distribuciones más complejas y realistas para la tasa de transición IR (por ejemplo, la distribución Erlang ). ^[13]${\displaystyle \gamma I}$${\estilo de visualización D}$${\displaystyle \gamma = 1/D}$

Para el caso especial en el que no hay eliminación del compartimento infeccioso ( ), el modelo SIR se reduce a un modelo SI muy simple, que tiene una solución logística , en la que cada individuo eventualmente se infecta.${\displaystyle \gamma = 0}$

La dinámica de una epidemia, por ejemplo, la gripe , suele ser mucho más rápida que la dinámica de nacimientos y muertes, por lo que los nacimientos y las muertes suelen omitirse en los modelos compartimentados simples. El sistema SIR sin la denominada dinámica vital (nacimientos y muertes, a veces llamada demografía) descrita anteriormente se puede expresar mediante el siguiente sistema de ecuaciones diferenciales ordinarias : ^{[8] [14]}

${\displaystyle \left\{{\begin{aligned}&{\frac {dS}{dt}}=-\beta IS,\\[6pt]&{\frac {dI}{dt}}=\beta IS-\gamma I,\\[6pt]&{\frac {dR}{dt}}=\gamma I,\end{aligned}}\right.}$

donde es el stock de población susceptible, es el stock de infectados, es el stock de población eliminada (ya sea por muerte o recuperación), y es la suma de estos tres.${\estilo de visualización S}$${\displaystyle I}$${\estilo de visualización R}$${\estilo de visualización N}$

Este modelo fue propuesto por primera vez por William Ogilvy Kermack y Anderson Gray McKendrick como un caso especial de lo que ahora llamamos teoría de Kermack-McKendrick , y siguió el trabajo que McKendrick había realizado con Ronald Ross . ^{[ cita requerida ]}

Este sistema no es lineal , sin embargo es posible derivar su solución analítica en forma implícita. ^[7] En primer lugar, observe que:

${\displaystyle {\frac {dS}{dt}}+{\frac {dI}{dt}}+{\frac {dR}{dt}}=0,}$

resulta que:

${\displaystyle S(t)+I(t)+R(t)={\text{constante}}=N,}$

Expresando en términos matemáticos la constancia de la población . Nótese que la relación anterior implica que solo es necesario estudiar la ecuación para dos de las tres variables.${\estilo de visualización N}$

En segundo lugar, observamos que la dinámica de la clase infecciosa depende de la siguiente relación:

${\displaystyle R_{0}={\frac {\beta }{\gamma }},}$

el llamado número básico de reproducción (también llamado índice básico de reproducción). Este índice se deriva como el número esperado de nuevas infecciones (estas nuevas infecciones a veces se denominan infecciones secundarias) a partir de una sola infección en una población donde todos los sujetos son susceptibles. ^{[15] [16]} Esta idea probablemente se puede ver más fácilmente si decimos que el tiempo típico entre contactos es , y el tiempo típico hasta la eliminación es . De aquí se deduce que, en promedio, el número de contactos de un individuo infeccioso con otros antes de que el infeccioso haya sido eliminado es:${\displaystyle T_{c}=\beta ^{-1}}$${\displaystyle T_{r}=\gamma ^{-1}}$${\displaystyle T_{r}/T_{c}.}$

Dividiendo la primera ecuación diferencial por la tercera, separando las variables e integrando obtenemos

${\displaystyle S(t)=S(0)e^{-R_{0}(R(t)-R(0))/N},}$

donde y son los números iniciales de, respectivamente, sujetos susceptibles y eliminados. Escribiendo para la proporción inicial de individuos susceptibles, y y para la proporción de individuos susceptibles y eliminados respectivamente en el límite se tiene${\estilo de visualización S(0)}$${\estilo de visualización R(0)}$$Estilo de visualización s_{0}=S(0)/N$${\displaystyle s_{\infty }=S(\infty )/N}$${\displaystyle r_{\infty }=R(\infty )/N}$${\displaystyle t\to \infty ,}$

${\displaystyle s_{\infty}=1-r_{\infty}=s_{0}e^{-R_{0}(r_{\infty}-r_{0})}}$

(nótese que el compartimento infeccioso se vacía en este límite). Esta ecuación trascendental tiene una solución en términos de la función W de Lambert , ^[17] a saber

${\displaystyle s_{\infty}=1-r_{\infty}=-R_{0}^{-1}\,W(-s_{0}R_{0}e^{-R_{0}(1-r_{0})}).}$

Esto demuestra que al final de una epidemia que se ajusta a los supuestos simples del modelo SIR, a menos que , no todos los individuos de la población hayan sido eliminados, por lo que algunos deben seguir siendo susceptibles. Una fuerza impulsora que conduce al final de una epidemia es una disminución en el número de individuos infecciosos. La epidemia no suele terminar debido a una falta total de individuos susceptibles.${\displaystyle s_{0}=0}$

El papel tanto del número básico de reproducción como de la susceptibilidad inicial son extremadamente importantes. De hecho, al reescribir la ecuación para los individuos infecciosos de la siguiente manera:

${\displaystyle {\frac {dI}{dt}}=\left(R_{0}{\frac {S}{N}}-1\right)\gamma I,}$

se obtiene que si:

${\displaystyle R_{0}\cdot S(0)>N,}$

entonces:

${\displaystyle {\frac {dI}{dt}}(0)>0,}$

Es decir, se producirá un brote epidémico propiamente dicho con un aumento del número de personas infectadas (que puede alcanzar una fracción considerable de la población). Por el contrario, si

${\displaystyle R_{0}\cdot S(0)<N,}$

entonces

${\displaystyle {\frac {dI}{dt}}(0)<0,}$

Es decir, independientemente del tamaño inicial de la población susceptible, la enfermedad nunca puede causar un brote epidémico propiamente dicho. En consecuencia, es evidente que tanto el número básico de reproducción como la susceptibilidad inicial son extremadamente importantes.

Tenga en cuenta que en el modelo anterior la función:

${\displaystyle F=\beta I,}$

modela la tasa de transición del compartimento de individuos susceptibles al compartimento de individuos infecciosos, de modo que se denomina fuerza de infección . Sin embargo, para grandes clases de enfermedades transmisibles es más realista considerar una fuerza de infección que no depende del número absoluto de sujetos infecciosos, sino de su fracción (con respecto a la población constante total ):${\displaystyle N}$

${\displaystyle F=\beta {\frac {I}{N}}.}$

Capasso ^[18] y, posteriormente, otros autores han propuesto fuerzas de infección no lineales para modelar de forma más realista el proceso de contagio.

En 2014, Harko y coautores derivaron una solución analítica exacta (que implica una integral que solo se puede calcular numéricamente) para el modelo SIR. ^[7] En el caso sin configuración de dinámica vital, para , etc., corresponde a la siguiente parametrización de tiempo${\displaystyle {\mathcal {S}}(u)=S(t)}$

${\displaystyle {\mathcal {S}}(u)=S(0)u}$

${\displaystyle {\mathcal {I}}(u)=N-{\mathcal {R}}(u)-{\mathcal {S}}(u)}$

${\displaystyle {\mathcal {R}}(u)=R(0)-\rho \ln(u)}$

para

${\displaystyle t={\frac {N}{\beta }}\int _{u}^{1}{\frac {du^{*}}{u^{*}{\mathcal {I}}(u^{*})}},\quad \rho ={\frac {\gamma N}{\beta }},}$

con condiciones iniciales

${\displaystyle ({\mathcal {S}}(1),{\mathcal {I}}(1),{\mathcal {R}}(1))=(S(0),N-R(0)-S(0),R(0)),\quad u_{T}<u<1,}$

donde satisface . Por la ecuación trascendental para anterior, se deduce que , si y .${\displaystyle u_{T}}$${\displaystyle {\mathcal {I}}(u_{T})=0}$${\displaystyle R_{\infty }}$${\displaystyle u_{T}=e^{-(R_{\infty }-R(0))/\rho }(=S_{\infty }/S(0)}$${\displaystyle S(0)\neq 0)}$${\displaystyle I_{\infty }=0}$

Una solución analítica equivalente (que implica una integral que solo se puede calcular numéricamente) encontrada por Miller ^{[19] [20]} produce

${\displaystyle {\begin{aligned}S(t)&=S(0)e^{-\xi (t)}\\[8pt]I(t)&=N-S(t)-R(t)\\[8pt]R(t)&=R(0)+\rho \xi (t)\\[8pt]\xi (t)&={\frac {\beta }{N}}\int _{0}^{t}I(t^{*})\,dt^{*}\end{aligned}}}$

Aquí se puede interpretar como el número esperado de transmisiones que ha recibido un individuo en el tiempo . Las dos soluciones están relacionadas por .${\displaystyle \xi (t)}$${\displaystyle t}$${\displaystyle e^{-\xi (t)}=u}$

En efecto, el mismo resultado se puede encontrar en el trabajo original de Kermack y McKendrick. ^[4]

Estas soluciones se pueden entender fácilmente si se observa que todos los términos en el lado derecho de las ecuaciones diferenciales originales son proporcionales a . Las ecuaciones se pueden dividir por , y el tiempo se puede reescalar de modo que el operador diferencial en el lado izquierdo se convierta simplemente en , donde , es decir . Las ecuaciones diferenciales ahora son todas lineales, y la tercera ecuación, de la forma const., muestra que y (y anteriores) están simplemente relacionadas linealmente.${\displaystyle I}$${\displaystyle I}$${\displaystyle d/d\tau }$${\displaystyle d\tau =Idt}$${\displaystyle \tau =\int Idt}$${\displaystyle dR/d\tau =}$${\displaystyle \tau }$${\displaystyle R}$${\displaystyle \xi }$

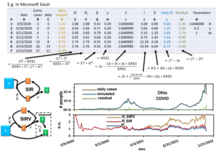
^{Kröger y Schlickeiser [9]} proporcionaron un aproximador analítico de alta precisión del modelo SIR, así como expresiones analíticas exactas para los valores finales , y , de modo que no es necesario realizar una integración numérica para resolver el modelo SIR ( aquí se puede encontrar un ejemplo práctico simplificado de simulación numérica de COVID-19 con Microsoft Excel ^[21] ), para obtener sus parámetros a partir de datos existentes o para predecir la dinámica futura de una epidemia modelada por el modelo SIR. El aproximador implica la función W de Lambert , que forma parte de todo el software básico de visualización de datos, como Microsoft Excel, MATLAB y Mathematica .${\displaystyle S_{\infty }}$${\displaystyle I_{\infty }}$${\displaystyle R_{\infty }}$

Mientras que Kendall ^[5] consideró el llamado modelo SIR de todos los tiempos, donde las condiciones iniciales , , y están acopladas a través de las relaciones anteriores, Kermack y McKendrick ^[4] propusieron estudiar el caso semitemporal más general, para el cual y son ambos arbitrarios. Esta última versión, denominada modelo SIR de semitiempo, ^[9] hace predicciones solo para tiempos futuros . También están disponibles una aproximación analítica y expresiones exactas para los valores finales para el modelo SIR de semitiempo. ^[10]${\displaystyle S(0)}$${\displaystyle I(0)}$${\displaystyle R(0)}$${\displaystyle S(0)}$${\displaystyle I(0)}$${\displaystyle t>0}$

En la literatura se pueden encontrar soluciones numéricas del modelo SIR. Un ejemplo es el uso del modelo para analizar los datos de propagación de COVID-19 . ^{[21] [22]} Se pueden extraer tres números de reproducción de los datos analizados con aproximación numérica,

El número básico de reproducción :

${\displaystyle R_{0}={\frac {\beta _{0}}{\gamma _{0}}}}$

el número de reproducción en tiempo real:

${\displaystyle R_{t}={\frac {\beta _{t}}{\gamma _{t}}}}$

y el número de reproducción efectiva en tiempo real:

${\displaystyle R_{e}={\frac {\beta _{t}S}{\gamma _{t}N}}}$

${\displaystyle R_{0}}$representa la velocidad de la tasa de reproducción al comienzo de la propagación cuando se supone que todas las poblaciones son susceptibles, p. ej., si y significa que una persona infecciosa en promedio infecta a 0,4 personas susceptibles por día y se recupera en 1/0,2 = 5 días. Por lo tanto, cuando esta persona se recupera, hay dos personas todavía infecciosas contraídas directamente de esta persona y , es decir, el número de personas infecciosas se duplicó en un ciclo de 5 días. Los datos simulados por el modelo con o datos reales ajustados producirán una duplicación del número de personas infecciosas más rápido que 5 días porque las dos personas infectadas están infectando a personas. A partir del modelo SIR, podemos decir que está determinado por la naturaleza de la enfermedad y también es una función de la frecuencia interactiva entre la persona infecciosa con las personas susceptibles y también la intensidad/duración de la interacción como qué tan cerca interactúan durante cuánto tiempo y si ambos usan o no máscaras, por lo tanto, cambia con el tiempo cuando cambia el comportamiento promedio de los portadores y las personas susceptibles. El modelo se utiliza para representar estos factores, pero en realidad se refiere a la etapa inicial, cuando no se toman medidas para evitar la propagación y toda la población es susceptible, por lo que todos los cambios son absorbidos por el cambio de .${\displaystyle \beta _{0}=0.4day^{-1}}$${\displaystyle \gamma _{0}=0.2day^{-1}}$${\displaystyle R_{0}=2}$${\displaystyle R_{0}=2}$${\displaystyle \beta }$${\displaystyle I}$${\displaystyle S}$${\displaystyle SI}$${\displaystyle \beta }$

${\displaystyle \gamma }$Por lo general, es más estable en el tiempo, suponiendo que cuando la persona infectada muestra síntomas, buscará atención médica o se autoaislará. Entonces, si encontramos cambios, lo más probable es que los comportamientos de las personas en la comunidad hayan cambiado de sus patrones normales antes del brote, o la enfermedad haya mutado a una nueva forma. La detección masiva y el aislamiento costosos de contactos cercanos susceptibles tienen efectos en la reducción, pero cuya eficiencia está en debate. Este debate se basa en gran medida en la incertidumbre del número de días reducidos desde después de la infección o la detección, lo que ocurra primero, hasta antes de que aparezca un síntoma para una persona susceptible infectada. Si la persona es infecciosa después de que aparecen los síntomas, o la detección solo funciona para una persona con síntomas, entonces estos métodos de prevención no son necesarios, y el autoaislamiento y/o la atención médica son la mejor manera de reducir los valores. El inicio típico del período infeccioso de COVID-19 es del orden de un día desde que aparecen los síntomas, lo que hace que la detección masiva con la frecuencia típica en unos pocos días sea inútil.${\displaystyle R_{t}}$${\displaystyle 1/\gamma }$${\displaystyle 1/\gamma }$

${\displaystyle R_{t}}$no nos dice si la propagación se acelerará o se ralentizará en las últimas etapas, cuando la fracción de personas susceptibles en la comunidad haya disminuido significativamente después de la recuperación o la vacunación. corrige este efecto de dilución multiplicando la fracción de la población susceptible sobre la población total. Corrige la interacción efectiva/transmisible entre una persona infecciosa y el resto de la comunidad cuando gran parte de la interacción es inmune en las etapas medias y tardías de la propagación de la enfermedad. Por lo tanto, cuando , veremos un brote de tipo exponencial; cuando , se alcanza un estado estable y no cambia el número de personas infecciosas con el tiempo; y cuando , la enfermedad decae y se desvanece con el tiempo.${\displaystyle R_{e}}$${\displaystyle R_{e}>1}$${\displaystyle R_{e}=1}$${\displaystyle R_{e}<1}$

Utilizando las ecuaciones diferenciales del modelo SIR y convirtiéndolas a formas numéricas discretas, se pueden establecer las ecuaciones recursivas y calcular las poblaciones S, I y R con cualquier condición inicial dada, pero acumular errores durante un largo tiempo de cálculo desde el punto de referencia. A veces se necesita una prueba de convergencia para estimar los errores. Dado un conjunto de condiciones iniciales y los datos de propagación de la enfermedad, también se pueden ajustar los datos con el modelo SIR y extraer los tres números de reproducción cuando los errores son generalmente insignificantes debido al corto paso de tiempo desde el punto de referencia. ^{[21] [22]} Cualquier punto del tiempo se puede utilizar como condición inicial para predecir el futuro después de él utilizando este modelo numérico con el supuesto de parámetros evolucionados en el tiempo, como la población, y . Sin embargo, lejos de este punto de referencia, los errores se acumularán con el tiempo, por lo que se necesita una prueba de convergencia para encontrar un paso de tiempo óptimo para obtener resultados más precisos.${\displaystyle R_{t}}$${\displaystyle \gamma }$

Entre estos tres números de reproducción, es muy útil juzgar la presión de control, por ejemplo, un valor grande significa que la enfermedad se propagará muy rápido y es muy difícil de controlar. es más útil para predecir tendencias futuras, por ejemplo, si sabemos que las interacciones sociales se han reducido un 50% con frecuencia desde antes del brote y las intensidades de interacción entre las personas son las mismas, entonces podemos establecer . Si el distanciamiento social y las mascarillas añaden otro 50% de reducción en la eficiencia de la infección, podemos establecer . se correlacionará perfectamente con las olas de propagación y siempre que , la propagación se acelere, y cuando , la propagación se desacelere, por lo que es útil para establecer una predicción sobre las tendencias a corto plazo. Además, se puede utilizar para calcular directamente la población umbral de vacunación/inmunización para la etapa de inmunidad colectiva estableciendo , y , es decir .${\displaystyle R_{0}}$${\displaystyle R_{t}}$${\displaystyle R_{t}=0.5R_{0}}$${\displaystyle R_{t}=0.25R_{0}}$${\displaystyle R_{e}}$${\displaystyle R_{e}>1}$${\displaystyle R_{e}<1}$${\displaystyle R_{t}=R_{0}}$${\displaystyle R_{E}=1}$${\displaystyle S=N/R_{0}}$

Consideremos una población caracterizada por una tasa de mortalidad y una tasa de natalidad , y donde se está propagando una enfermedad contagiosa. ^[8] El modelo con transmisión por acción masiva es:${\displaystyle \mu }$${\displaystyle \Lambda }$

${\displaystyle {\begin{aligned}{\frac {dS}{dt}}&=\Lambda -\mu S-{\frac {\beta IS}{N}}\\[8pt]{\frac {dI}{dt}}&={\frac {\beta IS}{N}}-\gamma I-\mu I\\[8pt]{\frac {dR}{dt}}&=\gamma I-\mu R\end{aligned}}}$

para el cual el equilibrio libre de enfermedad (ELE) es:

${\displaystyle \left(S(t),I(t),R(t)\right)=\left({\frac {\Lambda }{\mu }},0,0\right).}$

En este caso, podemos derivar un número de reproducción básico :

${\displaystyle R_{0}={\frac {\beta }{\mu +\gamma }},}$

que tiene propiedades de umbral. De hecho, independientemente de los valores iniciales biológicamente significativos, se puede demostrar que:

${\displaystyle R_{0}\leq 1\Rightarrow \lim _{t\to \infty }(S(t),I(t),R(t))={\textrm {DFE}}=\left({\frac {\Lambda }{\mu }},0,0\right)}$

${\displaystyle R_{0}>1,I(0)>0\Rightarrow \lim _{t\to \infty }(S(t),I(t),R(t))={\textrm {EE}}=\left({\frac {\gamma +\mu }{\beta }},{\frac {\mu }{\beta }}\left(R_{0}-1\right),{\frac {\gamma }{\beta }}\left(R_{0}-1\right)\right).}$

El punto EE se denomina Equilibrio Endémico (la enfermedad no se erradica totalmente y permanece en la población). Con argumentos heurísticos, se puede demostrar que puede leerse como el número promedio de infecciones causadas por un solo sujeto infeccioso en una población totalmente susceptible, la relación anterior significa biológicamente que si este número es menor o igual a uno la enfermedad se extingue, mientras que si este número es mayor que uno la enfermedad permanecerá permanentemente endémica en la población.${\displaystyle R_{0}}$

En 1927, WO Kermack y AG McKendrick crearon un modelo en el que consideraron una población fija con solo tres compartimentos: susceptible, ; infectado, ; y recuperado, . Los compartimentos utilizados para este modelo consisten en tres clases: ^[4]${\displaystyle S(t)}$${\displaystyle I(t)}$${\displaystyle R(t)}$

• ${\displaystyle S(t)}$Se utiliza para representar a los individuos que aún no están infectados con la enfermedad en el momento t, o aquellos susceptibles a la enfermedad de la población.
• ${\displaystyle I(t)}$designa a los individuos de la población que han sido infectados con la enfermedad y son capaces de transmitirla a aquellos en la categoría susceptible.
• ${\displaystyle R(t)}$Es el compartimento que se utiliza para los individuos de la población que han sido infectados y luego eliminados de la enfermedad, ya sea por inmunización o por muerte. Los que se encuentran en esta categoría no pueden volver a infectarse ni transmitir la infección a otros.

El flujo de este modelo puede considerarse de la siguiente manera:

${\displaystyle {\color {blue}{{\mathcal {S}}\rightarrow {\mathcal {I}}\rightarrow {\mathcal {R}}}}}$

Usando una población fija, en las tres funciones se resuelve que el valor debe permanecer constante dentro de la simulación, si se usa una simulación para resolver el modelo SIR. Alternativamente, el aproximante analítico ^[9] se puede usar sin realizar una simulación. El modelo se inicia con valores de , y . Estos son el número de personas en las categorías susceptibles, infectadas y eliminadas en el tiempo igual a cero. Si se supone que el modelo SIR se mantiene en todo momento, estas condiciones iniciales no son independientes. ^[9] Posteriormente, el modelo de flujo actualiza las tres variables para cada punto de tiempo con valores establecidos para y . La simulación primero actualiza la categoría infectada de la susceptible y luego la categoría eliminada se actualiza de la categoría infectada para el siguiente punto de tiempo (t = 1). Esto describe el flujo de personas entre las tres categorías. Durante una epidemia, la categoría susceptible no se desplaza con este modelo, cambia a lo largo de la epidemia y también lo hace . Estas variables determinan la duración de la epidemia y tendrían que actualizarse con cada ciclo.${\displaystyle N=S(t)+I(t)+R(t)}$${\displaystyle N}$${\displaystyle S(t=0)}$${\displaystyle I(t=0)}$${\displaystyle R(t=0)}$${\displaystyle \beta }$${\displaystyle \gamma }$${\displaystyle \beta }$${\displaystyle \gamma }$

${\displaystyle {\frac {dS}{dt}}=-\beta SI}$

${\displaystyle {\frac {dI}{dt}}=\beta SI-\gamma I}$

${\displaystyle {\frac {dR}{dt}}=\gamma I}$

Se hicieron varias suposiciones en la formulación de estas ecuaciones: primero, se debe considerar que un individuo en la población tiene una probabilidad igual a cualquier otro individuo de contraer la enfermedad con una tasa de y una fracción igual de personas con las que un individuo hace contacto por unidad de tiempo. Entonces, sea la multiplicación de y . Esta es la probabilidad de transmisión por la tasa de contacto. Además, un individuo infectado hace contacto con personas por unidad de tiempo mientras que solo una fracción, de ellas son susceptibles. Por lo tanto, tenemos que cada infectivo puede infectar a personas susceptibles y, por lo tanto, el número total de susceptibles infectados por infectivos por unidad de tiempo es . Para la segunda y tercera ecuaciones, considere la población que abandona la clase susceptible como igual al número que ingresa a la clase infectada. Sin embargo, un número igual a la fracción (que representa la tasa media de recuperación/muerte, o el período infectivo medio) de infectivos abandonan esta clase por unidad de tiempo para ingresar a la clase eliminada. Estos procesos que ocurren simultáneamente se conocen como la Ley de Acción de Masas, una idea ampliamente aceptada que sostiene que la tasa de contacto entre dos grupos de una población es proporcional al tamaño de cada uno de los grupos involucrados. Finalmente, se supone que la tasa de infección y recuperación es mucho más rápida que la escala temporal de nacimientos y muertes y, por lo tanto, estos factores se ignoran en este modelo. ^[23]${\displaystyle a}$${\displaystyle b}$${\displaystyle \beta }$${\displaystyle a}$${\displaystyle b}$${\displaystyle b}$${\displaystyle S/N}$${\displaystyle abS=\beta S}$${\displaystyle \beta SI}$${\displaystyle \gamma }$${\displaystyle 1/\gamma }$

La única solución de estado estable para el modelo SIR clásico, tal como se define en las ecuaciones diferenciales anteriores, es I=0; por lo tanto, S y R pueden adoptar cualquier valor. El modelo se puede modificar manteniendo los tres compartimentos para obtener una solución endémica de estado estable añadiendo alguna entrada al compartimento S.

Por ejemplo, se puede postular que la duración esperada de la susceptibilidad será donde refleja el tiempo de vida (esperanza de vida) y refleja el tiempo en el estado susceptible antes de infectarse, lo que se puede simplificar ^[24] a:${\displaystyle \operatorname {E} [\min(T_{L}\mid T_{S})]}$${\displaystyle T_{L}}$${\displaystyle T_{S}}$

${\displaystyle \operatorname {E} [\min(T_{L}\mid T_{S})]=\int _{0}^{\infty }e^{-(\mu +\delta )x}\,dx={\frac {1}{\mu +\delta }},}$

de modo que el número de personas susceptibles es el número que entra al compartimento susceptible multiplicado por la duración de la susceptibilidad:${\displaystyle \mu N}$

${\displaystyle S={\frac {\mu N}{\mu +\lambda }}.}$

De manera análoga, el número de personas infectadas en estado estable es el número de personas que entran al estado infectado desde el estado susceptible (número susceptible, multiplicado por la tasa de infección) multiplicado por la duración de la infecciosidad :${\displaystyle \lambda ={\tfrac {\beta I}{N}},}$${\displaystyle {\tfrac {1}{\mu +v}}}$

${\displaystyle I={\frac {\mu N}{\mu +\lambda }}\lambda {\frac {1}{\mu +v}}.}$

Existen muchas modificaciones del modelo SIR, incluidas aquellas que incluyen nacimientos y muertes, donde tras la recuperación no hay inmunidad (modelo SIS), donde la inmunidad dura solo por un corto período de tiempo (SIRS), donde hay un período latente de la enfermedad donde la persona no es infecciosa (SEIS y SEIR), y donde los bebés pueden nacer con inmunidad (MSIR). Los modelos compartimentados también se pueden utilizar para modelar múltiples grupos de riesgo, e incluso la interacción de múltiples patógenos. ^[25]

Algunas infecciones, como el resfriado común y la gripe , no confieren inmunidad duradera. Estas infecciones pueden generar resistencia temporal, pero no dan inmunidad a largo plazo una vez que se recuperan de la infección, y las personas se vuelven susceptibles nuevamente.

Tenemos el modelo:

${\displaystyle {\begin{aligned}{\frac {dS}{dt}}&=-{\frac {\beta SI}{N}}+\gamma I\\[6pt]{\frac {dI}{dt}}&={\frac {\beta SI}{N}}-\gamma I\end{aligned}}}$

Nótese que al denotar con N la población total se cumple que:

${\displaystyle {\frac {dS}{dt}}+{\frac {dI}{dt}}=0\Rightarrow S(t)+I(t)=N}$.

Resulta que:

${\displaystyle {\frac {dI}{dt}}=(\beta -\gamma )I-{\frac {\beta }{N}}I^{2}}$,

Es decir, la dinámica de las infecciones está regida por una función logística , de modo que :${\displaystyle \forall I(0)>0}$

${\displaystyle {\begin{aligned}&{\frac {\beta }{\gamma }}\leq 1\Rightarrow \lim _{t\to +\infty }I(t)=0,\\[6pt]&{\frac {\beta }{\gamma }}>1\Rightarrow \lim _{t\to +\infty }I(t)=\left(1-{\frac {\gamma }{\beta }}\right)N.\end{aligned}}}$

Es posible encontrar una solución analítica para este modelo (haciendo una transformación de variables: y sustituyéndola en las ecuaciones de campo medio), ^[26] de manera que la tasa básica de reproducción sea mayor que la unidad. La solución se da como${\displaystyle I=y^{-1}}$

${\displaystyle I(t)={\frac {I_{\infty }}{1+Ve^{-\chi t}}}}$.

donde es la población infecciosa endémica, y . Como se supone que el sistema está cerrado, la población susceptible es entonces .${\displaystyle I_{\infty }=(1-\gamma /\beta )N}$${\displaystyle \chi =\beta -\gamma }$${\displaystyle V=I_{\infty }/I_{0}-1}$${\displaystyle S(t)=N-I(t)}$

Siempre que la naturaleza entera del número de agentes es evidente (poblaciones con menos de decenas de miles de individuos), las fluctuaciones inherentes en el proceso de propagación de la enfermedad causadas por agentes discretos resultan en incertidumbres. ^[27] En este escenario, la evolución de la enfermedad predicha por ecuaciones compartimentales se desvía significativamente de los resultados observados. Estas incertidumbres pueden incluso hacer que la epidemia termine antes de lo previsto por las ecuaciones compartimentales.

Como caso especial, se obtiene la función logística habitual suponiendo . Esto también se puede considerar en el modelo SIR con , es decir, no se producirá ninguna eliminación. Ese es el modelo SI . ^[28] El sistema de ecuaciones diferenciales que utiliza se reduce así a:${\displaystyle \gamma =0}$${\displaystyle R=0}$${\displaystyle S=N-I}$

${\displaystyle {\frac {dI}{dt}}\propto I\cdot (N-I).}$

A largo plazo, en el modelo SI, todos los individuos se infectarán.

El modelo Susceptible-Infeccioso-Recuperado-Muerto diferencia entre Recuperado (es decir, específicamente individuos que han sobrevivido a la enfermedad y ahora son inmunes) y Muerto . ^[15] El modelo SIRD tiene soluciones semianalíticas basadas en el método de las cuatro partes. ^[29] Este modelo utiliza el siguiente sistema de ecuaciones diferenciales:

${\displaystyle {\begin{aligned}&{\frac {dS}{dt}}=-{\frac {\beta IS}{N}},\\[6pt]&{\frac {dI}{dt}}={\frac {\beta IS}{N}}-\gamma I-\mu I,\\[6pt]&{\frac {dR}{dt}}=\gamma I,\\[6pt]&{\frac {dD}{dt}}=\mu I,\end{aligned}}}$

donde son las tasas de infección, recuperación y mortalidad, respectivamente. ^[30]${\displaystyle \beta ,\gamma ,\mu }$

El modelo Susceptible-Infeccioso-Recuperado-Vacunado es un modelo SIR extendido que tiene en cuenta la vacunación de la población susceptible. ^[31] Este modelo utiliza el siguiente sistema de ecuaciones diferenciales:

${\displaystyle {\begin{aligned}&{\frac {dS}{dt}}=-{\frac {\beta (t)IS}{N}}-v(t)S,\\[6pt]&{\frac {dI}{dt}}={\frac {\beta (t)IS}{N}}-\gamma (t)I,\\[6pt]&{\frac {dR}{dt}}=\gamma (t)I,\\[6pt]&{\frac {dV}{dt}}=v(t)S,\end{aligned}}}$

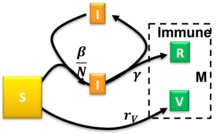
donde son las tasas de infección, recuperación y vacunación, respectivamente. Para las condiciones iniciales de semi-tiempo , , y proporciones constantes y el modelo se había resuelto de forma aproximada. ^[31] La ocurrencia de un brote pandémico requiere y hay una tasa de vacunación crítica reducida más allá de la cual el tamaño en estado estacionario del compartimento susceptible permanece relativamente cerca de . Las condiciones iniciales arbitrarias que satisfacen se pueden mapear al caso especial resuelto con . ^[31]${\displaystyle \beta ,\gamma ,v}$${\displaystyle S(0)=(1-\eta )N}$${\displaystyle I(0)=\eta N}$${\displaystyle R(0)=V(0)=0}$${\displaystyle k=\gamma (t)/\beta (t)}$${\displaystyle b=v(t)/\beta (t)}$${\displaystyle k+b<1-2\eta }$${\displaystyle b_{c}}$${\displaystyle S_{\infty }}$${\displaystyle S(0)}$${\displaystyle S(0)+I(0)+R(0)+V(0)=N}$${\displaystyle R(0)=V(0)=0}$

La solución numérica de este modelo para calcular el número de reproducción en tiempo real de COVID-19 se puede practicar en base a la información de las diferentes poblaciones de una comunidad. ^[22] La solución numérica es un método comúnmente utilizado para analizar redes cinéticas complicadas cuando la solución analítica es difícil de obtener o está limitada por requisitos tales como condiciones de contorno o parámetros especiales. Utiliza ecuaciones recursivas para calcular el siguiente paso convirtiendo la integración numérica en la suma de Riemann de pasos de tiempo discretos, por ejemplo, utilizar el capital y la tasa de interés de ayer para calcular el interés de hoy, lo que supone que la tasa de interés es fija durante el día. El cálculo contiene errores proyectados si no se incluyen las correcciones analíticas en el tamaño del paso numérico, por ejemplo, cuando la tasa de interés de la recaudación anual se simplifica a 12 veces la tasa mensual, se introduce un error proyectado. Por lo tanto, los resultados calculados conllevarán errores acumulativos cuando el paso de tiempo esté muy alejado del punto de referencia y se necesite una prueba de convergencia para estimar el error. Sin embargo, este error suele ser aceptable para el ajuste de datos. Al ajustar un conjunto de datos con un paso de tiempo cercano, el error es relativamente pequeño porque el punto de referencia está cerca en comparación con cuando se predice un largo período de tiempo después de un punto de referencia. Una vez que se extrae el tiempo real, se puede comparar con el número básico de reproducción . Antes de la vacunación, proporciona al responsable de las políticas y al público en general una medida de la eficiencia de las actividades de mitigación social, como el distanciamiento social y el uso de mascarillas, simplemente dividiendo . Con la vacunación masiva, el objetivo del control de la enfermedad es reducir el número efectivo de reproducción , donde es el número de población susceptible en ese momento y es la población total. Cuando , la propagación disminuye y los casos diarios de infección disminuyen.${\displaystyle R_{t}}$${\displaystyle R_{t}}$ ${\displaystyle R_{0}}$${\displaystyle R_{t}}$${\displaystyle {\frac {R_{t}}{R_{0}}}}$${\displaystyle R_{e}={\frac {R_{t}S}{N}}<1}$${\displaystyle S}$${\displaystyle N}$${\displaystyle R_{e}<1}$

El modelo de compartimento epidémico susceptible-infectado-recuperado-vacunado-fallecido (SIRVD) extiende el modelo SIR para incluir los efectos de las campañas de vacunación y las tasas de mortalidad dependientes del tiempo en los brotes epidémicos. Abarca los modelos SIR, SIRV, SIRD y SI como casos especiales, con tasas individuales dependientes del tiempo que rigen las transiciones entre diferentes fracciones. ^[32] Este modelo utiliza el siguiente sistema de ecuaciones diferenciales para las fracciones de población :${\displaystyle S,I,R,V,D}$

${\displaystyle {\begin{aligned}&{\frac {dS}{dt}}=-a(t)SI-v(t)S,\\[6pt]&{\frac {dI}{dt}}=a(t)SI-\mu (t)I-\psi (t)I,\\[6pt]&{\frac {dR}{dt}}=\mu (t)I,\\[6pt]&{\frac {dV}{dt}}=v(t)S,\\[6pt]&{\frac {dD}{dt}}=\psi (t)I\end{aligned}}}$

donde son las tasas de infección, vacunación, recuperación y mortalidad, respectivamente. Para las condiciones iniciales de semitiempo , , y proporciones constantes , , y el modelo se había resuelto de manera aproximada y exacta para algunos casos especiales, independientemente de la forma funcional de . ^[32] Esto se logra al reescribir las ecuaciones del modelo SIRVD anteriores en forma equivalente, pero reducida${\displaystyle a(t),v(t),\mu (t),\psi (t)}$${\displaystyle S(0)=1-\eta }$${\displaystyle I(0)=\eta }$${\displaystyle R(0)=V(0)=D(0)=0}$${\displaystyle k=\mu (t)/a(t)}$${\displaystyle b=v(t)/a(t)}$${\displaystyle q=\psi (t)/a(t)}$${\displaystyle a(t)}$

${\displaystyle {\begin{aligned}&{\frac {dS}{d\tau }}=-SI-b(\tau )S,\\[6pt]&{\frac {dI}{d\tau }}=SI-[k(\tau )+q(\tau )]I,\\[6pt]&{\frac {dR}{d\tau }}=k(\tau )I,\\[6pt]&{\frac {dV}{d\tau }}=b(\tau )S,\\[6pt]&{\frac {dD}{d\tau }}=q(\tau )S\end{aligned}}}$

dónde

${\displaystyle \tau (t)=\int _{0}^{t}a(\xi )d\xi }$

es un tiempo reducido y adimensional. La dependencia temporal de la fracción infectada y la tasa de nuevas infecciones difieren cuando se consideran los efectos de las vacunaciones y cuando la dependencia en tiempo real de las tasas de mortalidad y recuperación divergen. Estas diferencias se han destacado para las tasas de mortalidad estacionarias y las tasas de mortalidad que disminuyen gradualmente. ^[32] El caso de las tasas estacionarias permite construir un método de diagnóstico para extraer analíticamente todos los parámetros del modelo SIRVD a partir de los datos medidos de COVID-19 de una ola pandémica completa. ^[32]${\displaystyle I(\tau )}$${\displaystyle j(\tau )=S(\tau )I(\tau )}$

En el caso de muchas infecciones, incluida la del sarampión , los bebés no nacen en el compartimento susceptible, pero son inmunes a la enfermedad durante los primeros meses de vida debido a la protección que les brindan los anticuerpos maternos (que se transmiten a través de la placenta y, además, a través del calostro ). Esto se denomina inmunidad pasiva . Este detalle adicional se puede mostrar incluyendo una clase M (para la inmunidad derivada de la madre) al comienzo del modelo.

Para indicar esto matemáticamente, se añade un compartimento adicional, M ( t ) . Esto da como resultado las siguientes ecuaciones diferenciales:

${\displaystyle {\begin{aligned}{\frac {dM}{dt}}&=\Lambda -\delta M-\mu M\\[8pt]{\frac {dS}{dt}}&=\delta M-{\frac {\beta SI}{N}}-\mu S\\[8pt]{\frac {dI}{dt}}&={\frac {\beta SI}{N}}-\gamma I-\mu I\\[8pt]{\frac {dR}{dt}}&=\gamma I-\mu R\end{aligned}}}$

Algunas personas que han tenido una enfermedad infecciosa como la tuberculosis nunca se recuperan por completo y continúan siendo portadoras de la infección, aunque no sufren la enfermedad. Entonces pueden volver al compartimento infeccioso y sufrir síntomas (como en la tuberculosis) o pueden seguir infectando a otros en su estado de portadoras, aunque no presenten síntomas. El ejemplo más famoso de esto es probablemente el de Mary Mallon , que infectó a 22 personas con fiebre tifoidea . El compartimento portador está etiquetado como C.

En el caso de muchas infecciones importantes, existe un período de latencia significativo durante el cual las personas se han infectado pero aún no son infecciosas. Durante este período, la persona se encuentra en el compartimento E (expuesta).

Suponiendo que el periodo de latencia es una variable aleatoria con distribución exponencial con parámetro (es decir, el periodo de latencia promedio es ), y asumiendo también la presencia de una dinámica vital con tasa de natalidad igual a la tasa de mortalidad (de modo que el número total es constante), tenemos el modelo:${\displaystyle a}$${\displaystyle a^{-1}}$${\displaystyle \Lambda }$${\displaystyle N\mu }$${\displaystyle N}$

${\displaystyle {\begin{aligned}{\frac {dS}{dt}}&=\mu N-\mu S-{\frac {\beta IS}{N}}\\[8pt]{\frac {dE}{dt}}&={\frac {\beta IS}{N}}-(\mu +a)E\\[8pt]{\frac {dI}{dt}}&=aE-(\gamma +\mu )I\\[8pt]{\frac {dR}{dt}}&=\gamma I-\mu R.\end{aligned}}}$

Lo tenemos , pero esto es constante sólo debido al supuesto simplificador de que las tasas de natalidad y mortalidad son iguales; en general es una variable.${\displaystyle S+E+I+R=N,}$${\displaystyle N}$

Para este modelo, el número de reproducción básico es:

${\displaystyle R_{0}={\frac {a}{\mu +a}}{\frac {\beta }{\mu +\gamma }}.}$

De manera similar al modelo SIR, también en este caso tenemos un Equilibrio Libre de Enfermedades ( N ,0,0,0) y un Equilibrio Endémico EE, y se puede demostrar que, independientemente de las condiciones iniciales biológicamente significativas

${\displaystyle \left(S(0),E(0),I(0),R(0)\right)\in \left\{(S,E,I,R)\in [0,N]^{4}:S\geq 0,E\geq 0,I\geq 0,R\geq 0,S+E+I+R=N\right\}}$

Se sostiene que:

${\displaystyle R_{0}\leq 1\Rightarrow \lim _{t\to +\infty }\left(S(t),E(t),I(t),R(t)\right)=DFE=(N,0,0,0),}$

${\displaystyle R_{0}>1,I(0)>0\Rightarrow \lim _{t\to +\infty }\left(S(t),E(t),I(t),R(t)\right)=EE.}$

En el caso de una tasa de contacto que varía periódicamente, la condición para el atractivo global de DFE es que el siguiente sistema lineal con coeficientes periódicos:${\displaystyle \beta (t)}$

${\displaystyle {\begin{aligned}{\frac {dE_{1}}{dt}}&=\beta (t)I_{1}-(\gamma +a)E_{1}\\[8pt]{\frac {dI_{1}}{dt}}&=aE_{1}-(\gamma +\mu )I_{1}\end{aligned}}}$

es estable (es decir, tiene sus valores propios de Floquet dentro del círculo unitario en el plano complejo).

El modelo SEIS es como el modelo SEIR (arriba) excepto que no se adquiere inmunidad al final.

${\displaystyle {\color {blue}{{\mathcal {S}}\to {\mathcal {E}}\to {\mathcal {I}}\to {\mathcal {S}}}}}$

En este modelo, una infección no deja inmunidad, por lo que los individuos que se han recuperado vuelven a ser susceptibles y vuelven al compartimento S ( t ). Las siguientes ecuaciones diferenciales describen este modelo:

${\displaystyle {\begin{aligned}{\frac {dS}{dt}}&=\Lambda -{\frac {\beta SI}{N}}-\mu S+\gamma I\\[6pt]{\frac {dE}{dt}}&={\frac {\beta SI}{N}}-(\epsilon +\mu )E\\[6pt]{\frac {dI}{dt}}&=\varepsilon E-(\gamma +\mu )I\end{aligned}}}$

Para el caso de una enfermedad, con los factores de inmunidad pasiva y un periodo de latencia existe el modelo MSEIR.

${\displaystyle \color {blue}{{\mathcal {M}}\to {\mathcal {S}}\to {\mathcal {E}}\to {\mathcal {I}}\to {\mathcal {R}}}}$

${\displaystyle {\begin{aligned}{\frac {dM}{dt}}&=\Lambda -\delta M-\mu M\\[6pt]{\frac {dS}{dt}}&=\delta M-{\frac {\beta SI}{N}}-\mu S\\[6pt]{\frac {dE}{dt}}&={\frac {\beta SI}{N}}-(\varepsilon +\mu )E\\[6pt]{\frac {dI}{dt}}&=\varepsilon E-(\gamma +\mu )I\\[6pt]{\frac {dR}{dt}}&=\gamma I-\mu R\end{aligned}}}$

Un modelo MSEIRS es similar al MSEIR, pero la inmunidad en la clase R sería temporal, de modo que los individuos recuperarían su susceptibilidad cuando terminara la inmunidad temporal.

${\displaystyle {\color {blue}{{\mathcal {M}}\to {\mathcal {S}}\to {\mathcal {E}}\to {\mathcal {I}}\to {\mathcal {R}}\to {\mathcal {S}}}}}$

Es bien sabido que la probabilidad de contraer una enfermedad no es constante en el tiempo. A medida que avanza una pandemia, las reacciones a la misma pueden cambiar las tasas de contacto, que se suponen constantes en los modelos más simples. Las contramedidas, como el uso de mascarillas, el distanciamiento social y el confinamiento, alterarán la tasa de contacto de manera que reducirán la velocidad de la pandemia.

Además, algunas enfermedades son estacionales, como los virus del resfriado común , que son más frecuentes durante el invierno. En el caso de las enfermedades infantiles, como el sarampión, las paperas y la rubéola, existe una fuerte correlación con el calendario escolar, de modo que durante las vacaciones escolares la probabilidad de contraer una de ellas disminuye drásticamente. En consecuencia, para muchas clases de enfermedades, se debe considerar una fuerza de infección con una tasa de contacto que varía periódicamente ("estacional").

${\displaystyle F=\beta (t){\frac {I}{N}},\quad \beta (t+T)=\beta (t)}$

con período T igual a un año.

Así pues, nuestro modelo se convierte en

${\displaystyle {\begin{aligned}{\frac {dS}{dt}}&=\mu N-\mu S-\beta (t){\frac {I}{N}}S\\[8pt]{\frac {dI}{dt}}&=\beta (t){\frac {I}{N}}S-(\gamma +\mu )I\end{aligned}}}$

(la dinámica de la recuperación se deduce fácilmente de ), es decir, un conjunto no lineal de ecuaciones diferenciales con parámetros que varían periódicamente. Es bien sabido que esta clase de sistemas dinámicos puede experimentar fenómenos muy interesantes y complejos de resonancia paramétrica no lineal. Es fácil ver que si:${\displaystyle R=N-S-I}$

${\displaystyle {\frac {1}{T}}\int _{0}^{T}{\frac {\beta (t)}{\mu +\gamma }}\,dt<1\Rightarrow \lim _{t\to +\infty }(S(t),I(t))=DFE=(N,0),}$

mientras que si la integral es mayor que uno la enfermedad no se extinguirá y pueden existir tales resonancias. Por ejemplo, considerando la tasa de contacto que varía periódicamente como la 'entrada' del sistema, se tiene que la salida es una función periódica cuyo período es un múltiplo del período de la entrada. Esto permitió dar una contribución para explicar los brotes epidémicos polianuales (normalmente bienales) de algunas enfermedades infecciosas como interacción entre el período de las oscilaciones de la tasa de contacto y el pseudoperíodo de las oscilaciones amortiguadas cerca del equilibrio endémico. Cabe destacar que, en algunos casos, el comportamiento también puede ser cuasiperiódico o incluso caótico.

Los modelos compartimentados espaciotemporales no describen el número total, sino la densidad de personas susceptibles/infectantes/recuperadas. Por consiguiente, también permiten modelar la distribución de las personas infectadas en el espacio. En la mayoría de los casos, esto se hace combinando el modelo SIR con una ecuación de difusión.

${\displaystyle {\begin{aligned}&\partial _{t}S=D_{S}\nabla ^{2}S-{\frac {\beta IS}{N}},\\[6pt]&\partial _{t}I=D_{I}\nabla ^{2}I+{\frac {\beta IS}{N}}-\gamma I,\\[6pt]&\partial _{t}R=D_{R}\nabla ^{2}R+\gamma I,\end{aligned}}}$^[33]

donde , y son constantes de difusión. De este modo, se obtiene una ecuación de reacción-difusión. (Tenga en cuenta que, por razones dimensionales, el parámetro debe cambiarse en comparación con el modelo SIR simple). Los primeros modelos de este tipo se han utilizado para modelar la propagación de la peste negra en Europa. ^[34] Se han utilizado extensiones de este modelo para incorporar, por ejemplo, los efectos de intervenciones no farmacéuticas como el distanciamiento social. ^[35]${\displaystyle D_{S}}$${\displaystyle D_{I}}$${\displaystyle D_{R}}$${\displaystyle \beta }$

Como los contactos sociales, la gravedad y letalidad de la enfermedad, así como la eficacia de las medidas profilácticas pueden diferir sustancialmente entre subpoblaciones que interactúan, por ejemplo, los ancianos frente a los jóvenes, se pueden utilizar modelos SEIR separados para cada subgrupo que estén conectados mutuamente a través de vínculos de interacción. ^[33] Dichos modelos SEIR de subpoblaciones que interactúan se han utilizado para modelar la pandemia de COVID-19 a escala continental para desarrollar estrategias de vacunación personalizadas, aceleradas y dirigidas a subpoblaciones ^[36] que prometen un acortamiento de la pandemia y una reducción de los recuentos de casos y muertes en el contexto de un acceso limitado a las vacunas durante una ola de variantes de virus de preocupación.

El modelo SIR se ha estudiado en redes de diversos tipos con el fin de modelar una forma de conexión más realista que la condición de mezcla homogénea que se requiere habitualmente. Un modelo simple para epidemias en redes en las que un individuo tiene una probabilidad p de ser infectado por cada uno de sus vecinos infectados en un paso de tiempo dado conduce a resultados similares a la formación de componentes gigantes en los gráficos aleatorios de Erdos Renyi . ^[37]

La dinámica de las epidemias depende de cómo cambia el comportamiento de las personas con el tiempo. Por ejemplo, al principio de la epidemia, las personas son ignorantes y descuidadas, luego, después del brote de epidemias y la alarma, comienzan a cumplir con las diversas restricciones y la propagación de las epidemias puede disminuir. Con el tiempo, algunas personas se cansan/frustran por las restricciones y dejan de cumplirlas (agotamiento), especialmente si el número de nuevos casos disminuye. Después de descansar durante algún tiempo, pueden volver a cumplir con las restricciones. Pero durante esta pausa, la segunda ola puede llegar y volverse incluso más fuerte que la primera. Se debe considerar la dinámica social . Los modelos de física social del estrés social complementan los modelos clásicos de epidemias. ^[38]

El modelo de estrés social SIR más simple (SIR _SS ) se organiza de la siguiente manera. Los individuos susceptibles (S) se pueden dividir en tres subgrupos según los tipos de comportamiento: ignorantes o inconscientes de la epidemia (S _ign ), racionalmente resistentes (S _res ) y exhaustos (S _exh ) que no reaccionan a los estímulos externos (se trata de una especie de período refractario). En otras palabras: S(t) = S _ign (t) + S _res (t) + S _exh (t). Simbólicamente, el modelo de estrés social se puede presentar mediante el "esquema de reacción" (donde I denota a los individuos infectados):

• ${\displaystyle {\color {blue}{{\mathcal {S_{ign}}}+2{\mathcal {I}}\to {\mathcal {S_{res}}}+2{\mathcal {I}}}}}$– reacción de movilización (la forma autocatalítica aquí significa que la tasa de transición es proporcional al cuadrado de la fracción infectada I);
• ${\displaystyle {\color {blue}{{\mathcal {S_{res}}}\to {\mathcal {S_{exh}}}}}}$– proceso de agotamiento debido a la fatiga por las restricciones antiepidémicas;
• ${\displaystyle {\color {blue}{{\mathcal {S_{exh}}}\to {\mathcal {S_{ign}}}}}}$– relajación lenta hasta el estado inicial (fin del período refractario).

La principal reacción a la epidemia del SIR

• ${\displaystyle {\color {blue}{{\mathcal {S_{...}}}+{\mathcal {I}}\to {\mathcal {2I}}}}}$

tiene constantes de velocidad de reacción diferentes para S _ign , S _res y S _exh . Presumiblemente, para S _res , es menor que para S _ign y S _ign .${\displaystyle \beta }$${\displaystyle \beta }$

Las diferencias entre países se concentran en dos constantes cinéticas: la tasa de movilización y la tasa de agotamiento calculadas para la epidemia de COVID-19 en 13 países. ^[38] Estas constantes para esta epidemia en todos los países se pueden extraer mediante el ajuste del modelo SIR _SS a los datos disponibles públicamente ^[39].

Basándose en el modelo SIR clásico, se ha propuesto una ecuación Korteweg-de Vries (KdV)–SIR y su solución analítica para ilustrar la dinámica fundamental de una ola epidémica, la dependencia de las soluciones de los parámetros y la dependencia de los horizontes de predictibilidad de varios tipos de soluciones. ^[40] La ecuación KdV-SIR se escribe de la siguiente manera:

${\displaystyle {\frac {d^{2}I}{dt}}-\sigma _{o}^{2}I+{\frac {3}{2}}{\frac {\sigma _{o}^{2}}{I_{max}}}I^{2}=0}$.

Aquí,

${\displaystyle \sigma _{o}=\gamma (R_{o}-1)}$,

${\displaystyle R_{o}={\frac {\beta }{\gamma }}{\frac {S_{o}}{N}}}$,

y

${\displaystyle I_{max}={\frac {S_{o}}{2}}{\frac {(R_{o}-1)^{2}}{R_{o}^{2}}}}$.

${\displaystyle S_{o}}$indica el valor inicial de la variable de estado . Los parámetros (σ-cero) y (R-cero) son la tasa de crecimiento relativa independiente del tiempo y el número básico de reproducción, respectivamente. presenta el máximo de las variables de estado (para el número de personas infectadas). Una solución analítica para la ecuación KdV-SIR se escribe de la siguiente manera:${\displaystyle S}$${\displaystyle \sigma _{o}}$${\displaystyle R_{o}}$${\displaystyle I_{max}}$${\displaystyle I}$

${\displaystyle I=I_{max}sech^{2}\left({\frac {\sigma _{o}}{2}}t\right)}$,

que representa una solución de onda solitaria.

Modelar una población completa de posiblemente millones de personas usando dos constantes parece una tarea descabellada; cada individuo tiene características personales que influyen en la propagación: estado de inmunidad, hábitos de contacto, etc. Por lo tanto, es interesante saber qué sucede si, por ejemplo, y no son dos constantes sino algunas variables aleatorias (un par para cada individuo). Este procedimiento tiene varios nombres: "modelo heterogéneo", "estructuración" (ver también más abajo los modelos estructurados por edad) o visión "bayesiana". ^{[41] [42] [43]} Surgen resultados sorprendentes, por ejemplo, se demostró en ^[41] que el número de infectados en el pico de una epidemia heterogénea es menor que la epidemia determinista que tiene el mismo promedio ; lo mismo es válido para el tamaño total de la epidemia y otros modelos, por ejemplo, SEIR. ^[41]${\displaystyle \beta }$${\displaystyle \gamma }$${\displaystyle \beta }$${\displaystyle \gamma }$${\displaystyle \beta }$${\displaystyle S(0)-S(\infty )}$

El modelo SIR se puede modificar para modelar la vacunación. ^[44] Normalmente, estos introducen un compartimento adicional al modelo SIR, , para las personas vacunadas. A continuación se presentan algunos ejemplos.${\displaystyle V}$

En caso de enfermedades contagiosas, una de las principales tareas es erradicarlas mediante medidas de prevención y, si es posible, mediante el establecimiento de un programa de vacunación masiva. Consideremos una enfermedad para la que se vacuna a los recién nacidos (con una vacuna que otorga inmunidad de por vida) a un ritmo :${\displaystyle P\in (0,1)}$

${\displaystyle {\begin{aligned}{\frac {dS}{dt}}&=\nu N(1-P)-\mu S-\beta {\frac {I}{N}}S\\[8pt]{\frac {dI}{dt}}&=\beta {\frac {I}{N}}S-(\mu +\gamma )I\\[8pt]{\frac {dV}{dt}}&=\nu NP-\mu V\end{aligned}}}$

donde es la clase de sujetos vacunados. Es inmediato demostrar que:${\displaystyle V}$

${\displaystyle \lim _{t\to +\infty }V(t)=NP,}$

Así pues, trataremos el comportamiento a largo plazo de y , para lo cual se cumple que:${\displaystyle S}$${\displaystyle I}$

${\displaystyle R_{0}(1-P)\leq 1\Rightarrow \lim _{t\to +\infty }\left(S(t),I(t)\right)=DFE=\left(N\left(1-P\right),0\right)}$

${\displaystyle R_{0}(1-P)>1,\quad I(0)>0\Rightarrow \lim _{t\to +\infty }\left(S(t),I(t)\right)=EE=\left({\frac {N}{R_{0}(1-P)}},N\left(R_{0}(1-P)-1\right)\right).}$

En otras palabras, si

${\displaystyle P<P^{*}=1-{\frac {1}{R_{0}}}}$

El programa de vacunación no logra erradicar la enfermedad, por el contrario, ésta seguirá siendo endémica, aunque en niveles inferiores a los que se darían en caso de ausencia de vacunación. Esto significa que el modelo matemático sugiere que para una enfermedad cuyo número básico de reproducción puede llegar a 18, se debería vacunar al menos al 94,4% de los recién nacidos para erradicarla.

Las sociedades modernas se enfrentan al reto de la exención "racional", es decir, la decisión de la familia de no vacunar a los niños como consecuencia de una comparación "racional" entre el riesgo percibido de infección y el de sufrir daños por la vacuna. Para evaluar si este comportamiento es realmente racional, es decir, si puede conducir igualmente a la erradicación de la enfermedad, se puede suponer simplemente que la tasa de vacunación es una función creciente del número de sujetos infecciosos:

${\displaystyle P=P(I),\quad P'(I)>0.}$

En tal caso la condición de erradicación pasa a ser:

${\displaystyle P(0)\geq P^{*},}$

Es decir, la tasa de vacunación de referencia debería ser mayor que el umbral de "vacunación obligatoria", que, en caso de exención, no puede cumplirse. Por lo tanto, la exención "racional" podría ser miope, ya que se basa únicamente en la baja incidencia actual debido a la alta cobertura de vacunación, en lugar de tener en cuenta el resurgimiento futuro de la infección debido a la disminución de la cobertura.

En caso de que también haya vacunaciones de no recién nacidos a una tasa ρ la ecuación para el sujeto susceptible y vacunado debe modificarse de la siguiente manera:

${\displaystyle {\begin{aligned}{\frac {dS}{dt}}&=\mu N(1-P)-\mu S-\rho S-\beta {\frac {I}{N}}S\\[8pt]{\frac {dV}{dt}}&=\mu NP+\rho S-\mu V\end{aligned}}}$

conduciendo a la siguiente condición de erradicación:

${\displaystyle P\geq 1-\left(1+{\frac {\rho }{\mu }}\right){\frac {1}{R_{0}}}}$

Esta estrategia consiste en vacunar repetidamente a una cohorte de edad definida (como niños pequeños o ancianos) en una población susceptible a lo largo del tiempo. Con esta estrategia, el bloque de individuos susceptibles se elimina inmediatamente, lo que permite eliminar una enfermedad infecciosa (como el sarampión) de toda la población. Cada T unidades de tiempo, se vacuna una fracción constante p de sujetos susceptibles en un tiempo relativamente corto (con respecto a la dinámica de la enfermedad). Esto conduce a las siguientes ecuaciones diferenciales impulsivas para los sujetos susceptibles y vacunados:

${\displaystyle {\begin{aligned}{\frac {dS}{dt}}&=\mu N-\mu S-\beta {\frac {I}{N}}S,\quad S(nT^{+})=(1-p)S(nT^{-}),&&n=0,1,2,\ldots \\[8pt]{\frac {dV}{dt}}&=-\mu V,\quad V(nT^{+})=V(nT^{-})+pS(nT^{-}),&&n=0,1,2,\ldots \end{aligned}}}$

Es fácil ver que fijando I = 0 se obtiene que la dinámica de los sujetos susceptibles viene dada por:

${\displaystyle S^{*}(t)=1-{\frac {p}{1-(1-p)E^{-\mu T}}}E^{-\mu MOD(t,T)}}$

y que la condición de erradicación es:

${\displaystyle R_{0}\int _{0}^{T}S^{*}(t)\,dt<1}$

Una gran cantidad de literatura reconoce que la vacunación puede ser vista como un juego: en una población donde todos están vacunados, cualquier epidemia desaparecerá inmediatamente, por lo que una persona adicional no tendrá ningún interés en vacunarse. Por el contrario, una persona que llegue a una población donde nadie está vacunado tendrá todos los incentivos para vacunarse (la epidemia se desatará en esa población). Por lo tanto, parece que el individuo tiene interés en hacer lo contrario de la población en su conjunto. Pero la población es la suma de todos los individuos, y la afirmación anterior debería ser falsa. Por lo tanto, de hecho, se alcanza un equilibrio de Nash . ^{[45] [46] [47] [48] [49]} Las herramientas técnicas para tratar tales situaciones involucran la teoría de juegos o herramientas modernas como la teoría de juegos de campo medio . ^{[49] [50]}

La edad tiene una profunda influencia en la tasa de propagación de la enfermedad en una población, especialmente en la tasa de contacto. Esta tasa resume la efectividad de los contactos entre sujetos susceptibles e infecciosos. Teniendo en cuenta las edades de las clases epidémicas (para limitarnos al esquema susceptible-infeccioso-eliminado) de manera que:${\displaystyle s(t,a),i(t,a),r(t,a)}$

${\displaystyle S(t)=\int _{0}^{a_{M}}s(t,a)\,da}$

${\displaystyle I(t)=\int _{0}^{a_{M}}i(t,a)\,da}$

${\displaystyle R(t)=\int _{0}^{a_{M}}r(t,a)\,da}$

(donde es la edad máxima admisible) y su dinámica no se describe, como podría pensarse, mediante ecuaciones diferenciales parciales "simples", sino mediante ecuaciones integro-diferenciales :${\displaystyle a_{M}\leq +\infty }$

${\displaystyle \partial _{t}s(t,a)+\partial _{a}s(t,a)=-\mu (a)s(a,t)-s(a,t)\int _{0}^{a_{M}}k(a,a_{1};t)i(a_{1},t)\,da_{1}}$

${\displaystyle \partial _{t}i(t,a)+\partial _{a}i(t,a)=s(a,t)\int _{0}^{a_{M}}{k(a,a_{1};t)i(a_{1},t)da_{1}}-\mu (a)i(a,t)-\gamma (a)i(a,t)}$

${\displaystyle \partial _{t}r(t,a)+\partial _{a}r(t,a)=-\mu (a)r(a,t)+\gamma (a)i(a,t)}$

dónde:

${\displaystyle F(a,t,i(\cdot ,\cdot ))=\int _{0}^{a_{M}}k(a,a_{1};t)i(a_{1},t)\,da_{1}}$

es la fuerza de la infección, que, por supuesto, dependerá, aunque el núcleo de contacto, de las interacciones entre las edades.${\displaystyle k(a,a_{1};t)}$

La complejidad se ve aumentada por las condiciones iniciales para los recién nacidos (es decir, para a=0), que son sencillas para los infecciosos y se eliminan:

${\displaystyle i(t,0)=r(t,0)=0}$

pero que no son locales para la densidad de recién nacidos susceptibles:

${\displaystyle s(t,0)=\int _{0}^{a_{M}}\left(\varphi _{s}(a)s(a,t)+\varphi _{i}(a)i(a,t)+\varphi _{r}(a)r(a,t)\right)\,da}$

¿Dónde están las fertilidades de los adultos?${\displaystyle \varphi _{j}(a),j=s,i,r}$

Además, definiendo ahora la densidad de la población total se obtiene:${\displaystyle n(t,a)=s(t,a)+i(t,a)+r(t,a)}$

${\displaystyle \partial _{t}n(t,a)+\partial _{a}n(t,a)=-\mu (a)n(a,t)}$

En el caso más simple de fecundidad igual en las tres clases epidémicas, tenemos que para que haya equilibrio demográfico debe cumplirse la siguiente condición necesaria y suficiente que vincula la fecundidad con la mortalidad :${\displaystyle \varphi (.)}$${\displaystyle \mu (a)}$

${\displaystyle 1=\int _{0}^{a_{M}}\varphi (a)\exp \left(-\int _{0}^{a}{\mu (q)dq}\right)\,da}$