Intervalo de confianza

Este artículo tiene varios problemas. Ayúdenos a mejorarlo o a discutir estos problemas en la página de discusión . ( Aprenda cómo y cuándo eliminar estos mensajes ) Este artículo necesita la atención de un experto en estadística . El problema específico es el siguiente: muchas correcciones y correcciones indican que el idioma del artículo debe revisarse con cuidado. Es posible que WikiProject Statistics pueda ayudar a reclutar a un experto. ( Diciembre 2021 ) Este artículo puede ser demasiado técnico para que la mayoría de los lectores lo entiendan .Por favor, ayude a mejorarlo para que sea comprensible para los no expertos , sin eliminar los detalles técnicos. ( Marzo de 2021 )( Aprenda cómo y cuándo eliminar este mensaje ) ( Aprenda cómo y cuándo eliminar este mensaje )

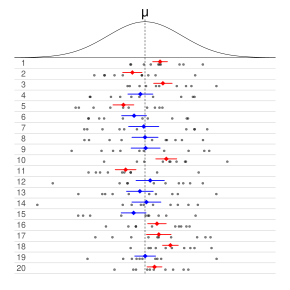
De manera informal, en las estadísticas frecuentistas , un intervalo de confianza ( IC ) es un intervalo que se espera que contenga típicamente el parámetro que se está estimando. Más específicamente, dado un nivel de confianza (95% y 99% son valores típicos), un IC es un intervalo aleatorio que contiene el parámetro que se está estimando % del tiempo. ^{[1] [2]} El nivel de confianza , grado de confianza o coeficiente de confianza representa la proporción a largo plazo de IC (en el nivel de confianza dado) que teóricamente contienen el valor verdadero del parámetro; esto es equivalente a la probabilidad de cobertura nominal . Por ejemplo, de todos los intervalos calculados al nivel del 95%, el 95% de ellos debería contener el valor verdadero del parámetro. ^[3]${\estilo de visualización \gamma}$${\estilo de visualización \gamma}$

Los factores que afectan la amplitud del IC incluyen el tamaño de la muestra , la variabilidad de la muestra y el nivel de confianza. ^[4] En igualdad de condiciones, una muestra más grande produce un intervalo de confianza más estrecho, una mayor variabilidad de la muestra produce un intervalo de confianza más amplio y un nivel de confianza más alto produce un intervalo de confianza más amplio. ^[5]

Los métodos para calcular intervalos de confianza para la proporción binomial aparecieron a partir de la década de 1920. ^{[6] [7]} Las ideas principales de los intervalos de confianza en general se desarrollaron a principios de la década de 1930, ^{[8] [9] [10]} y la primera explicación completa y general fue dada por Jerzy Neyman en 1937. ^[11]

Neyman describió el desarrollo de las ideas de la siguiente manera (los números de referencia han sido cambiados): ^[10]

[Mi trabajo sobre los intervalos de confianza] se originó alrededor de 1930 a partir de una simple pregunta de Waclaw Pytkowski, entonces estudiante mío en Varsovia, que estaba realizando un estudio empírico sobre economía agrícola. La pregunta era: ¿cómo caracterizar de manera no dogmática la precisión de un coeficiente de regresión estimado? ...

La monografía de Pytkowski... apareció impresa en 1932. ^[12] Ocurrió que, un poco antes, Fisher publicó su primer artículo ^[13] sobre distribuciones fiduciales y argumentos fiduciales. De manera bastante inesperada, si bien el marco conceptual del argumento fiducial es completamente diferente al de los intervalos de confianza, las soluciones específicas de varios problemas particulares coincidieron. Así, en el primer artículo en el que presenté la teoría de los intervalos de confianza, publicado en 1934, ^[8] reconocí la prioridad de Fisher por la idea de que la estimación de intervalos es posible sin ninguna referencia al teorema de Bayes y con la solución siendo independiente de las probabilidades a priori . Al mismo tiempo sugerí suavemente que el enfoque de Fisher al problema implicaba un pequeño malentendido.

En las revistas médicas, los intervalos de confianza se promovieron en la década de 1970, pero recién se empezaron a utilizar ampliamente en la década de 1980. ^[14] En 1988, las revistas médicas exigían la presentación de intervalos de confianza. ^[15]

Sea una muestra aleatoria de una distribución de probabilidad con parámetro estadístico , que es una cantidad a estimar, y , que representa cantidades que no son de interés inmediato. Un intervalo de confianza para el parámetro , con nivel de confianza o coeficiente , es un intervalo determinado por variables aleatorias y con la propiedad:${\estilo de visualización X}$ ${\estilo de visualización \theta}$${\estilo de visualización \varphi}$${\estilo de visualización \theta}$${\estilo de visualización \gamma}$${\displaystyle (u(X),v(X))}$ ${\displaystyle u(X)}$${\displaystyle v(X)}$

${\displaystyle P(u(X)<\theta <v(X))=\gamma \quad {\text{ para cada }}(\theta ,\varphi ).}$

El número , cuyo valor típico es cercano pero no mayor que 1, a veces se da en la forma (o como porcentaje ), donde es un número positivo pequeño, a menudo 0,05.${\estilo de visualización \gamma}$${\estilo de visualización 1-\alfa}$${\displaystyle 100\%\cdot (1-\alpha )}$${\estilo de visualización \alpha}$

Es importante que los límites y se especifiquen de tal manera que, siempre que se recopile aleatoriamente, cada vez que calculemos un intervalo de confianza, exista la probabilidad de que contenga , el valor verdadero del parámetro que se está estimando. Esto debería ser válido para cualquier valor real y . ^[2]${\displaystyle u(X)}$${\displaystyle v(X)}$${\estilo de visualización X}$${\estilo de visualización \gamma}$${\estilo de visualización \theta}$${\estilo de visualización \theta}$${\estilo de visualización \varphi}$

En muchas aplicaciones, es difícil construir intervalos de confianza que tengan exactamente el nivel de confianza requerido, pero se pueden calcular intervalos aproximados. La regla para construir el intervalo puede aceptarse como que proporciona un intervalo de confianza en el nivel si${\estilo de visualización \gamma}$

${\displaystyle P(u(X)<\theta <v(X))\approx \ \gamma \quad {\text{ para cada }}(\theta ,\varphi )}$

a un nivel aceptable de aproximación. Alternativamente, algunos autores ^[16] simplemente requieren que

${\displaystyle P(u(X)<\theta <v(X))\geq \ \gamma \quad {\text{ para cada }}(\theta ,\varphi ),}$

lo cual es útil si las probabilidades están solo parcialmente identificadas o son imprecisas , y también cuando se trabaja con distribuciones discretas . Límites de confianza de la forma

${\displaystyle P(u(X)<\theta )\geq \ \gamma }$   y   ${\displaystyle P(\theta <v(X))\geq \gamma }$

se denominan conservadores ; ^{[17] (p. 210)} en consecuencia, se habla de intervalos de confianza conservadores y, en general, de regiones.

Al aplicar procedimientos estadísticos estándar, a menudo habrá formas estándar de construir intervalos de confianza. Estos se habrán ideado de modo que cumplan con ciertas propiedades deseables, que se mantendrán siempre que los supuestos en los que se basa el procedimiento sean verdaderos. Estas propiedades deseables pueden describirse como: validez, optimalidad e invariancia.

De las tres, la "validez" es la más importante, seguida de cerca por la "optimalidad". La "invariancia" puede considerarse una propiedad del método de derivación de un intervalo de confianza, más que de la regla para construir el intervalo. En aplicaciones no estándar, se buscarían estas mismas propiedades deseables:

Esto significa que la probabilidad de cobertura nominal (nivel de confianza) del intervalo de confianza debe mantenerse, ya sea exactamente o con una buena aproximación.

Esto significa que la regla para construir el intervalo de confianza debe aprovechar al máximo la información del conjunto de datos.

Una forma de evaluar la optimalidad es mediante el ancho del intervalo, de modo que una regla para construir un intervalo de confianza se considera mejor que otra si conduce a intervalos cuyos anchos son típicamente más cortos.

En muchas aplicaciones, la cantidad que se está estimando podría no estar definida con precisión como tal.

Por ejemplo, una encuesta puede dar como resultado una estimación del ingreso medio de una población, pero también puede considerarse que proporciona una estimación del logaritmo del ingreso medio, dado que se trata de una escala común para presentar resultados gráficos. Sería deseable que el método utilizado para construir un intervalo de confianza para el ingreso medio diera resultados equivalentes cuando se aplicara para construir un intervalo de confianza para el logaritmo del ingreso medio: en concreto, los valores en los extremos del último intervalo serían los logaritmos de los valores en los extremos del primer intervalo.

En el caso de aplicaciones no estándar, existen varias vías que se pueden tomar para derivar una regla para la construcción de intervalos de confianza. Las reglas establecidas para procedimientos estándar se pueden justificar o explicar a través de varias de estas vías. Por lo general, una regla para construir intervalos de confianza está estrechamente vinculada a una forma particular de encontrar una estimación puntual de la cantidad que se está considerando.

Esto está estrechamente relacionado con el método de los momentos para la estimación. Un ejemplo sencillo surge cuando la cantidad que se va a estimar es la media de la población, en cuyo caso una estimación natural es la media de la muestra. De manera similar, la varianza de la muestra se puede utilizar para estimar la varianza de la población. Se puede construir un intervalo de confianza para la media verdadera centrado en la media de la muestra con un ancho que sea un múltiplo de la raíz cuadrada de la varianza de la muestra.

Las estimaciones se pueden construir utilizando el principio de máxima verosimilitud ; la teoría de verosimilitud proporciona dos formas de construir intervalos de confianza o regiones de confianza para las estimaciones.

El método de estimación que se utiliza en este caso puede considerarse tanto una generalización del método de momentos como una generalización del método de máxima verosimilitud. Existen generalizaciones correspondientes de los resultados de la teoría de máxima verosimilitud que permiten construir intervalos de confianza basados ​​en estimaciones derivadas de ecuaciones de estimación . ^{[ cita requerida ]}

Si existen pruebas de hipótesis para valores generales de un parámetro, entonces se pueden construir intervalos/regiones de confianza incluyendo en la región de confianza del 100 p  % todos aquellos puntos para los cuales la prueba de hipótesis de la hipótesis nula de que el valor verdadero es el valor dado no se rechaza a un nivel de significancia de (1 − p ). ^{[17] (§ 7.2 (iii))}

En situaciones en las que los supuestos distributivos de los métodos anteriores son inciertos o no se cumplen, los métodos de remuestreo permiten construir intervalos de confianza o intervalos de predicción. La distribución de datos observada y las correlaciones internas se utilizan como sustitutos de las correlaciones en la población más amplia.

El teorema del límite central es un refinamiento de la ley de los grandes números . Para un gran número de variables aleatorias independientes distribuidas de forma idéntica con varianza finita, el promedio tiene aproximadamente una distribución normal, sin importar cuál sea la distribución de , y la aproximación mejora aproximadamente en proporción a . ^[2]${\displaystyle X_{1},...,X_{n},}$${\displaystyle {\overline {X}}_{n}}$$Estilo de visualización X_{i}}$${\displaystyle {\sqrt {n}}}$

Supongamos que es una muestra independiente de una población distribuida normalmente con parámetros desconocidos media y varianza Sea${\displaystyle {X_{1},\ldots ,X_{n}}}$ ${\estilo de visualización \mu}$ ${\displaystyle \sigma ^{2}.}$

${\displaystyle {\bar {X}}={\frac {X_{1}+\cdots +X_{n}}{n}},}$

${\displaystyle S^{2}={\frac {1}{n-1}}\sum _{i=1}^{n}(X_{i}-{\bar {X}})^{2}.}$

¿Dónde está la media de la muestra y es la varianza de la muestra ? Entonces${\estilo de visualización {\bar {X}}}$$Estilo de visualización S2$

${\displaystyle T={\frac {{\bar {X}}-\mu }{S/{\sqrt {n}}}}}$

tiene una distribución t de Student con grados de libertad. ^[18] Nótese que la distribución de no depende de los valores de los parámetros no observables y ; es decir, es una cantidad fundamental . Supongamos que quisiéramos calcular un intervalo de confianza del 95% para Entonces, denotando como el percentil 97,5 de esta distribución,${\estilo de visualización n-1}$${\estilo de visualización T}$${\estilo de visualización \mu}$${\displaystyle \sigma ^{2}}$${\estilo de visualización \mu .}$${\estilo de visualización c}$

${\displaystyle P_{T}(-c\leq T\leq c)=0,95.}$

Tenga en cuenta que "97,5" y "0,95" son correctos en las expresiones anteriores. Hay una probabilidad del 2,5 % de que sea menor que y una probabilidad del 2,5 % de que sea mayor que Por lo tanto, la probabilidad de que esté entre y es del 95 %. es la medida de probabilidad según la distribución de Student.${\estilo de visualización T}$${\estilo de visualización -c}$${\estilo de visualización +c.}$${\estilo de visualización T}$${\estilo de visualización -c}$${\estilo de visualización +c}$$Estilo de visualización P_{T}$${\estilo de visualización t}$

Como consecuencia,

${\displaystyle P_{\mu }\left({\bar {X}}-{\frac {cS}{\sqrt {n}}}\leq \mu \leq {\bar {X}}+{\frac {cS}{\sqrt {n}}}\right)=0,95,}$

y tenemos un intervalo de confianza teórico (estocástico) del 95% para Aquí está la medida de probabilidad bajo una distribución desconocida de .${\estilo de visualización \mu .}$${\displaystyle P_{\mu}}$${\estilo de visualización \mu}$

Después de observar la muestra, encontramos valores para y para a partir de los cuales calculamos el intervalo de confianza.${\estilo de visualización {\barra {x}}}$${\estilo de visualización {\bar {X}}}$${\estilo de visualización s}$${\estilo de visualización S,}$

${\displaystyle \left[{\bar {x}}-{\frac {cs}{\sqrt {n}}},{\bar {x}}+{\frac {cs}{\sqrt {n}}}\right].}$

Se pueden dar varias interpretaciones de un intervalo de confianza (tomando como ejemplo a continuación el intervalo de confianza del 95%).

• El intervalo de confianza se puede expresar en términos de una frecuencia de largo plazo en muestras repetidas (o en un nuevo muestreo ): "Si este procedimiento se repitiera en numerosas muestras, la proporción de intervalos de confianza del 95% calculados que abarcaran el valor real del parámetro de población tendería hacia el 95%". ^[19]
• El intervalo de confianza se puede expresar en términos de probabilidad con respecto a una única muestra teórica (aún por realizarse): "Existe una probabilidad del 95% de que el intervalo de confianza del 95% calculado a partir de una muestra futura dada cubra el valor real del parámetro de población". ^[11] Esto esencialmente reformula la interpretación de las "muestras repetidas" como una probabilidad en lugar de una frecuencia.
• El intervalo de confianza se puede expresar en términos de significancia estadística, por ejemplo: "El intervalo de confianza del 95% representa valores que no son estadísticamente significativamente diferentes de la estimación puntual en el nivel .05". ^[20]

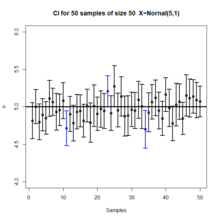
Los intervalos y niveles de confianza se malinterpretan con frecuencia, y estudios publicados han demostrado que incluso los científicos profesionales a menudo los malinterpretan. ^{[21] [22] [23] [24] [25] [26]}

• Un nivel de confianza del 95% no significa que para un intervalo determinado exista una probabilidad del 95% de que el parámetro de la población se encuentre dentro del intervalo (es decir, una probabilidad del 95% de que el intervalo cubra el parámetro de la población). ^[27] Según la interpretación frecuentista, una vez calculado un intervalo, este intervalo cubre el valor del parámetro o no lo hace; ya no es una cuestión de probabilidad. La probabilidad del 95% se relaciona con la confiabilidad del procedimiento de estimación, no con un intervalo calculado específico. ^{[28] El propio} Neyman (el defensor original de los intervalos de confianza) señaló este punto en su artículo original: ^[11]

  Se observará que en la descripción anterior, las afirmaciones de probabilidad se refieren a los problemas de estimación con los que se ocupará el estadístico en el futuro. De hecho, he afirmado repetidamente que la frecuencia de resultados correctos tenderá a α . Consideremos ahora el caso en el que ya se ha extraído una muestra y los cálculos han dado [límites particulares]. ¿Podemos decir que en este caso particular la probabilidad del valor verdadero [que se encuentre entre estos límites] es igual a α ? La respuesta es obviamente negativa. El parámetro es una constante desconocida y no se puede hacer ninguna afirmación de probabilidad sobre su valor...

• Un nivel de confianza del 95% no significa que el 95% de los datos de la muestra se encuentren dentro del intervalo de confianza.
• Un nivel de confianza del 95% no significa que exista una probabilidad del 95% de que la estimación del parámetro a partir de una repetición del experimento caiga dentro del intervalo de confianza calculado a partir de un experimento dado. ^[25]

Welch ^[29] presentó un ejemplo que muestra claramente la diferencia entre la teoría de los intervalos de confianza y otras teorías de estimación de intervalos (incluidos los intervalos fiduciales de Fisher y los intervalos bayesianos objetivos ). Robinson ^[30] llamó a este ejemplo "posiblemente el contraejemplo más conocido de la versión de Neyman de la teoría de los intervalos de confianza". Para Welch, mostraba la superioridad de la teoría de los intervalos de confianza; para los críticos de la teoría, muestra una deficiencia. Aquí presentamos una versión simplificada.

Supongamos que son observaciones independientes de una distribución uniforme . Entonces, el procedimiento óptimo con un 50 % de confianza para es ^[31]$Estilo de visualización X_{1}, X_{2}}$ ${\displaystyle (\theta -1/2,\theta +1/2)}$${\estilo de visualización \theta}$

${\displaystyle {\bar {X}}\pm {\begin{cases}{\dfrac {|X_{1}-X_{2}|}{2}}&{\text{if }}|X_{1}-X_{2}|<1/2\\[8pt]{\dfrac {1-|X_{1}-X_{2}|}{2}}&{\text{if }}|X_{1}-X_{2}|\geq 1/2.\end{cases}}}$

Se puede utilizar un argumento bayesiano fiducial u objetivo para derivar la estimación del intervalo

${\displaystyle {\bar {X}}\pm {\frac {1-|X_{1}-X_{2}|}{4}},}$

que también es un procedimiento de confianza del 50%. Welch demostró que el primer procedimiento de confianza domina al segundo, según los desiderata de la teoría del intervalo de confianza; para cada , la probabilidad de que el primer procedimiento contenga es menor o igual que la probabilidad de que el segundo procedimiento contenga . El ancho promedio de los intervalos del primer procedimiento es menor que el del segundo. Por lo tanto, el primer procedimiento es el preferido según la teoría clásica del intervalo de confianza.${\displaystyle \theta _{1}\neq \theta }$${\displaystyle \theta _{1}}$${\displaystyle \theta _{1}}$

Sin embargo, cuando , se garantiza que los intervalos del primer procedimiento contienen el valor verdadero : Por lo tanto, el coeficiente de confianza nominal del 50% no está relacionado con la incertidumbre que deberíamos tener de que un intervalo específico contenga el valor verdadero. El segundo procedimiento no tiene esta propiedad.${\displaystyle |X_{1}-X_{2}|\geq 1/2}$${\displaystyle \theta }$

Además, cuando el primer procedimiento genera un intervalo muy corto, esto indica que están muy próximos entre sí y, por lo tanto, solo ofrecen la información en un único punto de datos. Sin embargo, el primer intervalo excluirá casi todos los valores razonables del parámetro debido a su ancho reducido. El segundo procedimiento no tiene esta propiedad.${\displaystyle X_{1},X_{2}}$

Las dos propiedades contraintuitivas del primer procedimiento ( cobertura del 100 % cuando están muy separados y cobertura de casi el 0 % cuando están muy juntos) se equilibran para dar como resultado una cobertura del 50 % en promedio. Sin embargo, a pesar de que el primer procedimiento es óptimo, sus intervalos no ofrecen una evaluación de la precisión de la estimación ni una evaluación de la incertidumbre que uno debería tener de que el intervalo contenga el valor verdadero.${\displaystyle X_{1},X_{2}}$${\displaystyle X_{1},X_{2}}$

Este ejemplo se utiliza para argumentar en contra de las interpretaciones ingenuas de los intervalos de confianza. Si se afirma que un procedimiento de confianza tiene propiedades que van más allá de las de la cobertura nominal (como la relación con la precisión o una relación con la inferencia bayesiana), esas propiedades deben demostrarse; no se deducen del hecho de que un procedimiento sea un procedimiento de confianza.

Steiger ^[32] sugirió una serie de procedimientos de confianza para medidas de tamaño de efecto comunes en ANOVA . Morey et al. ^[27] señalan que varios de estos procedimientos de confianza, incluido el de ω ² , tienen la propiedad de que a medida que la estadística F se vuelve cada vez más pequeña (lo que indica un desajuste con todos los valores posibles de ω ^{2 )} , el intervalo de confianza se contrae e incluso puede contener solo el valor único ω ²  = 0; es decir, el IC es infinitesimalmente estrecho (esto ocurre cuando se trata de un IC).${\displaystyle p\geq 1-\alpha /2}$${\displaystyle 100(1-\alpha )\%}$

Este comportamiento es consistente con la relación entre el procedimiento de confianza y la prueba de significancia : como F se vuelve tan pequeño que las medias del grupo están mucho más cerca unas de otras de lo que esperaríamos por casualidad, una prueba de significancia podría indicar rechazo para la mayoría o todos los valores de ω ² . Por lo tanto, el intervalo será muy estrecho o incluso vacío (o, por una convención sugerida por Steiger, conteniendo solo 0). Sin embargo, esto no indica que la estimación de ω ² sea muy precisa. En cierto sentido, indica lo contrario: que la confiabilidad de los resultados mismos puede estar en duda. Esto es contrario a la interpretación común de los intervalos de confianza de que revelan la precisión de la estimación.

• Límites superiores de CL (física de partículas)
• Regla 68-95-99,7
• Banda de confianza , una estimación de intervalo para una curva
• Distribución de confianza
• Región de confianza , una generalización de dimensión superior
• Creencia (estadística)  : medida de la fuerza de la creencia utilizada en las estadísticas.Pages displaying wikidata descriptions as a fallback
• Intervalo creíble , una alternativa bayesiana para la estimación de intervalos
• Intervalo de confianza no paramétrico basado en funciones de distribución acumulativa  : clase de intervalos de confianza en torno a las funciones estadísticas de una distribución
• Barra de error  : Representaciones gráficas de la variabilidad de los datos
• Estadísticas de estimación  : enfoque de análisis de datos en estadísticas frecuentistas
• Margen de error , la mitad del ancho del CI
• Valor p  : función de los resultados de la muestra observada
• Intervalo de predicción , una estimación de intervalo para una variable aleatoria
• Error probable
• Intervalos de confianza robustos  : indicadores estadísticos de la desviación de una muestraPages displaying short descriptions of redirect targets

• Intervalo de confianza para la distribución binomial
• Intervalo de confianza para el exponente de la distribución de la ley de potencia
• Intervalo de confianza para la media de la distribución exponencial
• Intervalo de confianza para la media de la distribución de Poisson
• Intervalos de confianza para la media y la varianza de la distribución normal
• Intervalo de confianza para la respuesta prevista en regresión lineal simple

Wikimedia Commons tiene medios relacionados con Intervalo de confianza .

• El software exploratorio para intervalos de confianza es un tutorial de programas que se ejecutan en Excel
• Calculadoras de intervalos de confianza para R-cuadrados, coeficientes de regresión e intersecciones de regresión
• Weisstein, Eric W. "Intervalo de confianza". MathWorld .
• CAUSEweb.org Muchos recursos para la enseñanza de estadística, incluidos los intervalos de confianza.
• Una introducción interactiva a los intervalos de confianza
• Intervalos de confianza: nivel de confianza, tamaño de la muestra y margen de error por Eric Schulz, Wolfram Demonstrations Project .
• Intervalos de confianza en salud pública Archivado el 9 de agosto de 2016 en Wayback Machine . Descripción sencilla con ejemplos y qué hacer con muestras de tamaño pequeño o tasas cercanas a 0.