Espacio-tiempo

Parte de una serie sobre
Espacio-tiempo
Relatividad especial Relatividad general
Conceptos del espacio-tiempo Variedad espacio-temporal Principio de equivalencia Transformaciones de Lorentz Espacio Minkowski
Relatividad general Introducción a la relatividad general Matemáticas de la relatividad general Ecuaciones de campo de Einstein
Gravedad clásica Introducción a la gravitación Ley de gravitación universal de Newton
Matemáticas relevantes Cuatro vectores Derivaciones de la relatividad Diagramas del espacio-tiempo Geometría diferencial Espacio curvo Espacio-tiempo curvado Matemáticas de la relatividad general Topología del espacio-tiempo
Portal de física  Categoría
en a mi

En física , el espacio-tiempo , también llamado continuo espacio-tiempo , es un modelo matemático que fusiona las tres dimensiones del espacio y la única dimensión del tiempo en un único continuo de cuatro dimensiones . Los diagramas de espacio-tiempo son útiles para visualizar y comprender los efectos relativistas , como la forma en que los diferentes observadores perciben dónde y cuándo ocurren los eventos.

Hasta principios del siglo XX, se suponía que la geometría tridimensional del universo (su descripción en términos de ubicaciones, formas, distancias y direcciones) era distinta del tiempo (la medición de cuándo ocurren los eventos dentro del universo). Sin embargo, el espacio y el tiempo adquirieron nuevos significados con la transformación de Lorentz y la teoría especial de la relatividad .

En 1908, Hermann Minkowski presentó una interpretación geométrica de la relatividad especial que fusionaba el tiempo y las tres dimensiones espaciales del espacio en un único continuo de cuatro dimensiones, conocido hoy como espacio de Minkowski . Esta interpretación resultó vital para la teoría general de la relatividad , según la cual el espacio-tiempo está curvado por la masa y la energía .

La mecánica clásica no relativista trata el tiempo como una cantidad universal de medida que es uniforme en todo su alcance, está separada del espacio y es aceptada por todos los observadores. La mecánica clásica supone que el tiempo tiene una velocidad constante de paso, independiente del estado de movimiento del observador o de cualquier elemento externo. ^[1] Supone que el espacio es euclidiano : supone que el espacio sigue la geometría del sentido común. ^[2]

En el contexto de la relatividad especial , el tiempo no puede separarse de las tres dimensiones del espacio, porque la velocidad observada a la que pasa el tiempo para un objeto depende de la velocidad del objeto en relación con el observador. ^{[3] : 214–217} La relatividad general proporciona una explicación de cómo los campos gravitacionales pueden ralentizar el paso del tiempo de un objeto visto por un observador fuera del campo.

En el espacio ordinario, una posición se especifica mediante tres números, conocidos como dimensiones . En el sistema de coordenadas cartesianas , a menudo se denominan x , y y z . Un punto en el espacio-tiempo se denomina evento y requiere que se especifiquen cuatro números: la ubicación tridimensional en el espacio, más la posición en el tiempo (Fig. 1). Un evento se representa mediante un conjunto de coordenadas x , y , z y t . ^[4] El espacio-tiempo es, por tanto, cuatridimensional .

A diferencia de las analogías utilizadas en los escritos populares para explicar eventos, como los petardos o las chispas, los eventos matemáticos tienen duración cero y representan un único punto en el espacio-tiempo. ^[5] Aunque es posible estar en movimiento en relación con el estallido de un petardo o una chispa, no es posible que un observador esté en movimiento en relación con un evento.

La trayectoria de una partícula a través del espacio-tiempo puede considerarse una secuencia de eventos. La serie de eventos puede vincularse entre sí para formar una curva que representa el progreso de la partícula a través del espacio-tiempo. Esa trayectoria se denomina línea del universo de la partícula . ^{[6] : 105}

Matemáticamente, el espacio-tiempo es una variedad , es decir, parece localmente "plana" cerca de cada punto de la misma manera que, a escalas suficientemente pequeñas, la superficie de un globo parece ser plana. ^[7] Un factor de escala (convencionalmente llamado velocidad de la luz ) relaciona las distancias medidas en el espacio con las distancias medidas en el tiempo. La magnitud de este factor de escala (casi 300.000 kilómetros o 190.000 millas en el espacio son equivalentes a un segundo en el tiempo), junto con el hecho de que el espacio-tiempo es una variedad, implica que a velocidades ordinarias, no relativistas y a distancias ordinarias, a escala humana, hay poco que los humanos puedan observar que sea notablemente diferente de lo que podrían observar si el mundo fuera euclidiano. Fue recién con el advenimiento de mediciones científicas sensibles a mediados del siglo XIX, como el experimento de Fizeau y el experimento de Michelson-Morley , que comenzaron a notarse discrepancias desconcertantes entre las observaciones y las predicciones basadas en el supuesto implícito del espacio euclidiano. ^[8]${\displaystyle c}$

En la relatividad especial, un observador se refiere, en la mayoría de los casos, a un marco de referencia desde el cual se mide un conjunto de objetos o eventos. Este uso difiere significativamente del significado común del término en inglés. Los marcos de referencia son construcciones inherentemente no locales y, según este uso del término, no tiene sentido hablar de un observador como si tuviera una ubicación. ^[9]

En la figura 1-1, imaginemos que el marco en cuestión está equipado con una densa red de relojes, sincronizados dentro de este marco de referencia, que se extiende indefinidamente a lo largo de las tres dimensiones del espacio. Cualquier ubicación específica dentro de la red no es importante. La red de relojes se utiliza para determinar el tiempo y la posición de los eventos que tienen lugar dentro de todo el marco. El término observador se refiere a todo el conjunto de relojes asociados con un marco de referencia inercial. ^{[9] : 17–22}

En este caso idealizado, cada punto del espacio tiene un reloj asociado y, por lo tanto, los relojes registran cada evento instantáneamente, sin demora temporal entre un evento y su registro. Un observador real verá una demora entre la emisión de una señal y su detección debido a la velocidad de la luz. Para sincronizar los relojes, en la reducción de datos posterior a un experimento, se corregirá la hora en la que se recibe una señal para reflejar su hora real si hubiera sido registrada por una red idealizada de relojes. ^{[9] : 17–22}

En muchos libros sobre relatividad especial, especialmente en los más antiguos, la palabra "observador" se utiliza en el sentido más corriente de la palabra. El contexto suele dejar claro qué significado se ha adoptado.

Los físicos distinguen entre lo que se mide u observa , una vez descontados los retrasos en la propagación de la señal, y lo que se ve visualmente sin dichas correcciones. No entender la diferencia entre lo que se mide y lo que se ve es la fuente de mucha confusión entre los estudiantes de relatividad. ^[10]

A mediados del siglo XIX, varios experimentos, como la observación de la mancha de Arago y las mediciones diferenciales de la velocidad de la luz en el aire frente a la del agua, se consideraron que habían demostrado la naturaleza ondulatoria de la luz en oposición a una teoría corpuscular . ^[11] Entonces se asumió que la propagación de ondas requería la existencia de un medio ondulatorio ; en el caso de las ondas de luz, se consideró que este era un hipotético éter luminífero . ^{[nota 1]} Los diversos intentos de establecer las propiedades de este medio hipotético arrojaron resultados contradictorios. Por ejemplo, el experimento de Fizeau de 1851, realizado por el físico francés Hippolyte Fizeau , demostró que la velocidad de la luz en el agua en movimiento era menor que la suma de la velocidad de la luz en el aire más la velocidad del agua en una cantidad dependiente del índice de refracción del agua. ^[12]

Entre otras cuestiones, la dependencia del arrastre parcial del éter implicado por este experimento en el índice de refracción (que depende de la longitud de onda) llevó a la desagradable conclusión de que el éter fluye simultáneamente a diferentes velocidades para diferentes colores de luz. ^[13] El experimento de Michelson-Morley de 1887 (Fig. 1-2) no mostró ninguna influencia diferencial de los movimientos de la Tierra a través del éter hipotético en la velocidad de la luz, y la explicación más probable, el arrastre completo del éter, estaba en conflicto con la observación de la aberración estelar . ^[8]

George Francis FitzGerald en 1889, ^[14] y Hendrik Lorentz en 1892 propusieron de forma independiente que los cuerpos materiales que viajaban a través del éter fijo se veían afectados físicamente por su paso, contrayéndose en la dirección del movimiento en una cantidad que era exactamente la necesaria para explicar los resultados negativos del experimento de Michelson-Morley. No se producen cambios de longitud en direcciones transversales a la dirección del movimiento.

En 1904, Lorentz había ampliado su teoría de tal manera que había llegado a ecuaciones formalmente idénticas a las que Einstein derivaría más tarde, es decir, la transformación de Lorentz . ^[15] Como teoría de la dinámica (el estudio de las fuerzas y los pares y su efecto sobre el movimiento), su teoría suponía deformaciones físicas reales de los componentes físicos de la materia. ^{[16] : 163–174} Las ecuaciones de Lorentz predijeron una cantidad que llamó tiempo local , con la que podía explicar la aberración de la luz , el experimento de Fizeau y otros fenómenos.

Henri Poincaré fue el primero en combinar el espacio y el tiempo en el espacio-tiempo. ^{[17] [18] : 73–80, 93–95} Argumentó en 1898 que la simultaneidad de dos eventos es una cuestión de convención. ^{[19] [nota 2]} En 1900, reconoció que el "tiempo local" de Lorentz es en realidad lo que indican los relojes en movimiento aplicando una definición explícitamente operacional de sincronización de relojes asumiendo una velocidad de la luz constante. ^{[nota 3]} En 1900 y 1904, sugirió la indetectabilidad inherente del éter enfatizando la validez de lo que llamó el principio de relatividad . En 1905/1906 ^[20] perfeccionó matemáticamente la teoría de los electrones de Lorentz para ponerla de acuerdo con el postulado de la relatividad.

Mientras discutía varias hipótesis sobre la gravitación invariante de Lorentz, introdujo el concepto innovador de un espacio-tiempo de cuatro dimensiones al definir varios vectores de cuatro dimensiones , a saber, cuatro posiciones , cuatro velocidades y cuatro fuerzas . ^{[21] [22]} Sin embargo, no persiguió el formalismo de cuatro dimensiones en artículos posteriores, afirmando que esta línea de investigación parecía "implicar un gran dolor para un beneficio limitado", concluyendo finalmente "que el lenguaje tridimensional parece el más adecuado para la descripción de nuestro mundo". ^[22] Incluso en 1909, Poincaré continuó describiendo la interpretación dinámica de la transformada de Lorentz. ^{[16] : 163–174}

En 1905, Albert Einstein analizó la relatividad especial en términos de cinemática (el estudio de los cuerpos en movimiento sin referencia a fuerzas) en lugar de dinámica. Sus resultados eran matemáticamente equivalentes a los de Lorentz y Poincaré. Los obtuvo al reconocer que toda la teoría puede construirse sobre dos postulados: el principio de relatividad y el principio de la constancia de la velocidad de la luz. Su trabajo estaba lleno de vívidas imágenes que involucraban el intercambio de señales de luz entre relojes en movimiento, mediciones cuidadosas de las longitudes de varillas en movimiento y otros ejemplos similares. ^{[23] [nota 4]}

En 1905, Einstein superó los intentos previos de una relación electromagnética masa -energía al introducir la equivalencia general de masa y energía , que fue fundamental para su posterior formulación del principio de equivalencia en 1907, que declara la equivalencia de la masa inercial y gravitacional. Al utilizar la equivalencia masa-energía, Einstein demostró que la masa gravitacional de un cuerpo es proporcional a su contenido de energía, lo que fue uno de los primeros resultados en el desarrollo de la relatividad general . Si bien parecería que al principio no pensó geométricamente sobre el espacio-tiempo, ^{[3] : 219} en el desarrollo posterior de la relatividad general, Einstein incorporó plenamente el formalismo del espacio-tiempo.

Cuando Einstein publicó en 1905, otro de sus competidores, su antiguo profesor de matemáticas Hermann Minkowski , también había llegado a la mayoría de los elementos básicos de la relatividad especial. Max Born relató una reunión que había concertado con Minkowski, con la intención de ser su alumno/colaborador: ^[25]

Fui a Colonia, conocí a Minkowski y escuché su célebre conferencia «Espacio y tiempo», pronunciada el 2 de septiembre de 1908. [...] Más tarde me dijo que le causó un gran impacto cuando Einstein publicó su artículo en el que se afirmaba la equivalencia de los diferentes tiempos locales de los observadores que se movían unos con respecto a otros; pues había llegado a las mismas conclusiones de forma independiente, pero no las publicó porque deseaba primero elaborar la estructura matemática en todo su esplendor. Nunca reivindicó la prioridad y siempre concedió a Einstein su parte plena en el gran descubrimiento.

Minkowski se había interesado por el estado de la electrodinámica después de los experimentos disruptivos de Michelson al menos desde el verano de 1905, cuando Minkowski y David Hilbert dirigieron un seminario avanzado al que asistieron físicos notables de la época para estudiar los artículos de Lorentz, Poincaré y otros. Minkowski vio el trabajo de Einstein como una extensión del de Lorentz, y fue influenciado más directamente por Poincaré. ^[26]

El 5 de noviembre de 1907 (poco más de un año antes de su muerte), Minkowski presentó su interpretación geométrica del espacio-tiempo en una conferencia ante la Sociedad Matemática de Göttingen con el título El principio de relatividad ( Das Relativitätsprinzip ). ^{[nota 5]} El 21 de septiembre de 1908, Minkowski presentó su charla Espacio y tiempo ( Raum und Zeit ), ^[27] ante la Sociedad Alemana de Científicos y Médicos. Las palabras iniciales de Espacio y tiempo incluyen la declaración de Minkowski de que "de ahora en adelante, el espacio para sí mismo y el tiempo para sí mismo se reducirán completamente a una mera sombra, y solo algún tipo de unión de los dos preservará la independencia". Espacio y tiempo incluyó la primera presentación pública de diagramas de espacio-tiempo (Fig. 1-4), e incluyó una notable demostración de que el concepto de intervalo invariante (discutido más adelante), junto con la observación empírica de que la velocidad de la luz es finita, permite la derivación de la totalidad de la relatividad especial. ^{[nota 6]}

El concepto de espacio-tiempo y el grupo de Lorentz están estrechamente relacionados con ciertos tipos de geometrías esféricas , hiperbólicas o conformes y sus grupos de transformación ya desarrollados en el siglo XIX, en los que se utilizan intervalos invariantes análogos al intervalo espacio-tiempo . ^{[nota 7]}

Einstein, por su parte, inicialmente desestimó la interpretación geométrica de Minkowski de la relatividad especial, considerándola überflüssige Gelehrsamkeit (erudición superflua). Sin embargo, para completar su búsqueda de la relatividad general que comenzó en 1907, la interpretación geométrica de la relatividad resultó vital. En 1916, Einstein reconoció plenamente su deuda con Minkowski, cuya interpretación facilitó enormemente la transición a la relatividad general. ^{[16] : 151–152} Dado que existen otros tipos de espacio-tiempo, como el espacio-tiempo curvo de la relatividad general, el espacio-tiempo de la relatividad especial se conoce hoy como espacio-tiempo de Minkowski.

En tres dimensiones, la distancia entre dos puntos se puede definir utilizando el teorema de Pitágoras :${\displaystyle \Delta {d}}$

${\displaystyle (\Delta {d})^{2}=(\Delta {x})^{2}+(\Delta {y})^{2}+(\Delta {z})^{2}}$

Aunque dos observadores pueden medir la posición x , y y z de los dos puntos utilizando diferentes sistemas de coordenadas, la distancia entre los puntos será la misma para ambos, suponiendo que estén midiendo utilizando las mismas unidades. La distancia es "invariante".

Sin embargo, en la relatividad especial, la distancia entre dos puntos ya no es la misma si la miden dos observadores diferentes, cuando uno de ellos se mueve, debido a la contracción de Lorentz . La situación es aún más complicada si los dos puntos están separados tanto en el tiempo como en el espacio. Por ejemplo, si un observador ve que dos eventos ocurren en el mismo lugar, pero en diferentes momentos, una persona que se mueve con respecto al primer observador verá que los dos eventos ocurren en lugares diferentes, porque el punto de vista en movimiento se ve a sí mismo como estacionario, y la posición del evento como alejándose o acercándose. Por lo tanto, se debe utilizar una medida diferente para medir la "distancia" efectiva entre dos eventos. ^{[31] : 48–50, 100–102}

En el espacio-tiempo de cuatro dimensiones, el análogo de la distancia es el intervalo. Aunque el tiempo entra como una cuarta dimensión, se trata de manera diferente a las dimensiones espaciales. Por lo tanto, el espacio de Minkowski difiere en aspectos importantes del espacio euclidiano de cuatro dimensiones . La razón fundamental para fusionar el espacio y el tiempo en el espacio-tiempo es que el espacio y el tiempo no son invariantes por separado, lo que quiere decir que, en las condiciones adecuadas, diferentes observadores no estarán de acuerdo sobre la duración del tiempo entre dos eventos (debido a la dilatación del tiempo ) o la distancia entre los dos eventos (debido a la contracción de la longitud ). La relatividad especial proporciona un nuevo invariante, llamado intervalo espacio-temporal , que combina distancias en el espacio y en el tiempo. Todos los observadores que midan el tiempo y la distancia entre dos eventos cualesquiera terminarán calculando el mismo intervalo espacio-temporal. Supongamos que un observador mide dos eventos separados en el tiempo por y una distancia espacial . Entonces, el intervalo espacio-temporal al cuadrado entre los dos eventos que están separados por una distancia en el espacio y por en la coordenada es: ^[32]${\displaystyle \Delta t}$${\displaystyle \Delta x.}$${\displaystyle (\Delta {s})^{2}}$${\displaystyle \Delta {x}}$${\displaystyle \Delta {ct}=c\Delta t}$${\displaystyle ct}$

${\displaystyle (\Delta s)^{2}=(\Delta ct)^{2}-(\Delta x)^{2},}$

o para tres dimensiones espaciales,

${\displaystyle (\Delta s)^{2}=(\Delta ct)^{2}-(\Delta x)^{2}-(\Delta y)^{2}-(\Delta z)^{2}.}$

La constante de la velocidad de la luz convierte las unidades de tiempo (como los segundos) en unidades de espacio (como los metros). El intervalo al cuadrado es una medida de separación entre los eventos A y B que están separados en el tiempo y además separados en el espacio, ya sea porque hay dos objetos separados que experimentan eventos o porque un solo objeto en el espacio se mueve inercialmente entre sus eventos. El intervalo de separación es la diferencia entre el cuadrado de la distancia espacial que separa el evento B del evento A y el cuadrado de la distancia espacial recorrida por una señal de luz en ese mismo intervalo de tiempo . Si la separación de eventos se debe a una señal de luz, entonces esta diferencia se desvanece y .${\displaystyle c,}$${\displaystyle t}$${\displaystyle \Delta s^{2}}$${\displaystyle \Delta t}$${\displaystyle \Delta s=0}$

Cuando los eventos considerados son infinitesimalmente cercanos entre sí, entonces podemos escribir

${\displaystyle ds^{2}=c^{2}dt^{2}-dx^{2}-dy^{2}-dz^{2}.}$

En un marco inercial diferente, digamos con coordenadas , el intervalo espacio-temporal se puede escribir en la misma forma que arriba. Debido a la constancia de la velocidad de la luz, los eventos de luz en todos los marcos inerciales pertenecen al intervalo cero, . Para cualquier otro evento infinitesimal donde , se puede probar que lo que a su vez al integrar conduce a . ^{[33] : 2} La invariancia del intervalo espacio-temporal entre los mismos eventos para todos los marcos de referencia inerciales es uno de los resultados fundamentales de la teoría especial de la relatividad.${\displaystyle (t',x',y',z')}$${\displaystyle ds'}$${\displaystyle ds=ds'=0}$${\displaystyle ds\neq 0}$${\displaystyle ds^{2}=ds'^{2}}$${\displaystyle s=s'}$

Aunque por brevedad, con frecuencia se ven expresiones de intervalo expresadas sin deltas, incluso en la mayor parte de la discusión siguiente, debe entenderse que, en general, significa , etc. Siempre nos preocupan las diferencias de valores de coordenadas espaciales o temporales que pertenecen a dos eventos y, dado que no hay un origen preferido, los valores de coordenadas individuales no tienen un significado esencial.${\displaystyle x}$${\displaystyle \Delta {x}}$

La ecuación anterior es similar al teorema de Pitágoras, excepto que tiene un signo menos entre los términos y . El intervalo del espacio-tiempo es la cantidad, no en sí misma. La razón es que, a diferencia de las distancias en la geometría euclidiana, los intervalos en el espacio-tiempo de Minkowski pueden ser negativos. En lugar de tratar con raíces cuadradas de números negativos, los físicos suelen considerarlo como un símbolo distinto en sí mismo, en lugar del cuadrado de algo. ^{[3] : 217}${\displaystyle (ct)^{2}}$${\displaystyle x^{2}}$${\displaystyle s^{2},}$${\displaystyle s}$${\displaystyle s^{2}}$

Nota: Hay dos convenciones de signos en uso en la literatura sobre relatividad:

${\displaystyle s^{2}=(ct)^{2}-x^{2}-y^{2}-z^{2}}$

y

${\displaystyle s^{2}=-(ct)^{2}+x^{2}+y^{2}+z^{2}}$

Estas convenciones de signos están asociadas con las signaturas métricas (+−−−) y (−+++). Una variación menor es colocar la coordenada de tiempo al final en lugar de al principio. Ambas convenciones se utilizan ampliamente en el campo de estudio. ^[34]

En la siguiente discusión, utilizamos la primera convención.

En general, puede asumir cualquier valor de número real. Si es positivo, el intervalo de espacio-tiempo se denomina similar al tiempo . Dado que la distancia espacial recorrida por cualquier objeto masivo es siempre menor que la distancia recorrida por la luz durante el mismo intervalo de tiempo, los intervalos positivos son siempre similares al tiempo. Si es negativo, se dice que el intervalo de espacio-tiempo es similar al espacio . Los intervalos de espacio-tiempo son iguales a cero cuando En otras palabras, el intervalo de espacio-tiempo entre dos eventos en la línea del universo de algo que se mueve a la velocidad de la luz es cero. Tal intervalo se denomina similar a la luz o nulo . Un fotón que llega a nuestro ojo desde una estrella distante no habrá envejecido, a pesar de haber pasado (desde nuestra perspectiva) años en su paso. ^{[31] : 48–50}${\displaystyle s^{2}}$${\displaystyle s^{2}}$${\displaystyle s^{2}}$${\displaystyle x=\pm ct.}$

Un diagrama de espacio-tiempo se dibuja típicamente con un solo espacio y una sola coordenada de tiempo. La Fig. 2-1 presenta un diagrama de espacio-tiempo que ilustra las líneas del mundo (es decir, las trayectorias en el espacio-tiempo) de dos fotones, A y B, que se originan del mismo evento y van en direcciones opuestas. Además, C ilustra la línea del mundo de un objeto más lento que la velocidad de la luz. La coordenada de tiempo vertical está escalada de modo que tenga las mismas unidades (metros) que la coordenada espacial horizontal. Dado que los fotones viajan a la velocidad de la luz, sus líneas del mundo tienen una pendiente de ±1. ^{[31] : 23–25} En otras palabras, cada metro que un fotón viaja hacia la izquierda o la derecha requiere aproximadamente 3,3 nanosegundos de tiempo.${\displaystyle c}$

This section needs additional citations for verification. Please help improve this article by adding citations to reliable sources in this section. Unsourced material may be challenged and removed. (March 2024) (Learn how and when to remove this message)

Para comprender mejor cómo se comparan entre sí las coordenadas del espacio-tiempo medidas por observadores en diferentes marcos de referencia , es útil trabajar con una configuración simplificada con marcos en una configuración estándar. Con cuidado, esto permite simplificar las matemáticas sin perder generalidad en las conclusiones a las que se llega. En la figura 2-2, se muestran dos marcos de referencia galileanos (es decir, marcos convencionales de 3 espacios) en movimiento relativo. El marco S pertenece a un primer observador O, y el marco S′ (pronunciado "S prima") pertenece a un segundo observador O′.

• Los ejes x , y , z del marco S están orientados paralelos a los respectivos ejes primos del marco S′.
• El marco S′ se mueve en la dirección x del marco S con una velocidad constante v medida en el marco S.
• Los orígenes de los marcos S y S′ son coincidentes cuando el tiempo t = 0 para el marco S y t ′ = 0 para el marco S′. ^{[6] : 107}

La figura 2-3a vuelve a dibujar la figura 2-2 con una orientación diferente. La figura 2-3b ilustra un diagrama de espacio-tiempo relativista desde el punto de vista del observador O. Puesto que S y S′ están en configuración estándar, sus orígenes coinciden en los tiempos t  = 0 en el sistema de referencia S y t ′ = 0 en el sistema de referencia S′. El eje ct ′ pasa por los eventos en el sistema de referencia S′ que tienen x ′ = 0. Pero los puntos con x ′ = 0 se mueven en la dirección x del sistema de referencia S con velocidad v , de modo que no coinciden con el eje ct en ningún tiempo distinto de cero. Por lo tanto, el eje ct ′ está inclinado con respecto al eje ct en un ángulo θ dado por ^{[31] : 23–31}

${\displaystyle \tan(\theta )=v/c.}$

El eje x ′ también está inclinado con respecto al eje x . Para determinar el ángulo de esta inclinación, recordamos que la pendiente de la línea del universo de un pulso de luz es siempre ±1. La figura 2-3c presenta un diagrama de espacio-tiempo desde el punto de vista del observador O′. El evento P representa la emisión de un pulso de luz en x ′ = 0, ct ′ = − a . El pulso se refleja desde un espejo situado a una distancia a de la fuente de luz (evento Q), y regresa a la fuente de luz en x ′ = 0,  ct ′ =  a (evento R).

Los mismos eventos P, Q, R se representan en la Fig. 2-3b en el marco del observador O. Las trayectorias de la luz tienen pendientes = 1 y −1, de modo que △PQR forma un triángulo rectángulo con PQ y QR ambos a 45 grados respecto de los ejes x y ct . Como OP = OQ = OR, el ángulo entre x ′ y x también debe ser θ . ^{[6] : 113–118}

Mientras que el marco en reposo tiene ejes de espacio y tiempo que se encuentran en ángulos rectos, el marco en movimiento está dibujado con ejes que se encuentran en un ángulo agudo. Los marcos son en realidad equivalentes. ^{[31] : 23–31} La asimetría se debe a distorsiones inevitables en cómo las coordenadas del espacio-tiempo pueden mapearse en un plano cartesiano , y no debe considerarse más extraña que la manera en que, en una proyección Mercator de la Tierra, los tamaños relativos de las masas de tierra cerca de los polos (Groenlandia y la Antártida) son altamente exagerados en relación con las masas de tierra cerca del Ecuador.

En la figura 2-4, el evento O está en el origen de un diagrama de espacio-tiempo, y las dos líneas diagonales representan todos los eventos que tienen un intervalo de espacio-tiempo cero con respecto al evento de origen. Estas dos líneas forman lo que se llama el cono de luz del evento O, ya que al agregar una segunda dimensión espacial (figura 2-5) se crea la apariencia de dos conos circulares rectos que se encuentran con sus vértices en O. Un cono se extiende hacia el futuro (t>0), el otro hacia el pasado (t<0).

Un cono de luz (doble) divide el espacio-tiempo en regiones separadas con respecto a su vértice. El interior del cono de luz futuro consta de todos los eventos que están separados del vértice por más tiempo (distancia temporal) del necesario para cruzar su distancia espacial a la velocidad de la luz; estos eventos comprenden el futuro temporal del evento O. Del mismo modo, el pasado temporal comprende los eventos interiores del cono de luz pasado. Por lo tanto, en intervalos temporales Δ ct es mayor que Δ x , lo que hace que los intervalos temporales sean positivos. ^{[3] : 220}

La región exterior al cono de luz consiste en eventos que están separados del evento O por más espacio del que se puede cruzar a la velocidad de la luz en el tiempo dado . Estos eventos comprenden la llamada región espacial del evento O, denotada como "En otro lugar" en la Fig. 2-4. Se dice que los eventos en el propio cono de luz son similares a la luz (o separados nulamente ) de O. Debido a la invariancia del intervalo espacio-temporal, todos los observadores asignarán el mismo cono de luz a cualquier evento dado y, por lo tanto, estarán de acuerdo con esta división del espacio-tiempo. ^{[3] : 220}

El cono de luz tiene un papel esencial dentro del concepto de causalidad . Es posible que una señal que no viaja más rápido que la velocidad de la luz viaje desde la posición y el tiempo de O a la posición y el tiempo de D (Fig. 2-4). Por lo tanto, es posible que el evento O tenga una influencia causal en el evento D. El cono de luz futuro contiene todos los eventos que podrían ser influenciados causalmente por O. Del mismo modo, es posible que una señal que no viaja más rápido que la velocidad de la luz viaje desde la posición y el tiempo de A, a la posición y el tiempo de O. El cono de luz pasado contiene todos los eventos que podrían tener una influencia causal en O. En contraste, suponiendo que las señales no pueden viajar más rápido que la velocidad de la luz, cualquier evento, como por ejemplo B o C, en la región espacial (Elsewhere), no puede afectar al evento O, ni puede ser afectado por el evento O que emplee dicha señalización. Bajo este supuesto, se excluye cualquier relación causal entre el evento O y cualquier evento en la región espacial de un cono de luz. ^[35]

Todos los observadores estarán de acuerdo en que, para cualquier evento dado, un evento dentro del cono de luz futuro del evento dado ocurre después del evento dado. De la misma manera, para cualquier evento dado, un evento dentro del cono de luz pasado del evento dado ocurre antes del evento dado. La relación antes-después observada para eventos separados en el tiempo permanece invariable sin importar cuál sea el marco de referencia del observador, es decir, sin importar cómo se esté moviendo el observador. La situación es bastante diferente para eventos separados en el espacio. La figura 2-4 se dibujó a partir del marco de referencia de un observador que se mueve en v = 0. A partir de este marco de referencia, se observa que el evento C ocurre después del evento O, y se observa que el evento B ocurre antes del evento O. ^[36]

Desde un marco de referencia diferente, el orden de estos eventos no relacionados causalmente puede invertirse. En particular, se observa que si dos eventos son simultáneos en un marco de referencia particular, están necesariamente separados por un intervalo espacial y, por lo tanto, están relacionados de manera no causal. La observación de que la simultaneidad no es absoluta, sino que depende del marco de referencia del observador, se denomina relatividad de la simultaneidad . ^[36]

La figura 2-6 ilustra el uso de diagramas de espacio-tiempo en el análisis de la relatividad de la simultaneidad. Los eventos en el espacio-tiempo son invariantes, pero los marcos de coordenadas se transforman como se discutió anteriormente para la figura 2-3. Los tres eventos (A, B, C) son simultáneos desde el marco de referencia de un observador que se mueve en v = 0. Desde el marco de referencia de un observador que se mueve en v = 0.3 c , los eventos parecen ocurrir en el orden C, B, A. Desde el marco de referencia de un observador que se mueve en v = −0.5 c , los eventos parecen ocurrir en el orden A, B, C . La línea blanca representa un plano de simultaneidad que se mueve desde el pasado del observador al futuro del observador, resaltando los eventos que residen en él. El área gris es el cono de luz del observador, que permanece invariante.

Un intervalo de espacio-tiempo similar al espacio da la misma distancia que un observador mediría si los eventos que se están midiendo fueran simultáneos para el observador. Un intervalo de espacio-tiempo similar al espacio proporciona, por lo tanto, una medida de la distancia propia , es decir, la distancia verdadera = Del mismo modo, un intervalo de espacio-tiempo similar al tiempo da la misma medida del tiempo que se presentaría por el tictac acumulativo de un reloj que se mueve a lo largo de una línea de universo dada. Un intervalo de espacio-tiempo similar al tiempo proporciona, por lo tanto, una medida del tiempo propio = ^{[3] : 220–221}${\displaystyle {\sqrt {-s^{2}}}.}$${\displaystyle {\sqrt {s^{2}}}.}$

This section needs additional citations for verification. Please help improve this article by adding citations to reliable sources in this section. Unsourced material may be challenged and removed. (March 2024) (Learn how and when to remove this message)

En el espacio euclidiano (que tiene solo dimensiones espaciales), el conjunto de puntos equidistantes (usando la métrica euclidiana) de algún punto forman un círculo (en dos dimensiones) o una esfera (en tres dimensiones). En el espacio-tiempo de Minkowski (1+1)-dimensional (que tiene una dimensión temporal y una espacial), los puntos a un intervalo de espacio-tiempo constante desde el origen (usando la métrica de Minkowski) forman curvas dadas por las dos ecuaciones

${\displaystyle (ct)^{2}-x^{2}=\pm s^{2},}$

con alguna constante real positiva. Estas ecuaciones describen dos familias de hipérbolas en un diagrama de espacio-tiempo x – ct , que se denominan hipérbolas invariantes .${\displaystyle s^{2}}$

En la figura 2-7a, cada hipérbola magenta conecta todos los eventos que tienen una separación espacial fija desde el origen, mientras que las hipérbolas verdes conectan eventos con una separación temporal igual.

Las hipérbolas magenta, que cruzan el eje x , son curvas temporales, es decir, representan trayectorias reales que pueden recorrer partículas (constantemente aceleradas) en el espacio-tiempo: Entre dos eventos cualesquiera en una hipérbola es posible una relación de causalidad, porque la inversa de la pendiente (que representa la velocidad necesaria) para todas las secantes es menor que . Por otro lado, las hipérbolas verdes, que cruzan el eje ct , son curvas espaciales porque todos los intervalos a lo largo de estas hipérbolas son intervalos espaciales: No es posible ninguna causalidad entre dos puntos cualesquiera en una de estas hipérbolas, porque todas las secantes representan velocidades mayores que .${\displaystyle c}$${\displaystyle c}$

La figura 2-7b refleja la situación en el espacio-tiempo de Minkowski (1+2)-dimensional (una temporal y dos espaciales) con los hiperboloides correspondientes. Las hipérbolas invariantes desplazadas por intervalos espaciales desde el origen generan hiperboloides de una hoja, mientras que las hipérbolas invariantes desplazadas por intervalos temporales desde el origen generan hiperboloides de dos hojas.

El límite (1+2)-dimensional entre hiperboloides espaciales y temporales, establecido por los eventos que forman un intervalo de espacio-tiempo cero hasta el origen, se forma degenerando los hiperboloides hasta el cono de luz. En (1+1)-dimensionales las hipérbolas degeneran hasta las dos líneas grises de 45° representadas en la Fig. 2-7a.

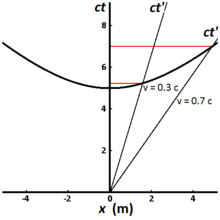
La figura 2-8 ilustra la hipérbola invariante para todos los eventos a los que se puede llegar desde el origen en un tiempo propio de 5 metros (aproximadamente1,67 × 10 ⁻⁸  s ). Diferentes líneas del universo representan relojes que se mueven a diferentes velocidades. Un reloj que está estacionario con respecto al observador tiene una línea del universo que es vertical, y el tiempo transcurrido medido por el observador es el mismo que el tiempo propio. Para un reloj que se mueve a 0,3  c , el tiempo transcurrido medido por el observador es de 5,24 metros (1,75 × 10 ⁻⁸  s ), mientras que para un reloj que viaja a 0,7  c , el tiempo transcurrido medido por el observador es de 7,00 metros (2,34 × 10 ⁻⁸  s ). ^{[3] : 220–221}

Esto ilustra el fenómeno conocido como dilatación del tiempo . Los relojes que viajan más rápido tardan más (en el marco del observador) en marcar la misma cantidad de tiempo propio, y viajan más lejos a lo largo del eje x dentro de ese tiempo propio de lo que lo hubieran hecho sin la dilatación del tiempo. ^{[3] : 220–221} La medición de la dilatación del tiempo por dos observadores en diferentes marcos de referencia inerciales es mutua. Si el observador O mide los relojes del observador O′ como si fueran más lentos en su marco, el observador O′ a su vez medirá los relojes del observador O como si fueran más lentos.

La contracción de la longitud , al igual que la dilatación del tiempo, es una manifestación de la relatividad de la simultaneidad. La medición de la longitud requiere la medición del intervalo espacio-temporal entre dos eventos que son simultáneos en nuestro marco de referencia. Pero los eventos que son simultáneos en un marco de referencia, en general, no lo son en otros marcos de referencia.

La figura 2-9 ilustra los movimientos de una varilla de 1 m que se desplaza a 0,5  c a lo largo del eje x . Los bordes de la banda azul representan las líneas de universo de los dos puntos finales de la varilla. La hipérbola invariante ilustra eventos separados del origen por un intervalo espacial de 1 m. Los puntos finales O y B medidos cuando t ′  = 0 son eventos simultáneos en el marco S′. Pero para un observador en el marco S, los eventos O y B no son simultáneos. Para medir la longitud, el observador en el marco S mide los puntos finales de la varilla tal como se proyectan sobre el eje x a lo largo de sus líneas de universo. La proyección de la lámina de universo de la varilla sobre el eje x produce la longitud escorzada OC. ^{[6] : 125}

(no ilustrado) Trazar una línea vertical a través de A de modo que intersecte el eje x ′ demuestra que, así como OB está acortado desde el punto de vista del observador O, OA también está acortado desde el punto de vista del observador O′. De la misma manera que cada observador mide los relojes del otro como si estuvieran atrasados, cada observador mide las reglas del otro como si estuvieran contraídas.

Con respecto a la contracción mutua de longitud, la figura 2-9 ilustra que los marcos primados y no primados se rotan mutuamente en un ángulo hiperbólico (análogo a los ángulos ordinarios en la geometría euclidiana). ^{[nota 8]} Debido a esta rotación, la proyección de una regla métrica primada sobre el eje x no primado se acorta, mientras que la proyección de una regla métrica no primada sobre el eje x′ primado también se acorta.

La dilatación mutua del tiempo y la contracción de la longitud tienden a parecer a los principiantes como conceptos inherentemente contradictorios. Si un observador en el marco S mide un reloj, en reposo en el marco S', como si funcionara más lento que el suyo, mientras que S' se mueve a una velocidad v en S, entonces el principio de relatividad requiere que un observador en el marco S' mida de la misma manera un reloj en el marco S, que se mueve a una velocidad − v en S', como si funcionara más lento que el suyo. Cómo pueden funcionar dos relojes más lentos que el otro es una pregunta importante que "va al corazón de la comprensión de la relatividad especial". ^{[3] : 198}

Esta aparente contradicción se debe a que no se han tenido en cuenta correctamente las diferentes configuraciones de las mediciones necesarias relacionadas. Estas configuraciones permiten una explicación coherente de la única contradicción aparente . No se trata del tictac abstracto de dos relojes idénticos, sino de cómo medir en un marco la distancia temporal de dos tictacs de un reloj en movimiento. Resulta que para observar mutuamente la duración entre tictacs de relojes, cada uno en movimiento en el marco respectivo, deben intervenir diferentes conjuntos de relojes. Para medir en el marco S la duración del tictac de un reloj en movimiento W′ (en reposo en S′), se utilizan dos relojes adicionales sincronizados W ₁ y W ₂ en reposo en dos puntos arbitrariamente fijos en S con la distancia espacial d .

Dos eventos pueden definirse por la condición "dos relojes están simultáneamente en un lugar", es decir, cuando W′ pasa cada uno por W ₁ y W ₂ . Para ambos eventos se registran las dos lecturas de los relojes colocados. La diferencia de las dos lecturas de W ₁ y W ₂ es la distancia temporal de los dos eventos en S, y su distancia espacial es d . La diferencia de las dos lecturas de W′ es la distancia temporal de los dos eventos en S′. En S′ estos eventos solo están separados en el tiempo, ocurren en el mismo lugar en S′. Debido a la invariancia del intervalo espacio-temporal abarcado por estos dos eventos, y la separación espacial no nula d en S, la distancia temporal en S′ debe ser menor que la de S: la distancia temporal menor entre los dos eventos, resultante de las lecturas del reloj en movimiento W′, pertenece al reloj de funcionamiento más lento W′.

Por el contrario, para juzgar en el marco S′ la distancia temporal de dos eventos en un reloj en movimiento W (en reposo en S), se necesitan dos relojes en reposo en S′.

En esta comparación, el reloj W se mueve con una velocidad de − v . Al registrar nuevamente las cuatro lecturas de los eventos, definidos por "dos relojes simultáneamente en un lugar", se obtienen las distancias temporales análogas de los dos eventos, ahora separados temporal y espacialmente en S′, y solo separados temporalmente pero ubicados en el mismo lugar en S. Para mantener invariable el intervalo espacio-temporal, la distancia temporal en S debe ser menor que en S′, debido a la separación espacial de los eventos en S′: ahora se observa que el reloj W corre más lento.

Los registros necesarios para los dos juicios, con "un reloj en movimiento" y "dos relojes en reposo" en S o S′ respectivamente, implican dos conjuntos diferentes, cada uno con tres relojes. Dado que hay diferentes conjuntos de relojes involucrados en las mediciones, no hay una necesidad inherente de que las mediciones sean recíprocamente "consistentes" de modo que, si un observador mide el reloj en movimiento como lento, el otro observador mide el reloj del primero como rápido. ^{[3] : 198–199}

La figura 2-10 ilustra la discusión previa de la dilatación mutua del tiempo con diagramas de Minkowski. La imagen superior refleja las mediciones como se ven desde el marco S "en reposo" con ejes rectangulares sin primar, y el marco S′ "moviéndose con v  > 0", coordinado por ejes oblicuos con primar, inclinados hacia la derecha; la imagen inferior muestra el marco S′ "en reposo" con coordenadas rectangulares con primar, y el marco S "moviéndose con − v  < 0", con ejes oblicuos sin primar, inclinados hacia la izquierda.

Cada línea trazada paralela a un eje espacial ( x , x ′ ) representa una línea de simultaneidad. Todos los eventos en dicha línea tienen el mismo valor temporal ( ct , ct ′ ). Del mismo modo, cada línea trazada paralela a un eje temporal ( ct , ct′ ) representa una línea de valores de coordenadas espaciales iguales ( x , x ′ ).

En ambas imágenes se puede designar el origen O (= O ′ ) como el evento, donde el respectivo "reloj en movimiento" se coloca junto con el "primer reloj en reposo" en ambas comparaciones. Obviamente, para este evento las lecturas en ambos relojes en ambas comparaciones son cero. Como consecuencia, las líneas de mundo de los relojes en movimiento son el eje ct ′ inclinado hacia la derecha (imágenes superiores, reloj W′) y los ejes ct inclinados hacia la izquierda (imágenes inferiores, reloj W). Las líneas de mundo de W ₁ y W′ ₁ son los ejes de tiempo verticales correspondientes ( ct en las imágenes superiores y ct ′ en las imágenes inferiores).

En la imagen superior, el lugar para W ₂ se toma como A _x > 0 y, por lo tanto, la línea de mundo (no se muestra en las imágenes) de este reloj intersecta la línea de mundo del reloj en movimiento (el eje ct ′) en el evento etiquetado A , donde "dos relojes están simultáneamente en un lugar". En la imagen inferior, el lugar para W′ ₂ se toma como C _{x ′}  < 0 y, por lo tanto, en esta medición, el reloj en movimiento W pasa por W′ ₂ en el evento C .

En la imagen superior, la coordenada ct A _t del evento A (la lectura de W ₂ ) está etiquetada como B , dando así el tiempo transcurrido entre los dos eventos, medidos con W ₁ y W ₂ , como OB . Para una comparación, la longitud del intervalo de tiempo OA , medido con W′, debe transformarse a la escala del eje ct . Esto se hace mediante la hipérbola invariante (ver también la Fig. 2-8) a través de A , conectando todos los eventos con el mismo intervalo de espacio-tiempo desde el origen como A . Esto produce el evento C en el eje ct y, obviamente: OC  <  OB , el reloj "en movimiento" W′ corre más lento.

Para mostrar la dilatación mutua del tiempo inmediatamente en la imagen superior, el evento D puede construirse como el evento en x ′ = 0 (la ubicación del reloj W′ en S′), que es simultáneo a C ( OC tiene el mismo intervalo de espacio-tiempo que OA ) en S′. Esto muestra que el intervalo de tiempo OD es más largo que OA , lo que demuestra que el reloj "en movimiento" corre más lento. ^{[6] : 124}

En la imagen inferior, el sistema S se mueve con velocidad − v en el sistema S′ en reposo. La línea de mundo del reloj W es el eje ct (inclinado hacia la izquierda), la línea de mundo de W′ ₁ es el eje vertical ct ′ y la línea de mundo de W′ ₂ es la vertical que pasa por el evento C , con la coordenada ct ′ D. La hipérbola invariante que pasa por el evento C escala el intervalo de tiempo OC a OA , que es más corto que OD ; además, B se construye (de manera similar a D en las imágenes superiores) como simultáneo a A en S, en x  = 0. El resultado OB  >  OC corresponde nuevamente al anterior.

La palabra "medida" es importante. En física clásica, un observador no puede afectar a un objeto observado, pero el estado de movimiento del objeto puede afectar las observaciones que el observador hace del objeto.

Muchas introducciones a la relatividad especial ilustran las diferencias entre la relatividad galileana y la relatividad especial planteando una serie de "paradojas". Estas paradojas son, de hecho, problemas mal planteados, resultado de nuestra falta de familiaridad con velocidades comparables a la velocidad de la luz. La solución es resolver muchos problemas de la relatividad especial y familiarizarse con sus llamadas predicciones contraintuitivas. El enfoque geométrico para estudiar el espacio-tiempo se considera uno de los mejores métodos para desarrollar una intuición moderna. ^[37]

La paradoja de los gemelos es un experimento mental que involucra a gemelos idénticos, uno de los cuales hace un viaje al espacio en un cohete de alta velocidad, regresa a casa y descubre que el gemelo que permaneció en la Tierra ha envejecido más. Este resultado parece desconcertante porque cada gemelo observa al otro gemelo moverse, y por lo tanto, a primera vista, parecería que cada uno debería encontrar que el otro ha envejecido menos. La paradoja de los gemelos elude la justificación de la dilatación mutua del tiempo presentada anteriormente al evitar el requisito de un tercer reloj. ^{[3] : 207} Sin embargo, la paradoja de los gemelos no es una verdadera paradoja porque se entiende fácilmente dentro del contexto de la relatividad especial.

La impresión de que existe una paradoja surge de una mala interpretación de lo que afirma la relatividad especial. La relatividad especial no declara que todos los marcos de referencia sean equivalentes, sino sólo los marcos inerciales. El marco de la gemela viajera no es inercial durante los períodos en que está acelerando. Además, la diferencia entre las gemelas es detectable observacionalmente: la gemela viajera necesita encender sus cohetes para poder regresar a casa, mientras que la gemela que se queda en casa no. ^{[38] [nota 9]}

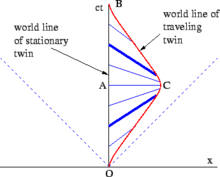
Estas distinciones deberían dar como resultado una diferencia en las edades de los gemelos. El diagrama de espacio-tiempo de la figura 2-11 presenta el caso simple de un gemelo que sale en línea recta a lo largo del eje x y regresa inmediatamente. Desde el punto de vista del gemelo que se queda en casa, no hay nada desconcertante en la paradoja de los gemelos en absoluto. El tiempo propio medido a lo largo de la línea del mundo del gemelo viajero de O a C, más el tiempo propio medido de C a B, es menor que el tiempo propio del gemelo que se queda en casa medido de O a A a B. Las trayectorias más complejas requieren integrar el tiempo propio entre los respectivos eventos a lo largo de la curva (es decir, la integral de trayectoria ) para calcular la cantidad total de tiempo propio experimentado por el gemelo viajero. ^[38]

Surgen complicaciones si se analiza la paradoja de los gemelos desde el punto de vista del gemelo viajero.

De ahora en adelante se utilizará la nomenclatura de Weiss, que designa al gemelo que se queda en casa como Terence y a la gemela que viaja como Stella. ^[38]

Stella no está en un marco inercial. Dado este hecho, a veces se afirma incorrectamente que la resolución completa de la paradoja de los gemelos requiere la relatividad general: ^[38]

Un análisis SR puro sería el siguiente: Analizado en el marco de reposo de Stella, ella está inmóvil durante todo el viaje. Cuando dispara sus cohetes para el cambio de dirección, experimenta una pseudofuerza que se asemeja a una fuerza gravitacional. ^[38] Las figuras 2-6 y 2-11 ilustran el concepto de líneas (planos) de simultaneidad: las líneas paralelas al eje x del observador (plano xy ) representan conjuntos de eventos que son simultáneos en el marco del observador. En la figura 2-11, las líneas azules conectan eventos en la línea del mundo de Terence que, desde el punto de vista de Stella , son simultáneos con eventos en su línea del mundo. (Terence, a su vez, observaría un conjunto de líneas horizontales de simultaneidad). A lo largo de los tramos de ida y vuelta del viaje de Stella, ella mide los relojes de Terence como si fueran más lentos que el suyo. Pero durante el giro (es decir, entre las líneas azules en negrita de la figura), se produce un cambio en el ángulo de sus líneas de simultaneidad, que corresponde a un rápido salto de los acontecimientos en la línea del mundo de Terence que Stella considera simultáneos con el suyo. Por lo tanto, al final de su viaje, Stella descubre que Terence ha envejecido más que ella. ^[38]

Aunque no se requiere la relatividad general para analizar la paradoja de los gemelos, la aplicación del principio de equivalencia de la relatividad general sí proporciona una visión adicional del tema. Stella no está estacionaria en un marco inercial. Analizada en el marco de reposo de Stella, está inmóvil durante todo el viaje. Cuando se desplaza por inercia, su marco de reposo es inercial, y el reloj de Terence parecerá ir más lento. Pero cuando dispara sus cohetes para dar la vuelta, su marco de reposo es un marco acelerado y experimenta una fuerza que la empuja como si estuviera en un campo gravitatorio. Terence parecerá estar muy arriba en ese campo y, debido a la dilatación del tiempo gravitacional , su reloj parecerá ir más rápido, tanto que el resultado neto será que Terence ha envejecido más que Stella cuando vuelvan a estar juntos. ^[38] Los argumentos teóricos que predicen la dilatación del tiempo gravitacional no son exclusivos de la relatividad general. Cualquier teoría de la gravedad predecirá la dilatación del tiempo gravitacional si respeta el principio de equivalencia, incluida la teoría de Newton. ^{[3] : 16}

Esta sección introductoria se ha centrado en el espacio-tiempo de la relatividad especial, ya que es el más fácil de describir. El espacio-tiempo de Minkowski es plano, no tiene en cuenta la gravedad, es uniforme en todas partes y no sirve más que como un fondo estático para los eventos que tienen lugar en él. La presencia de la gravedad complica enormemente la descripción del espacio-tiempo. En la relatividad general, el espacio-tiempo ya no es un fondo estático, sino que interactúa activamente con los sistemas físicos que contiene. El espacio-tiempo se curva en presencia de materia, puede propagar ondas, doblar la luz y exhibe una serie de otros fenómenos. ^{[3] : 221} Algunos de estos fenómenos se describen en las secciones posteriores de este artículo.

Un objetivo básico es poder comparar las mediciones realizadas por observadores en movimiento relativo. Si hay un observador O en el sistema S que ha medido las coordenadas de tiempo y espacio de un evento, asignando a este evento tres coordenadas cartesianas y el tiempo medido en su red de relojes sincronizados ( x , y , z , t ) (ver Fig. 1-1). Un segundo observador O′ en un sistema diferente S′ mide el mismo evento en su sistema de coordenadas y su red de relojes sincronizados ( x ′ , y ′ , z ′ , t ′ ) . Con sistemas inerciales, ninguno de los observadores está bajo aceleración, y un conjunto simple de ecuaciones nos permite relacionar las coordenadas ( x , y , z , t ) con ( x ′ , y ′ , z ′ , t ′ ) . Dado que los dos sistemas de coordenadas están en configuración estándar, es decir, están alineados con coordenadas paralelas ( x , y , z ) y que t = 0 cuando t ′ = 0 , la transformación de coordenadas es la siguiente: ^{[39] [40]}

${\displaystyle x'=x-vt}$

${\displaystyle y'=y}$

${\displaystyle z'=z}$

${\displaystyle t'=t.}$

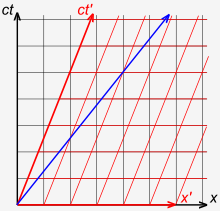
La figura 3-1 ilustra que en la teoría de Newton, el tiempo es universal, no la velocidad de la luz. ^{[41] : 36–37} Considere el siguiente experimento mental: La flecha roja ilustra un tren que se mueve a 0,4 c con respecto a la plataforma. Dentro del tren, un pasajero dispara una bala con una velocidad de 0,4 c en el marco del tren. La flecha azul ilustra que una persona parada en las vías del tren mide la bala como viajando a 0,8 c. Esto está de acuerdo con nuestras expectativas ingenuas.

En términos más generales, suponiendo que el marco S′ se mueve a una velocidad v con respecto al marco S, entonces, dentro del marco S′, el observador O′ mide un objeto que se mueve con velocidad u ′ . La velocidad u con respecto al marco S, dado que x = ut , x ′ = x − vt y t = t ′ , se puede escribir como x ′ = ut − vt = ( u − v ) t = ( u − v ) t ′ . Esto conduce a u ′ = x ′ / t ′ y, en última instancia,

${\displaystyle u'=u-v}$  o  ${\displaystyle u=u'+v,}$

que es la ley galileana de sentido común para la suma de velocidades .

La composición de las velocidades es bastante diferente en el espacio-tiempo relativista. Para reducir ligeramente la complejidad de las ecuaciones, introducimos una abreviatura común para la relación entre la velocidad de un objeto y la de la luz,

${\displaystyle \beta =v/c}$

La figura 3-2a ilustra un tren rojo que avanza a una velocidad dada por v / c = β = s / a . Desde el marco preparado del tren, un pasajero dispara una bala con una velocidad dada por u ′ / c = β ′ = n / m , donde la distancia se mide a lo largo de una línea paralela al eje x ′ rojo en lugar de paralela al eje x negro . ¿Cuál es la velocidad compuesta u de la bala con respecto a la plataforma, como se representa mediante la flecha azul? Con referencia a la figura 3-2b:

1. Desde la plataforma, la velocidad compuesta de la bala viene dada por u = c ( s + r )/( a + b ) .
2. Los dos triángulos amarillos son semejantes porque son triángulos rectángulos que comparten un ángulo común α . En el triángulo amarillo grande, la razón s / a = v / c = β .
3. Las razones de los lados correspondientes de los dos triángulos amarillos son constantes, de modo que r / a = b / s = n / m = β ′ . Por lo tanto, b = u ′ s / c y r = u ′ a / c .
4. Sustituya las expresiones para b y r en la expresión para u en el paso 1 para obtener la fórmula de Einstein para la suma de velocidades: ^{[41] : 42–48}

   ${\displaystyle u={v+u' \over 1+(vu'/c^{2})}.}$

La fórmula relativista para la suma de velocidades presentada anteriormente presenta varias características importantes:

• Si u ′ y v son muy pequeñas comparadas con la velocidad de la luz, entonces el producto vu ′ / c ² se vuelve extremadamente pequeño y el resultado general se vuelve indistinguible de la fórmula galileana (fórmula de Newton) para la adición de velocidades: u  =  u ′  +  v . La fórmula galileana es un caso especial de la fórmula relativista aplicable a bajas velocidades.
• Si u ′ se establece igual a c , entonces la fórmula arroja u  =  c independientemente del valor inicial de v . La velocidad de la luz es la misma para todos los observadores independientemente de sus movimientos relativos a la fuente emisora. ^{[41] : 49}

This section needs additional citations for verification. Please help improve this article by adding citations to reliable sources in this section. Unsourced material may be challenged and removed. (March 2024) (Learn how and when to remove this message)

Es fácil obtener expresiones cuantitativas para la dilatación del tiempo y la contracción de la longitud. La figura 3-3 es una imagen compuesta que contiene fotogramas individuales tomados de dos animaciones anteriores, simplificadas y reetiquetadas para los fines de esta sección.

Para reducir ligeramente la complejidad de las ecuaciones, existen distintas notaciones abreviadas para ct :

${\displaystyle \mathrm {T} =ct}$y son comunes.${\displaystyle w=ct}$

También se ve muy frecuentemente el uso de la convención${\displaystyle c=1.}$

En la figura 3-3a, los segmentos OA y OK representan intervalos de espacio-tiempo iguales. La dilatación del tiempo está representada por la relación OB / OK . La hipérbola invariante tiene la ecuación w = √ x ² + k ² donde k  =  OK , y la línea roja que representa la línea del universo de una partícula en movimiento tiene la ecuación w  =  x / β  =  xc / v . Un poco de manipulación algebraica da como resultado${\textstyle OB=OK/{\sqrt {1-v^{2}/c^{2}}}.}$

La expresión que implica el símbolo de la raíz cuadrada aparece muy frecuentemente en relatividad, y una expresión adicional se llama factor de Lorentz, denotado por la letra griega gamma : ^[42]${\displaystyle \gamma }$

${\displaystyle \gamma ={\frac {1}{\sqrt {1-v^{2}/c^{2}}}}={\frac {1}{\sqrt {1-\beta ^{2}}}}}$

Si v es mayor o igual que c , la expresión para pierde todo significado físico, lo que implica que c es la velocidad máxima posible en la naturaleza. Para cualquier v mayor que cero, el factor de Lorentz será mayor que uno, aunque la forma de la curva es tal que para velocidades bajas, el factor de Lorentz es extremadamente cercano a uno.${\displaystyle \gamma }$

En la Fig. 3-3b, los segmentos OA y OK representan intervalos de espacio-tiempo iguales. La contracción de longitud está representada por la razón OB / OK . La hipérbola invariante tiene la ecuación x = √ w ² + k ² , donde k  =  OK , y los bordes de la banda azul que representan las líneas del universo de los puntos finales de una varilla en movimiento tienen pendiente 1/ β  =  c / v . El evento A tiene coordenadas ( x ,  w ) = ( γk ,  γβk ). Dado que la línea tangente a través de A y B tiene la ecuación w  = ( x  −  OB )/ β , tenemos γβk  = ( γk  −  OB )/ β y

${\displaystyle OB/OK=\gamma (1-\beta ^{2})={\frac {1}{\gamma }}}$

Las transformaciones de Galileo y la consiguiente ley de sentido común de la suma de velocidades funcionan bien en nuestro mundo ordinario de baja velocidad de aviones, automóviles y pelotas. Sin embargo, a partir de mediados del siglo XIX, la instrumentación científica sensible comenzó a detectar anomalías que no encajaban bien con la suma ordinaria de velocidades.

Las transformaciones de Lorentz se utilizan para transformar las coordenadas de un evento de un marco a otro en relatividad especial.

El factor de Lorentz aparece en las transformaciones de Lorentz:

${\displaystyle {\begin{aligned}t'&=\gamma \left(t-{\frac {vx}{c^{2}}}\right)\\x'&=\gamma \left(x-vt\right)\\y'&=y\\z'&=z\end{aligned}}}$

Las transformaciones inversas de Lorentz son:

${\displaystyle {\begin{aligned}t&=\gamma \left(t'+{\frac {vx'}{c^{2}}}\right)\\x&=\gamma \left(x'+vt'\right)\\y&=y'\\z&=z'\end{aligned}}}$

Cuando v  ≪  c y x es suficientemente pequeño, los términos v ² / c ² y vx / c ² se acercan a cero, y las transformaciones de Lorentz se aproximan a las transformaciones galileanas.

${\displaystyle t'=\gamma (t-vx/c^{2}),}$ ${\displaystyle x'=\gamma (x-vt)}$etc., la mayoría de las veces realmente significan etc. Aunque para abreviar las ecuaciones de transformación de Lorentz se escriben sin deltas, x significa Δ x , etc. En general, siempre nos preocupan las diferencias de espacio y tiempo entre eventos.${\displaystyle \Delta t'=\gamma (\Delta t-v\Delta x/c^{2}),}$ ${\displaystyle \Delta x'=\gamma (\Delta x-v\Delta t)}$

Llamar a un conjunto de transformaciones transformaciones normales de Lorentz y al otro transformaciones inversas es engañoso, ya que no hay diferencia intrínseca entre los sistemas de referencia. Diferentes autores llaman a uno u otro conjunto de transformaciones el conjunto "inverso". Las transformaciones hacia delante y hacia atrás están trivialmente relacionadas entre sí, ya que el sistema de referencia S solo puede moverse hacia delante o hacia atrás con respecto a S ′ . Por lo tanto, invertir las ecuaciones simplemente implica intercambiar las variables primadas y no primadas y reemplazar v por − v . ^{[43] : 71–79}

Ejemplo: Terence y Stella participan en una carrera espacial de la Tierra a Marte. Terence es un oficial en la línea de partida, mientras que Stella es una participante. En el momento t = t ′ = 0 , la nave espacial de Stella acelera instantáneamente a una velocidad de 0,5  c . La distancia de la Tierra a Marte es de 300 segundos luz (aproximadamente90,0 × 10 ⁶  km ). Terence observa a Stella cruzando el reloj de la línea de meta en t  = 600,00 s . Pero Stella observa que el tiempo en el cronómetro de su barco es ⁠ ⁠${\displaystyle t^{\prime }=\gamma \left(t-vx/c^{2}\right)=519.62\ {\text{s}}}$ cuando pasa la línea de meta, y calcula que la distancia entre las líneas de salida y llegada, medida en su marco, es de 259,81 segundos luz (aproximadamente77,9 × 10 ⁶  kilómetros ). 1).

Ha habido muchas docenas de derivaciones de las transformaciones de Lorentz desde el trabajo original de Einstein en 1905, cada una con su enfoque particular. Aunque la derivación de Einstein se basó en la invariancia de la velocidad de la luz, hay otros principios físicos que pueden servir como puntos de partida. En última instancia, estos puntos de partida alternativos pueden considerarse diferentes expresiones del principio subyacente de localidad , que establece que la influencia que una partícula ejerce sobre otra no puede transmitirse instantáneamente. ^[44]

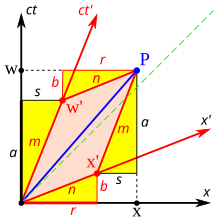
La derivación dada aquí e ilustrada en la Fig. 3-5 se basa en una presentada por Bais ^{[41] : 64–66} y hace uso de resultados previos de las secciones Composición relativista de velocidades, Dilatación del tiempo y Contracción de longitud. El evento P tiene coordenadas ( w ,  x ) en el "sistema de reposo" negro y coordenadas ( w ′ ,  x ′ ) en el marco rojo que se mueve con el parámetro de velocidad β  =  v / c . Para determinar w ′ y x ′ en términos de w y x (o al revés) es más fácil al principio derivar la transformación inversa de Lorentz.

1. No puede haber expansión/contracción de longitud en las direcciones transversales. y ' debe ser igual a y y z ′ debe ser igual a z , de lo contrario, si una pelota de 1 m que se mueve rápidamente podría pasar por un agujero circular de 1 m dependería del observador. El primer postulado de la relatividad establece que todos los marcos inerciales son equivalentes, y la expansión/contracción transversal violaría esta ley. ^{[43] : 27–28}
2. Del dibujo, w = a + b y x  =  r  +  s
3. De resultados anteriores usando triángulos similares, sabemos que s / a  =  b / r = v / c  =  β .
4. Debido a la dilatación del tiempo, a  =  γw ′
5. Sustituyendo la ecuación (4) en s / a  =  β se obtiene s  =  γw ′ β .
6. La contracción de longitud y los triángulos similares nos dan r  =  γx ′ y b  =  βr = βγx ′
7. Sustituyendo las expresiones para s , a , r y b en las ecuaciones del Paso 2 obtenemos inmediatamente

   ${\displaystyle w=\gamma w'+\beta \gamma x'}$

   ${\displaystyle x=\gamma x'+\beta \gamma w'}$

Las ecuaciones anteriores son expresiones alternativas para las ecuaciones t y x de la transformación inversa de Lorentz, como se puede ver al sustituir ct por w , ct ′ por w ′ y v / c por β . A partir de la transformación inversa, las ecuaciones de la transformación hacia adelante se pueden derivar al resolver para t ′ y x ′ .

Las transformaciones de Lorentz tienen una propiedad matemática llamada linealidad, ya que x ′ y t ′ se obtienen como combinaciones lineales de x y t , sin potencias superiores involucradas. La linealidad de la transformación refleja una propiedad fundamental del espacio-tiempo que se asumió tácitamente en la derivación, a saber, que las propiedades de los marcos de referencia inerciales son independientes de la ubicación y el tiempo. En ausencia de gravedad, el espacio-tiempo parece el mismo en todas partes. ^{[41] : 67} Todos los observadores inerciales estarán de acuerdo en lo que constituye un movimiento acelerado y no acelerado. ^{[43] : 72–73} Cualquier observador puede usar sus propias mediciones de espacio y tiempo, pero no hay nada absoluto en ellas. Las convenciones de otro observador funcionarán igual de bien. ^{[3] : 190}

Un resultado de la linealidad es que si se aplican secuencialmente dos transformaciones de Lorentz, el resultado también es una transformación de Lorentz.

Ejemplo: Terence observa a Stella alejándose de él a una velocidad de 0,500  c y puede usar las transformaciones de Lorentz con β  = 0,500 para relacionar las mediciones de Stella con las suyas. Stella, en su marco, observa a Ursula alejándose de él a una velocidad de 0,250  c y puede usar las transformaciones de Lorentz con β  = 0,250 para relacionar las mediciones de Ursula con las suyas. Debido a la linealidad de las transformaciones y a la composición relativista de las velocidades, Terence puede usar las transformaciones de Lorentz con β  = 0,666 para relacionar las mediciones de Ursula con las suyas.

El efecto Doppler es el cambio de frecuencia o longitud de onda de una onda para un receptor y una fuente en movimiento relativo. Para simplificar, consideramos aquí dos escenarios básicos: (1) Los movimientos de la fuente y/o el receptor se producen exactamente a lo largo de la línea que los une (efecto Doppler longitudinal), y (2) los movimientos forman ángulos rectos con respecto a dicha línea ( efecto Doppler transversal ). Ignoramos los escenarios en los que se mueven a lo largo de ángulos intermedios.

El análisis Doppler clásico se ocupa de las ondas que se propagan en un medio, como las ondas sonoras o las ondulaciones del agua, y que se transmiten entre fuentes y receptores que se acercan o se alejan entre sí. El análisis de dichas ondas depende de si la fuente, el receptor o ambos se mueven en relación con el medio. Dado el escenario en el que el receptor está estacionario con respecto al medio y la fuente se aleja directamente del receptor a una velocidad de v _s para un parámetro de velocidad de β _s , la longitud de onda aumenta y la frecuencia observada f viene dada por

${\displaystyle f={\frac {1}{1+\beta _{s}}}f_{0}}$

Por otra parte, dado el escenario donde la fuente es estacionaria y el receptor se aleja directamente de la fuente a una velocidad de v _r para un parámetro de velocidad de β _r , la longitud de onda no cambia, pero la velocidad de transmisión de las ondas en relación con el receptor disminuye, y la frecuencia observada f está dada por

${\displaystyle f=(1-\beta _{r})f_{0}}$

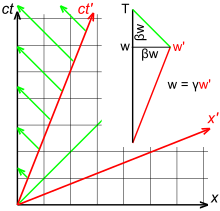
La luz, a diferencia del sonido o las ondas del agua, no se propaga a través de un medio y no hay distinción entre una fuente que se aleja del receptor o un receptor que se aleja de la fuente. La figura 3-6 ilustra un diagrama de espacio-tiempo relativista que muestra una fuente que se separa del receptor con un parámetro de velocidad de modo que la separación entre la fuente y el receptor en el tiempo es . Debido a la dilatación del tiempo, Puesto que la pendiente del rayo de luz verde es −1, Por lo tanto, el efecto Doppler relativista está dado por ^{[41] : 58–59}${\displaystyle \beta ,}$${\displaystyle w}$${\displaystyle \beta w}$${\displaystyle w=\gamma w'.}$${\displaystyle T=w+\beta w=\gamma w'(1+\beta ).}$

${\displaystyle f={\sqrt {\frac {1-\beta }{1+\beta }}}\,f_{0}.}$

Supongamos que una fuente y un receptor, que se aproximan entre sí en un movimiento inercial uniforme a lo largo de líneas que no se intersecan, están en su punto más cercano de aproximación entre sí. Parecería que el análisis clásico predice que el receptor no detecta ningún desplazamiento Doppler. Debido a sutilezas en el análisis, esa expectativa no es necesariamente cierta. Sin embargo, cuando se define adecuadamente, el desplazamiento Doppler transversal es un efecto relativista que no tiene análogo clásico. Las sutilezas son las siguientes: ^{[45] : 541–543}

<!—fin de la lista simple—>

En el escenario (a), el punto de aproximación más cercano es independiente del marco y representa el momento en el que no hay cambio en la distancia en función del tiempo (es decir, dr/dt = 0, donde r es la distancia entre el receptor y la fuente) y, por lo tanto, no hay desplazamiento Doppler longitudinal. La fuente observa que el receptor está iluminado por una luz de frecuencia f ′ , pero también observa que el receptor tiene un reloj dilatado en el tiempo. En el marco S, el receptor está, por lo tanto, iluminado por una luz desplazada al azul de frecuencia

${\displaystyle f=f'\gamma =f'/{\sqrt {1-\beta ^{2}}}}$

En el escenario (b), la ilustración muestra que el receptor está iluminado por la luz que proviene del momento en que la fuente estaba más cerca del receptor, a pesar de que la fuente se ha movido. Debido a que los relojes de la fuente están dilatados en el tiempo, medidos en el marco S, y dado que dr/dt era igual a cero en este punto, la luz de la fuente, emitida desde este punto más cercano, se desplaza hacia el rojo con la frecuencia.

${\displaystyle f=f'/\gamma =f'{\sqrt {1-\beta ^{2}}}}$

Los escenarios (c) y (d) pueden analizarse mediante argumentos simples de dilatación del tiempo. En (c), el receptor observa que la luz de la fuente está desplazada hacia el azul por un factor de , y en (d), la luz está desplazada hacia el rojo. La única complicación aparente es que los objetos en órbita están en movimiento acelerado. Sin embargo, si un observador inercial mira un reloj que se acelera, solo la velocidad instantánea del reloj es importante al calcular la dilatación del tiempo. (Sin embargo, lo inverso no es cierto.) ^{[45] : 541–543} La mayoría de los informes sobre el desplazamiento Doppler transversal se refieren al efecto como un desplazamiento hacia el rojo y analizan el efecto en términos de los escenarios (b) o (d). ^{[nota 11]}${\displaystyle \gamma }$

En mecánica clásica, el estado de movimiento de una partícula se caracteriza por su masa y su velocidad. El momento lineal , producto de la masa de una partícula por su velocidad, es una cantidad vectorial que posee la misma dirección que la velocidad: p  =  m v . Es una cantidad que se conserva , lo que significa que si un sistema cerrado no se ve afectado por fuerzas externas, su momento lineal total no puede cambiar.

En la mecánica relativista, el vector de momento se extiende a cuatro dimensiones. Al vector de momento se le añade un componente temporal que permite que el vector de momento del espacio-tiempo se transforme como el vector de posición del espacio-tiempo ⁠ ⁠${\displaystyle (x,t)}$ . Al explorar las propiedades del momento del espacio-tiempo, comenzamos, en la figura 3-8a, examinando cómo se ve una partícula en reposo. En el marco de reposo, el componente espacial del momento es cero, es decir, p  = 0 , pero el componente temporal es igual a mc .

Podemos obtener los componentes transformados de este vector en el marco móvil utilizando las transformaciones de Lorentz, o podemos leerlo directamente de la figura porque sabemos que ⁠ ⁠${\displaystyle (mc)^{\prime }=\gamma mc}$ y ⁠ ⁠${\displaystyle p^{\prime }=-\beta \gamma mc}$ , ya que los ejes rojos están reescalados por gamma. La figura 3-8b ilustra la situación tal como aparece en el marco móvil. Es evidente que los componentes de espacio y tiempo del cuadrimpulso tienden al infinito a medida que la velocidad del marco móvil se acerca a c . ^{[41] : 84–87}

Utilizaremos esta información en breve para obtener una expresión para el tetra-momento .

Las partículas de luz, o fotones, viajan a la velocidad de c , la constante que se conoce convencionalmente como velocidad de la luz . Esta afirmación no es una tautología, ya que muchas formulaciones modernas de la relatividad no parten de la velocidad constante de la luz como postulado. Por lo tanto, los fotones se propagan a lo largo de una línea de universo similar a la luz y, en unidades apropiadas, tienen componentes espaciales y temporales iguales para cada observador.

Una consecuencia de la teoría del electromagnetismo de Maxwell es que la luz transporta energía y momento, y que su relación es constante: ⁠ ⁠${\displaystyle E/p=c}$ . Reordenando, ⁠ ⁠${\displaystyle E/c=p}$ , y dado que para los fotones, los componentes de espacio y tiempo son iguales, E / c debe, por lo tanto, igualarse con el componente de tiempo del vector de momento del espacio-tiempo.

Los fotones viajan a la velocidad de la luz, pero tienen un momento y una energía finitos. Para que esto sea así, el término de masa en γmc debe ser cero, lo que significa que los fotones son partículas sin masa . El infinito por cero es una cantidad mal definida, pero E / c está bien definida.

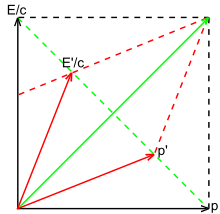
Según este análisis, si la energía de un fotón es igual a E en el sistema en reposo, es igual a ⁠ ⁠${\displaystyle E^{\prime }=(1-\beta )\gamma E}$ en un sistema en movimiento. Este resultado se puede derivar mediante la inspección de la figura 3-9 o mediante la aplicación de las transformaciones de Lorentz, y es coherente con el análisis del efecto Doppler dado anteriormente. ^{[41] : 88}

La consideración de las interrelaciones entre los diversos componentes del vector de momento relativista llevó a Einstein a varias conclusiones importantes.

• En el límite de baja velocidad, cuando β = v / c se acerca a cero, γ se acerca a 1, por lo que el componente espacial del momento relativista ⁠ ⁠${\displaystyle \beta \gamma mc=\gamma mv}$ se acerca a mv , el término clásico para el momento. Siguiendo esta perspectiva, γm puede interpretarse como una generalización relativista de m . Einstein propuso que la masa relativista de un objeto aumenta con la velocidad según la fórmula ⁠ ⁠${\displaystyle m_{\text{rel}}=\gamma m}$ .
• De la misma manera, comparando el componente temporal del momento relativista con el del fotón, ⁠ ⁠${\displaystyle \gamma mc=m_{\text{rel}}c=E/c}$ , de modo que Einstein llegó a la relación ⁠ ⁠${\displaystyle E=m_{\text{rel}}c^{2}}$ . Simplificada al caso de velocidad cero, esta es la ecuación de Einstein que relaciona energía y masa.

Otra forma de ver la relación entre masa y energía es considerar una expansión en serie de γmc ² a baja velocidad:

${\displaystyle E=\gamma mc^{2}={\frac {mc^{2}}{\sqrt {1-\beta ^{2}}}}}$ ${\displaystyle \approx mc^{2}+{\frac {1}{2}}mv^{2}...}$

El segundo término es simplemente una expresión de la energía cinética de la partícula. La masa, en efecto, parece ser otra forma de energía. ^{[41] : 90–92  [43] : 129–130, 180}

El concepto de masa relativista que Einstein introdujo en 1905, m _rel , aunque se valida ampliamente cada día en los aceleradores de partículas de todo el mundo (o en cualquier instrumentación cuyo uso dependa de partículas de alta velocidad, como los microscopios electrónicos, ^[46] los antiguos televisores en color, etc.), no ha demostrado ser un concepto fructífero en física en el sentido de que no es un concepto que haya servido de base para otros desarrollos teóricos. La masa relativista, por ejemplo, no desempeña ningún papel en la relatividad general.

Por esta razón, así como por cuestiones pedagógicas, la mayoría de los físicos prefieren actualmente una terminología diferente cuando se refieren a la relación entre masa y energía. ^[47] "Masa relativista" es un término en desuso. El término "masa" por sí mismo se refiere a la masa en reposo o masa invariante , y es igual a la longitud invariante del vector de momento relativista. Expresado como una fórmula,

${\displaystyle E^{2}-p^{2}c^{2}=m_{\text{rest}}^{2}c^{4}}$

Esta fórmula se aplica a todas las partículas, tanto sin masa como con masa. Para los fotones donde m _{en reposo} es igual a cero, se obtiene: ⁠ ⁠${\displaystyle E=\pm pc}$ . ^{[41] : 90–92}

Debido a la estrecha relación entre masa y energía, el cuatrimomento (también llamado 4-momento) también se denomina 4-vector de energía-momento. Si se utiliza una P mayúscula para representar el cuatrimomento y una p minúscula para denotar el momento espacial, el cuatrimomento se puede escribir como

${\displaystyle P\equiv (E/c,{\vec {p}})=(E/c,p_{x},p_{y},p_{z})}$o alternativamente,

${\displaystyle P\equiv (E,{\vec {p}})=(E,p_{x},p_{y},p_{z})}$utilizando la convención que ^{[43] : 129–130, 180}${\displaystyle c=1.}$

En física, las leyes de conservación establecen que ciertas propiedades particulares mensurables de un sistema físico aislado no cambian a medida que el sistema evoluciona con el tiempo. En 1915, Emmy Noether descubrió que subyacente a cada ley de conservación hay una simetría fundamental de la naturaleza. ^[48] El hecho de que a los procesos físicos no les importe en qué lugar del espacio tienen lugar ( simetría de traslación espacial ) produce la conservación del momento , el hecho de que a dichos procesos no les importe cuándo tienen lugar ( simetría de traslación temporal ) produce la conservación de la energía , y así sucesivamente. En esta sección, examinamos las opiniones newtonianas de la conservación de la masa, el momento y la energía desde una perspectiva relativista.

Para entender cómo debe modificarse la visión newtoniana de la conservación del momento en un contexto relativista, examinamos el problema de dos cuerpos en colisión limitados a una sola dimensión.

En la mecánica newtoniana se pueden distinguir dos casos extremos de este problema que producen matemáticas de mínima complejidad:

(1) Los dos cuerpos rebotan uno contra el otro en una colisión completamente elástica.

(2) Los dos cuerpos se quedan pegados y continúan moviéndose como una sola partícula. Este segundo caso es el de una colisión completamente inelástica.

En ambos casos (1) y (2), el momento, la masa y la energía total se conservan. Sin embargo, la energía cinética no se conserva en casos de colisión inelástica. Una determinada fracción de la energía cinética inicial se convierte en calor.

En el caso (2), dos masas con momentos ⁠ ⁠${\displaystyle {\boldsymbol {p}}_{\boldsymbol {1}}=m_{1}{\boldsymbol {v}}_{\boldsymbol {1}}}$ y ⁠ ⁠${\displaystyle {\boldsymbol {p}}_{\boldsymbol {2}}=m_{2}{\boldsymbol {v}}_{\boldsymbol {2}}}$ chocan para producir una única partícula de masa conservada ⁠ ⁠${\displaystyle m=m_{1}+m_{2}}$ que viaja a la velocidad del centro de masa del sistema original, . El momento total ⁠ ⁠ se conserva.${\displaystyle {\boldsymbol {v_{cm}}}=\left(m_{1}{\boldsymbol {v_{1}}}+m_{2}{\boldsymbol {v_{2}}}\right)/\left(m_{1}+m_{2}\right)}$${\displaystyle {\boldsymbol {p=p_{1}+p_{2}}}}$

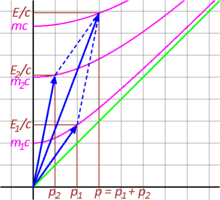
La figura 3-10 ilustra la colisión inelástica de dos partículas desde una perspectiva relativista. Los componentes temporales ⁠ ⁠${\displaystyle E_{1}/c}$ y ⁠ ⁠${\displaystyle E_{2}/c}$ se suman para formar la E/c total del vector resultante, lo que significa que la energía se conserva. Asimismo, los componentes espaciales ⁠ ⁠${\displaystyle {\boldsymbol {p_{1}}}}$ y ⁠ ⁠${\displaystyle {\boldsymbol {p_{2}}}}$ se suman para formar p del vector resultante. El cuadri-momento es, como se esperaba, una cantidad conservada. Sin embargo, la masa invariante de la partícula fusionada, dada por el punto donde la hipérbola invariante del momento total intersecta el eje de energía, no es igual a la suma de las masas invariantes de las partículas individuales que colisionaron. De hecho, es mayor que la suma de las masas individuales: ⁠ ⁠${\displaystyle m>m_{1}+m_{2}}$ . ^{[41] : 94–97}

Si analizamos los acontecimientos de este escenario en orden inverso, vemos que la no conservación de la masa es un fenómeno común: cuando una partícula elemental inestable se desintegra espontáneamente en dos partículas más ligeras, la energía total se conserva, pero no la masa. Parte de la masa se convierte en energía cinética. ^{[43] : 134–138}

La libertad de elegir cualquier marco en el que realizar un análisis nos permite escoger uno que sea particularmente conveniente. Para el análisis de problemas de momento y energía, el marco más conveniente es generalmente el " marco del centro del momento " (también llamado marco de momento cero o marco COM). Este es el marco en el que el componente espacial del momento total del sistema es cero. La figura 3-11 ilustra la ruptura de una partícula de alta velocidad en dos partículas hijas. En el marco de laboratorio, las partículas hijas se emiten preferentemente en una dirección orientada a lo largo de la trayectoria de la partícula original. Sin embargo, en el marco COM, las dos partículas hijas se emiten en direcciones opuestas, aunque sus masas y la magnitud de sus velocidades generalmente no son las mismas. ^[49]

En un análisis newtoniano de partículas en interacción, la transformación entre sistemas es sencilla porque todo lo que se necesita es aplicar la transformación galileana a todas las velocidades. Dado que ⁠ ⁠${\displaystyle v'=v-u}$ , el momento ⁠ ⁠${\displaystyle p'=p-mu}$ . Si se observa que el momento total de un sistema de partículas en interacción se conserva en un sistema, se observará asimismo que se conserva en cualquier otro sistema. ^{[43] : 241–245}

La conservación del momento en el marco COM equivale al requisito de que p  = 0 tanto antes como después de la colisión. En el análisis newtoniano, la conservación de la masa dicta que ⁠ ⁠${\displaystyle m=m_{1}+m_{2}}$ . En los escenarios unidimensionales simplificados que hemos estado considerando, solo es necesaria una restricción adicional antes de que se puedan determinar los momentos salientes de las partículas: una condición de energía. En el caso unidimensional de una colisión completamente elástica sin pérdida de energía cinética, las velocidades salientes de las partículas que rebotan en el marco COM serán exactamente iguales y opuestas a sus velocidades entrantes. En el caso de una colisión completamente inelástica con pérdida total de energía cinética, las velocidades salientes de las partículas que rebotan serán cero. ^{[43] : 241–245}

Los momentos newtonianos, calculados como ⁠ ⁠${\displaystyle p=mv}$ , no se comportan adecuadamente bajo la transformación de Lorentz. La transformación lineal de velocidades ⁠ ⁠${\displaystyle v'=v-u}$ se reemplaza por la altamente no lineal ⁠ ⁠${\displaystyle v^{\prime }=(v-u)/(1-{vu}/{c^{2}})}$ de modo que un cálculo que demuestre la conservación del momento en un marco será inválido en otros marcos. Einstein se enfrentó a tener que renunciar a la conservación del momento o cambiar la definición de momento. Esta segunda opción fue la que eligió. ^{[41] : 104}

La ley relativista de conservación de la energía y el momento sustituye a las tres leyes clásicas de conservación de la energía, el momento y la masa. La masa ya no se conserva de forma independiente, porque ha sido subsumida en la energía relativista total. Esto hace que la conservación relativista de la energía sea un concepto más simple que en la mecánica no relativista, porque la energía total se conserva sin ninguna calificación. La energía cinética convertida en calor o energía potencial interna se manifiesta como un aumento de la masa. ^{[43] : 127}

Las teorías de Newton suponían que el movimiento se produce en el contexto de un marco de referencia euclidiano rígido que se extiende por todo el espacio y todo el tiempo. La gravedad está mediada por una fuerza misteriosa, que actúa instantáneamente a través de una distancia, cuyas acciones son independientes del espacio intermedio. ^{[nota 12]} Por el contrario, Einstein negó que exista un marco de referencia euclidiano de fondo que se extienda por todo el espacio. Tampoco existe nada parecido a una fuerza de gravitación, solo la estructura del espacio-tiempo en sí. ^{[51] : 175–190}

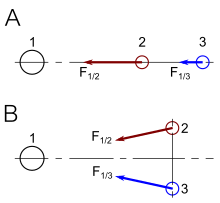
En términos de espacio-tiempo, la trayectoria de un satélite que orbita la Tierra no está determinada por las influencias distantes de la Tierra, la Luna y el Sol. En cambio, el satélite se mueve a través del espacio solo en respuesta a las condiciones locales. Dado que el espacio-tiempo es en todas partes localmente plano cuando se lo considera en una escala suficientemente pequeña, el satélite siempre sigue una línea recta en su marco inercial local. Decimos que el satélite siempre sigue la trayectoria de una geodésica . No se puede descubrir ninguna evidencia de que la gravitación siga los movimientos de una sola partícula. ^{[51] : 175–190}

En cualquier análisis del espacio-tiempo, la evidencia de la gravitación requiere que se observen las aceleraciones relativas de dos cuerpos o dos partículas separadas. En la figura 5-1, dos partículas separadas, en caída libre en el campo gravitacional de la Tierra, exhiben aceleraciones de marea debido a inhomogeneidades locales en el campo gravitacional de tal manera que cada partícula sigue un camino diferente a través del espacio-tiempo. Las aceleraciones de marea que exhiben estas partículas entre sí no requieren fuerzas para su explicación. Más bien, Einstein las describió en términos de la geometría del espacio-tiempo, es decir, la curvatura del espacio-tiempo. Estas aceleraciones de marea son estrictamente locales. Es el efecto total acumulativo de muchas manifestaciones locales de curvatura lo que resulta en la apariencia de una fuerza gravitacional que actúa a gran distancia de la Tierra. ^{[51] : 175–190}

Distintos observadores que analizan los escenarios presentados en esta figura interpretan los escenarios de manera diferente según su conocimiento de la situación. (i) Un primer observador, en el centro de masa de las partículas 2 y 3 pero sin saber que la masa 1 es grande, concluye que existe una fuerza de repulsión entre las partículas en el escenario A, mientras que existe una fuerza de atracción entre las partículas en el escenario B. (ii) Un segundo observador, consciente de la gran masa 1, sonríe ante la ingenuidad del primer reportero. Este segundo observador sabe que, en realidad, las fuerzas aparentes entre las partículas 2 y 3 representan en realidad efectos de marea resultantes de su atracción diferencial por la masa 1. (iii) Un tercer observador, entrenado en relatividad general, sabe que, de hecho, no hay fuerzas en absoluto que actúen entre los tres objetos. Más bien, los tres objetos se mueven a lo largo de geodésicas en el espacio-tiempo.

Dos proposiciones centrales subyacen a la relatividad general.

• El primer concepto crucial es la independencia de coordenadas: las leyes de la física no pueden depender del sistema de coordenadas que se utilice. Se trata de una importante ampliación del principio de relatividad a partir de la versión utilizada en la relatividad especial, que establece que las leyes de la física deben ser las mismas para todo observador que se mueva en sistemas de referencia no acelerados (inerciales). En la relatividad general, para utilizar las propias palabras de Einstein (traducidas), "las leyes de la física deben ser de tal naturaleza que se apliquen a sistemas de referencia en cualquier tipo de movimiento". ^{[52] : 113} Esto nos lleva a un problema inmediato: en sistemas acelerados, uno siente fuerzas que aparentemente le permitirían evaluar su estado de aceleración en un sentido absoluto. Einstein resolvió este problema mediante el principio de equivalencia. ^{[53] : 137–149}

• El principio de equivalencia establece que en cualquier región suficientemente pequeña del espacio, los efectos de la gravitación son los mismos que los de la aceleración.
  En la figura 5-2, la persona A está en una nave espacial, lejos de cualquier objeto masivo, que experimenta una aceleración uniforme de g . La persona B está en una caja que reposa sobre la Tierra. Siempre que la nave espacial sea suficientemente pequeña para que los efectos de marea no sean medibles (dada la sensibilidad de la instrumentación de medición de la gravedad actual, A y B presumiblemente deberían ser liliputienses ), no hay experimentos que A y B puedan realizar que les permitan decir en qué entorno están. ^{[53] : 141–149}
  Una expresión alternativa del principio de equivalencia es señalar que en la ley de gravitación universal de Newton, F = GMm _g /r ² = m _g g y en la segunda ley de Newton, F = m _i a , no hay ninguna razón a priori por la que la masa gravitacional m _g deba ser igual a la masa inercial m _i . El principio de equivalencia establece que estas dos masas son idénticas. ^{[53] : 141–149}

Para pasar de la descripción elemental del espacio-tiempo curvo que se acaba de mencionar a una descripción completa de la gravitación se requieren cálculos tensoriales y geometría diferencial, dos temas que requieren un estudio considerable. Sin estas herramientas matemáticas, es posible escribir sobre la relatividad general, pero no es posible demostrar ninguna derivación no trivial.

En la visión convencionalista de Poincaré , los criterios esenciales según los cuales se debería seleccionar una geometría euclidiana frente a una no euclidiana serían la economía y la simplicidad. Un realista diría que Einstein descubrió que el espacio-tiempo no es euclidiano. Un convencionalista diría que Einstein simplemente encontró más conveniente utilizar una geometría no euclidiana. El convencionalista mantendría que el análisis de Einstein no decía nada acerca de cuál es realmente la geometría del espacio-tiempo . ^[54]

Dicho esto,

1. ¿Es posible representar la relatividad general en términos de espacio-tiempo plano?
2. ¿Existen situaciones en las que una interpretación del espacio-tiempo plano de la relatividad general puede ser más conveniente que la interpretación habitual del espacio-tiempo curvo?

En respuesta a la primera pregunta, varios autores, entre ellos Deser, Grishchuk, Rosen, Weinberg, etc., han proporcionado diversas formulaciones de la gravitación como un campo en una variedad plana. Esas teorías se denominan de diversas formas: " gravedad bimétrica ", "enfoque teórico de campo para la relatividad general", etc. ^{[55] [56] [57] [58]} Kip Thorne ha proporcionado una revisión popular de estas teorías. ^{[59] : 397–403}

El paradigma del espacio-tiempo plano postula que la materia crea un campo gravitatorio que hace que las reglas se encojan cuando se las gira de una orientación circunferencial a una radial, y que eso hace que el ritmo de los relojes se dilate. El paradigma del espacio-tiempo plano es totalmente equivalente al paradigma del espacio-tiempo curvo en el sentido de que ambos representan los mismos fenómenos físicos. Sin embargo, sus formulaciones matemáticas son completamente diferentes. Los físicos en activo alternan rutinariamente entre el uso de técnicas de espacio-tiempo curvo y plano según los requisitos del problema. El paradigma del espacio-tiempo plano es conveniente cuando se realizan cálculos aproximados en campos débiles. Por lo tanto, las técnicas de espacio-tiempo plano tienden a usarse para resolver problemas de ondas gravitacionales, mientras que las técnicas de espacio-tiempo curvo tienden a usarse en el análisis de agujeros negros. ^{[59] : 397–403}

El grupo de simetría del espacio-tiempo para la Relatividad Especial es el grupo de Poincaré , que es un grupo de diez dimensiones de tres impulsos de Lorentz, tres rotaciones y cuatro traslaciones del espacio-tiempo. Es lógico preguntar qué simetrías, si las hay, podrían aplicarse en la Relatividad General . Un caso manejable podría ser considerar las simetrías del espacio-tiempo tal como las ven los observadores ubicados lejos de todas las fuentes del campo gravitacional. La expectativa ingenua para simetrías del espacio-tiempo asintóticamente planas podría ser simplemente extender y reproducir las simetrías del espacio-tiempo plano de la relatividad especial, es decir , el grupo de Poincaré.

En 1962, Hermann Bondi , MG van der Burg, AW Metzner ^[60] y Rainer K. Sachs ^[61] abordaron este problema de simetría asintótica para investigar el flujo de energía en el infinito debido a la propagación de ondas gravitacionales . Su primer paso fue decidir sobre algunas condiciones de contorno físicamente sensatas para colocar en el campo gravitacional en el infinito similar a la luz para caracterizar lo que significa decir que una métrica es asintóticamente plana, sin hacer suposiciones a priori sobre la naturaleza del grupo de simetría asintótica, ni siquiera la suposición de que tal grupo existe. Luego, después de diseñar lo que consideraron que eran las condiciones de contorno más sensatas, investigaron la naturaleza de las transformaciones de simetría asintótica resultantes que dejan invariante la forma de las condiciones de contorno apropiadas para campos gravitacionales asintóticamente planos. ^{[62] : 35}

Lo que encontraron fue que las transformaciones de simetría asintótica realmente forman un grupo y la estructura de este grupo no depende del campo gravitatorio particular que esté presente. Esto significa que, como se esperaba, uno puede separar la cinemática del espacio-tiempo de la dinámica del campo gravitatorio al menos en el infinito espacial. La sorpresa desconcertante en 1962 fue su descubrimiento de un rico grupo de dimensión infinita (el llamado grupo BMS) como el grupo de simetría asintótica, en lugar del grupo de Poincaré de dimensión finita, que es un subgrupo del grupo BMS. No solo las transformaciones de Lorentz son transformaciones de simetría asintótica, también hay transformaciones adicionales que no son transformaciones de Lorentz sino que son transformaciones de simetría asintótica. De hecho, encontraron una infinidad adicional de generadores de transformaciones conocidos como supertraslaciones . Esto implica la conclusión de que la Relatividad General (RG) no se reduce a la relatividad especial en el caso de campos débiles a largas distancias. ^{[62] : 35}

Por razones físicas, un continuo espacio-temporal se define matemáticamente como una variedad lorentziana tetradimensional, suave y conectada . Esto significa que la métrica suave de Lorentz tiene una firma . La métrica determina la${\displaystyle (M,g)}$ ${\displaystyle g}$ ${\displaystyle (3,1)}$geometría del espacio-tiempo , así como la determinación de lasgeodésicasde partículas y rayos de luz. Sobre cada punto (evento) en esta variedad,gráficos de coordenadaspara representar a los observadores en sistemas de referencia. Por lo general, se utilizan coordenadas cartesianas. Además, por simplicidad, las unidades de medida suelen elegirse de modo que la velocidad de la luzsea igual a 1.^[64]${\displaystyle (x,y,z,t)}$${\displaystyle c}$

Un marco de referencia (observador) puede identificarse con uno de estos cuadros de coordenadas; cualquier observador de este tipo puede describir cualquier evento . Otro marco de referencia puede identificarse mediante un segundo cuadro de coordenadas sobre . Dos observadores (uno en cada marco de referencia) pueden describir el mismo evento pero obtener descripciones diferentes. ^[64]${\displaystyle p}$${\displaystyle p}$${\displaystyle p}$

Por lo general, se necesitan muchos diagramas de coordenadas superpuestos para cubrir una variedad. Dados dos diagramas de coordenadas, uno que contiene (representa a un observador) y otro que contiene (representa a otro observador), la intersección de los diagramas representa la región del espacio-tiempo en la que ambos observadores pueden medir cantidades físicas y, por lo tanto, comparar resultados. La relación entre los dos conjuntos de mediciones está dada por una transformación de coordenadas no singular en esta intersección. La idea de los diagramas de coordenadas como observadores locales que pueden realizar mediciones en su vecindad también tiene mucho sentido físico, ya que así es como uno realmente recopila datos físicos: localmente. ^[64]${\displaystyle p}$${\displaystyle q}$

Por ejemplo, dos observadores, uno de los cuales está en la Tierra, pero el otro que está en un cohete rápido a Júpiter, pueden observar un cometa chocando contra Júpiter (este es el evento ). En general, no estarán de acuerdo sobre la ubicación exacta y el momento de este impacto, es decir, tendrán diferentes 4-tuplas (ya que están usando diferentes sistemas de coordenadas). Aunque sus descripciones cinemáticas diferirán, las leyes dinámicas (físicas), como la conservación del momento y la primera ley de la termodinámica, seguirán siendo válidas. De hecho, la teoría de la relatividad requiere más que esto en el sentido de que estipula que estas (y todas las demás leyes físicas) deben tomar la misma forma en todos los sistemas de coordenadas. Esto introduce tensores en la relatividad, por los cuales se representan todas las cantidades físicas.${\displaystyle p}$${\displaystyle (x,y,z,t)}$

Se dice que las geodésicas son temporales, nulas o espaciales si el vector tangente a un punto de la geodésica es de esta naturaleza. Las trayectorias de partículas y rayos de luz en el espacio-tiempo se representan mediante geodésicas temporales y nulas (espaciales), respectivamente. ^[64]

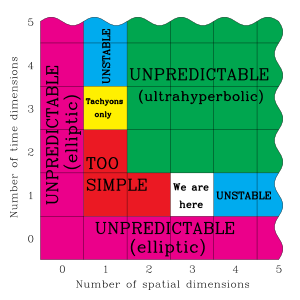
Hay dos tipos de dimensiones: espacial (bidireccional) y temporal (unidireccional). ^[66] Sea N el número de dimensiones espaciales y T el número de dimensiones temporales . Que N = 3 y T = 1 , dejando de lado las dimensiones compactificadas invocadas por la teoría de cuerdas e indetectables hasta la fecha, se puede explicar apelando a las consecuencias físicas de dejar que N difiera de 3 y que T difiera de 1. El argumento es a menudo de carácter antrópico y posiblemente el primero de su tipo, aunque antes de que el concepto completo se pusiera de moda.

La noción implícita de que la dimensionalidad del universo es especial se atribuye por primera vez a Gottfried Wilhelm Leibniz , quien en el Discurso sobre la metafísica sugirió que el mundo es "aquel que es al mismo tiempo el más simple en hipótesis y el más rico en fenómenos". ^[67] Immanuel Kant sostuvo que el espacio tridimensional era una consecuencia de la ley del cuadrado inverso de la gravitación universal . Si bien el argumento de Kant es históricamente importante, John D. Barrow dijo que "recibe el mensaje al revés: es la tridimensionalidad del espacio lo que explica por qué vemos leyes de fuerza del cuadrado inverso en la naturaleza, no al revés" (Barrow 2002:204). ^{[nota 13]}

En 1920, Paul Ehrenfest demostró que si sólo hay una única dimensión temporal y más de tres dimensiones espaciales, la órbita de un planeta alrededor de su Sol no puede permanecer estable. Lo mismo es cierto de la órbita de una estrella alrededor del centro de su galaxia . ^[68] Ehrenfest también demostró que si hay un número par de dimensiones espaciales, entonces las diferentes partes de un impulso de onda viajarán a diferentes velocidades. Si hay dimensiones espaciales, donde k es un número entero positivo, entonces los impulsos de onda se distorsionan. En 1922, Hermann Weyl afirmó que la teoría del electromagnetismo de Maxwell puede expresarse en términos de una acción sólo para una variedad de cuatro dimensiones. ^[69] Finalmente, Tangherlini demostró en 1963 que cuando hay más de tres dimensiones espaciales, los orbitales de los electrones alrededor de los núcleos no pueden ser estables; los electrones caerían en el núcleo o se dispersarían. ^[70]${\displaystyle 5+2k}$

Max Tegmark amplía el argumento precedente de la siguiente manera antrópica. ^[71] Si T difiere de 1, el comportamiento de los sistemas físicos no podría predecirse de manera confiable a partir del conocimiento de las ecuaciones diferenciales parciales relevantes . En un universo así, no podría surgir vida inteligente capaz de manipular la tecnología. Además, si T > 1 , Tegmark mantiene que los protones y electrones serían inestables y podrían desintegrarse en partículas con mayor masa que ellos mismos. (Esto no es un problema si las partículas tienen una temperatura suficientemente baja). ^[71] Por último, si N < 3 , la gravitación de cualquier tipo se vuelve problemática, y el universo probablemente sería demasiado simple para contener observadores. Por ejemplo, cuando N < 3 , los nervios no pueden cruzarse sin intersecar. ^[71] Por lo tanto, los argumentos antrópicos y otros descartan todos los casos excepto N = 3 y T = 1 , que describe el mundo que nos rodea.

Por otra parte, en vista de la creación de agujeros negros a partir de un gas monoatómico ideal bajo su propia gravedad, Wei-Xiang Feng demostró que el espacio-tiempo (3 + 1) -dimensional es la dimensionalidad marginal. Además, es la única dimensionalidad que puede permitir una esfera de gas "estable" con una constante cosmológica "positiva" . Sin embargo, un gas autogravitante no puede estar ligado de manera estable si la esfera de masa es mayor que ~10 ²¹ masas solares, debido a la pequeña positividad de la constante cosmológica observada. ^[72]

En 2019, James Scargill sostuvo que la vida compleja puede ser posible con dos dimensiones espaciales. Según Scargill, una teoría puramente escalar de la gravedad puede permitir una fuerza gravitacional local, y las redes 2D pueden ser suficientes para las redes neuronales complejas. ^{[73] [74]}

• Barrow, John D. ; Tipler, Frank J. (1986). El principio cosmológico antrópico (1.ª ed.). Oxford University Press . ISBN 978-0-19-282147-8. Código LCCN  87028148.
• George F. Ellis y Ruth M. Williams (1992) Espacios-tiempos planos y curvos . Oxford University Press. ISBN 0-19-851164-7 
• Lorentz, HA , Einstein, Albert , Minkowski, Hermann y Weyl, Hermann (1952) El principio de relatividad: una colección de memorias originales . Dover.
• Lucas, John Randolph (1973) Tratado sobre el tiempo y el espacio . Londres: Methuen.
• Penrose, Roger (2004). El camino hacia la realidad . Oxford: Oxford University Press. ISBN 0-679-45443-8.Capítulos 17–18.
• Taylor, EF; Wheeler, John A. (1992). Física del espacio-tiempo, segunda edición. Archivo de Internet: WH Freeman. ISBN 0-7167-2327-1.
• Arkani-Hamed, Nima (1 de diciembre de 2017). La perdición del espacio-tiempo: por qué debe disolverse en estructuras más fundamentales (discurso). La 2384.ª reunión de la Sociedad. Washington, DC . Consultado el 16 de julio de 2022 .

Wikiquote tiene citas relacionadas con Espacio-tiempo .

Wikilibros tiene un libro sobre el tema: Relatividad especial

• Medios relacionados con el espacio-tiempo en Wikimedia Commons
• Albert Einstein sobre el espacio-tiempo 13.ª edición Encyclopædia Britannica Histórico: Artículo de Albert Einstein de 1926
• Enciclopedia del espacio-tiempo y la gravitación Artículos de expertos de Scholarpedia
• Enciclopedia de Filosofía de Stanford : "Espacio y tiempo: marcos inerciales" de Robert DiSalle.