Agujero negro
Un agujero negro es una región del espacio-tiempo donde la gravedad es tan fuerte que nada, ni siquiera la luz y otras ondas electromagnéticas , es capaz de poseer suficiente energía para escapar de ella. [2] La teoría de la relatividad general de Einstein predice que una masa suficientemente compacta puede deformar el espacio-tiempo para formar un agujero negro. [3] [4] El límite de no escape se llama horizonte de sucesos . Un agujero negro tiene un gran efecto en el destino y las circunstancias de un objeto que lo cruza, pero no tiene características detectables localmente según la relatividad general. [5] En muchos sentidos, un agujero negro actúa como un cuerpo negro ideal , ya que no refleja luz. [6] [7] La teoría cuántica de campos en el espacio-tiempo curvo predice que los horizontes de sucesos emiten radiación de Hawking , con el mismo espectro que un cuerpo negro de una temperatura inversamente proporcional a su masa. Esta temperatura es del orden de milmillonésimas de kelvin para los agujeros negros estelares , lo que hace que sea esencialmente imposible de observar directamente.
Los objetos cuyos campos gravitatorios son demasiado fuertes para que la luz escape fueron considerados por primera vez en el siglo XVIII por John Michell y Pierre-Simon Laplace . [8] En 1916, Karl Schwarzschild encontró la primera solución moderna de la relatividad general que caracterizaría a un agujero negro. Debido a su influyente investigación, la métrica de Schwarzschild lleva su nombre. David Finkelstein , en 1958, publicó por primera vez la interpretación de "agujero negro" como una región del espacio de la que nada puede escapar. Los agujeros negros fueron considerados durante mucho tiempo una curiosidad matemática; no fue hasta la década de 1960 que el trabajo teórico demostró que eran una predicción genérica de la relatividad general. El descubrimiento de las estrellas de neutrones por Jocelyn Bell Burnell en 1967 despertó el interés en los objetos compactos colapsados gravitacionalmente como una posible realidad astrofísica. El primer agujero negro conocido fue Cygnus X-1 , identificado por varios investigadores de forma independiente en 1971. [9] [10]
Los agujeros negros de masa estelar se forman cuando las estrellas masivas colapsan al final de su ciclo de vida. Una vez que se ha formado un agujero negro, puede crecer absorbiendo masa de su entorno. Los agujeros negros supermasivos de millones de masas solares ( M ☉ ) pueden formarse absorbiendo otras estrellas y fusionándose con otros agujeros negros, o mediante el colapso directo de nubes de gas . Existe consenso en que los agujeros negros supermasivos existen en los centros de la mayoría de las galaxias .
La presencia de un agujero negro se puede inferir a través de su interacción con otra materia y con la radiación electromagnética como la luz visible. Cualquier materia que cae hacia un agujero negro puede formar un disco de acreción externo calentado por fricción , formando cuásares , algunos de los objetos más brillantes del universo. Las estrellas que pasan demasiado cerca de un agujero negro supermasivo pueden ser trituradas en serpentinas que brillan muy intensamente antes de ser "tragadas". [11] Si otras estrellas están orbitando un agujero negro, sus órbitas se pueden utilizar para determinar la masa y la ubicación del agujero negro. Tales observaciones se pueden utilizar para excluir posibles alternativas como las estrellas de neutrones. De esta manera, los astrónomos han identificado numerosos candidatos a agujeros negros estelares en sistemas binarios y han establecido que la fuente de radio conocida como Sagitario A* , en el núcleo de la galaxia Vía Láctea , contiene un agujero negro supermasivo de aproximadamente 4,3 millones de masas solares .
Historia
La idea de un cuerpo tan grande que ni siquiera la luz pudiera escapar fue propuesta brevemente por el pionero astrónomo y clérigo inglés John Michell en una carta publicada en noviembre de 1784. Los cálculos simplistas de Michell asumieron que un cuerpo así podría tener la misma densidad que el Sol, y concluyeron que uno se formaría cuando el diámetro de una estrella exceda al del Sol por un factor de 500, y su velocidad de escape superficial exceda la velocidad habitual de la luz. Michell señaló correctamente que tales cuerpos supermasivos pero no radiantes podrían ser detectables a través de sus efectos gravitacionales sobre los cuerpos visibles cercanos. [8] [12] [13] Los académicos de la época se entusiasmaron inicialmente con la propuesta de que gigantescas pero invisibles "estrellas oscuras" podrían estar escondidas a simple vista, pero el entusiasmo se enfrió cuando la naturaleza ondulatoria de la luz se hizo evidente a principios del siglo XIX, [14] como si la luz fuera una onda en lugar de una partícula, no estaba claro qué influencia, si es que tenía alguna, tendría la gravedad sobre las ondas de luz que escapan. [8] [13]
La teoría moderna de la gravedad, la relatividad general, desacredita la noción de Michell de que un rayo de luz se dispara directamente desde la superficie de una estrella supermasiva, es desacelerado por la gravedad de la estrella, se detiene y luego cae libremente de nuevo a la superficie de la estrella. [15] En cambio, el espacio-tiempo en sí mismo está curvado de tal manera que la geodésica por la que viaja la luz nunca abandona la superficie de la "estrella" (agujero negro).
Relatividad general
| Relatividad general |
|---|
 |
En 1915, Albert Einstein desarrolló su teoría de la relatividad general , habiendo demostrado anteriormente que la gravedad influye en el movimiento de la luz. Solo unos meses después, Karl Schwarzschild encontró una solución a las ecuaciones de campo de Einstein que describe el campo gravitatorio de una masa puntual y una masa esférica. [16] [17] Unos meses después de Schwarzschild, Johannes Droste , un estudiante de Hendrik Lorentz , dio de forma independiente la misma solución para la masa puntual y escribió más extensamente sobre sus propiedades. [18] [19] Esta solución tuvo un comportamiento peculiar en lo que ahora se llama el radio de Schwarzschild , donde se volvió singular , lo que significa que algunos de los términos en las ecuaciones de Einstein se volvieron infinitos. La naturaleza de esta superficie no se entendió bien en ese momento.
En 1924, Arthur Eddington demostró que la singularidad desaparecía tras un cambio de coordenadas. En 1933, Georges Lemaître se dio cuenta de que esto significaba que la singularidad en el radio de Schwarzschild era una singularidad de coordenadas no física . [20] Arthur Eddington comentó sobre la posibilidad de una estrella con masa comprimida al radio de Schwarzschild en un libro de 1926, señalando que la teoría de Einstein nos permite descartar densidades demasiado grandes para estrellas visibles como Betelgeuse porque "una estrella de 250 millones de kilómetros de radio no podría tener una densidad tan alta como el Sol. En primer lugar, la fuerza de la gravedad sería tan grande que la luz no podría escapar de ella, los rayos caerían de nuevo a la estrella como una piedra a la tierra. En segundo lugar, el desplazamiento hacia el rojo de las líneas espectrales sería tan grande que el espectro se desplazaría hasta dejar de existir. En tercer lugar, la masa produciría tanta curvatura de la métrica del espacio-tiempo que el espacio se cerraría alrededor de la estrella, dejándonos fuera (es decir, en ninguna parte)". [21] [22]
En 1931, Subrahmanyan Chandrasekhar calculó, utilizando la relatividad especial, que un cuerpo no giratorio de materia degenerada en electrones por encima de una cierta masa límite (ahora llamada límite de Chandrasekhar en 1,4 M ☉ ) no tiene soluciones estables. [23] Sus argumentos fueron rechazados por muchos de sus contemporáneos como Eddington y Lev Landau , quienes argumentaron que algún mecanismo aún desconocido detendría el colapso. [24] Estaban parcialmente en lo cierto: una enana blanca ligeramente más masiva que el límite de Chandrasekhar colapsará en una estrella de neutrones , [25] que es en sí misma estable.
En 1939, Robert Oppenheimer y otros predijeron que las estrellas de neutrones por encima de otro límite, el límite de Tolman-Oppenheimer-Volkoff , colapsarían aún más por las razones presentadas por Chandrasekhar, y concluyeron que no era probable que ninguna ley de la física interviniera y detuviera al menos algunas estrellas de colapsar en agujeros negros. [26] Sus cálculos originales, basados en el principio de exclusión de Pauli , lo dieron como 0,7 M ☉ . La consideración posterior de la repulsión neutrón-neutrón mediada por la fuerza fuerte elevó la estimación a aproximadamente 1,5 M ☉ a 3,0 M ☉ . [27] Las observaciones de la fusión de estrellas de neutrones GW170817 , que se cree que generó un agujero negro poco después, han refinado la estimación del límite TOV a ~2,17 M ☉ . [28] [29] [30] [31] [32]
Oppenheimer y sus coautores interpretaron la singularidad en el límite del radio de Schwarzschild como una indicación de que se trataba del límite de una burbuja en la que el tiempo se detenía. Este es un punto de vista válido para los observadores externos, pero no para los observadores que caen sobre la estrella. Las hipotéticas estrellas colapsadas se denominaron "estrellas congeladas", porque un observador externo vería la superficie de la estrella congelada en el tiempo en el instante en que su colapso la lleva al radio de Schwarzschild. [33]
En 1939, Einstein intentó demostrar que los agujeros negros eran imposibles en su artículo "Sobre un sistema estacionario con simetría esférica que consta de muchas masas gravitantes", utilizando su teoría de la relatividad general para defender su argumento. [34] Meses después, Oppenheimer y su alumno Hartland Snyder proporcionaron el modelo de Oppenheimer-Snyder en su artículo "Sobre la contracción gravitacional continua", [35] que predijo la existencia de agujeros negros. En el artículo, que no hacía referencia a la reciente publicación de Einstein, Oppenheimer y Snyder utilizaron la propia teoría de la relatividad general de Einstein para mostrar las condiciones en las que un agujero negro podría desarrollarse, por primera vez en la física contemporánea. [34]
Edad de oro
En 1958, David Finkelstein identificó la superficie de Schwarzschild como un horizonte de sucesos , "una membrana unidireccional perfecta: las influencias causales pueden atravesarla sólo en una dirección". [36] Esto no contradecía estrictamente los resultados de Oppenheimer, pero los amplió para incluir el punto de vista de los observadores que caen. La solución de Finkelstein extendió la solución de Schwarzschild para el futuro de los observadores que caen en un agujero negro. Martin Kruskal ya había encontrado una extensión completa , a quien se le instó a publicarla. [37]
Estos resultados se produjeron al comienzo de la edad de oro de la relatividad general , que se caracterizó por la conversión de la relatividad general y los agujeros negros en temas de investigación de primer orden. Este proceso se vio facilitado por el descubrimiento de los púlsares por Jocelyn Bell Burnell en 1967, [38] [39] que, en 1969, se demostró que eran estrellas de neutrones que giraban rápidamente. [40] Hasta ese momento, las estrellas de neutrones, al igual que los agujeros negros, se consideraban meras curiosidades teóricas; pero el descubrimiento de los púlsares mostró su relevancia física y estimuló un mayor interés en todos los tipos de objetos compactos que podrían formarse por colapso gravitacional. [41]
En este período se encontraron soluciones más generales para los agujeros negros. En 1963, Roy Kerr encontró la solución exacta para un agujero negro giratorio . Dos años después, Ezra Newman encontró la solución axisimétrica para un agujero negro que rota y está cargado eléctricamente . [42] A través del trabajo de Werner Israel , [43] Brandon Carter , [44] [45] y David Robinson [46] surgió el teorema de no-hair , que establece que una solución de agujero negro estacionario está completamente descrita por los tres parámetros de la métrica de Kerr-Newman : masa , momento angular y carga eléctrica. [47]
Al principio, se sospechó que las características extrañas de las soluciones de los agujeros negros eran artefactos patológicos de las condiciones de simetría impuestas, y que las singularidades no aparecerían en situaciones genéricas. Esta opinión fue sostenida en particular por Vladimir Belinsky , Isaak Khalatnikov y Evgeny Lifshitz , quienes intentaron demostrar que no aparecen singularidades en soluciones genéricas. Sin embargo, a finales de la década de 1960 Roger Penrose [48] y Stephen Hawking utilizaron técnicas globales para demostrar que las singularidades aparecen de forma genérica. [49] Por este trabajo, Penrose recibió la mitad del Premio Nobel de Física de 2020 , ya que Hawking murió en 2018. [50] Basándose en observaciones en Greenwich y Toronto a principios de la década de 1970, Cygnus X-1 , una fuente de rayos X galáctica descubierta en 1964, se convirtió en el primer objeto astronómico comúnmente aceptado como un agujero negro. [51] [52]
El trabajo de James Bardeen , Jacob Bekenstein , Carter y Hawking a principios de la década de 1970 condujo a la formulación de la termodinámica de los agujeros negros . [53] Estas leyes describen el comportamiento de un agujero negro en estrecha analogía con las leyes de la termodinámica al relacionar la masa con la energía, el área con la entropía y la gravedad superficial con la temperatura . La analogía se completó cuando Hawking, en 1974, demostró que la teoría cuántica de campos implica que los agujeros negros deberían radiar como un cuerpo negro con una temperatura proporcional a la gravedad superficial del agujero negro, prediciendo el efecto ahora conocido como radiación de Hawking . [54]
Observación
El 11 de febrero de 2016, la Colaboración Científica LIGO y la colaboración Virgo anunciaron la primera detección directa de ondas gravitacionales , lo que representa la primera observación de una fusión de agujeros negros. [55] El 10 de abril de 2019, se publicó la primera imagen directa de un agujero negro y sus alrededores, luego de las observaciones realizadas por el Event Horizon Telescope (EHT) en 2017 del agujero negro supermasivo en el centro galáctico de Messier 87. [56] [57] [58] A partir de 2023 , el cuerpo más cercano conocido que se cree que es un agujero negro, Gaia BH1 , está a unos 1560 años luz (480 parsecs ) de distancia. [59] Aunque hasta ahora solo se han encontrado un par de docenas de agujeros negros en la Vía Láctea , se cree que hay cientos de millones, la mayoría de los cuales son solitarios y no causan emisión de radiación. [60] Por lo tanto, sólo serían detectables mediante lentes gravitacionales .[update]
Etimología
John Michell utilizó el término "estrella oscura" en una carta de noviembre de 1783 a Henry Cavendish [ cita requerida ] , y a principios del siglo XX, los físicos utilizaron el término "objeto colapsado gravitacionalmente". La escritora científica Marcia Bartusiak rastrea el término "agujero negro" hasta el físico Robert H. Dicke , quien a principios de la década de 1960, según se informa, comparó el fenómeno con el Agujero Negro de Calcuta , famoso por ser una prisión donde la gente entraba pero nunca salía con vida. [61]
El término "agujero negro" fue utilizado en forma impresa por las revistas Life y Science News en 1963, [61] y por la periodista científica Ann Ewing en su artículo " 'Agujeros negros' en el espacio", fechado el 18 de enero de 1964, que era un informe sobre una reunión de la Asociación Americana para el Avance de la Ciencia celebrada en Cleveland, Ohio. [62] [63]
En diciembre de 1967, un estudiante supuestamente sugirió la frase "agujero negro" en una conferencia de John Wheeler ; [62] Wheeler adoptó el término por su brevedad y "valor publicitario", y rápidamente se popularizó, [64] lo que llevó a algunos a atribuirle a Wheeler la creación de la frase. [65]
Propiedades y estructura
El teorema de la ausencia de pelo postula que, una vez que alcanza una condición estable después de su formación, un agujero negro tiene solo tres propiedades físicas independientes: masa, carga eléctrica y momento angular; el agujero negro no tiene otras características. Si la conjetura es cierta, dos agujeros negros cualesquiera que compartan los mismos valores para estas propiedades o parámetros son indistinguibles entre sí. El grado en que la conjetura es cierta para los agujeros negros reales bajo las leyes de la física moderna es actualmente un problema sin resolver. [47]
Estas propiedades son especiales porque son visibles desde el exterior de un agujero negro. Por ejemplo, un agujero negro cargado repele otras cargas similares al igual que cualquier otro objeto cargado. De manera similar, la masa total dentro de una esfera que contiene un agujero negro se puede encontrar utilizando el análogo gravitacional de la ley de Gauss (a través de la masa ADM ), lejos del agujero negro. [66] De la misma manera, el momento angular (o giro) se puede medir desde lejos utilizando el arrastre de marcos por el campo gravitomagnético , a través, por ejemplo, del efecto Lense-Thirring . [67]

Cuando un objeto cae en un agujero negro, cualquier información sobre la forma del objeto o la distribución de la carga en él se distribuye uniformemente a lo largo del horizonte del agujero negro y se pierde para los observadores externos. El comportamiento del horizonte en esta situación es un sistema disipativo que es muy análogo al de una membrana elástica conductora con fricción y resistencia eléctrica : el paradigma de la membrana . [68] Esto es diferente de otras teorías de campo como el electromagnetismo, que no tienen fricción ni resistividad a nivel microscópico, porque son reversibles en el tiempo . [69] [70]
Como un agujero negro finalmente alcanza un estado estable con solo tres parámetros, no hay forma de evitar la pérdida de información sobre las condiciones iniciales: los campos gravitatorios y eléctricos de un agujero negro brindan muy poca información sobre lo que entró. La información que se pierde incluye todas las cantidades que no se pueden medir lejos del horizonte del agujero negro, incluidos los números cuánticos aproximadamente conservados , como el número bariónico total y el número leptónico . Este comportamiento es tan desconcertante que se lo ha llamado la paradoja de la pérdida de información del agujero negro . [69] [71]
Propiedades físicas
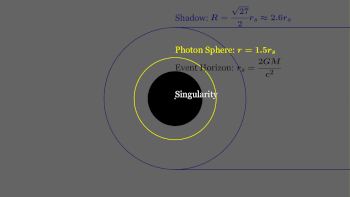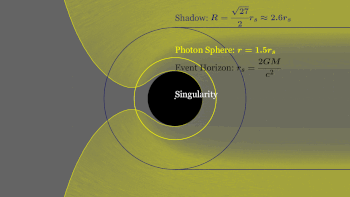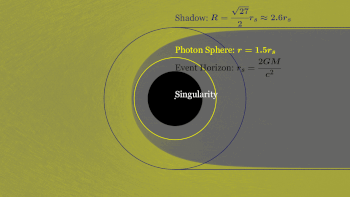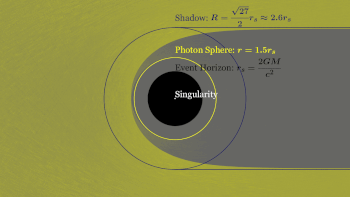
Los agujeros negros estáticos más simples tienen masa pero no carga eléctrica ni momento angular. A estos agujeros negros se los suele denominar agujeros negros de Schwarzschild en honor a Karl Schwarzschild, quien descubrió esta solución en 1916. [17] Según el teorema de Birkhoff , es la única solución de vacío que es esféricamente simétrica . [72] Esto significa que no hay diferencia observable a distancia entre el campo gravitatorio de un agujero negro de este tipo y el de cualquier otro objeto esférico de la misma masa. Por lo tanto, la noción popular de un agujero negro que "absorbe todo" a su alrededor es correcta solo cerca del horizonte de un agujero negro; lejos, el campo gravitatorio externo es idéntico al de cualquier otro cuerpo de la misma masa. [73]
También existen soluciones que describen agujeros negros más generales. Los agujeros negros cargados que no giran se describen mediante la métrica de Reissner-Nordström , mientras que la métrica de Kerr describe un agujero negro giratorio sin carga. La solución de agujero negro estacionario más general conocida es la métrica de Kerr-Newman, que describe un agujero negro con carga y momento angular. [74]
Si bien la masa de un agujero negro puede tomar cualquier valor positivo, la carga y el momento angular están limitados por la masa. Se espera que la carga eléctrica total Q y el momento angular total J satisfagan la desigualdad
para un agujero negro de masa M . Los agujeros negros con la mínima masa posible que satisface esta desigualdad se denominan extremos . Existen soluciones de las ecuaciones de Einstein que violan esta desigualdad, pero no poseen un horizonte de sucesos. Estas soluciones tienen las llamadas singularidades desnudas que se pueden observar desde el exterior y, por lo tanto, se consideran no físicas . La hipótesis de la censura cósmica descarta la formación de tales singularidades, cuando se crean a través del colapso gravitacional de materia realista . [3] Esto está respaldado por simulaciones numéricas. [75]
Debido a la fuerza relativamente grande de la fuerza electromagnética , se espera que los agujeros negros que se forman a partir del colapso de estrellas conserven la carga casi neutra de la estrella. Sin embargo, se espera que la rotación sea una característica universal de los objetos astrofísicos compactos. La fuente binaria de rayos X candidata a agujero negro GRS 1915+105 [76] parece tener un momento angular cercano al valor máximo permitido. Ese límite sin carga es [77]
permitiendo la definición de un parámetro de espín adimensional tal que [77]
- [77] [Nota 1]
| Clase | Masa aproximada | Radio aproximado |
|---|---|---|
| Agujero negro ultramasivo | 109 –1011 M ☉ | >1.000 UA |
| Agujero negro supermasivo | 106 –109 M ☉ | 0,001–400 UA |
| Agujero negro de masa intermedia | 102 –105 millones ☉ | 10 3 km ≈ R Tierra |
| Agujero negro estelar | 2-150 millones ☉ | 30 kilómetros |
| Microagujero negro | hasta M Luna | hasta 0,1 mm |
Los agujeros negros se clasifican comúnmente según su masa, independientemente del momento angular, J . El tamaño de un agujero negro, determinado por el radio del horizonte de sucesos, o radio de Schwarzschild, es proporcional a la masa, M , a través de
donde r s es el radio de Schwarzschild y M ☉ es la masa del Sol . [79] Para un agujero negro con espín y/o carga eléctrica distintos de cero, el radio es menor, [Nota 2] hasta que un agujero negro extremal podría tener un horizonte de eventos cercano a [80]
Horizonte de eventos
La característica que define a un agujero negro es la aparición de un horizonte de sucesos, un límite en el espacio-tiempo a través del cual la materia y la luz pueden pasar solo hacia el interior, en dirección a la masa del agujero negro. Nada, ni siquiera la luz, puede escapar del interior del horizonte de sucesos. [82] [83] Se hace referencia al horizonte de sucesos como tal porque si un suceso ocurre dentro del límite, la información de ese suceso no puede llegar a un observador externo, lo que hace imposible determinar si tal suceso ocurrió. [84]
Como predice la relatividad general, la presencia de una masa deforma el espacio-tiempo de tal manera que los caminos tomados por las partículas se desvían hacia la masa. [85] En el horizonte de sucesos de un agujero negro, esta deformación se vuelve tan fuerte que no hay caminos que se alejen del agujero negro. [86]
Para un observador distante, los relojes cerca de un agujero negro parecerían funcionar más lentamente que aquellos más alejados del agujero negro. [87] Debido a este efecto, conocido como dilatación del tiempo gravitacional , un objeto que cae en un agujero negro parece desacelerarse a medida que se acerca al horizonte de sucesos, y tarda una cantidad infinita de tiempo en alcanzarlo. [88] Al mismo tiempo, todos los procesos en este objeto se desaceleran, desde el punto de vista de un observador externo fijo, lo que hace que cualquier luz emitida por el objeto parezca más roja y tenue, un efecto conocido como corrimiento al rojo gravitacional . [89] Finalmente, el objeto que cae se desvanece hasta que ya no se puede ver. Normalmente, este proceso ocurre muy rápidamente y un objeto desaparece de la vista en menos de un segundo. [90]
Por otra parte, los observadores indestructibles que caen en un agujero negro no notan ninguno de estos efectos al cruzar el horizonte de sucesos. Según sus propios relojes, que les parecen funcionar normalmente, cruzan el horizonte de sucesos después de un tiempo finito sin notar ningún comportamiento singular; en la relatividad general clásica, es imposible determinar la ubicación del horizonte de sucesos a partir de observaciones locales, debido al principio de equivalencia de Einstein . [91] [92]
La topología del horizonte de sucesos de un agujero negro en equilibrio es siempre esférica. [Nota 4] [95] Para los agujeros negros no rotatorios (estáticos), la geometría del horizonte de sucesos es precisamente esférica, mientras que para los agujeros negros rotatorios el horizonte de sucesos es achatado. [96] [97] [98]
Singularidad
En el centro de un agujero negro, como se describe en la relatividad general, puede haber una singularidad gravitacional , una región donde la curvatura del espacio-tiempo se vuelve infinita. [99] Para un agujero negro que no gira, esta región toma la forma de un único punto; para un agujero negro que gira, se extiende hasta formar una singularidad de anillo que se encuentra en el plano de rotación. [100] En ambos casos, la región singular tiene volumen cero. También se puede demostrar que la región singular contiene toda la masa de la solución del agujero negro. [101] Por lo tanto, se puede pensar que la región singular tiene una densidad infinita . [102]
Los observadores que caen en un agujero negro de Schwarzschild (es decir, que no gira y no tiene carga) no pueden evitar ser arrastrados hacia la singularidad una vez que cruzan el horizonte de sucesos. Pueden prolongar la experiencia acelerando para frenar su descenso, pero sólo hasta cierto límite. [103] Cuando alcanzan la singularidad, son aplastados hasta una densidad infinita y su masa se suma a la total del agujero negro. Antes de que eso suceda, habrán sido destrozados por las crecientes fuerzas de marea en un proceso que a veces se denomina espaguetificación o "efecto fideo". [104]
En el caso de un agujero negro cargado (Reissner–Nordström) o rotatorio (Kerr), es posible evitar la singularidad. Extendiendo estas soluciones lo más posible se revela la posibilidad hipotética de salir del agujero negro hacia un espacio-tiempo diferente con el agujero negro actuando como un agujero de gusano . [105] La posibilidad de viajar a otro universo es, sin embargo, solo teórica ya que cualquier perturbación destruiría esta posibilidad. [106] También parece ser posible seguir curvas temporales cerradas (regresando al propio pasado) alrededor de la singularidad de Kerr, lo que conduce a problemas con la causalidad como la paradoja del abuelo . [107] Se espera que ninguno de estos efectos peculiares sobreviva en un tratamiento cuántico adecuado de los agujeros negros rotatorios y cargados. [108]
La aparición de singularidades en la relatividad general se percibe comúnmente como una señal del colapso de la teoría. [109] Sin embargo, este colapso es esperado; ocurre en una situación en la que los efectos cuánticos deberían describir estas acciones, debido a la densidad extremadamente alta y, por lo tanto, a las interacciones de partículas. Hasta la fecha, no ha sido posible combinar los efectos cuánticos y gravitacionales en una sola teoría, aunque existen intentos de formular tal teoría de la gravedad cuántica . En general, se espera que dicha teoría no presente ninguna singularidad. [110] [111]
Esfera de fotones
La esfera de fotones es un límite esférico donde los fotones que se mueven tangentes a esa esfera quedarían atrapados en una órbita no estable pero circular alrededor del agujero negro. [112] Para los agujeros negros que no giran, la esfera de fotones tiene un radio 1,5 veces el radio de Schwarzschild. Sus órbitas serían dinámicamente inestables , por lo tanto, cualquier pequeña perturbación, como una partícula de materia que caiga, causaría una inestabilidad que crecería con el tiempo, ya sea colocando al fotón en una trayectoria hacia afuera haciendo que escape del agujero negro, o en una espiral hacia adentro donde eventualmente cruzaría el horizonte de eventos. [113]
Aunque la luz todavía puede escapar de la esfera de fotones, cualquier luz que la cruce en una trayectoria de entrada será capturada por el agujero negro. Por lo tanto, cualquier luz que llegue a un observador externo desde la esfera de fotones debe haber sido emitida por objetos entre la esfera de fotones y el horizonte de sucesos. [113] Para un agujero negro de Kerr, el radio de la esfera de fotones depende del parámetro de giro y de los detalles de la órbita del fotón, que puede ser prograda (el fotón gira en el mismo sentido del giro del agujero negro) o retrógrada. [114] [115]
Ergosfera
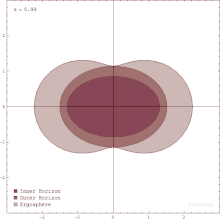
Los agujeros negros que giran están rodeados por una región del espacio-tiempo en la que es imposible permanecer inmóvil, llamada ergosfera. Este es el resultado de un proceso conocido como arrastre de marco ; la relatividad general predice que cualquier masa que gira tenderá a "arrastrarse" ligeramente a lo largo del espacio-tiempo que la rodea inmediatamente. Cualquier objeto cerca de la masa que gira tenderá a comenzar a moverse en la dirección de rotación. Para un agujero negro que gira, este efecto es tan fuerte cerca del horizonte de sucesos que un objeto tendría que moverse más rápido que la velocidad de la luz en la dirección opuesta para simplemente permanecer inmóvil. [117]
La ergosfera de un agujero negro es un volumen delimitado por el horizonte de sucesos del agujero negro y la ergosuperficie , que coincide con el horizonte de sucesos en los polos pero está a una distancia mucho mayor alrededor del ecuador. [116]
Los objetos y la radiación pueden escapar normalmente de la ergosfera. A través del proceso de Penrose , los objetos pueden emerger de la ergosfera con más energía de la que tenían al entrar. La energía extra se toma de la energía rotacional del agujero negro. De ese modo, la rotación del agujero negro se ralentiza. [118] Una variación del proceso de Penrose en presencia de fuertes campos magnéticos, el proceso de Blandford-Znajek se considera un mecanismo probable para la enorme luminosidad y los chorros relativistas de los cuásares y otros núcleos galácticos activos .
Órbita circular estable más interna (CIUO)
En la gravedad newtoniana , las partículas de prueba pueden orbitar de manera estable a distancias arbitrarias de un objeto central. Sin embargo, en la relatividad general, existe una órbita circular estable más interna (a menudo llamada ISCO), para la cual cualquier perturbación infinitesimal hacia adentro de una órbita circular conducirá a una espiral hacia el agujero negro, y cualquier perturbación hacia afuera, dependiendo de la energía, resultará en una espiral hacia adentro, orbitando de manera estable entre el apastrón y el periastrón, o escapando al infinito. [119] La ubicación de la ISCO depende del giro del agujero negro, en el caso de un agujero negro de Schwarzschild (espín cero) es:
y disminuye a medida que aumenta el giro del agujero negro para las partículas que orbitan en la misma dirección que el giro. [120]
Región de hundimiento
La última región observable del espacio-tiempo alrededor de un agujero negro se denomina región de caída. En esta zona la materia ya no puede seguir órbitas circulares ni detener su descenso final hacia el agujero negro, sino que se precipitará rápidamente hacia el agujero negro a una velocidad cercana a la de la luz. [121] [122]
Formación y evolución
Dada la extraña naturaleza de los agujeros negros, durante mucho tiempo se cuestionó si tales objetos podían existir realmente en la naturaleza o si eran simplemente soluciones patológicas a las ecuaciones de Einstein. El propio Einstein pensó erróneamente que los agujeros negros no se formarían, porque sostenía que el momento angular de las partículas que colapsan estabilizaría su movimiento en un radio determinado. [123] Esto llevó a la comunidad de la relatividad general a descartar todos los resultados en sentido contrario durante muchos años. Sin embargo, una minoría de relativistas siguió sosteniendo que los agujeros negros eran objetos físicos, [124] y a finales de la década de 1960, habían persuadido a la mayoría de los investigadores en el campo de que no hay ningún obstáculo para la formación de un horizonte de sucesos. [125]
Penrose demostró que una vez que se forma un horizonte de eventos, la relatividad general sin mecánica cuántica requiere que se forme una singularidad en su interior. [48] Poco después, Hawking demostró que muchas soluciones cosmológicas que describen el Big Bang tienen singularidades sin campos escalares u otra materia exótica . [ aclaración necesaria ] La solución de Kerr , el teorema sin pelo y las leyes de la termodinámica de los agujeros negros demostraron que las propiedades físicas de los agujeros negros eran simples y comprensibles, lo que los convertía en temas respetables para la investigación. [126] Los agujeros negros convencionales se forman por el colapso gravitacional de objetos pesados como las estrellas, pero en teoría también pueden formarse por otros procesos. [127] [128]
Colapso gravitacional

El colapso gravitacional ocurre cuando la presión interna de un objeto es insuficiente para resistir la propia gravedad del objeto. En el caso de las estrellas, esto suele ocurrir porque a la estrella le queda muy poco "combustible" para mantener su temperatura mediante la nucleosíntesis estelar o porque una estrella que habría sido estable recibe materia adicional de una manera que no aumenta su temperatura central. En cualquier caso, la temperatura de la estrella ya no es lo suficientemente alta como para evitar que colapse por su propio peso. [130]
El colapso puede ser detenido por la presión de degeneración de los constituyentes de la estrella, permitiendo la condensación de la materia en un estado exótico más denso . El resultado es uno de los varios tipos de estrella compacta . El tipo que se forma depende de la masa del remanente de la estrella original que queda si las capas externas han sido expulsadas (por ejemplo, en una supernova de tipo II ). La masa del remanente, el objeto colapsado que sobrevive a la explosión, puede ser sustancialmente menor que la de la estrella original. Los remanentes que superan los 5 M☉ son producidos por estrellas que tenían más de 20 M☉ antes del colapso. [130]
Si la masa del remanente excede aproximadamente 3–4 M☉ (el límite de Tolman–Oppenheimer–Volkoff [ 26] ), ya sea porque la estrella original era muy pesada o porque el remanente acumuló masa adicional mediante la acreción de materia, incluso la presión de degeneración de neutrones es insuficiente para detener el colapso. Ningún mecanismo conocido (excepto posiblemente la presión de degeneración de quarks) es lo suficientemente poderoso para detener la implosión y el objeto colapsará inevitablemente para formar un agujero negro. [130]
Se supone que el colapso gravitacional de estrellas pesadas es responsable de la formación de agujeros negros de masa estelar . La formación de estrellas en el universo temprano puede haber dado lugar a estrellas muy masivas, que al colapsar habrían producido agujeros negros de hasta 103 M ☉ . Estos agujeros negros podrían ser las semillas de los agujeros negros supermasivos que se encuentran en los centros de la mayoría de las galaxias. [131] Se ha sugerido además que los agujeros negros masivos con masas típicas de ~105 M ☉ podría haberse formado a partir del colapso directo de nubes de gas en el universo joven. [127] Estos objetos masivos han sido propuestos como las semillas que eventualmente formaron los primeros cuásares observados ya en el corrimiento al rojo. [132] Algunos candidatos para tales objetos se han encontrado en observaciones del universo joven. [127]
Aunque la mayor parte de la energía liberada durante el colapso gravitacional se emite muy rápidamente, un observador externo no ve realmente el final de este proceso. Aunque el colapso lleva una cantidad finita de tiempo desde el marco de referencia de la materia que cae, un observador distante vería que el material que cae se ralentiza y se detiene justo por encima del horizonte de sucesos, debido a la dilatación del tiempo gravitacional. La luz del material que colapsa tarda cada vez más en llegar al observador, y la luz emitida justo antes de que se forme el horizonte de sucesos se retrasa una cantidad infinita de tiempo. Por lo tanto, el observador externo nunca ve la formación del horizonte de sucesos; en cambio, el material que colapsa parece volverse más tenue y cada vez más desplazado hacia el rojo, hasta que finalmente se desvanece. [133]
Los agujeros negros primordiales y el Big Bang
El colapso gravitacional requiere una gran densidad. En la época actual del universo, estas altas densidades se encuentran solo en las estrellas, pero en el universo primitivo, poco después del Big Bang, las densidades eran mucho mayores, lo que posiblemente permitió la creación de agujeros negros. La alta densidad por sí sola no es suficiente para permitir la formación de agujeros negros, ya que una distribución de masa uniforme no permitirá que la masa se amontone. Para que los agujeros negros primordiales se hayan formado en un medio tan denso, debe haber habido perturbaciones iniciales de densidad que luego pudieron crecer bajo su propia gravedad. Diferentes modelos para el universo primitivo varían ampliamente en sus predicciones de la escala de estas fluctuaciones. Varios modelos predicen la creación de agujeros negros primordiales que varían en tamaño desde una masa de Planck ( ≈1,2 × 10 19 GeV/ c 2 ≈2,2 × 10 −8 kg ) a cientos de miles de masas solares. [128]
A pesar de que el universo primitivo era extremadamente denso , no volvió a colapsar en un agujero negro durante el Big Bang, ya que la tasa de expansión fue mayor que la atracción. Siguiendo la teoría de la inflación, hubo una gravitación neta repulsiva en el comienzo hasta el final de la inflación. Desde entonces, el flujo de Hubble se vio frenado por la densidad energética del universo.
Los modelos para el colapso gravitacional de objetos de tamaño relativamente constante, como las estrellas , no necesariamente se aplican de la misma manera al espacio en rápida expansión, como el Big Bang. [134]
Colisiones de alta energía
El colapso gravitacional no es el único proceso que podría crear agujeros negros. En principio, los agujeros negros podrían formarse en colisiones de alta energía que alcancen una densidad suficiente. Hasta 2002, no se había detectado ningún evento de este tipo, ni directa ni indirectamente como una deficiencia del balance de masa en los experimentos con aceleradores de partículas . [135] Esto sugiere que debe haber un límite inferior para la masa de los agujeros negros. Teóricamente, se espera que este límite se encuentre alrededor de la masa de Planck, donde se espera que los efectos cuánticos invaliden las predicciones de la relatividad general. [136]
Esto dejaría la creación de agujeros negros firmemente fuera del alcance de cualquier proceso de alta energía que ocurra en la Tierra o cerca de ella. Sin embargo, ciertos avances en la gravedad cuántica sugieren que la masa mínima del agujero negro podría ser mucho menor: algunos escenarios de branaworld , por ejemplo, establecen el límite tan bajo como1 TeV/ c 2 . [137] Esto haría concebible que se crearan microagujeros negros en las colisiones de alta energía que ocurren cuando los rayos cósmicos golpean la atmósfera de la Tierra, o posiblemente en el Gran Colisionador de Hadrones del CERN . Estas teorías son muy especulativas, y muchos especialistas consideran improbable la creación de agujeros negros en estos procesos. [138] Incluso si pudieran formarse microagujeros negros, se espera que se evaporarían en unos 10 −25 segundos, sin representar una amenaza para la Tierra. [139]
Crecimiento
Una vez que se ha formado un agujero negro, puede seguir creciendo absorbiendo materia adicional . Cualquier agujero negro absorberá continuamente gas y polvo interestelar de sus alrededores. Este proceso de crecimiento es una forma posible a través de la cual se pueden haber formado algunos agujeros negros supermasivos, aunque la formación de agujeros negros supermasivos todavía es un campo de investigación abierto. [131] Se ha sugerido un proceso similar para la formación de agujeros negros de masa intermedia que se encuentran en cúmulos globulares . [140] Los agujeros negros también pueden fusionarse con otros objetos como estrellas o incluso otros agujeros negros. Se cree que esto ha sido importante, especialmente en el crecimiento temprano de los agujeros negros supermasivos, que podrían haberse formado a partir de la agregación de muchos objetos más pequeños. [131] El proceso también se ha propuesto como el origen de algunos agujeros negros de masa intermedia. [141] [142]
Evaporación
En 1974, Hawking predijo que los agujeros negros no son completamente negros, sino que emiten pequeñas cantidades de radiación térmica a una temperatura ħc 3 /(8 πGM k B ); [54] este efecto se ha conocido como radiación de Hawking. Al aplicar la teoría cuántica de campos a un fondo de agujero negro estático, determinó que un agujero negro debería emitir partículas que muestren un espectro de cuerpo negro perfecto . Desde la publicación de Hawking, muchos otros han verificado el resultado a través de varios enfoques. [143] Si la teoría de Hawking sobre la radiación de los agujeros negros es correcta, entonces se espera que los agujeros negros se encojan y se evaporen con el tiempo a medida que pierden masa por la emisión de fotones y otras partículas. [54] La temperatura de este espectro térmico ( temperatura de Hawking ) es proporcional a la gravedad superficial del agujero negro, que, para un agujero negro de Schwarzschild, es inversamente proporcional a la masa. Por lo tanto, los agujeros negros grandes emiten menos radiación que los agujeros negros pequeños. [144]
Un agujero negro estelar de 1 M☉ tiene una temperatura de Hawking de 62 nanokelvins . [145] Esto es mucho menor que la temperatura de 2,7 K de la radiación de microondas de fondo cósmico . Los agujeros negros de masa estelar o mayores reciben más masa del fondo cósmico de microondas de la que emiten a través de la radiación de Hawking y, por lo tanto, crecerán en lugar de encogerse. [ 146] Para tener una temperatura de Hawking mayor que 2,7 K (y poder evaporarse), un agujero negro necesitaría una masa menor que la de la Luna . Un agujero negro de este tipo tendría un diámetro de menos de una décima de milímetro. [147]
Si un agujero negro es muy pequeño, se espera que los efectos de la radiación sean muy fuertes. Un agujero negro con la masa de un automóvil tendría un diámetro de aproximadamente 10 −24 m y tardaría un nanosegundo en evaporarse, tiempo durante el cual tendría brevemente una luminosidad de más de 200 veces la del Sol. Se espera que los agujeros negros de menor masa se evaporen aún más rápido; por ejemplo, un agujero negro de masa 1 TeV/ c 2 tardaría menos de 10 −88 segundos en evaporarse por completo. Para un agujero negro tan pequeño, se espera que los efectos de la gravedad cuántica desempeñen un papel importante y podrían hipotéticamente hacer que un agujero negro tan pequeño sea estable, aunque los avances actuales en gravedad cuántica no indican que este sea el caso. [148] [149]
Se prevé que la radiación de Hawking de un agujero negro astrofísico sea muy débil y, por lo tanto, sería extremadamente difícil de detectar desde la Tierra. Sin embargo, una posible excepción es el destello de rayos gamma emitido en la última etapa de la evaporación de los agujeros negros primordiales. Las búsquedas de tales destellos han resultado infructuosas y proporcionan límites estrictos a la posibilidad de existencia de agujeros negros primordiales de baja masa. [150] El telescopio espacial de rayos gamma Fermi de la NASA , lanzado en 2008, continuará la búsqueda de estos destellos. [151]
Si los agujeros negros se evaporan a través de la radiación de Hawking, un agujero negro de masa solar se evaporará (comenzando una vez que la temperatura del fondo cósmico de microondas caiga por debajo de la del agujero negro) durante un período de 10 64 años. [152] Un agujero negro supermasivo con una masa de 1011 M ☉ se evaporarán en alrededor de 2×10 100 años. [153] Se predice que algunos agujeros negros monstruosos en el universo seguirán creciendo hasta quizás 1014 M ☉ durante el colapso de supercúmulos de galaxias. Incluso estos se evaporarían en un lapso de tiempo de hasta 10 106 años. [152]
Evidencia observacional
Por naturaleza, los agujeros negros no emiten ninguna radiación electromagnética aparte de la hipotética radiación de Hawking , por lo que los astrofísicos que buscan agujeros negros generalmente deben basarse en observaciones indirectas. Por ejemplo, la existencia de un agujero negro a veces se puede inferir observando su influencia gravitatoria sobre sus alrededores. [154]
Interferometría directa


El Event Horizon Telescope (EHT) es un programa activo que observa directamente el entorno inmediato de los horizontes de eventos de los agujeros negros, como el agujero negro en el centro de la Vía Láctea. En abril de 2017, el EHT comenzó a observar el agujero negro en el centro de Messier 87. [ 155] [156] "En total, ocho observatorios de radio en seis montañas y cuatro continentes observaron la galaxia en Virgo de forma intermitente durante 10 días en abril de 2017" para proporcionar los datos que dieron lugar a la imagen en abril de 2019. [157]
Después de dos años de procesamiento de datos, el EHT publicó la primera imagen directa de un agujero negro. En concreto, del agujero negro supermasivo que se encuentra en el centro de la galaxia antes mencionada. [158] [159] Lo que se ve no es el agujero negro, que se muestra en negro debido a la pérdida de toda la luz dentro de esta región oscura, sino los gases en el borde del horizonte de sucesos, que se muestran en naranja o rojo, que definen el agujero negro. [160]
El 12 de mayo de 2022, el EHT publicó la primera imagen de Sagitario A* , el agujero negro supermasivo situado en el centro de la Vía Láctea. La imagen publicada mostraba la misma estructura en forma de anillo y la misma sombra circular que se observa en el agujero negro M87* , y la imagen se creó utilizando las mismas técnicas que para el agujero negro M87. El proceso de obtención de imágenes de Sagitario A*, que es más de mil veces más pequeño y menos masivo que M87*, fue significativamente más complejo debido a la inestabilidad de su entorno. [161] La imagen de Sagitario A* estaba parcialmente borrosa por el plasma turbulento en su camino hacia el centro galáctico, un efecto que impide la resolución de la imagen en longitudes de onda más largas. [162]
Se cree que el brillo de este material en la mitad "inferior" de la imagen EHT procesada se debe a la radiación Doppler , por la que el material que se acerca al observador a velocidades relativistas se percibe como más brillante que el material que se aleja. En el caso de un agujero negro, este fenómeno implica que el material visible está rotando a velocidades relativistas (>1000 km/s [2 200 000 mph]), las únicas velocidades a las que es posible equilibrar centrífugamente la inmensa atracción gravitatoria de la singularidad y, por lo tanto, permanecer en órbita por encima del horizonte de sucesos. Esta configuración de material brillante implica que el EHT observó a M87* desde una perspectiva que captaba el disco de acreción del agujero negro casi de canto, mientras todo el sistema giraba en el sentido de las agujas del reloj. [163] [164]
La lente gravitacional extrema asociada con los agujeros negros produce la ilusión de una perspectiva que ve el disco de acreción desde arriba. En realidad, la mayor parte del anillo en la imagen del EHT se creó cuando la luz emitida por el lado más alejado del disco de acreción se dobló alrededor del pozo de gravedad del agujero negro y se escapó, lo que significa que la mayoría de las perspectivas posibles sobre M87* pueden ver el disco completo, incluso el que está directamente detrás de la "sombra".
En 2015, el EHT detectó campos magnéticos justo fuera del horizonte de sucesos de Sagitario A* e incluso discernió algunas de sus propiedades. Las líneas de campo que pasan a través del disco de acreción eran una mezcla compleja de ordenadas y enredadas. Los estudios teóricos de los agujeros negros habían predicho la existencia de campos magnéticos. [165] [166]
En abril de 2023 se presentó una imagen de la sombra del agujero negro Messier 87 y del chorro de alta energía relacionado, vistos juntos por primera vez. [167] [168]
Detección de ondas gravitacionales a partir de agujeros negros en fusión

El 14 de septiembre de 2015, el observatorio de ondas gravitacionales LIGO realizó la primera observación directa exitosa de ondas gravitacionales . [55] [169] La señal fue consistente con las predicciones teóricas para las ondas gravitacionales producidas por la fusión de dos agujeros negros: uno con aproximadamente 36 masas solares y el otro alrededor de 29 masas solares. [55] [170] Esta observación proporciona la evidencia más concreta de la existencia de agujeros negros hasta la fecha. Por ejemplo, la señal de onda gravitacional sugiere que la separación de los dos objetos antes de la fusión fue de solo 350 km, o aproximadamente cuatro veces el radio de Schwarzschild correspondiente a las masas inferidas. Por lo tanto, los objetos deben haber sido extremadamente compactos, lo que deja a los agujeros negros como la interpretación más plausible. [55]
Más importante aún, la señal observada por LIGO también incluía el inicio del ringdown posterior a la fusión , la señal producida cuando el objeto compacto recién formado se asienta en un estado estacionario. Podría decirse que el ringdown es la forma más directa de observar un agujero negro. [171] A partir de la señal de LIGO, es posible extraer la frecuencia y el tiempo de amortiguamiento del modo dominante del ringdown. A partir de estos, es posible inferir la masa y el momento angular del objeto final, que coinciden con las predicciones independientes de las simulaciones numéricas de la fusión. [172] La frecuencia y el tiempo de decaimiento del modo dominante están determinados por la geometría de la esfera de fotones. Por lo tanto, la observación de este modo confirma la presencia de una esfera de fotones; sin embargo, no puede excluir posibles alternativas exóticas a los agujeros negros que sean lo suficientemente compactos como para tener una esfera de fotones. [171] [173]
La observación también proporciona la primera evidencia observacional de la existencia de sistemas binarios de agujeros negros de masa estelar. Además, es la primera evidencia observacional de agujeros negros de masa estelar que pesan 25 masas solares o más. [174]
Desde entonces, se han observado muchos más eventos de ondas gravitacionales . [175]
Estrellas orbitando Sagitario A*

Los movimientos propios de las estrellas cercanas al centro de nuestra Vía Láctea proporcionan una fuerte evidencia observacional de que estas estrellas están orbitando un agujero negro supermasivo. [176] Desde 1995, los astrónomos han seguido los movimientos de 90 estrellas que orbitan un objeto invisible coincidente con la fuente de radio Sagitario A*. Al ajustar sus movimientos a las órbitas keplerianas , los astrónomos pudieron inferir, en 1998, que unaUn objeto de 2,6 × 10 6 M ☉ debe estar contenido en un volumen con un radio de 0,02 años luz para provocar los movimientos de esas estrellas. [177]
Desde entonces, una de las estrellas, llamada S2 , ha completado una órbita completa. A partir de los datos orbitales, los astrónomos pudieron refinar los cálculos de la masa para4,3 × 10 6 M ☉ y un radio de menos de 0,002 años luz para el objeto que causa el movimiento orbital de esas estrellas. [176] El límite superior del tamaño del objeto todavía es demasiado grande para probar si es más pequeño que su radio de Schwarzschild. Sin embargo, estas observaciones sugieren firmemente que el objeto central es un agujero negro supermasivo, ya que no hay otros escenarios plausibles para confinar tanta masa invisible en un volumen tan pequeño. [177] Además, hay alguna evidencia observacional de que este objeto podría poseer un horizonte de sucesos, una característica exclusiva de los agujeros negros. [178]
Acreción de materia
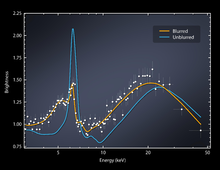
Debido a la conservación del momento angular , [180] el gas que cae en el pozo gravitacional creado por un objeto masivo normalmente formará una estructura en forma de disco alrededor del objeto. Las impresiones artísticas, como la representación que acompaña a la imagen de un agujero negro con corona, suelen representar el agujero negro como si fuera un cuerpo espacial plano que oculta la parte del disco que se encuentra justo detrás de él, pero en realidad el efecto de lente gravitacional distorsionaría en gran medida la imagen del disco de acreción. [181]
Dentro de un disco de este tipo, la fricción haría que el momento angular se transportara hacia afuera, lo que permitiría que la materia cayera más hacia adentro, liberando así energía potencial y aumentando la temperatura del gas. [182]
Cuando el objeto que se acumula es una estrella de neutrones o un agujero negro, el gas en el disco de acreción interior orbita a velocidades muy altas debido a su proximidad al objeto compacto . La fricción resultante es tan significativa que calienta el disco interior a temperaturas a las que emite grandes cantidades de radiación electromagnética (principalmente rayos X). Estas brillantes fuentes de rayos X pueden detectarse mediante telescopios. Este proceso de acreción es uno de los procesos de producción de energía más eficientes que se conocen. Hasta el 40% de la masa en reposo del material acumulado puede emitirse como radiación. [182] En la fusión nuclear, solo alrededor del 0,7% de la masa en reposo se emitirá como energía. En muchos casos, los discos de acreción están acompañados de chorros relativistas que se emiten a lo largo de los polos, que se llevan gran parte de la energía. El mecanismo de creación de estos chorros no se entiende bien actualmente, en parte debido a la falta de datos. [183]
Por ello, muchos de los fenómenos más energéticos del universo se han atribuido a la acreción de materia en los agujeros negros. En particular, se cree que los núcleos galácticos activos y los cuásares son los discos de acreción de los agujeros negros supermasivos. [184] De manera similar, se acepta generalmente que los sistemas binarios de rayos X son sistemas binarios de estrellas en los que una de las dos estrellas es un objeto compacto que acrecienta materia de su compañera. [184] También se ha sugerido que algunas fuentes de rayos X ultraluminosas pueden ser los discos de acreción de agujeros negros de masa intermedia. [185]
Se ha observado que las fuerzas de marea desgarran estrellas en las inmediaciones de agujeros negros supermasivos en los núcleos de las galaxias, en lo que se conoce como evento de disrupción de marea (TDE, por sus siglas en inglés) . Parte del material de la estrella desgarrada forma un disco de acreción alrededor del agujero negro, que emite radiación electromagnética observable.
En noviembre de 2011 se informó de la primera observación directa de un disco de acreción de un cuásar alrededor de un agujero negro supermasivo. [186] [187]
Sistemas binarios de rayos X

Los sistemas binarios de rayos X son sistemas estelares binarios que emiten la mayor parte de su radiación en la parte de rayos X del espectro. Generalmente se cree que estas emisiones de rayos X se producen cuando una de las estrellas (objeto compacto) acrecienta materia de otra estrella (normal). La presencia de una estrella normal en un sistema de este tipo ofrece la oportunidad de estudiar el objeto central y determinar si podría ser un agujero negro. [184]
Si un sistema de este tipo emite señales que pueden rastrearse directamente hasta el objeto compacto, no puede ser un agujero negro. Sin embargo, la ausencia de dicha señal no excluye la posibilidad de que el objeto compacto sea una estrella de neutrones. Al estudiar la estrella compañera, a menudo es posible obtener los parámetros orbitales del sistema y obtener una estimación de la masa del objeto compacto. Si esta es mucho mayor que el límite de Tolman-Oppenheimer-Volkoff (la masa máxima que puede tener una estrella sin colapsar), entonces el objeto no puede ser una estrella de neutrones y generalmente se espera que sea un agujero negro. [184]
El primer candidato fuerte para un agujero negro, Cygnus X-1 , fue descubierto de esta manera por Charles Thomas Bolton , [188] Louise Webster y Paul Murdin [189] en 1972. [190] [191] Quedaban algunas dudas, debido a las incertidumbres que resultan de que la estrella compañera sea mucho más pesada que el agujero negro candidato. Actualmente, los mejores candidatos para agujeros negros se encuentran en una clase de sistemas binarios de rayos X llamados transitorios de rayos X suaves. En esta clase de sistema, la estrella compañera tiene una masa relativamente baja, lo que permite estimaciones más precisas de la masa del agujero negro. Estos sistemas emiten rayos X de forma activa solo durante varios meses una vez cada 10 a 50 años. Durante el período de baja emisión de rayos X, llamado quiescencia, el disco de acreción es extremadamente débil, lo que permite una observación detallada de la estrella compañera durante este período. Uno de los mejores candidatos de este tipo es V404 Cygni . [184]
Oscilaciones cuasi-periódicas
Las emisiones de rayos X de los discos de acreción a veces parpadean a ciertas frecuencias. Estas señales se denominan oscilaciones cuasiperiódicas y se cree que son causadas por material que se mueve a lo largo del borde interior del disco de acreción (la órbita circular estable más interna). Como tal, su frecuencia está vinculada a la masa del objeto compacto. Por lo tanto, pueden usarse como una forma alternativa de determinar la masa de los agujeros negros candidatos. [192]
Núcleos galácticos

Los astrónomos utilizan el término "galaxia activa" para describir galaxias con características inusuales, como una emisión de líneas espectrales inusual y una emisión de radio muy fuerte. Estudios teóricos y observacionales han demostrado que la actividad en estos núcleos galácticos activos (AGN) puede explicarse por la presencia de agujeros negros supermasivos, que pueden ser millones de veces más masivos que los estelares. Los modelos de estos AGN consisten en un agujero negro central que puede ser millones o miles de millones de veces más masivo que el Sol ; un disco de gas y polvo interestelar llamado disco de acreción; y dos chorros perpendiculares al disco de acreción. [194] [195]
Aunque se espera que se encuentren agujeros negros supermasivos en la mayoría de los AGN, solo los núcleos de algunas galaxias han sido estudiados con más cuidado en los intentos de identificar y medir las masas reales de los candidatos a agujeros negros supermasivos centrales. Algunas de las galaxias más notables con candidatos a agujeros negros supermasivos incluyen la Galaxia de Andrómeda , M32 , M87 , NGC 3115 , NGC 3377 , NGC 4258 , NGC 4889 , NGC 1277 , OJ 287 , APM 08279+5255 y la Galaxia del Sombrero . [196]
En la actualidad se acepta ampliamente que el centro de casi todas las galaxias, no solo las activas, contiene un agujero negro supermasivo. [197] La estrecha correlación observacional entre la masa de este agujero y la dispersión de velocidad del bulbo de la galaxia anfitriona , conocida como relación M–sigma , sugiere firmemente una conexión entre la formación del agujero negro y la de la galaxia misma. [198]
Microlente
Otra forma de comprobar la naturaleza de agujero negro de un objeto es mediante la observación de los efectos provocados por un fuerte campo gravitacional en sus proximidades. Uno de estos efectos es el efecto de lente gravitacional: la deformación del espacio-tiempo alrededor de un objeto masivo hace que los rayos de luz se desvíen, como la luz que pasa a través de una lente óptica . Se han realizado observaciones de lente gravitacional débil, en la que los rayos de luz se desvían solo unos pocos segundos de arco . El efecto de microlente se produce cuando las fuentes no están resueltas y el observador ve un pequeño aumento de brillo. El cambio de milenio vio las primeras 3 detecciones candidatas de agujeros negros de esta manera, [199] [200] y en enero de 2022, los astrónomos informaron de la primera detección confirmada de un evento de microlente de un agujero negro aislado. [201]
Otra posibilidad para observar el efecto de lente gravitacional de un agujero negro sería observar estrellas que orbitan alrededor de él. Hay varios candidatos para tal observación en órbita alrededor de Sagitario A* . [202]
Alternativas
La evidencia de los agujeros negros estelares se basa en gran medida en la existencia de un límite superior para la masa de una estrella de neutrones. El tamaño de este límite depende en gran medida de las suposiciones realizadas sobre las propiedades de la materia densa. Nuevas fases exóticas de la materia podrían hacer subir este límite. [184] Una fase de quarks libres a alta densidad podría permitir la existencia de estrellas densas de quarks, [203] y algunos modelos supersimétricos predicen la existencia de estrellas Q. [204] Algunas extensiones del modelo estándar postulan la existencia de preones como bloques de construcción fundamentales de quarks y leptones , que hipotéticamente podrían formar estrellas de preones . [205] Estos modelos hipotéticos podrían explicar potencialmente una serie de observaciones de candidatos a agujeros negros estelares. Sin embargo, se puede demostrar a partir de argumentos de la relatividad general que cualquier objeto de este tipo tendrá una masa máxima. [184]
Dado que la densidad media de un agujero negro dentro de su radio de Schwarzschild es inversamente proporcional al cuadrado de su masa, los agujeros negros supermasivos son mucho menos densos que los agujeros negros estelares. La densidad media de un agujero negro de 10 La masa de un agujero negro de 8 M☉ es comparable a la del agua. [184] En consecuencia, la física de la materia que forma un agujero negro supermasivo se entiende mucho mejor y las posibles explicaciones alternativas para las observaciones de agujeros negros supermasivos son mucho más mundanas. Por ejemplo, un agujero negro supermasivo podría ser modelado por un gran cúmulo de objetos muy oscuros. Sin embargo, tales alternativas normalmente no son lo suficientemente estables para explicar los candidatos a agujero negro supermasivo. [184]
La evidencia de la existencia de agujeros negros estelares y supermasivos implica que para que los agujeros negros no se formen, la relatividad general debe fallar como teoría de la gravedad, tal vez debido al inicio de las correcciones de la mecánica cuántica . Una característica muy esperada de una teoría de la gravedad cuántica es que no presentará singularidades u horizontes de eventos y, por lo tanto, los agujeros negros no serían artefactos reales. [206] Por ejemplo, en el modelo de bola de pelusa [207] basado en la teoría de cuerdas , los estados individuales de una solución de agujero negro generalmente no tienen un horizonte de eventos o singularidad, pero para un observador clásico/semiclásico el promedio estadístico de tales estados aparece como un agujero negro ordinario tal como se deduce de la relatividad general. [208]
Se ha conjeturado que algunos objetos teóricos coinciden de manera idéntica o casi idéntica con las observaciones de candidatos a agujeros negros astronómicos [173] , pero que funcionan a través de un mecanismo diferente. Entre ellos se incluyen la gravastar [209] , la estrella negra [210] , la nestar relacionada [211] y la estrella de energía oscura [212] .
Preguntas abiertas
Entropía y termodinámica
En 1971, Hawking demostró en condiciones generales [Nota 5] que el área total de los horizontes de sucesos de cualquier conjunto de agujeros negros clásicos nunca puede disminuir, incluso si colisionan y se fusionan. [213] Este resultado, ahora conocido como la segunda ley de la mecánica de los agujeros negros , es notablemente similar a la segunda ley de la termodinámica , que establece que la entropía total de un sistema aislado nunca puede disminuir. Al igual que con los objetos clásicos a temperatura cero absoluta , se suponía que los agujeros negros tenían entropía cero. Si este fuera el caso, la segunda ley de la termodinámica sería violada por materia cargada de entropía que entrara en un agujero negro, lo que resultaría en una disminución de la entropía total del universo. Por lo tanto, Bekenstein propuso que un agujero negro debería tener una entropía, y que debería ser proporcional al área de su horizonte. [214]
El vínculo con las leyes de la termodinámica se fortaleció aún más con el descubrimiento de Hawking en 1974 de que la teoría cuántica de campos predice que un agujero negro irradia radiación de cuerpo negro a una temperatura constante. Esto aparentemente causa una violación de la segunda ley de la mecánica de agujeros negros, ya que la radiación se llevará energía del agujero negro haciendo que se encoja. La radiación también se lleva entropía, y se puede demostrar bajo supuestos generales que la suma de la entropía de la materia que rodea a un agujero negro y una cuarta parte del área del horizonte medida en unidades de Planck de hecho siempre está aumentando. Esto permite la formulación de la primera ley de la mecánica de agujeros negros como un análogo de la primera ley de la termodinámica , con la masa actuando como energía, la gravedad superficial como temperatura y el área como entropía. [214]
Una característica desconcertante es que la entropía de un agujero negro aumenta con su área en lugar de aumentar con su volumen, ya que la entropía es normalmente una cantidad extensiva que aumenta linealmente con el volumen del sistema. Esta extraña propiedad llevó a Gerard 't Hooft y Leonard Susskind a proponer el principio holográfico , que sugiere que todo lo que sucede en un volumen de espacio-tiempo puede describirse mediante datos sobre el límite de ese volumen. [215]
Aunque la relatividad general puede utilizarse para realizar un cálculo semiclásico de la entropía de un agujero negro, esta situación es teóricamente insatisfactoria. En mecánica estadística , la entropía se entiende como el recuento del número de configuraciones microscópicas de un sistema que tienen las mismas cualidades macroscópicas, como masa, carga, presión, etc. Sin una teoría satisfactoria de la gravedad cuántica, no se puede realizar dicho cálculo para los agujeros negros. Se han logrado algunos avances en varios enfoques de la gravedad cuántica. En 1995, Andrew Strominger y Cumrun Vafa demostraron que contar los microestados de un agujero negro supersimétrico específico en la teoría de cuerdas reproducía la entropía de Bekenstein-Hawking. [216] Desde entonces, se han informado resultados similares para diferentes agujeros negros tanto en la teoría de cuerdas como en otros enfoques de la gravedad cuántica como la gravedad cuántica de bucles . [217]
Paradoja de la pérdida de información
Como un agujero negro tiene sólo unos pocos parámetros internos, la mayor parte de la información sobre la materia que se utilizó para formar el agujero negro se pierde. Independientemente del tipo de materia que entra en un agujero negro, parece que sólo se conserva la información relativa a la masa total, la carga y el momento angular. Mientras se haya pensado que los agujeros negros persisten para siempre, esta pérdida de información no es tan problemática, ya que se puede pensar que la información existe dentro del agujero negro, inaccesible desde el exterior, pero representada en el horizonte de sucesos de acuerdo con el principio holográfico. Sin embargo, los agujeros negros se evaporan lentamente emitiendo radiación de Hawking. Esta radiación no parece llevar ninguna información adicional sobre la materia que formó el agujero negro, lo que significa que esta información parece haber desaparecido para siempre. [218]
La cuestión de si la información se pierde realmente en los agujeros negros (la paradoja de la información de los agujeros negros ) ha dividido a la comunidad de la física teórica. En mecánica cuántica, la pérdida de información corresponde a la violación de una propiedad llamada unitaridad , y se ha argumentado que la pérdida de unitaridad también implicaría la violación de la conservación de la energía, [219] aunque esto también ha sido discutido. [220] En los últimos años se ha ido acumulando evidencia de que, de hecho, la información y la unitaridad se conservan en un tratamiento gravitacional cuántico completo del problema. [221]
Un intento de resolver la paradoja de la información del agujero negro se conoce como complementariedad del agujero negro . En 2012, se introdujo la " paradoja del cortafuegos " con el objetivo de demostrar que la complementariedad del agujero negro no resuelve la paradoja de la información. Según la teoría cuántica de campos en el espacio-tiempo curvado , una única emisión de radiación de Hawking involucra dos partículas entrelazadas entre sí . La partícula saliente escapa y se emite como un cuanto de radiación de Hawking; la partícula entrante es tragada por el agujero negro. Supongamos que un agujero negro se formó un tiempo finito en el pasado y se evaporará por completo en algún tiempo finito en el futuro. Entonces, emitirá solo una cantidad finita de información codificada dentro de su radiación de Hawking. Según la investigación de físicos como Don Page [222] [223] y Leonard Susskind, eventualmente llegará un momento en el que una partícula saliente debe estar entrelazada con toda la radiación de Hawking que el agujero negro ha emitido previamente.
Esto aparentemente crea una paradoja: un principio llamado " monogamia del entrelazamiento " requiere que, como cualquier sistema cuántico, la partícula saliente no pueda estar completamente entrelazada con otros dos sistemas al mismo tiempo; sin embargo, aquí la partícula saliente parece estar entrelazada tanto con la partícula entrante como, independientemente, con la radiación de Hawking anterior. [224] Para resolver esta contradicción, los físicos pueden verse eventualmente obligados a renunciar a uno de los tres principios probados por el tiempo: el principio de equivalencia de Einstein, la unitaridad o la teoría cuántica de campos local. Una posible solución, que viola el principio de equivalencia, es que un "cortafuegos" destruya las partículas entrantes en el horizonte de sucesos. [225] En general, cuál de estos supuestos debería abandonarse (si es que debería abandonarse alguno) sigue siendo un tema de debate. [220]
En ciencia ficción
La epopeya de ciencia ficción de 2014 de Christopher Nolan , Interstellar, presenta un agujero negro conocido como Gargantúa, que es el objeto central de un sistema planetario en una galaxia distante. La humanidad accedió a este sistema a través de un agujero de gusano en el sistema solar exterior , cerca de Saturno .
Véase también
- Brana negra o cuerda negra
- Iniciativa Agujero Negro
- Nave espacial del agujero negro
- Agujeros negros en la ficción
- Blanet
- Agujero negro BTZ
- Binario dorado
- Agujero negro hipotético (desambiguación)
- Kugelblitz (astrofísica)
- Lista de agujeros negros
- Lista de agujeros negros más cercanos
- Contorno de los agujeros negros
- Agujero negro sónico
- Agujero negro virtual
- Batalla de Susskind y Hawking
- Cronología de la física de los agujeros negros
- Agujero blanco
- Estrella de Planck
- Estrella oscura (materia oscura)
Notas
- ^ El valor de cJ/GM2 puede superar 1 para objetos distintos de los agujeros negros. El valor más alto conocido para una estrella de neutrones es ≤ 0,4, y las ecuaciones de estado de uso común limitarían ese valor a < 0,7. [78]
- ^ El radio del horizonte de eventos (exterior) se escala como sigue:
- ^ El conjunto de posibles caminos, o más precisamente el futuro cono de luz que contiene todas las posibles líneas del mundo (en este diagrama el cono de luz está representado por la región en forma de V delimitada por flechas que representan las líneas del mundo de los rayos de luz), está inclinado de esta manera en las coordenadas de Eddington-Finkelstein (el diagrama es una versión "animada" de un diagrama de coordenadas de Eddington-Finkelstein), pero en otras coordenadas los conos de luz no están inclinados de esta manera, por ejemplo en las coordenadas de Schwarzschild se estrechan sin inclinarse a medida que uno se acerca al horizonte de eventos, y en las coordenadas de Kruskal-Szekeres los conos de luz no cambian de forma ni de orientación en absoluto. [81]
- ^ Esto es cierto sólo para los espacios-tiempos de cuatro dimensiones. En dimensiones superiores son posibles topologías de horizonte más complicadas, como un anillo negro . [93] [94]
- ^ En particular, asumió que toda la materia satisface la condición de energía débil .
Referencias
- ^ Oldham, LJ; Auger, MW (marzo de 2016). "Estructura de galaxias a partir de múltiples trazadores – II. M87 desde escalas de parsec a megaparsec". Monthly Notices of the Royal Astronomical Society . 457 (1): 421–439. arXiv : 1601.01323 . Bibcode :2016MNRAS.457..421O. doi : 10.1093/mnras/stv2982 . ISSN 0035-8711. S2CID 119166670.
- ^ Wald 1984, págs. 299-300
- ^ ab Wald, RM (1997). "Colapso gravitacional y censura cósmica". En Iyer, BR; Bhawal, B. (eds.). Agujeros negros, radiación gravitacional y el universo . Dordrecht: Springer. págs. 69–86. arXiv : gr-qc/9710068 . doi :10.1007/978-94-017-0934-7. ISBN . 978-9401709347.
- ^ Overbye, Dennis (8 de junio de 2015). «Black Hole Hunters». NASA . Archivado desde el original el 9 de junio de 2015. Consultado el 8 de junio de 2015 .
- ^ Hamilton, A. "Viaje a un agujero negro de Schwarzschild". jila.colorado.edu . Archivado desde el original el 3 de septiembre de 2019. Consultado el 28 de junio de 2020 .
- ^ Schutz, Bernard F. (2003). Gravedad desde el suelo. Cambridge University Press . pág. 110. ISBN 978-0-521-45506-0Archivado desde el original el 2 de diciembre de 2016.
- ^ Davies, PCW (1978). "Termodinámica de los agujeros negros" (PDF) . Informes sobre el progreso en física . 41 (8): 1313–1355. Bibcode :1978RPPh...41.1313D. doi :10.1088/0034-4885/41/8/004. S2CID 250916407. Archivado desde el original (PDF) el 10 de mayo de 2013.
- ^ abc Montgomery, Colin; Orchiston, Wayne; Whittingham, Ian (2009). "Michell, Laplace y el origen del concepto de agujero negro" (PDF) . Revista de Historia y Patrimonio Astronómico . 12 (2): 90–96. Bibcode :2009JAHH...12...90M. doi :10.3724/SP.J.1440-2807.2009.02.01. S2CID 55890996.
- ^ Webster, B. Louise; Murdin, Paul (1972), "Cygnus X-1: ¿una binaria espectroscópica con un compañero pesado?", Nature , 235 (5332): 37–38, Bibcode :1972Natur.235...37W, doi :10.1038/235037a0, S2CID 4195462
- ^ Bolton, CT (1972), "Identificación de Cygnus X-1 con HDE 226868", Nature , 235 (5336): 271–273, Bibcode :1972Natur.235..271B, doi :10.1038/235271b0, S2CID 4222070
- ^ Clery D (2020). "Agujeros negros atrapados en el acto de tragarse estrellas". Science . 367 (6477): 495. Bibcode :2020Sci...367..495C. doi :10.1126/science.367.6477.495. PMID 32001633. S2CID 210984462.
- ^ Michell, J. (1784). "Sobre los medios para descubrir la distancia, magnitud, etc. de las estrellas fijas, como consecuencia de la disminución de la velocidad de su luz, en caso de que se encuentre que tal disminución tiene lugar en cualquiera de ellas, y se obtengan otros datos a partir de observaciones, según sea necesario para ese propósito". Philosophical Transactions of the Royal Society . 74 : 35–57. Bibcode :1784RSPT...74...35M. doi : 10.1098/rstl.1784.0008 . JSTOR 106576.
- ^ de Thorne 1994, págs. 123-124
- ^ Slayter, Elizabeth M.; Slayter, Henry S. (1992). Microscopía óptica y electrónica. Cambridge University Press . ISBN 978-0-521-33948-3Archivado desde el original el 30 de noviembre de 2017.
- ^ Crass, Instituto de Astronomía – Diseño de DR Wilkins y SJ «Light escaping from black holes» (La luz escapa de los agujeros negros). www.ast.cam.ac.uk. Archivado desde el original el 6 de julio de 2019. Consultado el 10 de marzo de 2018 .
- ^ Levy, Adam (11 de enero de 2021). «Cómo los agujeros negros pasaron de la teoría a la realidad». Revista Knowable . doi : 10.1146/knowable-010921-1 . Consultado el 25 de marzo de 2022 .
- ^ ab Schwarzschild, K. (1916). "Über das Gravitationsfeld eines Massenpunktes nach der Einsteinschen Theorie". Sitzungsberichte der Königlich Preussischen Akademie der Wissenschaften . 7 : 189–196. Código Bib :1916SPAW.......189S.
- Traducción: Antoci, S.; Loinger, A. (1999). "Sobre el campo gravitatorio de un punto de masa según la teoría de Einstein". arXiv : physics/9905030 .y Schwarzschild, K. (1916). "Über das Gravitationsfeld einer Kugel aus inkcompressibler Flüssigkeit nach der Einsteinschen Theorie". Sitzungsberichte der Königlich Preussischen Akademie der Wissenschaften . 18 : 424–434. Código bibliográfico : 1916skpa.conf..424S.
- Traducción: Antoci, S. (1999). "Sobre el campo gravitatorio de una esfera de fluido incompresible según la teoría de Einstein". arXiv : physics/9912033 .
- ^ Droste, J. (1917). «Sobre el campo de un único centro en la teoría de la gravitación de Einstein y el movimiento de una partícula en ese campo» (PDF) . Actas de la Royal Academy of Sciences de Ámsterdam . 19 (1): 197–215. Archivado desde el original (PDF) el 18 de mayo de 2013. Consultado el 16 de septiembre de 2012 .
- ^ Kox, AJ (1992). "Relatividad general en los Países Bajos: 1915-1920". En Eisenstaedt, Jean; Kox, AJ (eds.). Estudios sobre la historia de la relatividad general . Birkhäuser. pág. 41. ISBN 978-0-8176-3479-7Archivado desde el original el 10 de agosto de 2016 . Consultado el 23 de febrero de 2016 .
- ^ 't Hooft, G. (2009). «Introducción a la teoría de los agujeros negros» (PDF) . Instituto de Física Teórica/Instituto Spinoza. pp. 47–48. Archivado desde el original (PDF) el 21 de mayo de 2009. Consultado el 24 de junio de 2010 .
- ^ Eddington, Arthur (1926). La constitución interna de las estrellas. Science. Vol. 52. Cambridge University Press. págs. 233–40. Bibcode :1920Sci....52..233E. doi :10.1126/science.52.1341.233. ISBN 978-0-521-33708-3. PMID 17747682. Archivado desde el original el 11 de agosto de 2016.
- ^ Thorne, Kip S.; Hawking, Stephen (1994). Agujeros negros y distorsiones temporales: el escandaloso legado de Einstein . WW Norton & Company. págs. 134-135. ISBN. 978-0-393-31276-8. Recuperado el 12 de abril de 2019.
La primera conclusión fue la versión newtoniana de que la luz no escapa; la segunda fue una descripción relativista semiprecisa; y la tercera fue una hipérbole típica de Eddington ... cuando una estrella es tan pequeña como la circunferencia crítica, la curvatura es fuerte pero no infinita, y el espacio definitivamente no envuelve a la estrella. Eddington puede haberlo sabido, pero su descripción fue una buena historia y captó de una manera caprichosa el espíritu de la curvatura del espacio-tiempo de Schwarzschild".
- ^ Venkataraman, G. (1992). Chandrasekhar y su límite. Universities Press. pág. 89. ISBN 978-81-7371-035-3Archivado desde el original el 11 de agosto de 2016.
- ^ Detweiler, S. (1981). "Carta de recursos BH-1: Agujeros negros". American Journal of Physics . 49 (5): 394–400. Código Bibliográfico :1981AmJPh..49..394D. doi :10.1119/1.12686.
- ^ Harpaz, A. (1994). Evolución estelar. AK Peters . pag. 105.ISBN 978-1-56881-012-6Archivado desde el original el 11 de agosto de 2016.
- ^ ab Oppenheimer, JR ; Volkoff, GM (1939). "Sobre núcleos de neutrones masivos". Physical Review . 55 (4): 374–381. Código Bibliográfico :1939PhRv...55..374O. doi :10.1103/PhysRev.55.374.
- ^ Bombaci, I. (1996). "La masa máxima de una estrella de neutrones". Astronomía y astrofísica . 305 : 871–877. Bibcode :1996A&A...305..871B.
- ^ Cho, A. (16 de febrero de 2018). "A weight limit emerge for neutron stars" (Surge un límite de peso para las estrellas de neutrones). Science . 359 (6377): 724–725. Bibcode :2018Sci...359..724C. doi :10.1126/science.359.6377.724. PMID 29449468.
- ^ Margalit, B.; Metzger, BD (1 de diciembre de 2017). "Restricción de la masa máxima de estrellas de neutrones a partir de observaciones de múltiples mensajeros de GW170817". The Astrophysical Journal . 850 (2): L19. arXiv : 1710.05938 . Bibcode :2017ApJ...850L..19M. doi : 10.3847/2041-8213/aa991c . S2CID 119342447.
- ^ Shibata, M.; Fujibayashi, S.; Hotokezaka, K.; Kiuchi, K.; Kyutoku, K.; Sekiguchi, Y.; Tanaka, M. (22 de diciembre de 2017). "Modelado de GW170817 basado en la relatividad numérica y sus implicaciones". Physical Review D . 96 (12): 123012. arXiv : 1710.07579 . Código Bibliográfico :2017PhRvD..96l3012S. doi :10.1103/PhysRevD.96.123012. S2CID 119206732.
- ^ Ruiz, M.; Shapiro, SL; Tsokaros, A. (11 de enero de 2018). "GW170817, simulaciones magnetohidrodinámicas relativistas generales y la masa máxima de la estrella de neutrones". Physical Review D . 97 (2): 021501. arXiv : 1711.00473 . Bibcode :2018PhRvD..97b1501R. doi :10.1103/PhysRevD.97.021501. PMC 6036631 . PMID 30003183.
- ^ Rezzolla, L.; Most, ER; Weih, LR (9 de enero de 2018). "Uso de observaciones de ondas gravitacionales y relaciones cuasi-universales para limitar la masa máxima de las estrellas de neutrones". Astrophysical Journal . 852 (2): L25. arXiv : 1711.00314 . Bibcode :2018ApJ...852L..25R. doi : 10.3847/2041-8213/aaa401 . S2CID 119359694.
- ^ Ruffini, R. ; Wheeler, JA (1971). "Introducing the black hole" (PDF) . Physics Today . 24 (1): 30–41. Bibcode :1971PhT....24a..30R. doi :10.1063/1.3022513. Archivado desde el original (PDF) el 25 de julio de 2011 . Consultado el 5 de diciembre de 2009 .
- ^ ab Bernstein, Jeremy (2007). "El padre reacio de los agujeros negros". Scientific American . 17 : 4–11. doi :10.1038/scientificamerican0407-4sp . Consultado el 3 de agosto de 2023 .
- ^ Oppenheimer, JR; Snyder, H. (1939). "Sobre la contracción gravitacional continua". Physical Review . 56 (5): 455–459. Bibcode :1939PhRv...56..455O. doi : 10.1103/PhysRev.56.455 .
- ^ Finkelstein, D. (1958). "Asimetría pasado-futuro del campo gravitatorio de una partícula puntual". Physical Review . 110 (4): 965–967. Bibcode :1958PhRv..110..965F. doi :10.1103/PhysRev.110.965.
- ^ Kruskal, M. (1960). "Extensión máxima de la métrica de Schwarzschild". Physical Review . 119 (5): 1743. Bibcode :1960PhRv..119.1743K. doi :10.1103/PhysRev.119.1743.
- ^ Hewish, A. ; et al. (1968). "Observación de una fuente de radio de pulsación rápida". Nature . 217 (5130): 709–713. Código Bibliográfico :1968Natur.217..709H. doi :10.1038/217709a0. S2CID 4277613.
- ^ Pilkington, JDH; et al. (1968). "Observaciones de algunas fuentes de radio pulsadas adicionales". Nature . 218 (5137): 126–129. Código Bibliográfico :1968Natur.218..126P. doi :10.1038/218126a0. S2CID 4253103.
- ^ Hewish, A. (1970). "Pulsars". Revista anual de astronomía y astrofísica . 8 (1): 265–296. Código Bibliográfico :1970ARA&A...8..265H. doi :10.1146/annurev.aa.08.090170.001405.
- ^ Boissoneault, Lorraine (28 de febrero de 2018). «Hace cincuenta años, el descubrimiento de un estudiante de posgrado cambió el curso de la astrofísica». Revista Smithsonian . Consultado el 22 de diciembre de 2023 .
- ^ Newman, ET ; et al. (1965). "Métrica de una masa cargada rotatoria". Revista de física matemática . 6 (6): 918. Bibcode :1965JMP.....6..918N. doi :10.1063/1.1704351.
- ^ Israel, W. (1967). "Horizontes de sucesos en espacios-tiempos de vacío estático". Physical Review . 164 (5): 1776. Bibcode :1967PhRv..164.1776I. doi :10.1103/PhysRev.164.1776.
- ^ Carter, B. (1971). "Un agujero negro axisimétrico tiene sólo dos grados de libertad". Physical Review Letters . 26 (6): 331. Bibcode :1971PhRvL..26..331C. doi :10.1103/PhysRevLett.26.331.
- ^ Carter, B. (1977). "El teorema de unicidad del agujero negro en el vacío y sus generalizaciones concebibles". Actas de la 1.ª reunión de Marcel Grossmann sobre relatividad general . pp. 243–254.
- ^ Robinson, D. (1975). "Singularidad del agujero negro de Kerr". Physical Review Letters . 34 (14): 905. Código Bibliográfico :1975PhRvL..34..905R. doi :10.1103/PhysRevLett.34.905.
- ^ ab Heusler, M. (2012). "Agujeros negros estacionarios: singularidad y más allá". Living Reviews in Relativity . 15 (7): 7. arXiv : 1205.6112 . Código Bibliográfico :2012LRR....15....7C. doi : 10.12942/lrr-2012-7 . PMC 5255892 . PMID 28179837.
- ^ ab Penrose, R. (1965). "Colapso gravitacional y singularidades espacio-temporales" (PDF) . Physical Review Letters . 14 (3): 57. Bibcode :1965PhRvL..14...57P. doi :10.1103/PhysRevLett.14.57. S2CID 116755736. Archivado desde el original (PDF) el 11 de octubre de 2020.
- ^ Ford, LH (2003). "Los teoremas de singularidad clásicos y sus lagunas cuánticas". Revista internacional de física teórica . 42 (6): 1219–1227. arXiv : gr-qc/0301045 . Código Bibliográfico :2003gr.qc.....1045F. doi :10.1023/A:1025754515197. S2CID 14404560.
- ^ "El Premio Nobel de Física 2020". NobelPrize.org . Archivado desde el original el 24 de abril de 2021. Consultado el 8 de octubre de 2020 .
- ^ Rolston, Bruce (10 de noviembre de 1997), The First Black Hole, Universidad de Toronto, archivado desde el original el 7 de marzo de 2008 , consultado el 11 de marzo de 2008
- ^ Shipman, HL; Yu, Z; Du, YW (1975), "La historia improbable de los modelos de estrellas triples para Cygnus X-1 Evidencia de un agujero negro", Astrophysical Letters , 16 (1): 9–12, Bibcode :1975ApL....16....9S, doi :10.1016/S0304-8853(99)00384-4
- ^ Bardeen, JM ; Carter, B. ; Hawking, SW (1973). "Las cuatro leyes de la mecánica de los agujeros negros". Communications in Mathematical Physics . 31 (2): 161–170. Bibcode :1973CMaPh..31..161B. doi :10.1007/BF01645742. MR 0334798. S2CID 54690354. Zbl 1125.83309. Archivado desde el original el 16 de mayo de 2020 . Consultado el 4 de junio de 2021 .
- ^ abc Hawking, SW (1974). "¿Explosiones de agujeros negros?". Nature . 248 (5443): 30–31. Bibcode :1974Natur.248...30H. doi :10.1038/248030a0. S2CID 4290107.
- ^ abcd Abbott, BP; et al. (2016). "Observación de ondas gravitacionales a partir de una fusión de agujeros negros binarios". Phys. Rev. Lett. 116 (6): 061102. arXiv : 1602.03837 . Bibcode :2016PhRvL.116f1102A. doi :10.1103/PhysRevLett.116.061102. PMID 26918975. S2CID 124959784.
- ^ Event Horizon Telescope, The (2019). "Resultados del primer telescopio de horizonte de sucesos M87. I. La sombra del agujero negro supermasivo". The Astrophysical Journal . 875 (1): L1. arXiv : 1906.11238 . Código Bibliográfico :2019ApJ...875L...1E. doi : 10.3847/2041-8213/ab0ec7 . S2CID 145906806.
- ^ Bouman, Katherine L. ; Johnson, Michael D.; Zoran, Daniel; Fish, Vincent L.; Doeleman, Sheperd S.; Freeman, William T. (2016). "Imágenes computacionales para reconstrucción de imágenes VLBI". Conferencia IEEE de 2016 sobre visión artificial y reconocimiento de patrones (CVPR) . págs. 913–922. arXiv : 1512.01413 . doi :10.1109/CVPR.2016.105. hdl :1721.1/103077. ISBN 978-1-4673-8851-1.S2CID 9085016 .
- ^ Gardiner, Aidan (12 de abril de 2018). «Cuando un agujero negro finalmente se revela, es útil tener nuestro propio reportero cósmico: los astrónomos anunciaron el miércoles que habían capturado la primera imagen de un agujero negro. Dennis Overbye, del Times, responde a las preguntas de los lectores». The New York Times . Archivado desde el original el 1 de enero de 2022 . Consultado el 15 de abril de 2019 .
- ^ El-Badry, Kareem; Rix, Hans-Walter; Quataert, Eliot; Howard, Andrew W.; Isaacson, Howard; Fuller, Jim; Hawkins, Keith; Breivik, Katelyn; Wong, Kaze WK; Rodriguez, Antonio C.; Conroy, Charlie; Shahaf, Sahar; Mazeh, Tsevi; Arenou, Frédéric; Burdge, Kevin B.; Bashi, Dolev; Faigler, Simchon; Weisz, Daniel R.; Seeburger, Rhys; Monter, Silvia Almada; Wojno, Jennifer (2023). "Una estrella similar al Sol orbitando un agujero negro". Monthly Notices of the Royal Astronomical Society . 518 : 1057–1085. arXiv : 2209.06833 . doi : 10.1093/mnras/stac3140 .
- ^ «El instrumento de ESO encuentra el agujero negro más cercano a la Tierra». Observatorio Europeo Austral . 6 de mayo de 2020. Archivado desde el original el 6 de mayo de 2020. Consultado el 2 de abril de 2021 .
- ^ ab "Marcia Bartusiak del MIT sobre la comprensión de nuestro lugar en el universo". www.wbur.org . 9 de octubre de 2018. Archivado desde el original el 12 de abril de 2019 . Consultado el 12 de abril de 2019 .
- ^ ab Siegfried, Tom (23 de diciembre de 2013). "50 años después, es difícil decir quién nombró a los agujeros negros". Science News . Archivado desde el original el 9 de marzo de 2017 . Consultado el 24 de septiembre de 2017 .
Parece que la etiqueta de "agujero negro" también se mencionó en enero de 1964 en Cleveland en una reunión de la Asociación Estadounidense para el Avance de la Ciencia. La reportera de Science News Letter, Ann Ewing, informó desde esa reunión, describiendo cómo un campo gravitatorio intenso podría hacer que una estrella colapsara sobre sí misma. "Una estrella así forma entonces un 'agujero negro' en el universo", escribió Ewing.
- ^ Brown, Emma (3 de agosto de 2010). «Ann E. Ewing, periodista que informó por primera vez sobre los agujeros negros». Boston.com . Archivado desde el original el 24 de septiembre de 2017. Consultado el 24 de septiembre de 2017 .
- ^ "El físico pionero John Wheeler muere a los 96 años". Scientific American . Archivado desde el original el 28 de noviembre de 2016. Consultado el 27 de noviembre de 2016 .
- ^ Overbye, Dennis (14 de abril de 2008). «John A. Wheeler, el físico que acuñó el término «agujero negro», ha muerto a los 96 años». The New York Times . Archivado desde el original el 22 de noviembre de 2016. Consultado el 27 de noviembre de 2016 .
- ^ Carroll 2004, pág. 253
- ^ Reynolds, Christopher S. (enero de 2019). «Observando el giro de los agujeros negros». Nature Astronomy . 3 (1): 41–47. arXiv : 1903.11704 . Código Bibliográfico : 2019NatAs...3...41R. doi : 10.1038/s41550-018-0665-z. ISSN 2397-3366. S2CID 85543351. Archivado desde el original el 18 de noviembre de 2020. Consultado el 21 de agosto de 2020 .
- ^ Thorne, KS ; Price, RH (1986). Agujeros negros: el paradigma de la membrana . Yale University Press. ISBN 978-0-300-03770-8.
- ^ ab Anderson, Warren G. (1996). "El problema de la pérdida de información en los agujeros negros". Usenet Physics FAQ . Archivado desde el original el 22 de enero de 2009. Consultado el 24 de marzo de 2009 .
- ^ Preskill, J. (21 de octubre de 1994). Agujeros negros e información: una crisis en la física cuántica (PDF) . Seminario de teoría de Caltech. Archivado desde el original (PDF) el 18 de mayo de 2008. Consultado el 17 de mayo de 2009 .
- ^ Preskill, J. (21 de octubre de 1994). Agujeros negros e información: una crisis en la física cuántica (PDF) . Seminario de teoría de Caltech. Archivado desde el original (PDF) el 18 de mayo de 2008. Consultado el 17 de mayo de 2009 .
- ^ Hawking y Ellis 1973, Apéndice B
- ^ Seeds, Michael A.; Backman, Dana E. (2007). Perspectivas sobre la astronomía. Cengage Learning. pág. 167. ISBN 978-0-495-11352-2Archivado desde el original el 10 de agosto de 2016.
- ^ Shapiro, SL; Teukolsky, SA (1983). Agujeros negros, enanas blancas y estrellas de neutrones: la física de los objetos compactos . John Wiley and Sons. pág. 357. ISBN 978-0-471-87316-7.
- ^ Berger, BK (2002). "Enfoques numéricos para las singularidades del espacio-tiempo". Living Reviews in Relativity . 5 (1): 2002–1. arXiv : gr-qc/0201056 . Código Bibliográfico :2002LRR.....5....1B. doi : 10.12942/lrr-2002-1 . PMC 5256073 . PMID 28179859.
- ^ McClintock, JE; Shafee, R.; Narayan, R.; Remillard, RA; Davis, SW; Li, L.-X. (2006). "El giro del agujero negro casi extremo de Kerr GRS 1915+105". Astrophysical Journal . 652 (1): 518–539. arXiv : astro-ph/0606076 . Código Bibliográfico :2006ApJ...652..518M. doi :10.1086/508457. S2CID 1762307.
- ^ abc Abbott, BP; et al. ( Colaboración científica LIGO y Colaboración Virgo ) (1 de junio de 2017). "GW170104: Observación de una coalescencia de un agujero negro binario de 50 masas solares con un corrimiento al rojo de 0,2". Physical Review Letters . 118 (22): 221101. arXiv : 1706.01812 . Código Bibliográfico :2017PhRvL.118v1101A. doi :10.1103/PhysRevLett.118.221101. PMID 28621973. S2CID 206291714.
- ^ Abbott, BP; et al. ( Colaboración científica LIGO y Colaboración Virgo ) (16 de octubre de 2017). "GW170817: Observación de ondas gravitacionales desde una espiral de estrellas de neutrones binarias". Physical Review Letters . 119 (16): 161101. arXiv : 1710.05832 . Código Bibliográfico :2017PhRvL.119p1101A. doi :10.1103/PhysRevLett.119.161101. PMID 29099225. S2CID 217163611.
- ^ Wald 1984, págs. 124-125
- ^ Saa, Alberto; Santarelli, Raphael (18 de julio de 2011). "Destrucción de un agujero negro de Kerr-Newman casi extremo". Physical Review D . 84 (2): 027501. arXiv : 1105.3950 . Código Bibliográfico :2011PhRvD..84b7501S. doi :10.1103/PhysRevD.84.027501. S2CID 118487989.
- ^ Misner, Thorne y Wheeler 1973, pág. 848
- ^ Davies, Paul (1992). The New Physics (edición ilustrada). Cambridge University Press. pág. 26. ISBN 978-0-521-43831-5Archivado del original el 17 de agosto de 2021 . Consultado el 25 de septiembre de 2020 .Extracto de la página 26 Archivado el 15 de agosto de 2021 en Wayback Machine.
- ^ Fleisch, Daniel; Kregenow, Julia (2013). Guía para estudiantes de las matemáticas de la astronomía (edición ilustrada). Cambridge University Press. pág. 168. ISBN 978-1-107-03494-5Archivado del original el 17 de agosto de 2021 . Consultado el 25 de septiembre de 2020 .Extracto de la página 168 Archivado el 17 de agosto de 2021 en Wayback Machine.
- ^ Wheeler 2007, pág. 179
- ^ Carroll 2004, cap. 5.4 y 7.3
- ^ "Singularidades y agujeros negros > Conos de luz y estructura causal". plato.stanford.edu . Stanford Encyclopedia of Philosophy . Archivado desde el original el 17 de mayo de 2019 . Consultado el 11 de marzo de 2018 .
- ^ Carroll 2004, pág. 217
- ^ Carroll 2004, pág. 218
- ^ "Dentro de un agujero negro". Conociendo el universo y sus secretos . Archivado desde el original el 23 de abril de 2009. Consultado el 26 de marzo de 2009 .
- ^ "¿Qué te pasa si caes en un agujero negro?". math.ucr.edu . John Baez . Archivado desde el original el 13 de febrero de 2019 . Consultado el 11 de marzo de 2018 .
- ^ Carroll 2004, pág. 222
- ^ "Mira: Tres formas en las que un astronauta podría caer en un agujero negro". 1 de febrero de 2014. Archivado desde el original el 15 de abril de 2019. Consultado el 13 de marzo de 2018 .
- ^ Emparan, R.; Reall, HS (2008). "Agujeros negros en dimensiones superiores". Living Reviews in Relativity . 11 (6): 6. arXiv : 0801.3471 . Bibcode :2008LRR....11....6E. doi : 10.12942/lrr-2008-6 . PMC 5253845 . PMID 28163607.
- ^ Obers, NA (2009). Papantonopoulos, Eleftherios (ed.). Física de agujeros negros (PDF) . Lecture Notes in Physics. Vol. 769. Berlín, Heidelberg. pp. 211–258. arXiv : 0802.0519 . Bibcode :2009LNP...769.....P. doi :10.1007/978-3-540-88460-6. ISBN . 978-3-540-88459-0. Archivado (PDF) del original el 26 de julio de 2018 . Consultado el 27 de julio de 2018 .
{{cite book}}: CS1 maint: location missing publisher (link) - ^ Hawking y Ellis 1973, cap. 9.3
- ^ Smarr, L. (1973). "Geometría superficial de agujeros negros giratorios cargados". Physical Review D . 7 (2): 289–295. Código Bibliográfico :1973PhRvD...7..289S. doi :10.1103/PhysRevD.7.289.
- ^ Visser, M. (22 de enero de 2009). "El espacio-tiempo de Kerr: una breve introducción". En Wiltshire, DL; Visser, M.; Scott, SM (eds.). El espacio-tiempo de Kerr: agujeros negros en rotación en la relatividad general. Cambridge University Press. arXiv : 0706.0622 . ISBN 978-052188512-6Archivado del original el 20 de mayo de 2020 . Consultado el 12 de enero de 2020 .
- ^ Delgado, JFM; Herdeiro, CAR; Radu, E. (2018). "Geometría del horizonte para agujeros negros de Kerr con pelo sincronizado". Physical Review D . 97 (12): 124012. arXiv : 1804.04910 . Bibcode :2018PhRvD..97l4012D. doi :10.1103/PhysRevD.97.124012. hdl :10773/24121. S2CID 55732213.
- ^ Carroll 2004, pág. 205
- ^ Carroll 2004, págs. 264-265
- ^ Carroll 2004, pág. 252
- ^ "¿Tamaños de agujeros negros? ¿Qué tan grande es un agujero negro?". Sky & Telescope . 22 de julio de 2014. Archivado desde el original el 3 de abril de 2019. Consultado el 9 de octubre de 2018 .
- ^ Lewis, GF; Kwan, J. (2007). "No hay vuelta atrás: maximizar el tiempo de supervivencia por debajo del horizonte de sucesos de Schwarzschild". Publicaciones de la Sociedad Astronómica de Australia . 24 (2): 46–52. arXiv : 0705.1029 . Código Bibliográfico :2007PASA...24...46L. doi :10.1071/AS07012. S2CID 17261076.
- ^ Wheeler 2007, pág. 182
- ^ Carroll 2004, págs. 257-259 y 265-266
- ^ Droz, S.; Israel, W.; Morsink, SM (1996). "Agujeros negros: la historia desde dentro". Physics World . 9 (1): 34–37. Bibcode :1996PhyW....9...34D. doi :10.1088/2058-7058/9/1/26.
- ^ Carroll 2004, pág. 266
- ^ Poisson, E.; Israel, W. (1990). "Estructura interna de los agujeros negros". Physical Review D . 41 (6): 1796–1809. Bibcode :1990PhRvD..41.1796P. doi :10.1103/PhysRevD.41.1796. PMID 10012548.
- ^ Wald 1984, pág. 212
- ^ Hamade, R. (1996). «Agujeros negros y gravedad cuántica». Cambridge Relativity and Cosmology . Universidad de Cambridge. Archivado desde el original el 7 de abril de 2009. Consultado el 26 de marzo de 2009 .
- ^ Palmer, D. "Pregúntele a un astrofísico: Gravedad cuántica y agujeros negros". NASA. Archivado desde el original el 28 de marzo de 2009. Consultado el 26 de marzo de 2009 .
- ^ Cramer, Claes R. (1997). "Usando el agujero negro no cargado de Kerr como espejo gravitacional". Relatividad general y gravitación . 29 (4): 445–454. arXiv : gr-qc/9510053 . Código Bibliográfico :1997GReGr..29..445C. doi :10.1023/A:1018878515046. S2CID 9517046.
- ^ ab Nitta, Daisuke; Chiba, Takeshi; Sugiyama, Naoshi (septiembre de 2011). "Sombras de agujeros negros en colisión". Physical Review D . 84 (6): 063008. arXiv : 1106.2425 . Código Bibliográfico :2011PhRvD..84f3008N. doi :10.1103/PhysRevD.84.063008. S2CID 119264596.
- ^ Bardeen, James M.; Press, William H.; Teukolsky, Saul A. (1 de diciembre de 1972). "Agujeros negros giratorios: marcos localmente no giratorios, extracción de energía y radiación sincrotrón escalar". The Astrophysical Journal . 178 : 347–370. Bibcode :1972ApJ...178..347B. doi :10.1086/151796.
- ^ "Calculadora de agujeros negros". Fabio Pacucci . Archivado desde el original el 21 de octubre de 2020. Consultado el 29 de septiembre de 2020 .
- ^ ab Visser, Matt (2007). "El espacio-tiempo de Kerr: una breve introducción". página 35, Fig. 3. arXiv : 0706.0622 [gr-qc].
- ^ Carroll 2004, cap. 6.6
- ^ Carroll 2004, cap. 6.7
- ^ Misner, Thorne y Wheeler 1973, Caja 25.6
- ^ Bardeen, JM (1972). "Agujeros negros rotatorios: marcos localmente no rotatorios, extracción de energía y radiación sincrotrón escalar". The Astrophysical Journal . 178 : 347–370. Bibcode :1972ApJ...178..347B. doi :10.1086/151796.
- ^ "Primera prueba de la existencia de 'regiones de hundimiento' de agujeros negros". Departamento de Física. Universidad de Oxford . 16 de mayo de 2024.
- ^ Mummery, Andrew; Ingram, Adam; Davis, Shane; Fabian, Andrew (junio de 2024). "Emisión continua desde dentro de la región de hundimiento de los discos de los agujeros negros". Monthly Notices of the Royal Astronomical Society . 531 (1): 366–386. arXiv : 2405.09175 . doi : 10.1093/mnras/stae1160 .
- ^ Einstein, A. (1939). "Sobre un sistema estacionario con simetría esférica que consta de muchas masas gravitantes" (PDF) . Anales de Matemáticas . 40 (4): 922–936. Código Bibliográfico :1939AnMat..40..922E. doi :10.2307/1968902. JSTOR 1968902. S2CID 55495712. Archivado desde el original (PDF) el 28 de febrero de 2019.
- ^ Kerr, RP (2009). "Las métricas de Kerr y Kerr-Schild". En Wiltshire, DL; Visser, M.; Scott, SM (eds.). El espacio-tiempo de Kerr . Cambridge University Press. arXiv : 0706.1109 . Bibcode :2007arXiv0706.1109K. ISBN. 978-0-521-88512-6.
- ^ Findley, Kate (27 de diciembre de 2019). «El descubrimiento de los agujeros negros: de la teoría a la realidad». Wondrium Daily . Consultado el 29 de junio de 2022 .[ enlace muerto permanente ]
- ^ Hawking, SW ; Penrose, R. (enero de 1970). "Las singularidades del colapso gravitacional y la cosmología". Actas de la Royal Society A . 314 (1519): 529–548. Bibcode :1970RSPSA.314..529H. doi : 10.1098/rspa.1970.0021 . JSTOR 2416467.
- ^ abc Pacucci, F.; Ferrara, A.; Grazian, A.; Fiore, F.; Giallongo, E. (2016). "Primera identificación de candidatos a agujero negro por colapso directo en el universo temprano en CANDELS/GOODS-S". Mon. Not. R. Astron. Soc . 459 (2): 1432. arXiv : 1603.08522 . Bibcode :2016MNRAS.459.1432P. doi : 10.1093/mnras/stw725 . S2CID: 118578313.
- ^ ab Carr, BJ (2005). "Agujeros negros primordiales: ¿existen y son útiles?". En Suzuki, H.; Yokoyama, J.; Suto, Y.; Sato, K. (eds.). Horizonte inflado de astrofísica y cosmología de partículas . Universal Academy Press. pp. astro–ph/0511743. arXiv : astro-ph/0511743 . Código Bibliográfico :2005astro.ph.11743C. ISBN 978-4-946443-94-7.
- ^ "Desgarrado por un agujero negro". Nota de prensa de la ESO . Archivado desde el original el 21 de julio de 2013. Consultado el 19 de julio de 2013 .
- ^ abc Carroll 2004, Sección 5.8
- ^ abc Rees, MJ; Volonteri, M. (2007). Karas, V.; Matt, G. (eds.). Agujeros negros masivos: formación y evolución . Actas de la Unión Astronómica Internacional. Vol. 238. págs. 51–58. arXiv : astro-ph/0701512 . Bibcode :2007IAUS..238...51R. doi :10.1017/S1743921307004681. ISBN . 978-0-521-86347-6. Número de identificación del sujeto 14844338.
{{cite book}}:|journal=ignorado ( ayuda ) - ^ Bañados, Eduardo; Venemans, Bram P.; Mazzucchelli, Chiara; Farina, Emanuele P.; Walter, Fabian; Wang, Feige; Decarli, Roberto; Stern, Daniel; Fan, Xiaohui; Davies, Frederick B.; Hennawi, Joseph F. (1 de enero de 2018). "Un agujero negro de 800 millones de masas solares en un universo significativamente neutral con un corrimiento al rojo de 7,5". Nature . 553 (7689): 473–476. arXiv : 1712.01860 . Código Bibliográfico :2018Natur.553..473B. doi :10.1038/nature25180. PMID 29211709. S2CID 205263326.
- ^ Penrose, R. (2002). "Colapso gravitacional: el papel de la relatividad general" (PDF) . Relatividad general y gravitación . 34 (7): 1141. Código Bibliográfico :2002GReGr..34.1141P. doi :10.1023/A:1016578408204. S2CID 117459073. Archivado desde el original (PDF) el 26 de mayo de 2013.
- ^ Philip Gibbs. "¿Es el Big Bang un agujero negro?". John Baez . Archivado desde el original el 31 de diciembre de 2018. Consultado el 16 de marzo de 2018 .
- ^ Giddings, SB; Thomas, S. (2002). "Colisionadores de alta energía como fábricas de agujeros negros: el fin de la física de corta distancia". Physical Review D . 65 (5): 056010. arXiv : hep-ph/0106219 . Código Bibliográfico :2002PhRvD..65e6010G. doi :10.1103/PhysRevD.65.056010. S2CID 1203487.
- ^ Harada, T. (2006). "¿Existe una masa mínima para los agujeros negros?". Physical Review D. 74 ( 8): 084004. arXiv : gr-qc/0609055 . Bibcode :2006PhRvD..74h4004H. doi :10.1103/PhysRevD.74.084004. S2CID : 119375284.
- ^ Arkani–Hamed, N.; Dimopoulos, S.; Dvali, G. (1998). "El problema de la jerarquía y nuevas dimensiones en un milímetro". Physics Letters B . 429 (3–4): 263–272. arXiv : hep-ph/9803315 . Código Bibliográfico :1998PhLB..429..263A. doi :10.1016/S0370-2693(98)00466-3. S2CID 15903444.
- ^ LHC Safety Assessment Group (2008). "Revisión de la seguridad de las colisiones del LHC" (PDF) . Journal of Physics G: Nuclear Physics . 35 (11): 115004. arXiv : 0806.3414 . Bibcode :2008JPhG...35k5004E. doi :10.1088/0954-3899/35/11/115004. S2CID 53370175. Archivado (PDF) desde el original el 14 de abril de 2010.
- ^ Cavaglià, M. (2010). «¿Aceleradores de partículas como fábricas de agujeros negros?». Einstein-Online . 4 : 1010. Archivado desde el original el 8 de mayo de 2013. Consultado el 8 de mayo de 2013 .
- ^ Vesperini, E.; McMillan, SLW; d'Ercole, A.; et al. (2010). "Agujeros negros de masa intermedia en cúmulos globulares tempranos". The Astrophysical Journal Letters . 713 (1): L41–L44. arXiv : 1003.3470 . Código Bibliográfico :2010ApJ...713L..41V. doi :10.1088/2041-8205/713/1/L41. S2CID 119120429.
- ^ Zwart, SFP; Baumgardt, H.; Hut, P.; et al. (2004). "Formación de agujeros negros masivos a través de colisiones descontroladas en cúmulos estelares jóvenes densos". Nature . 428 (6984): 724–726. arXiv : astro-ph/0402622 . Bibcode :2004Natur.428..724P. doi :10.1038/nature02448. PMID 15085124. S2CID 4408378.
- ^ O'Leary, RM; Rasio, FA; Fregeau, JM; et al. (2006). "Fusiones binarias y crecimiento de agujeros negros en cúmulos estelares densos". The Astrophysical Journal . 637 (2): 937–951. arXiv : astro-ph/0508224 . Código Bibliográfico :2006ApJ...637..937O. doi :10.1086/498446. S2CID 1509957.
- ^ Page, DN (2005). "Radiación de Hawking y termodinámica de agujeros negros". New Journal of Physics . 7 (1): 203. arXiv : hep-th/0409024 . Código Bibliográfico :2005NJPh....7..203P. doi :10.1088/1367-2630/7/1/203. S2CID 119047329.
- ^ Carroll 2004, cap. 9.6
- ^ Siegel, Ethan (2017). "Pregúntale a Ethan: ¿Los agujeros negros crecen más rápido de lo que se evaporan?". Forbes (blog "Starts With A Bang") . Archivado desde el original el 22 de noviembre de 2018. Consultado el 17 de marzo de 2018 .
- ^ Sivaram, C. (2001). "¡La radiación de Hawking en los agujeros negros tal vez nunca sea observada!". Relatividad general y gravitación . 33 (2): 175–181. Bibcode :2001GReGr..33..175S. doi :10.1023/A:1002753400430. S2CID 118913634.
- ^ "¿Agujeros negros en evaporación?". Einstein en línea . Instituto Max Planck de Física Gravitacional. 2010. Archivado desde el original el 22 de julio de 2011. Consultado el 12 de diciembre de 2010 .
- ^ Giddings, SB; Mangano, ML (2008). "Implicaciones astrofísicas de los hipotéticos agujeros negros estables a escala de TeV". Physical Review D . 78 (3): 035009. arXiv : 0806.3381 . Código Bibliográfico :2008PhRvD..78c5009G. doi :10.1103/PhysRevD.78.035009. S2CID 17240525.
- ^ Peskin, ME (2008). "¿El fin del mundo en el Gran Colisionador de Hadrones?". Física . 1 : 14. Bibcode :2008PhyOJ...1...14P. doi : 10.1103/Physics.1.14 .
- ^ Fichtel, CE; Bertsch, DL; Dingus, BL ; et al. (1994). "Búsqueda de datos del telescopio experimental de rayos gamma energéticos (EGRET) para estallidos de microsegundos de rayos gamma de alta energía". Astrophysical Journal . 434 (2): 557–559. Bibcode :1994ApJ...434..557F. doi :10.1086/174758.
- ^ Naeye, R. "Testing Fundamental Physics". NASA. Archivado desde el original el 31 de agosto de 2008. Consultado el 16 de septiembre de 2008 .
- ^ ab Frautschi, S. (1982). "Entropía en un universo en expansión". Science . 217 (4560): 593–599. Bibcode :1982Sci...217..593F. doi :10.1126/science.217.4560.593. PMID 17817517. S2CID 27717447.Véase la página 596: tabla 1 y la sección “desintegración del agujero negro” y la oración anterior en esa página.
- ^ Page, Don N. (1976). "Tasas de emisión de partículas de un agujero negro: partículas sin masa de un agujero no cargado y no rotatorio". Physical Review D . 13 (2): 198–206. Bibcode :1976PhRvD..13..198P. doi :10.1103/PhysRevD.13.198.. Véase en particular la ecuación (27).
- ^ "Agujeros negros | Dirección de misiones científicas". NASA. Archivado desde el original el 17 de noviembre de 2017. Consultado el 17 de marzo de 2018 .
- ^ "Observaciones de abril de 2017". Event Horizon Telescope . Archivado desde el original el 10 de abril de 2019. Consultado el 11 de abril de 2019 .
- ^ Overbye, Dennis (24 de enero de 2024). «Ese famoso agujero negro recibe una segunda mirada: estudios repetidos del agujero negro supermasivo en la galaxia Messier 87 confirman que sigue actuando como la teoría de Einstein predijo que lo haría». The New York Times . Archivado desde el original el 24 de enero de 2024. Consultado el 25 de enero de 2024 .
- ^ Overbye, Dennis (10 de abril de 2019). «La oscuridad es visible, por fin: los astrónomos captan la primera imagen de un agujero negro». The New York Times . Archivado desde el original el 21 de mayo de 2019. Consultado el 11 de abril de 2019 .
- ^ AP (10 de abril de 2019). «Los astrónomos revelan la primera imagen de un agujero negro». The New York Times (video). Archivado desde el original el 22 de mayo de 2019. Consultado el 11 de abril de 2019 .
- ^ Doeleman, Shep (4 de abril de 2016). "El telescopio del horizonte de sucesos: obtención de imágenes y resolución temporal de un agujero negro". Physics @ Berkeley . El evento se produce a las 46:50. Archivado desde el original el 1 de diciembre de 2016. Consultado el 8 de julio de 2016 .
- ^ Grossman, Lisa; Conover, Emily (10 de abril de 2019). «La primera imagen de un agujero negro abre una nueva era en la astrofísica». Science News . Archivado desde el original el 27 de abril de 2019. Consultado el 11 de abril de 2019 .
- ^ Este artículo incorpora texto disponible bajo la licencia CC BY 4.0. «Los astrónomos revelan la primera imagen del agujero negro en el corazón de nuestra galaxia». eventhorizontelescope.org . 12 de mayo de 2022 . Consultado el 22 de junio de 2022 .
- ^ C. Bower, Geoffrey (mayo de 2022). "Enfoque en los primeros resultados de Sgr A* del Event Horizon Telescope". The Astrophysical Journal Letters (2041–8205).
- ^ Event Horizon Telescope Collaboration (2021). "Primeros resultados del Event Horizon Telescope M87. VII. Polarización del anillo". The Astrophysical Journal . 910 (1): L12. arXiv : 2105.01169 . Código Bibliográfico :2021ApJ...910L..12E. doi : 10.3847/2041-8213/abe71d . S2CID 233851995.
- ^ "La primera imagen de un agujero negro abre una nueva era en la astrofísica". Science News . 10 de abril de 2019. Archivado desde el original el 27 de abril de 2019 . Consultado el 30 de septiembre de 2019 .
- ^ Johnson, MD; Fish, VL; Doeleman, SS; Marrone, DP; Plambeck, RL; Wardle, JFC; Akiyama, K.; Asada, K.; Beaudoin, C. (4 de diciembre de 2015). "Estructura y variabilidad del campo magnético resuelto cerca del horizonte de sucesos de Sagitario A*". Science . 350 (6265): 1242–1245. arXiv : 1512.01220 . Bibcode :2015Sci...350.1242J. doi :10.1126/science.aac7087. PMID 26785487. S2CID 21730194.
- ^ "Event Horizon Telescope revela campos magnéticos en el agujero negro central de la Vía Láctea". cfa.harvard.edu . 3 de diciembre de 2015. Archivado desde el original el 31 de diciembre de 2015 . Consultado el 12 de enero de 2016 .
- ^ Overbye, Dennis (26 de abril de 2023). «Una nueva visión de un agujero negro cada vez más conocido: los radioastrónomos han captado una imagen de gran angular de uno de los lugares más violentos del cosmos». The New York Times . Archivado desde el original el 26 de abril de 2023. Consultado el 26 de abril de 2023 .
- ^ Lu, Ru-Sen; et al. (26 de abril de 2023). "Una estructura de acreción en forma de anillo en M87 que conecta su agujero negro y chorro". Nature . 616 (7958): 686–690. arXiv : 2304.13252 . Bibcode :2023Natur.616..686L. doi :10.1038/s41586-023-05843-w. PMC 10132962 . PMID 37100940.
- ^ Overbye, Dennis (11 de febrero de 2016). «Los físicos detectan ondas gravitacionales y demuestran que Einstein tenía razón». The New York Times . Archivado desde el original el 11 de febrero de 2016. Consultado el 11 de febrero de 2016 .
- ^ Abbott, Benjamin P.; et al. ( Colaboración científica LIGO y Colaboración Virgo ) (11 de febrero de 2016). "Propiedades de la fusión de agujeros negros binarios GW150914". Physical Review Letters . 116 (24): 241102. arXiv : 1602.03840 . Código Bibliográfico :2016PhRvL.116x1102A. doi :10.1103/PhysRevLett.116.241102. PMID 27367378. S2CID 217406416.
- ^ ab Cardoso, V.; Franzin, E.; Pani, P. (2016). "¿Es el anillo de ondas gravitacionales una sonda del horizonte de sucesos?". Physical Review Letters . 116 (17): 171101. arXiv : 1602.07309 . Bibcode :2016PhRvL.116q1101C. doi :10.1103/PhysRevLett.116.171101. PMID 27176511. S2CID 206273829.
- ^ Abbott, Benjamin P.; et al. ( LIGO Scientific Collaboration & Virgo Collaboration ) (11 de febrero de 2016). "Pruebas de relatividad general con GW150914". Physical Review Letters . 116 (22): 221101. arXiv : 1602.03841 . Código Bibliográfico :2016PhRvL.116v1101A. doi :10.1103/PhysRevLett.116.221101. PMID 27314708. S2CID 217275338. Archivado desde el original el 15 de febrero de 2016 . Consultado el 12 de febrero de 2016 .
- ^ ab Murk, Sebastian (2023). "Nomen non est omen: Por qué es demasiado pronto para identificar objetos ultracompactos como agujeros negros". Revista Internacional de Física Moderna D . 32 (14): 2342012–2342235. arXiv : 2210.03750 . Código Bibliográfico :2023IJMPD..3242012M. doi :10.1142/S0218271823420129. S2CID 252781040.
- ^ Abbott, BP; et al. ( Colaboración científica LIGO y Colaboración Virgo ) (2016). "Implicaciones astrofísicas de la fusión de agujeros negros binarios GW150914". Astrophys. J. Lett . 818 (2): L22. arXiv : 1602.03846 . Bibcode :2016ApJ...818L..22A. doi : 10.3847/2041-8205/818/2/L22 . hdl :1826/11732. S2CID 209315965. Archivado desde el original el 16 de marzo de 2016.
- ^ "Detección de ondas gravitacionales". LIGO . Archivado desde el original el 20 de mayo de 2020 . Consultado el 9 de abril de 2018 .
- ^ ab Gillessen, S.; Eisenhauer, F.; Trippe, S.; et al. (2009). "Monitoreo de órbitas estelares alrededor del agujero negro masivo en el centro galáctico". The Astrophysical Journal . 692 (2): 1075–1109. arXiv : 0810.4674 . Bibcode :2009ApJ...692.1075G. doi :10.1088/0004-637X/692/2/1075. S2CID 1431308.
- ^ ab Ghez, AM; Klein, BL; Morris, M.; et al. (1998). "Estrellas de alto movimiento propio en las proximidades de Sagitario A*: evidencia de un agujero negro supermasivo en el centro de nuestra galaxia". The Astrophysical Journal . 509 (2): 678–686. arXiv : astro-ph/9807210 . Código Bibliográfico :1998ApJ...509..678G. doi :10.1086/306528. S2CID 18243528.
- ^ Broderick, Avery; Loeb, Abraham; Narayan, Ramesh (agosto de 2009). "El horizonte de sucesos de Sagitario A*". The Astrophysical Journal . 701 (2): 1357–1366. arXiv : 0903.1105 . Código Bibliográfico :2009ApJ...701.1357B. doi :10.1088/0004-637X/701/2/1357. S2CID 12991878.
- ^ "El telescopio NuSTAR de la NASA detecta una rara distorsión de la luz de un agujero negro". NASA . 12 de agosto de 2014. Archivado desde el original el 13 de agosto de 2014 . Consultado el 12 de agosto de 2014 .
- ^ "Los investigadores aclaran la dinámica de la energía rotacional de los agujeros negros". Archivado desde el original el 17 de septiembre de 2018. Consultado el 17 de septiembre de 2018 .
- ^ Marck, Jean-Alain (1 de marzo de 1996). "Método abreviado de solución de ecuaciones geodésicas para el agujero negro de Schwarzchild". Gravedad clásica y cuántica . 13 (3): 393–402. arXiv : gr-qc/9505010 . Código Bibliográfico :1996CQGra..13..393M. doi :10.1088/0264-9381/13/3/007. ISSN 0264-9381. S2CID 119508131.
- ^ ab McClintock, JE; Remillard, RA (2006). "Binarias de agujeros negros". En Lewin, W.; van der Klis, M. (eds.). Fuentes compactas de rayos X estelares . p. 157. arXiv : astro-ph/0306213 . Código Bibliográfico :2006csxs.book..157M. ISBN 978-0-521-82659-4.Sección 4.1.5.
- ^ "¿Qué impulsa los poderosos chorros de un agujero negro?". Ciencia | AAAS . 19 de noviembre de 2014. Archivado desde el original el 5 de mayo de 2019 . Consultado el 19 de marzo de 2018 .
- ^ abcdefghi Celotti, A.; Miller, JC; Sciama, DW (1999). "Evidencia astrofísica de la existencia de agujeros negros" (PDF) . Gravedad clásica y cuántica . 16 (12A): A3–A21. arXiv : astro-ph/9912186 . Código Bibliográfico :1999CQGra..16A...3C. doi :10.1088/0264-9381/16/12A/301. S2CID 17677758. Archivado (PDF) desde el original el 27 de julio de 2018 . Consultado el 27 de julio de 2018 .
- ^ Winter, LM; Mushotzky, RF; Reynolds, CS (2006). "Estudio archivístico XMM-Newton de la población de rayos X ultraluminosos en galaxias cercanas". The Astrophysical Journal . 649 (2): 730–752. arXiv : astro-ph/0512480 . Código Bibliográfico :2006ApJ...649..730W. doi :10.1086/506579. S2CID 118445260.
- ^ [email protected]. «Hubble observa directamente el disco alrededor de un agujero negro». www.spacetelescope.org . Archivado desde el original el 8 de marzo de 2016. Consultado el 7 de marzo de 2016 .
- ^ Muñoz, José A.; Mediavilla, Evencio; Kochanek, Christopher S.; Falcó, Emilio; Mosquera, Ana María (1 de diciembre de 2011). "Un estudio de la cromaticidad de la lente gravitacional con el telescopio espacial Hubble". La revista astrofísica . 742 (2): 67. arXiv : 1107.5932 . Código Bib : 2011ApJ...742...67M. doi :10.1088/0004-637X/742/2/67. S2CID 119119359.
- ^ Bolton, CT (1972). "Identificación de Cygnus X-1 con HDE 226868". Nature . 235 (5336): 271–273. Código Bibliográfico :1972Natur.235..271B. doi :10.1038/235271b0. S2CID 4222070.
- ^ Webster, BL; Murdin, P. (1972). "Cygnus X-1: ¿una binaria espectroscópica con un compañero pesado?". Nature . 235 (5332): 37–38. Bibcode :1972Natur.235...37W. doi :10.1038/235037a0. S2CID 4195462.
- ^ Rolston, B. (10 de noviembre de 1997). "El primer agujero negro". El boletín . Universidad de Toronto. Archivado desde el original el 2 de mayo de 2008 . Consultado el 11 de marzo de 2008 .
- ^ Shipman, HL (1 de enero de 1975). "La improbable historia de los modelos de estrellas triples para Cygnus X-1: evidencia de un agujero negro". Astrophysical Letters . 16 (1): 9–12. Bibcode :1975ApL....16....9S.
- ^ "Los científicos de la NASA identifican el agujero negro más pequeño conocido" (Nota de prensa). Goddard Space Flight Center . 1 de abril de 2008. Archivado desde el original el 27 de diciembre de 2008. Consultado el 14 de marzo de 2009 .
- ^ Chou, Felicia; Anderson, Janet; Watzke, Megan (5 de enero de 2015). "RELEASE 15-001 – NASA's Chandra Detects Record-Breaking Outburst from Milky Way's Black Hole". NASA . Archivado desde el original el 6 de enero de 2015 . Consultado el 6 de enero de 2015 .
- ^ Krolik, JH (1999). Núcleos galácticos activos. Princeton University Press. Cap. 1.2. ISBN 978-0-691-01151-6Archivado del original el 14 de agosto de 2021 . Consultado el 16 de octubre de 2020 .
- ^ Sparke, LS ; Gallagher, JS (2000). Galaxias en el universo: una introducción. Cambridge University Press. Cap. 9.1. ISBN 978-0-521-59740-1Archivado del original el 22 de marzo de 2022 . Consultado el 16 de octubre de 2020 .
- ^ Kormendy, J.; Richstone, D. (1995). "Inward Bound – La búsqueda de agujeros negros supermasivos en núcleos galácticos". Revista anual de astronomía y astrofísica . 33 (1): 581–624. Bibcode :1995ARA&A..33..581K. doi :10.1146/annurev.aa.33.090195.003053.
- ^ King, A. (2003). "Agujeros negros, formación de galaxias y la relación MBH-σ". The Astrophysical Journal Letters . 596 (1): 27–29. arXiv : astro-ph/0308342 . Código Bibliográfico :2003ApJ...596L..27K. doi :10.1086/379143. S2CID 9507887.
- ^ Ferrarese, L.; Merritt, D. (2000). "Una relación fundamental entre los agujeros negros supermasivos y sus galaxias anfitrionas". The Astrophysical Journal Letters . 539 (1): 9–12. arXiv : astro-ph/0006053 . Código Bibliográfico :2000ApJ...539L...9F. doi :10.1086/312838. S2CID 6508110.
- ^ Bennett, DP; Becker, AC; Quinn, JL; Tomaney, AB; Alcock, C.; Allsman, RA; Alves, DR; Axelrod, TS; Calitz, JJ; Cook, KH; Drake, AJ; Fragile, PC; Freeman, KC; Geha, M.; Griest, K. (1 de noviembre de 2002). "Eventos de microlente gravitacional debidos a agujeros negros de masa estelar". The Astrophysical Journal . 579 (2): 639–659. arXiv : astro-ph/0109467 . Código Bibliográfico :2002ApJ...579..639B. doi :10.1086/342225. ISSN 0004-637X.
- ^ Mao, Shude; Smith, Martin C.; Woźniak, P.; Udalski, A.; Szymański, M.; Kubiak, M.; Pietrzyński, G.; Soszyński, I.; Żebruń, K. (1 de enero de 2002). "Experimento de lente gravitacional óptica OGLE-1999-BUL-32: el evento de microlente más largo jamás visto - ¿evidencia de un agujero negro de masa estelar?". Monthly Notices of the Royal Astronomical Society . 329 (2): 349–354. arXiv : astro-ph/0108312 . Código Bibliográfico :2002MNRAS.329..349M. doi : 10.1046/j.1365-8711.2002.04986.x . Revista de Ciencias Sociales y Humanidades (Revista de Ciencias Sociales y Humanidades).
- ^ Sahu, KC (2022). "Un agujero negro aislado de masa estelar detectado mediante microlente astrométrica". Astrophysical Journal . 933 (1): 83. arXiv : 2201.13296 . Código Bibliográfico :2022ApJ...933...83S. doi : 10.3847/1538-4357/ac739e . S2CID 246430448.
- ^ Bozza, V. (2010). "Lentes gravitacionales por agujeros negros". Relatividad general y gravitación . 42 (9): 2269–2300. arXiv : 0911.2187 . Código Bibliográfico :2010GReGr..42.2269B. doi :10.1007/s10714-010-0988-2. S2CID 118635353.
- ^ Kovacs, Z.; Cheng, KS; Harko, T. (2009). "¿Pueden los agujeros negros de masa estelar ser estrellas de quarks?". Monthly Notices of the Royal Astronomical Society . 400 (3): 1632–1642. arXiv : 0908.2672 . Bibcode :2009MNRAS.400.1632K. doi : 10.1111/j.1365-2966.2009.15571.x . S2CID 18263809.
- ^ Kusenko, A. (2006). "Propiedades y firmas de bolas Q supersimétricas". arXiv : hep-ph/0612159 .
- ^ Hansson, J.; Sandin, F. (2005). "Estrellas preón: una nueva clase de objetos compactos cósmicos". Physics Letters B . 616 (1–2): 1–7. arXiv : astro-ph/0410417 . Código Bibliográfico :2005PhLB..616....1H. doi :10.1016/j.physletb.2005.04.034. S2CID 119063004.
- ^ Kiefer, C. (2006). "Gravedad cuántica: introducción general y desarrollos recientes". Annalen der Physik . 15 (1–2): 129–148. arXiv : gr-qc/0508120 . Código Bibliográfico :2006AnP...518..129K. doi :10.1002/andp.200510175. S2CID 12984346.
- ^ Mathur, Samir D. (2005). "La propuesta fuzzball para los agujeros negros: una revisión elemental". Fortschritte der Physik . 53 (7–8): 793. arXiv : hep-th/0502050 . Código bibliográfico : 2005 para Ph..53..793M. doi :10.1002/prop.200410203. S2CID 15083147.
- ^ Skenderis, K.; Taylor, M. (2008). "La propuesta de bola de pelusa para los agujeros negros". Physics Reports . 467 (4–5): 117. arXiv : 0804.0552 . Bibcode :2008PhR...467..117S. doi :10.1016/j.physrep.2008.08.001. S2CID 118403957.
- ^ Mazur, Pawel O.; Mottola, Emil (2004). "Estrellas de condensado de vacío gravitacional". Actas de la Academia Nacional de Ciencias de los Estados Unidos de América . 101 (26): 9545–9550. arXiv : gr-qc/0407075 . Bibcode :2004PNAS..101.9545M. doi : 10.1073/pnas.0402717101 . PMC 470711 . PMID 15210982. S2CID 2607263.
- ^ Choi, Charles Q. (2018). «Los pretendientes a agujeros negros podrían ser realmente estrellas cuánticas extrañas». Scientific American . Archivado desde el original el 17 de junio de 2019. Consultado el 17 de marzo de 2018 .
- ^ McRae, Mike (20 de febrero de 2024). «Estrellas dentro de estrellas que parecen burbujas podrían explicar la rareza de los agujeros negros». ScienceAlert . Archivado desde el original el 20 de febrero de 2024 . Consultado el 20 de febrero de 2024 .
- ^ Ball, Philip (31 de marzo de 2005). "Los agujeros negros 'no existen'"". Naturaleza . doi :10.1038/news050328-8.
- ^ Hawking, SW (1971). "Radiación gravitacional de agujeros negros en colisión". Physical Review Letters . 26 (21): 1344–1346. Código Bibliográfico :1971PhRvL..26.1344H. doi :10.1103/PhysRevLett.26.1344.
- ^ ab Wald, RM (2001). "La termodinámica de los agujeros negros". Living Reviews in Relativity . 4 (1): 6. arXiv : gr-qc/9912119 . Bibcode :2001LRR.....4....6W. doi : 10.12942/lrr-2001-6 . PMC 5253844 . PMID 28163633.
- ^ 't Hooft, G. (2001). "El principio holográfico". En Zichichi, A. (ed.). Fundamentos y aspectos destacados de la física fundamental . Serie subnuclear. Vol. 37. World Scientific Publishing . págs. 72–100. arXiv : hep-th/0003004 . Código Bibliográfico : 2001bhfp.conf...72T. doi : 10.1142/9789812811585_0005. ISBN . 978-981-02-4536-8.S2CID119383028 .
- ^ Strominger, A.; Vafa, C. (1996). "Origen microscópico de la entropía de Bekenstein-Hawking". Physics Letters B . 379 (1–4): 99–104. arXiv : hep-th/9601029 . Código Bibliográfico :1996PhLB..379...99S. doi :10.1016/0370-2693(96)00345-0. S2CID 1041890.
- ^ Carlip, S. (2009). "Termodinámica de agujeros negros y mecánica estadística". Física de agujeros negros . Apuntes de clase de física. Vol. 769. Berlín, Heidelberg. págs. 89–123. arXiv : 0807.4520 . Código Bibliográfico :2009LNP...769...89C. doi :10.1007/978-3-540-88460-6_3. ISBN: 978-3-540-88459-0. Número de identificación del sujeto 15877702.
{{cite book}}: CS1 maint: location missing publisher (link) - ^ Hawking, SW "¿Dios juega a los dados?". www.hawking.org.uk . Archivado desde el original el 11 de enero de 2012. Consultado el 14 de marzo de 2009 .
- ^ Giddings, SB (1995). "La paradoja de la información del agujero negro". Partículas, cuerdas y cosmología . Taller de Johns Hopkins sobre problemas actuales en teoría de partículas 19 y simposio interdisciplinario PASCOS 5. arXiv : hep-th/9508151 . Bibcode :1995hep.th....8151G.
- ^ ab Unruh, William G. ; Wald, Robert M. (2017). "Pérdida de información". Informes sobre el progreso en física . 80 (9): 092002. arXiv : 1703.02140 . Bibcode :2017RPPh...80i2002U. doi :10.1088/1361-6633/aa778e. PMID 28585922. S2CID 39957660.
- ^ Mathur, SD (2011). La paradoja de la información: conflictos y resoluciones . XXV Simposio Internacional sobre Interacciones Leptón-Fotónicas a Altas Energías. Pramana . Vol. 79, núm. 5. págs. 1059–1073. arXiv : 1201.2079 . Bibcode :2012Prama..79.1059M. doi :10.1007/s12043-012-0417-z.
- ^ Page, Don N. (1993). "Información en la radiación de los agujeros negros". Phys. Rev. Lett. 71 (23): 3743–3746. arXiv : hep-th/9306083 . Código Bibliográfico :1993PhRvL..71.3743P. CiteSeerX 10.1.1.267.174 . doi :10.1103/PhysRevLett.71.3743. PMID 10055062. S2CID 9363821.
- ^ Page, Don N. (1993). "Entropía media de un subsistema". Phys. Rev. Lett. 71 (9): 1291–1294. arXiv : gr-qc/9305007 . Código Bibliográfico :1993PhRvL..71.1291P. CiteSeerX 10.1.1.339.7694 . doi :10.1103/PhysRevLett.71.1291. PMID 10055503. S2CID 17058654.
- ^ Merali, Zeeya (3 de abril de 2013). "Astrofísica: ¡Fuego en el agujero!". Nature . 496 (7443): 20–23. Bibcode :2013Natur.496...20M. doi : 10.1038/496020a . PMID 23552926.
- ^ Amheiri, Ahmed; Marolf, Donald; Polchinski, Joseph; Sully, James (2013). "Agujeros negros: ¿complementariedad o cortafuegos?". Journal of High Energy Physics . 2013 (2): 62. arXiv : 1207.3123 . Bibcode :2013JHEP...02..062A. doi :10.1007/JHEP02(2013)062. S2CID 55581818.
Fuentes
- Carroll, Sean M. (2004). Espacio-tiempo y geometría . Addison Wesley. ISBN 978-0-8053-8732-2.Las notas de clase en las que se basó el libro están disponibles de forma gratuita en el sitio web de Sean Carroll Archivado el 23 de marzo de 2017 en Wayback Machine.
- Hawking, SW ; Ellis, GFR (1973). Estructura a gran escala del espacio-tiempo. Cambridge University Press. ISBN 978-0-521-09906-6Archivado del original el 21 de julio de 2020 . Consultado el 16 de mayo de 2020 .
- Misner, Charles ; Thorne, Kip S .; Wheeler, John (1973). Gravitación . WH Freeman and Company. ISBN 978-0-7167-0344-0.
- Thorne, Kip S. (1994). Agujeros negros y distorsiones temporales . Norton, WW & Company, Inc. ISBN 978-0-393-31276-8.
- Wald, Robert M. (1984). Relatividad general. University of Chicago Press. ISBN 978-0-226-87033-5Archivado desde el original el 11 de agosto de 2016 . Consultado el 23 de febrero de 2016 .
- Wheeler, J. Craig (2007). Catástrofes cósmicas (2.ª ed.). Cambridge University Press. ISBN 978-0-521-85714-7.
Lectura adicional
Lectura popular
- Begelman, Mitchell C.; Rees, Martin J. (2021). La atracción fatal de la gravedad: agujeros negros en el universo (3.ª ed.). Cambridge, Reino Unido; Nueva York, NY: Cambridge University Press. ISBN 978-1-108-87112-9.
- Ferguson, Kitty (1991). Agujeros negros en el espacio-tiempo . Watts Franklin. ISBN 978-0-531-12524-3.
- Hawking, Stephen (1988). Una breve historia del tiempo . Bantam Books, Inc. ISBN 978-0-553-38016-3.
- Hawking, Stephen ; Penrose, Roger (1996). La naturaleza del espacio y el tiempo. Princeton University Press. ISBN 978-0-691-03791-2Archivado del original el 18 de octubre de 2021 . Consultado el 16 de mayo de 2020 .
- Levin, Janna (2020). Guía de supervivencia en agujeros negros. Nueva York: Alfred A. Knopf. ISBN 9780525658221Archivado del original el 22 de marzo de 2022 . Consultado el 6 de noviembre de 2021 .
- Melia, Fulvio (2003). El agujero negro en el centro de nuestra galaxia . Princeton U Press. ISBN 978-0-691-09505-9.
- Melia, Fulvio (2003). El borde del infinito. Agujeros negros supermasivos en el universo . Cambridge U Press. ISBN 978-0-521-81405-8.
- Pickover, Clifford (1998). Agujeros negros: guía para viajeros . Wiley, John & Sons, Inc. ISBN 978-0-471-19704-1.
- Susskind, Leonard (2008). La guerra de los agujeros negros: mi batalla con Stephen Hawking para hacer del mundo un lugar seguro para la mecánica cuántica (1.ª ed.). Nueva York: Little, Brown. ISBN 978-0-316-01640-7.OCLC 181603165 .
Libros de texto y monografías universitarias
- Carter, B. (1973). "Estados de equilibrio de agujeros negros". En DeWitt-Morette, Cécile; DeWitt, Bryce S. (eds.). Agujeros negros . Nueva York: Gordon and Breach. ISBN 978-0-677-15610-1.
- Chandrasekhar, Subrahmanyan (1999). Teoría matemática de los agujeros negros . Oxford University Press. ISBN 978-0-19-850370-5.
- Frolov, Valeri P.; Novikov, Igor D. (1998). Física de agujeros negros . Teorías fundamentales de la física. Vol. 96. doi :10.1007/978-94-011-5139-9. ISBN 978-0-7923-5146-7.
- Frolov, Valeri P.; Zelnikov, Andrei (2011). Introducción a la física de los agujeros negros. Oxford: Oxford University Press. ISBN 978-0-19-969229-3. Zbl 1234.83001. Archivado desde el original el 22 de marzo de 2022 . Consultado el 2 de enero de 2022 .
- Melia, Fulvio (2007). El agujero negro supermasivo galáctico . Princeton U Press. ISBN 978-0-691-13129-0.
- Taylor, Edwin F.; Wheeler, John Archibald (2000). Explorando agujeros negros . Addison Wesley Longman. ISBN 978-0-201-38423-9.
- Wald, Robert M. (1992). Espacio, tiempo y gravedad: la teoría del Big Bang y los agujeros negros . University of Chicago Press. ISBN 978-0-226-87029-8.
- Price, Richard; Creighton, Teviet (2008). "Agujeros negros". Scholarpedia . 3 (1): 4277. Bibcode :2008SchpJ...3.4277C. doi : 10.4249/scholarpedia.4277 .
Artículos de revisión
- Hughes, Scott A. (2005). "Confiar pero verificar: el caso de los agujeros negros astrofísicos". arXiv : hep-ph/0511217 .Notas de conferencias del Instituto de Verano SLAC 2005 .
- Gallo, Elena; Marolf, Donald (2009). "Resource Letter BH-2: Black Holes". Revista estadounidense de física . 77 (4): 294–307. arXiv : 0806.2316 . Código Bibliográfico :2009AmJPh..77..294G. doi :10.1119/1.3056569. S2CID 118494056.
- Cardoso, Vitor; Pani, Paolo (2019). "Prueba de la naturaleza de los objetos compactos oscuros: un informe de situación". Living Reviews in Relativity . 22 (1): 4. arXiv : 1904.05363 . Código Bibliográfico :2019LRR....22....4C. doi :10.1007/s41114-019-0020-4. S2CID 256465740.
- Mann, Robert B.; Murk, Sebastian; Terno, Daniel R. (2022). "Agujeros negros y sus horizontes en teorías semiclásicas y modificadas de la gravedad". Revista Internacional de Física Moderna D . 31 (9): 2230015–2230276. arXiv : 2112.06515 . Código Bibliográfico :2022IJMPD..3130015M. doi :10.1142/S0218271822300154. S2CID 245123647.
Enlaces externos
- Agujeros negros en In Our Time en la BBC
- Enciclopedia de Filosofía de Stanford : "Singularidades y agujeros negros" de Erik Curiel y Peter Bokulich.
- Agujeros negros: la atracción implacable de la gravedad – Sitio web multimedia interactivo sobre la física y la astronomía de los agujeros negros del Instituto Científico del Telescopio Espacial (HubbleSite)
- Visualización de un agujero negro por parte de la ESA Archivado el 3 de mayo de 2019 en Wayback Machine
- Preguntas frecuentes sobre los agujeros negros
- Geometría de Schwarzschild
- Agujeros negros: lo básico (NYT; abril de 2021)
Vídeos
- Estudio de 16 años rastrea estrellas que orbitan Sagitario A*
- Película del candidato a agujero negro del Instituto Max Planck
- Cowen, Ron (20 de abril de 2015). «Las simulaciones 3D de agujeros negros en colisión son las más realistas hasta el momento». Nature . doi : 10.1038/nature.2015.17360 .
- Visualización por ordenador de la señal detectada por LIGO
- Dos agujeros negros se fusionan en uno (según la señal GW150914)

























