Computación cuántica

Un ordenador cuántico es un ordenador que explota fenómenos mecánicos cuánticos . En escalas pequeñas, la materia física exhibe propiedades tanto de partículas como de ondas , y la computación cuántica aprovecha este comportamiento utilizando hardware especializado. La física clásica no puede explicar el funcionamiento de estos dispositivos cuánticos, y un ordenador cuántico escalable podría realizar algunos cálculos exponencialmente más rápido ^[a] que cualquier ordenador "clásico" moderno. Teóricamente, un ordenador cuántico a gran escala podría romper esquemas de cifrado ampliamente utilizados y ayudar a los físicos a realizar simulaciones físicas ; sin embargo, el estado actual de la técnica es en gran parte experimental y poco práctico, con varios obstáculos para aplicaciones útiles.

La unidad básica de información en computación cuántica, el qubit (o "bit cuántico"), cumple la misma función que el bit en computación clásica. Sin embargo, a diferencia de un bit clásico, que puede estar en uno de dos estados (un binario ), un qubit puede existir en una superposición de sus dos estados "base", lo que significa, en términos generales, que está en ambos estados simultáneamente. Al medir un qubit, el resultado es una salida probabilística de un bit clásico. Si un ordenador cuántico manipula el qubit de una manera particular, los efectos de interferencia de ondas pueden amplificar los resultados de medición deseados. El diseño de algoritmos cuánticos implica la creación de procedimientos que permitan a un ordenador cuántico realizar cálculos de manera eficiente y rápida.

La ingeniería física de cúbits de alta calidad ha demostrado ser un desafío. Si un cúbit físico no está lo suficientemente aislado de su entorno, sufre de decoherencia cuántica , lo que introduce ruido en los cálculos. Los gobiernos nacionales han invertido mucho en investigación experimental que apunta a desarrollar cúbits escalables con tiempos de coherencia más largos y tasas de error más bajas. Entre los ejemplos de implementaciones se incluyen los superconductores (que aíslan una corriente eléctrica eliminando la resistencia eléctrica ) y las trampas de iones (que confinan una sola partícula atómica utilizando campos electromagnéticos ).

En principio, un ordenador clásico puede resolver los mismos problemas computacionales que un ordenador cuántico, si se le da el tiempo suficiente. La ventaja cuántica se presenta en forma de complejidad temporal en lugar de computabilidad , y la teoría de la complejidad cuántica muestra que algunos algoritmos cuánticos son exponencialmente más eficientes que los algoritmos clásicos más conocidos. En teoría, un ordenador cuántico a gran escala podría resolver problemas computacionales que no serían solucionables por un ordenador clásico en un tiempo razonable. Este concepto de capacidad adicional se ha denominado " supremacía cuántica ". Si bien estas afirmaciones han atraído una atención significativa hacia la disciplina, los casos de uso práctico a corto plazo siguen siendo limitados.

Durante muchos años, los campos de la mecánica cuántica y la informática formaron comunidades académicas distintas. ^[1] La teoría cuántica moderna se desarrolló en la década de 1920 para explicar la dualidad onda-partícula observada a escala atómica, ^[2] y las computadoras digitales surgieron en las décadas siguientes para reemplazar a las computadoras humanas para los cálculos tediosos. ^[3] Ambas disciplinas tuvieron aplicaciones prácticas durante la Segunda Guerra Mundial ; las computadoras desempeñaron un papel importante en la criptografía en tiempos de guerra , ^[4] y la física cuántica fue esencial para la física nuclear utilizada en el Proyecto Manhattan . ^[5]

A medida que los físicos aplicaron modelos mecánicos cuánticos a problemas computacionales e intercambiaron bits digitales por qubits , los campos de la mecánica cuántica y la informática comenzaron a converger. En 1980, Paul Benioff presentó la máquina cuántica de Turing , que utiliza la teoría cuántica para describir una computadora simplificada. ^[6] Cuando las computadoras digitales se volvieron más rápidas, los físicos enfrentaron un aumento exponencial en la sobrecarga al simular la dinámica cuántica , ^[7] lo que llevó a Yuri Manin y Richard Feynman a sugerir de forma independiente que el hardware basado en fenómenos cuánticos podría ser más eficiente para la simulación por computadora. ^{[8] [9] [10]} En un artículo de 1984, Charles Bennett y Gilles Brassard aplicaron la teoría cuántica a los protocolos de criptografía y demostraron que la distribución de claves cuánticas podría mejorar la seguridad de la información . ^{[11] [12]}

Luego surgieron algoritmos cuánticos para resolver problemas de oráculo , como el algoritmo de Deutsch en 1985, ^[13] el algoritmo de Bernstein-Vazirani en 1993, ^[14] y el algoritmo de Simon en 1994. ^[15] Estos algoritmos no resolvieron problemas prácticos, pero demostraron matemáticamente que uno podía obtener más información consultando una caja negra con un estado cuántico en superposición , a veces denominado paralelismo cuántico . ^[16]

Peter Shor se basó en estos resultados con su algoritmo de 1994 para romper los protocolos de cifrado RSA y Diffie-Hellman ampliamente utilizados, ^[17] lo que atrajo una atención significativa al campo de la computación cuántica. ^[18] En 1996, el algoritmo de Grover estableció una aceleración cuántica para el problema de búsqueda no estructurada de amplia aplicación. ^{[19] [20]} El mismo año, Seth Lloyd demostró que las computadoras cuánticas podían simular sistemas cuánticos sin la sobrecarga exponencial presente en las simulaciones clásicas, ^[21] validando la conjetura de Feynman de 1982. ^[22]

A lo largo de los años, los experimentalistas han construido computadoras cuánticas a pequeña escala utilizando iones atrapados y superconductores . ^[23] En 1998, una computadora cuántica de dos qubits demostró la viabilidad de la tecnología, ^{[24] [25]} y experimentos posteriores han aumentado el número de qubits y reducido las tasas de error. ^[23]

En 2019, Google AI y la NASA anunciaron que habían logrado la supremacía cuántica con una máquina de 54 qubits, realizando un cálculo que es imposible para cualquier computadora clásica. ^{[26] [27] [28]} Sin embargo, la validez de esta afirmación todavía se está investigando activamente. ^{[29] [30]}

En diciembre de 2023, los físicos informaron por primera vez sobre el entrelazamiento de moléculas individuales, lo que puede tener aplicaciones significativas en la computación cuántica. ^[31]

Los ingenieros informáticos suelen describir el funcionamiento de una computadora moderna en términos de electrodinámica clásica . Dentro de estas computadoras "clásicas", algunos componentes (como semiconductores y generadores de números aleatorios ) pueden depender del comportamiento cuántico, pero estos componentes no están aislados de su entorno, por lo que cualquier información cuántica se descoherencia rápidamente . Si bien los programadores pueden depender de la teoría de la probabilidad al diseñar un algoritmo aleatorio , las nociones de mecánica cuántica como la superposición y la interferencia son en gran medida irrelevantes para el análisis de programas .

Los programas cuánticos , por el contrario, se basan en un control preciso de sistemas cuánticos coherentes . Los físicos describen estos sistemas matemáticamente utilizando álgebra lineal . Los números complejos modelan amplitudes de probabilidad , los vectores modelan estados cuánticos y las matrices modelan las operaciones que se pueden realizar en estos estados. Programar un ordenador cuántico es entonces una cuestión de componer operaciones de tal manera que el programa resultante calcule un resultado útil en teoría y sea implementable en la práctica.

Como describe el físico Charlie Bennett la relación entre las computadoras cuánticas y clásicas, ^[32]

Un ordenador clásico es un ordenador cuántico... así que no deberíamos preguntarnos de dónde vienen las aceleraciones cuánticas. Deberíamos decir: "Bueno, todos los ordenadores son cuánticos... ¿De dónde vienen las desaceleraciones clásicas?"

Así como el bit es el concepto básico de la teoría clásica de la información, el qubit es la unidad fundamental de la información cuántica . El mismo término qubit se utiliza para referirse a un modelo matemático abstracto y a cualquier sistema físico que esté representado por ese modelo. Un bit clásico, por definición, existe en cualquiera de dos estados físicos, que pueden denotarse 0 y 1. Un qubit también se describe por un estado, y dos estados a menudo escritos y sirven como las contrapartes cuánticas de los estados clásicos 0 y 1. Sin embargo, los estados cuánticos y pertenecen a un espacio vectorial , lo que significa que pueden multiplicarse por constantes y sumarse, y el resultado es nuevamente un estado cuántico válido. Tal combinación se conoce como superposición de y . ^{[33] [34]}${\displaystyle |0\rangle}$${\displaystyle |1\rangle}$${\displaystyle |0\rangle}$${\displaystyle |1\rangle}$${\displaystyle |0\rangle}$${\displaystyle |1\rangle}$

Un vector bidimensional representa matemáticamente un estado de qubit. Los físicos suelen utilizar la notación de Dirac para el álgebra lineal mecánica cuántica , escribiendo ' ket psi ' para un vector etiquetado . Debido a que un qubit es un sistema de dos estados, cualquier estado de qubit toma la forma , donde y son los estados base estándar , ^[b] y y son las amplitudes de probabilidad , que son en general números complejos . ^[34] Si o es cero, el qubit es efectivamente un bit clásico; cuando ambos son distintos de cero, el qubit está en superposición. Un vector de estado cuántico de este tipo actúa de forma similar a un vector de probabilidad (clásico) , con una diferencia clave: a diferencia de las probabilidades, las amplitudes de probabilidad no son necesariamente números positivos. ^[36] Las amplitudes negativas permiten la interferencia de ondas destructivas.${\displaystyle |\psi \rangle }$ ${\estilo de visualización \psi}$${\displaystyle \alpha |0\rangle +\beta |1\rangle }$${\displaystyle |0\rangle}$${\displaystyle |1\rangle}$${\estilo de visualización \alpha}$${\estilo de visualización \beta}$${\estilo de visualización \alpha}$${\estilo de visualización \beta}$

Cuando se mide un qubit en la base estándar , el resultado es un bit clásico. La regla de Born describe la correspondencia de norma al cuadrado entre amplitudes y probabilidades: cuando se mide un qubit , el estado colapsa a con probabilidad o a con probabilidad . Cualquier estado válido de qubit tiene coeficientes y tales que . Como ejemplo, medir el qubit produciría o con igual probabilidad.${\displaystyle \alpha |0\rangle +\beta |1\rangle }$${\displaystyle |0\rangle}$${\displaystyle |\alpha |^{2}}$${\displaystyle |1\rangle}$${\estilo de visualización |\beta |^{2}}$${\estilo de visualización \alpha}$${\estilo de visualización \beta}$${\displaystyle |\alpha |^{2}+|\beta |^{2}=1}$${\displaystyle 1/{\sqrt {2}}|0\rangle +1/{\sqrt {2}}|1\rangle }$${\displaystyle |0\rangle}$${\displaystyle |1\rangle}$

Cada qubit adicional duplica la dimensión del espacio de estados . ^[35] Como ejemplo, el vector ⁠1/√2⁠ |00⟩ + ⁠1/√2⁠ |01⟩ representa un estado de dos qubits, un producto tensorial del qubit |0⟩ con el qubit ⁠1/√2⁠ |0⟩ + ⁠1/√2⁠ |1⟩ . Este vector habita en un espacio vectorial de cuatro dimensionesgenerado por los vectores base |00⟩ , |01⟩ , |10⟩ y |11⟩ . El estado de Bell ⁠1/√2⁠ |00⟩ + ⁠1/√2⁠ |11⟩ es imposible de descomponer en el producto tensorial de dos qubits individuales: los dos qubits están entrelazados porque sus amplitudes de probabilidad están correlacionadas . En general, el espacio vectorial para unsistema de n -qubits es 2 ⁿ -dimensional, y esto hace que sea un desafío para una computadora clásica simular uno cuántico: representar un sistema de 100 qubits requiere almacenar 2 ¹⁰⁰ valores clásicos.

El estado de esta memoria cuántica de un cúbito se puede manipular aplicando puertas lógicas cuánticas , de manera análoga a cómo se puede manipular la memoria clásica con puertas lógicas clásicas . Una puerta importante tanto para la computación clásica como para la cuántica es la puerta NOT, que se puede representar mediante una matriz. Matemáticamente, la aplicación de una puerta lógica de este tipo a un vector de estado cuántico se modela con la multiplicación de matrices . Por lo tanto,$${\displaystyle X:={\begin{pmatrix}0&1\\1&0\end{pmatrix}}.}$$

${\displaystyle X|0\rangle =|1\rangle }$y .${\displaystyle X|1\rangle =|0\rangle }$

Las matemáticas de las puertas de un solo cúbit se pueden extender para operar en memorias cuánticas de múltiples cúbits de dos maneras importantes. Una forma es simplemente seleccionar un cúbit y aplicar esa puerta al cúbit objetivo mientras se deja el resto de la memoria intacta. Otra forma es aplicar la puerta a su objetivo solo si otra parte de la memoria está en un estado deseado. Estas dos opciones se pueden ilustrar utilizando otro ejemplo. Los estados posibles de una memoria cuántica de dos cúbits son La puerta NOT controlada (CNOT) se puede representar utilizando la siguiente matriz: Como consecuencia matemática de esta definición, , , y . En otras palabras, la CNOT aplica una puerta NOT ( de antes) al segundo cúbit si y solo si el primer cúbit está en el estado . Si el primer cúbit es , no se hace nada a ninguno de los cúbits.$${\displaystyle |00\rangle :={\begin{pmatrix}1\\0\\0\\0\end{pmatrix}};\quad |01\rangle :={\begin{pmatrix}0\\1\\0\\0\end{pmatrix}};\quad |10\rangle :={\begin{pmatrix}0\\0\\1\\0\end{pmatrix}};\quad |11\rangle :={\begin{pmatrix}0\\0\\0\\1\end{pmatrix}}.}$$$${\displaystyle \operatorname {CNOT} :={\begin{pmatrix}1&0&0&0\\0&1&0&0\\0&0&0&1\\0&0&1&0\end{pmatrix}}.}$$${\textstyle \operatorname {CNOT} |00\rangle =|00\rangle }$${\textstyle \operatorname {CNOT} |01\rangle =|01\rangle }$${\textstyle \operatorname {CNOT} |10\rangle =|11\rangle }$${\textstyle \operatorname {CNOT} |11\rangle =|10\rangle }$${\textstyle X}$${\textstyle |1\rangle }$${\textstyle |0\rangle }$

En resumen, la computación cuántica puede describirse como una red de puertas lógicas cuánticas y mediciones. Sin embargo, cualquier medición puede posponerse hasta el final de la computación cuántica, aunque este aplazamiento puede tener un costo computacional, por lo que la mayoría de los circuitos cuánticos representan una red que consta solo de puertas lógicas cuánticas y ninguna medición.

El paralelismo cuántico es la heurística que permite pensar que los ordenadores cuánticos evalúan una función para múltiples valores de entrada simultáneamente. Esto se puede lograr preparando un sistema cuántico en una superposición de estados de entrada y aplicando una transformación unitaria que codifica la función que se va a evaluar. El estado resultante codifica los valores de salida de la función para todos los valores de entrada en la superposición, lo que permite el cálculo de múltiples salidas simultáneamente. Esta propiedad es clave para la aceleración de muchos algoritmos cuánticos. Sin embargo, el "paralelismo" en este sentido es insuficiente para acelerar un cálculo, porque la medición al final del cálculo da solo un valor. Para ser útil, un algoritmo cuántico también debe incorporar algún otro ingrediente conceptual. ^{[37] [38]}

Existen varios modelos de computación para la computación cuántica, que se distinguen por los elementos básicos en que se descompone el cálculo.

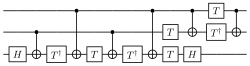
Una matriz de puertas cuánticas descompone el cálculo en una secuencia de puertas cuánticas de unos pocos cúbits . Un cálculo cuántico puede describirse como una red de puertas lógicas cuánticas y mediciones. Sin embargo, cualquier medición puede posponerse hasta el final del cálculo cuántico, aunque este aplazamiento puede tener un costo computacional, por lo que la mayoría de los circuitos cuánticos representan una red que consta solo de puertas lógicas cuánticas y ninguna medición.

Cualquier computación cuántica (que es, en el formalismo anterior, cualquier matriz unitaria de tamaño sobre qubits) puede representarse como una red de puertas lógicas cuánticas de una familia bastante pequeña de puertas. Una elección de familia de puertas que permite esta construcción se conoce como un conjunto de puertas universales , ya que una computadora que puede ejecutar tales circuitos es una computadora cuántica universal . Un conjunto común de este tipo incluye todas las puertas de un solo qubit, así como la puerta CNOT de arriba. Esto significa que cualquier computación cuántica puede realizarse ejecutando una secuencia de puertas de un solo qubit junto con puertas CNOT. Aunque este conjunto de puertas es infinito, puede reemplazarse con un conjunto de puertas finito apelando al teorema de Solovay-Kitaev . Aquí se presenta la implementación de funciones booleanas utilizando las puertas cuánticas de pocos qubits. ^[39]${\displaystyle 2^{n}\times 2^{n}}$${\displaystyle n}$

Una computadora cuántica basada en mediciones descompone el cálculo en una secuencia de mediciones de estados de Bell y puertas cuánticas de un solo qubit aplicadas a un estado inicial altamente enredado (un estado de clúster ), utilizando una técnica llamada teletransportación de puertas cuánticas .

Una computadora cuántica adiabática , basada en recocido cuántico , descompone el cálculo en una transformación lenta y continua de un hamiltoniano inicial en un hamiltoniano final, cuyos estados fundamentales contienen la solución. ^[40]

La computación cuántica neuromórfica (abreviada como 'computación cuántica n.') es un tipo de computación no convencional que utiliza la computación neuromórfica para realizar operaciones cuánticas. Se sugirió que los algoritmos cuánticos , que son algoritmos que se ejecutan en un modelo realista de computación cuántica, se pueden calcular con la misma eficiencia que la computación cuántica neuromórfica. Tanto la computación cuántica tradicional como la computación cuántica neuromórfica son enfoques de computación no convencionales basados ​​en la física para los cálculos y no siguen la arquitectura de von Neumann . Ambos construyen un sistema (un circuito) que representa el problema físico en cuestión y luego aprovechan sus respectivas propiedades físicas del sistema para buscar el "mínimo". La computación cuántica neuromórfica y la computación cuántica comparten propiedades físicas similares durante el cálculo.

Una computadora cuántica topológica descompone el cálculo en el trenzado de aniones en una red 2D. ^[41]

Una máquina de Turing cuántica es el análogo cuántico de una máquina de Turing . ^[6] Se ha demostrado que todos estos modelos de computación (circuitos cuánticos, ^[42] computación cuántica unidireccional , ^[43] computación cuántica adiabática, ^[44] y computación cuántica topológica ^[45] ) son equivalentes a la máquina de Turing cuántica; dada una implementación perfecta de una de esas computadoras cuánticas, puede simular todas las demás con una sobrecarga no mayor que un polinomio. Esta equivalencia no tiene por qué ser válida para las computadoras cuánticas prácticas, ya que la sobrecarga de la simulación puede ser demasiado grande para ser práctica.

El teorema del umbral muestra cómo aumentar el número de qubits puede mitigar los errores, ^[46] aunque la computación cuántica totalmente tolerante a fallos sigue siendo "un sueño bastante lejano". ^[47] Según algunos investigadores, las máquinas cuánticas ruidosas de escala intermedia ( NISQ ) pueden tener usos especializados en un futuro próximo, pero el ruido en las puertas cuánticas limita su fiabilidad. ^[47] Los científicos de la Universidad de Harvard crearon con éxito "circuitos cuánticos" que corrigen errores de forma más eficiente que los métodos alternativos, lo que puede eliminar potencialmente un obstáculo importante para las computadoras cuánticas prácticas. ^{[48] [49]} El equipo de investigación de Harvard recibió el apoyo del MIT , QuEra Computing , Caltech y la Universidad de Princeton y fue financiado por el programa Optimización con dispositivos cuánticos ruidosos de escala intermedia (ONISQ) de DARPA. [ ^{50] [51]}

La computación cuántica tiene importantes aplicaciones potenciales en los campos de la criptografía y la ciberseguridad. La criptografía cuántica, que se basa en los principios de la mecánica cuántica, ofrece la posibilidad de canales de comunicación seguros que son resistentes a las escuchas clandestinas. Los protocolos de distribución de claves cuánticas (QKD), como BB84, permiten el intercambio seguro de claves criptográficas entre partes, lo que garantiza la confidencialidad e integridad de la comunicación. Además, los generadores de números aleatorios cuánticos (QRNG) pueden producir números aleatorios de alta calidad, que son esenciales para un cifrado seguro.

Sin embargo, la computación cuántica también plantea desafíos a los sistemas criptográficos tradicionales. El algoritmo de Shor , un algoritmo cuántico para la factorización de números enteros, podría potencialmente romper esquemas de criptografía de clave pública ampliamente utilizados como RSA, que se basan en la dificultad de factorizar números grandes. La criptografía poscuántica, que implica el desarrollo de algoritmos criptográficos que sean resistentes a ataques tanto de computadoras clásicas como cuánticas, es un área activa de investigación destinada a abordar esta preocupación.

La investigación en curso en criptografía cuántica y criptografía post-cuántica es crucial para garantizar la seguridad de la comunicación y los datos ante la evolución de las capacidades de computación cuántica. Los avances en estos campos, como el desarrollo de nuevos protocolos QKD, la mejora de los QRNG y la estandarización de algoritmos criptográficos post-cuánticos, desempeñarán un papel clave en el mantenimiento de la integridad y confidencialidad de la información en la era cuántica. ^[52]

La criptografía cuántica permite nuevas formas de transmitir datos de forma segura; por ejemplo, la distribución de claves cuánticas utiliza estados cuánticos entrelazados para establecer claves criptográficas seguras . ^[53] Cuando un emisor y un receptor intercambian estados cuánticos, pueden garantizar que un adversario no intercepte el mensaje, ya que cualquier espía no autorizado perturbaría el delicado sistema cuántico e introduciría un cambio detectable. ^[54] Con protocolos criptográficos apropiados , el emisor y el receptor pueden establecer así información privada compartida resistente a las escuchas clandestinas. ^{[11] [55]}

Los cables de fibra óptica modernos pueden transmitir información cuántica a distancias relativamente cortas. La investigación experimental en curso tiene como objetivo desarrollar hardware más confiable (como repetidores cuánticos), con la esperanza de escalar esta tecnología a redes cuánticas de larga distancia con entrelazamiento de extremo a extremo. Teóricamente, esto podría permitir nuevas aplicaciones tecnológicas, como la computación cuántica distribuida y la detección cuántica mejorada . ^{[56] [57]}

Los avances en la búsqueda de algoritmos cuánticos se centran generalmente en este modelo de circuito cuántico, aunque existen excepciones como el algoritmo adiabático cuántico . Los algoritmos cuánticos se pueden clasificar aproximadamente según el tipo de aceleración que logran con respecto a los algoritmos clásicos correspondientes. ^[58]

Los algoritmos cuánticos que ofrecen más que una aceleración polinómica sobre el algoritmo clásico más conocido incluyen el algoritmo de Shor para factorización y los algoritmos cuánticos relacionados para calcular logaritmos discretos , resolver la ecuación de Pell y, de manera más general, resolver el problema del subgrupo oculto para grupos finitos abelianos . ^[58] Estos algoritmos dependen de la primitiva de la transformada cuántica de Fourier . No se ha encontrado ninguna prueba matemática que demuestre que no se puede descubrir un algoritmo clásico igualmente rápido, pero la evidencia sugiere que esto es poco probable. ^[59] Ciertos problemas de oráculo como el problema de Simon y el problema de Bernstein-Vazirani dan aceleraciones demostrables, aunque esto es en el modelo de consulta cuántica , que es un modelo restringido donde los límites inferiores son mucho más fáciles de demostrar y no necesariamente se traducen en aceleraciones para problemas prácticos.

Otros problemas, incluida la simulación de procesos físicos cuánticos a partir de la química y la física del estado sólido, la aproximación de ciertos polinomios de Jones y el algoritmo cuántico para sistemas lineales de ecuaciones, tienen algoritmos cuánticos que parecen dar aceleraciones superpolinómicas y son BQP -completos. Debido a que estos problemas son BQP-completos, un algoritmo clásico igualmente rápido para ellos implicaría que ningún algoritmo cuántico da una aceleración superpolinómica, lo que se cree que es poco probable. ^[60]

Algunos algoritmos cuánticos, como el algoritmo de Grover y la amplificación de amplitud , dan aceleraciones polinómicas sobre los algoritmos clásicos correspondientes. ^[58] Aunque estos algoritmos dan una aceleración cuadrática comparativamente modesta, son ampliamente aplicables y por lo tanto dan aceleraciones para una amplia gama de problemas. ^[20]

Dado que la química y la nanotecnología dependen de la comprensión de los sistemas cuánticos, y dichos sistemas son imposibles de simular de manera eficiente de manera clásica, la simulación cuántica puede ser una aplicación importante de la computación cuántica. ^[61] La simulación cuántica también podría usarse para simular el comportamiento de átomos y partículas en condiciones inusuales, como las reacciones dentro de un colisionador . ^[62] En junio de 2023, los científicos informáticos de IBM informaron que una computadora cuántica produjo mejores resultados para un problema de física que una supercomputadora convencional. ^{[63] [64]}

Alrededor del 2% de la producción energética mundial anual se utiliza para la fijación de nitrógeno para producir amoníaco para el proceso Haber en la industria de fertilizantes agrícolas (aunque los organismos naturales también producen amoníaco). Se podrían utilizar simulaciones cuánticas para comprender este proceso y aumentar la eficiencia energética de la producción. ^[65] Se espera que un uso temprano de la computación cuántica sea el modelado que mejore la eficiencia del proceso Haber-Bosch ^[66] para mediados de la década de 2020 ^[67], aunque algunos han predicho que tomará más tiempo. ^[68]

Una aplicación notable de la computación cuántica es para ataques a sistemas criptográficos que están actualmente en uso. Se cree que la factorización de enteros , que sustenta la seguridad de los sistemas criptográficos de clave pública , es computacionalmente inviable con una computadora ordinaria para enteros grandes si son el producto de pocos números primos (por ejemplo, productos de dos primos de 300 dígitos). ^[69] En comparación, una computadora cuántica podría resolver este problema exponencialmente más rápido usando el algoritmo de Shor para encontrar sus factores. ^[70] Esta capacidad permitiría a una computadora cuántica romper muchos de los sistemas criptográficos en uso hoy en día, en el sentido de que habría un algoritmo de tiempo polinomial (en el número de dígitos del entero) para resolver el problema. En particular, la mayoría de los cifrados de clave pública populares se basan en la dificultad de factorizar números enteros o el problema del logaritmo discreto , los cuales pueden resolverse mediante el algoritmo de Shor. En particular, se podrían descifrar los algoritmos RSA , Diffie–Hellman y Diffie–Hellman de curva elíptica , que se utilizan para proteger páginas web seguras, correo electrónico cifrado y muchos otros tipos de datos. Descifrarlos tendría ramificaciones significativas para la privacidad y la seguridad electrónicas.

La identificación de sistemas criptográficos que puedan ser seguros contra algoritmos cuánticos es un tema de investigación activa en el campo de la criptografía postcuántica . ^{[71] [72]} Algunos algoritmos de clave pública se basan en problemas distintos a los problemas de factorización de enteros y logaritmos discretos a los que se aplica el algoritmo de Shor, como el criptosistema de McEliece basado en un problema de teoría de codificación . ^{[71] [73] Tampoco se sabe que} los criptosistemas basados ​​en red sean rotos por computadoras cuánticas, y encontrar un algoritmo de tiempo polinomial para resolver el problema del subgrupo oculto diedro , que rompería muchos criptosistemas basados ​​en red, es un problema abierto bien estudiado. ^[74] Se ha demostrado que aplicar el algoritmo de Grover para romper un algoritmo simétrico (clave secreta) por fuerza bruta requiere un tiempo igual a aproximadamente 2 ^{n /2} invocaciones del algoritmo criptográfico subyacente, en comparación con aproximadamente 2 ⁿ en el caso clásico, ^[75] lo que significa que las longitudes de clave simétrica se reducen efectivamente a la mitad: AES-256 tendría la misma seguridad contra un ataque que use el algoritmo de Grover que AES-128 contra la búsqueda clásica por fuerza bruta (ver Tamaño de clave ).

El ejemplo más conocido de un problema que permite una aceleración cuántica polinómica es la búsqueda no estructurada , que implica encontrar un elemento marcado en una lista de elementos en una base de datos. Esto se puede resolver mediante el algoritmo de Grover utilizando consultas a la base de datos, cuadráticamente menos que las consultas requeridas para los algoritmos clásicos. En este caso, la ventaja no solo es demostrable sino también óptima: se ha demostrado que el algoritmo de Grover brinda la máxima probabilidad posible de encontrar el elemento deseado para cualquier número de búsquedas de oráculo. Muchos ejemplos de aceleraciones cuánticas demostrables para problemas de consulta se basan en el algoritmo de Grover, incluido el algoritmo de Brassard, Høyer y Tapp para encontrar colisiones en funciones dos a uno, ^[76] y el algoritmo de Farhi, Goldstone y Gutmann para evaluar árboles NAND. ^[77]${\displaystyle n}$${\displaystyle O({\sqrt {n}})}$${\displaystyle \Omega (n)}$

Los problemas que pueden abordarse eficientemente con el algoritmo de Grover tienen las siguientes propiedades: ^{[78] [79]}

1. No existe una estructura de búsqueda en la colección de posibles respuestas,
2. El número de posibles respuestas a comprobar es el mismo que el número de entradas al algoritmo, y
3. Existe una función booleana que evalúa cada entrada y determina si es la respuesta correcta.

En el caso de problemas con todas estas propiedades, el tiempo de ejecución del algoritmo de Grover en un ordenador cuántico se escala como la raíz cuadrada del número de entradas (o elementos en la base de datos), a diferencia del escalamiento lineal de los algoritmos clásicos. Una clase general de problemas a los que se puede aplicar el algoritmo de Grover ^[80] es un problema de satisfacibilidad booleana , donde la base de datos a través de la cual itera el algoritmo es la de todas las respuestas posibles. Un ejemplo y una posible aplicación de esto es un descifrador de contraseñas que intenta adivinar una contraseña. Descifrar cifrados simétricos con este algoritmo es de interés para las agencias gubernamentales. ^[81]

El recocido cuántico se basa en el teorema adiabático para realizar los cálculos. Un sistema se coloca en el estado fundamental de un hamiltoniano simple, que evoluciona lentamente hacia un hamiltoniano más complicado cuyo estado fundamental representa la solución al problema en cuestión. El teorema adiabático establece que si la evolución es lo suficientemente lenta, el sistema permanecerá en su estado fundamental en todo momento durante el proceso.La optimización adiabática puede ser útil para resolver problemas de biología computacional . ^[82]

Dado que las computadoras cuánticas pueden producir resultados que las computadoras clásicas no pueden producir de manera eficiente, y dado que la computación cuántica es fundamentalmente algebraica lineal, algunos expresan esperanza en el desarrollo de algoritmos cuánticos que puedan acelerar las tareas de aprendizaje automático . ^{[47] [83]}

Por ejemplo, se cree que el algoritmo HHL , llamado así por sus descubridores Harrow, Hassidim y Lloyd, proporciona una aceleración sobre sus contrapartes clásicas. ^{[47] [84]} Algunos grupos de investigación han explorado recientemente el uso de hardware de recocido cuántico para entrenar máquinas de Boltzmann y redes neuronales profundas . ^{[85] [86] [87]}

Los modelos de química generativa profunda surgen como herramientas poderosas para acelerar el descubrimiento de fármacos . Sin embargo, el inmenso tamaño y la complejidad del espacio estructural de todas las posibles moléculas similares a fármacos plantean obstáculos significativos, que podrían ser superados en el futuro por las computadoras cuánticas. Las computadoras cuánticas son naturalmente buenas para resolver problemas complejos de muchos cuerpos cuánticos ^[21] y, por lo tanto, pueden ser fundamentales en aplicaciones que involucran química cuántica. Por lo tanto, se puede esperar que los modelos generativos mejorados cuánticamente ^[88], incluidas las GAN cuánticas ^[89], puedan eventualmente desarrollarse en algoritmos de química generativa definitivos.

A partir de 2023, ^[update]las computadoras clásicas superarán a las computadoras cuánticas en todas las aplicaciones del mundo real. Si bien las computadoras cuánticas actuales pueden acelerar las soluciones a problemas matemáticos particulares, no brindan ninguna ventaja computacional para tareas prácticas. Los científicos e ingenieros están explorando múltiples tecnologías para el hardware de computación cuántica y esperan desarrollar arquitecturas cuánticas escalables, pero aún quedan serios obstáculos. ^{[90] [91]}

Existen varios desafíos técnicos a la hora de construir un ordenador cuántico a gran escala. ^[92] El físico David DiVincenzo ha enumerado estos requisitos para un ordenador cuántico práctico: ^[93]

• Físicamente escalable para aumentar el número de qubits
• Qubits que pueden inicializarse con valores arbitrarios
• Puertas cuánticas que son más rápidas que el tiempo de decoherencia
• Juego de puerta universal
• Qubits que se pueden leer fácilmente.

La obtención de componentes para ordenadores cuánticos también es muy difícil. Los ordenadores cuánticos superconductores , como los construidos por Google e IBM , necesitan helio-3 , un subproducto de la investigación nuclear , y cables superconductores especiales fabricados únicamente por la empresa japonesa Coax Co. ^[94]

El control de sistemas multi-qubit requiere la generación y coordinación de una gran cantidad de señales eléctricas con una resolución temporal precisa y determinista. Esto ha llevado al desarrollo de controladores cuánticos que permiten la interconexión con los qubits. Escalar estos sistemas para que admitan una cantidad creciente de qubits es un desafío adicional. ^[95]

Uno de los mayores desafíos que implica la construcción de computadoras cuánticas es controlar o eliminar la decoherencia cuántica . Esto generalmente significa aislar el sistema de su entorno, ya que las interacciones con el mundo externo hacen que el sistema se descoherencie. Sin embargo, también existen otras fuentes de decoherencia. Los ejemplos incluyen las puertas cuánticas y las vibraciones reticulares y el espín termonuclear de fondo del sistema físico utilizado para implementar los qubits. La decoherencia es irreversible, ya que es efectivamente no unitaria, y generalmente es algo que debe controlarse altamente, si no evitarse. Los tiempos de decoherencia para los sistemas candidatos en particular, el tiempo de relajación transversal T ₂ (para la tecnología de RMN y MRI , también llamado tiempo de desfase ), generalmente varían entre nanosegundos y segundos a baja temperatura. ^[96] Actualmente, algunas computadoras cuánticas requieren que sus qubits se enfríen a 20 milikelvin (generalmente usando un refrigerador de dilución ^[97] ) para evitar una decoherencia significativa. ^[98] Un estudio de 2020 sostiene que la radiación ionizante, como los rayos cósmicos , pueden provocar que ciertos sistemas pierdan la coherencia en cuestión de milisegundos. ^[99]

Como resultado, las tareas que consumen mucho tiempo pueden hacer que algunos algoritmos cuánticos sean inoperantes, ya que intentar mantener el estado de los qubits durante un período lo suficientemente largo eventualmente corromperá las superposiciones. ^[100]

Estos problemas son más difíciles para los enfoques ópticos, ya que las escalas de tiempo son órdenes de magnitud más cortas y un enfoque que se cita a menudo para superarlos es la conformación de pulsos ópticos . Las tasas de error suelen ser proporcionales a la relación entre el tiempo de operación y el tiempo de decoherencia, por lo tanto, cualquier operación debe completarse mucho más rápido que el tiempo de decoherencia.

Como se describe en el teorema del umbral , si la tasa de error es lo suficientemente pequeña, se cree que es posible utilizar la corrección de error cuántico para suprimir errores y decoherencia. Esto permite que el tiempo total de cálculo sea mayor que el tiempo de decoherencia si el esquema de corrección de error puede corregir errores más rápido de lo que la decoherencia los introduce. Una cifra que se cita a menudo para la tasa de error requerida en cada compuerta para el cálculo tolerante a fallas es 10 ⁻³ , suponiendo que el ruido es despolarizante.

Cumplir con esta condición de escalabilidad es posible para una amplia gama de sistemas. Sin embargo, el uso de la corrección de errores conlleva el coste de un número mucho mayor de qubits necesarios. El número necesario para factorizar números enteros utilizando el algoritmo de Shor sigue siendo polinomial, y se cree que está entre L y L ² , donde L es el número de dígitos del número a factorizar; los algoritmos de corrección de errores inflarían esta cifra con un factor adicional de L . Para un número de 1000 bits, esto implica una necesidad de unos 10 ⁴ bits sin corrección de errores. ^[101] Con la corrección de errores, la cifra aumentaría a unos 10 ⁷ bits. El tiempo de cálculo es de unos L ² o unos 10 ⁷ pasos y, a 1  MHz, unos 10 segundos. Sin embargo, los costes de codificación y corrección de errores aumentan el tamaño de una computadora cuántica tolerante a fallos real en varios órdenes de magnitud. Estimaciones cuidadosas ^{[102] [103]} muestran que al menos 3  millones de cúbits físicos factorizarían un entero de 2048 bits en 5 meses en una computadora cuántica de iones atrapados con corrección total de errores. En términos de la cantidad de cúbits físicos, hasta la fecha, esta sigue siendo la estimación más baja ^[104] para un problema de factorización de enteros prácticamente útil con un tamaño de 1024 bits o más.

Otro enfoque para el problema de estabilidad-decoherencia es crear una computadora cuántica topológica con aniones , cuasipartículas utilizadas como hilos, y confiar en la teoría de trenzas para formar puertas lógicas estables. ^{[105] [106]}

El físico John Preskill acuñó el término supremacía cuántica para describir la hazaña de ingeniería de demostrar que un dispositivo cuántico programable puede resolver un problema más allá de las capacidades de las computadoras clásicas de última generación. ^{[107] [108] [109]} El problema no necesita ser útil, por lo que algunos ven la prueba de supremacía cuántica solo como un posible punto de referencia futuro. ^[110]

En octubre de 2019, Google AI Quantum, con la ayuda de la NASA, se convirtió en el primero en afirmar haber alcanzado la supremacía cuántica al realizar cálculos en la computadora cuántica Sycamore más de 3.000.000 de veces más rápido de lo que podrían hacerse en Summit , generalmente considerada la computadora más rápida del mundo. ^{[27] [111] [112]} Esta afirmación ha sido posteriormente cuestionada: IBM ha declarado que Summit puede realizar muestras mucho más rápido de lo que se afirma, ^{[113] [114]} y desde entonces los investigadores han desarrollado mejores algoritmos para el problema de muestreo utilizado para afirmar la supremacía cuántica, dando reducciones sustanciales a la brecha entre Sycamore y las supercomputadoras clásicas ^{[115] [116] [117]} e incluso superándola. ^{[118] [119] [120]}

En diciembre de 2020, un grupo de la USTC implementó un tipo de muestreo de bosones en 76 fotones con una computadora cuántica fotónica , Jiuzhang , para demostrar la supremacía cuántica. ^{[121] [122] [123]} Los autores afirman que una supercomputadora contemporánea clásica requeriría un tiempo computacional de 600 millones de años para generar la cantidad de muestras que su procesador cuántico puede generar en 20 segundos. ^[124]

Las afirmaciones de supremacía cuántica han generado un revuelo en torno a la computación cuántica, ^[125] pero se basan en tareas de referencia artificiales que no implican directamente aplicaciones útiles en el mundo real. ^{[90] [126]}

En enero de 2024, un estudio publicado en Physical Review Letters proporcionó una verificación directa de los experimentos de supremacía cuántica al calcular amplitudes exactas para cadenas de bits generadas experimentalmente utilizando una supercomputadora Sunway de nueva generación, lo que demuestra un salto significativo en la capacidad de simulación basada en un algoritmo de contracción de red tensorial de amplitud múltiple. Este desarrollo subraya el panorama cambiante de la computación cuántica, destacando tanto el progreso como las complejidades involucradas en la validación de las afirmaciones de supremacía cuántica. ^[127]

A pesar de las grandes esperanzas en la computación cuántica, el progreso significativo en hardware y el optimismo sobre las aplicaciones futuras, un artículo destacado de Nature de 2023 resumió las computadoras cuánticas actuales como "por ahora, [no sirven para] absolutamente nada". ^[90] El artículo explicó que las computadoras cuánticas aún no son más útiles o eficientes que las computadoras convencionales en cualquier caso, aunque también argumentó que a largo plazo es probable que dichas computadoras sean útiles. Un artículo de Communications of the ACM de 2023 ^[91] encontró que los algoritmos de computación cuántica actuales son "insuficientes para una ventaja cuántica práctica sin mejoras significativas en la pila de software/hardware". Sostiene que los candidatos más prometedores para lograr una aceleración con las computadoras cuánticas son "problemas de datos pequeños", por ejemplo, en química y ciencia de los materiales. Sin embargo, el artículo también concluye que una gran variedad de las aplicaciones potenciales que consideró, como el aprendizaje automático, "no lograrán una ventaja cuántica con los algoritmos cuánticos actuales en el futuro previsible", e identificó restricciones de E/S que hacen que la aceleración sea poco probable para "problemas de big data, sistemas lineales no estructurados y búsqueda de bases de datos basada en el algoritmo de Grover".

Esta situación se puede atribuir a varias consideraciones actuales y de largo plazo.

• El hardware y los algoritmos informáticos convencionales no sólo están optimizados para tareas prácticas, sino que siguen mejorando rápidamente, en particular los aceleradores de GPU .
• El hardware de computación cuántica actual genera solo una cantidad limitada de entrelazamiento antes de verse abrumado por el ruido.
• Los algoritmos cuánticos permiten acelerar el proceso en comparación con los algoritmos convencionales solo en algunas tareas, y hacer que estas tareas se adapten a aplicaciones prácticas resultó un desafío. Algunas tareas y aplicaciones prometedoras requieren recursos que van mucho más allá de los disponibles en la actualidad. ^{[128] [129]} En particular, procesar grandes cantidades de datos no cuánticos es un desafío para las computadoras cuánticas. ^[91]
• Algunos algoritmos prometedores han sido "descuantizados", es decir, se han encontrado análogos no cuánticos con una complejidad similar.
• Si se utiliza la corrección de errores cuánticos para escalar las computadoras cuánticas a aplicaciones prácticas, su sobrecarga puede socavar la aceleración ofrecida por muchos algoritmos cuánticos. ^[91]
• El análisis de la complejidad de los algoritmos a veces hace suposiciones abstractas que no se aplican a las aplicaciones. Por ejemplo, es posible que los datos de entrada no estén disponibles codificados en estados cuánticos y las "funciones oráculo" utilizadas en el algoritmo de Grover suelen tener una estructura interna que se puede aprovechar para algoritmos más rápidos.

En particular, construir computadoras con una gran cantidad de cúbits puede ser inútil si esos cúbits no están conectados lo suficientemente bien y no pueden mantener un grado de entrelazamiento suficientemente alto durante mucho tiempo. Cuando intentan superar a las computadoras convencionales, los investigadores de computación cuántica a menudo buscan nuevas tareas que se puedan resolver en computadoras cuánticas, pero esto deja la posibilidad de que se desarrollen técnicas no cuánticas eficientes en respuesta, como se vio en las demostraciones de supremacía cuántica . Por lo tanto, es deseable demostrar límites inferiores en la complejidad de los mejores algoritmos no cuánticos posibles (que pueden ser desconocidos) y demostrar que algunos algoritmos cuánticos mejoran asintomáticamente esos límites.

Algunos investigadores han expresado su escepticismo respecto de que algún día se puedan construir computadoras cuánticas escalables, generalmente debido al problema de mantener la coherencia a gran escala, pero también por otras razones.

Bill Unruh dudó de la viabilidad de las computadoras cuánticas en un artículo publicado en 1994. ^[130] Paul Davies argumentó que una computadora de 400 qubits incluso entraría en conflicto con el límite de información cosmológica implícito en el principio holográfico . ^[131] Escépticos como Gil Kalai dudan de que alguna vez se logre la supremacía cuántica. ^{[132] [133] [134]} El físico Mikhail Dyakonov ha expresado su escepticismo sobre la computación cuántica de la siguiente manera:

"Por lo tanto, el número de parámetros continuos que describen el estado de un ordenador cuántico tan útil en un momento dado debe ser... aproximadamente 10 ³⁰⁰ ... ¿Podríamos aprender a controlar los más de 10 ³⁰⁰ parámetros continuamente variables que definen el estado cuántico de un sistema de este tipo? Mi respuesta es sencilla: no, nunca " . ^{[135] [136]}

Una computadora cuántica práctica debe utilizar un sistema físico como un registro cuántico programable. ^[138] Los investigadores están explorando varias tecnologías como candidatas para implementaciones confiables de qubits. ^[139] Los superconductores y los iones atrapados son algunas de las propuestas más desarrolladas, pero los experimentalistas también están considerando otras posibilidades de hardware. ^[140]

Las primeras puertas lógicas cuánticas se implementaron con iones atrapados y se han creado prototipos de máquinas de uso general con hasta 20 cúbits. Sin embargo, la tecnología detrás de estos dispositivos combina equipos de vacío complejos, láseres, microondas y equipos de radiofrecuencia, lo que hace que los procesadores a gran escala sean difíciles de integrar con equipos informáticos estándar. Además, el propio sistema de iones atrapados tiene desafíos de ingeniería que superar. ^[141]

Los sistemas comerciales más grandes se basan en dispositivos superconductores y han alcanzado una escala de 2000 qubits. Sin embargo, las tasas de error para máquinas más grandes han sido del orden del 5%. Tecnológicamente, todos estos dispositivos son criogénicos y la ampliación a grandes cantidades de qubits requiere una integración a escala de oblea, un serio desafío de ingeniería en sí mismo. ^[142]

Los esfuerzos de investigación para crear cúbits más estables para la computación cuántica incluyen enfoques de computación cuántica topológica . Por ejemplo, Microsoft está trabajando en una computadora basada en las propiedades cuánticas de cuasipartículas bidimensionales llamadas anyones . ^{[143] [144] [145]}

Centrándose en el punto de vista de la gestión empresarial, las aplicaciones potenciales de la computación cuántica en cuatro categorías principales son la ciberseguridad, el análisis de datos y la inteligencia artificial, la optimización y la simulación, y la gestión y búsqueda de datos. ^[146]

La inversión en investigación sobre computación cuántica ha aumentado en los sectores público y privado. ^{[147] [148]} Como resumió una empresa consultora, ^[149]

...  los dólares de inversión están llegando a raudales y las empresas emergentes de computación cuántica están proliferando.  ... Si bien la computación cuántica promete ayudar a las empresas a resolver problemas que están más allá del alcance y la velocidad de las computadoras convencionales de alto rendimiento , los casos de uso son en gran medida experimentales e hipotéticos en esta etapa inicial.

Cualquier problema computacional solucionable por una computadora clásica también es solucionable por una computadora cuántica. ^[150] Intuitivamente, esto se debe a que se cree que todos los fenómenos físicos, incluido el funcionamiento de las computadoras clásicas, se pueden describir utilizando la mecánica cuántica , que subyace al funcionamiento de las computadoras cuánticas.

Por el contrario, cualquier problema que pueda resolver un ordenador cuántico también puede resolverlo un ordenador clásico. Es posible simular tanto ordenadores cuánticos como clásicos manualmente con solo un papel y un bolígrafo, si se le da suficiente tiempo. Más formalmente, cualquier ordenador cuántico puede ser simulado por una máquina de Turing . En otras palabras, los ordenadores cuánticos no proporcionan ningún poder adicional sobre los ordenadores clásicos en términos de computabilidad . Esto significa que los ordenadores cuánticos no pueden resolver problemas indecidibles como el problema de la detención , y la existencia de ordenadores cuánticos no refuta la tesis de Church-Turing . ^[151]

Si bien las computadoras cuánticas no pueden resolver ningún problema que las computadoras clásicas ya no puedan resolver, se sospecha que pueden resolver ciertos problemas más rápido que las computadoras clásicas. Por ejemplo, se sabe que las computadoras cuánticas pueden factorizar números enteros de manera eficiente , mientras que no se cree que este sea el caso de las computadoras clásicas.

La clase de problemas que puede resolverse eficientemente mediante un ordenador cuántico con error acotado se denomina BQP , por "error acotado, cuántico, tiempo polinomial". Más formalmente, BQP es la clase de problemas que puede resolver una máquina de Turing cuántica de tiempo polinomial con una probabilidad de error de como máximo 1/3. Como clase de problemas probabilísticos, BQP es la contraparte cuántica de BPP ("error acotado, probabilístico, tiempo polinomial"), la clase de problemas que pueden resolverse mediante máquinas de Turing probabilísticas de tiempo polinomial con error acotado. ^[152] Se sabe que y se sospecha ampliamente que , lo que intuitivamente significaría que los ordenadores cuánticos son más potentes que los ordenadores clásicos en términos de complejidad temporal . ^[153]${\displaystyle {\mathsf {BPP\subseteq BQP}}}$${\displaystyle {\mathsf {BQP\subsetneq BPP}}}$

No se conoce la relación exacta de BQP con P , NP y PSPACE . Sin embargo, se sabe que ; es decir, todos los problemas que pueden ser resueltos eficientemente por una computadora clásica determinista también pueden ser resueltos eficientemente por una computadora cuántica, y todos los problemas que pueden ser resueltos eficientemente por una computadora cuántica también pueden ser resueltos por una computadora clásica determinista con recursos espaciales polinomiales. Se sospecha además que BQP es un superconjunto estricto de P, lo que significa que hay problemas que son eficientemente solucionables por computadoras cuánticas que no son eficientemente solucionables por computadoras clásicas deterministas. Por ejemplo, se sabe que la factorización de enteros y el problema del logaritmo discreto están en BQP y se sospecha que están fuera de P. Sobre la relación de BQP con NP, se sabe poco más allá del hecho de que algunos problemas NP que se cree que no están en P también están en BQP (la factorización de enteros y el problema del logaritmo discreto están ambos en NP, por ejemplo). Se sospecha que ; es decir, se cree que existen problemas comprobables de manera eficiente que no son solucionables de manera eficiente por una computadora cuántica. Como consecuencia directa de esta creencia, también se sospecha que BQP es disjunto de la clase de problemas NP-completos (si un problema NP-completo estuviera en BQP, entonces se seguiría de la NP-dureza que todos los problemas en NP están en BQP). ^[154]${\displaystyle {\mathsf {P\subseteq BQP\subseteq PSPACE}}}$${\displaystyle {\mathsf {NP\nsubseteq BQP}}}$

Wikimedia Commons tiene medios relacionados con Computación cuántica .

• Aaronson, Scott (2013). Computación cuántica desde Demócrito . Cambridge University Press. doi :10.1017/CBO9780511979309. ISBN. 978-0-521-19956-8.OCLC 829706638  .
• Grumbling, Emily; Horowitz, Mark, eds. (2019). Computación cuántica: progreso y perspectivas . Washington, DC: The National Academies Press. doi :10.17226/25196. ISBN 978-0-309-47970-7. OCLC  1091904777. S2CID  125635007.
• Mermin, N. David (2007). Informática cuántica: una introducción . doi :10.1017/CBO9780511813870. ISBN 978-0-511-34258-5.OCLC 422727925  .
• Nielsen, Michael ; Chuang, Isaac (2010). Computación cuántica e información cuántica (edición del décimo aniversario). doi :10.1017/CBO9780511976667. ISBN 978-0-511-99277-3. OCLC  700706156. S2CID  59717455.
• Shor, Peter W. (1994). Algoritmos para computación cuántica: logaritmos discretos y factorización . Simposio sobre fundamentos de la informática . Santa Fe, Nuevo México : IEEE . pp. 124–134. doi :10.1109/SFCS.1994.365700. ISBN . 978-0-8186-6580-6.

• Medios relacionados con Computadora cuántica en Wikimedia Commons
• Materiales de aprendizaje relacionados con la computación cuántica en Wikiversidad
• Enciclopedia de Filosofía de Stanford : "Computación cuántica" por Amit Hagar y Michael E. Cuffaro.
• "Computación cuántica, teoría de la computación", Enciclopedia de Matemáticas , EMS Press , 2001 [1994]
• Computación cuántica para los más curiosos, por Andy Matuschak y Michael Nielsen

Conferencias

• Computación cuántica para personas determinadas: 22 videoconferencias de Michael Nielsen
• Videoconferencias de David Deutsch
• Conferencias en el Instituto Henri Poincaré (diapositivas y vídeos)
• Conferencia en línea sobre Introducción a la computación cuántica, de Edward Gerjuoy (2008)
• Lomonaco, Sam. Cuatro conferencias sobre computación cuántica dictadas en la Universidad de Oxford en julio de 2006