Fatiga (material)

It has been suggested that Static fatigue be merged into this article. (Discuss) Proposed since August 2024.

En la ciencia de los materiales , la fatiga es la iniciación y propagación de grietas en un material debido a una carga cíclica. Una vez que se ha iniciado una grieta por fatiga , crece un poco con cada ciclo de carga, lo que generalmente produce estrías en algunas partes de la superficie de la fractura. La grieta seguirá creciendo hasta que alcance un tamaño crítico, lo que ocurre cuando el factor de intensidad de tensión de la grieta excede la tenacidad de fractura del material, lo que produce una propagación rápida y, por lo general, una fractura completa de la estructura.

Tradicionalmente, la fatiga se ha asociado con el fallo de los componentes metálicos, lo que dio lugar al término fatiga del metal . En el siglo XIX, se pensaba que el fallo repentino de los ejes metálicos de los ferrocarriles se debía a la cristalización del metal debido a la apariencia frágil de la superficie de la fractura, pero desde entonces esto ha sido desmentido. ^[1] La mayoría de los materiales, como los compuestos, los plásticos y las cerámicas, parecen experimentar algún tipo de fallo relacionado con la fatiga. ^[2]

Para ayudar a predecir la vida útil por fatiga de un componente, se realizan pruebas de fatiga utilizando cupones para medir la tasa de crecimiento de grietas mediante la aplicación de una carga cíclica de amplitud constante y promediando el crecimiento medido de una grieta a lo largo de miles de ciclos. Sin embargo, también hay una serie de casos especiales que deben considerarse donde la tasa de crecimiento de grietas es significativamente diferente en comparación con la obtenida a partir de pruebas de amplitud constante, como la tasa de crecimiento reducida que se produce para cargas pequeñas cerca del umbral o después de la aplicación de una sobrecarga , y la mayor tasa de crecimiento de grietas asociada con grietas cortas o después de la aplicación de una subcarga . ^[2]

Si las cargas superan un cierto umbral, comenzarán a iniciarse grietas microscópicas en concentraciones de tensión como agujeros, bandas de deslizamiento persistentes (PSB), interfaces compuestas o límites de grano en metales. ^[3] Los valores de tensión que causan daños por fatiga suelen ser mucho menores que la resistencia al rendimiento del material.

Históricamente, la fatiga se ha dividido en regiones de fatiga de alto ciclo que requieren más de 10 ⁴ ciclos para fallar, donde la tensión es baja y principalmente elástica , y fatiga de bajo ciclo donde hay una plasticidad significativa. Los experimentos han demostrado que la fatiga de bajo ciclo también es causa de crecimiento de grietas. ^[4]

Las fallas por fatiga, tanto para ciclos altos como bajos, siguen todos los mismos pasos básicos: inicio de la grieta, crecimiento de grietas en etapas I y II y, finalmente, falla definitiva. Para comenzar el proceso, las grietas deben nuclearse dentro de un material. Este proceso puede ocurrir en los puntos de aumento de tensión en muestras metálicas o en áreas con una alta densidad de huecos en muestras de polímeros. Estas grietas se propagan lentamente al principio durante el crecimiento de grietas en etapa I a lo largo de planos cristalográficos, donde las tensiones de corte son más altas. Una vez que las grietas alcanzan un tamaño crítico, se propagan rápidamente durante el crecimiento de grietas en etapa II en una dirección perpendicular a la fuerza aplicada. Estas grietas pueden eventualmente conducir a la falla definitiva del material, a menudo de una manera frágil y catastrófica.

La formación de grietas iniciales que preceden a la falla por fatiga es un proceso independiente que consta de cuatro pasos discretos en muestras metálicas. El material desarrollará estructuras celulares y se endurecerá en respuesta a la carga aplicada. Esto hace que la amplitud de la tensión aplicada aumente dadas las nuevas restricciones a la deformación. Estas estructuras celulares recién formadas finalmente se romperán con la formación de bandas de deslizamiento persistentes (PSB). El deslizamiento en el material se localiza en estas PSB, y el deslizamiento exagerado ahora puede servir como un concentrador de tensión para la formación de una grieta. La nucleación y el crecimiento de una grieta hasta un tamaño detectable explican la mayor parte del proceso de agrietamiento. Es por esta razón que las fallas por fatiga cíclicas parecen ocurrir tan repentinamente que la mayor parte de los cambios en el material no son visibles sin pruebas destructivas. Incluso en materiales normalmente dúctiles, las fallas por fatiga se parecerán a fallas frágiles repentinas.

Los planos de deslizamiento inducidos por PSB dan lugar a intrusiones y extrusiones a lo largo de la superficie de un material, que a menudo se producen en pares. ^[5] Este deslizamiento no es un cambio microestructural dentro del material, sino más bien una propagación de dislocaciones dentro del material. En lugar de una interfaz suave, las intrusiones y extrusiones harán que la superficie del material se parezca al borde de una baraja de cartas, donde no todas las cartas están perfectamente alineadas. Las intrusiones y extrusiones inducidas por deslizamiento crean estructuras superficiales extremadamente finas en el material. Como el tamaño de la estructura de la superficie está inversamente relacionado con los factores de concentración de tensión, el deslizamiento de la superficie inducido por PSB puede provocar que se inicien fracturas.

Estos pasos también se pueden omitir por completo si las grietas se forman en un concentrador de tensión preexistente, como por ejemplo una inclusión en el material o un concentrador de tensión geométrico causado por una esquina interna afilada o un filete.

La mayor parte de la vida útil por fatiga se consume generalmente en la fase de crecimiento de la grieta. La tasa de crecimiento depende principalmente del rango de carga cíclica, aunque otros factores como la tensión media, el entorno, las sobrecargas y las subcargas también pueden afectar la tasa de crecimiento. El crecimiento de la grieta puede detenerse si las cargas son lo suficientemente pequeñas como para caer por debajo de un umbral crítico.

Las grietas por fatiga pueden surgir de defectos de material o de fabricación de hasta 10 μm.

Cuando la tasa de crecimiento se vuelve lo suficientemente grande, se pueden ver estrías de fatiga en la superficie de la fractura. Las estrías marcan la posición de la punta de la grieta y el ancho de cada estría representa el crecimiento de un ciclo de carga. Las estrías son el resultado de la plasticidad en la punta de la grieta.

Cuando la intensidad de la tensión supera un valor crítico conocido como tenacidad de fractura, se producirá una fractura rápida insostenible, generalmente por un proceso de coalescencia de microhuecos . Antes de la fractura final, la superficie de la fractura puede contener una mezcla de áreas de fatiga y fractura rápida.

Los siguientes efectos modifican la tasa de crecimiento: ^[2]

• Efecto de la tensión media: una tensión media más alta aumenta la tasa de crecimiento de las grietas.
• Medio ambiente: El aumento de la humedad aumenta la velocidad de crecimiento de las grietas. En el caso del aluminio, las grietas generalmente crecen desde la superficie, donde el vapor de agua de la atmósfera puede alcanzar la punta de la grieta y disociarse en hidrógeno atómico, lo que provoca la fragilización por hidrógeno . Las grietas que crecen internamente están aisladas de la atmósfera y crecen en el vacío , donde la velocidad de crecimiento suele ser un orden de magnitud más lenta que una grieta superficial. ^[6]
• Efecto de grieta corta: En 1975, Pearson observó que las grietas cortas crecen más rápido de lo esperado. ^[7] Las posibles razones para el efecto de grieta corta incluyen la presencia de la tensión T, el estado de tensión triaxial en la punta de la grieta, la falta de cierre de la grieta asociada con las grietas cortas y la gran zona plástica en comparación con la longitud de la grieta. Además, las grietas largas suelen experimentar un umbral que las grietas cortas no tienen. ^[8] Hay una serie de criterios para las grietas cortas: ^[9]
  • Las grietas suelen ser más pequeñas que 1 mm.
  • Las grietas son más pequeñas que el tamaño de la microestructura del material, como el tamaño del grano, o
  • La longitud de la grieta es pequeña en comparación con la zona plástica.
• Subcargas: Un pequeño número de subcargas aumenta la tasa de crecimiento y puede contrarrestar el efecto de las sobrecargas.
• Sobrecargas: Las sobrecargas iniciales (> 1,5 la carga máxima en una secuencia) provocan un pequeño aumento en la tasa de crecimiento seguido de una larga reducción en la tasa de crecimiento.

• En las aleaciones metálicas, y para el caso simplificado de que no existen discontinuidades macroscópicas ni microscópicas, el proceso se inicia con movimientos de dislocación a nivel microscópico, que eventualmente forman bandas de deslizamiento persistentes que se convierten en el núcleo de grietas cortas.
• Las discontinuidades macroscópicas y microscópicas (a escala de grano cristalino), así como las características de diseño de los componentes que causan concentraciones de tensión (agujeros, chaveteros , cambios bruscos de dirección de carga, etc.) son ubicaciones comunes en las que comienza el proceso de fatiga.
• La fatiga es un proceso que tiene un grado de aleatoriedad ( estocástico ) y que a menudo muestra una dispersión considerable incluso en muestras aparentemente idénticas en entornos bien controlados.
• La fatiga suele estar asociada a tensiones de tracción, pero se han reportado grietas por fatiga debido a cargas de compresión. ^[10]
• Cuanto mayor sea el rango de tensión aplicado, más corta será la vida útil.
• La dispersión de la vida útil por fatiga tiende a aumentar cuanto más prolongada es la vida útil por fatiga.
• El daño es irreversible. Los materiales no se recuperan cuando descansan.
• La vida útil por fatiga está influenciada por una variedad de factores, como la temperatura , el acabado de la superficie , la microestructura metalúrgica, la presencia de productos químicos oxidantes o inertes , tensiones residuales , contacto por roce ( fretting ), etc.
• Algunos materiales (por ejemplo, algunas aleaciones de acero y titanio ) presentan un límite de fatiga teórico por debajo del cual la carga continua no conduce a falla por fatiga.
• La resistencia a la fatiga por ciclos elevados (aproximadamente entre 104 ^y 108 ^ciclos ) se puede describir mediante parámetros basados ​​en la tensión. En estas pruebas se suele utilizar un banco de pruebas servohidráulico controlado por carga, con frecuencias de alrededor de 20 a 50 Hz. También se pueden utilizar otros tipos de máquinas, como máquinas magnéticas resonantes, para alcanzar frecuencias de hasta 250 Hz.
• La fatiga de bajo ciclo (carga que generalmente causa falla en menos de 10 ⁴ ciclos) está asociada con un comportamiento plástico localizado en los metales; por lo tanto, se debe utilizar un parámetro basado en la deformación para predecir la vida útil por fatiga en los metales. Las pruebas se realizan con amplitudes de deformación constantes, generalmente de 0,01 a 5 Hz.

• 1837: Wilhelm Albert publica el primer artículo sobre la fatiga. Ideó una máquina de prueba para las cadenas transportadoras utilizadas en las minas de Clausthal . ^[11]
• 1839: Jean-Victor Poncelet describe los metales como "cansados" en sus conferencias en la escuela militar de Metz .
• 1842: William John Macquorn Rankine reconoce la importancia de las concentraciones de tensión en su investigación de las fallas de los ejes de los ferrocarriles . El accidente del tren de Versalles fue causado por una falla por fatiga de un eje de locomotora. ^[12]
• 1843: Joseph Glynn informa sobre la fatiga de un eje de un ténder de locomotora. Identifica la ranura de la chaveta como el origen de la grieta.
• 1848: La Inspección de Ferrocarriles informa de una de las primeras fallas de neumáticos, probablemente causada por un agujero de remache en la banda de rodadura de una rueda de vagón de ferrocarril. Probablemente se trató de una falla por fatiga.
• 1849: Eaton Hodgkinson recibe una "pequeña suma de dinero" para informar al Parlamento del Reino Unido sobre su trabajo en "determinar mediante experimentos directos los efectos de los cambios continuos de carga sobre las estructuras de hierro y hasta qué punto podrían cargarse sin peligro para su seguridad final".
• 1854: F. Braithwaite informa sobre fallas comunes en el servicio por fatiga y acuña el término fatiga . ^[13]
• 1860: Sir William Fairbairn y August Wöhler realizan pruebas sistemáticas de fatiga .
• 1870: A. Wöhler resume su trabajo sobre ejes de ferrocarril. Concluye que el rango de tensión cíclica es más importante que la tensión máxima e introduce el concepto de límite de resistencia . ^[11]
• 1903: Sir James Alfred Ewing demuestra el origen de la falla por fatiga en grietas microscópicas.
• 1910: OH Basquin propone una relación logaritmo-logaritmo para las curvas SN, utilizando los datos de prueba de Wöhler. ^[14]
• 1940: Sidney M. Cadwell publica el primer estudio riguroso sobre la fatiga del caucho. ^[15]
• 1945: AM Miner populariza la hipótesis de daño lineal de Palmgren (1924) como una herramienta de diseño práctica. ^{[16] [17]}
• 1952: W. Weibull Un modelo de curva SN. ^[18]
• 1954: El primer avión comercial a reacción del mundo, el de Havilland Comet , sufre un desastre cuando tres aviones se rompen en el aire, lo que obliga a De Havilland y a todos los demás fabricantes a rediseñar los aviones de gran altitud y, en particular, a sustituir las aberturas cuadradas como las ventanas por unas ovaladas.
• 1954: LF Coffin y SS Manson explican el crecimiento de grietas por fatiga en términos de deformación plástica en la punta de las grietas.
• 1961: PC Paris propone métodos para predecir la tasa de crecimiento de grietas por fatiga individuales frente al escepticismo inicial y la defensa popular del enfoque fenomenológico de Miner.
• 1968: Tatsuo Endo y M. Matsuishi idean el algoritmo de conteo de flujo de lluvia y permiten la aplicación confiable de la regla de Miner a cargas aleatorias . ^[19]
• 1970: Smith, Watson y Topper desarrollaron un modelo de corrección de tensión media, donde el daño por fatiga en un ciclo está determinado por el producto de la tensión máxima y la amplitud de la deformación. ^[20]
• 1970: W. Elber explica los mecanismos y la importancia del cierre de grietas para frenar el crecimiento de una grieta por fatiga debido al efecto de cuña de la deformación plástica que queda detrás de la punta de la grieta. ^{[21] [22]}
• 1973: MW Brown y KJ Miller observan que la vida útil por fatiga en condiciones multiaxiales está determinada por la experiencia del plano que recibe el mayor daño, y que deben considerarse tanto las cargas de tensión como las de corte en el plano crítico . ^[23]

La Sociedad Americana para Pruebas y Materiales define la vida por fatiga , N _f , como el número de ciclos de tensión de un carácter específico que soporta una muestra antes de que se produzca una falla de una naturaleza específica. ^[24] Para algunos materiales, en particular el acero y el titanio , existe un valor teórico para la amplitud de la tensión por debajo del cual el material no fallará durante ningún número de ciclos, llamado límite de fatiga o límite de resistencia . ^[25] Sin embargo, en la práctica, varios trabajos realizados en un mayor número de ciclos sugieren que no existen límites de fatiga para ningún metal. ^{[26] [27] [28]}

Los ingenieros han utilizado varios métodos para determinar la vida útil por fatiga de un material: ^[29]

1. El método del estrés-vida,
2. El método de la tensión-vida,
3. El método de crecimiento de grietas y
4. métodos probabilísticos, que pueden basarse en métodos de vida útil o de crecimiento de grietas.

Ya sea que se utilice el enfoque de tensión/deformación-vida o el enfoque de crecimiento de grietas, la carga de amplitud compleja o variable se reduce a una serie de cargas cíclicas simples equivalentes a la fatiga utilizando una técnica como el algoritmo de conteo de flujo de lluvia .

Una pieza mecánica suele estar expuesta a una secuencia compleja y, a menudo , aleatoria de cargas, grandes y pequeñas. Para evaluar la vida útil segura de una pieza de este tipo mediante los métodos de daño por fatiga o de vida útil por tensión/deformación, se suele realizar la siguiente serie de pasos:

1. La carga compleja se reduce a una serie de cargas cíclicas simples utilizando una técnica como el análisis del flujo de lluvia ;
2. Se crea un histograma de estrés cíclico a partir del análisis del flujo de lluvia para formar un espectro de daño por fatiga;
3. Para cada nivel de estrés, el grado de daño acumulado se calcula a partir de la curva SN; y
4. El efecto de las contribuciones individuales se combina utilizando un algoritmo como la regla de Miner .

Dado que las curvas SN se generan normalmente para cargas uniaxiales , se necesita alguna regla de equivalencia siempre que la carga sea multiaxial. Para historiales de cargas simples y proporcionales (carga lateral en una relación constante con la axial), se puede aplicar la regla de senos. Para situaciones más complejas, como cargas no proporcionales, se debe aplicar el análisis del plano crítico .

En 1945, Milton A. Miner popularizó una regla que había sido propuesta por primera vez por Arvid Palmgren en 1924. ^[16] La regla, llamada de diversas formas regla de Miner o hipótesis de daño lineal de Palmgren-Miner , establece que cuando hay k magnitudes de tensión diferentes en un espectro, S _i (1 ≤ i ≤ k ), cada una contribuyendo con n _i ( S _i ) ciclos, entonces si N _i ( S _i ) es el número de ciclos hasta la falla de una inversión de tensión constante S _i (determinada por pruebas de fatiga uniaxial), la falla ocurre cuando:

${\displaystyle \sum _{i=1}^{k}{\frac {n_{i}}{N_{i}}}=C}$

Generalmente, para fines de diseño, se supone que C es 1. Esto puede considerarse como una evaluación de qué proporción de la vida se consume mediante una combinación lineal de inversiones de tensión en magnitudes variables.

Aunque la regla de Miner puede ser una aproximación útil en muchas circunstancias, tiene varias limitaciones importantes:

1. No reconoce la naturaleza probabilística de la fatiga y no existe una manera sencilla de relacionar la vida útil predicha por la regla con las características de una distribución de probabilidad. Los analistas de la industria a menudo utilizan curvas de diseño, ajustadas para tener en cuenta la dispersión, para _{calcular Ni} ( Si ) .
2. La secuencia en la que se aplican ciclos de tensión alta y baja a una muestra afecta de hecho la vida útil por fatiga, algo que la regla de Miner no tiene en cuenta. En algunas circunstancias, los ciclos de tensión baja seguidos de tensión alta causan más daño del que predeciría la regla. ^[30] No considera el efecto de una sobrecarga o tensión alta que puede resultar en una tensión residual compresiva que puede retardar el crecimiento de la grieta. Una tensión alta seguida de una tensión baja puede tener menos daño debido a la presencia de tensión residual compresiva (o daños plásticos localizados alrededor de la punta de la grieta).

El rendimiento de fatiga de los materiales se caracteriza comúnmente por una curva SN , también conocida como curva de Wöhler . Esto a menudo se representa con la tensión cíclica ( S ) contra los ciclos hasta la falla ( N ) en una escala logarítmica . ^[31] Las curvas SN se derivan de pruebas en muestras del material a caracterizar (a menudo llamadas cupones o especímenes) donde se aplica una tensión sinusoidal regular mediante una máquina de prueba que también cuenta el número de ciclos hasta la falla. Este proceso a veces se conoce como prueba de cupón . Para una mayor precisión pero una generalidad menor, se utilizan pruebas de componentes. ^[32] Cada prueba de cupón o componente genera un punto en el gráfico, aunque en algunos casos hay un desfase donde el tiempo hasta la falla excede el disponible para la prueba (ver censura ). El análisis de datos de fatiga requiere técnicas de estadística , especialmente análisis de supervivencia y regresión lineal .

La progresión de la curva SN puede verse influenciada por muchos factores, como la relación de tensiones (tensión media), ^[33] la frecuencia de carga, la temperatura , la corrosión , las tensiones residuales y la presencia de entallas. Un diagrama de vida de fatiga constante (CFL) ^[34] es útil para el estudio del efecto de la relación de tensiones. La línea de Goodman es un método utilizado para estimar la influencia de la tensión media en la resistencia a la fatiga .

Un diagrama de vida de fatiga constante (CFL) es útil para el efecto de la relación de tensiones en la curva SN. ^[35] Además, en presencia de una tensión constante superpuesta a la carga cíclica, se puede utilizar la relación de Goodman para estimar una condición de falla. Grafica la amplitud de la tensión contra la tensión media con el límite de fatiga y la resistencia máxima a la tracción del material como los dos extremos. Los criterios de falla alternativos incluyen Soderberg y Gerber. ^[36]

Como los cupones muestreados de un marco homogéneo mostrarán una variación en su número de ciclos hasta la falla, la curva SN debería ser más apropiadamente una curva de estrés-ciclo-probabilidad (SNP) para capturar la probabilidad de falla después de un número dado de ciclos de un cierto estrés.

En el caso de los materiales cúbicos centrados en el cuerpo (bcc), la curva de Wöhler suele convertirse en una línea horizontal con una amplitud de tensión decreciente, es decir, existe una resistencia a la fatiga que se puede asignar a estos materiales. En el caso de los metales cúbicos centrados en las caras (fcc), la curva de Wöhler generalmente desciende de forma continua, de modo que solo se puede asignar un límite de fatiga a estos materiales. ^[37]

Cuando las deformaciones ya no son elásticas, como en presencia de concentraciones de tensión, se puede utilizar la deformación total en lugar de la tensión como parámetro de similitud. Esto se conoce como el método de deformación-vida. La amplitud de la deformación total es la suma de la amplitud de la deformación elástica y la amplitud de la deformación plástica y se expresa mediante ^{[2] [38]}${\displaystyle \Delta \varepsilon /2}$${\displaystyle \Delta \varepsilon _{\text{e}}/2}$${\displaystyle \Delta \varepsilon _{\text{p}}/2}$

${\displaystyle {\Delta \varepsilon \over 2}={\Delta \varepsilon _{\text{e}} \over 2}+{\Delta \varepsilon _{\text{p}} \over 2}}$.

La ecuación de Basquin para la amplitud de la deformación elástica es

${\displaystyle {\Delta \varepsilon _{\text{e}} \over 2}={\frac {\Delta \sigma }{2E}}={\frac {\sigma _{\text{a}}}{E}}}$

¿Dónde está el módulo de Young ?${\displaystyle E}$

La relación para la fatiga de alto ciclo se puede expresar utilizando la amplitud de deformación elástica.

${\displaystyle {\Delta \varepsilon _{\text{e}} \over 2}={\frac {\sigma _{\text{f}}^{\prime }}{E}}(2N_{\text{f}})^{b}}$

donde es un parámetro que escala con la resistencia a la tracción obtenida al ajustar los datos experimentales, es el número de ciclos hasta la falla y es la pendiente de la curva logarítmica-logarítmica determinada nuevamente mediante el ajuste de la curva.${\displaystyle \sigma _{\text{f}}^{\prime }}$${\displaystyle N_{\text{f}}}$${\displaystyle b}$

En 1954, Coffin y Manson propusieron que la vida útil por fatiga de un componente estaba relacionada con la amplitud de la deformación plástica utilizando

${\displaystyle {\Delta \varepsilon _{\text{p}} \over 2}=\varepsilon _{\text{f}}^{\prime }(2N_{\text{f}})^{c}}$.

La combinación de las partes elásticas y plásticas proporciona la amplitud de deformación total que tiene en cuenta tanto la fatiga de ciclo alto como la de ciclo bajo.

${\displaystyle {\Delta \varepsilon \over 2}={\frac {\sigma _{\text{f}}^{\prime }}{E}}(2N_{\text{f}})^{b}+\varepsilon _{\text{f}}^{\prime }(2N_{\text{f}})^{c}}$.

donde es el coeficiente de resistencia a la fatiga, es el exponente de resistencia a la fatiga, es el coeficiente de ductilidad por fatiga, es el exponente de ductilidad por fatiga y es el número de ciclos hasta la falla ( siendo el número de reversiones hasta la falla).${\displaystyle \sigma _{f}'}$${\displaystyle b}$${\displaystyle \varepsilon _{f}'}$${\displaystyle c}$${\displaystyle N_{f}}$${\displaystyle 2N_{f}}$

Se puede hacer una estimación de la vida útil por fatiga de un componente utilizando una ecuación de crecimiento de grietas sumando el ancho de cada incremento de crecimiento de grietas para cada ciclo de carga. Se aplican factores de seguridad o de dispersión a la vida útil calculada para tener en cuenta cualquier incertidumbre y variabilidad asociada con la fatiga. La tasa de crecimiento utilizada en las predicciones de crecimiento de grietas se mide típicamente aplicando miles de ciclos de amplitud constante a una muestra y midiendo la tasa de crecimiento a partir del cambio en la conformidad de la muestra o midiendo el crecimiento de la grieta en la superficie de la muestra. ASTM International ha desarrollado métodos estándar para medir la tasa de crecimiento. ^[9]

Las ecuaciones de crecimiento de grietas, como la ecuación de París-Erdoğan, se utilizan para predecir la vida útil de un componente. Se pueden utilizar para predecir el crecimiento de una grieta desde 10 um hasta la falla. Para acabados de fabricación normales, esto puede cubrir la mayor parte de la vida útil por fatiga de un componente donde el crecimiento puede comenzar desde el primer ciclo. ^[4] Las condiciones en la punta de la grieta de un componente generalmente están relacionadas con las condiciones de la muestra de prueba utilizando un parámetro característico como la intensidad de la tensión, la integral J o el desplazamiento de apertura de la punta de la grieta . Todas estas técnicas tienen como objetivo hacer coincidir las condiciones de la punta de la grieta en el componente con las de las muestras de prueba que dan la tasa de crecimiento de la grieta.

Puede ser necesario contar con modelos adicionales para incluir los efectos de retardo y aceleración asociados con sobrecargas o subcargas en la secuencia de carga. Además, puede ser necesario contar con datos de crecimiento de grietas pequeñas para que coincidan con la mayor tasa de crecimiento observada en las grietas pequeñas. ^[39]

Por lo general, se utiliza una técnica de conteo de ciclos, como el conteo de ciclos de lluvia, para extraer los ciclos de una secuencia compleja. Se ha demostrado que esta técnica, junto con otras, funciona con métodos de crecimiento de grietas. ^[40]

Los métodos de crecimiento de grietas tienen la ventaja de que pueden predecir el tamaño intermedio de las grietas. Esta información se puede utilizar para programar inspecciones en una estructura para garantizar la seguridad, mientras que los métodos de deformación/vida solo proporcionan una vida útil hasta la falla.

Un diseño confiable contra fallas por fatiga requiere una educación exhaustiva y experiencia supervisada en ingeniería estructural , ingeniería mecánica o ciencia de los materiales . Existen al menos cinco enfoques principales para asegurar la vida útil de las piezas mecánicas que muestran grados crecientes de sofisticación: ^[41]

1. Diseño para mantener la tensión por debajo del umbral del límite de fatiga (concepto de vida útil infinita);
2. Diseño a prueba de fallos , con degradación gradual y tolerante a fallos : indique al usuario que reemplace las piezas cuando fallen. Diseñe de manera que no haya un único punto de falla y que, cuando una pieza falle por completo, no se produzca una falla catastrófica de todo el sistema.
3. Diseño de vida segura : Diseño (conservador) para una vida útil fija después de la cual se le indica al usuario que reemplace la pieza por una nueva (una práctica de diseño denominada pieza de vida útil finita, concepto de vida útil finita o "vida segura"); la obsolescencia planificada y los productos desechables son variantes que se diseñan para una vida útil fija después de la cual se le indica al usuario que reemplace todo el dispositivo;
4. Tolerancia al daño : es un enfoque que garantiza la seguridad de la aeronave al asumir la presencia de grietas o defectos incluso en aeronaves nuevas. Se pueden utilizar cálculos de crecimiento de grietas, inspecciones periódicas y reparación o reemplazo de componentes para garantizar que los componentes críticos que puedan contener grietas sigan siendo seguros. Las inspecciones generalmente utilizan pruebas no destructivas para limitar o monitorear el tamaño de las posibles grietas y requieren una predicción precisa de la tasa de crecimiento de grietas entre inspecciones. El diseñador establece un programa de controles de mantenimiento de la aeronave con la frecuencia suficiente para que las piezas se reemplacen mientras la grieta aún está en la fase de "crecimiento lento". Esto a menudo se conoce como diseño tolerante al daño o "retirada por causa justificada".
5. Gestión de riesgos : garantiza que la probabilidad de falla se mantenga por debajo de un nivel aceptable. Este enfoque se utiliza normalmente para aeronaves donde los niveles aceptables pueden basarse en la probabilidad de falla durante un solo vuelo o durante la vida útil de una aeronave. Se supone que un componente tiene una grieta con una distribución de probabilidad de tamaños de grietas. Este enfoque puede considerar la variabilidad en valores como las tasas de crecimiento de grietas, el uso y el tamaño crítico de grietas. ^[42] También es útil para considerar daños en múltiples ubicaciones que pueden interactuar para producir daños por fatiga generalizados o en múltiples sitios . Las distribuciones de probabilidad que son comunes en el análisis de datos y en el diseño contra la fatiga incluyen la distribución log-normal , la distribución de valores extremos , la distribución de Birnbaum-Saunders y la distribución de Weibull .

Las pruebas de fatiga se pueden utilizar para componentes como un cupón o un artículo de prueba a escala real para determinar:

1. la tasa de crecimiento de grietas y la vida útil por fatiga de componentes como un cupón o un artículo de prueba a escala real.
2. Ubicación de regiones críticas
3. Grado de seguridad ante fallos cuando falla parte de la estructura.
4. el origen y la causa del defecto iniciador de la grieta a partir del examen fractográfico de la grieta.

Estas pruebas pueden formar parte del proceso de certificación, como por ejemplo la certificación de aeronavegabilidad .

1. Detener la perforación Las grietas por fatiga que han comenzado a propagarse a veces se pueden detener perforando agujeros , llamados topes de perforación , en la punta de la grieta. ^[43] Existe la posibilidad de que se inicie una nueva grieta en el costado del agujero.
2. Mezclar . Las pequeñas grietas se pueden difuminar y la superficie se puede trabajar en frío o granallar.
3. Orificios de gran tamaño . Los orificios con grietas que crecen a partir de ellos se pueden perforar para hacer un orificio más grande para eliminar las grietas y colocar casquillos para restaurar el orificio original. Los casquillos se pueden encoger en frío con ajuste por interferencia para inducir tensiones residuales de compresión beneficiosas. El orificio de gran tamaño también se puede trabajar en frío introduciendo un mandril de gran tamaño a través del orificio. ^[44]
4. Parche . Las grietas se pueden reparar instalando un parche o un accesorio de reparación. Los parches compuestos se han utilizado para restaurar la resistencia de las alas de los aviones después de que se han detectado grietas o para reducir la tensión antes del agrietamiento con el fin de mejorar la vida útil por fatiga. ^[45] Los parches pueden restringir la capacidad de monitorear las grietas por fatiga y es posible que sea necesario quitarlos y reemplazarlos para las inspecciones.

1. Cambio de material . Los cambios en los materiales utilizados en las piezas también pueden mejorar la resistencia a la fatiga. Por ejemplo, las piezas pueden fabricarse con metales con mejor resistencia a la fatiga. El reemplazo completo y el rediseño de las piezas también pueden reducir, si no eliminar, los problemas de fatiga. Por lo tanto, las palas de rotor y las hélices de los helicópteros de metal se están reemplazando por equivalentes compuestos . No solo son más ligeros, sino también mucho más resistentes a la fatiga. Son más caros, pero el costo adicional se compensa ampliamente por su mayor integridad, ya que la pérdida de una pala de rotor generalmente conduce a la pérdida total de la aeronave. Un argumento similar se ha presentado para el reemplazo de fuselajes, alas y colas de metal de las aeronaves. ^[46]
2. Inducir tensiones residuales El granallado de una superficie puede reducir dichas tensiones de tracción y crear una tensión residual de compresión , que evita la iniciación de grietas. Las formas de granallado incluyen: granallado , utilizando proyectiles de alta velocidad, tratamiento de impacto de alta frecuencia (también llamado impacto mecánico de alta frecuencia) utilizando un martillo mecánico, ^{[47] [48]} y granallado láser que utiliza pulsos láser de alta energía. El bruñido de baja plasticidad también se puede utilizar para inducir tensiones de compresión en filetes y se pueden utilizar mandriles de trabajo en frío para agujeros. ^[49] Los aumentos en la vida útil y la resistencia a la fatiga están proporcionalmente relacionados con la profundidad de las tensiones residuales de compresión impartidas. El granallado imparte tensiones residuales de compresión de aproximadamente 0,005 pulgadas (0,1 mm) de profundidad, mientras que el granallado láser puede llegar a 0,040 a 0,100 pulgadas (1 a 2,5 mm) de profundidad, o más. ^{[50] [ verificación fallida ]}
3. Tratamiento criogénico profundo . Se ha demostrado que el uso del tratamiento criogénico profundo aumenta la resistencia a la fatiga. Se ha demostrado que los resortes utilizados en la industria, las carreras de autos y las armas de fuego duran hasta seis veces más cuando se tratan. La corrosión por calor, que es una forma de fatiga cíclica térmica, se ha retrasado considerablemente. ^[51]
4. Reperfilado . El cambio de forma de una concentración de tensión, como un orificio o un corte, se puede utilizar para prolongar la vida útil de un componente. La optimización de la forma mediante algoritmos de optimización numérica se ha utilizado para reducir la concentración de tensión en las alas y aumentar su vida útil. ^[52]

Los materiales compuestos pueden ofrecer una excelente resistencia a la carga de fatiga. En general, los materiales compuestos presentan una buena tenacidad a la fractura y, a diferencia de los metales, aumentan la tenacidad a la fractura a medida que aumenta la resistencia. El tamaño crítico del daño en los materiales compuestos también es mayor que en los metales. ^[53]

El modo principal de daño en una estructura metálica es el agrietamiento. En el caso del metal, las grietas se propagan de una manera relativamente bien definida con respecto a la tensión aplicada, y el tamaño crítico de la grieta y la velocidad de propagación de la grieta se pueden relacionar con los datos de la muestra a través de la mecánica de fractura analítica. Sin embargo, en el caso de las estructuras compuestas, no hay un único modo de daño que predomine. El agrietamiento de la matriz, la delaminación, el desprendimiento, los huecos, la fractura de las fibras y el agrietamiento del material compuesto pueden ocurrir por separado y en combinación, y el predominio de uno o más de ellos depende en gran medida de las orientaciones del laminado y las condiciones de carga. ^[54] Además, las uniones y los accesorios únicos utilizados para las estructuras compuestas a menudo introducen modos de falla diferentes de los tipificados por el propio laminado. ^[55]

El daño compuesto se propaga de una manera menos regular y los modos de daño pueden cambiar. La experiencia con los compuestos indica que la tasa de propagación del daño no exhibe las dos regiones distintas de iniciación y propagación como los metales. El rango de iniciación de grietas en los metales es de propagación, y hay una diferencia cuantitativa significativa en la tasa, mientras que la diferencia parece ser menos evidente con los compuestos. ^[54] Las grietas por fatiga de los compuestos pueden formarse en la matriz y propagarse lentamente ya que la matriz soporta una fracción tan pequeña de la tensión aplicada . Y las fibras en la estela de la grieta experimentan daño por fatiga. En muchos casos, la tasa de daño se acelera por interacciones perjudiciales con el medio ambiente como la oxidación o corrosión de las fibras. ^[56]

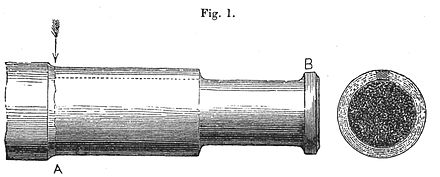
En mayo de 1842 , tras las celebraciones del rey Luis Felipe I en el Palacio de Versalles , un tren que regresaba a París se estrelló en Meudon después de que la locomotora que iba delante rompiera un eje. Los vagones que iban detrás se amontonaron contra las locomotoras destrozadas y se incendiaron. Al menos 55 pasajeros murieron atrapados en los vagones bloqueados, incluido el explorador Jules Dumont d'Urville . Este accidente se conoce en Francia como la "Catástrofe ferroviaria de Meudon" . El accidente fue presenciado por el ingeniero de locomotoras británico Joseph Locke y se difundió ampliamente en Gran Bretaña. Los ingenieros lo discutieron extensamente, buscando una explicación.

El descarrilamiento se había producido por la rotura de un eje de locomotora . La investigación de Rankine sobre los ejes rotos en Gran Bretaña puso de relieve la importancia de la concentración de tensiones y el mecanismo de crecimiento de las grietas con cargas repetidas. Sin embargo, sus artículos y otros que sugerían un mecanismo de crecimiento de las grietas mediante tensiones repetidas fueron ignorados, y las fallas por fatiga se produjeron a un ritmo cada vez mayor en el sistema ferroviario en expansión. Otras teorías falsas parecían ser más aceptables, como la idea de que el metal se había "cristalizado" de alguna manera. La idea se basaba en el aspecto cristalino de la región de fractura rápida de la superficie de la grieta, pero ignoraba el hecho de que el metal ya era altamente cristalino.

En 1954, dos aviones de pasajeros De Havilland Comet se despedazaron en pleno vuelo y se estrellaron con unos meses de diferencia. Como resultado, se realizaron pruebas sistemáticas en un fuselaje sumergido y presurizado en un tanque de agua. Después de un equivalente a 3.000 vuelos, los investigadores del Royal Aircraft Establishment (RAE) pudieron concluir que el accidente se había debido a un fallo en la cabina de presión en la ventana delantera del radiogoniómetro automático en el techo. Esta "ventana" era, de hecho, una de las dos aberturas para las antenas de un sistema de navegación electrónico en el que paneles opacos de fibra de vidrio ocupaban el lugar del "cristal" de la ventana. El fallo se debió a la fatiga del metal causada por la repetida presurización y despresurización de la cabina del avión. Además, los soportes alrededor de las ventanas estaban remachados, no pegados, como exigían las especificaciones originales del avión. El problema se vio agravado por la técnica de construcción con remaches perforados empleada. A diferencia del remachado con taladro, la naturaleza imperfecta del orificio creado mediante el remachado con punzón provocó grietas por defectos de fabricación que pueden haber provocado la aparición de grietas por fatiga alrededor del remache.

La cabina de presión del Comet había sido diseñada con un factor de seguridad cómodamente superior al requerido por los Requisitos de Aeronavegabilidad Civil Británicos (2,5 veces la presión de prueba de la cabina en comparación con el requisito de 1,33 veces y una carga máxima de 2,0 veces la presión de la cabina) y el accidente provocó una revisión en las estimaciones de los requisitos de resistencia de carga segura de las cabinas de presión de los aviones de pasajeros.

Además, se descubrió que las tensiones en torno a las aberturas de la cabina de presión eran considerablemente mayores de lo que se había previsto, especialmente alrededor de los recortes con esquinas agudas, como las ventanas. Como resultado, todos los futuros aviones a reacción tendrían ventanas con esquinas redondeadas, lo que reduciría en gran medida la concentración de tensiones. Esta fue una característica distintiva notable de todos los modelos posteriores del Comet. Los investigadores de la RAE dijeron en una investigación pública que las esquinas agudas cerca de las aberturas de las ventanas de los Comet actuaban como sitios de inicio de grietas. El revestimiento del avión también era demasiado delgado y había grietas en las esquinas debido a las tensiones de fabricación.

El Alexander L. Kielland era una plataforma de perforación semisumergible noruega que volcó mientras trabajaba en el campo petrolífero de Ekofisk en marzo de 1980, matando a 123 personas. El naufragio fue el peor desastre en aguas noruegas desde la Segunda Guerra Mundial. La plataforma, ubicada aproximadamente a 320 km al este de Dundee , Escocia, era propiedad de la Stavanger Drilling Company de Noruega y estaba alquilada a la empresa estadounidense Phillips Petroleum en el momento del desastre. Bajo una lluvia torrencial y niebla, a primera hora de la tarde del 27 de marzo de 1980, más de 200 hombres estaban fuera de servicio en el alojamiento del Alexander L. Kielland . El viento soplaba con ráfagas de 40 nudos y las olas alcanzaban los 12 m de altura. La plataforma acababa de ser retirada de la plataforma de producción Edda . Minutos antes de las 18:30, los que estaban a bordo sintieron un "crujido agudo" seguido de "una especie de temblor". De repente, la plataforma se inclinó más de 30° y luego se estabilizó. Cinco de los seis cables de anclaje se habían roto y el único que quedaba impedía que la plataforma volcara. La escora seguía aumentando y a las 18:53 se rompió el cable de anclaje restante y la plataforma volcó.

Un año después, en marzo de 1981, el informe de investigación ^[58] concluyó que la plataforma se derrumbó debido a una grieta por fatiga en uno de sus seis arriostramientos (arriostramiento D-6), que conectaba la pata D colapsada con el resto de la plataforma. Esto se atribuyó a una pequeña soldadura de filete de 6 mm que unía una placa de brida que no soportaba carga a este arriostramiento D-6. Esta placa de brida sostenía un dispositivo de sonar utilizado durante las operaciones de perforación. El perfil deficiente de la soldadura de filete contribuyó a una reducción de su resistencia a la fatiga. Además, la investigación encontró cantidades considerables de desgarro laminar en la placa de brida y grietas frías en la soldadura a tope. Las grietas frías en las soldaduras, el aumento de las concentraciones de tensión debido a la placa de brida debilitada, el perfil deficiente de la soldadura y las tensiones cíclicas (que serían comunes en el Mar del Norte ), parecieron desempeñar colectivamente un papel en el colapso de la plataforma.

• El desastre de la mina de carbón Hartley de 1862 fue causado por la fractura de la viga de una máquina de vapor y mató a 204 personas.
• La gran inundación de melaza de Boston de 1919 se ha atribuido a una falla por fatiga.
• El accidente del vuelo 421 de Northwest Airlines en 1948 debido a una falla por fatiga en la raíz del larguero del ala
• El "Mt. Pinatubo" de 1957 , avión presidencial del presidente filipino Ramon Magsaysay , se estrelló debido a una falla del motor causada por fatiga del metal.
• El vuelco en 1965 de la primera plataforma petrolífera marina del Reino Unido, el Sea Gem , se debió a la fatiga en parte del sistema de suspensión que une el casco a las patas.
• El vuelo 417 de Los Angeles Airways de 1968 perdió una de sus palas del rotor principal debido a una falla por fatiga.
• El vuelo 1750 de MacRobertson Miller Airlines de 1968 perdió un ala debido a un mantenimiento inadecuado que provocó una falla por fatiga.
• El accidente del F-111A en 1969 debido a una falla por fatiga del pivote del ala debido a un defecto del material resultó en el desarrollo de un enfoque tolerante a daños para el diseño por fatiga. ^[59]
• El accidente del Boeing 707 de Dan-Air en 1977 fue causado por una falla por fatiga que provocó la pérdida del estabilizador horizontal derecho.
• El vuelo 191 de American Airlines de 1979 se estrelló después de una separación del motor atribuida a daños por fatiga en la estructura del pilón que sujeta el motor al ala, causado por procedimientos de mantenimiento inadecuados.
• El vuelo 7 de LOT de 1980 se estrelló debido a la fatiga en el eje de la turbina del motor, lo que provocó la desintegración del motor y la pérdida de control.
• El vuelo 123 de Japan Airlines de 1985 se estrelló después de que el avión perdiera su estabilizador vertical debido a reparaciones defectuosas en el mamparo trasero.
• El vuelo 243 de Aloha Airlines de 1988 sufrió una descompresión explosiva a 24.000 pies (7.300 m) después de una falla por fatiga.
• El vuelo 232 de United Airlines de 1989 perdió su motor de cola debido a una falla por fatiga en el cubo del disco del ventilador.
• El vuelo 1862 de El Al de 1992 perdió ambos motores en su ala derecha debido a una falla por fatiga en el montaje del pilón del motor n.° 3.
• El desastre del tren de Eschede de 1998 fue causado por una falla por fatiga de una sola rueda compuesta.
• El accidente ferroviario de Hatfield del año 2000 probablemente fue causado por fatiga por contacto rodante .
• El retiro del mercado en 2000 de 6,5 millones de neumáticos Firestone en Ford Explorers se originó por el crecimiento de grietas por fatiga que provocaron la separación de la banda de rodadura del neumático. ^[60]
• El vuelo 611 de China Airlines de 2002 se desintegró en pleno vuelo debido a una falla por fatiga.
• El vuelo 101 de Chalk's Ocean Airways de 2005 perdió su ala derecha debido a una falla por fatiga provocada por prácticas de mantenimiento inadecuadas.
• El descarrilamiento del tren de Viareggio en 2009 debido a una falla por fatiga.
• El accidente de la central eléctrica de Sayano-Shushenskaya en 2009 se debió a la fatiga del metal de los soportes de la turbina.
• El vuelo 66 de Air France de 2017 tuvo una falla en el motor durante el vuelo debido a una fractura por fatiga en frío en el cubo del ventilador.
• Se cree que la implosión del sumergible Titán 2023 se produjo debido a la delaminación por fatiga del material de fibra de carbono utilizado para el casco.

• Seguridad de la aviación  – Estado en el que los riesgos asociados con la aviación se encuentran en un nivel aceptable
• Ley de la fatiga de Basquin
• Análisis del plano crítico  – Análisis de tensiones y deformaciones multiaxiales
• Incrustación
• Ingeniería de materiales forenses  : rama de la ingeniería forensePages displaying wikidata descriptions as a fallback
• Fractografía  – Estudio de las superficies de fractura de los materiales.
• Diagrama de resistencia a la fatiga de Smith  [de] , un diagrama del ingeniero mecánico británico James Henry Smith  [de]
• Fatiga de la soldadura  : degradación de la soldadura debido a la deformación bajo carga cíclica
• Fatiga termomecánica
• Fatiga por vibración
• Revista internacional sobre la fatiga

• Personal de PDL (1995). Fatiga y propiedades tribológicas de plásticos y elastómeros . Biblioteca de diseño de plásticos. ISBN 978-1-884207-15-0.
• Leary, M.; Burvill, C. (2009). "Aplicabilidad de los datos publicados para el diseño limitado por la fatiga". Quality and Reliability Engineering International . 25 (8): 921–932. doi :10.1002/qre.1010. S2CID  206432498.
• Dieter, GE (2013). Metalurgia mecánica . McGraw-Hill . ISBN. 978-1259064791.
• Little, RE; Jebe, EH (1975). Diseño estadístico de experimentos de fatiga . John Wiley & Sons . ISBN 978-0-470-54115-9.
• Schijve, J. (2009). Fatiga de Estructuras y Materiales . Saltador . ISBN 978-1-4020-6807-2.
• Lalanne, C. (2009). Daño por fatiga . ISTE - Wiley . ISBN 978-1-84821-125-4.
• Pook, L. (2007). Fatiga de metales: qué es y por qué es importante . Springer. ISBN 978-1-4020-5596-6.
• Draper, J. (2008). Análisis moderno de fatiga de metales . EMAS. ISBN 978-0-947817-79-4.
• Suresh, S. (2004). Fatiga de materiales . Cambridge University Press . ISBN 978-0-521-57046-6.
• Kim, HS (2018). Mecánica de sólidos y fracturas, 3.ª ed. Bookboon, Londres. ISBN 978-87-403-2393-1.

Wikimedia Commons alberga una categoría multimedia sobre Fatiga material .

• Fatiga Shawn M. Kelly
• Nota de aplicación sobre la propagación de grietas por fatiga en UHMWPE Archivado el 4 de noviembre de 2013 en Wayback Machine
• Vídeo de la prueba de fatiga de la Universidad de Ciencias Aplicadas de Karlsruhe
• Método de vida de la cepa G. Glinka
• Fatiga por carga de amplitud variable A. Fatemi