Leyes de Kepler sobre el movimiento planetario

- Las órbitas son elipses, con focos F 1 y F 2 para el Planeta 1, y F 1 y F 3 para el Planeta 2. El Sol está en F 1 .
- Las áreas sombreadas A 1 y A 2 son iguales y son barridas en tiempos iguales por la órbita del Planeta 1.
- La relación entre el tiempo de órbita del Planeta 1 y el del Planeta 2 es .
| Parte de una serie sobre |
| Astrodinámica |
|---|
En astronomía , las leyes de Kepler sobre el movimiento planetario , publicadas por Johannes Kepler en 1609 (sin la tercera ley) y publicadas en su totalidad en 1619, describen las órbitas de los planetas alrededor del Sol. Estas leyes reemplazaron las órbitas circulares y los epiciclos de la teoría heliocéntrica de Nicolás Copérnico por órbitas elípticas y explicaron cómo varían las velocidades planetarias. Las tres leyes establecen que: [1] [2]
- La órbita de un planeta es una elipse con el Sol en uno de los dos focos .
- Un segmento de línea que une un planeta y el Sol barre áreas iguales durante intervalos de tiempo iguales.
- El cuadrado del período orbital de un planeta es proporcional al cubo de la longitud del semieje mayor de su órbita.
Las órbitas elípticas de los planetas fueron indicadas mediante cálculos de la órbita de Marte . A partir de esto, Kepler dedujo que otros cuerpos del Sistema Solar , incluidos los más alejados del Sol, también tienen órbitas elípticas. La segunda ley establece que cuando un planeta está más cerca del Sol, viaja más rápido. La tercera ley expresa que cuanto más lejos está un planeta del Sol, mayor es su período orbital.
Isaac Newton demostró en 1687 que relaciones como las de Kepler se aplicarían en el Sistema Solar como consecuencia de sus propias leyes de movimiento y la ley de gravitación universal .
Un enfoque histórico más preciso se encuentra en Astronomia nova y Epitome Astronomiae Copernicanae .
Comparación con Copérnico
Las leyes de Johannes Kepler mejoraron el modelo de Copérnico . Según Copérnico: [3] [4]
- La órbita planetaria es un círculo con epiciclos.
- El Sol está aproximadamente en el centro de la órbita.
- La velocidad del planeta en la órbita principal es constante.
A pesar de tener razón al afirmar que los planetas giraban alrededor del Sol, Copérnico se equivocó al definir sus órbitas. Al introducir explicaciones físicas para el movimiento en el espacio más allá de la mera geometría, Kepler definió correctamente la órbita de los planetas de la siguiente manera: [1] [2] [5] : 53–54
- La órbita planetaria no es un círculo con epiciclos, sino una elipse .
- El Sol no está en el centro sino en un punto focal de la órbita elíptica.
- Ni la velocidad lineal ni la velocidad angular del planeta en la órbita son constantes, pero la velocidad de área (estrechamente vinculada históricamente con el concepto de momento angular ) es constante.
La excentricidad de la órbita de la Tierra hace que el tiempo transcurrido entre el equinoccio de marzo y el de septiembre , de unos 186 días, sea distinto del tiempo transcurrido entre el equinoccio de septiembre y el de marzo, de unos 179 días. Un diámetro cortaría la órbita en partes iguales, pero el plano que pasa por el Sol paralelo al ecuador de la Tierra corta la órbita en dos partes con áreas en una proporción de 186 a 179, por lo que la excentricidad de la órbita de la Tierra es aproximadamente
que está cerca del valor correcto (0,016710218). La precisión de este cálculo requiere que las dos fechas elegidas estén a lo largo del eje menor de la órbita elíptica y que los puntos medios de cada mitad estén a lo largo del eje mayor. Como las dos fechas elegidas aquí son equinoccios, esto será correcto cuando el perihelio , la fecha en la que la Tierra está más cerca del Sol, caiga en un solsticio . El perihelio actual, cerca del 4 de enero, está bastante cerca del solsticio del 21 o 22 de diciembre.
Nomenclatura
La formulación actual de la obra de Kepler tardó casi dos siglos en adoptar su forma establecida. Los Elementos de la filosofía de Newton de Voltaire de 1738 fueron la primera publicación en utilizar la terminología de «leyes». [6] [7] La Enciclopedia biográfica de astrónomos, en su artículo sobre Kepler (p. 620), afirma que la terminología de las leyes científicas para estos descubrimientos era vigente al menos desde la época de Joseph de Lalande . [8] Fue la exposición de Robert Small , en Un relato de los descubrimientos astronómicos de Kepler (1814), la que conformó el conjunto de tres leyes, añadiendo la tercera. [9] Small también afirmó, en contra de la historia, que se trataba de leyes empíricas , basadas en el razonamiento inductivo . [7] [10]
Además, el uso actual de la “Segunda Ley de Kepler” es un nombre poco apropiado. Kepler tenía dos versiones, relacionadas en un sentido cualitativo: la “ley de distancia” y la “ley de área”. La “ley de área” es la que se convirtió en la Segunda Ley en el conjunto de tres; pero el propio Kepler no la privilegió de esa manera. [11]
Historia
Kepler publicó sus dos primeras leyes sobre el movimiento planetario en 1609, [12] habiéndolas encontrado al analizar las observaciones astronómicas de Tycho Brahe . [13] [14] [15] [5] : 53 La tercera ley de Kepler fue publicada en 1619. [16] [14] Kepler había creído en el modelo copernicano del Sistema Solar, que exigía órbitas circulares, pero no podía conciliar las observaciones altamente precisas de Brahe con un ajuste circular a la órbita de Marte – Marte casualmente tiene la excentricidad más alta de todos los planetas excepto Mercurio. [17] Su primera ley reflejó este descubrimiento.
En 1621, Kepler observó que su tercera ley se aplicaba a las cuatro lunas más brillantes de Júpiter . [Nb 1] Godefroy Wendelin también hizo esta observación en 1643. [Nb 2] La segunda ley, en la forma de "ley de área", fue impugnada por Nicolaus Mercator en un libro de 1664, pero en 1670 sus Philosophical Transactions estaban a su favor. [18] [19] A medida que avanzaba el siglo, se fue aceptando más ampliamente. [20] La recepción en Alemania cambió notablemente entre 1688, año en el que se publicaron los Principia de Newton y se los consideró básicamente copernicanos, y 1690, momento en el que se había publicado el trabajo de Gottfried Leibniz sobre Kepler. [21]
A Newton se le atribuye la comprensión de que la segunda ley no es específica de la ley del cuadrado inverso de la gravitación, sino que es una consecuencia de la naturaleza radial de esa ley, mientras que las otras leyes dependen de la forma del cuadrado inverso de la atracción. Carl Runge y Wilhelm Lenz identificaron mucho más tarde un principio de simetría en el espacio de fases del movimiento planetario (el grupo ortogonal O(4) en acción) que explica la primera y la tercera ley en el caso de la gravitación newtoniana, como lo hace la conservación del momento angular a través de la simetría rotacional para la segunda ley. [22]
Formulario
El modelo matemático de la cinemática de un planeta sujeto a las leyes permite una amplia gama de cálculos posteriores.
Primera ley
La primera ley de Kepler establece que:
La órbita de cada planeta es una elipse con el Sol en uno de sus dos focos .


Matemáticamente, una elipse se puede representar mediante la fórmula:
donde es el semilato recto , ε es la excentricidad de la elipse, r es la distancia del Sol al planeta y θ es el ángulo hasta la posición actual del planeta desde su aproximación más cercana, visto desde el Sol. Entonces ( r , θ ) son coordenadas polares .
Para una elipse 0 < ε < 1; en el caso límite ε = 0, la órbita es un círculo con el Sol en el centro (es decir, donde hay excentricidad cero).
En θ = 0°, perihelio , la distancia es mínima
En θ = 90° y en θ = 270° la distancia es igual a .
En θ = 180°, afelio , la distancia es máxima (por definición, el afelio es – invariablemente – el perihelio más 180°)
El semieje mayor a es la media aritmética entre r min y r max :
El semieje menor b es la media geométrica entre r min y r max :
El semi-lato recto p es la media armónica entre r min y r max :
La excentricidad ε es el coeficiente de variación entre r min y r max :
El área de la elipse es
El caso especial de un círculo es ε = 0, lo que resulta en r = p = r min = r max = a = b y A = πr 2 .
Segunda ley
La segunda ley de Kepler establece que:
Una línea que une un planeta y el Sol barre áreas iguales durante intervalos de tiempo iguales. [23]

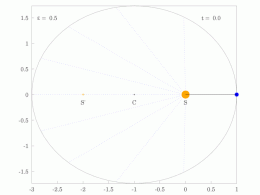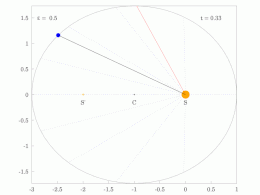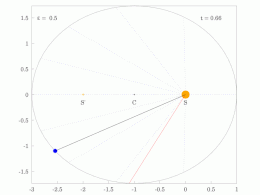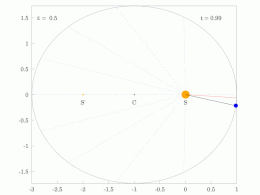
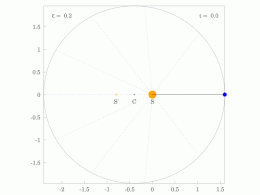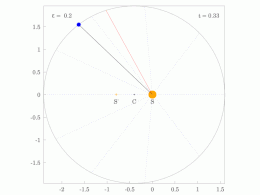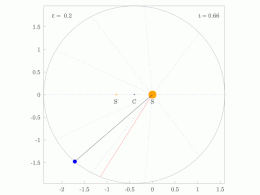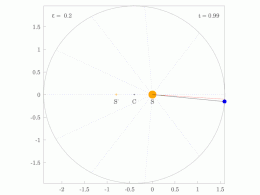
El radio orbital y la velocidad angular del planeta en la órbita elíptica variarán. Esto se muestra en la animación: el planeta se desplaza más rápido cuando está más cerca del Sol y más lento cuando está más lejos. La segunda ley de Kepler establece que el sector azul tiene un área constante.
Historia y pruebas
Kepler llegó a esta ley basándose en suposiciones que eran sólo aproximadamente verdaderas o completamente falsas y que pueden resumirse de la siguiente manera:
- Los planetas son empujados alrededor del Sol por una fuerza del Sol. Esta falsa suposición se basa en la física aristotélica incorrecta que sostiene que un objeto necesita ser empujado para mantener el movimiento.
- La fuerza propulsora del Sol es inversamente proporcional a la distancia al Sol. Kepler razonó esto, creyendo que la gravedad que se propaga en tres dimensiones sería un desperdicio, ya que los planetas habitaban en un plano. Por lo tanto, una ley inversa en lugar de la [correcta] ley del cuadrado inverso.
- Como Kepler creía que la fuerza sería proporcional a la velocidad, de las afirmaciones 1 y 2 se deducía que la velocidad sería inversa a la distancia al Sol. Este también es un principio incorrecto de la física aristotélica.
- Como la velocidad es inversa al tiempo, la distancia al Sol sería proporcional al tiempo que se tarda en recorrer una pequeña parte de la órbita. Esto es aproximadamente cierto en el caso de las órbitas elípticas.
- El área barrida es proporcional al tiempo total. Esto también es aproximadamente cierto.
- Las órbitas de un planeta son circulares (Kepler descubrió su Segunda Ley antes de su Primera Ley, que contradice ésta).
Sin embargo, el resultado de la Segunda Ley es exactamente cierto, ya que es lógicamente equivalente a la conservación del momento angular, que es cierta para cualquier cuerpo que experimente una fuerza radialmente simétrica. [24] Una prueba correcta se puede mostrar a través de esto. Dado que el producto vectorial de dos vectores da el área de un paralelogramo que posee lados de esos vectores, el área triangular dA barrida en un corto período de tiempo está dada por la mitad del producto vectorial de los vectores r y dx , para un pequeño trozo de la órbita, dx .
para un pequeño trozo de la órbita dx y el tiempo para recorrerla dt .
De este modo
Como la expresión final es proporcional al momento angular total , la ley de áreas iguales de Kepler se cumplirá para cualquier sistema que conserve el momento angular. Como cualquier fuerza radial no producirá ningún par en el movimiento del planeta, el momento angular se conservará.
En términos de parámetros elípticos
En poco tiempo el planeta barre un pequeño triángulo que tiene una línea de base , una altura y un área , por lo que la velocidad del área constante es
El área encerrada por la órbita elíptica es . Por lo tanto, el período satisface
y el movimiento medio del planeta alrededor del Sol
satisface
Y entonces,
Tercera ley
La tercera ley de Kepler establece que:
La relación entre el cuadrado del período orbital de un objeto y el cubo del semieje mayor de su órbita es la misma para todos los objetos que orbitan alrededor del mismo eje primario.
Esto captura la relación entre la distancia de los planetas al Sol y sus períodos orbitales.
Kepler enunció en 1619 [16] esta tercera ley en un laborioso intento de determinar lo que él consideraba la " música de las esferas " según leyes precisas, y expresarla en términos de notación musical. [25] Por lo tanto, se la conoció como la ley armónica . [26] La forma original de esta ley (que no se refiere al semieje mayor, sino más bien a una "distancia media") es válida sólo para planetas con pequeñas excentricidades cercanas a cero. [27]
Utilizando la ley de gravitación de Newton (publicada en 1687), esta relación se puede encontrar en el caso de una órbita circular estableciendo la fuerza centrípeta igual a la fuerza gravitacional:
Luego, al expresar la velocidad angular ω en términos del período orbital y luego reordenar, obtenemos la Tercera Ley de Kepler:
Se puede hacer una derivación más detallada con órbitas elípticas generales, en lugar de círculos, así como orbitando el centro de masas, en lugar de solo la masa grande. Esto da como resultado reemplazar un radio circular, , con el semieje mayor, , del movimiento relativo elíptico de una masa en relación con la otra, así como reemplazar la masa grande con . Sin embargo, como las masas de los planetas son mucho más pequeñas que el Sol, esta corrección a menudo se ignora. La fórmula completa correspondiente es:
donde es la masa del Sol , es la masa del planeta, es la constante gravitacional , es el periodo orbital y es el semieje mayor elíptico, y es la unidad astronómica , la distancia media de la Tierra al Sol.
Mesa
La siguiente tabla muestra los datos utilizados por Kepler para derivar empíricamente su ley:
| Planeta | Distancia media al sol (UA) | Periodo (días) | (10-6 AU 3 / día 2 ) |
|---|---|---|---|
| Mercurio | 0,389 | 87,77 | 7.64 |
| Venus | 0,724 | 224,70 | 7.52 |
| Tierra | 1 | 365,25 | 7,50 |
| Marte | 1.524 | 686,95 | 7,50 |
| Júpiter | 5.20 | 4332.62 | 7,49 |
| Saturno | 9.510 | 10759.2 | 7.43 |
Kepler se enteró de la reciente invención de los logaritmos y los gráficos logarítmicos de John Napier antes de descubrir el patrón. [28]
Al encontrar este patrón, Kepler escribió: [29]
Al principio creí que estaba soñando... Pero es absolutamente cierto y exacto que la relación que existe entre los períodos de dos planetas cualesquiera es precisamente la relación entre la potencia 3/2 de la distancia media.
— traducido de Armonías del mundo de Kepler (1619)

A modo de comparación, he aquí unas estimaciones modernas: [ cita requerida ]
| Planeta | Semieje mayor (UA) | Periodo (días) | (10-6 AU 3 / día 2 ) |
|---|---|---|---|
| Mercurio | 0,38710 | 87.9693 | 7.496 |
| Venus | 0,72333 | 224.7008 | 7.496 |
| Tierra | 1 | 365.2564 | 7.496 |
| Marte | 1.52366 | 686.9796 | 7.495 |
| Júpiter | 5.20336 | 4332.8201 | 7.504 |
| Saturno | 9.53707 | 10775.599 | 7.498 |
| Urano | 19.1913 | 30687.153 | 7.506 |
| Neptuno | 30.0690 | 60190.03 | 7.504 |
Aceleración planetaria
Isaac Newton calculó en su Philosophiæ Naturalis Principia Mathematica la aceleración de un planeta que se mueve según la primera y la segunda ley de Kepler.
- La dirección de la aceleración es hacia el Sol.
- La magnitud de la aceleración es inversamente proporcional al cuadrado de la distancia del planeta al Sol ( ley del cuadrado inverso ).
Esto implica que el Sol puede ser la causa física de la aceleración de los planetas. Sin embargo, Newton afirma en sus Principia que considera las fuerzas desde un punto de vista matemático, no físico, adoptando así una visión instrumentalista. [30] Además, no asigna una causa a la gravedad. [31]
Newton definió la fuerza que actúa sobre un planeta como el producto de su masa por la aceleración (ver las leyes del movimiento de Newton ). Por lo tanto:
- Cada planeta es atraído hacia el Sol.
- La fuerza que actúa sobre un planeta es directamente proporcional a la masa del planeta y es inversamente proporcional al cuadrado de su distancia al Sol.
- Todos los cuerpos del Sistema Solar se atraen entre sí.
- La fuerza entre dos cuerpos es directamente proporcional al producto de sus masas e inversamente proporcional al cuadrado de la distancia entre ellos.
Como los planetas tienen masas pequeñas en comparación con la del Sol, las órbitas se ajustan aproximadamente a las leyes de Kepler. El modelo de Newton mejora el modelo de Kepler y se ajusta a las observaciones reales con mayor precisión. (Véase el problema de los dos cuerpos ).
A continuación se muestra el cálculo detallado de la aceleración de un planeta en movimiento según la primera y la segunda ley de Kepler.
Vector de aceleración
Desde el punto de vista heliocéntrico considere el vector al planeta donde es la distancia al planeta y es un vector unitario que apunta hacia el planeta.
donde es el vector unitario cuya dirección es 90 grados en sentido antihorario de , y es el ángulo polar, y donde un punto en la parte superior de la variable significa diferenciación con respecto al tiempo.
Derivamos el vector de posición dos veces para obtener el vector de velocidad y el vector de aceleración:
Entonces, ¿dónde está la aceleración radial y la aceleración transversal ?
Ley del cuadrado inverso
La segunda ley de Kepler dice que es constante.
La aceleración transversal es cero:
Entonces, la aceleración de un planeta que obedece la segunda ley de Kepler está dirigida hacia el Sol.
La aceleración radial es
La primera ley de Kepler establece que la órbita se describe mediante la ecuación:
Diferenciando con respecto al tiempo o
Diferenciando una vez más
La aceleración radial satisface
Sustituyendo la ecuación de la elipse se obtiene
La relación da el resultado final simple
Esto significa que el vector de aceleración de cualquier planeta que obedezca la primera y la segunda ley de Kepler satisface la ley del cuadrado inverso , donde es una constante, y es el vector unitario que apunta desde el Sol hacia el planeta, y es la distancia entre el planeta y el Sol.
Dado que el movimiento medio , donde es el período, según la tercera ley de Kepler, tiene el mismo valor para todos los planetas, la ley del cuadrado inverso para las aceleraciones planetarias se aplica en todo el Sistema Solar.
La ley del cuadrado inverso es una ecuación diferencial . Las soluciones de esta ecuación diferencial incluyen los movimientos keplerianos, como se muestra, pero también incluyen movimientos en los que la órbita es una hipérbola , una parábola o una línea recta . (Véase órbita de Kepler ).
Ley de gravitación de Newton
Por la segunda ley de Newton , la fuerza gravitacional que actúa sobre el planeta es:
donde es la masa del planeta y tiene el mismo valor para todos los planetas del Sistema Solar. Según la tercera ley de Newton , el Sol es atraído hacia el planeta por una fuerza de la misma magnitud. Dado que la fuerza es proporcional a la masa del planeta, bajo la consideración simétrica, también debería ser proporcional a la masa del Sol, . Entonces, donde es la constante gravitacional .
La aceleración del cuerpo número i del Sistema Solar es, según las leyes de Newton: donde es la masa del cuerpo j , es la distancia entre el cuerpo i y el cuerpo j , es el vector unitario del cuerpo i hacia el cuerpo j , y la suma vectorial es sobre todos los cuerpos del Sistema Solar, además del propio i .
En el caso especial en el que sólo hay dos cuerpos en el Sistema Solar, la Tierra y el Sol, la aceleración se convierte en la aceleración del movimiento de Kepler. Por lo tanto, la Tierra se mueve alrededor del Sol según las leyes de Kepler.
Si los dos cuerpos del Sistema Solar son la Luna y la Tierra, la aceleración de la Luna se convierte en
Así que en esta aproximación, la Luna se mueve alrededor de la Tierra según las leyes de Kepler.
En el caso de los tres cuerpos las aceleraciones son
Estas aceleraciones no son las de las órbitas de Kepler, y el problema de los tres cuerpos es complicado. Pero la aproximación kepleriana es la base para los cálculos de perturbación . (Véase Teoría lunar ).
Posición en función del tiempo
Kepler utilizó sus dos primeras leyes para calcular la posición de un planeta en función del tiempo. Su método implica la solución de una ecuación trascendental llamada ecuación de Kepler .
El procedimiento para calcular las coordenadas polares heliocéntricas ( r , θ ) de un planeta en función del tiempo t desde el perihelio , consta de los cinco pasos siguientes:
- Calcular el movimiento medio n = (2 π rad)/ P , donde P es el período.
- Calcule la anomalía media M = nt , donde t es el tiempo transcurrido desde el perihelio.
- Calcule la anomalía excéntrica E resolviendo la ecuación de Kepler: donde es la excentricidad.
- Calcule la anomalía verdadera θ resolviendo la ecuación:
- Calcular la distancia heliocéntrica r : donde es el semieje mayor.
Las coordenadas polares de posición ( r , θ ) ahora se pueden escribir como un vector cartesiano y el vector de velocidad cartesiana se puede calcular como , donde es el parámetro gravitacional estándar . [32]
El caso especial importante de la órbita circular, ε = 0, da θ = E = M. Debido a que el movimiento circular uniforme se consideraba normal , una desviación de este movimiento se consideraba una anomalía.
La prueba de este procedimiento se muestra a continuación.
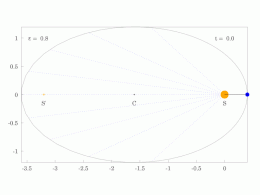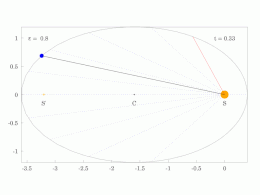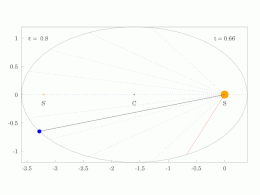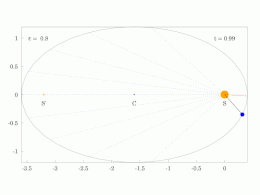
Anomalía media,METRO
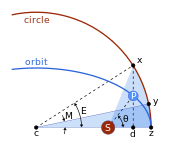
El problema kepleriano supone una órbita elíptica y los cuatro puntos:
- s el Sol (en un foco de la elipse);
- z el perihelio
- c el centro de la elipse
- p el planeta
y
- distancia entre el centro y el perihelio, el semieje mayor,
- La excentricidad,
- el semieje menor,
- la distancia entre el Sol y el planeta.
- la dirección del planeta visto desde el Sol, la verdadera anomalía .
El problema es calcular las coordenadas polares ( r , θ ) del planeta a partir del tiempo transcurrido desde el perihelio, t .
Se resuelve por pasos. Kepler consideró el círculo con el eje mayor como diámetro, y
- la proyección del planeta al círculo auxiliar
- el punto del círculo tal que las áreas del sector | zcy | y | zsx | son iguales,
- La anomalía media .
Las áreas sectoriales están relacionadas por
El área del sector circular
El área barrida desde el perihelio es, según la segunda ley de Kepler, proporcional al tiempo transcurrido desde el perihelio. Por lo tanto, la anomalía media, M , es proporcional al tiempo transcurrido desde el perihelio, t . donde n es el movimiento medio .
Anomalía excéntrica,mi
Cuando se calcula la anomalía media M , el objetivo es calcular la anomalía verdadera θ . Sin embargo, la función θ = f ( M ) no es elemental. [33] La solución de Kepler es utilizar x como se ve desde el centro, la anomalía excéntrica como variable intermedia y calcular primero E como una función de M resolviendo la ecuación de Kepler a continuación, y luego calcular la anomalía verdadera θ a partir de la anomalía excéntrica E . Aquí están los detalles.
La división por 2/2 da la ecuación de Kepler
Esta ecuación da M como función de E. Determinar E para una M dada es el problema inverso. Los algoritmos numéricos iterativos se utilizan comúnmente.
Una vez calculada la anomalía excéntrica E , el siguiente paso es calcular la anomalía verdadera θ .
Pero tenga en cuenta: las coordenadas de posición cartesianas con referencia al centro de la elipse son ( a cos E , b sen E )
Con referencia al Sol (con coordenadas ( c ,0) = ( ae ,0) ), r = ( a cos E – ae , b sen E )
La verdadera anomalía sería arctan( r y / r x ), la magnitud de r sería √ r · r .
Verdadera anomalía,θ
Nótese en la figura que para que
Dividiendo por e insertando desde la primera ley de Kepler para obtener
El resultado es una relación utilizable entre la anomalía excéntrica E y la anomalía verdadera θ .
Se obtiene una forma computacionalmente más conveniente sustituyendo en la identidad trigonométrica :
Conseguir
Multiplicando por 1 + ε obtenemos el resultado
Este es el tercer paso en la conexión entre el tiempo y la posición en la órbita.
Distancia,a
El cuarto paso es calcular la distancia heliocéntrica r desde la anomalía verdadera θ mediante la primera ley de Kepler:
Utilizando la relación anterior entre θ y E, la ecuación final para la distancia r es:
Véase también
- Movimiento circular
- Tiempo de caída libre
- Gravedad
- Órbita de Kepler
- Problema de Kepler
- Ecuación de Kepler
- Vector de Laplace-Runge-Lenz
- Momento angular relativo específico , derivación relativamente fácil de las leyes de Kepler comenzando con la conservación del momento angular
Notas explicativas
- ^ En 1621, Johannes Kepler señaló que las lunas de Júpiter obedecen (aproximadamente) su tercera ley en su Epitome Astronomiae Copernicanae [Epítome de la astronomía copernicana] (Linz ("Lentiis ad Danubium"), (Austria): Johann Planck, 1622), libro 4 , parte 2, páginas 554–555. De las págs. 554–555: "... plane ut est cum sex planet circa Solem, ... prodit Marius in suo mundo Ioviali ista 3.5.8.13 (vel 14. Galilæo) ... Periodica vero tempora prodit idem Marius .. . sunt maiora simplis, minora vero duplis." (... así como es claramente [cierto] entre los seis planetas alrededor del Sol, así también lo es entre las cuatro [lunas] de Júpiter, porque alrededor del cuerpo de Júpiter cualquier [satélite] que pueda alejarse de él, órbitas más lentas, e incluso eso [el período de la órbita] no es en la misma proporción, sino mayor [que la distancia a Júpiter]; es decir, 3/2 ( sescupla ) de la proporción de cada una de las distancias a Júpiter, lo que es claramente la misma [proporción] que se usa para los seis planetas de arriba. En su [libro] El mundo de Júpiter [ Mundus Jovialis , 1614], [Simon Mayr o] "Marius" [1573–1624] presenta estas distancias, desde Júpiter, de las cuatro [lunas] de Júpiter: 3, 5, 8, 13 (o 14 [según] Galileo) [Nota: Las distancias de las lunas de Júpiter a Júpiter se expresan como múltiplos de Diámetro de Júpiter.] ... Mayr presenta sus períodos de tiempo: 1 día 18 1/2 horas, 3 días 13 1/3 horas, 7 días 2 horas, 16 días 18 horas: para todos [estos datos] la proporción es mayor que el doble, es decir mayor que [la proporción] de las distancias 3, 5, 8, 13 o 14, aunque menor que [la proporción] de los cuadrados, que duplican las proporciones de las distancias, a saber, 9, 25, 64, 169 o 196, así como [una potencia de] 3/2 también es mayor que 1 pero menor que 2.)
- ^ Godefroy Wendelin escribió una carta a Giovanni Battista Riccioli sobre la relación entre las distancias de las lunas jovianas a Júpiter y los períodos de sus órbitas, mostrando que los períodos y distancias se ajustaban a la tercera ley de Kepler. Véase: Joanne Baptista Riccioli, Almagestum novum ... (Bolonia (Bononia), (Italia): Victor Benati, 1651), tomo 1, página 492 Scholia III. En el margen al lado del párrafo correspondiente está impreso: Vendelini ingeniosa speculatio circa motus & intervalola satellitum Jovis . (La inteligente especulación de Wendelin sobre el movimiento y las distancias de los satélites de Júpiter.) De la p. 492: "III. Non minus Kepleriana ingeniosa est Vendelini... & D. 7. 164/1000. pro penextimo, & D. 16. 756/1000. pro extimo". (No menos inteligente que la de Kepler es la investigación del perspicaz astrónomo Wendelin sobre la proporción de los períodos y las distancias de los satélites de Júpiter, que me había comunicado con gran generosidad en una carta muy larga y muy erudita. Así pues, como en [el caso de] los planetas más grandes, las distancias medias de los planetas al Sol están respectivamente en la proporción 3/2 de sus períodos; así las distancias de estos planetas menores de Júpiter a Júpiter (que son 3, 5, 8 , y 14) están respectivamente en la proporción 3/2 de [sus] períodos (que son 1,769 días para el más interior [Io], 3,554 días para el siguiente al más interior [Europa], 7,164 días para el siguiente al más exterior [ Ganimedes], y 16.756 días para el más externo [Calisto]).)
Referencias
- ^ ab "Leyes de Kepler". hyperphysics.phy-astr.gsu.edu . Consultado el 13 de diciembre de 2022 .
- ^ ab "Órbitas y leyes de Kepler". Exploración del Sistema Solar de la NASA . Consultado el 13 de diciembre de 2022 .
- ^ "Movimiento planetario: la historia de una idea que impulsó la revolución científica". earthobservatory.nasa.gov . 2009-07-07 . Consultado el 2022-12-13 .
- ^ "Nicolaus Copernicus". history.com . Consultado el 13 de diciembre de 2022 .
- ^ ab Gingerich, Owen (2011). "La gran catástrofe marciana y cómo Kepler la arregló" (PDF) . Physics Today . 64 (9): 50–54. Bibcode :2011PhT....64i..50G. doi :10.1063/PT.3.1259 . Consultado el 27 de julio de 2023 .
- ^ Voltaire, Eléments de la philosophie de Newton [Elementos de la filosofía de Newton] (Londres: 1738). Véase, por ejemplo:
- De la pág. 162: "Par une des grandes loix de Kepler, toute Planete décrit des aires égales en temp égaux: par une autre loi non-moins sûre, chaque Planete fait sa révolution autour du Soleil en telle sort, que si, sa moyenne Distance au Soleil est 10. prenez le cube de este nombre, ce qui sera 1000., & le tems de la révolution de cette Planete autour du Soleil será proporcional a la racine quarrée de ce nombre 1000." (Por una de las grandes leyes de Kepler, cada planeta describe áreas iguales en tiempos iguales; por otra ley no menos cierta, cada planeta hace su revolución alrededor del sol de tal manera que si su distancia media al sol es 10, tomemos el cubo de ese número, que será 1000, y el tiempo de la revolución de ese planeta alrededor del sol será proporcional a la raíz cuadrada de ese número 1000.)
- De la pág. 205: "Il est donc prouvé par la loi de Kepler & par celle de Neuton, que chaque Planete gravite vers le Soleil, ..." (Se demuestra así por la ley de Kepler y por la de Newton, que cada planeta gira alrededor del sol...)
- ^ ab Wilson, Curtis (mayo de 1994). "Las llamadas leyes de Kepler" (PDF) . HAD News (31): 1–2 . Consultado el 27 de diciembre de 2016 .
- ^ De la Lande, Astronomía , vol. 1 (París: Desaint & Saillant, 1764). Véase, por ejemplo:
- De la pág. 390: "... mais suivant la famause loi de Kepler, qui sera expliquée dans le Livre suivant (892), le rapport des temps périodiques est toujours plus grand que celui des distancias, une planete cinq fois plus éloignée du soleil, emploie à faire sa révolution douze fois plus de temps ou environ..." (... pero según la famosa ley de Kepler, que será explicada en el siguiente libro [es decir, capítulo] (párr. 892), la relación de los períodos son siempre mayores que el de las distancias [de modo que, por ejemplo,] un planeta cinco veces más lejos del sol, requiere alrededor de doce veces más tiempo para hacer su revolución [alrededor del sol]...)
- De la pág. 429: "Les Quarrés des Temps périodiques sont comme les Cubes des Distances. 892. La plus famause loi du mouvement des planetes découverte par Kepler, est celle du report qu'il ya entre les grandeurs de leurs orbites, & le temps qu'elles emploient à les parcourir..." (Los cuadrados de los períodos son como los cubos de las distancias. 892. La ley más famosa del movimiento de los planetas descubierta por Kepler es la de la relación entre los tamaños de sus órbitas y los tiempos que requieren los [planetas] para recorrerlos...)
- De la pág. 430: "Los aires son proporcionales al tiempo. 895. Cette loi générale du mouvement des planetes devenue si importante dans l'Astronomie, sçavior, que les aires sont proporcionalnelles au temps, est encore une des découvertes de Kepler; ..." ( Las áreas son proporcionales a los tiempos. 895. Esta ley general del movimiento de los planetas [que ha] llegado a ser tan importante en astronomía, a saber, que las áreas son proporcionales a los tiempos, es uno de los descubrimientos de Kepler...)
- De la pág. 435: "On appellé cette loi des aires proporcionalnelles aux temps, Loi de Kepler, aussi bien que celle de l'article 892, du nome de ce célebre Inventeur; ..." (Uno llamó a esta ley de áreas proporcionales a tiempos ( la ley de Kepler) así como la del párr. 892, por el nombre de ese célebre inventor...)
- ^ Robert Small, Un relato de los descubrimientos astronómicos de Kepler (Londres: J Mawman, 1804), págs. 298-299.
- ^ Robert Small, Un relato de los descubrimientos astronómicos de Kepler (Londres: J. Mawman, 1804).
- ^ Bruce Stephenson (1994). Astronomía física de Kepler. Princeton University Press. pág. 170. ISBN 978-0-691-03652-6.
- ^ Astronomia nova Aitiologitis, seu Physica Coelestis tradita Commentariis de Motibus stellae Martis ex observeibus GV Tychnonis.Praga 1609; ingles. tr. WH Donahue, Cambridge 1992.
- ↑ En su Astronomia nova , Kepler presentó solamente una prueba de que la órbita de Marte es elíptica. La evidencia de que las órbitas de los otros planetas conocidos son elípticas fue presentada recién en 1621.
Véase: Johannes Kepler, Astronomia nova ... (1609), p. 285. Después de haber rechazado las órbitas circulares y ovaladas, Kepler concluyó que la órbita de Marte debía ser elíptica. Desde la parte superior de la página 285: "Ergo ellipsis est Planetæ iter;..." (Por lo tanto, una elipse es la trayectoria del planeta [es decir, Marte];...) Más adelante en la misma página: "... ut sequenti capite patescet: ubi simul etiam demonstrabitur, nullam Planetæ relinqui figuram Orbitæ, præterquam perfecte ellipticam;..." (... como se revelará en el próximo capítulo : donde también se demostrará que se debe renunciar a cualquier figura de la órbita del planeta, excepto una elipse perfecta; ... ) Y luego: "Caput LIX. Demonstratio, quod orbita Martis, ... , fiat perfecta ellipsis: ... " (Capítulo 59. Prueba de que la órbita de Marte, ... es una elipse perfecta: ... ) La prueba geométrica de que la órbita de Marte es una elipse aparece como Proteorema XI en las páginas 289–290.
Kepler afirmó que cada planeta viaja en órbitas elípticas con el Sol en un foco en: Johannes Kepler, Epitome Astronomiae Copernicanae [Resumen de la astronomía copernicana] (Linz ("Lentiis ad Danubium"), (Austria): Johann Planck, 1622), libro 5, parte 1, III. De Figura Orbitæ (III. Sobre la figura [es decir, la forma] de las órbitas), páginas 658–665. De la pág. 658: "Ellipsin fieri orbitam planetæ..." (De una elipse se hace la órbita de un planeta...). De la pág. 659: "... Sole (Foco altero huius ellipsis)..." (... el Sol (el otro foco de esta elipse)...). - ^ ab Holton, Gerald James; Brush, Stephen G. (2001). Física, la aventura humana: de Copérnico a Einstein y más allá (3.ª edición de bolsillo). Piscataway, Nueva Jersey: Rutgers University Press. pp. 40–41. ISBN 978-0-8135-2908-0. Recuperado el 27 de diciembre de 2009 .
- ^ En su Astronomia nova ... (1609), Kepler no expuso su segunda ley en su forma moderna, sino en su Epítome de 1621. Además, en 1609, expuso su segunda ley en dos formas diferentes, que los eruditos denominan "ley de distancia" y "ley de área".
- Su "ley de la distancia" se presenta en: "Caput XXXII. Virtutem quam Planetam movet in circulum attenuari cum discessu a fonte". (Capítulo 32. La fuerza que mueve un planeta circularmente se debilita con la distancia desde la fuente.) Ver: Johannes Kepler, Astronomia nova ... (1609), págs. 165-167. En la página 167, Kepler afirma: "... quanto longior est αδ quam αε, tanto diutius moratur Planeta in certo aliquo arcui excentrici apud δ, quam in æquali arcu excentrici apud ε". (..., como αδ es más largo que αε, un planeta permanecerá mucho más tiempo en un cierto arco del excéntrico cerca de δ que en un arco igual del excéntrico cerca de ε.) Es decir, cuanto más lejos esté un planeta del El Sol (en el punto α), cuanto más lento se mueve a lo largo de su órbita, por lo que un radio desde el Sol hasta un planeta pasa por áreas iguales en tiempos iguales. Sin embargo, tal como lo presentó Kepler, su argumento es preciso solo para círculos, no para elipses. .
- Su "ley del área" se presenta en: "Caput LIX. Demonstratio, quod orbita Martis,..., fiat perfecta ellipsis:..." (Capítulo 59. Prueba de que la órbita de Marte,..., es una elipse perfecta: ... ), Proteorema XIV y XV, págs. En la parte superior pág. 294, dice: "Arcum ellipseos, cujus moras metitur area AKN, debere terminari in LK, ut sit AM". (El arco de la elipse, cuya duración está delimitada [es decir, medida] por el área AKM, debe terminar en LK, de modo que [es decir, el arco] sea AM.) En otras palabras, el tiempo que Marte requiere moverse a lo largo de un arco AM de su órbita elíptica se mide por el área del segmento AMN de la elipse (donde N es la posición del Sol), que a su vez es proporcional a la sección AKN del círculo que rodea la elipse y que es tangente a ella. Por lo tanto, el área que recorre un radio desde el Sol hasta Marte cuando Marte se mueve a lo largo de un arco de su órbita elíptica es proporcional al tiempo que Marte necesita para moverse a lo largo de ese arco. Por lo tanto, un El radio del Sol a Marte barre áreas iguales en tiempos iguales.
- ^ de Johannes Kepler, Harmonices Mundi [La armonía del mundo] (Linz, (Austria): Johann Planck, 1619), libro 5, capítulo 3, pág. 189. Desde el final de la pág. 189: "Sed res est certissima exactitudexactissimaque quod proportio qua est inter binorum quorumcunque Planetarum tempora periodia, sit præcise sesquialtera proporcionalis mediarum distantiarum,..." (Pero es absolutamente seguro y exacto que la proporción entre los tiempos periódicos de dos planetas cualesquiera es precisamente la proporción sesquialterna [es decir, la relación de 3:2] de sus distancias medias,... ")
Una traducción al inglés de Kepler Harmonices Mundi está disponible como: Johannes Kepler con EJ Aiton, AM Duncan y JV Field , trad., The Harmony of the World (Filadelfia, Pensilvania: American Philosophical Society, 1997); - ^ Asociación Nacional de Profesores de Ciencias de la Tierra (9 de octubre de 2008). «Tabla de datos de planetas y planetas enanos». Ventanas al Universo . Consultado el 2 de agosto de 2018 .
- ^ Mercator, Nicolás (1664). Nicolai Mercatoris Hypothesis astronomica nova, et consenso eius cum observeibus [ La nueva hipótesis astronómica de Nicolaus Mercator y su concordancia con las observaciones ] (en latín). Londres, Inglaterra: Leybourn.
- ^ Mercator, Nic. (25 de marzo de 1670). "Algunas consideraciones del señor Nic. Mercator, concernientes al método geométrico y directo del señor Cassini para hallar los apogeos, excentricidades y anomalías de los planetas; ..." . Philosophical Transactions of the Royal Society of London (en latín). 5 (57): 1168–1175. doi :10.1098/rstl.1670.0018. Mercator criticó el método de Cassini para hallar, a partir de tres observaciones, la línea de ápsides de una órbita. Cassini había asumido (erróneamente) que los planetas se mueven uniformemente a lo largo de sus órbitas elípticas. De la página 1174: "Sed cum id Observationibus nequaquam congruere animadverteret, mutavit sententiam, & lineam veri motus Planetæ æqualibus temporibus æquales areas Ellipticas verrere professus est: ... " (Pero cuando se dio cuenta de que no concordaba en absoluto con las observaciones, cambió su pensamiento y declaró que una línea [desde el Sol hasta un planeta, que denota] el movimiento verdadero de un planeta, barre áreas iguales de una elipse en períodos de tiempo iguales: ... [que es la forma de "área" de la segunda ley de Kepler])
- ^ Wilbur Applebaum (2000). Enciclopedia de la revolución científica: desde Copérnico hasta Newton. Routledge. p. 603. Bibcode :2000esrc.book.....A. ISBN 978-1-135-58255-5.
- ^ Roy Porter (1992). La revolución científica en el contexto nacional . Cambridge University Press. pág. 102. ISBN 978-0-521-39699-8.
- ^ Victor Guillemin; Shlomo Sternberg (2006). Variaciones sobre un tema de Kepler. American Mathematical Soc. p. 5. ISBN 978-0-8218-4184-6.
- ^ Bryant, Jeff; Pavlyk, Oleksandr. "Segunda ley de Kepler", Wolfram Demonstrations Project . Consultado el 27 de diciembre de 2009.
- ^ Holton, Gerald; Brush, Stephen (2001). Brush y Holton - Física: la aventura humana . Princeton University Press. págs. 42-43. ISBN 978-0813529080.
- ^ Burtt, Edwin . Los fundamentos metafísicos de la ciencia física moderna . pág. 52.
- ^ Gerald James Holton, Stephen G. Brush (2001). Física, la aventura humana. Rutgers University Press. pág. 45. ISBN 978-0-8135-2908-0.
- ^ Vijaya, GK (2019). "Forma original de la Tercera Ley de Kepler y su aplicación incorrecta en las Proposiciones XXXII-XXXVII de los Principia de Newton (Libro I)". Heliyon . 5 (2): e01274. Bibcode :2019Heliy...501274V. doi : 10.1016/j.heliyon.2019.e01274 . PMC 6395789 . PMID 30886926.
- ^ Caspar, Max (1993). Kepler . Nueva York: Dover. pág. 304. ISBN 9780486676050.
- ^ Caspar, Max (1993). Kepler . Nueva York: Dover. pág. 286. ISBN 9780486676050.
- ^ I. Newton, Principia , pág. 408 en la traducción de IB Cohen y A. Whitman
- ^ I. Newton, Principia , pág. 943 en la traducción de IB Cohen y A. Whitman
- ^ Schwarz, René. «Memorando n.º 1: Elementos de la órbita kepleriana → Vectores de estado cartesianos» (PDF) . Consultado el 4 de mayo de 2018 .
- ^ Müller, M (1995). "Ecuación del tiempo: problema en astronomía". Acta Physica Polonica A. Consultado el 23 de febrero de 2013 .
Bibliografía general
- La vida de Kepler se resume en las páginas 523-627 y el Libro V de su obra magna , Harmonice Mundi ( Armonías del mundo ), se reimprime en: Hawking, Stephen , ed. (2002). Sobre los hombros de gigantes: las grandes obras de física y astronomía . Filadelfia: Running Press . pp. 635-732. ISBN 978-0-7624-1348-5.
- La derivación de la tercera ley de Kepler sobre el movimiento planetario es un tema habitual en las clases de mecánica de ingeniería. Véase, por ejemplo: Meriam, JL (1971) [1966]. Dynamics (2.ª ed.). Nueva York: Wiley . pp. 161–164. ISBN. 978-0-471-59601-1..
- Murray, Carl D. ; Dermott, SF (1999). Dinámica del sistema solar. Cambridge ; Nueva York: Cambridge University Press . ISBN 978-0-521-57295-8.
- Arnolʹd, VI (1997). "Capítulo 2: Investigación de las ecuaciones de movimiento". Métodos matemáticos de mecánica clásica . Textos de posgrado en matemáticas (2.ª ed.). Nueva York: Springer Publishing . ISBN 978-0-387-96890-2.
Enlaces externos
- B. Surendranath Reddy; animación de las leyes de Kepler: subprograma Archivado el 6 de octubre de 2013 en Wayback Machine.
- Crowell, Benjamin, Light and Matter , un libro en línea que ofrece una prueba de la primera ley sin el uso del cálculo (ver sección 15.7)
- David McNamara y Gianfranco Vidali, "Segunda ley de Kepler: tutorial interactivo de Java", una aplicación Java interactiva que ayuda a comprender la segunda ley de Kepler.
- Cain, Gay (10 de mayo de 2010), Astronomy Cast , "Ep. 189: Johannes Kepler y sus leyes del movimiento planetario"
- Departamento de Física y Astronomía de la Universidad de Tennessee: Astronomía 161, "Johannes Kepler: Las leyes del movimiento planetario"
- Simulador del sistema solar (applet interactivo) Archivado el 13 de diciembre de 2018 en Wayback Machine
- "Kepler y sus leyes" en De astrónomos a naves espaciales , de David P. Stern (10 de octubre de 2016)
- "Las tres leyes del movimiento planetario de Kepler" en YouTube por Jens Puhle (27 de diciembre de 2023): un video que explica y visualiza las tres leyes del movimiento planetario de Kepler






![{\displaystyle {\begin{aligned}a&={\frac {r_{\max}+r_{\min}}{2}}\\[3pt]a&={\frac {p}{1-\varepsilon ^{2}}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/82847fc5b12e705011877c295e4ed5b439a1ed30)
![{\displaystyle {\begin{aligned}b&={\sqrt {r_{\max }r_{\min }}}\\[3pt]b&={\frac {p}{\sqrt {1-\varepsilon ^{2}}}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/03d3ca95934b7178477b3e16f3364de18f5fe6a9)

































































































![{\displaystyle {\begin{aligned}\tan ^{2}{\frac {E}{2}}&={\frac {1-\cos E}{1+\cos E}}={\frac { 1-{\frac {\varepsilon +\cos \theta }{1+\varepsilon \cos \theta }}}{1+{\frac {\varepsilon +\cos \theta }{1+\varepsilon \cos \theta }}}}\\[8pt]&={\frac {(1+\varepsilon \cos \theta )-(\varepsilon +\cos \theta )}{(1+\varepsilon \cos \theta )+(\ varepsilon +\cos \theta )}}={\frac {1-\varepsilon }{1+\varepsilon }}\cdot {\frac {1-\cos \theta }{1+\cos \theta }}={\frac {1-\varepsilon }{1+\varepsilon }}\tan ^{2}{\frac {\theta }{2}}.\end{alineado}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1bc0a064e24ecffca17176902230ccd78625ad9a)







