Homomorfismo
En álgebra , un homomorfismo es una función que preserva la estructura entre dos estructuras algebraicas del mismo tipo (como dos grupos , dos anillos o dos espacios vectoriales ). La palabra homomorfismo proviene del griego antiguo : ὁμός ( homos ), que significa "mismo", y μορφή ( morphe ), que significa "forma". Sin embargo, la palabra aparentemente se introdujo en las matemáticas debido a una (mala) traducción del alemán ähnlich, que significa "similar", a ὁμός, que significa "mismo". [1] El término "homomorfismo" apareció ya en 1892, cuando se le atribuyó al matemático alemán Felix Klein (1849-1925). [2]
Los homomorfismos de espacios vectoriales también se denominan mapas lineales y su estudio es el tema del álgebra lineal .
El concepto de homomorfismo se ha generalizado, bajo el nombre de morfismo , a muchas otras estructuras que o bien no tienen un conjunto subyacente, o bien no son algebraicas. Esta generalización es el punto de partida de la teoría de categorías .
Un homomorfismo también puede ser un isomorfismo , un endomorfismo , un automorfismo , etc. (ver más abajo). Cada uno de ellos puede definirse de manera que pueda generalizarse a cualquier clase de morfismos.
Definición
Un homomorfismo es una función entre dos estructuras algebraicas del mismo tipo (por ejemplo, dos grupos, dos cuerpos, dos espacios vectoriales), que conserva las operaciones de las estructuras. Esto significa una función entre dos conjuntos , dotados de la misma estructura de manera que, si es una operación de la estructura (supuesta aquí, para simplificar, una operación binaria ), entonces
para cada par , de elementos de . [nota 1] Se dice a menudo que conserva la operación o es compatible con la operación.
Formalmente, un mapa conserva una operación de aridad , definida tanto en como si
para todos los elementos en .
Las operaciones que deben conservarse mediante un homomorfismo incluyen las operaciones 0-arias , es decir, las constantes. En particular, cuando un elemento de identidad es requerido por el tipo de estructura, el elemento de identidad de la primera estructura debe mapearse al elemento de identidad correspondiente de la segunda estructura.
Por ejemplo:
- Un homomorfismo de semigrupos es una función entre semigrupos que preserva la operación de semigrupo.
- Un homomorfismo monoide es un mapa entre monoides que preserva la operación monoide y mapea el elemento identidad del primer monoide al del segundo monoide (el elemento identidad es una operación 0-aria ).
- Un homomorfismo de grupo es una función entre grupos que preserva la operación de grupo. Esto implica que el homomorfismo de grupo asigna el elemento identidad del primer grupo al elemento identidad del segundo grupo, y asigna el inverso de un elemento del primer grupo al inverso de la imagen de este elemento. Por lo tanto, un homomorfismo de semigrupo entre grupos es necesariamente un homomorfismo de grupo.
- Un homomorfismo de anillo es una función entre anillos que preserva la adición de anillos, la multiplicación de anillos y la identidad multiplicativa . La preservación de la identidad multiplicativa depende de la definición de anillo que se utilice. Si no se preserva la identidad multiplicativa, se tiene un homomorfismo de anillo .
- Un mapa lineal es un homomorfismo de espacios vectoriales ; es decir, un homomorfismo de grupo entre espacios vectoriales que preserva la estructura del grupo abeliano y la multiplicación escalar .
- Un homomorfismo de módulo , también llamado mapa lineal entre módulos , se define de manera similar.
- Un homomorfismo de álgebra es un mapa que preserva las operaciones del álgebra .
Una estructura algebraica puede tener más de una operación, y se requiere un homomorfismo para preservar cada operación. Por lo tanto, una función que preserva sólo algunas de las operaciones no es un homomorfismo de la estructura, sino sólo un homomorfismo de la subestructura que se obtiene al considerar sólo las operaciones preservadas. Por ejemplo, una función entre monoides que preserva la operación monoide y no el elemento identidad, no es un homomorfismo monoide, sino sólo un homomorfismo de semigrupo.
La notación de las operaciones no necesita ser la misma en el origen y el destino de un homomorfismo. Por ejemplo, los números reales forman un grupo para la suma y los números reales positivos forman un grupo para la multiplicación. La función exponencial
satisface
y es por tanto un homomorfismo entre estos dos grupos. Es incluso un isomorfismo (véase más abajo), ya que su función inversa , el logaritmo natural , satisface
y también es un homomorfismo de grupo.
Ejemplos
Los números reales son un anillo , que tiene tanto suma como multiplicación. El conjunto de todas las matrices 2×2 también es un anillo, bajo la suma y la multiplicación de matrices . Si definimos una función entre estos anillos de la siguiente manera:
donde r es un número real, entonces f es un homomorfismo de anillos, ya que f conserva ambas sumas:
y multiplicación:
Para otro ejemplo, los números complejos distintos de cero forman un grupo bajo la operación de multiplicación, al igual que los números reales distintos de cero. (El cero debe excluirse de ambos grupos ya que no tiene un inverso multiplicativo , que es necesario para los elementos de un grupo). Defina una función de los números complejos distintos de cero a los números reales distintos de cero mediante
Es decir, es el valor absoluto (o módulo) del número complejo . Entonces es un homomorfismo de grupos, ya que conserva la multiplicación:
Nótese que f no puede extenderse a un homomorfismo de anillos (de los números complejos a los números reales), ya que no preserva la adición:
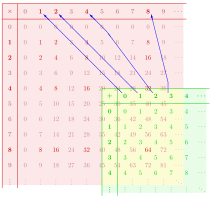
Como otro ejemplo, el diagrama muestra un homomorfismo de monoide del monoide al monoide . Debido a los diferentes nombres de las operaciones correspondientes, las propiedades de conservación de la estructura satisfechas por ascienden a y .
Un álgebra de composición sobre un cuerpo tiene una forma cuadrática , llamada norma , que es un homomorfismo de grupo del grupo multiplicativo de al grupo multiplicativo de .
Homomorfismos especiales
Varios tipos de homomorfismos tienen un nombre específico, que también se define para los morfismos generales .

Isomorfismo
Un isomorfismo entre estructuras algebraicas del mismo tipo se define comúnmente como un homomorfismo biyectivo . [3] : 134 [4] : 28
En el contexto más general de la teoría de categorías , un isomorfismo se define como un morfismo que tiene un inverso que también es un morfismo. En el caso específico de las estructuras algebraicas, las dos definiciones son equivalentes, aunque pueden diferir para las estructuras no algebraicas, que tienen un conjunto subyacente.
Más precisamente, si
es un (homo)morfismo, tiene inverso si existe un homomorfismo
de tal manera que
Si y tienen conjuntos subyacentes, y tiene una inversa , entonces es biyectiva. De hecho, es inyectiva , como implica , y es sobreyectiva , ya que, para cualquier en , se tiene , y es la imagen de un elemento de .
Por el contrario, si es un homomorfismo biyectivo entre estructuras algebraicas, sea la función tal que es el único elemento de tal que . Se tiene y sólo queda demostrar que g es un homomorfismo. Si es una operación binaria de la estructura, para cada par , de elementos de , se tiene
y por lo tanto es compatible con Como la prueba es similar para cualquier aridad , esto demuestra que es un homomorfismo.
Esta prueba no funciona para estructuras no algebraicas. Por ejemplo, para espacios topológicos , un morfismo es una función continua y la inversa de una función continua biyectiva no es necesariamente continua. Un isomorfismo de espacios topológicos, llamado homeomorfismo o función bicontinua , es entonces una función continua biyectiva, cuya inversa también es continua.
Endomorfismo
Un endomorfismo es un homomorfismo cuyo dominio es igual al codominio o, más generalmente, un morfismo cuyo origen es igual a su destino. [3] : 135
Los endomorfismos de una estructura algebraica, o de un objeto de una categoría , forman un monoide bajo composición.
Los endomorfismos de un espacio vectorial o de un módulo forman un anillo . En el caso de un espacio vectorial o de un módulo libre de dimensión finita , la elección de una base induce un isomorfismo de anillo entre el anillo de endomorfismos y el anillo de matrices cuadradas de la misma dimensión.
Automorfismo
Un automorfismo es un endomorfismo que también es un isomorfismo. [3] : 135
Los automorfismos de una estructura algebraica o de un objeto de una categoría forman un grupo bajo composición, que se denomina grupo de automorfismos de la estructura.
Muchos grupos que han recibido un nombre son grupos de automorfismos de alguna estructura algebraica. Por ejemplo, el grupo lineal general es el grupo de automorfismos de un espacio vectorial de dimensión sobre un cuerpo .
Los grupos de automorfismos de campos fueron introducidos por Évariste Galois para estudiar las raíces de los polinomios y son la base de la teoría de Galois .
Monomorfismo
Para las estructuras algebraicas, los monomorfismos se definen comúnmente como homomorfismos inyectivos . [3] : 134 [4] : 29
En el contexto más general de la teoría de categorías , un monomorfismo se define como un morfismo que se deja cancelable . [5] Esto significa que un (homo)morfismo es un monomorfismo si, para cualquier par , de morfismos de cualquier otro objeto a , entonces implica .
Estas dos definiciones de monomorfismo son equivalentes para todas las estructuras algebraicas comunes. Más precisamente, son equivalentes para los cuerpos , para los cuales todo homomorfismo es un monomorfismo, y para las variedades del álgebra universal , es decir, estructuras algebraicas para las cuales las operaciones y los axiomas (identidades) están definidos sin ninguna restricción (los cuerpos no forman una variedad, ya que el inverso multiplicativo está definido como una operación unaria o como una propiedad de la multiplicación, que están, en ambos casos, definidas solo para elementos no nulos).
En particular, las dos definiciones de un monomorfismo son equivalentes para conjuntos , magmas , semigrupos , monoides , grupos , anillos , campos , espacios vectoriales y módulos .
Un monomorfismo dividido es un homomorfismo que tiene un inverso izquierdo y, por lo tanto, es en sí mismo un inverso derecho de ese otro homomorfismo. Es decir, un homomorfismo es un monomorfismo dividido si existe un homomorfismo tal que Un monomorfismo dividido es siempre un monomorfismo, para ambos significados de monomorfismo . Para conjuntos y espacios vectoriales, cada monomorfismo es un monomorfismo dividido, pero esta propiedad no se cumple para la mayoría de las estructuras algebraicas comunes.
Prueba de la equivalencia de las dos definiciones de monomorfismos |
|---|
Un homomorfismo inyectivo se deja cancelable : Si se tiene para cada uno en , la fuente común de y . Si es inyectivo, entonces , y por lo tanto . Esta prueba no sólo funciona para estructuras algebraicas, sino también para cualquier categoría cuyos objetos sean conjuntos y las flechas sean aplicaciones entre estos conjuntos. Por ejemplo, una aplicación continua inyectiva es un monomorfismo en la categoría de espacios topológicos . Para probar que, a la inversa, un homomorfismo cancelable por la izquierda es inyectivo, es útil considerar un objeto libre en . Dada una variedad de estructuras algebraicas, un objeto libre en es un par que consiste en una estructura algebraica de esta variedad y un elemento de que satisface la siguiente propiedad universal : para cada estructura de la variedad, y cada elemento de , hay un homomorfismo único tal que . Por ejemplo, para conjuntos, el objeto libre en es simplemente ; para semigrupos , el objeto libre en es que, como, un semigrupo, es isomorfo al semigrupo aditivo de los enteros positivos; para monoides , el objeto libre en es que, como, un monoide, es isomorfo al monoide aditivo de los enteros no negativos; para grupos , el objeto libre en es el grupo cíclico infinito que, como, un grupo, es isomorfo al grupo aditivo de los enteros; para anillos , el objeto libre en es el anillo polinomial , para espacios vectoriales o módulos , el objeto libre en es el espacio vectorial o módulo libre que tiene como base. Si existe un objeto libre sobre , entonces todo homomorfismo cancelable por la izquierda es inyectivo : sea un homomorfismo cancelable por la izquierda, y y dos elementos de tal . Por definición del objeto libre , existen homomorfismos y de a tales que y . Como , se tiene por la unicidad en la definición de una propiedad universal. Como es cancelable por la izquierda, se tiene , y por tanto . Por lo tanto, es inyectivo. Existencia de un objeto libre en para una variedad (ver también Objeto libre § Existencia ): Para construir un objeto libre sobre , considere el conjunto de las fórmulas bien formadas construidas a partir de y las operaciones de la estructura. Dos de estas fórmulas se dicen equivalentes si se puede pasar de una a la otra aplicando los axiomas ( identidades de la estructura). Esto define una relación de equivalencia , si las identidades no están sujetas a condiciones, es decir, si se trabaja con una variedad. Entonces las operaciones de la variedad están bien definidas en el conjunto de clases de equivalencia de para esta relación. Es sencillo demostrar que el objeto resultante es un objeto libre en . |
Epimorfismo
En álgebra , los epimorfismos se definen a menudo como homomorfismos sobreyectivos . [3] : 134 [4] : 43 Por otro lado, en teoría de categorías , los epimorfismos se definen como morfismos cancelables por la derecha . [5] Esto significa que un (homo)morfismo es un epimorfismo si, para cualquier par , de morfismos de a cualquier otro objeto , la igualdad implica .
Un homomorfismo sobreyectivo siempre es cancelable por la derecha, pero lo inverso no siempre es cierto para las estructuras algebraicas. Sin embargo, las dos definiciones de epimorfismo son equivalentes para conjuntos , espacios vectoriales , grupos abelianos , módulos (ver más abajo una prueba) y grupos . [6] La importancia de estas estructuras en todas las matemáticas, especialmente en álgebra lineal y álgebra homológica , puede explicar la coexistencia de dos definiciones no equivalentes.
Las estructuras algebraicas para las que existen epimorfismos no sobreyectivos incluyen semigrupos y anillos . El ejemplo más básico es la inclusión de números enteros en números racionales , que es un homomorfismo de anillos y de semigrupos multiplicativos. Para ambas estructuras es un monomorfismo y un epimorfismo no sobreyectivo, pero no un isomorfismo. [5] [7]
Una amplia generalización de este ejemplo es la localización de un anillo por un conjunto multiplicativo. Toda localización es un epimorfismo de anillo, que no es, en general, sobreyectivo. Como las localizaciones son fundamentales en el álgebra conmutativa y la geometría algebraica , esto puede explicar por qué en estas áreas, la definición de epimorfismos como homomorfismos cancelables por la derecha es generalmente preferida.
Un epimorfismo dividido es un homomorfismo que tiene un inverso derecho y, por lo tanto, es en sí mismo un inverso izquierdo de ese otro homomorfismo. Es decir, un homomorfismo es un epimorfismo dividido si existe un homomorfismo tal que Un epimorfismo dividido es siempre un epimorfismo, para ambos significados de epimorfismo . Para conjuntos y espacios vectoriales, cada epimorfismo es un epimorfismo dividido, pero esta propiedad no se cumple para la mayoría de las estructuras algebraicas comunes.
En resumen, uno tiene
La última implicación es una equivalencia para conjuntos, espacios vectoriales, módulos, grupos abelianos y grupos; la primera implicación es una equivalencia para conjuntos y espacios vectoriales.
Equivalencia de las dos definiciones de epimorfismo |
|---|
Sea un homomorfismo. Queremos demostrar que si no es sobreyectivo, no es cancelable por la derecha. En el caso de conjuntos, sea un elemento de que no pertenece a , y se define de manera que sea la función identidad , y que para cada uno excepto que sea cualquier otro elemento de . Claramente no es cancelable por derecho, ya que y En el caso de espacios vectoriales, grupos abelianos y módulos, la demostración se basa en la existencia de conúcleos y en el hecho de que las aplicaciones cero son homomorfismos: sea el conúcleo de , y sea la aplicación canónica, tal que . Sea la aplicación cero. Si no es sobreyectiva, , y por lo tanto (una es una aplicación cero, mientras que la otra no lo es). Por lo tanto no es cancelable, ya que (ambas son la aplicación cero de a ). |
Núcleo
Cualquier homomorfismo define una relación de equivalencia en por si y sólo si . La relación se llama núcleo de . Es una relación de congruencia en . Al conjunto cociente se le puede dar entonces una estructura del mismo tipo que , de manera natural, definiendo las operaciones del conjunto cociente por , para cada operación de . En ese caso la imagen de en bajo el homomorfismo es necesariamente isomorfa a ; este hecho es uno de los teoremas de isomorfismo .
Cuando la estructura algebraica es un grupo para alguna operación, la clase de equivalencia del elemento identidad de esta operación basta para caracterizar la relación de equivalencia. En este caso, el cociente por la relación de equivalencia se denota por (que normalmente se lee como " mod "). También en este caso, es , en lugar de , lo que se llama núcleo de . Los núcleos de homomorfismos de un tipo dado de estructura algebraica están naturalmente dotados de alguna estructura. Este tipo de estructura de los núcleos es el mismo que la estructura considerada, en el caso de grupos abelianos , espacios vectoriales y módulos , pero es diferente y ha recibido un nombre específico en otros casos, como subgrupo normal para núcleos de homomorfismos de grupo e ideales para núcleos de homomorfismos de anillo (en el caso de anillos no conmutativos, los núcleos son los ideales bilaterales ).
Estructuras relacionales
En la teoría de modelos , la noción de estructura algebraica se generaliza a estructuras que involucran tanto operaciones como relaciones. Sea L una firma que consiste en símbolos de función y relación, y A , B dos estructuras L. Entonces, un homomorfismo de A a B es una aplicación h del dominio de A al dominio de B tal que
- h ( F A ( a 1 ,…, a n )) = F B ( h ( a 1 ),…, h ( a n )) para cada símbolo de función n -aria F en L ,
- R A ( a 1 ,…, a n ) implica R B ( h ( a 1 ),…, h ( a n )) para cada símbolo de relación n -aria R en L .
En el caso especial con sólo una relación binaria, obtenemos la noción de homomorfismo de grafos . [8]
Teoría del lenguaje formal
Los homomorfismos también se utilizan en el estudio de lenguajes formales [9] y a menudo se los denomina brevemente morfismos . [10] Dados alfabetos y , una función tal que para todos se llama homomorfismo en . [nota 2] Si es un homomorfismo en y denota la cadena vacía, entonces se llama homomorfismo libre de cuando para todos en .
Un homomorfismo que satisface para todos se llama homomorfismo -uniforme . [11] Si para todos (es decir, es 1-uniforme), entonces también se llama codificación o proyección . [ cita requerida ]
El conjunto de palabras formado a partir del alfabeto puede considerarse como el monoide libre generado por . Aquí la operación monoide es la concatenación y el elemento identidad es la palabra vacía. Desde esta perspectiva, un homomorfismo de lenguaje es precisamente un homomorfismo monoide. [nota 3]
Véase también
- Difeomorfismo
- Cifrado homomórfico
- Intercambio de secretos homomórficos : un protocolo de votación descentralizado y simplista
- Morfismo
- Cuasimorfismo
Notas
- ^ Como suele suceder, aunque no siempre, aquí se utilizó el mismo símbolo para el funcionamiento de ambos .
- ^ El ∗ denota la operación de estrella de Kleene , mientras que Σ ∗ denota el conjunto de palabras formadas a partir del alfabeto Σ, incluida la palabra vacía. La yuxtaposición de términos denota concatenación . Por ejemplo, h ( u ) h ( v ) denota la concatenación de h ( u ) con h ( v ).
- ^ Estamos seguros de que un homomorfismo de lenguaje h asigna la palabra vacía ε a la palabra vacía. Dado que h ( ε ) = h ( εε ) = h ( ε ) h ( ε ), el número w de caracteres en h ( ε ) es igual al número 2 w de caracteres en h ( ε ) h ( ε ). Por lo tanto, w = 0 y h ( ε ) tiene una longitud nula.
Citas
- ^ Fricke, Robert (1897-1912). Vorlesungen über die Theorie der automorphen Functionen. BG Teubner. OCLC 29857037.
- ^ Ver:
- Ritter, Ernst (1892). "Die eindeutigen automorphen Formen vom Geschlecht Null, eine Revision und Erweiterung der Poincaré'schen Sätze" [Las formas automórficas únicas del género cero, una revisión y ampliación del teorema de Poincaré]. Mathematische Annalen (en alemán). 41 : 1–82. doi :10.1007/BF01443449. S2CID 121524108. De la nota a pie de página de la pág. 22: "Ich will nach einem Vorschlage von Hrn. Prof. Klein statt der umständlichen und nicht immer ausreichenden Bezeichnungen: "holoedrisch, bezw. hemiedrisch usw isomorph" die Benennung "isomorph" auf den Fall des holoedrischen Isomorphismus zweier Gruppen einschränken, sonst aber von "Homomorphismus" sprechen, … " (Siguiendo una sugerencia del Prof. Klein, en lugar de las engorrosas y no siempre satisfactorias designaciones "holohédricas, o hemiédrico, etc. isomorfismo", limitaré la denominación "isomorfismo" al caso de un isomorfismo holoédrico de dos grupos; en caso contrario, sin embargo, [hablaré] de un "homomorfismo",... )
- Fricke, Robert (1892). "Ueber den arithmetischen Charakter der zu den Verzweigungen (2,3,7) und (2,4,7) gehörenden Dreiecksfunctionen" [Sobre el carácter aritmético de las funciones triangulares que pertenecen a los puntos de ramificación (2,3,7) y ( 2,4,7)]. Mathematische Annalen (en alemán). 41 (3): 443–468. doi :10.1007/BF01443421. S2CID 120022176. De la pág. 466: "Hierdurch ist, wie man sofort überblickt, eine homomorphe*) Beziehung der Gruppe Γ (63) auf die Gruppe der mod. n incongruenten Substitutionen mit racionalen ganzen Coficienten der Determinante 1 begründet". (Así, como se ve inmediatamente, una relación homomórfica del grupo Γ (63) se basa en el grupo de sustituciones incongruentes módulo n con coeficientes enteros racionales del determinante 1.) De la nota al pie de la p. 466: "*) Im Anschluss an einen von Hrn. Klein bei seinen neueren Vorlesungen eingeführten Brauch schreibe ich an Stelle der bisherigen Bezeichnung "meroedrischer Isomorphismus" die sinngemässere "Homomorphismus"." (Siguiendo un uso que ha sido introducido por el Sr. Klein durante sus conferencias más recientes, escribo en lugar de la designación anterior "isomorfismo meroédrico", el más lógico "homomorfismo".)
- ^ abcde Birkhoff, Garrett (1967) [1940], Teoría de celosías , Publicaciones del Colloquium de la American Mathematical Society, vol. 25 (3.ª ed.), Providence, RI: American Mathematical Society , ISBN 978-0-8218-1025-5, Sr. 0598630
- ^ abc Mac Lane, Saunders (1971). Categorías para el matemático en activo . Textos de posgrado en matemáticas . Vol. 5. Springer-Verlag . Ejercicio 4 en la sección I.5. ISBN 0-387-90036-5.Zbl 0232.18001 .
- ^ Linderholm, CE (1970). Un epimorfismo de grupo es sobreyectivo. The American Mathematical Monthly , 77(2), 176-177.
- ^ Dăscălescu, Sorin; Năstăsescu, Constantin; Raianu, Șerban (2001). Álgebra de Hopf: una introducción . Matemática Pura y Aplicada. vol. 235. Nueva York, Nueva York: Marcel Dekker. pag. 363.ISBN 0824704819.Zbl 0962.16026 .
- ^ Para una discusión detallada de los homomorfismos e isomorfismos relacionales, véase la Sección 17.3, en Gunther Schmidt , 2010. Matemáticas relacionales . Cambridge University Press, ISBN 978-0-521-76268-7
- ^ Seymour Ginsburg , Propiedades teóricas algebraicas y de autómatas de los lenguajes formales , Holanda Septentrional, 1975, ISBN 0-7204-2506-9 ,
- ^ T. Harju, J. Karhumғki, Morfismos en Manual de lenguajes formales , Volumen I, editado por G. Rozenberg, A. Salomaa, Springer, 1997, ISBN 3-540-61486-9 .
- ^ Krieger (2006) pág. 287
Referencias
- Krieger, Dalia (2006). "Sobre exponentes críticos en puntos fijos de morfismos que no se borran". En Ibarra, Oscar H.; Dang, Zhe (eds.). Desarrollos en teoría del lenguaje: 10.ª conferencia internacional, DLT 2006, Santa Bárbara, CA, EE. UU., 26-29 de junio de 2006: actas . Berlín: Springer. pp. 280–291. ISBN. 978-3-540-35430-7.OCLC 262693179 .
- Stanley N. Burris; HP Sankappanavar (2012). Un curso de álgebra universal (PDF) . S. Burris y HP Sankappanavar. ISBN 978-0-9880552-0-9.
- Mac Lane, Saunders (1971), Categorías para el matemático en activo , Textos de posgrado en matemáticas , vol. 5, Springer-Verlag , ISBN 0-387-90036-5, Zbl0232.18001
- Fraleigh, John B.; Katz, Victor J. (2003), Un primer curso de álgebra abstracta , Addison-Wesley, ISBN 978-1-292-02496-7






























































![{\displaystyle \mathbb {Z} [x];}](https://wikimedia.org/api/rest_v1/media/math/render/svg/568ff090582d151fc35f9fc40684023ac3a4b75d)


























![{\displaystyle [x]\ast [y]=[x\ast y]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8eae43c9e78efb8d7d20d28c28b73805f76b3f02)


















