La ciencia en la antigüedad clásica

La ciencia en la antigüedad clásica abarca las investigaciones sobre el funcionamiento del mundo o el universo dirigidas tanto a objetivos prácticos (por ejemplo, establecer un calendario fiable o determinar cómo curar una variedad de enfermedades) como a investigaciones más abstractas pertenecientes a la filosofía natural . La antigüedad clásica se define tradicionalmente como el período comprendido entre el siglo VIII a. C. (inicio de la Grecia arcaica ) y el siglo VI d. C. (después del cual hubo ciencia medieval ). Por lo general, se limita geográficamente al Occidente grecorromano , la cuenca mediterránea y el Antiguo Cercano Oriente , excluyendo así las tradiciones de la ciencia en el mundo antiguo en regiones como China y el subcontinente indio .

Las ideas sobre la naturaleza que se teorizaron durante la antigüedad clásica no se limitaban a la ciencia, sino que incluían mitos y religión. Aquellos que ahora se consideran los primeros científicos pueden haberse considerado filósofos naturales , practicantes de una profesión especializada (por ejemplo, médicos) o seguidores de una tradición religiosa (por ejemplo, curanderos del templo). Algunas de las figuras más conocidas activas en este período incluyen a Hipócrates , Aristóteles , Euclides , Arquímedes , Hiparco , Galeno y Ptolomeo . Sus contribuciones y comentarios se difundieron por todo el mundo oriental , islámico y latino y contribuyeron al nacimiento de la ciencia moderna . Sus obras abarcaron muchas categorías diferentes, incluidas las matemáticas , la cosmología , la medicina y la física .

Este tema de investigación sobre la naturaleza de las cosas comenzó a partir de preocupaciones prácticas entre los antiguos griegos . Por ejemplo, un intento de establecer un calendario se ejemplifica por primera vez en Los trabajos y los días del poeta griego Hesíodo , que vivió alrededor del 700 a. C. El calendario de Hesíodo estaba destinado a regular las actividades estacionales mediante las apariciones y desapariciones estacionales de las estrellas, así como por las fases de la Luna, que se consideraban propicias u ominosas. ^[3] Alrededor del 450 a. C. comenzamos a ver compilaciones de las apariciones y desapariciones estacionales de las estrellas en textos conocidos como parapegmata , que se usaban para regular los calendarios civiles de las ciudades-estado griegas sobre la base de observaciones astronómicas. ^[4]

La medicina es otro campo en el que se llevaron a cabo investigaciones de la naturaleza orientadas a la práctica durante este período. La medicina griega no era el territorio de una única profesión capacitada y no había un método aceptado de calificación para la licencia. Los médicos de la tradición hipocrática , los curanderos de los templos asociados con el culto de Asclepio , los recolectores de hierbas, los vendedores de drogas, las parteras y los entrenadores de gimnasia afirmaban estar calificados como curanderos en contextos específicos y competían activamente por los pacientes. ^[5] Esta rivalidad entre estas tradiciones en competencia contribuyó a un debate público activo sobre las causas y el tratamiento adecuado de las enfermedades, y sobre los enfoques metodológicos generales de sus rivales.

Un ejemplo de la búsqueda de explicaciones causales se encuentra en el texto hipocrático Sobre la enfermedad sagrada , que trata sobre la naturaleza de la epilepsia. En él, el autor ataca a sus rivales (los curanderos del templo) por su ignorancia al atribuir la epilepsia a la ira divina, y por su amor al lucro. Aunque el autor insiste en que la epilepsia tiene una causa natural, cuando se trata de explicar cuál es esa causa y cuál sería el tratamiento adecuado, la explicación es tan escasa en evidencia específica y el tratamiento tan vago como el de sus rivales. ^[6] No obstante, se siguieron recopilando observaciones de fenómenos naturales en un esfuerzo por determinar sus causas, como por ejemplo en las obras de Aristóteles y Teofrasto , que escribieron extensamente sobre animales y plantas. Teofrasto también produjo el primer intento sistemático de clasificar minerales y rocas, un resumen del cual se encuentra en la Historia natural de Plinio .

El legado de la ciencia griega en esta era incluyó avances sustanciales en el conocimiento fáctico debido a la investigación empírica (por ejemplo, en zoología, botánica, mineralogía y astronomía), una conciencia de la importancia de ciertos problemas científicos (por ejemplo, el problema del cambio y sus causas) y un reconocimiento de la importancia metodológica de establecer criterios para la verdad (por ejemplo, aplicar las matemáticas a los fenómenos naturales), a pesar de la falta de consenso universal en cualquiera de estas áreas. ^[7]

Los primeros filósofos griegos , conocidos como presocráticos , eran materialistas que proporcionaban respuestas alternativas a la misma pregunta que se encuentra en los mitos de sus vecinos: "¿Cómo llegó a existir el cosmos ordenado en el que vivimos?" ^[8] Aunque la pregunta es muy similar, sus respuestas y su actitud hacia las respuestas son marcadamente diferentes. Como informaron escritores posteriores como Aristóteles, sus explicaciones tendían a centrarse en la fuente material de las cosas.

Tales de Mileto (624-546 a. C.) consideraba que todas las cosas surgían del agua y se sustentaban en ella. Anaximandro (610-546 a. C.) sugirió que las cosas no podían provenir de una sustancia específica como el agua, sino de algo que él llamaba "lo ilimitado". No se sabe exactamente qué quería decir, pero se ha sugerido que era ilimitado en su cantidad, de modo que la creación no fracasaría; en sus cualidades, de modo que no sería dominado por su contrario; en el tiempo, ya que no tiene principio ni fin; y en el espacio, ya que abarca todas las cosas. ^[9] Anaxímenes (585-525 a. C.) volvió a una sustancia material concreta, el aire, que podía alterarse por rarefacción y condensación. Adujo observaciones comunes (el ladrón de vino) para demostrar que el aire era una sustancia y un experimento simple (respirar sobre la propia mano) para demostrar que podía alterarse por rarefacción y condensación. ^[10]

Heráclito de Éfeso (535-475 a. C. aproximadamente) sostuvo que el cambio, más que cualquier sustancia, era lo fundamental, aunque el elemento fuego parecía desempeñar un papel central en este proceso. ^[11] Finalmente, Empédocles de Acragas (490-430 a. C.) parece haber combinado las opiniones de sus predecesores, afirmando que hay cuatro elementos (Tierra, Agua, Aire y Fuego) que producen cambios al mezclarse y separarse bajo la influencia de dos "fuerzas" opuestas que él llamó Amor y Lucha. ^[12]

Todas estas teorías implican que la materia es una sustancia continua. Dos filósofos griegos, Leucipo (primera mitad del siglo V a. C.) y Demócrito, propusieron la idea de que existían dos entidades reales: los átomos , que eran pequeñas partículas indivisibles de materia, y el vacío, que era el espacio vacío en el que se encontraba la materia. ^[13] Aunque todas las explicaciones desde Tales hasta Demócrito involucran a la materia, lo que es más importante es el hecho de que estas explicaciones rivales sugieren un proceso continuo de debate en el que se propusieron y criticaron teorías alternativas.

Jenófanes de Colofón prefiguró la paleontología y la geología al pensar que periódicamente la tierra y el mar se mezclan y convierten todo en barro, citando varios fósiles de criaturas marinas que había visto. ^[14]

Las explicaciones materialistas de los orígenes del cosmos fueron intentos de responder a la pregunta de cómo llegó a existir un universo organizado; sin embargo, la idea de un conjunto aleatorio de elementos (por ejemplo, fuego o agua) que produzca un universo ordenado sin la existencia de algún principio ordenador siguió siendo problemática para algunos.

Una respuesta a este problema fue propuesta por los seguidores de Pitágoras (c. 582–507 a. C.), quienes veían el número como la entidad fundamental e inmutable que subyace a toda la estructura del universo. Aunque es difícil separar los hechos de la leyenda, parece que algunos pitagóricos creían que la materia estaba formada por disposiciones ordenadas de puntos según principios geométricos: triángulos, cuadrados, rectángulos u otras figuras. Otros pitagóricos veían el universo organizado sobre la base de números, razones y proporciones, de forma muy similar a las escalas musicales. Filolao , por ejemplo, sostenía que había diez cuerpos celestes porque la suma de 1 + 2 + 3 + 4 da el número perfecto 10. Así, los pitagóricos fueron unos de los primeros en aplicar principios matemáticos para explicar la base racional de un universo ordenado, una idea que tendría inmensas consecuencias en el desarrollo del pensamiento científico. ^[15]

Según la tradición, el médico Hipócrates de Cos (460-370 a. C.) es considerado el «padre de la medicina» porque fue el primero en hacer uso del pronóstico y la observación clínica, en categorizar las enfermedades y en formular las ideas que sustentan la teoría humoral . ^[16] Sin embargo, la mayor parte del Corpus Hipocrático —una colección de teorías, prácticas y diagnósticos médicos— se atribuyó a menudo a Hipócrates con muy poca justificación, lo que dificulta saber lo que Hipócrates realmente pensó, escribió e hizo. ^[17]

A pesar de su amplia variabilidad en términos de estilo y método, los escritos del Corpus Hipocrático tuvieron una influencia significativa en la práctica médica de la medicina islámica y occidental durante más de mil años. ^[18]

La primera institución de educación superior en la Antigua Grecia fue fundada por Platón (c. 427 – c. 347 a. C.), un ateniense que , tal vez bajo la influencia de Pitágoras , parece haber identificado el principio ordenador del universo como uno basado en el número y la geometría. Un relato posterior sostiene que Platón había inscrito en la entrada de la Academia las palabras "Que no entre nadie que ignore la geometría". ^[19] Aunque lo más probable es que la historia sea un mito, no deja de dar testimonio del interés de Platón por las matemáticas, al que se alude en varios de sus diálogos. ^[20]

La filosofía de Platón sostenía que todas las cosas materiales son reflejos imperfectos de ideas eternas e inmutables , así como todos los diagramas matemáticos son reflejos de verdades matemáticas eternas e inmutables. Puesto que Platón creía que las cosas materiales tenían un tipo inferior de realidad, consideró que no se puede lograr un conocimiento demostrativo observando el mundo material imperfecto. La verdad se encuentra a través de la argumentación racional, análoga a las demostraciones de los matemáticos. ^[21] Por ejemplo, Platón recomendó que la astronomía se estudiara en términos de modelos geométricos abstractos en lugar de observaciones empíricas, ^[22] y propuso que los líderes se formaran en matemáticas como preparación para la filosofía. ^[23]

Aristóteles (384-322 a. C.) estudió en la Academia y, sin embargo, discrepaba de Platón en varios aspectos importantes. Si bien estaba de acuerdo en que la verdad debe ser eterna e inmutable, Aristóteles sostenía que el mundo es cognoscible a través de la experiencia y que llegamos a conocer la verdad por lo que percibimos con nuestros sentidos. Para él, las cosas directamente observables son reales; las ideas (o, como él las llamaba, formas) solo existen cuando se expresan en la materia, como en los seres vivos, o en la mente de un observador o artesano. ^[24]

La teoría de la realidad de Aristóteles dio lugar a un enfoque diferente de la ciencia. A diferencia de Platón, Aristóteles hizo hincapié en la observación de las entidades materiales que encarnan las formas. También restó importancia (pero no negó) a las matemáticas en el estudio de la naturaleza. El proceso de cambio prevaleció sobre el enfoque de Platón sobre las ideas eternas e inmutables en la filosofía de Aristóteles. Por último, redujo la importancia de las formas de Platón a uno de cuatro factores causales.

Aristóteles distinguió así cuatro causas : ^[25]

• la materia de la que está hecha una cosa (la causa material ).
• la forma en que fue creado (la causa formal ; similar a las ideas de Platón).
• el agente que hizo la cosa (la causa motora o eficiente ).
• el propósito para el cual se hizo la cosa (la causa final ).

Aristóteles insistió en que el conocimiento científico (griego antiguo: ἐπιστήμη , latín: scientia ) es el conocimiento de las causas necesarias. Él y sus seguidores no aceptarían la mera descripción o predicción como ciencia. La más característica de las causas de Aristóteles es su causa final, el propósito para el cual se hace algo. Llegó a esta idea a través de sus investigaciones biológicas , como las de los animales marinos en Lesbos , en las que observó que los órganos de los animales cumplen una función particular:

La ausencia de azar y la búsqueda de fines se dan sobre todo en las obras de la naturaleza. Y el fin para el cual una cosa ha sido construida o ha llegado a existir pertenece a lo bello. ^[26]

Tras la muerte de Platón, Aristóteles abandonó la Academia y viajó mucho antes de regresar a Atenas para fundar una escuela adyacente al Liceo. Como uno de los filósofos naturales más prolíficos de la Antigüedad, Aristóteles escribió y dio conferencias sobre muchos temas de interés científico, incluyendo biología , meteorología , psicología , lógica y física . Desarrolló una teoría física integral que era una variación de la teoría clásica de los elementos ( tierra , agua , fuego , aire y éter ). En su teoría, los elementos ligeros (fuego y aire) tienen una tendencia natural a alejarse del centro del universo mientras que los elementos pesados ​​(tierra y agua) tienen una tendencia natural a moverse hacia el centro del universo, formando así una Tierra esférica. Dado que se veía que los cuerpos celestes (es decir, los planetas y las estrellas ) se movían en círculos, concluyó que debían estar hechos de un quinto elemento, al que llamó éter . ^[27]

Aristóteles utilizó ideas intuitivas para justificar su razonamiento y podía señalar la caída de una piedra, el ascenso de las llamas o el vertido de agua para ilustrar su teoría. Sus leyes del movimiento enfatizaban la observación común de que la fricción era un fenómeno omnipresente: que cualquier cuerpo en movimiento, a menos que se actúe sobre él, llegaría al reposo . También propuso que los objetos más pesados ​​caen más rápido y que los huecos son imposibles.

El sucesor de Aristóteles en el Liceo fue Teofrasto , que escribió valiosos libros que describen la vida vegetal y animal. Sus obras se consideran las primeras en poner la botánica y la zoología sobre una base sistemática. El trabajo de Teofrasto sobre mineralogía proporcionó descripciones de minerales y menas conocidos en el mundo en ese momento, haciendo algunas observaciones agudas de sus propiedades. Por ejemplo, hizo la primera referencia conocida al fenómeno de que el mineral turmalina atrae paja y trozos de madera cuando se calienta, que ahora se sabe que es causado por piroelectricidad . ^[28] Plinio el Viejo hace claras referencias a su uso de la obra en su Historia natural , al tiempo que actualizaba y ponía a disposición mucha información nueva sobre los minerales . De estos dos primeros textos surgió la ciencia de la mineralogía y, en última instancia, la geología . Ambos autores describen las fuentes de los minerales que discuten en las diversas minas explotadas en su tiempo, por lo que sus obras deben considerarse no solo como textos científicos tempranos, sino también importantes para la historia de la ingeniería y la historia de la tecnología . ^[7]

Otros peripatéticos notables incluyen a Estratón , que fue tutor en la corte de los Ptolomeos y que dedicó tiempo a la investigación física, Eudemo , que editó las obras de Aristóteles y escribió los primeros libros sobre la historia de la ciencia , y Demetrio de Falero , que gobernó Atenas durante un tiempo y más tarde puede haber ayudado a establecer la Biblioteca de Alejandría .

Las campañas militares de Alejandro Magno difundieron el pensamiento griego en Egipto , Asia Menor , Persia y hasta el río Indo . La migración resultante de muchas poblaciones de habla griega a través de estos territorios proporcionó el impulso para la fundación de varias sedes de aprendizaje, como las de Alejandría , Antioquía y Pérgamo .

La ciencia helenística difería de la ciencia griega en al menos dos aspectos: primero, se benefició de la fertilización cruzada de las ideas griegas con las que se habían desarrollado en otras civilizaciones no helénicas; segundo, en cierta medida, fue apoyada por mecenas reales en los reinos fundados por los sucesores de Alejandro . La ciudad de Alejandría , en particular, se convirtió en un importante centro de investigación científica en el siglo III a. C. Dos instituciones establecidas allí durante los reinados de Ptolomeo I Sóter (367-282 a. C.) y Ptolomeo II Filadelfo (309-246 a. C.) fueron la Biblioteca y el Museo . A diferencia de la Academia de Platón y el Liceo de Aristóteles , estas instituciones fueron apoyadas oficialmente por los Ptolomeos, aunque el alcance del mecenazgo podía ser precario dependiendo de las políticas del gobernante de turno. ^[29]

Los eruditos helenísticos emplearon a menudo los principios desarrollados en el pensamiento griego anterior en sus investigaciones científicas, como la aplicación de las matemáticas a los fenómenos o la recopilación deliberada de datos empíricos. ^[30] Sin embargo, la evaluación de la ciencia helenística varía ampliamente. En un extremo está la opinión del erudito clásico inglés Cornford, quien creía que "todo el trabajo más importante y original se realizó en los tres siglos que van desde el 600 al 300 a. C." ^[31] En el otro extremo está la opinión del físico y matemático italiano Lucio Russo , quien afirma que el método científico nació en realidad en el siglo III a. C., solo para ser olvidado en gran medida durante el período romano y no revivido nuevamente hasta el Renacimiento. ^[32]

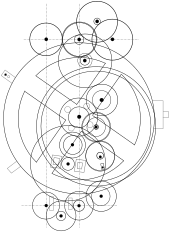
Un buen ejemplo del nivel de logro en el conocimiento astronómico y la ingeniería durante la era helenística se puede ver en el mecanismo de Antikythera (150-100 a. C.). Es una computadora mecánica de 37 engranajes que calculaba los movimientos del Sol, la Luna y posiblemente los otros cinco planetas conocidos por los antiguos. El mecanismo de Antikythera incluía eclipses lunares y solares predichos sobre la base de períodos astronómicos que se cree que se aprendieron de los babilonios . ^[33] El dispositivo puede haber sido parte de una antigua tradición griega de tecnología mecánica compleja que luego se transmitió, al menos en parte, a los mundos bizantino e islámico, donde se construyeron dispositivos mecánicos que eran complejos, aunque más simples que el mecanismo de Antikythera, durante la Edad Media . Se han encontrado fragmentos de un calendario de engranajes unido a un reloj de sol, del Imperio bizantino del siglo V o VI ; el calendario puede haber sido utilizado para ayudar a decir el tiempo. El científico al-Biruni describió alrededor del año 1000 un calendario con engranajes similar al dispositivo bizantino, y un astrolabio del siglo XIII que aún se conserva también contiene un mecanismo de relojería similar. ^{[34] [35]}

En Alejandría se formó una importante escuela de medicina desde finales del siglo IV hasta el siglo II a. C. ^[36] A partir de Ptolomeo I Sóter , a los funcionarios médicos se les permitió abrir y examinar cadáveres con el fin de aprender cómo funcionaban los cuerpos humanos. El primer uso de cuerpos humanos para la investigación anatómica ocurrió en el trabajo de Herófilo (335-280 a. C.) y Erasístrato (c. 304 - c. 250 a. C.), quienes obtuvieron permiso para realizar disecciones en vivo, o vivisecciones , en criminales condenados en Alejandría bajo los auspicios de la dinastía ptolemaica . ^[37]

Herófilo desarrolló un cuerpo de conocimiento anatómico mucho más informado por la estructura real del cuerpo humano que los trabajos anteriores. También revirtió la noción de larga data hecha por Aristóteles de que el corazón era la "sede de la inteligencia", argumentando en su lugar a favor del cerebro . ^[38] Herófilo también escribió sobre la distinción entre venas y arterias , e hizo muchas otras observaciones precisas sobre la estructura del cuerpo humano, especialmente el sistema nervioso . ^[39] Erasístrato diferenció entre la función de los nervios sensoriales y motores , y los relacionó con el cerebro. Se le atribuye una de las primeras descripciones en profundidad del cerebro y el cerebelo . ^[40] Por sus contribuciones, a Herófilo a menudo se le llama el "padre de la anatomía ", mientras que Erasístrato es considerado por algunos como el "fundador de la fisiología ". ^[41]

Las matemáticas griegas en el período helenístico alcanzaron un nivel de sofisticación que no se igualó durante varios siglos después, ya que gran parte del trabajo representado por los eruditos activos en este momento era de un nivel muy avanzado. ^[42] También hay evidencia de combinar el conocimiento matemático con altos niveles de experiencia técnica, como se encuentra, por ejemplo, en la construcción de proyectos de construcción masivos (por ejemplo, Syracusia ), o en la medición de Eratóstenes (276-195 a. C.) de la distancia entre el Sol y la Tierra y el tamaño de la Tierra . ^[43]

Aunque eran pocos en número, los matemáticos helenísticos se comunicaban activamente entre sí; la publicación consistía en pasar y copiar el trabajo de alguien entre colegas. ^[44] Entre los más reconocibles está el trabajo de Euclides (325-265 a. C.), quien presumiblemente fue autor de una serie de libros conocidos como los Elementos , un canon de geometría y teoría elemental de números durante muchos siglos. ^[45] Los Elementos de Euclides sirvieron como el principal libro de texto para la enseñanza de las matemáticas teóricas hasta principios del siglo XX.

Arquímedes (287–212 a. C.), un griego siciliano , escribió alrededor de una docena de tratados donde comunicó muchos resultados notables, como la suma de una serie geométrica infinita en la Cuadratura de la Parábola , una aproximación al valor π en la Medición del Círculo , y una nomenclatura para expresar números muy grandes en el Calculador de Arena . ^[46]

El producto más característico de las matemáticas griegas es la teoría de las secciones cónicas , desarrollada en gran medida en el período helenístico, principalmente por Apolonio (262-190 a. C.). Los métodos utilizados no hacían uso explícito del álgebra ni de la trigonometría, que apareció en la época de Hiparco (190-120 a. C.).

Los avances en la astronomía matemática también tuvieron lugar durante la era helenística. Aristarco de Samos (310–230 a. C.) fue un astrónomo y matemático griego antiguo que presentó el primer modelo heliocéntrico conocido que colocaba al Sol en el centro del universo conocido, con la Tierra girando alrededor del Sol una vez al año y rotando sobre su eje una vez al día. Aristarco también estimó los tamaños del Sol y la Luna en comparación con el tamaño de la Tierra, y las distancias al Sol y la Luna. Su modelo heliocéntrico no encontró muchos adeptos en la antigüedad, pero sí influyó en algunos astrónomos modernos tempranos, como Nicolás Copérnico , que conocía la teoría heliocéntrica de Aristarco. ^[47]

En el siglo II a. C., Hiparco descubrió la precesión , calculó el tamaño y la distancia de la Luna e inventó los primeros dispositivos astronómicos conocidos, como el astrolabio . ^[48] Hiparco también creó un catálogo completo de 1020 estrellas, y la mayoría de las constelaciones del hemisferio norte derivan de la astronomía griega . ^{[49] [50]} Recientemente se ha afirmado que un globo celeste basado en el catálogo de estrellas de Hiparco se encuentra sobre los anchos hombros de una gran estatua romana del siglo II conocida como Atlas Farnesio . ^[51]

La ciencia durante el Imperio Romano se ocupó de sistematizar el conocimiento adquirido en la época helenística anterior y el conocimiento de las vastas áreas que los romanos habían conquistado. Fue en gran parte el trabajo de los autores activos en este período el que se transmitiría ininterrumpidamente a las civilizaciones posteriores. ^{[ cita requerida ]}

Aunque la ciencia continuó bajo el dominio romano, los textos latinos eran principalmente compilaciones que se basaban en trabajos griegos anteriores. La investigación y la enseñanza científica avanzadas continuaron llevándose a cabo en griego. Las obras griegas y helenísticas que sobrevivieron se preservaron y desarrollaron más tarde en el Imperio bizantino y luego en el mundo islámico . Los intentos de los últimos romanos de traducir escritos griegos al latín tuvieron un éxito limitado (por ejemplo, Boecio ), y el conocimiento directo de la mayoría de los textos griegos antiguos solo llegó a Europa occidental a partir del siglo XII. ^[52]

Plinio el Viejo publicó la Naturalis Historia en el año 77 d. C., una de las recopilaciones más extensas sobre el mundo natural que sobrevivió hasta la Edad Media . Plinio no se limitó a enumerar materiales y objetos, sino que también registró explicaciones de fenómenos. Por lo tanto, es el primero en describir correctamente el origen del ámbar como la resina fosilizada de los pinos. Hace la inferencia a partir de la observación de insectos atrapados dentro de algunas muestras de ámbar.

La obra de Plinio se divide claramente en el mundo orgánico de las plantas y los animales, y el reino de la materia inorgánica, aunque hay frecuentes digresiones en cada sección. Está especialmente interesado no solo en describir la existencia de plantas, animales e insectos, sino también su explotación (o abuso) por parte del hombre. La descripción de metales y minerales es particularmente detallada y valiosa por ser la recopilación más extensa aún disponible del mundo antiguo. Aunque gran parte de la obra se recopiló mediante un uso juicioso de fuentes escritas, Plinio da un relato de testigo ocular de la minería de oro en España , donde estaba destinado como oficial. Plinio es especialmente significativo porque proporciona detalles bibliográficos completos de los autores anteriores y sus obras que utiliza y consulta. Debido a que su enciclopedia sobrevivió a la Edad Oscura , conocemos estas obras perdidas , incluso si los textos mismos han desaparecido. El libro fue uno de los primeros en imprimirse en 1489 y se convirtió en una obra de referencia estándar para los eruditos del Renacimiento , así como en una inspiración para el desarrollo de un enfoque científico y racional del mundo. ^{[ cita requerida ]}

Herón de Alejandría fue un matemático e ingeniero grecoegipcio que a menudo se considera el mayor experimentador de la antigüedad. ^[53] Entre sus inventos más famosos se encontraba un molino de viento, que constituye el primer ejemplo de aprovechamiento del viento en tierra, y una descripción bien reconocida de un dispositivo impulsado por vapor llamado eolípila, que fue la primera máquina de vapor registrada.

El mayor médico y filósofo de esta era fue Galeno , activo en el siglo II d. C. Sobreviven alrededor de 100 de sus obras (la mayor cantidad para cualquier autor griego antiguo) y llenan 22 volúmenes de texto moderno. ^[54] Galeno nació en la antigua ciudad griega de Pérgamo (ahora en Turquía ), hijo de un exitoso arquitecto que le dio una educación liberal. Galeno fue instruido en todas las principales escuelas filosóficas (platonismo, aristotelismo, estoicismo y epicureísmo) hasta que su padre, movido por un sueño de Asclepio , decidió que debía estudiar medicina. Después de la muerte de su padre, Galeno viajó mucho en busca de los mejores médicos en Esmirna , Corinto y finalmente Alejandría . ^[55]

Galeno recopiló gran parte del conocimiento obtenido por sus predecesores y amplió la investigación sobre la función de los órganos realizando disecciones y vivisecciones en monos de Berbería , bueyes , cerdos y otros animales. ^[56] En 158 d. C., Galeno sirvió como médico jefe de los gladiadores en su Pérgamo natal y pudo estudiar todo tipo de heridas sin realizar ninguna disección humana real. Sin embargo, fue a través de sus experimentos que Galeno pudo revocar muchas creencias sostenidas durante mucho tiempo, como la teoría de que las arterias contenían aire que lo transportaba a todas las partes del cuerpo desde el corazón y los pulmones. ^[57] Esta creencia se basó originalmente en las arterias de animales muertos, que parecían estar vacías. Galeno pudo demostrar que las arterias vivas contienen sangre, pero su error, que se convirtió en la ortodoxia médica establecida durante siglos, fue asumir que la sangre va y viene del corazón en un movimiento de flujo y reflujo. ^[58]

La anatomía fue una parte importante de la educación médica de Galeno y fue una fuente importante de interés a lo largo de su vida. Escribió dos grandes obras anatómicas, Sobre el procedimiento anatómico y Sobre los usos de las partes del cuerpo humano . La información contenida en estos tratados se convirtió en la base de autoridad para todos los escritores médicos y médicos durante los siguientes 1300 años hasta que fueron cuestionados por Vesalio y Harvey en el siglo XVI. ^{[59] [60]}

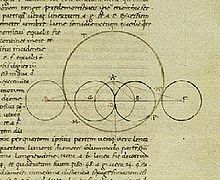
Claudio Ptolomeo (c. 100-170 d. C.), que vivió en Alejandría o sus alrededores , llevó a cabo un programa científico centrado en la redacción de una docena de libros sobre astronomía , astrología , cartografía , armónica y óptica . A pesar de su estilo severo y su alto nivel técnico, una gran parte de ellos han sobrevivido, en algunos casos los únicos restos de su tipo de escritura de la antigüedad. Dos temas principales que recorren las obras de Ptolomeo son el modelado matemático de los fenómenos físicos y los métodos de representación visual de la realidad física. ^[61]

El programa de investigación de Ptolomeo implicó una combinación de análisis teórico con consideraciones empíricas, como se vio, por ejemplo, en su estudio sistematizado de la astronomía. La Sintaxis matemática de Ptolomeo ( en griego antiguo : Μαθηματικὴ Σύνταξις ), más conocida como Almagesto , buscaba mejorar el trabajo de sus predecesores al construir la astronomía no solo sobre una base matemática segura, sino también al demostrar la relación entre las observaciones astronómicas y la teoría astronómica resultante. ^[62] En sus Hipótesis planetarias , Ptolomeo describe en detalle las representaciones físicas de sus modelos matemáticos que se encuentran en el Almagesto , presumiblemente con fines didácticos. ^[63] Del mismo modo, la Geografía se ocupaba del dibujo de mapas precisos utilizando información astronómica, al menos en principio. ^[64] Además de la astronomía, tanto la Armónica como la Óptica contienen (además de análisis matemáticos del sonido y la vista, respectivamente) instrucciones sobre cómo construir y utilizar instrumentos experimentales para corroborar la teoría. ^{[65] [66]} En retrospectiva, es evidente que Ptolomeo ajustó algunas mediciones reportadas para que se ajustaran a su suposición (incorrecta) de que el ángulo de refracción es proporcional al ángulo de incidencia . ^{[67] [68]}

La minuciosidad de Ptolomeo y su preocupación por la facilidad de presentación de los datos (por ejemplo, en su uso generalizado de tablas ^[69] ) prácticamente garantizaron que los trabajos anteriores sobre estos temas se descuidaran o se consideraran obsoletos, hasta el punto de que casi nada queda de las obras a las que Ptolomeo a menudo se refiere. ^[70] Su trabajo astronómico en particular definió el método y el tema de la investigación futura durante siglos, y el sistema ptolemaico se convirtió en el modelo dominante para los movimientos de los cielos hasta el siglo XVII . ^[71]

• La ciencia forense en la antigüedad
• Protociencia
• Tecnología romana
• Teorías científicas obsoletas