Hélice

Una hélice ( / ˈh iː l ɪ k s / ; pl.  hélices ) es una forma similar a un resorte helicoidal cilíndrico o la rosca de un tornillo de máquina . Es un tipo de curva espacial suave con líneas tangentes en un ángulo constante con respecto a un eje fijo. Las hélices son importantes en biología , ya que la molécula de ADN está formada como dos hélices entrelazadas , y muchas proteínas tienen subestructuras helicoidales, conocidas como hélices alfa . La palabra hélice proviene de la palabra griega ἕλιξ , "retorcido, curvado". ^[1] Una hélice "rellena" -por ejemplo, una rampa "espiral" (helicoidal)- es una superficie llamada helicoide . ^[2]

El paso de una hélice es la altura de una vuelta completa de la hélice , medida paralelamente al eje de la hélice.

Una doble hélice consta de dos hélices (normalmente congruentes ) con el mismo eje, que se diferencian por una traslación a lo largo del eje. ^[3]

Una hélice circular (es decir, una con radio constante) tiene una curvatura de banda constante y una torsión constante . La pendiente de una hélice circular se define comúnmente como la relación entre la circunferencia del cilindro circular alrededor del cual gira en espiral y su paso (la altura de una vuelta completa de la hélice).

Una hélice cónica , también conocida como espiral cónica , puede definirse como una espiral sobre una superficie cónica, donde la distancia al vértice es una función exponencial del ángulo que indica la dirección desde el eje.

Una curva se denomina hélice general o hélice cilíndrica ^[4] si su tangente forma un ángulo constante con una línea fija en el espacio. Una curva es una hélice general si y solo si la razón entre la curvatura y la torsión es constante. ^[5]

Una curva se denomina hélice oblicua si su normal principal forma un ángulo constante con una línea fija en el espacio. ^[6] Se puede construir aplicando una transformación al marco móvil de una hélice general. ^[7]

Para encontrar curvas espaciales más generales de tipo hélice, véase espiral espacial ; por ejemplo, espiral esférica .

Las hélices pueden ser dextrógiras o levógiras. Si la línea de visión va a lo largo del eje de la hélice, si un movimiento de giro en el sentido de las agujas del reloj aleja la hélice del observador, se denomina hélice dextrógirada; si se dirige hacia el observador, se denomina hélice levógirada. La quiralidad es una propiedad de la hélice, no de la perspectiva: una hélice dextrógirada no se puede girar para que parezca levógirada a menos que se la mire en un espejo, y viceversa.

En matemáticas , una hélice es una curva en un espacio tridimensional . La siguiente parametrización en coordenadas cartesianas define una hélice particular; ^[8] quizás la ecuación más simple para una sea

${\displaystyle {\begin{aligned}x(t)&=\cos(t),\\y(t)&=\sin(t),\\z(t)&=t.\end{aligned}}}$

A medida que aumenta el parámetro t , el punto traza una hélice dextrógira de paso 2 π (o pendiente 1) y radio 1 alrededor del eje z , en un sistema de coordenadas dextrógiro.${\displaystyle (x(t),y(t),z(t))}$

En coordenadas cilíndricas ( r , θ , h ) , la misma hélice está parametrizada por:

${\displaystyle {\begin{aligned}r(t)&=1,\\\theta (t)&=t,\\h(t)&=t.\end{aligned}}}$

Una hélice circular de radio a y pendiente ⁠a/b⁠ (o tono 2 πb ) se describe mediante la siguiente parametrización:

${\displaystyle {\begin{aligned}x(t)&=a\cos(t),\\y(t)&=a\sin(t),\\z(t)&=bt.\end{aligned}}}$

Otra forma de construir matemáticamente una hélice es trazar la función compleja e ^xi como una función del número real x (ver la fórmula de Euler ). El valor de x y las partes real e imaginaria del valor de la función le dan a este gráfico tres dimensiones reales.

A excepción de las rotaciones , las traslaciones y los cambios de escala, todas las hélices dextrógiras son equivalentes a la hélice definida anteriormente. La hélice levógiras equivalente se puede construir de varias maneras, siendo la más simple negar cualquiera de los componentes x , y o z .

Una hélice circular de radio a y pendiente ⁠a/b⁠ (o paso 2 πb ) expresado en coordenadas cartesianas como la ecuación paramétrica

${\displaystyle t\mapsto (a\cos t,a\sin t,bt),t\in [0,T]}$

tiene una longitud de arco de

${\displaystyle A=T\cdot {\sqrt {a^{2}+b^{2}}},}$

una curvatura de

${\displaystyle {\frac {|a|}{a^{2}+b^{2}}},}$

y una torsión de

${\displaystyle {\frac {b}{a^{2}+b^{2}}}.}$

Una hélice tiene una curvatura y torsión constantes y distintas de cero.

Una hélice es la función con valor vectorial

$${\displaystyle {\begin{aligned}\mathbf {r} &=a\cos t\mathbf {i} +a\sin t\mathbf {j} +bt\mathbf {k} \\[6px]\mathbf {v} &=-a\sin t\mathbf {i} +a\cos t\mathbf {j} +b\mathbf {k} \\[6px]\mathbf {a} &=-a\cos t\mathbf {i} -a\sin t\mathbf {j} +0\mathbf {k} \\[6px]|\mathbf {v} |&={\sqrt {(-a\sin t)^{2}+(a\cos t)^{2}+b^{2}}}={\sqrt {a^{2}+b^{2}}}\\[6px]|\mathbf {a} |&={\sqrt {(-a\sin t)^{2}+(a\cos t)^{2}}}=a\\[6px]s(t)&=\int _{0}^{t}{\sqrt {a^{2}+b^{2}}}d\tau ={\sqrt {a^{2}+b^{2}}}t\end{aligned}}}$$

Por lo tanto, una hélice se puede repararmetrizar en función de s , que debe ser la velocidad unitaria:

$${\displaystyle \mathbf {r} (s)=a\cos {\frac {s}{\sqrt {a^{2}+b^{2}}}}\mathbf {i} +a\sin {\frac {s}{\sqrt {a^{2}+b^{2}}}}\mathbf {j} +{\frac {bs}{\sqrt {a^{2}+b^{2}}}}\mathbf {k} }$$

El vector tangente unitario es

$${\displaystyle {\frac {d\mathbf {r} }{ds}}=\mathbf {T} ={\frac {-a}{\sqrt {a^{2}+b^{2}}}}\sin {\frac {s}{\sqrt {a^{2}+b^{2}}}}\mathbf {i} +{\frac {a}{\sqrt {a^{2}+b^{2}}}}\cos {\frac {s}{\sqrt {a^{2}+b^{2}}}}\mathbf {j} +{\frac {b}{\sqrt {a^{2}+b^{2}}}}\mathbf {k} }$$

El vector normal es

$${\displaystyle {\frac {d\mathbf {T} }{ds}}=\kappa \mathbf {N} ={\frac {-a}{a^{2}+b^{2}}}\cos {\frac {s}{\sqrt {a^{2}+b^{2}}}}\mathbf {i} +{\frac {-a}{a^{2}+b^{2}}}\sin {\frac {s}{\sqrt {a^{2}+b^{2}}}}\mathbf {j} +0\mathbf {k} }$$

Su curvatura es

$${\displaystyle \kappa =\left|{\frac {d\mathbf {T} }{ds}}\right|={\frac {|a|}{a^{2}+b^{2}}}}$$.

El vector normal unitario es

$${\displaystyle \mathbf {N} =-\cos {\frac {s}{\sqrt {a^{2}+b^{2}}}}\mathbf {i} -\sin {\frac {s}{\sqrt {a^{2}+b^{2}}}}\mathbf {j} +0\mathbf {k} }$$

El vector binormal es

$${\displaystyle {\begin{aligned}\mathbf {B} =\mathbf {T} \times \mathbf {N} &={\frac {1}{\sqrt {a^{2}+b^{2}}}}\left(b\sin {\frac {s}{\sqrt {a^{2}+b^{2}}}}\mathbf {i} -b\cos {\frac {s}{\sqrt {a^{2}+b^{2}}}}\mathbf {j} +a\mathbf {k} \right)\\[12px]{\frac {d\mathbf {B} }{ds}}&={\frac {1}{a^{2}+b^{2}}}\left(b\cos {\frac {s}{\sqrt {a^{2}+b^{2}}}}\mathbf {i} +b\sin {\frac {s}{\sqrt {a^{2}+b^{2}}}}\mathbf {j} +0\mathbf {k} \right)\end{aligned}}}$$

Su torsión es$${\displaystyle \tau =\left|{\frac {d\mathbf {B} }{ds}}\right|={\frac {b}{a^{2}+b^{2}}}.}$$

Un ejemplo de doble hélice en biología molecular es la doble hélice del ácido nucleico .

Un ejemplo de hélice cónica es la montaña rusa Corkscrew del parque de atracciones Cedar Point .

Algunas curvas que se encuentran en la naturaleza consisten en múltiples hélices de diferente orientación unidas entre sí por transiciones conocidas como perversiones de zarcillo .

La mayoría de las roscas de los tornillos de hardware son hélices dextrógiras. La hélice alfa en biología, así como las formas A y B del ADN, también son hélices dextrógiras. La forma Z del ADN es levógiras.

En música , el espacio tonal a menudo se modela con hélices o hélices dobles, que generalmente se extienden fuera de un círculo como el círculo de quintas , para representar la equivalencia de octavas .

En aviación, el paso geométrico es la distancia que avanzaría un elemento de la hélice de un avión en una revolución si se moviera a lo largo de una hélice que tiene un ángulo igual al que existe entre la cuerda del elemento y un plano perpendicular al eje de la hélice; véase también: ángulo de paso (aviación) .

• 
  Estructura cristalina de una hélice molecular plegada reportada por Lehn et al. ^[9]
• 
  Una hélice zurda natural, formada por una planta trepadora .
• 
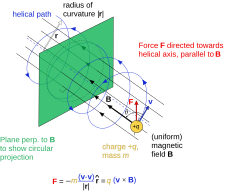
  Una partícula cargada en un campo magnético uniforme que sigue una trayectoria helicoidal.
• 
  Un resorte helicoidal

Busque hélice en Wikcionario, el diccionario libre.