Análisis complejo
Este artículo incluye una lista de referencias generales , pero carece de suficientes citas en línea correspondientes . ( Marzo de 2021 ) |
| Mathematical analysis → Complex analysis |
| Complex analysis |
|---|
 |
| Complex numbers |
| Complex functions |
|
| Basic theory |
| Geometric function theory |
| People |
El análisis complejo , tradicionalmente conocido como teoría de funciones de una variable compleja , es la rama del análisis matemático que investiga las funciones de números complejos . Es útil en muchas ramas de las matemáticas, incluidas la geometría algebraica , la teoría de números , la combinatoria analítica y las matemáticas aplicadas , así como en la física , incluidas las ramas de la hidrodinámica , la termodinámica , la mecánica cuántica y la teoría de twistores . Por extensión, el uso del análisis complejo también tiene aplicaciones en campos de ingeniería como la ingeniería nuclear , aeroespacial , mecánica y eléctrica . [1]
Como una función diferenciable de una variable compleja es igual a su serie de Taylor (es decir, es analítica ), el análisis complejo se ocupa particularmente de las funciones analíticas de una variable compleja, es decir, las funciones holomorfas . El concepto puede extenderse a funciones de varias variables complejas .
Historia

El análisis complejo es una de las ramas clásicas de las matemáticas, con raíces en el siglo XVIII y justo antes. Entre los matemáticos importantes asociados con los números complejos se incluyen Euler , Gauss , Riemann , Cauchy , Gösta Mittag-Leffler , Weierstrass y muchos más en el siglo XX. El análisis complejo, en particular la teoría de las aplicaciones conformes , tiene muchas aplicaciones físicas y también se utiliza en toda la teoría analítica de números . En los tiempos modernos, se ha vuelto muy popular a través de un nuevo impulso de la dinámica compleja y las imágenes de fractales producidas al iterar funciones holomorfas . Otra aplicación importante del análisis complejo es en la teoría de cuerdas , que examina los invariantes conformes en la teoría cuántica de campos .
Funciones complejas

Una función compleja es una función que va de números complejos a números complejos. En otras palabras, es una función que tiene un subconjunto (no necesariamente propio) de los números complejos como dominio y los números complejos como codominio . Generalmente se supone que las funciones complejas tienen un dominio que contiene un subconjunto abierto no vacío del plano complejo .
Para cualquier función compleja, los valores del dominio y sus imágenes en el rango pueden separarse en partes reales e imaginarias :
donde todos tienen valor real.
En otras palabras, una función compleja puede descomponerse en
- y
es decir, en dos funciones de valor real ( , ) de dos variables reales ( , ).
De manera similar, cualquier función de valor complejo f en un conjunto arbitrario X (es isomorfa a, y por lo tanto, en ese sentido, es) puede considerarse como un par ordenado de dos funciones de valor real : (Re f , Im f ) o, alternativamente, como una función de valor vectorial de X en
Algunas propiedades de funciones complejas (como la continuidad ) no son más que las propiedades correspondientes de funciones vectoriales de dos variables reales. Otros conceptos de análisis complejo, como la diferenciabilidad , son generalizaciones directas de conceptos similares para funciones reales, pero pueden tener propiedades muy diferentes. En particular, toda función compleja diferenciable es analítica (véase la siguiente sección), y dos funciones diferenciables que son iguales en una vecindad de un punto son iguales en la intersección de su dominio (si los dominios son conexos ). La última propiedad es la base del principio de continuación analítica que permite extender cada función analítica real de una manera única para obtener una función analítica compleja cuyo dominio es todo el plano complejo con un número finito de arcos de curva eliminados. Muchas funciones complejas básicas y especiales se definen de esta manera, incluyendo la función exponencial compleja , las funciones logarítmicas complejas y las funciones trigonométricas .
Funciones holomorfas
Las funciones complejas que son diferenciables en cada punto de un subconjunto abierto del plano complejo se denominan holomorfas en . En el contexto del análisis complejo, la derivada de at se define como [2]
Superficialmente, esta definición es formalmente análoga a la de la derivada de una función real. Sin embargo, las derivadas complejas y las funciones diferenciables se comportan de maneras significativamente diferentes en comparación con sus contrapartes reales. En particular, para que exista este límite, el valor del cociente de diferencias debe acercarse al mismo número complejo, independientemente de la manera en que nos acerquemos en el plano complejo. En consecuencia, la diferenciabilidad compleja tiene implicaciones mucho más fuertes que la diferenciabilidad real. Por ejemplo, las funciones holomorfas son infinitamente diferenciables , mientras que la existencia de la derivada n -ésima no necesariamente implica la existencia de la derivada ( n + 1)-ésima para funciones reales. Además, todas las funciones holomorfas satisfacen la condición más fuerte de analiticidad , lo que significa que la función está, en cada punto de su dominio, dada localmente por una serie de potencias convergentes. En esencia, esto significa que las funciones holomorfas en pueden aproximarse arbitrariamente bien por polinomios en alguna vecindad de cada punto en . Esto contrasta marcadamente con las funciones reales diferenciables; Hay funciones reales infinitamente diferenciables que no son analíticas en ningún caso ; véase Función suave no analítica § Una función suave que no es analítica en ningún caso real .
La mayoría de las funciones elementales, incluidas la función exponencial , las funciones trigonométricas y todas las funciones polinómicas , extendidas apropiadamente a argumentos complejos como funciones , son holomorfas en todo el plano complejo, lo que las convierte en funciones enteras , mientras que las funciones racionales , donde p y q son polinomios, son holomorfas en dominios que excluyen puntos donde q es cero. Tales funciones que son holomorfas en todas partes excepto en un conjunto de puntos aislados se conocen como funciones meromórficas . Por otro lado, las funciones , , y no son holomorfas en ninguna parte del plano complejo, como se puede demostrar por su incapacidad para satisfacer las condiciones de Cauchy-Riemann (ver más abajo).
Una propiedad importante de las funciones holomorfas es la relación entre las derivadas parciales de sus componentes reales e imaginarias, conocidas como condiciones de Cauchy-Riemann . Si , definida por , donde , es holomorfa en una región , entonces para todo ,
En términos de las partes real e imaginaria de la función, u y v , esto es equivalente al par de ecuaciones y , donde los subíndices indican diferenciación parcial. Sin embargo, las condiciones de Cauchy-Riemann no caracterizan a las funciones holomorfas, sin condiciones de continuidad adicionales (véase el teorema de Looman-Menchoff ).
Las funciones holomorfas presentan algunas características notables. Por ejemplo, el teorema de Picard afirma que el rango de una función completa puede tomar solo tres formas posibles: , o para algún . En otras palabras, si dos números complejos distintos y no están en el rango de una función completa , entonces es una función constante. Además, una función holomorfa en un conjunto abierto conexo está determinada por su restricción a cualquier subconjunto abierto no vacío.
Mapa conforme

En matemáticas , un mapa conforme es una función que preserva localmente los ángulos , pero no necesariamente las longitudes.
Más formalmente, sean y subconjuntos abiertos de . Una función se denomina conforme (o preservadora de ángulos) en un punto si preserva los ángulos entre curvas dirigidas a través de , así como la orientación. Las funciones conformes preservan tanto los ángulos como las formas de figuras infinitesimalmente pequeñas, pero no necesariamente su tamaño o curvatura .
La propiedad conforme puede describirse en términos de la matriz derivada jacobiana de una transformación de coordenadas . La transformación es conforme siempre que el jacobiano en cada punto sea un escalar positivo multiplicado por una matriz de rotación ( ortogonal con determinante uno). Algunos autores definen la conformidad para incluir aplicaciones de inversión de orientación cuyos jacobianos pueden escribirse como cualquier escalar multiplicado por cualquier matriz ortogonal. [3]
En el caso de las aplicaciones en dos dimensiones, las aplicaciones conformes (que preservan la orientación) son precisamente las funciones analíticas complejas localmente invertibles . En tres dimensiones y dimensiones superiores, el teorema de Liouville limita drásticamente las aplicaciones conformes a unos pocos tipos.
La noción de conformidad se generaliza de manera natural a aplicaciones entre variedades riemannianas o semi-riemannianas .Resultados principales
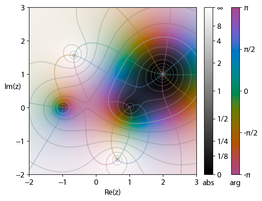
el brillo la magnitud.
Una de las herramientas centrales en el análisis complejo es la integral de línea . La integral de línea alrededor de un camino cerrado de una función que es holomorfa en todas partes dentro del área limitada por el camino cerrado es siempre cero, como lo establece el teorema de la integral de Cauchy . Los valores de una función holomorfa de este tipo dentro de un disco se pueden calcular mediante una integral de camino en el límite del disco (como se muestra en la fórmula integral de Cauchy ). Las integrales de camino en el plano complejo se utilizan a menudo para determinar integrales reales complicadas, y aquí es aplicable la teoría de residuos , entre otras (ver métodos de integración de contorno ). Un "polo" (o singularidad aislada ) de una función es un punto donde el valor de la función se vuelve ilimitado o "explota". Si una función tiene un polo de este tipo, entonces se puede calcular el residuo de la función allí, que se puede utilizar para calcular integrales de camino que involucran a la función; este es el contenido del poderoso teorema del residuo . El comportamiento notable de las funciones holomorfas cerca de singularidades esenciales se describe mediante el teorema de Picard . Las funciones que solo tienen polos pero no tienen singularidades esenciales se denominan meromórficas . Las series de Laurent son el equivalente complejo de las series de Taylor , pero se pueden utilizar para estudiar el comportamiento de funciones cercanas a singularidades mediante sumas infinitas de funciones más conocidas, como los polinomios.
Una función acotada que es holomorfa en todo el plano complejo debe ser constante; este es el teorema de Liouville . Puede utilizarse para proporcionar una prueba natural y breve del teorema fundamental del álgebra que establece que el campo de los números complejos es algebraicamente cerrado .
Si una función es holomorfa en todo un dominio conexo , entonces sus valores están completamente determinados por sus valores en cualquier subdominio más pequeño. Se dice que la función en el dominio más grande es una continuación analítica a partir de sus valores en el dominio más pequeño. Esto permite la extensión de la definición de funciones, como la función zeta de Riemann , que se definen inicialmente en términos de sumas infinitas que convergen solo en dominios limitados a casi todo el plano complejo. A veces, como en el caso del logaritmo natural , es imposible continuar analíticamente una función holomorfa a un dominio no simplemente conexo en el plano complejo, pero es posible extenderla a una función holomorfa en una superficie estrechamente relacionada conocida como superficie de Riemann .
Todo esto se refiere al análisis complejo en una variable. También existe una teoría muy rica de análisis complejo en más de una dimensión compleja en la que las propiedades analíticas, como la expansión en serie de potencias, se mantienen, mientras que la mayoría de las propiedades geométricas de las funciones holomorfas en una dimensión compleja (como la conformidad ) no se mantienen. El teorema de mapeo de Riemann sobre la relación conforme de ciertos dominios en el plano complejo, que puede ser el resultado más importante en la teoría unidimensional, falla dramáticamente en dimensiones superiores.
Una aplicación importante de ciertos espacios complejos es la mecánica cuántica como funciones de onda .
Véase también
- Geometría compleja
- Análisis hipercomplejo
- Cálculo vectorial
- Lista de temas de análisis complejos
- Teorema de monodromía
- Análisis real
- Teorema de Riemann-Roch
- Teorema de Runge
Referencias
- ^ "Aplicaciones industriales del análisis complejo". Newton Gateway to Mathematics . 30 de octubre de 2019 . Consultado el 20 de noviembre de 2023 .
- ^ Rudin, Walter (1987). Análisis real y complejo (PDF) . McGraw-Hill Education. pág. 197. ISBN. 978-0-07-054234-1.
- ^ Blair, David (17 de agosto de 2000). Teoría de la inversión y mapeo conforme . Biblioteca de matemáticas para estudiantes. Vol. 9. Providence, Rhode Island: American Mathematical Society. doi :10.1090/stml/009. ISBN. 978-0-8218-2636-2. Número de identificación del sujeto 118752074.
Fuentes
- Ablowitz, MJ y AS Fokas , Variables complejas: Introducción y aplicaciones (Cambridge, 2003).
- Ahlfors, L. , Análisis complejo (McGraw-Hill, 1953).
- Cartan, H. , Teoría elemental de las funciones analíticas de uno o más complejos de variables. (Hermann, 1961). Traducción al inglés, Teoría elemental de funciones analíticas de una o varias variables complejas. (Addison-Wesley, 1963).
- Carathéodory, C. , Funktionentheorie. (Birkhäuser, 1950). Traducción al inglés, Theory of Functions of a Complex Variable (Chelsea, 1954). [2 volúmenes.]
- Carrier, GF , M. Krook y CE Pearson, Funciones de una variable compleja: teoría y técnica. (McGraw-Hill, 1966).
- Conway, JB , Funciones de una variable compleja. (Springer, 1973).
- Fisher, S., Variables complejas. (Wadsworth y Brooks/Cole, 1990).
- Forsyth, A. , Teoría de funciones de una variable compleja (Cambridge, 1893).
- Freitag, E. y R. Busam, Funktionentheorie . (Springer, 1995). Traducción al inglés, Análisis complejo . (Springer, 2005).
- Goursat, E. , Cours d'analyse mathématique, tomo 2. (Gauthier-Villars, 1905). Traducción al inglés, Un curso de análisis matemático, vol. 2, parte 1: Funciones de una variable compleja. (Ginn, 1916).
- Henrici, P. , Análisis complejo computacional y aplicado (Wiley). [Tres volúmenes: 1974, 1977, 1986.]
- Kreyszig, E. , Matemáticas avanzadas de ingeniería. (Wiley, 1962).
- Lavrentyev, M. & B. Shabat, Методы теории функций комплексного переменного. ( Métodos de la Teoría de Funciones de una Variable Compleja ). (1951, en ruso).
- Markushevich, AI , Teoría de funciones de una variable compleja , (Prentice-Hall, 1965). [Tres volúmenes.]
- Marsden y Hoffman, Análisis complejo básico. (Freeman, 1973).
- Needham, T. , Análisis visual complejo. (Oxford, 1997). http://usf.usfca.edu/vca/
- Remmert, R. , Teoría de funciones complejas . (Springer, 1990).
- Rudin, W. , Análisis real y complejo. (McGraw-Hill, 1966).
- Shaw, WT, Análisis complejo con Mathematica (Cambridge, 2006).
- Stein, E. y R. Shakarchi, Análisis complejo. (Princeton, 2003).
- Sveshnikov, AG & AN Tikhonov , Теория функций комплексной переменной. (Nauka, 1967). Traducción al inglés, Teoría de funciones de una variable compleja (MIR, 1978).
- Titchmarsh, EC , La teoría de funciones. (Oxford, 1932).
- Wegert, E., Funciones complejas visuales . (Birkhäuser, 2012).
- Whittaker, ET y GN Watson , Un curso de análisis moderno (Cambridge, 1902). 3.ª ed. (1920 )
Enlaces externos
- Página de análisis complejo de MathWorld de Wolfram Research










































