Síntesis de modulación de frecuencia
Forma de síntesis del sonido
Síntesis FM utilizando 2 operadores
Un tono portador f c de 220 Hz modulado por un tono modulador f m de 440 Hz , con varias opciones de índice de modulación de frecuencia , β . Las señales del dominio temporal se ilustran arriba y los espectros correspondientes se muestran a continuación (amplitudes del espectro en dB ).
Formas de onda para cada β

Espectros para cada β

La síntesis de modulación de frecuencia (o síntesis FM ) es una forma de síntesis de sonido en la que se modifica la frecuencia de una forma de onda modulando su frecuencia con un modulador. La frecuencia (instantánea) de un oscilador se modifica de acuerdo con la amplitud de una señal moduladora. [1]

La síntesis FM puede crear sonidos tanto armónicos como inarmónicos . Para sintetizar sonidos armónicos, la señal moduladora debe tener una relación armónica con la señal portadora original. A medida que aumenta la cantidad de modulación de frecuencia, el sonido se vuelve progresivamente más complejo. Mediante el uso de moduladores con frecuencias que son múltiplos no enteros de la señal portadora (es decir, inarmónicos), se pueden crear espectros inarmónicos de percusión y de campana.

Aplicaciones

La síntesis FM mediante osciladores analógicos puede dar lugar a inestabilidad de tono. [2] Sin embargo, la síntesis FM también se puede implementar digitalmente, lo que es más estable y se convirtió en una práctica estándar. La síntesis FM digital (equivalente a la modulación de fase utilizando la integración temporal de la frecuencia instantánea ) fue la base de varios instrumentos musicales a partir de 1974. Yamaha construyó el primer prototipo de sintetizador digital en 1974, basado en la síntesis FM, [3] antes de lanzar comercialmente el Yamaha GS-1 en 1980. [4] El Synclavier I , fabricado por New England Digital Corporation a partir de 1978, incluía un sintetizador FM digital, que utilizaba un algoritmo de síntesis FM con licencia de Yamaha. [5] El innovador sintetizador Yamaha DX7 de Yamaha , lanzado en 1983, llevó a la FM a la vanguardia de la síntesis a mediados de la década de 1980. [6]

Uso recreativo: chips de sonido FM en PC, salas de juegos, consolas de juegos y teléfonos móviles

La síntesis FM también se convirtió en la configuración habitual para juegos y software hasta mediados de los noventa. Para los sistemas compatibles con IBM PC , las tarjetas de sonido como AdLib y Sound Blaster popularizaron los chips Yamaha como el OPL2 y OPL3 . Otros ordenadores como el Sharp X68000 y el MSX ( unidad de ordenador Yamaha CX5M ) utilizan el chip de sonido OPM (que también se utilizó comúnmente para máquinas arcade hasta mediados de los noventa) con unidades CX5M posteriores que utilizan el chip de sonido OPP , y los ordenadores NEC PC-88 y PC-98 utilizan el OPN y el OPNA . Para los sistemas arcade y las consolas de juegos, el OPNB se utilizó como placa generadora de sonido básica principal en las placas arcade de Taito (con una variante del OPNB que se utilizó en el Taito Z System ) y se utilizó notablemente en las máquinas arcade Neo Geo (MVS) y consolas domésticas (AES) de SNK . El OPN2 relacionado se utilizó en la Mega Drive (Genesis) de Sega y en el FM Towns Marty de Fujitsu como uno de sus chips generadores de sonido. A lo largo de la década de 2000, la síntesis FM también se utilizó en una amplia gama de teléfonos para reproducir tonos de llamada y otros sonidos, generalmente en el formato Yamaha SMAF .

Historia

Don Buchla (mediados de la década de 1960)

Don Buchla implementó la modulación de frecuencia en sus instrumentos a mediados de los años 1960, antes de la patente de Chowning. Sus módulos de oscilador dual 158, 258 y 259 tenían una entrada de voltaje de control de FM específica, [7] y el modelo 208 (Music Easel) tenía un oscilador de modulación cableado para permitir la modulación de frecuencia y de amplitud del oscilador primario. [8] Estas primeras aplicaciones utilizaban osciladores analógicos, y esta capacidad también fue seguida por otros sintetizadores modulares y portátiles, incluidos Minimoog y ARP Odyssey .

John Chowning (finales de la década de 1960 y década de 1970)

La síntesis de modulación de frecuencia digital fue desarrollada por John Chowning

A mediados del siglo XX, la modulación de frecuencia (FM), un medio para transportar sonido, se había comprendido durante décadas y se estaba utilizando para transmitir transmisiones de radio . La síntesis FM fue desarrollada desde 1967 en la Universidad de Stanford , California, por John Chowning , quien estaba tratando de crear sonidos diferentes de la síntesis analógica [ cita requerida ] . Su algoritmo [ cita requerida ] fue licenciado a la empresa japonesa Yamaha en 1973. [3] La implementación comercializada por Yamaha (patente estadounidense 4018121 de abril de 1977 [9] o patente estadounidense 4.018.121 [10] ) en realidad se basa en la modulación de fase [ cita requerida ] , pero los resultados terminan siendo matemáticamente equivalentes ya que ambos son esencialmente un caso especial de modulación de amplitud en cuadratura [ cita requerida ] . [11]

Década de 1970 y 1980

Expansiones de Yamaha

Los ingenieros de Yamaha comenzaron a adaptar el algoritmo de Chowning para su uso en un sintetizador digital comercial, añadiendo mejoras como el método de "escalado de clave" para evitar la introducción de distorsión que normalmente se producía en los sistemas analógicos durante la modulación de frecuencia [ cita requerida ] , aunque pasarían varios años antes de que Yamaha lanzara sus sintetizadores digitales FM. [12] En la década de 1970, Yamaha obtuvo una serie de patentes, bajo el antiguo nombre de la empresa "Nippon Gakki Seizo Kabushiki Kaisha", que evolucionaban el trabajo de Chowning. [10] Yamaha construyó el primer prototipo de sintetizador digital FM en 1974. [3] Yamaha finalmente comercializó la tecnología de síntesis FM con el Yamaha GS-1, el primer sintetizador digital FM, lanzado en 1980. [4]

Sintetizador digital FM Yamaha DX7 (1983)

La síntesis FM fue la base de algunas de las primeras generaciones de sintetizadores digitales , en particular los de Yamaha, así como los de New England Digital Corporation bajo licencia de Yamaha. [5] El sintetizador DX7 de Yamaha , lanzado en 1983, fue omnipresente durante la década de 1980. Varios otros modelos de Yamaha proporcionaron variaciones y evoluciones de la síntesis FM durante esa década. [13]

Yamaha había patentado su implementación de hardware de FM en la década de 1970, [10] lo que le permitió casi monopolizar el mercado de la tecnología FM hasta mediados de la década de 1990.

Casio desarrolló una forma de síntesis relacionada llamada síntesis de distorsión de fase , utilizada en su gama de sintetizadores CZ . Tenía una calidad de sonido similar (pero ligeramente diferente) a la de la serie DX.

Década de 1990

Popularización tras la expiración de la patente

Con la expiración de la patente de FM de la Universidad de Stanford en 1995, la síntesis FM digital ahora puede ser implementada libremente por otros fabricantes. La patente de síntesis FM le reportó a Stanford 20 millones de dólares antes de que expirara, convirtiéndola (en 1994) en "el segundo acuerdo de licencia más lucrativo en la historia de Stanford". [14] Hoy en día, la FM se encuentra principalmente en sintetizadores basados ​​en software como FM8 de Native Instruments o Sytrus de Image-Line , pero también se ha incorporado al repertorio de síntesis de algunos sintetizadores digitales modernos, generalmente coexistiendo como una opción junto con otros métodos de síntesis como la síntesis sustractiva , la síntesis basada en muestras , la síntesis aditiva y otras técnicas. El grado de complejidad de la FM en tales sintetizadores de hardware puede variar desde la simple FM de 2 operadores, hasta los motores de 6 operadores altamente flexibles de Korg Kronos y Alesis Fusion , hasta la creación de FM en motores ampliamente modulares como los de los últimos sintetizadores de Kurzweil Music Systems . [ cita requerida ]

Convolución y modulación en tiempo real (AFM + muestra) y síntesis de modelado de formantes

Los nuevos sintetizadores de hardware comercializados específicamente por sus capacidades FM desaparecieron del mercado después del lanzamiento del Yamaha SY99 [15] y FS1R [16], e incluso aquellos comercializaban sus capacidades FM altamente poderosas como contrapartes de la síntesis basada en muestras y la síntesis de formantes respectivamente. Sin embargo, las opciones de síntesis FM bien desarrolladas son una característica de los sintetizadores Nord Lead fabricados por Clavia, la gama Alesis Fusion , el Korg Oasys y Kronos y el Modor NF-1. Varios otros sintetizadores ofrecen capacidades FM limitadas para complementar sus motores principales. [ cita requerida ]

La combinación de conjuntos de 8 operadores FM con formas de onda multiespectrales comenzó en 1999 por parte de Yamaha en el FS1R. El FS1R tenía 16 operadores, 8 operadores FM estándar y 8 operadores adicionales que usaban una fuente de ruido en lugar de un oscilador como fuente de sonido. Al agregar fuentes de ruido ajustables, el FS1R podía modelar los sonidos producidos en la voz humana y en un instrumento de viento, además de producir sonidos de instrumentos de percusión. El FS1R también contenía una forma de onda adicional llamada forma de onda Formant. Los formantes se pueden usar para modelar sonidos de instrumentos corporales resonantes como el violonchelo, el violín, la guitarra acústica, el fagot, la trompa inglesa o la voz humana. Los formantes incluso se pueden encontrar en el espectro armónico de varios instrumentos de viento. [17]

Década de 2000-presente

Modulación de fase variable, síntesis FM-X, FM alterada, etc.

En 2016, Korg lanzó el Korg Volca FM, una iteración FM de 3 voces y 6 operadores de la serie Korg Volca de módulos de escritorio compactos y asequibles. [18] Más recientemente, Korg lanzó el opsix (2020) y el opsix SE (2023) que integran síntesis FM de 6 operadores con modelado sustractivo, analógico, aditivo, semimodular y Waveshaping. Yamaha lanzó el Montage , que combina un motor basado en muestras de 128 voces con un motor FM de 128 voces. Esta iteración de FM se llama FM-X y presenta 8 operadores; cada operador tiene la opción de varias formas de onda básicas, pero cada forma de onda tiene varios parámetros para ajustar su espectro. [19] El Yamaha Montage fue seguido por el Yamaha MODX más asequible en 2018, con una arquitectura FM-X de 64 voces y 8 operadores además de un motor basado en muestras de 128 voces. [20] En 2018, Elektron lanzó Digitone , un sintetizador FM de 8 voces y 4 operadores que incorpora el reconocido motor de secuencia de Elektron. [21]

La síntesis FM-X se introdujo con los sintetizadores Yamaha Montage en 2016. FM-X utiliza 8 operadores. Cada operador FM-X tiene un conjunto de formas de onda multiespectrales para elegir, lo que significa que cada operador FM-X puede ser equivalente a una pila de 3 o 4 operadores FM DX7. La lista de formas de onda seleccionables incluye ondas sinusoidales, las formas de onda All1 y All2, las formas de onda Odd1 e Odd2 y las formas de onda Res1 y Res2. La selección de ondas sinusoidales funciona igual que las formas de onda DX7. Las formas de onda All1 y All2 son formas de onda de dientes de sierra. Las formas de onda Odd1 e Odd2 son ondas de pulso o cuadradas. Estos dos tipos de formas de onda se pueden utilizar para modelar los picos armónicos básicos en la parte inferior del espectro armónico de la mayoría de los instrumentos. Las formas de onda Res1 y Res2 mueven el pico espectral a un armónico específico y se pueden utilizar para modelar grupos de armónicos triangulares o redondeados más arriba en el espectro de un instrumento. La combinación de una forma de onda All1 o Odd1 con múltiples formas de onda Res1 (o Res2) (y el ajuste de sus amplitudes) puede modelar el espectro armónico de un instrumento o sonido. [17] [ cita requerida ]

Análisis espectral

Demostración de 2 operadores: si la frecuencia del modulador es menor que la de la portadora, la nota de salida será la del modulador.

Existen múltiples variaciones de síntesis FM, entre ellas:

  • Diversos arreglos de operadores (conocidos como "algoritmos FM" en la terminología de Yamaha)
    • 2 operadores
    • FM en serie (múltiples etapas)
    • FM paralela (múltiples moduladores, múltiples portadoras),
    • Mezcla de ellos
  • Varias formas de onda de los operadores
    • Forma de onda sinusoidal
    • Otras formas de onda
  • Modulación adicional

etc .

Como base de estas variaciones, analizamos el espectro de 2 operadores (síntesis FM lineal utilizando dos operadores sinusoidales) a continuación.

2 operadores

El espectro generado por la síntesis FM con un modulador se expresa de la siguiente manera: [22] [23]

Para la señal de modulación , la señal portadora es: [nota 1] m ( t ) = B sin ⁡ ( ω m t ) {\displaystyle m(t)=B\,\sin(\omega _{m}t)\,}

F M ( t )   =   A sin ⁡ ( ∫ 0 t ( ω c + B sin ⁡ ( ω m τ ) ) d τ )   =   A sin ⁡ ( ω c t − B ω m ( cos ⁡ ( ω m t ) − 1 ) )   =   A sin ⁡ ( ω c t + B ω m ( sin ⁡ ( ω m t − π / 2 ) + 1 ) ) {\displaystyle {\begin{aligned}FM(t)&\ =\ A\,\sin \left(\,\int _{0}^{t}\left(\omega _{c}+B\,\sin(\omega _{m}\,\tau )\right)d\tau \right)\\&\ =\ A\,\sin \left(\omega _{c}\,t-{\frac {B}{\omega _{m}}}\left(\cos(\omega _{m}\,t)-1\right)\right)\\&\ =\ A\,\sin \left(\omega _{c}\,t+{\frac {B}{\omega _{m}}}\left(\sin(\omega _{m}\,t-\pi /2)+1\right)\right)\\\end{aligned}}}

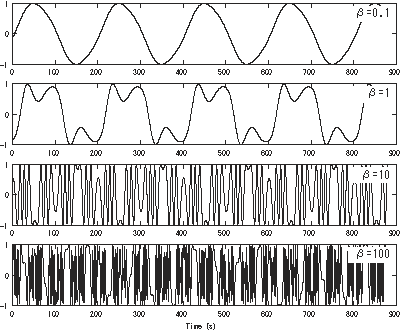
Si ignoráramos los términos de fase constante en la portadora y el modulador , finalmente obtendríamos la siguiente expresión, como se ve en Chowning 1973 y Roads 1996, p. 232: ϕ c = B / ω m {\displaystyle \phi _{c}=B/\omega _{m}\,} ϕ m = − π / 2 {\displaystyle \phi _{m}=-\pi /2\,}

F M ( t )   ≈   A sin ⁡ ( ω c t + β sin ⁡ ( ω m t ) )   =   A ( J 0 ( β ) sin ⁡ ( ω c t ) + ∑ n = 1 ∞ J n ( β ) [ sin ⁡ ( ( ω c + n ω m ) t )   +   ( − 1 ) n sin ⁡ ( ( ω c − n ω m ) t ) ] )   =   A ∑ n = − ∞ ∞ J n ( β ) sin ⁡ ( ( ω c + n ω m ) t ) {\displaystyle {\begin{aligned}FM(t)&\ \approx \ A\,\sin \left(\omega _{c}\,t+\beta \,\sin(\omega _{m}\,t)\right)\\&\ =\ A\left(J_{0}(\beta )\sin(\omega _{c}\,t)+\sum _{n=1}^{\infty }J_{n}(\beta )\left[\,\sin((\omega _{c}+n\,\omega _{m})\,t)\ +\ (-1)^{n}\sin((\omega _{c}-n\,\omega _{m})\,t)\,\right]\right)\\&\ =\ A\sum _{n=-\infty }^{\infty }J_{n}(\beta )\,\sin((\omega _{c}+n\,\omega _{m})\,t)\end{aligned}}}

donde son las frecuencias angulares ( ) de la portadora y del modulador, es el índice de modulación de frecuencia , y las amplitudes son la -ésima función de Bessel de primer tipo , respectivamente. [nota 2] ω c , ω m {\displaystyle \omega _{c}\,,\,\omega _{m}\,} ω = 2 π f {\displaystyle \,\omega =2\pi f\,} β = B / ω m {\displaystyle \beta =B/\omega _{m}\,} J n ( β ) {\displaystyle J_{n}(\beta )\,} n {\displaystyle n\,}

Véase también

Referencias

Notas al pie

  1. ^ Nótese que la señal de modulación como frecuencia instantánea se convierte a la fase de la señal portadora , mediante la integral de tiempo entre . m ( t ) {\displaystyle m(t)} F M ( t ) {\displaystyle FM(t)} [ 0 , t ] {\displaystyle [0,t]}
  2. ^ La expresión anterior se transforma utilizando fórmulas de adición trigonométrica
    sin ⁡ ( x ± y ) = sin ⁡ x cos ⁡ y ± cos ⁡ x sin ⁡ y {\displaystyle {\begin{aligned}\sin(x\pm y)&=\sin x\cos y\pm \cos x\sin y\end{aligned}}}
    y un lema de la función de Bessel
    cos ⁡ ( β sin ⁡ θ ) = J 0 ( β ) + 2 ∑ n = 1 ∞ J 2 n ( β ) cos ⁡ ( 2 n θ ) sin ⁡ ( β sin ⁡ θ ) = 2 ∑ n = 0 ∞ J 2 n + 1 ( β ) sin ⁡ ( ( 2 n + 1 ) θ ) {\displaystyle {\begin{aligned}\cos(\beta \sin \theta )&=J_{0}(\beta )+2\sum _{n=1}^{\infty }J_{2n}(\beta )\cos(2n\theta )\\\sin(\beta \sin \theta )&=2\sum _{n=0}^{\infty }J_{2n+1}(\beta )\sin((2n+1)\theta )\end{aligned}}}
    ( Fuente : Kreh 2012)
    Como sigue:
    sin ⁡ ( θ c + β sin ⁡ ( θ m ) )   =   sin ⁡ ( θ c ) cos ⁡ ( β sin ⁡ ( θ m ) ) + cos ⁡ ( θ c ) sin ⁡ ( β sin ⁡ ( θ m ) )   =   sin ⁡ ( θ c ) [ J 0 ( β ) + 2 ∑ n = 1 ∞ J 2 n ( β ) cos ⁡ ( 2 n θ m ) ] + cos ⁡ ( θ c ) [ 2 ∑ n = 0 ∞ J 2 n + 1 ( β ) sin ⁡ ( ( 2 n + 1 ) θ m ) ]   =   J 0 ( β ) sin ⁡ ( θ c ) + J 1 ( β ) 2 cos ⁡ ( θ c ) sin ⁡ ( θ m ) + J 2 ( β ) 2 sin ⁡ ( θ c ) cos ⁡ ( 2 θ m ) + J 3 ( β ) 2 cos ⁡ ( θ c ) sin ⁡ ( 3 θ m ) + . . .   =   J 0 ( β ) sin ⁡ ( θ c ) + ∑ n = 1 ∞ J n ( β ) [ sin ⁡ ( θ c + n θ m )   +   ( − 1 ) n sin ⁡ ( θ c − n θ m ) ]   =   ∑ n = − ∞ ∞ J n ( β ) sin ⁡ ( θ c + n θ m ) ( ∵   J − n ( x ) = ( − 1 ) n J n ( x ) ) {\displaystyle {\begin{aligned}&\sin \left(\theta _{c}+\beta \,\sin(\theta _{m})\right)\\&\ =\ \sin(\theta _{c})\cos(\beta \sin(\theta _{m}))+\cos(\theta _{c})\sin(\beta \sin(\theta _{m}))\\&\ =\ \sin(\theta _{c})\left[J_{0}(\beta )+2\sum _{n=1}^{\infty }J_{2n}(\beta )\cos(2n\theta _{m})\right]+\cos(\theta _{c})\left[2\sum _{n=0}^{\infty }J_{2n+1}(\beta )\sin((2n+1)\theta _{m})\right]\\&\ =\ J_{0}(\beta )\sin(\theta _{c})+J_{1}(\beta )2\cos(\theta _{c})\sin(\theta _{m})+J_{2}(\beta )2\sin(\theta _{c})\cos(2\theta _{m})+J_{3}(\beta )2\cos(\theta _{c})\sin(3\theta _{m})+...\\&\ =\ J_{0}(\beta )\sin(\theta _{c})+\sum _{n=1}^{\infty }J_{n}(\beta )\left[\,\sin(\theta _{c}+n\theta _{m})\ +\ (-1)^{n}\sin(\theta _{c}-n\theta _{m})\,\right]\\&\ =\ \sum _{n=-\infty }^{\infty }J_{n}(\beta )\,\sin(\theta _{c}+n\theta _{m})\qquad (\because \ J_{-n}(x)=(-1)^{n}J_{n}(x))\end{aligned}}}

Citas

  1. ^ Dodge y Jerse 1997, pág. 115
  2. ^ McGuire, Sam; Matějů, Zbyněk (28 de diciembre de 2020). El arte de la orquestación digital. Prensa CRC. ISBN 978-1-000-28699-1.
  3. ^ abc "[Capítulo 2] Generadores de tonos FM y el nacimiento de la producción musical en casa". 40.º aniversario del sintetizador Yamaha: historia . Yamaha Corporation. 2014. Archivado desde el original el 11 de mayo de 2017.
  4. ^ de Curtis Roads (1996). El tutorial de música por ordenador. MIT Press . p. 226. ISBN 0-262-68082-3. Consultado el 5 de junio de 2011 .
  5. ^ ab "1978 New England Digital Synclavier". Mezcla . Penton Media. 1 de septiembre de 2006.
  6. ^ "Los 10 mejores presets de sintetizadores clásicos (y dónde puedes escucharlos)". MusicRadar . Consultado el 19 de octubre de 2018 .
  7. ^ Dr. Hubert Howe (1960s). Buchla Electronic Music System: Users Manual written for CBS Musical Instruments (Buchla 100 Owner's Manual). Educational Research Department, CBS Musical Instruments, Columbia Broadcasting System. p. 7. En este punto podemos considerar varias modificaciones adicionales de la señal que podríamos desear hacer a la serie de tonos producidos por el ejemplo anterior. Por ejemplo, si quisiéramos agregar modulación de frecuencia a los tonos, es necesario conectar otra señal de audio al conector conectado por una línea al dial central del oscilador de diente de sierra de doble seno modelo 158. ...
  8. ^ Atten Strange (1974). Programación y metaprogramación en el electroorganismo: una directiva operativa para el caballete musical. Buchla y asociados.
  9. ^ "Patente estadounidense 4018121 de abril de 1977". patft.uspto.gov . Consultado el 30 de abril de 2017 .
  10. ^ abc «Patente US4018121 - Método de sintetizar un sonido musical - Google Patents» . Consultado el 30 de abril de 2017 .
  11. ^ Rob Hordijk. "Síntesis FM en Modular". Consejos y trucos de Nord Modular y Micro Modular V3.03 . Clavia DMI AB. Archivado desde el original el 7 de abril de 2007. Consultado el 23 de marzo de 2013 .
  12. ^ Holmes, Thom (2008). "Early Computer Music". Música electrónica y experimental: tecnología, música y cultura (3.ª ed.). Taylor & Francis . pp. 257–8. ISBN 978-0-415-95781-6. Consultado el 4 de junio de 2011 .
  13. ^ Gordon Reid (septiembre de 2001). «Sonidos de los 80, parte 2: Yamaha DX1 y sus sucesores (retro)». Sound on Sound . Archivado desde el original el 17 de septiembre de 2011. Consultado el 29 de junio de 2011 .
  14. ^ Stanford University News Service (07/06/94), La síntesis musical se acerca a la calidad del sonido de los instrumentos reales
  15. ^ "Especificaciones de Yamaha SY99". Yamaha Corporation (en japonés).
  16. ^ Poyser, Debbie; Johnson, Derek (1998). "Yamaha FS1R - Generador de tonos de síntesis FM/conformación de formantes". Sound on Sound . N.º de diciembre de 1998.
  17. ^ de Zollinger, W. Thor (diciembre de 2017). "FM_Synthesis_of_Real_Instruments" (PDF) . Archivado (PDF) desde el original el 25 de septiembre de 2017.
  18. ^ Página del producto Volca FM
  19. ^ Página de características del producto Yamaha Montage
  20. ^ Página de características del producto Yamaha MODX
  21. ^ Página del producto Digitone
  22. ^ Chowning 1973, págs. 1-2
  23. ^ Doering, Ed. "Matemáticas de modulación de frecuencia" . Consultado el 11 de abril de 2013 .

Bibliografía

  • Chowning, J. (1973). "La síntesis de espectros de audio complejos mediante modulación de frecuencia" (PDF) . Revista de la Sociedad de Ingeniería de Audio . 21 (7).
  • Chowning, John; Bristow, David (1986). Teoría y aplicaciones de FM: de músicos para músicos . Tokio: Yamaha. ISBN 4-636-17482-8.
  • Dodge, Charles; Jerse, Thomas A. (1997). Música por computadora: síntesis, composición e interpretación . Nueva York: Schirmer Books. ISBN 0-02-864682-7.
  • Kreh, Martin (2012), "Funciones de Bessel" (PDF) , The Pennsylvania State University , pp. 5–6, archivado desde el original (PDF) el 2017-11-18 , consultado el 2014-08-22
  • Roads, Curtis (1996). El tutorial de música por ordenador. MIT Press. ISBN 978-0-262-68082-0.
  • Introducción a FM, por Bill Schottstaedt
  • Tutorial de FM
  • Secretos de sintetizador, parte 12: Introducción a la modulación de frecuencia, por Gordon Reid
  • Secretos de sintetizador, parte 13: Más sobre modulación de frecuencia, por Gordon Reid
  • Escuela de sintetizadores de Paul Wiffens: Parte 3
  • Sitio espejo de FM Synthesis que incluye análisis de operadores complejos, 2019
Retrieved from "https://en.wikipedia.org/w/index.php?title=Frequency_modulation_synthesis&oldid=1241677476"