Respuesta de impulso finito

En el procesamiento de señales , un filtro de respuesta de impulso finito ( FIR ) es un filtro cuya respuesta de impulso (o respuesta a cualquier entrada de longitud finita) tiene una duración finita , porque se establece en cero en un tiempo finito. Esto contrasta con los filtros de respuesta de impulso infinito (IIR), que pueden tener retroalimentación interna y pueden continuar respondiendo indefinidamente (generalmente decayendo). ^{[ cita requerida ]}

La respuesta al impulso (es decir, la salida en respuesta a una entrada delta de Kronecker ) de un filtro FIR de tiempo discreto de orden N dura exactamente ^muestras (desde el primer elemento distinto de cero hasta el último elemento distinto de cero) antes de establecerse en cero.${\estilo de visualización N+1}$

Los filtros FIR pueden ser de tiempo discreto o de tiempo continuo , y digitales o analógicos .

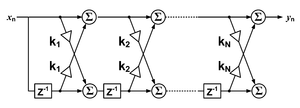
Para un filtro FIR causal de tiempo discreto de orden N , cada valor de la secuencia de salida es una suma ponderada de los valores de entrada más recientes :

${\displaystyle {\begin{aligned}y[n]&=b_{0}x[n]+b_{1}x[n-1]+\cdots +b_{N}x[nN]\\&=\sum _{i=0}^{N}b_{i}\cdot x[ni],\end{aligned}}}$

dónde :

• ${\textstyle x[n]}$es la señal de entrada,
• ${\textstyle y[n]}$es la señal de salida,
• ${\textstyle N}$es el orden del filtro; un filtro de orden ^th tiene términos en el lado derecho${\textstyle N}$${\textstyle N+1}$
• ${\textstyle b_{i}}$es el valor de la respuesta al impulso en el instante i' de un filtro FIR de orden . Si el filtro es un filtro FIR de forma directa, entonces es también un coeficiente del filtro.${\textstyle 0\leq i\leq N}$${\textstyle N^{\text{ésimo}}}$${\textstyle b_{i}}$

Este cálculo también se conoce como convolución discreta .

En estos términos se hace referencia comúnmente como${\textstyle x[ni]}$tap s, basado en la estructura de unalínea de retardo con tomasque en muchas implementaciones o diagramas de bloques proporciona las entradas retardadas a las operaciones de multiplicación. Se puede hablar de unfiltro de 5.º orden/6 tomas, por ejemplo.

La respuesta al impulso del filtro, tal como se define, no es cero durante un período finito. Si se incluyen los ceros, la respuesta al impulso es la secuencia infinita :

${\displaystyle h[n]=\sum _{i=0}^{N}b_{i}\cdot \delta [ni]={\begin{cases}b_{n}&0\leq n\leq N\\0&{\text{de lo contrario}}.\end{cases}}}$

Si un filtro FIR no es causal, el rango de valores distintos de cero en su respuesta al impulso puede comenzar antes de , con la fórmula definitoria generalizada apropiadamente.${\estilo de visualización n=0}$

Un filtro FIR tiene una serie de propiedades útiles que a veces lo hacen preferible a un filtro de respuesta de impulso infinito (IIR). Filtros FIR:

• No requiere retroalimentación. Esto significa que los errores de redondeo no se suman con las iteraciones sumadas. El mismo error relativo ocurre en cada cálculo. Esto también simplifica la implementación.
• Son inherentemente estables , ya que la salida es una suma de un número finito de múltiplos finitos de los valores de entrada, por lo que no puede ser mayor que veces el valor más grande que aparece en la entrada.${\textstyle \suma |b_{i}|}$
• Se puede diseñar fácilmente para que sea de fase lineal haciendo que la secuencia de coeficientes sea simétrica. Esta propiedad a veces es deseable para aplicaciones sensibles a la fase, por ejemplo, comunicaciones de datos, sismología , filtros de cruce y masterización .

La principal desventaja de los filtros FIR es que se requiere una potencia de cálculo considerablemente mayor en un procesador de propósito general en comparación con un filtro IIR con una nitidez o selectividad similar , especialmente cuando se necesitan cortes de baja frecuencia (en relación con la frecuencia de muestreo). Sin embargo, muchos procesadores de señales digitales proporcionan características de hardware especializadas para que los filtros FIR sean aproximadamente tan eficientes como los IIR para muchas aplicaciones.

El efecto del filtro sobre la secuencia se describe en el dominio de la frecuencia mediante el teorema de convolución :${\displaystyle x[n]}$

${\displaystyle \underbrace {{\mathcal {F}}\{x*h\}} _{Y(\omega )}=\underbrace {{\mathcal {F}}\{x\}} _{X(\omega )}\cdot \underbrace {{\mathcal {F}}\{h\}} _{H(\omega )}}$     y     ${\displaystyle y[n]=x[n]*h[n]={\mathcal {F}}^{-1}{\big \{}X(\omega )\cdot H(\omega ){\big \}},}$

donde los operadores y denotan respectivamente la transformada de Fourier de tiempo discreto (DTFT) y su inversa. Por lo tanto, la función multiplicativa de valor complejo es la respuesta de frecuencia del filtro . Se define mediante una serie de Fourier :${\displaystyle {\mathcal {F}}}$${\displaystyle {\mathcal {F}}^{-1}}$${\displaystyle H(\omega )}$

${\displaystyle H_{2\pi}(\omega )\ \triánguloq \suma _{n=-\infty }^{\infty }h[n]\cdot \left({e^{i\omega }}\right)^{-n}=\suma _{n=0}^{N}b_{n}\cdot \left({e^{i\omega }}\right)^{-n},}$

donde el subíndice añadido denota -periodicidad. Aquí representa la frecuencia en unidades normalizadas ( radianes por muestra ). La función tiene una periodicidad de con en unidades de ciclos por muestra , lo que es favorecido por muchas aplicaciones de diseño de filtros. ^[A]   El valor , llamado frecuencia de Nyquist , corresponde a   Cuando la secuencia tiene una tasa de muestreo conocida (en muestras por segundo ), la frecuencia ordinaria está relacionada con la frecuencia normalizada por ciclos por segundo ( Hz ). Por el contrario, si uno quiere diseñar un filtro para frecuencias ordinarias , etc., usando una aplicación que espera ciclos por muestra , uno ingresaría   etc.${\estilo de visualización 2\pi}$${\estilo de visualización \omega}$${\displaystyle H_{2\pi }(2\pi f')}$${\estilo de visualización 1}$${\estilo de visualización f'}$${\displaystyle \omega =\pi}$${\displaystyle f'={\tfrac {1}{2}}.}$${\displaystyle x[n]}$${\displaystyle f_{s}}$${\displaystyle f=f'\cdot f_{s}={\tfrac {\omega }{2\pi }}\cdot f_{s}}$ $estilo de visualización f_{1},}$ $estilo de visualización f_{2},}$${\displaystyle f_{1}/f_{s},}$  ${\displaystyle f_{2}/f_{s},}$

${\displaystyle H_{2\pi }(\omega )}$También se puede expresar en términos de la transformada Z de la respuesta al impulso del filtro:

${\displaystyle {\widehat {H}}(z)\ \triangleq \sum _{n=-\infty }^{\infty }h[n]\cdot z^{-n}.}$

${\displaystyle H_{2\pi}(\omega )=\left.{\widehat {H}}(z)\,\right|_{z=e^{j\omega }}={\widehat {H}}(e^{j\omega }).}$

Los filtros FIR se diseñan buscando los coeficientes y el orden de los filtros que cumplen con ciertas especificaciones, que pueden ser en el dominio del tiempo (por ejemplo, un filtro adaptado ) o en el dominio de la frecuencia (el más común). Los filtros adaptados realizan una correlación cruzada entre la señal de entrada y una forma de pulso conocida. La convolución FIR es una correlación cruzada entre la señal de entrada y una copia invertida en el tiempo de la respuesta al impulso. Por lo tanto, la respuesta al impulso del filtro adaptado se "diseña" muestreando la forma de pulso conocida y utilizando esas muestras en orden inverso como los coeficientes del filtro. ^[1]

Cuando se desea una respuesta de frecuencia particular, existen varios métodos de diseño comunes:

1. Método de diseño de ventanas
2. Método de muestreo de frecuencia
3. Método del mínimo error cuadrático medio (MSE)
4. Método de Parks-McClellan (también conocido como método equiripple, óptimo o minimax). El algoritmo de intercambio de Remez se utiliza comúnmente para encontrar un conjunto de coeficientes equiripple óptimo. Aquí el usuario especifica una respuesta de frecuencia deseada, una función de ponderación para los errores de esta respuesta y un orden de filtro N . Luego, el algoritmo encuentra el conjunto de coeficientes que minimizan la desviación máxima del ideal. Intuitivamente, esto encuentra el filtro que está lo más cerca posible de la respuesta deseada dado que solo se pueden usar coeficientes. Este método es particularmente fácil en la práctica ya que al menos un texto ^[2] incluye un programa que toma el filtro deseado y N , y devuelve los coeficientes óptimos.${\textstyle N+1}$${\textstyle N+1}$
5. Los filtros FIR de ondulación equitativa también se pueden diseñar utilizando algoritmos DFT. ^[3] El algoritmo es de naturaleza iterativa. La DFT de un diseño de filtro inicial se calcula utilizando el algoritmo FFT (si no se dispone de una estimación inicial, se puede utilizar h[n]=delta[n]). En el dominio de Fourier, o dominio DFT, la respuesta de frecuencia se corrige de acuerdo con las especificaciones deseadas y luego se calcula la DFT inversa. En el dominio del tiempo, solo se mantienen los primeros N coeficientes (los otros coeficientes se establecen en cero). Luego, el proceso se repite de forma iterativa: se calcula la DFT una vez más, se aplica la corrección en el dominio de la frecuencia, y así sucesivamente.

Los paquetes de software como MATLAB , GNU Octave , Scilab y SciPy proporcionan formas convenientes de aplicar estos diferentes métodos.

En el método de diseño de ventana, primero se diseña un filtro IIR ideal y luego se trunca la respuesta de impulso infinita multiplicándola por una función de ventana de longitud finita . El resultado es un filtro de respuesta de impulso finito cuya respuesta de frecuencia se modifica con respecto a la del filtro IIR. Al multiplicar el impulso infinito por la función de ventana en el dominio del tiempo, se obtiene como resultado que la respuesta de frecuencia del IIR se convolucione con la transformada de Fourier (o DTFT) de la función de ventana. Si el lóbulo principal de la ventana es angosto, la respuesta de frecuencia compuesta permanece cercana a la del filtro IIR ideal.

La respuesta ideal es a menudo rectangular, y el IIR correspondiente es una función sinc . El resultado de la convolución del dominio de frecuencia es que los bordes del rectángulo se estrechan y aparecen ondulaciones en la banda de paso y la banda de supresión. Trabajando hacia atrás, se puede especificar la pendiente (o ancho) de la región estrechada ( banda de transición ) y la altura de las ondulaciones, y de ese modo derivar los parámetros del dominio de frecuencia de una función de ventana apropiada. Continuar hacia atrás hasta una respuesta de impulso se puede hacer iterando un programa de diseño de filtros para encontrar el orden de filtro mínimo. Otro método es restringir el conjunto de soluciones a la familia paramétrica de ventanas de Kaiser , que proporciona relaciones de forma cerrada entre los parámetros del dominio del tiempo y del dominio de la frecuencia. En general, ese método no logrará el orden de filtro mínimo posible, pero es particularmente conveniente para aplicaciones automatizadas que requieren un diseño de filtro dinámico sobre la marcha.

El método de diseño de ventana también es ventajoso para crear filtros de media banda eficientes , porque la función sinc correspondiente es cero en cada uno de los otros puntos de muestra (excepto el central). El producto con la función de ventana no altera los ceros, por lo que casi la mitad de los coeficientes de la respuesta al impulso final son cero. Una implementación adecuada de los cálculos FIR puede aprovechar esa propiedad para duplicar la eficiencia del filtro.

Meta:

Para diseñar un filtro FIR en el sentido MSE, minimizamos el error cuadrático medio entre el filtro que obtuvimos y el filtro deseado.

${\displaystyle {\text{MSE}}=f_{s}^{-1}\int _{-f_{s}/2}^{f_{s}/2}|H(f)-H_{d}(f)|^{2}\,df}$, donde es la frecuencia de muestreo, es el espectro del filtro que obtuvimos y es el espectro del filtro deseado.${\displaystyle f_{s}\,}$${\displaystyle H(f)\,}$$Estilo de visualización H_{d}(f)\,}$

Método:

Dado un filtro FIR de N puntos , y .${\displaystyle h[n]}$${\displaystyle r[n]=h[n+k],k={\frac {(N-1)}{2}}}$

Paso 1: Supongamos que incluso simétrica. Entonces, la transformada de Fourier de tiempo discreto de se define como${\displaystyle h[n]}$${\displaystyle r[n]}$

${\displaystyle R(F)=e^{j2\pi Fk}H(F)=\sum _ {n=0}^{k}s[n]\cos(2\pi nF)}$

Paso 2: Calcular el error cuadrático medio.

${\displaystyle {\text{MSE}}=\int _{-1/2}^{1/2}|R(F)-H_{d}(F)|^{2}\,dF}$

Por lo tanto,

${\displaystyle {\text{MSE}}=\int _{-1/2}^{1/2}\sum _{n=0}^{k}s[n]\cos(2\pi nF)\sum _{\tau =0}^{k}s[\tau ]\cos(2\pi \tau F)\,dF-2\int _{-1/2}^{1/2}\sum _{n=0}^{k}s[n]\cos(2\pi nF)H_{d}\,dF+\int _{-1/2}^{1/2}H_{d}(F)^{2}\,dF}$

Paso 3: Minimizar el error cuadrático medio haciendo la derivada parcial de MSE con respecto a${\displaystyle s[n]}$

${\displaystyle {\frac {\partial {\text{MSE}}}{\partial s[n]}}=2\sum _{\tau =0}^{k}s[\tau ]\int _{-1/2}^{1/2}\cos(2\pi nF)\cos(2\pi \tau F)\,dF-2\int _{-1/2}^{1/2}H_{d}(F)^{2}\cos(2\pi nF)\,dF=0}$

Después de la organización, tenemos

${\displaystyle s[0]=\int _{-1/2}^{1/2}H_{d}(F)\,dF}$

${\displaystyle s[n]=\int _{-1/2}^{1/2}\cos(2\pi nF)H_{d}(F)\,dF,\ {\text{ for }}n\neq 0}$

Paso 4: Vuelva a la presentación de${\displaystyle s[n]}$${\displaystyle h[n]}$

${\displaystyle h[k]=s[0],h[k+n]=s[n]/2,h[k-n]=s[n]/2,\;for\;n=1,2,3,\ldots ,k,{\text{ where }}k=(N-1)/2}$y${\displaystyle h[n]=0{\text{ for }}n<0{\text{ and }}n\geq N}$

Además, podemos tratar la importancia de la banda de paso y la banda de supresión de manera diferente según nuestras necesidades agregando una función ponderada. Entonces, el error MSE se convierte en${\displaystyle W(f)}$

${\displaystyle {\text{MSE}}=\int _{-1/2}^{1/2}W(F)|R(F)-H_{d}(F)|^{2}\,dF}$

Un filtro de media móvil es un filtro FIR muy simple. A veces se lo denomina filtro boxcar , especialmente cuando va seguido de una decimación o de una sinc-in-frequency . Los coeficientes del filtro, , se obtienen mediante la siguiente ecuación:${\textstyle b_{0},\ldots ,b_{N}}$

${\displaystyle b_{i}={\frac {1}{N+1}}}$

Para proporcionar un ejemplo más específico, seleccionamos el orden de filtro:

${\displaystyle N=2}$

La respuesta al impulso del filtro resultante es :

${\displaystyle h[n]={\frac {1}{3}}\delta [n]+{\frac {1}{3}}\delta [n-1]+{\frac {1}{3}}\delta [n-2]}$

El diagrama de bloques de la derecha muestra el filtro de promedio móvil de segundo orden que se analiza a continuación. La función de transferencia es :

${\displaystyle H(z)={\frac {1}{3}}+{\frac {1}{3}}z^{-1}+{\frac {1}{3}}z^{-2}={\frac {1}{3}}{\frac {z^{2}+z+1}{z^{2}}}.}$

La siguiente figura muestra el diagrama polo-cero correspondiente . La frecuencia cero (DC) corresponde a (1, 0), las frecuencias positivas avanzan en sentido antihorario alrededor del círculo hasta la frecuencia de Nyquist en (−1, 0). Dos polos se encuentran en el origen y dos ceros en , .${\textstyle z_{1}=-{\frac {1}{2}}+j{\frac {\sqrt {3}}{2}}}$${\textstyle z_{2}=-{\frac {1}{2}}-j{\frac {\sqrt {3}}{2}}}$

La respuesta de frecuencia, en términos de frecuencia normalizada ω , es :

${\displaystyle {\begin{aligned}H\left(e^{j\omega }\right)&={\frac {1}{3}}+{\frac {1}{3}}e^{-j\omega }+{\frac {1}{3}}e^{-j2\omega }\\&={\frac {1}{3}}e^{-j\omega }\left(1+2\cos(\omega )\right).\end{aligned}}}$

Los componentes de magnitud y fase de se representan gráficamente en la figura. Pero también se pueden generar gráficos como estos haciendo una transformada de Fourier discreta (DFT) de la respuesta al impulso. ^[B] Y debido a la simetría, el diseño del filtro o el software de visualización a menudo muestran solo la región [0, π]. El gráfico de magnitud indica que el filtro de promedio móvil pasa frecuencias bajas con una ganancia cercana a 1 y atenúa frecuencias altas, y por lo tanto es un filtro de paso bajo rudimentario . El gráfico de fase es lineal excepto por las discontinuidades en las dos frecuencias donde la magnitud tiende a cero. El tamaño de las discontinuidades es π, lo que representa una inversión de signo. No afectan la propiedad de fase lineal, como se ilustra en la figura final.${\textstyle H\left(e^{j\omega }\right)}$

• Filtro peine integrador en cascada
• Soporte compacto
• Línea de retardo digital
• Filtro electrónico
• Filtro (procesamiento de señales)
• Diseño de filtros
• Función de transferencia FIR
• Filtro de respuesta de impulso infinito (IIR)
• Transformada Z (específicamente ecuación de diferencia lineal de coeficientes constantes )