Decagramo (geometría)
| Decagramo regular | |
|---|---|
 Un decagramo regular | |
| Tipo | Polígono estrellado regular |
| Aristas y vértices | 10 |
| Símbolo de Schläfli | {10/3} y {5/3} |
| Diagramas de Coxeter-Dynkin |       |
| Grupo de simetría | Diédrico (D 10 ) |
| Angulo interno ( grados ) | 72° |
| Propiedades | estrella , cíclica , equilátera , isogonal , isotoxal |
| Polígono dual | ser |
| Polígonos estelares |
|---|
En geometría , un decagrama es un polígono en forma de estrella de 10 puntas . Existe un decagrama regular, que contiene los vértices de un decágono regular , pero que se conectan entre sí por cada tercer punto. Su símbolo de Schläfli es {10/3}. [1]
El nombre decagramo combina un prefijo numeral , deca- , con el sufijo griego -gramo . El sufijo -gramo deriva de γραμμῆς ( grammēs ), que significa línea. [2]
Decagramo regular
Para un decagramo regular con longitudes de arista unitarias, las proporciones de los puntos de cruce en cada arista son las que se muestran a continuación.
Aplicaciones
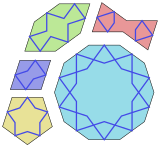
Los decagramas se han utilizado como uno de los motivos decorativos en los azulejos girih . [3]
Variaciones isotoxales
Un polígono isotoxal tiene dos vértices y una arista. Existen formas de decagramas isotoxales, que alternan vértices en dos radios. Cada forma tiene la libertad de un ángulo. La primera es una variación de un pentágono de doble vuelta {5}, y la última es una variación de un pentagrama de doble vuelta {5/2}. La del medio es una variación de un decagrama regular, {10/3}.
 (5/2) α } |  (5/3) α } |  (5/4) α } |
Cifras relacionadas
Un decagrama regular es un poligrama de diez lados , representado por el símbolo {10/n}, que contiene los mismos vértices que un decágono regular. Solo uno de estos poligramas, {10/3} (que conecta cada tercer punto), forma un polígono estrellado regular , pero también hay tres poligramas de diez vértices que pueden interpretarse como compuestos regulares:
- {10/5} es un compuesto de cinco dígonos degenerados 5{2}
- {10/4} es un compuesto de dos pentagramas 2{5/2}
- {10/2} es un compuesto de dos pentágonos 2{5}. [4] [5]
| Forma | Convexo | Compuesto | Polígono estrellado | Compuestos | |
|---|---|---|---|---|---|
| Imagen |  | 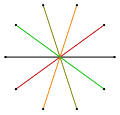.svg/1280px-Regular_star_figure_2(5,1).svg.png) | | .svg/1280px-Regular_star_figure_2(5,2).svg.png) | .svg/1280px-Regular_star_figure_5(2,1).svg.png) |
| Símbolo | {10/1} = {10} | {10/2} = 2{5} | {10/3} | {10/4} = 2{5/2} | {10/5} = 5{2} |
.svg){kind=link}
.svg){kind=link}
.svg){kind=link}
{10/2} puede verse como el equivalente 2D del compuesto 3D del dodecaedro y el icosaedro y del compuesto 4D de 120 celdas y 600 celdas ; es decir, el compuesto de dos politopos pentagonales en sus respectivas posiciones duales.
{10/4} puede considerarse como el equivalente bidimensional del compuesto tridimensional de un pequeño dodecaedro estrellado y un gran dodecaedro o del compuesto de un gran icosaedro y un gran dodecaedro estrellado por razones similares. Tiene seis análogos cuatridimensionales, dos de los cuales son compuestos de dos politopos estelares autoduales, como el propio pentagrama; el compuesto de dos grandes 120 celdas y el compuesto de dos grandes 120 celdas estelares. Se puede ver una lista completa en Compuesto politópico#Compuestos con duales .
Truncamientos más profundos del pentágono regular y del pentagrama pueden producir formas intermedias de polígonos estelares con diez vértices igualmente espaciados y dos longitudes de arista que permanecen transitivas en relación con los vértices (cualesquiera dos vértices pueden transformarse entre sí mediante una simetría de la figura). [6] [7] [8]
| Cuasiregular | Isogonal | Cobertura doble cuasirregular | |
|---|---|---|---|
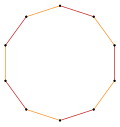 t{5} = {10} | 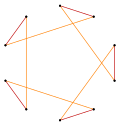 |  |  t{5/4} = {10/4} = 2{5/2} |
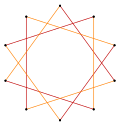 t{5/3} = {10/3} |  | 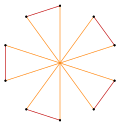 |  t{5/2} = {10/2} = 2{5} |
Véase también
Referencias
- ^ Barnes, John (2012), Gemas de geometría, Springer, págs. 28-29, ISBN 9783642309649.
- ^ γραμμή, Henry George Liddell, Robert Scott, Un léxico griego-inglés , sobre Perseo
- ^ Sarhangi, Reza (2012), "Modularidad poliédrica en una clase especial de polígonos estelares entrelazados basados en decagramas", Bridges 2012: Mathematics, Music, Art, Architecture, Culture (PDF) , págs. 165-174.
- ^ Politopos regulares, pág. 93-95, polígonos estelares regulares, compuestos estelares regulares
- ^ Coxeter, Introducción a la geometría, segunda edición, 2.8 Polígonos estelares , págs. 36-38
- ^ El lado más luminoso de las matemáticas: Actas de la Conferencia conmemorativa Eugène Strens sobre matemáticas recreativas y su historia, (1994), Metamorfosis de polígonos , Branko Grünbaum .
- ^ * Coxeter, Harold Scott MacDonald ; Longuet-Higgins, MS; Miller, JCP (1954). "Poliedros uniformes". Philosophical Transactions of the Royal Society of London. Series A. Ciencias matemáticas y físicas . 246 (916). The Royal Society : 411. Bibcode :1954RSPTA.246..401C. doi :10.1098/rsta.1954.0003. ISSN 0080-4614. JSTOR 91532. MR 0062446. S2CID 202575183.
- ^ Coxeter, The Densities of the Regular polytopes I, p.43 Si d es impar, el truncamiento del polígono {p/q} es naturalmente {2n/d}. Pero si no lo es, consta de dos {n/(d/2)} coincidentes; dos, porque cada lado surge de un lado original y uno de un vértice original. Por lo tanto, la densidad de un polígono no se altera por el truncamiento.
