Análisis factorial

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed. Find sources: "Factor analysis" – news · newspapers · books · scholar · JSTOR (August 2023) (Learn how and when to remove this message)

El análisis factorial es un método estadístico utilizado para describir la variabilidad entre variables observadas y correlacionadas en términos de un número potencialmente menor de variables no observadas llamadas factores . Por ejemplo, es posible que las variaciones en seis variables observadas reflejen principalmente las variaciones en dos variables no observadas (subyacentes). El análisis factorial busca tales variaciones conjuntas en respuesta a variables latentes no observadas . Las variables observadas se modelan como combinaciones lineales de los factores potenciales más los términos de " error ", por lo tanto, el análisis factorial puede considerarse como un caso especial de modelos de errores en las variables . ^[1]

En términos simples, la carga factorial de una variable cuantifica el grado en que la variable está relacionada con un factor dado. ^[2]

Una razón común detrás de los métodos de análisis factorial es que la información obtenida sobre las interdependencias entre las variables observadas se puede utilizar más tarde para reducir el conjunto de variables en un conjunto de datos. El análisis factorial se utiliza comúnmente en psicometría , psicología de la personalidad , biología, marketing , gestión de productos , investigación de operaciones , finanzas y aprendizaje automático . Puede ayudar a tratar con conjuntos de datos donde hay un gran número de variables observadas que se cree que reflejan un número menor de variables subyacentes/latentes. Es una de las técnicas de interdependencia más utilizadas y se utiliza cuando el conjunto relevante de variables muestra una interdependencia sistemática y el objetivo es descubrir los factores latentes que crean una similitud.

El modelo intenta explicar un conjunto de observaciones en cada uno de los individuos con un conjunto de factores comunes ( ) donde hay menos factores por unidad que observaciones por unidad ( ). Cada individuo tiene sus propios factores comunes, y estos se relacionan con las observaciones a través de la matriz de carga factorial ( ), para una sola observación, según${\displaystyle p}$${\displaystyle n}$${\displaystyle k}$ ${\displaystyle f_{i,j}}$${\displaystyle k<p}$${\displaystyle k}$${\displaystyle L\in \mathbb {R} ^{p\times k}}$

${\displaystyle x_{i,m}-\mu _{i}=l_{i,1}f_{1,m}+\dots +l_{i,k}f_{k,m}+\varepsilon _{i,m}}$

dónde

• ${\displaystyle x_{i,m}}$es el valor de la observación del individuo,${\displaystyle i}$${\displaystyle m}$
• ${\displaystyle \mu _{i}}$es la media de observación para la observación ésima,${\displaystyle i}$
• ${\displaystyle l_{i,j}}$es la carga para la observación ésima del factor ésimo,${\displaystyle i}$${\displaystyle j}$
• ${\displaystyle f_{j,m}}$es el valor del factor ésimo del individuo ésimo, y${\displaystyle j}$${\displaystyle m}$
• ${\displaystyle \varepsilon _{i,m}}$es el término de error estocástico no observado con media cero y varianza finita.${\displaystyle (i,m)}$

En notación matricial

${\displaystyle X-\mathrm {M} =LF+\varepsilon }$

donde matriz de observación , matriz de carga , matriz de factores , matriz de términos de error y matriz de media donde el elemento th es simplemente .${\displaystyle X\in \mathbb {R} ^{p\times n}}$${\displaystyle L\in \mathbb {R} ^{p\times k}}$${\displaystyle F\in \mathbb {R} ^{k\times n}}$${\displaystyle \varepsilon \in \mathbb {R} ^{p\times n}}$${\displaystyle \mathrm {M} \in \mathbb {R} ^{p\times n}}$${\displaystyle (i,m)}$${\displaystyle \mathrm {M} _{i,m}=\mu _{i}}$

También impondremos las siguientes suposiciones :${\displaystyle F}$

1. ${\displaystyle F}$y son independientes.${\displaystyle \varepsilon }$
2. ${\displaystyle \mathrm {E} (F)=0}$;¿Dónde está la expectativa?${\displaystyle \mathrm {E} }$
3. ${\displaystyle \mathrm {Cov} (F)=I}$donde es la matriz de covarianza , para asegurarse de que los factores no estén correlacionados, y es la matriz identidad .${\displaystyle \mathrm {Cov} }$${\displaystyle I}$

Supongamos que... Entonces${\displaystyle \mathrm {Cov} (X-\mathrm {M} )=\Sigma }$

${\displaystyle \Sigma =\mathrm {Cov} (X-\mathrm {M} )=\mathrm {Cov} (LF+\varepsilon ),\,}$

y por lo tanto, de las condiciones 1 y 2 impuestas anteriormente , y , dando${\displaystyle F}$${\displaystyle E[LF]=LE[F]=0}$${\displaystyle Cov(LF+\epsilon )=Cov(LF)+Cov(\epsilon )}$

${\displaystyle \Sigma =L\mathrm {Cov} (F)L^{T}+\mathrm {Cov} (\varepsilon ),\,}$

o, configuración ,${\displaystyle \Psi :=\mathrm {Cov} (\varepsilon )}$

${\displaystyle \Sigma =LL^{T}+\Psi .\,}$

Para cualquier matriz ortogonal , si establecemos y , los criterios para ser factores y cargas factoriales aún se mantienen. Por lo tanto, un conjunto de factores y cargas factoriales es único solo hasta una transformación ortogonal .${\displaystyle Q}$${\displaystyle L^{\prime }=\ LQ}$${\displaystyle F^{\prime }=Q^{T}F}$

Supongamos que un psicólogo tiene la hipótesis de que hay dos tipos de inteligencia , la "inteligencia verbal" y la "inteligencia matemática", ninguna de las cuales se observa directamente. ^{[nota 1] Se busca} evidencia de la hipótesis en las calificaciones de los exámenes de cada uno de los 10 campos académicos diferentes de 1000 estudiantes. Si cada estudiante se elige al azar de una gran población , entonces las 10 calificaciones de cada estudiante son variables aleatorias. La hipótesis del psicólogo puede decir que para cada uno de los 10 campos académicos, la calificación promediada sobre el grupo de todos los estudiantes que comparten algún par común de valores para las "inteligencias" verbal y matemática es una constante multiplicada por su nivel de inteligencia verbal más otra constante multiplicada por su nivel de inteligencia matemática, es decir, es una combinación lineal de esos dos "factores". Los números para una materia en particular, por los que se multiplican los dos tipos de inteligencia para obtener la calificación esperada, son postulados por la hipótesis como los mismos para todos los pares de niveles de inteligencia, y se denominan "carga factorial" para esta materia. ^{[ aclaración necesaria ]} Por ejemplo, la hipótesis puede sostener que la aptitud promedio prevista del estudiante en el campo de la astronomía es

{10 × la inteligencia verbal del estudiante} + {6 × la inteligencia matemática del estudiante}.

Los números 10 y 6 son las cargas factoriales asociadas con la astronomía. Otras materias académicas pueden tener cargas factoriales diferentes.

Dos estudiantes que se supone que tienen grados idénticos de inteligencia verbal y matemática pueden tener diferentes aptitudes medidas en astronomía porque las aptitudes individuales difieren de las aptitudes promedio (predichas anteriormente) y debido al error de medición en sí. Tales diferencias conforman lo que colectivamente se denomina el "error", un término estadístico que significa la cantidad en la que un individuo, según se mide, difiere de lo que es promedio o predicho por sus niveles de inteligencia (ver errores y residuos en estadística ).

Los datos observables que se incluyen en el análisis factorial serían 10 puntuaciones de cada uno de los 1000 estudiantes, lo que supone un total de 10 000 números. Las cargas factoriales y los niveles de los dos tipos de inteligencia de cada estudiante deben inferirse a partir de los datos.

En lo que sigue, las matrices se indicarán mediante variables indexadas. Los índices de "sujeto" se indicarán mediante las letras , y , con valores que van desde hasta que es igual a en el ejemplo anterior. Los índices de "factor" se indicarán mediante las letras , y , con valores que van desde hasta que es igual a en el ejemplo anterior. Los índices de "instancia" o "muestra" se indicarán mediante las letras , y , con valores que van desde hasta . En el ejemplo anterior, si una muestra de estudiantes participó en los exámenes, la puntuación del estudiante número uno para el examen número uno viene dada por . El propósito del análisis factorial es caracterizar las correlaciones entre las variables de las que son una instancia particular o un conjunto de observaciones. Para que las variables estén en igualdad de condiciones, se normalizan en puntuaciones estándar :${\displaystyle a}$${\displaystyle b}$${\displaystyle c}$${\displaystyle 1}$${\displaystyle p}$${\displaystyle 10}$${\displaystyle p}$${\displaystyle q}$${\displaystyle r}$${\displaystyle 1}$${\displaystyle k}$${\displaystyle 2}$${\displaystyle i}$${\displaystyle j}$${\displaystyle k}$${\displaystyle 1}$${\displaystyle N}$${\displaystyle N=1000}$${\displaystyle p=10}$${\displaystyle i}$${\displaystyle a}$${\displaystyle x_{ai}}$${\displaystyle x_{a}}$${\displaystyle x_{ai}}$${\displaystyle z}$

${\displaystyle z_{ai}={\frac {x_{ai}-{\hat {\mu }}_{a}}{{\hat {\sigma }}_{a}}}}$

donde la media de la muestra es:

${\displaystyle {\hat {\mu }}_{a}={\tfrac {1}{N}}\sum _{i}x_{ai}}$

y la varianza de la muestra viene dada por:

${\displaystyle {\hat {\sigma }}_{a}^{2}={\tfrac {1}{N-1}}\sum _{i}(x_{ai}-{\hat {\mu }}_{a})^{2}}$

El modelo de análisis factorial para esta muestra particular es entonces:

${\displaystyle {\begin{matrix}z_{1,i}&=&\ell _{1,1}F_{1,i}&+&\ell _{1,2}F_{2,i}&+&\varepsilon _{1,i}\\\vdots &&\vdots &&\vdots &&\vdots \\z_{10,i}&=&\ell _{10,1}F_{1,i}&+&\ell _{10,2}F_{2,i}&+&\varepsilon _{10,i}\end{matrix}}}$

o, más sucintamente:

${\displaystyle z_{ai}=\sum _{p}\ell _{ap}F_{pi}+\varepsilon _{ai}}$

dónde

• ${\displaystyle F_{1i}}$es la "inteligencia verbal" del estudiante,${\displaystyle i}$
• ${\displaystyle F_{2i}}$es la "inteligencia matemática" del estudiante,${\displaystyle i}$
• ${\displaystyle \ell _{ap}}$son las cargas factoriales para el sujeto , para .${\displaystyle a}$${\displaystyle p=1,2}$

En notación matricial , tenemos

${\displaystyle Z=LF+\varepsilon }$

Obsérvese que duplicar la escala en la que se mide la "inteligencia verbal" (el primer componente de cada columna de ) y reducir simultáneamente a la mitad las cargas factoriales de la inteligencia verbal no produce ninguna diferencia en el modelo. Por lo tanto, no se pierde ninguna generalidad al suponer que la desviación estándar de los factores de la inteligencia verbal es . Lo mismo ocurre con la inteligencia matemática. Además, por razones similares, no se pierde ninguna generalidad al suponer que los dos factores no están correlacionados entre sí. En otras palabras:${\displaystyle F}$${\displaystyle 1}$

${\displaystyle \sum _{i}F_{pi}F_{qi}=\delta _{pq}}$

donde es el delta de Kronecker ( cuando y cuando ). Se supone que los errores son independientes de los factores:${\displaystyle \delta _{pq}}$${\displaystyle 0}$${\displaystyle p\neq q}$${\displaystyle 1}$${\displaystyle p=q}$

${\displaystyle \sum _{i}F_{pi}\varepsilon _{ai}=0}$

Dado que cualquier rotación de una solución es también una solución, esto dificulta la interpretación de los factores. Vea las desventajas a continuación. En este ejemplo particular, si no sabemos de antemano que los dos tipos de inteligencia no están correlacionados, entonces no podemos interpretar los dos factores como dos tipos diferentes de inteligencia. Incluso si no están correlacionados, no podemos decir qué factor corresponde a la inteligencia verbal y cuál corresponde a la inteligencia matemática sin un argumento externo.

Los valores de las cargas , los promedios y las varianzas de los "errores" deben estimarse a partir de los datos observados y (el supuesto sobre los niveles de los factores es fijo para un determinado ). El "teorema fundamental" puede derivarse de las condiciones anteriores:${\displaystyle L}$${\displaystyle \mu }$${\displaystyle \varepsilon }$${\displaystyle X}$${\displaystyle F}$${\displaystyle F}$

${\displaystyle \sum _{i}z_{ai}z_{bi}=\sum _{j}\ell _{aj}\ell _{bj}+\sum _{i}\varepsilon _{ai}\varepsilon _{bi}}$

El término de la izquierda es el término de la matriz de correlación (una matriz derivada como el producto de la matriz de observaciones estandarizadas con su transpuesta) de los datos observados, y sus elementos diagonales serán s. El segundo término de la derecha será una matriz diagonal con términos menores que la unidad. El primer término de la derecha es la "matriz de correlación reducida" y será igual a la matriz de correlación excepto por sus valores diagonales que serán menores que la unidad. Estos elementos diagonales de la matriz de correlación reducida se denominan "comunalidades" (que representan la fracción de la varianza en la variable observada que se explica por los factores):${\displaystyle (a,b)}$${\displaystyle p\times p}$${\displaystyle p\times N}$${\displaystyle p}$${\displaystyle 1}$

${\displaystyle h_{a}^{2}=1-\psi _{a}=\sum _{j}\ell _{aj}\ell _{aj}}$

Los datos de muestra no obedecerán exactamente a la ecuación fundamental dada anteriormente debido a errores de muestreo, insuficiencia del modelo, etc. El objetivo de cualquier análisis del modelo anterior es encontrar los factores y las cargas que proporcionen un "mejor ajuste" a los datos. En el análisis factorial, el mejor ajuste se define como el mínimo del error cuadrático medio en los residuos fuera de la diagonal de la matriz de correlación: ^[3]${\displaystyle z_{ai}}$${\displaystyle F_{pi}}$${\displaystyle \ell _{ap}}$

${\displaystyle \varepsilon ^{2}=\sum _{a\neq b}\left[\sum _{i}z_{ai}z_{bi}-\sum _{j}\ell _{aj}\ell _{bj}\right]^{2}}$

Esto equivale a minimizar los componentes fuera de la diagonal de la covarianza del error que, en las ecuaciones del modelo, tienen valores esperados de cero. Esto debe contrastarse con el análisis de componentes principales que busca minimizar el error cuadrático medio de todos los residuos. ^[3] Antes de la llegada de las computadoras de alta velocidad, se dedicaba un esfuerzo considerable a encontrar soluciones aproximadas al problema, particularmente en la estimación de las comunalidades por otros medios, lo que luego simplificaba considerablemente el problema al producir una matriz de correlación reducida conocida. Esto luego se usaba para estimar los factores y las cargas. Con la llegada de las computadoras de alta velocidad, el problema de minimización se puede resolver iterativamente con la velocidad adecuada, y las comunalidades se calculan en el proceso, en lugar de ser necesarias de antemano. El algoritmo MinRes es particularmente adecuado para este problema, pero no es el único medio iterativo para encontrar una solución.

Si se permite que los factores de la solución estén correlacionados (como en la rotación 'oblimin', por ejemplo), entonces el modelo matemático correspondiente utiliza coordenadas sesgadas en lugar de coordenadas ortogonales.

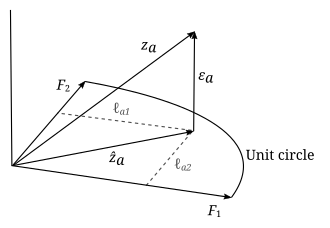
Los parámetros y variables del análisis factorial pueden recibir una interpretación geométrica. Los datos ( ), los factores ( ) y los errores ( ) pueden verse como vectores en un espacio euclidiano (espacio muestral) de dimensión 1, representados como , y , respectivamente. Dado que los datos están estandarizados, los vectores de datos tienen una longitud unitaria ( ). Los vectores factoriales definen un subespacio lineal de dimensión 1 (es decir, un hiperplano) en este espacio, sobre el cual se proyectan ortogonalmente los vectores de datos. Esto se desprende de la ecuación del modelo ${\displaystyle z_{ai}}$${\displaystyle F_{pi}}$${\displaystyle \varepsilon _{ai}}$${\displaystyle N}$${\displaystyle \mathbf {z} _{a}}$${\displaystyle \mathbf {F} _{p}}$${\displaystyle {\boldsymbol {\varepsilon }}_{a}}$${\displaystyle ||\mathbf {z} _{a}||=1}$${\displaystyle k}$

${\displaystyle \mathbf {z} _{a}=\sum _{p}\ell _{ap}\mathbf {F} _{p}+{\boldsymbol {\varepsilon }}_{a}}$

y la independencia de los factores y los errores: . En el ejemplo anterior, el hiperplano es simplemente un plano bidimensional definido por los dos vectores de factores. La proyección de los vectores de datos sobre el hiperplano está dada por ${\displaystyle \mathbf {F} _{p}\cdot {\boldsymbol {\varepsilon }}_{a}=0}$

${\displaystyle {\hat {\mathbf {z} }}_{a}=\sum _{p}\ell _{ap}\mathbf {F} _{p}}$

y los errores son vectores desde ese punto proyectado hasta el punto de datos y son perpendiculares al hiperplano. El objetivo del análisis factorial es encontrar un hiperplano que sea un "ajuste óptimo" para los datos en algún sentido, por lo que no importa cómo se elijan los vectores factoriales que definen este hiperplano, siempre que sean independientes y se encuentren en el hiperplano. Somos libres de especificarlos como ortogonales y normales ( ) sin pérdida de generalidad. Después de encontrar un conjunto adecuado de factores, también se pueden rotar arbitrariamente dentro del hiperplano, de modo que cualquier rotación de los vectores factoriales definirá el mismo hiperplano y también será una solución. Como resultado, en el ejemplo anterior, en el que el hiperplano de ajuste es bidimensional, si no sabemos de antemano que los dos tipos de inteligencia no están correlacionados, entonces no podemos interpretar los dos factores como los dos tipos diferentes de inteligencia. Incluso si no están correlacionados, no podemos decir qué factor corresponde a la inteligencia verbal y cuál corresponde a la inteligencia matemática, o si los factores son combinaciones lineales de ambos, sin un argumento externo.${\displaystyle \mathbf {F} _{p}\cdot \mathbf {F} _{q}=\delta _{pq}}$

Los vectores de datos tienen longitud unitaria. Las entradas de la matriz de correlación para los datos se dan por . La matriz de correlación se puede interpretar geométricamente como el coseno del ángulo entre los dos vectores de datos y . Los elementos diagonales serán claramente s y los elementos fuera de la diagonal tendrán valores absolutos menores o iguales a la unidad. La "matriz de correlación reducida" se define como ${\displaystyle \mathbf {z} _{a}}$${\displaystyle r_{ab}=\mathbf {z} _{a}\cdot \mathbf {z} _{b}}$${\displaystyle \mathbf {z} _{a}}$${\displaystyle \mathbf {z} _{b}}$${\displaystyle 1}$

${\displaystyle {\hat {r}}_{ab}={\hat {\mathbf {z} }}_{a}\cdot {\hat {\mathbf {z} }}_{b}}$.

El objetivo del análisis factorial es elegir el hiperplano de ajuste de modo que la matriz de correlación reducida reproduzca la matriz de correlación lo más fielmente posible, excepto los elementos diagonales de la matriz de correlación que se sabe que tienen un valor unitario. En otras palabras, el objetivo es reproducir con la mayor exactitud posible las correlaciones cruzadas en los datos. Específicamente, para el hiperplano de ajuste, el error cuadrático medio en los componentes fuera de la diagonal

${\displaystyle \varepsilon ^{2}=\sum _{a\neq b}\left(r_{ab}-{\hat {r}}_{ab}\right)^{2}}$

se debe minimizar, y esto se logra minimizándolo con respecto a un conjunto de vectores de factores ortonormales. Se puede ver que

${\displaystyle r_{ab}-{\hat {r}}_{ab}={\boldsymbol {\varepsilon }}_{a}\cdot {\boldsymbol {\varepsilon }}_{b}}$

El término de la derecha es simplemente la covarianza de los errores. En el modelo, se afirma que la covarianza de los errores es una matriz diagonal, por lo que el problema de minimización anterior producirá de hecho un "ajuste óptimo" para el modelo: producirá una estimación de muestra de la covarianza de los errores cuyos componentes no diagonales se minimizan en el sentido del cuadrado medio. Se puede ver que, dado que son proyecciones ortogonales de los vectores de datos, su longitud será menor o igual que la longitud del vector de datos proyectado, que es la unidad. El cuadrado de estas longitudes son simplemente los elementos diagonales de la matriz de correlación reducida. Estos elementos diagonales de la matriz de correlación reducida se conocen como "comunalidades":${\displaystyle {\hat {z}}_{a}}$

${\displaystyle {h_{a}}^{2}=||{\hat {\mathbf {z} }}_{a}||^{2}=\sum _{p}{\ell _{ap}}^{2}}$

Los valores elevados de las comunalidades indicarán que el hiperplano de ajuste reproduce con bastante precisión la matriz de correlación. Los valores medios de los factores también deben limitarse a cero, de lo que se deduce que los valores medios de los errores también serán cero.

This section needs additional citations for verification. Please help improve this article by adding citations to reliable sources in this section. Unsourced material may be challenged and removed. (April 2012) (Learn how and when to remove this message)

El análisis factorial exploratorio (AFE) se utiliza para identificar interrelaciones complejas entre elementos y grupos de elementos que forman parte de conceptos unificados. ^[4] El investigador no hace suposiciones a priori sobre las relaciones entre los factores. ^[4]

El análisis factorial confirmatorio (AFC) es un enfoque más complejo que prueba la hipótesis de que los elementos están asociados con factores específicos. ^[4] El AFC utiliza modelos de ecuaciones estructurales para probar un modelo de medición mediante el cual la carga en los factores permite la evaluación de las relaciones entre las variables observadas y las variables no observadas. ^[4] Los enfoques de modelos de ecuaciones estructurales pueden acomodar el error de medición y son menos restrictivos que la estimación de mínimos cuadrados . ^[4] Los modelos hipotéticos se prueban contra datos reales, y el análisis demostraría cargas de variables observadas en las variables latentes (factores), así como la correlación entre las variables latentes. ^[4]

El análisis de componentes principales (PCA) es un método ampliamente utilizado para la extracción de factores, que es la primera fase del EFA. ^[4] Los pesos de los factores se calculan para extraer la máxima varianza posible, y la factorización sucesiva continúa hasta que no quede más varianza significativa. ^[4] Luego, el modelo factorial debe rotarse para su análisis. ^[4]

El análisis factorial canónico, también llamado factorización canónica de Rao, es un método diferente para calcular el mismo modelo que el PCA, que utiliza el método del eje principal. El análisis factorial canónico busca los factores que tienen la correlación canónica más alta con las variables observadas. El análisis factorial canónico no se ve afectado por el reescalamiento arbitrario de los datos.

El análisis factorial común, también llamado análisis factorial principal (PFA) o factorización de ejes principales (PAF), busca la menor cantidad de factores que puedan explicar la varianza común (correlación) de un conjunto de variables.

La factorización de imágenes se basa en la matriz de correlación de variables predichas en lugar de variables reales, donde cada variable se predice a partir de las demás mediante regresión múltiple .

La factorización alfa se basa en maximizar la fiabilidad de los factores, suponiendo que las variables se seleccionan aleatoriamente de un universo de variables. Todos los demás métodos suponen que se seleccionan casos y que las variables son fijas.

El modelo de regresión factorial es un modelo combinatorio de modelo factorial y modelo de regresión; o alternativamente, puede verse como el modelo factorial híbrido, ^[5] cuyos factores son parcialmente conocidos.

Cargas factoriales

La comunalidad es el cuadrado de la carga externa estandarizada de un elemento. De manera análoga a la r-cuadrada de Pearson , la carga factorial al cuadrado es el porcentaje de varianza en esa variable indicadora explicada por el factor. Para obtener el porcentaje de varianza en todas las variables explicadas por cada factor, sume la suma de las cargas factoriales al cuadrado para ese factor (columna) y divida por el número de variables. (El número de variables es igual a la suma de sus varianzas, ya que la varianza de una variable estandarizada es 1). Esto es lo mismo que dividir el valor propio del factor por el número de variables.

En el análisis factorial confirmatorio, según una regla general, las cargas factoriales deben ser de 0,7 o más para confirmar que las variables independientes identificadas a priori están representadas por un factor en particular, partiendo del supuesto de que el nivel 0,7 corresponde aproximadamente a la mitad de la varianza del indicador que explica el factor. Sin embargo, el estándar 0,7 es alto y los datos de la vida real pueden no cumplir este criterio, por lo que algunos investigadores, en particular con fines exploratorios, utilizarán un nivel inferior, como 0,4 para el factor central y 0,25 para otros factores. En cualquier caso, las cargas factoriales deben interpretarse a la luz de la teoría, no mediante niveles de corte arbitrarios.

En la rotación oblicua , se puede examinar tanto una matriz de patrón como una matriz de estructura. La matriz de estructura es simplemente la matriz de carga de factores como en la rotación ortogonal, que representa la varianza en una variable medida explicada por un factor sobre una base de contribuciones únicas y comunes. La matriz de patrón, en cambio, contiene coeficientes que sólo representan contribuciones únicas. Cuantos más factores, más bajos serán los coeficientes de patrón, por regla general, ya que habrá más contribuciones comunes a la varianza explicada. En el caso de la rotación oblicua, el investigador observa tanto los coeficientes de estructura como los de patrón al atribuir una etiqueta a un factor. Los principios de la rotación oblicua se pueden derivar tanto de la entropía cruzada como de su entropía dual. ^[6]

Comunalidad

La suma de las cargas factoriales al cuadrado de todos los factores de una variable dada (fila) es la varianza de esa variable explicada por todos los factores. La comunalidad mide el porcentaje de varianza de una variable dada explicada por todos los factores en conjunto y puede interpretarse como la confiabilidad del indicador en el contexto de los factores postulados.

Soluciones espurias

Si la comunalidad excede 1,0, existe una solución espuria, que puede reflejar una muestra demasiado pequeña o la decisión de extraer demasiados o muy pocos factores.

Unicidad de una variable

La variabilidad de una variable menos su comunalidad.

Valores propios/raíces características

Los valores propios miden la cantidad de variación en la muestra total que explica cada factor. La relación de valores propios es la relación de la importancia explicativa de los factores con respecto a las variables. Si un factor tiene un valor propio bajo, entonces contribuye poco a la explicación de las variaciones en las variables y puede ignorarse por ser menos importante que los factores con valores propios más altos.

Sumas de extracción de cargas al cuadrado

Los valores propios iniciales y los valores propios después de la extracción (enumerados por SPSS como "sumas de extracción de cargas al cuadrado") son los mismos para la extracción de PCA, pero para otros métodos de extracción, los valores propios después de la extracción serán inferiores a sus contrapartes iniciales. SPSS también imprime "sumas de rotación de cargas al cuadrado" e incluso para PCA, estos valores propios diferirán de los valores propios iniciales y de extracción, aunque su total será el mismo.

Puntuaciones factoriales

Puntuaciones de los componentes (en PCA)

Explicado desde la perspectiva de PCA, no desde la perspectiva del análisis factorial.

Las puntuaciones de cada caso (fila) en cada factor (columna). Para calcular la puntuación factorial de un caso determinado para un factor determinado, se toma la puntuación estandarizada del caso en cada variable, se multiplica por las cargas correspondientes de la variable para el factor determinado y se suman estos productos. El cálculo de las puntuaciones factoriales permite buscar valores atípicos en los factores. Además, las puntuaciones factoriales se pueden utilizar como variables en modelos posteriores.

Los investigadores desean evitar criterios subjetivos o arbitrarios para la retención de factores como "para mí tenía sentido". Se han desarrollado varios métodos objetivos para resolver este problema, lo que permite a los usuarios determinar un rango apropiado de soluciones para investigar. ^[7] Sin embargo, estos diferentes métodos a menudo no están de acuerdo entre sí en cuanto al número de factores que se deben retener. Por ejemplo, el análisis paralelo puede sugerir 5 factores mientras que el MAP de Velicer sugiere 6, por lo que el investigador puede solicitar soluciones de 5 y 6 factores y discutir cada una en términos de su relación con los datos externos y la teoría.

Análisis paralelo de Horn (PA): ^[8] Un método de simulación basado en Monte-Carlo que compara los valores propios observados con los obtenidos a partir de variables normales no correlacionadas. Se retiene un factor o componente si el valor propio asociado es mayor que el percentil 95 de la distribución de valores propios derivados de los datos aleatorios. PA es una de las reglas más comúnmente recomendadas para determinar el número de componentes a retener, ^{[7] [9]} pero muchos programas no incluyen esta opción (una notable excepción es R ). ^[10] Sin embargo, Formann proporcionó evidencia tanto teórica como empírica de que su aplicación podría no ser apropiada en muchos casos ya que su desempeño está considerablemente influenciado por el tamaño de la muestra , la discriminación de ítems y el tipo de coeficiente de correlación . ^[11]

La prueba MAP de Velicer (1976) ^[12] , como la describe Courtney (2013) ^[13], “implica un análisis completo de los componentes principales seguido del examen de una serie de matrices de correlaciones parciales” (p. 397 (aunque esta cita no aparece en Velicer (1976) y el número de página citado está fuera de las páginas de la cita). La correlación al cuadrado para el Paso “0” (ver Figura 4) es la correlación al cuadrado promedio fuera de la diagonal para la matriz de correlación no parcializada. En el Paso 1, se eliminan parcialmente el primer componente principal y sus elementos asociados. A continuación, se calcula la correlación al cuadrado promedio fuera de la diagonal para la matriz de correlación posterior para el Paso 1. En el Paso 2, se eliminan parcialmente los dos primeros componentes principales y se calcula nuevamente la correlación al cuadrado promedio fuera de la diagonal resultante. Los cálculos se llevan a cabo para k menos un paso (k representa el número total de variables en la matriz). A continuación, se calculan todas las correlaciones al cuadrado promedio para cada paso. alineados y el número de paso en los análisis que dieron como resultado la correlación parcial cuadrática promedio más baja determina el número de componentes o factores a retener. ^[12] Mediante este método, los componentes se mantienen siempre que la varianza en la matriz de correlación represente la varianza sistemática, en oposición a la varianza residual o de error. Aunque metodológicamente similar al análisis de componentes principales, se ha demostrado que la técnica MAP funciona bastante bien para determinar el número de factores a retener en estudios de simulación múltiple. ^{[7] [14] [15] [16]} Este procedimiento está disponible a través de la interfaz de usuario de SPSS, ^[13] así como el paquete psych para el lenguaje de programación R. [ ^{17] [18]}

Criterio de Kaiser: La regla de Kaiser consiste en descartar todos los componentes con valores propios inferiores a 1,0 (este es el valor propio igual a la información que representa un elemento individual promedio). ^[19] El criterio de Kaiser es el predeterminado en SPSS y la mayoría del software estadístico , pero no se recomienda cuando se utiliza como único criterio de corte para estimar el número de factores, ya que tiende a extraer demasiados factores. ^[20] Se ha creado una variación de este método en la que un investigador calcula intervalos de confianza para cada valor propio y retiene solo los factores que tienen el intervalo de confianza completo mayor que 1,0. ^{[14] [21]}

Gráfico de scree : ^[22] El test de scree de Cattell traza los componentes como el eje X y los valores propios correspondientes como el eje Y. A medida que uno se mueve hacia la derecha, hacia los componentes posteriores, los valores propios caen. Cuando la caída cesa y la curva forma un codo hacia un declive menos pronunciado, el test de scree de Cattell dice que se deben descartar todos los componentes posteriores al que comienza en el codo. Esta regla a veces es criticada por ser susceptible de "manipulación" controlada por el investigador. Es decir, como elegir el "codo" puede ser subjetivo porque la curva tiene múltiples codos o es una curva suave, el investigador puede verse tentado a establecer el punto de corte en el número de factores deseados por su agenda de investigación. ^{[ cita requerida ]}

Criterios de explicación de la varianza: algunos investigadores simplemente utilizan la regla de mantener suficientes factores para explicar el 90 % (a veces el 80 %) de la variación. Cuando el objetivo del investigador enfatiza la parsimonia (explicar la varianza con la menor cantidad posible de factores), el criterio podría ser tan bajo como el 50 %.

Al colocar una distribución previa sobre el número de factores latentes y luego aplicar el teorema de Bayes, los modelos bayesianos pueden devolver una distribución de probabilidad sobre el número de factores latentes. Esto se ha modelado utilizando el proceso de buffet indio ^[23] , pero se puede modelar de manera más simple al colocar cualquier distribución previa discreta (por ejemplo, una distribución binomial negativa ) sobre el número de componentes.

El resultado del PCA maximiza la varianza explicada por el primer factor primero, luego por el segundo factor, etc. Una desventaja de este procedimiento es que la mayoría de los elementos se cargan en los factores iniciales, mientras que muy pocos elementos se cargan en las variables posteriores. Esto dificulta la interpretación de los factores mediante la lectura de una lista de preguntas y cargas, ya que cada pregunta está fuertemente correlacionada con los primeros componentes, mientras que muy pocas preguntas están fuertemente correlacionadas con los últimos componentes.

La rotación sirve para que los resultados sean más fáciles de interpretar. Al elegir una base diferente para los mismos componentes principales (es decir, elegir factores diferentes para expresar la misma estructura de correlación), es posible crear variables que sean más fáciles de interpretar.

Las rotaciones pueden ser ortogonales u oblicuas; las rotaciones oblicuas permiten que los factores se correlacionen. ^[24] Esta mayor flexibilidad significa que son posibles más rotaciones, algunas de las cuales pueden ser mejores para lograr un objetivo específico. Sin embargo, esto también puede hacer que los factores sean más difíciles de interpretar, ya que cierta información se "cuenta dos veces" y se incluye varias veces en diferentes componentes; algunos factores incluso pueden parecer casi duplicados entre sí.

Existen dos grandes clases de rotaciones ortogonales: aquellas que buscan filas dispersas (donde cada fila es un caso, es decir, un sujeto) y aquellas que buscan columnas dispersas (donde cada columna es una variable).

• Factores simples: estas rotaciones intentan explicar todos los factores utilizando solo unas pocas variables importantes. Este efecto se puede lograr utilizando Varimax (la rotación más común).
• Variables simples: estas rotaciones intentan explicar todas las variables utilizando solo unos pocos factores importantes. Este efecto se puede lograr utilizando Quartimax o los componentes no rotados del PCA.
• Ambos: estas rotaciones intentan alcanzar un equilibrio entre los dos objetivos anteriores, pero en el proceso pueden lograr un ajuste deficiente en ambas tareas; por lo tanto, son impopulares en comparación con los métodos anteriores. Equamax es una de esas rotaciones.

Puede resultar difícil interpretar una estructura factorial cuando cada variable se basa en múltiples factores. Pequeños cambios en los datos pueden a veces inclinar la balanza en el criterio de rotación de factores de modo que se produzca una rotación de factores completamente diferente. Esto puede dificultar la comparación de los resultados de diferentes experimentos. Este problema se ilustra mediante una comparación de diferentes estudios sobre diferencias culturales en todo el mundo. Cada estudio ha utilizado diferentes medidas de variables culturales y ha producido un resultado de análisis factorial rotado de forma diferente. Los autores de cada estudio creyeron que habían descubierto algo nuevo e inventaron nuevos nombres para los factores que encontraron. Una comparación posterior de los estudios descubrió que los resultados eran bastante similares cuando se comparaban los resultados no rotados. La práctica común de la rotación de factores ha oscurecido la similitud entre los resultados de los diferentes estudios. ^[25]

This article may be confusing or unclear to readers. Please help clarify the article. There might be a discussion about this on the talk page. (March 2010) (Learn how and when to remove this message)

El análisis factorial de orden superior es un método estadístico que consiste en repetir los pasos de análisis factorial – rotación oblicua – análisis factorial de factores rotados. Su mérito es permitir al investigador ver la estructura jerárquica de los fenómenos estudiados. Para interpretar los resultados, se procede ya sea por post-multiplicación de la matriz de patrón de factores primarios por las matrices de patrón de factores de orden superior (Gorsuch, 1983) y quizás aplicando una rotación Varimax al resultado (Thompson, 1990) o utilizando una solución Schmid-Leiman (SLS, Schmid & Leiman, 1957, también conocida como transformación Schmid-Leiman) que atribuye la variación de los factores primarios a los factores de segundo orden.

El análisis factorial está relacionado con el análisis de componentes principales (PCA), pero no son idénticos. ^[26] Ha habido una controversia significativa en el campo sobre las diferencias entre las dos técnicas. El PCA puede considerarse como una versión más básica del análisis factorial exploratorio (EFA) que se desarrolló en los primeros días antes de la llegada de las computadoras de alta velocidad. Tanto el PCA como el análisis factorial tienen como objetivo reducir la dimensionalidad de un conjunto de datos, pero los enfoques adoptados para hacerlo son diferentes para las dos técnicas. El análisis factorial está claramente diseñado con el objetivo de identificar ciertos factores no observables a partir de las variables observadas, mientras que el PCA no aborda directamente este objetivo; en el mejor de los casos, el PCA proporciona una aproximación a los factores requeridos. ^[27] Desde el punto de vista del análisis exploratorio, los valores propios del PCA son cargas de componentes infladas, es decir, contaminadas con varianza de error. ^{[28] [29] [30] [31] [32] [33]}

Aunque el EFA y el PCA se consideran técnicas sinónimas en algunos campos de la estadística, esto ha sido criticado. ^{[34] [35]} El análisis factorial "se ocupa de la suposición de una estructura causal subyacente : [supone] que la covariación en las variables observadas se debe a la presencia de una o más variables latentes (factores) que ejercen influencia causal sobre estas variables observadas". ^[36] Por el contrario, el PCA no supone ni depende de dicha relación causal subyacente. Los investigadores han argumentado que las distinciones entre las dos técnicas pueden significar que existen beneficios objetivos para preferir una sobre la otra en función del objetivo analítico. Si el modelo factorial está incorrectamente formulado o no se cumplen las suposiciones, entonces el análisis factorial dará resultados erróneos. El análisis factorial se ha utilizado con éxito cuando la comprensión adecuada del sistema permite buenas formulaciones del modelo inicial. El PCA emplea una transformación matemática de los datos originales sin suposiciones sobre la forma de la matriz de covarianza. El objetivo del PCA es determinar combinaciones lineales de las variables originales y seleccionar algunas que puedan usarse para resumir el conjunto de datos sin perder mucha información. ^[37]

Fabrigar et al. (1999) ^[34] abordan una serie de razones utilizadas para sugerir que el PCA no es equivalente al análisis factorial:

1. A veces se sugiere que el PCA es computacionalmente más rápido y requiere menos recursos que el análisis factorial. Fabrigar et al. sugieren que los recursos informáticos fácilmente disponibles han hecho que esta preocupación práctica sea irrelevante.
2. El PCA y el análisis factorial pueden producir resultados similares. Este punto también lo abordan Fabrigar et al.; en ciertos casos, en los que las comunalidades son bajas (por ejemplo, 0,4), las dos técnicas producen resultados divergentes. De hecho, Fabrigar et al. sostienen que en los casos en los que los datos corresponden a los supuestos del modelo de factores comunes, los resultados del PCA son inexactos.
3. Existen ciertos casos en los que el análisis factorial conduce a "casos Heywood". Estos incluyen situaciones en las que se estima que el 100% o más de la varianza en una variable medida está explicada por el modelo. Fabrigar et al. sugieren que estos casos son en realidad informativos para el investigador, ya que indican un modelo especificado incorrectamente o una violación del modelo de factor común. La falta de casos Heywood en el enfoque PCA puede significar que tales problemas pasan desapercibidos.
4. Los investigadores obtienen información adicional de un enfoque de PCA, como la puntuación de un individuo en un componente determinado; dicha información no se obtiene del análisis factorial. Sin embargo, como sostienen Fabrigar et al., el objetivo típico del análisis factorial (es decir, determinar los factores que explican la estructura de las correlaciones entre las variables medidas) no requiere el conocimiento de las puntuaciones factoriales y, por lo tanto, esta ventaja se anula. También es posible calcular las puntuaciones factoriales a partir de un análisis factorial.

El análisis factorial tiene en cuenta el error aleatorio inherente a la medición, mientras que el PCA no lo hace. Este punto lo ejemplifica Brown (2009), ^[38] quien indicó que, con respecto a las matrices de correlación involucradas en los cálculos:

"En el PCA, los 1.00 se colocan en la diagonal, lo que significa que se debe tener en cuenta toda la varianza de la matriz (incluida la varianza única de cada variable, la varianza común entre las variables y la varianza de error). Por lo tanto, por definición, eso incluiría toda la varianza de las variables. En cambio, en el EFA, las comunalidades se colocan en la diagonal, lo que significa que solo se debe tener en cuenta la varianza compartida con otras variables (excluyendo la varianza única de cada variable y la varianza de error). Por lo tanto, por definición, eso incluiría solo la varianza que es común entre las variables".

—  Brown (2009), Análisis de componentes principales y análisis factorial exploratorio: definiciones, diferencias y opciones

Por esta razón, Brown (2009) recomienda utilizar el análisis factorial cuando existen ideas teóricas sobre relaciones entre variables, mientras que el ACP debe utilizarse si el objetivo del investigador es explorar patrones en sus datos.

Suhr (2009) ilustra con más detalle las diferencias entre el PCA y el análisis factorial (AF): ^[35]

• El PCA da como resultado componentes principales que explican una cantidad máxima de varianza para las variables observadas; el AF da cuenta de la varianza común en los datos.
• PCA inserta unos en las diagonales de la matriz de correlación; FA ajusta las diagonales de la matriz de correlación con los factores únicos.
• PCA minimiza la suma de las distancias perpendiculares al cuadrado al eje del componente; FA estima los factores que influyen en las respuestas a las variables observadas.
• Las puntuaciones de los componentes en PCA representan una combinación lineal de las variables observadas ponderadas por vectores propios ; las variables observadas en FA son combinaciones lineales de los factores subyacentes y únicos.
• En PCA, los componentes obtenidos no son interpretables, es decir, no representan "construcciones" subyacentes; en FA, las construcciones subyacentes se pueden etiquetar e interpretar fácilmente, dada una especificación precisa del modelo.

Charles Spearman fue el primer psicólogo en analizar el análisis de factores comunes ^[39] y lo hizo en su artículo de 1904. ^[40] Proporcionó pocos detalles sobre sus métodos y se ocupó de modelos de un solo factor. ^[41] Descubrió que las puntuaciones de los niños en edad escolar en una amplia variedad de temas aparentemente no relacionados estaban correlacionados positivamente, lo que lo llevó a postular que una única capacidad mental general, o g , subyace y da forma al rendimiento cognitivo humano.

El desarrollo inicial del análisis factorial común con múltiples factores fue dado por Louis Thurstone en dos artículos a principios de la década de 1930, ^{[42] [43]} resumidos en su libro de 1935, The Vector of Mind . ^[44] Thurstone introdujo varios conceptos importantes de análisis factorial, incluyendo comunalidad, singularidad y rotación. ^[45] Abogó por una "estructura simple" y desarrolló métodos de rotación que podrían usarse como una forma de lograr dicha estructura. ^[39]

En la metodología Q , William Stephenson , alumno de Spearman, distingue entre el análisis factorial R , orientado al estudio de las diferencias interindividuales, y el análisis factorial Q orientado a las diferencias subjetivas intraindividuales. ^{[46] [47]}

Raymond Cattell fue un firme defensor del análisis factorial y la psicometría y utilizó la teoría multifactorial de Thurstone para explicar la inteligencia. Cattell también desarrolló el test de detección de errores y los coeficientes de similitud.

El análisis factorial se utiliza para identificar los "factores" que explican una variedad de resultados en diferentes pruebas. Por ejemplo, la investigación sobre inteligencia descubrió que las personas que obtienen una puntuación alta en una prueba de habilidad verbal también son buenas en otras pruebas que requieren habilidades verbales. Los investigadores explicaron esto utilizando el análisis factorial para aislar un factor, a menudo llamado inteligencia verbal, que representa el grado en el que alguien es capaz de resolver problemas que involucran habilidades verbales. ^{[ cita requerida ]}

El análisis factorial en psicología se asocia con mayor frecuencia a la investigación sobre inteligencia. Sin embargo, también se ha utilizado para encontrar factores en una amplia gama de dominios, como la personalidad, las actitudes, las creencias, etc. Está vinculado a la psicometría , ya que puede evaluar la validez de un instrumento al determinar si el instrumento mide efectivamente los factores postulados. ^{[ cita requerida ]}

• Reducción del número de variables, mediante la combinación de dos o más variables en un único factor. Por ejemplo, el rendimiento en carreras, lanzamiento de pelota, bateo, salto y levantamiento de pesas se podría combinar en un único factor, como la capacidad atlética general. Por lo general, en una matriz de elementos por personas, los factores se seleccionan agrupando elementos relacionados. En la técnica de análisis de factores Q, la matriz se transpone y los factores se crean agrupando personas relacionadas. Por ejemplo, los liberales, libertarios, conservadores y socialistas podrían formar grupos separados.
• Identificación de grupos de variables interrelacionadas, para ver cómo se relacionan entre sí. Por ejemplo, Carroll utilizó el análisis factorial para construir su teoría de los tres estratos . Descubrió que un factor llamado "percepción visual amplia" se relaciona con la capacidad de un individuo para realizar tareas visuales. También encontró un factor de "percepción auditiva amplia", relacionado con la capacidad para realizar tareas auditivas. Además, encontró un factor global, llamado "g" o inteligencia general, que se relaciona tanto con la "percepción visual amplia" como con la "percepción auditiva amplia". Esto significa que es probable que alguien con una "g" alta tenga tanto una capacidad de "percepción visual" alta como una capacidad de "percepción auditiva" alta, y que "g" explica, por lo tanto, una buena parte de por qué alguien es bueno o malo en ambos dominios.

• "...cada orientación es igualmente aceptable matemáticamente. Pero diferentes teorías factoriales demostraron diferir tanto en términos de las orientaciones de los ejes factoriales para una solución dada como en términos de cualquier otra cosa, de modo que el ajuste del modelo no resultó útil para distinguir entre teorías" (Sternberg, 1977 ^[48] ). Esto significa que todas las rotaciones representan diferentes procesos subyacentes, pero todas las rotaciones son resultados igualmente válidos de la optimización del análisis factorial estándar. Por lo tanto, es imposible elegir la rotación adecuada utilizando únicamente el análisis factorial.
• El análisis factorial solo puede ser tan bueno como lo permitan los datos. En psicología, donde los investigadores a menudo tienen que depender de medidas menos válidas y confiables, como los autoinformes, esto puede ser problemático.
• La interpretación del análisis factorial se basa en el uso de una “heurística”, que es una solución “conveniente aunque no sea absolutamente verdadera”. ^[49] Se puede hacer más de una interpretación de los mismos datos factorizados de la misma manera, y el análisis factorial no puede identificar causalidad.

El análisis factorial es una técnica que se utiliza con frecuencia en la investigación transcultural. Sirve para extraer dimensiones culturales . Los modelos de dimensiones culturales más conocidos son los elaborados por Geert Hofstede , Ronald Inglehart , Christian Welzel , Shalom Schwartz y Michael Minkov. Una visualización popular es el mapa cultural del mundo de Inglehart y Welzel . ^[25]

En un estudio de principios de 1965, se examinan los sistemas políticos de todo el mundo mediante análisis factorial para construir modelos teóricos e investigaciones relacionadas, comparar sistemas políticos y crear categorías tipológicas. ^[50] Para estos fines, en este estudio se identifican siete dimensiones políticas básicas, que están relacionadas con una amplia variedad de comportamiento político: estas dimensiones son Acceso, Diferenciación, Consenso, Seccionalismo, Legitimación, Interés y Teoría e Investigación del Liderazgo.

Otros politólogos exploran la medición de la eficacia política interna utilizando cuatro nuevas preguntas agregadas al Estudio Nacional de Elecciones de 1988. Aquí se utiliza el análisis factorial para descubrir que estos ítems miden un solo concepto distinto de la eficacia externa y la confianza política, y que estas cuatro preguntas proporcionaban la mejor medida de la eficacia política interna hasta ese momento. ^[51]

Los pasos básicos son:

• Identifique los atributos destacados que utilizan los consumidores para evaluar los productos de esta categoría.
• Utilice técnicas de investigación de marketing cuantitativa (como encuestas ) para recopilar datos de una muestra de clientes potenciales sobre sus calificaciones de todos los atributos del producto.
• Introduzca los datos en un programa estadístico y ejecute el procedimiento de análisis factorial. La computadora generará un conjunto de atributos subyacentes (o factores).
• Utilice estos factores para construir mapas perceptivos y otros dispositivos de posicionamiento del producto .

La etapa de recopilación de datos suele estar a cargo de profesionales de la investigación de mercados. Las preguntas de la encuesta piden al encuestado que califique una muestra de producto o descripciones de conceptos de productos en función de una serie de atributos. Se eligen entre cinco y veinte atributos, como por ejemplo: facilidad de uso, peso, precisión, durabilidad, colorido, precio o tamaño. Los atributos elegidos variarán según el producto que se esté estudiando. Se formula la misma pregunta sobre todos los productos del estudio. Los datos de varios productos se codifican y se introducen en un programa estadístico como R , SPSS , SAS , Stata , STATISTICA , JMP y SYSTAT.

El análisis aislará los factores subyacentes que explican los datos utilizando una matriz de asociaciones. ^[52] El análisis factorial es una técnica de interdependencia. Se examina el conjunto completo de relaciones interdependientes. No hay especificación de variables dependientes, variables independientes o causalidad. El análisis factorial supone que todos los datos de calificación de diferentes atributos se pueden reducir a unas pocas dimensiones importantes. Esta reducción es posible porque algunos atributos pueden estar relacionados entre sí. La calificación otorgada a cualquier atributo es parcialmente el resultado de la influencia de otros atributos. El algoritmo estadístico deconstruye la calificación (llamada puntuación bruta) en sus diversos componentes y reconstruye las puntuaciones parciales en puntuaciones factoriales subyacentes. El grado de correlación entre la puntuación bruta inicial y la puntuación factorial final se llama carga factorial .

• Se pueden utilizar atributos tanto objetivos como subjetivos, siempre que los primeros se puedan convertir en puntuaciones.
• El análisis factorial puede identificar dimensiones latentes o constructos que el análisis directo no puede identificar.
• Es fácil y económico.

• La utilidad depende de la capacidad de los investigadores para recopilar un conjunto suficiente de atributos del producto. Si se excluyen o se descuidan atributos importantes, el valor del procedimiento se reduce.
• Si los conjuntos de variables observadas son muy similares entre sí y distintos de otros elementos, el análisis factorial les asignará un único factor. Esto puede ocultar factores que representan relaciones más interesantes. ^{[ Aclaración necesaria ]}
• Para nombrar factores puede ser necesario tener conocimientos de teoría porque atributos aparentemente disímiles pueden correlacionarse fuertemente por razones desconocidas.

El análisis factorial también se ha utilizado ampliamente en ciencias físicas como la geoquímica , la hidroquímica , ^[53] la astrofísica y la cosmología , así como en ciencias biológicas, como la ecología , la biología molecular , la neurociencia y la bioquímica .

En la gestión de la calidad de las aguas subterráneas, es importante relacionar la distribución espacial de los diferentes parámetros químicos con las diferentes fuentes posibles, que tienen diferentes firmas químicas. Por ejemplo, es probable que una mina de sulfuro esté asociada con altos niveles de acidez, sulfatos disueltos y metales de transición. Estas firmas pueden identificarse como factores a través del análisis factorial en modo R, y la ubicación de las posibles fuentes puede sugerirse trazando un contorno de las puntuaciones de los factores. ^[54]

En geoquímica , diferentes factores pueden corresponder a diferentes asociaciones minerales y, por lo tanto, a la mineralización. ^[55]

El análisis factorial se puede utilizar para resumir los datos de microarrays de ADN de oligonucleótidos de alta densidad a nivel de sonda para los GeneChips de Affymetrix . En este caso, la variable latente corresponde a la concentración de ARN en una muestra. ^[56]

El análisis factorial se ha implementado en varios programas de análisis estadístico desde la década de 1980:

• BMDP
• JMP (software estadístico)
• Mplus (software estadístico)]
• Python : módulo scikit-learn ^[57]
• R (con la función base factanal o la función fa en el paquete psych ). Las rotaciones se implementan en el paquete R GPArotation .
• SAS (utilizando PROC FACTOR o PROC CALIS)
• Sistema operativo SPSS ^[58]
• Estado

• Factor [1] - software gratuito de análisis factorial desarrollado por la Universidad Rovira i Virgili

• Child, Dennis (2006), Lo esencial del análisis factorial (3.ª ed.), Continuum International , ISBN 978-0-8264-8000-2.
• Fabrigar, LR; Wegener, DT; MacCallum, RC; Strahan, EJ (septiembre de 1999). "Evaluación del uso del análisis factorial exploratorio en la investigación psicológica". Psychological Methods . 4 (3): 272–299. doi :10.1037/1082-989X.4.3.272.
• BT Gray (1997) Análisis factorial de orden superior (artículo de conferencia)
• Jennrich, Robert I., "Rotación a cargas simples utilizando la función de pérdida de componentes: el caso oblicuo", Psychometrika , vol. 71, n.º 1, págs. 173-191, marzo de 2006.
• Katz, Jeffrey Owen y Rohlf, F. James. Función del producto primario en el plano: una rotación oblicua hacia una estructura simple. Multivariate Behavioral Research , abril de 1975, vol. 10, págs. 219-232.
• Katz, Jeffrey Owen y Rohlf, F. James. Functionplane: Un nuevo enfoque para la rotación de estructuras simples. Psychometrika , marzo de 1974, vol. 39, n.º 1, págs. 37–51.
• Katz, Jeffrey Owen y Rohlf, F. James. Análisis de conglomerados de puntos funcionales. Systematic Zoology , septiembre de 1973, vol. 22, núm. 3, págs. 295–301.
• Mulaik, SA (2010), Fundamentos del análisis factorial , Chapman & Hall.
• Preacher, KJ; MacCallum, RC (2003). "Reparación de la máquina de análisis factorial eléctrico de Tom Swift" (PDF) . Entendiendo las estadísticas . 2 (1): 13–43. doi :10.1207/S15328031US0201_02. hdl : 1808/1492 .
• J. Schmid y JM Leiman (1957). El desarrollo de soluciones factoriales jerárquicas. Psychometrika , 22(1), 53–61.
• Thompson, B. (2004), Análisis factorial exploratorio y confirmatorio: comprensión de conceptos y aplicaciones , Washington DC: American Psychological Association , ISBN 978-1591470939.

• Hans-Georg Wolff, Katja Preising (2005)Exploración de la estructura factorial de ítems y de orden superior con la solución Schmid-Leiman: códigos de sintaxis para SPSS y SAS Métodos, instrumentos y computadoras de investigación del comportamiento , 37 (1), 48-58

Wikimedia Commons tiene medios relacionados con Análisis factorial .

• Guía para principiantes sobre análisis factorial
• Análisis factorial exploratorio. Manuscrito de un libro de Tucker, L. y MacCallum R. (1993). Recuperado el 8 de junio de 2006 de: [2] Archivado el 23 de mayo de 2013 en Wayback Machine.
• Garson, G. David, "Factor Analysis", de Statnotes: Topics in Multivariate Analysis . Recuperado el 13 de abril de 2009, de StatNotes: Topics in Multivariate Analysis, de G. David Garson en la Universidad Estatal de Carolina del Norte, Programa de Administración Pública
• Análisis factorial a los 100 años: material de conferencia
• FARMS — Análisis factorial para el resumen robusto de microarrays, un paquete R