Álgebra exterior

En matemáticas, el álgebra exterior o álgebra de Grassmann de un espacio vectorial es un álgebra asociativa que contiene que tiene un producto, llamado producto exterior o producto cuña y denotado con , tal que para cada vector en El álgebra exterior lleva el nombre de Hermann Grassmann , ^[3] y los nombres del producto provienen del símbolo "cuña" y del hecho de que el producto de dos elementos de es "exterior"${\estilo de visualización V}$${\estilo de visualización V,}$${\displaystyle \cuña}$${\displaystyle v\cuña v=0}$${\estilo de visualización v}$${\estilo de visualización V.}$${\displaystyle \cuña}$${\estilo de visualización V}$${\estilo de visualización V.}$

El producto de cuña de vectores se llama cuchilla de grado o cuchilla - . El producto de cuña se introdujo originalmente como una construcción algebraica utilizada en geometría para estudiar áreas , volúmenes y sus análogos de dimensiones superiores: La magnitud de una cuchilla 2 es el área del paralelogramo definido por y y, de manera más general, la magnitud de una cuchilla - es el (hiper)volumen del paralelotopo definido por los vectores constituyentes. La propiedad alternante que implica una propiedad antisimétrica que y de manera más general, cualquier cuchilla cambia de signo siempre que se intercambian dos de sus vectores constituyentes, lo que corresponde a un paralelotopo de orientación opuesta. ${\estilo de visualización k}$${\displaystyle v_{1}\cuña v_{2}\cuña \puntos \cuña v_{k}}$ ${\estilo de visualización k}$${\estilo de visualización k}$ ${\displaystyle v\cuña w}$${\estilo de visualización v}$${\estilo de visualización w,}$${\estilo de visualización k}$${\displaystyle v\cuña v=0}$${\displaystyle v\cuña w=-w\cuña v,}$

El álgebra exterior completa contiene objetos que no son en sí mismos cuchillas, sino combinaciones lineales de cuchillas; una suma de cuchillas de grado homogéneo se llama k - vector , mientras que una suma más general de cuchillas de grado arbitrario se llama multivector . ^[4] El espacio lineal de las -cuchillas se llama -ésima potencia exterior de El álgebra exterior es la suma directa de las -ésimas potencias exteriores de y esto hace que el álgebra exterior sea un álgebra graduada .${\estilo de visualización k}$${\estilo de visualización k}$${\estilo de visualización k}$${\estilo de visualización V.}$${\estilo de visualización k}$${\estilo de visualización V,}$

El álgebra exterior es universal en el sentido de que toda ecuación que relaciona elementos de en el álgebra exterior también es válida en toda álgebra asociativa que contiene y en la que el cuadrado de cada elemento de es cero.${\estilo de visualización V}$${\estilo de visualización V}$${\estilo de visualización V}$

La definición del álgebra exterior puede extenderse para espacios construidos a partir de espacios vectoriales, como cuerpos vectoriales y funciones cuyo dominio es un espacio vectorial. Además, el cuerpo de escalares puede ser cualquier cuerpo (sin embargo, para cuerpos de característica dos, la condición anterior debe reemplazarse por que sea equivalente en otras características). De manera más general, el álgebra exterior puede definirse para módulos sobre un anillo conmutativo . En particular, el álgebra de formas diferenciales en variables es un álgebra exterior sobre el anillo de las funciones suaves en variables.${\displaystyle v\cuña v=0}$${\displaystyle v\cuña w+w\cuña v=0,}$${\estilo de visualización k}$${\estilo de visualización k}$

El espacio vectorial euclidiano bidimensional es un espacio vectorial real dotado de una base formada por un par de vectores unitarios ortogonales.${\displaystyle \mathbf {R} ^{2}}$

${\displaystyle {\mathbf {e} }_{1}={\begin{bmatrix}1\\0\end{bmatrix}},\quad {\mathbf {e} }_{2}={\begin{ bmatrix}0\\1\end{bmatrix}}.}$

Supongamos que

${\displaystyle \mathbf {v} ={\begin{bmatrix}a\\b\end{bmatrix}}=a\mathbf {e} _{1}+b\mathbf {e} _{2},\quad \mathbf {w} ={\begin{bmatrix}c\\d\end{bmatrix}}=c\mathbf {e} _{1}+d\mathbf {e} _{2}}$

son un par de vectores dados en ⁠ ⁠${\displaystyle \mathbf {R} ^{2}}$ , escritos en componentes. Existe un paralelogramo único que tiene y como dos de sus lados. El área de este paralelogramo está dada por la fórmula del determinante estándar:${\displaystyle \mathbf {v}}$${\displaystyle \mathbf {w}}$

${\displaystyle {\text{Área}}={\Bigl |}\det {\begin{bmatrix}\mathbf {v} &\mathbf {w} \end{bmatrix}}{\Bigr |}={\Biggl |}\det {\begin{bmatrix}a&c\\b&d\end{bmatrix}}{\Biggr |}=\left|ad-bc\right|.}$

Consideremos ahora el producto exterior de y ⁠ ⁠ :${\displaystyle \mathbf {v}}$${\displaystyle \mathbf {w}}$

${\displaystyle {\begin{aligned}\mathbf {v} \wedge \mathbf {w} &=(a\mathbf {e} _{1}+b\mathbf {e} _{2})\wedge (c\mathbf {e} _{1}+d\mathbf {e} _{2})\\&=ac\mathbf {e} _{1}\wedge \mathbf {e} _{1}+ad\mathbf {e} _{1}\wedge \mathbf {e} _{2}+bc\mathbf {e} _{2}\wedge \mathbf {e} _{1}+bd\mathbf {e} _{2}\wedge \mathbf {e} _{2}\\&=\left(ad-bc\right)\mathbf {e} _{1}\wedge \mathbf {e} _{2}\end{alineado}}}$

donde el primer paso utiliza la ley distributiva para el producto exterior, y el último utiliza el hecho de que el producto exterior es una función alternada , y en particular (El hecho de que el producto exterior sea una función alternada también obliga a ) Nótese que el coeficiente en esta última expresión es precisamente el determinante de la matriz [ v w ] . El hecho de que esto pueda ser positivo o negativo tiene el significado intuitivo de que v y w pueden estar orientados en sentido antihorario o horario como los vértices del paralelogramo que definen. Tal área se llama área con signo del paralelogramo: el valor absoluto del área con signo es el área ordinaria, y el signo determina su orientación.${\displaystyle \mathbf {e}_{2}\wedge \mathbf {e}_{1}=-(\mathbf {e}_{1}\wedge \mathbf {e}_{2}).}$${\displaystyle \mathbf {e}_{1}\wedge \mathbf {e}_{1}=\mathbf {e}_{2}\wedge \mathbf {e}_{2}=0.}$

El hecho de que este coeficiente sea el área con signo no es casual. De hecho, es relativamente fácil ver que el producto exterior debería estar relacionado con el área con signo si uno intenta axiomatizar esta área como una construcción algebraica. En detalle, si A( v , w ) denota el área con signo del paralelogramo del cual el par de vectores v y w forman dos lados adyacentes, entonces A debe satisfacer las siguientes propiedades:

1. A( r v , s w ) = rs A( v , w ) para cualquier número real r y s , ya que al reescalar cualquiera de los lados se reescala el área en la misma cantidad (y al invertir la dirección de uno de los lados se invierte la orientación del paralelogramo).
2. A( v , v ) = 0 , ya que el área del paralelogramo degenerado determinado por v (es decir, un segmento de línea ) es cero.
3. A( w , v ) = −A( v , w ) , ya que intercambiar los roles de v y w invierte la orientación del paralelogramo.
4. A( v + r w , w ) = A( v , w ) para cualquier número real r , ya que sumar un múltiplo de w a v no afecta ni a la base ni a la altura del paralelogramo y en consecuencia preserva su área.
5. A( e ₁ , e ₂ ) = 1 , ya que el área del cuadrado unitario es uno.

Con excepción de la última propiedad, el producto exterior de dos vectores satisface las mismas propiedades que el área. En cierto sentido, el producto exterior generaliza la propiedad final al permitir que el área de un paralelogramo se compare con la de cualquier paralelogramo elegido en un plano paralelo (aquí, el de lados e ₁ y e ₂ ). En otras palabras, el producto exterior proporciona una formulación del área independiente de la base . ^[5]

Para los vectores en R ³ , el álgebra exterior está estrechamente relacionada con el producto vectorial y el producto triple . Utilizando la base estándar { e ₁ , e ₂ , e ₃ } , el producto exterior de un par de vectores

${\displaystyle \mathbf {u} =u_ {1}\mathbf {e} _ {1}+u_ {2}\mathbf {e} _ {2}+u_ {3}\mathbf {e} _ {3} }$

y

${\displaystyle \mathbf {v} =v_{1}\mathbf {e} _{1}+v_{2}\mathbf {e} _{2}+v_{3}\mathbf {e} _{3} }$

es

${\displaystyle \mathbf {u} \wedge \mathbf {v} =(u_{1}v_{2}-u_{2}v_{1})(\mathbf {e} _{1}\wedge \mathbf {e} _{2})+(u_{3}v_{1}-u_{1}v_{3})(\mathbf {e} _{3}\wedge \mathbf {e} _{1})+(u_{2}v_{3}-u_{3}v_{2})(\mathbf {e} _{2}\wedge \mathbf {e} _{3})}$

donde { e ₁ ∧ e ₂ , e ₃ ∧ e _​​1 , e ₂ ∧ e ₃ } es la base del espacio tridimensional ⋀ ² ( R ³ ). Los coeficientes anteriores son los mismos que los de la definición habitual del producto vectorial de vectores en tres dimensiones, con la única diferencia de que el producto exterior no es un vector ordinario, sino un bivector .

Incorporando un tercer vector

${\displaystyle \mathbf {w} =w_{1}\mathbf {e} _{1}+w_{2}\mathbf {e} _{2}+w_{3}\mathbf {e} _{3},}$

El producto exterior de tres vectores es

${\displaystyle \mathbf {u} \wedge \mathbf {v} \wedge \mathbf {w} =(u_{1}v_{2}w_{3}+u_{2}v_{3}w_{1}+u_{3}v_{1}w_{2}-u_{1}v_{3}w_{2}-u_{2}v_{1}w_{3}-u_{3}v_{2}w_{1})(\mathbf {e} _{1}\wedge \mathbf {e} _{2}\wedge \mathbf {e} _{3})}$

donde e ₁ ∧ e ₂ ∧ e ₃ es el vector base del espacio unidimensional ⋀ ³ ( R ³ ). El coeficiente escalar es el triple producto de los tres vectores.

El producto vectorial y el producto triple en tres dimensiones admiten interpretaciones tanto geométricas como algebraicas. El producto vectorial u × v puede interpretarse como un vector que es perpendicular tanto a u como a v y cuya magnitud es igual al área del paralelogramo determinado por los dos vectores. También puede interpretarse como el vector que consiste en los menores de la matriz con columnas u y v . El producto triple de u , v y w es geométricamente un volumen (con signo). Algebraicamente, es el determinante de la matriz con columnas u , v y w . El producto exterior en tres dimensiones permite interpretaciones similares. De hecho, en presencia de una base ortonormal orientada positivamente , el producto exterior generaliza estas nociones a dimensiones superiores.

El álgebra exterior de un espacio vectorial sobre un cuerpo se define como el álgebra cociente del álgebra tensorial por el ideal bilateral generado por todos los elementos de la forma tales que . ^[6] Simbólicamente,${\displaystyle \bigwedge (V)}$${\displaystyle V}$ ${\displaystyle K}$ ${\displaystyle I}$${\displaystyle x\otimes x}$${\displaystyle x\in V}$

${\displaystyle \bigwedge (V):=T(V)/I.\,}$

El producto exterior de dos elementos de se define por${\displaystyle \wedge }$${\displaystyle \bigwedge (V)}$

${\displaystyle \alpha \wedge \beta =\alpha \otimes \beta {\pmod {I}}.}$

El producto exterior es por construcción alternante en elementos de ⁠ ⁠${\displaystyle V}$ , lo que significa que para todo por la construcción anterior. Se deduce que el producto también es anticonmutativo en elementos de ⁠ ⁠ , pues suponiendo que ⁠ ⁠ ,${\displaystyle x\wedge x=0}$${\displaystyle x\in V,}$${\displaystyle V}$${\displaystyle x,y\in V}$

${\displaystyle 0=(x+y)\wedge (x+y)=x\wedge x+x\wedge y+y\wedge x+y\wedge y=x\wedge y+y\wedge x}$

por eso

${\displaystyle x\wedge y=-(y\wedge x).}$

De manera más general, si es una permutación de los números enteros ⁠ ⁠ , y ⁠ ⁠ , ⁠ ⁠ , ..., ⁠ ⁠ son elementos de ⁠ ⁠ , se deduce que${\displaystyle \sigma }$${\displaystyle [1,\dots ,k]}$${\displaystyle x_{1}}$${\displaystyle x_{2}}$${\displaystyle x_{k}}$${\displaystyle V}$

${\displaystyle x_{\sigma (1)}\wedge x_{\sigma (2)}\wedge \cdots \wedge x_{\sigma (k)}=\operatorname {sgn}(\sigma )x_{1}\wedge x_{2}\wedge \cdots \wedge x_{k},}$

donde es la firma de la permutación ⁠ ⁠ . ^[7]${\displaystyle \operatorname {sgn}(\sigma )}$ ${\displaystyle \sigma }$

En particular, si para algún ⁠ ⁠ , entonces también se cumple la siguiente generalización de la propiedad alterna:${\displaystyle x_{i}=x_{j}}$${\displaystyle i\neq j}$

${\displaystyle x_{1}\wedge x_{2}\wedge \cdots \wedge x_{k}=0.}$

Junto con la propiedad distributiva del producto exterior, una generalización adicional es que una condición necesaria y suficiente para que un conjunto de vectores sea linealmente dependiente es que${\displaystyle \{x_{1},x_{2},\dots ,x_{k}\}}$

${\displaystyle x_{1}\wedge x_{2}\wedge \cdots \wedge x_{k}=0.}$

La k -ésima potencia exterior de ⁠ ⁠${\displaystyle V}$ , denotada ⁠ ⁠${\displaystyle {\textstyle \bigwedge }^{\!k}(V)}$ , es el subespacio vectorial de ⁠ ⁠ ${\displaystyle {\textstyle \bigwedge }(V)}$ generado por elementos de la forma

${\displaystyle x_{1}\wedge x_{2}\wedge \cdots \wedge x_{k},\quad x_{i}\in V,i=1,2,\dots ,k.}$

Si ⁠ ⁠${\displaystyle \alpha \in {\textstyle \bigwedge }^{\!k}(V)}$ , entonces se dice que es un k -vector . Si, además, se puede expresar como un producto exterior de elementos de ⁠ ⁠ , entonces se dice que es descomponible (o  simple , por algunos autores; o una  cuchilla , por otros). Aunque los ⁠ ⁠ -vectores descomponibles abarcan ⁠ ⁠ , no todos los elementos de son descomponibles. Por ejemplo, dado ⁠ ⁠ con una base ⁠ ⁠ , el siguiente 2-vector no es descomponible:${\displaystyle \alpha }$${\displaystyle \alpha }$${\displaystyle k}$${\displaystyle V}$${\displaystyle \alpha }$${\displaystyle k}$${\displaystyle {\textstyle \bigwedge }^{\!k}(V)}$${\displaystyle {\textstyle \bigwedge }^{\!k}(V)}$${\displaystyle \mathbf {R} ^{4}}$${\displaystyle \{e_{1},e_{2},e_{3},e_{4}\}}$

${\displaystyle \alpha =e_{1}\wedge e_{2}+e_{3}\wedge e_{4}.}$

Si la dimensión de es y es una base para , entonces el conjunto${\displaystyle V}$${\displaystyle n}$${\displaystyle \{e_{1},\dots ,e_{n}\}}$${\displaystyle V}$

${\displaystyle \{\,e_{i_{1}}\wedge e_{i_{2}}\wedge \cdots \wedge e_{i_{k}}~{\big |}~~1\leq i_{1}<i_{2}<\cdots <i_{k}\leq n\,\}}$

es una base para ⁠ ⁠${\displaystyle {\textstyle \bigwedge }^{\!k}(V)}$ . La razón es la siguiente: dado cualquier producto exterior de la forma

${\displaystyle v_{1}\wedge \cdots \wedge v_{k},}$

cada vector puede escribirse como una combinación lineal de los vectores base ⁠ ⁠ ; utilizando la bilinealidad del producto exterior, esto puede expandirse a una combinación lineal de productos exteriores de esos vectores base. Cualquier producto exterior en el que el mismo vector base aparezca más de una vez es cero; cualquier producto exterior en el que los vectores base no aparezcan en el orden adecuado puede reordenarse, cambiando el signo siempre que dos vectores base cambien de lugar. En general, los coeficientes resultantes de los k -vectores base pueden calcularse como los menores de la matriz que describe los vectores en términos de la base ⁠ ⁠ .${\displaystyle v_{j}}$${\displaystyle e_{i}}$${\displaystyle v_{j}}$${\displaystyle e_{i}}$

Contando los elementos base, la dimensión de es igual a un coeficiente binomial :${\displaystyle {\textstyle \bigwedge }^{\!k}(V)}$

${\displaystyle \dim {\textstyle \bigwedge }^{\!k}(V)={\binom {n}{k}},}$

donde ⁠ ⁠${\displaystyle n}$ es la dimensión de los vectores , y ⁠ ⁠${\displaystyle k}$ es el número de vectores en el producto. El coeficiente binomial produce el resultado correcto, incluso para casos excepcionales; en particular, para ⁠ ⁠ .${\displaystyle {\textstyle \bigwedge }^{\!k}(V)=\{0\}}$${\displaystyle k>n}$

Cualquier elemento del álgebra exterior puede escribirse como una suma de k -vectores . Por lo tanto, como espacio vectorial, el álgebra exterior es una suma directa.

${\displaystyle {\textstyle \bigwedge }(V)={\textstyle \bigwedge }^{\!0}(V)\oplus {\textstyle \bigwedge }^{\!1}(V)\oplus {\textstyle \bigwedge }^{\!2}(V)\oplus \cdots \oplus {\textstyle \bigwedge }^{\!n}(V)}$

(donde, por convención, ⁠ ⁠${\displaystyle {\textstyle \bigwedge }^{\!0}(V)=K}$ , el campo subyacente ⁠ ⁠${\displaystyle V}$ , y ⁠ ⁠${\displaystyle {\textstyle \bigwedge }^{\!1}(V)=V}$ ), y por lo tanto su dimensión es igual a la suma de los coeficientes binomiales, que es ⁠ ⁠${\displaystyle 2^{n}}$ .

Si ⁠ ⁠${\displaystyle \alpha \in {\textstyle \bigwedge }^{\!k}(V)}$ , entonces es posible expresar como una combinación lineal de k -vectores descomponibles :${\displaystyle \alpha }$

${\displaystyle \alpha =\alpha ^{(1)}+\alpha ^{(2)}+\cdots +\alpha ^{(s)}}$

donde cada uno es descomponible, digamos${\displaystyle \alpha ^{(i)}}$

${\displaystyle \alpha ^{(i)}=\alpha _{1}^{(i)}\wedge \cdots \wedge \alpha _{k}^{(i)},\quad i=1,2,\ldots ,s.}$

El rango del k -vector es el número mínimo de k -vectores descomponibles en dicha expansión de ⁠ ⁠ . Esto es similar a la noción de rango tensorial .${\displaystyle \alpha }$${\displaystyle \alpha }$

El rango es particularmente importante en el estudio de 2-vectores (Sternberg 1964, §III.6) (Bryant et al. 1991). El rango de un 2-vector puede identificarse con la mitad del rango de la matriz de coeficientes de en una base. Por lo tanto, si es una base para ⁠ ⁠ , entonces puede expresarse de forma única como${\displaystyle \alpha }$${\displaystyle \alpha }$${\displaystyle e_{i}}$${\displaystyle V}$${\displaystyle \alpha }$

${\displaystyle \alpha =\sum _{i,j}a_{ij}e_{i}\wedge e_{j}}$

donde (la matriz de coeficientes es antisimétrica ). Por lo tanto, el rango de la matriz es par y es el doble del rango de la forma .${\displaystyle a_{ij}=-a_{ji}}$${\displaystyle a_{ij}}$${\displaystyle \alpha }$

En la característica 0, el 2-vector tiene rango si y sólo si${\displaystyle \alpha }$${\displaystyle p}$

${\displaystyle {\underset {p}{\underbrace {\alpha \wedge \cdots \wedge \alpha } }}\neq 0\ }$y${\displaystyle \ {\underset {p+1}{\underbrace {\alpha \wedge \cdots \wedge \alpha } }}=0.}$

El producto exterior de un vector k con un vector p es un vector , lo que nuevamente invoca la bilinealidad. En consecuencia, la descomposición de suma directa de la sección anterior${\displaystyle (k+p)}$

${\displaystyle {\textstyle \bigwedge }(V)={\textstyle \bigwedge }^{\!0}(V)\oplus {\textstyle \bigwedge }^{\!1}(V)\oplus {\textstyle \bigwedge }^{\!2}(V)\oplus \cdots \oplus {\textstyle \bigwedge }^{\!n}(V)}$

da al álgebra exterior la estructura adicional de un álgebra graduada , es decir

${\displaystyle {\textstyle \bigwedge }^{\!k}(V)\wedge {\textstyle \bigwedge }^{\!p}(V)\subset {\textstyle \bigwedge }^{\!k+p}(V).}$

Además, si K es el campo base, tenemos

${\displaystyle {\textstyle \bigwedge }^{\!0}(V)=K}$y${\displaystyle {\textstyle \bigwedge }^{\!1}(V)=V.}$

El producto exterior es anticonmutativo graduado, lo que significa que si y ⁠ ⁠ , entonces${\displaystyle \alpha \in {\textstyle \bigwedge }^{\!k}(V)}$${\displaystyle \beta \in {\textstyle \bigwedge }^{\!p}(V)}$

${\displaystyle \alpha \wedge \beta =(-1)^{kp}\beta \wedge \alpha .}$

Además de estudiar la estructura graduada en el álgebra exterior, Bourbaki (1989) estudia estructuras graduadas adicionales en álgebras exteriores, como aquellas del álgebra exterior de un módulo graduado (un módulo que ya tiene su propia gradación).

Sea V un espacio vectorial sobre el cuerpo K . De manera informal, la multiplicación en se realiza manipulando símbolos e imponiendo una ley distributiva , una ley asociativa y usando la identidad para v ∈ V . Formalmente, es el álgebra "más general" en la que se cumplen estas reglas para la multiplicación, en el sentido de que cualquier K -álgebra asociativa unital que contenga V con multiplicación alternada en V debe contener una imagen homomórfica de ⁠ ⁠ . En otras palabras, el álgebra exterior tiene la siguiente propiedad universal : ^[8]${\displaystyle {\textstyle \bigwedge }(V)}$${\displaystyle v\wedge v=0}$${\displaystyle {\textstyle \bigwedge }(V)}$${\displaystyle {\textstyle \bigwedge }(V)}$

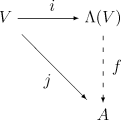
Para construir el álgebra más general que contiene a V y cuya multiplicación es alternada en V , es natural comenzar con el álgebra asociativa más general que contiene a V , el álgebra tensorial T ( V ) , y luego hacer cumplir la propiedad alternada tomando un cociente adecuado. Por lo tanto, tomamos el ideal bilateral I en T ( V ) generado por todos los elementos de la forma v ⊗ v para v en V , y definimos como el cociente${\displaystyle {\textstyle \bigwedge }(V)}$

${\displaystyle {\textstyle \bigwedge }(V)=T(V)\,/\,I}$

(y use ∧ como símbolo de multiplicación en ⁠ ⁠${\displaystyle {\textstyle \bigwedge }(V)}$ ). Entonces es sencillo demostrar que contiene V y satisface la propiedad universal anterior.${\displaystyle {\textstyle \bigwedge }(V)}$

Como consecuencia de esta construcción, la operación de asignar a un espacio vectorial V su álgebra exterior es un funtor de la categoría de espacios vectoriales a la categoría de álgebras.${\displaystyle {\textstyle \bigwedge }(V)}$

En lugar de definir primero y luego identificar las potencias externas como ciertos subespacios, se pueden definir alternativamente los espacios primero y luego combinarlos para formar el álgebra . Este enfoque se utiliza a menudo en geometría diferencial y se describe en la siguiente sección.${\displaystyle {\textstyle \bigwedge }(V)}$${\displaystyle {\textstyle \bigwedge }^{\!k}(V)}$${\displaystyle {\textstyle \bigwedge }^{\!k}(V)}$${\displaystyle {\textstyle \bigwedge }(V)}$

Dado un anillo conmutativo y un módulo - ⁠ ⁠ , podemos definir el álgebra exterior tal como se indicó anteriormente, como un cociente adecuado del álgebra tensorial ⁠ ⁠ . Satisfará la propiedad universal análoga. Muchas de las propiedades de también requieren que sea un módulo proyectivo . Cuando se utiliza dimensionalidad finita, las propiedades requieren además que sea finitamente generada y proyectiva. Se pueden encontrar generalizaciones para las situaciones más comunes en Bourbaki (1989).${\displaystyle R}$${\displaystyle R}$ ${\displaystyle M}$${\displaystyle {\textstyle \bigwedge }(M)}$${\displaystyle \mathrm {T} (M)}$${\displaystyle {\textstyle \bigwedge }(M)}$${\displaystyle M}$${\displaystyle M}$

Las álgebras exteriores de fibrados vectoriales se consideran con frecuencia en geometría y topología. No existen diferencias esenciales entre las propiedades algebraicas del álgebra exterior de fibrados vectoriales de dimensión finita y las del álgebra exterior de módulos proyectivos finitamente generados, según el teorema de Serre-Swan . Se pueden definir álgebras exteriores más generales para haces de módulos.

Para un cuerpo de característica distinta de 2, ^[9] el álgebra exterior de un espacio vectorial sobre puede identificarse canónicamente con el subespacio vectorial de que consiste en tensores antisimétricos . Para característica 0 (o mayor que ⁠ ⁠ ), el espacio vectorial de tensores antisimétricos -lineales es transversal al ideal ⁠ ⁠ , por lo tanto, una buena opción para representar el cociente. Pero para característica distinta de cero, el espacio vectorial de tensores antisimétricos ⁠ ⁠ -lineales podría no ser transversal al ideal (en realidad, para ⁠ ⁠ , el espacio vectorial de tensores antisimétricos -lineales está contenido en ); Sin embargo, transversal o no, se puede definir un producto en este espacio de modo que el álgebra resultante sea isomorfa al álgebra exterior: en el primer caso la elección natural para el producto es simplemente el producto cociente (usando la proyección disponible), en el segundo caso, este producto debe modificarse ligeramente como se indica a continuación (según la configuración de Arnold), pero de modo que el álgebra permanezca isomorfa con el álgebra exterior, es decir, el cociente de por el ideal generado por elementos de la forma ⁠ ⁠ . Por supuesto, para la característica ⁠ ⁠ (o mayor que la dimensión del espacio vectorial), se podría usar una u otra definición del producto, ya que las dos álgebras son isomorfas (ver VI Arnold o Kobayashi-Nomizu).${\displaystyle V}$${\displaystyle K}$${\displaystyle \mathrm {T} (V)}$${\displaystyle \dim V}$${\displaystyle k}$${\displaystyle I}$${\displaystyle K}$${\displaystyle k\geq \operatorname {char} K}$${\displaystyle K}$${\displaystyle I}$${\displaystyle \mathrm {T} (V)}$${\displaystyle I}$${\displaystyle x\otimes x}$${\displaystyle 0}$

Sea el espacio de tensores homogéneos de grado . Éste está abarcado por tensores descomponibles${\displaystyle \mathrm {T} ^{r}(V)}$${\displaystyle r}$

${\displaystyle v_{1}\otimes \cdots \otimes v_{r},\quad v_{i}\in V.}$

La antisimetrización (o a veces la simetrización sesgada ) de un tensor descomponible se define por

${\displaystyle \operatorname {{\mathcal {A}}^{(r)}} (v_{1}\otimes \cdots \otimes v_{r})=\sum _{\sigma \in {\mathfrak {S}}_{r}}\operatorname {sgn} (\sigma )v_{\sigma (1)}\otimes \cdots \otimes v_{\sigma (r)}}$

y, cuando (para un campo característico distinto de cero podría ser 0):${\displaystyle r!\neq 0}$${\displaystyle r!}$

${\displaystyle \operatorname {Alt} ^{(r)}(v_{1}\otimes \cdots \otimes v_{r})={\frac {1}{r!}}\operatorname {{\mathcal {A}}^{(r)}} (v_{1}\otimes \cdots \otimes v_{r})}$

donde la suma se toma sobre el grupo simétrico de permutaciones en los símbolos ⁠ ⁠${\displaystyle \{1,\dots ,r\}}$ . Esto se extiende por linealidad y homogeneidad a una operación, también denotada por y , en el álgebra tensorial completa ⁠ ⁠ .${\displaystyle {\mathcal {A}}}$${\displaystyle {\rm {Alt}}}$${\displaystyle \mathrm {T} (V)}$

Tenga en cuenta que

${\displaystyle \operatorname {{\mathcal {A}}^{(r)}} \operatorname {{\mathcal {A}}^{(r)}} =r!\operatorname {{\mathcal {A}}^{(r)}} .}$

De modo que, cuando se define, es la proyección para el álgebra exterior (cociente) sobre el subespacio tensorial alterno homogéneo r. Por otra parte, la imagen es siempre el subespacio tensorial alterno graduado (aún no un álgebra, ya que el producto aún no está definido), denotado ⁠ ⁠ . Este es un subespacio vectorial de ⁠ ⁠ , y hereda la estructura de un espacio vectorial graduado de aquel en ⁠ ⁠ . Además, el núcleo de es precisamente ⁠ ⁠ , el subconjunto homogéneo del ideal ⁠ ⁠ , o el núcleo de es ⁠ ⁠ . Cuando se define, lleva un producto graduado asociativo definido por (el mismo que el producto de cuña)${\displaystyle \operatorname {Alt} ^{(r)}}$${\displaystyle {\mathcal {A}}(\mathrm {T} (V))}$${\displaystyle A(V)}$${\displaystyle \mathrm {T} (V)}$${\displaystyle \mathrm {T} (V)}$${\displaystyle {\mathcal {A}}^{(r)}}$${\displaystyle I^{(r)}}$${\displaystyle I}$${\displaystyle {\mathcal {A}}}$${\displaystyle I}$${\displaystyle \operatorname {Alt} }$${\displaystyle A(V)}$${\displaystyle {\widehat {\otimes }}}$

${\displaystyle t\wedge s=t~{\widehat {\otimes }}~s=\operatorname {Alt} (t\otimes s).}$

Suponiendo que tiene característica 0, ya que es un suplemento de en ⁠ ⁠ , con el producto dado anteriormente, existe un isomorfismo canónico${\displaystyle K}$${\displaystyle A(V)}$${\displaystyle I}$${\displaystyle \mathrm {T} (V)}$

${\displaystyle A(V)\cong {\textstyle \bigwedge }(V).}$

Cuando la característica del campo no es cero, se hará lo mismo que antes, pero el producto no se puede definir como se indica más arriba. En tal caso, el isomorfismo sigue siendo válido, a pesar de no ser un complemento del ideal , pero entonces, el producto se debe modificar como se indica a continuación ( producto, configuración de Arnold).${\displaystyle {\mathcal {A}}}$${\displaystyle {\rm {Alt}}}$${\displaystyle A(V)\cong {\textstyle \bigwedge }(V)}$${\displaystyle A(V)}$${\displaystyle I}$${\displaystyle {\dot {\wedge }}}$

Finalmente, siempre obtenemos ⁠ ⁠${\displaystyle A(V)}$ isomorfo con ⁠ ⁠${\displaystyle {\textstyle \bigwedge }(V)}$ , pero el producto podría (o debería) elegirse de dos maneras (o solo una). En realidad, el producto podría elegirse de muchas maneras, reescalándolo en espacios homogéneos como para una secuencia arbitraria en el cuerpo, siempre que la división tenga sentido (esto es tal que el producto redefinido también es asociativo, es decir, define un álgebra en ⁠ ⁠ ). También tenga en cuenta que la definición del producto interior debe cambiarse en consecuencia, para mantener su propiedad de derivación sesgada.${\displaystyle c(r+p)/c(r)c(p)}$${\displaystyle c(r)}$${\displaystyle A(V)}$

Supóngase que V tiene dimensión finita n , y que se da una base e ₁ , ..., e _n de V. Entonces cualquier tensor alterno t ∈ A ^r ( V ) ⊂ T ^r ( V ) se puede escribir en notación de índice con la convención de suma de Einstein como

${\displaystyle t=t^{i_{1}i_{2}\cdots i_{r}}\,{\mathbf {e} }_{i_{1}}\otimes {\mathbf {e} }_{i_{2}}\otimes \cdots \otimes {\mathbf {e} }_{i_{r}},}$

donde t ^{i ₁ ⋅⋅⋅ i _r} es completamente antisimétrico en sus índices.

El producto exterior de dos tensores alternos t y s de rangos r y p está dado por

${\displaystyle t~{\widehat {\otimes }}~s={\frac {1}{(r+p)!}}\sum _{\sigma \in {\mathfrak {S}}_{r+p}}\operatorname {sgn} (\sigma )t^{i_{\sigma (1)}\cdots i_{\sigma (r)}}s^{i_{\sigma (r+1)}\cdots i_{\sigma (r+p)}}{\mathbf {e} }_{i_{1}}\otimes {\mathbf {e} }_{i_{2}}\otimes \cdots \otimes {\mathbf {e} }_{i_{r+p}}.}$

Los componentes de este tensor son precisamente la parte sesgada de los componentes del producto tensorial s ⊗ t , denotados por corchetes en los índices:

${\displaystyle (t~{\widehat {\otimes }}~s)^{i_{1}\cdots i_{r+p}}=t^{[i_{1}\cdots i_{r}}s^{i_{r+1}\cdots i_{r+p}]}.}$

El producto interior también puede describirse en notación de índice de la siguiente manera. Sea un tensor antisimétrico de rango ⁠ ⁠ . Entonces, para α ∈ V ^∗ , ⁠ ⁠ es un tensor alterno de rango ⁠ ⁠ , dado por${\displaystyle t=t^{i_{0}i_{1}\cdots i_{r-1}}}$${\displaystyle r}$${\displaystyle \iota _{\alpha }t}$${\displaystyle r-1}$

${\displaystyle (\iota _{\alpha }t)^{i_{1}\cdots i_{r-1}}=r\sum _{j=0}^{n}\alpha _{j}t^{ji_{1}\cdots i_{r-1}}.}$

donde n es la dimensión de V .

Dados dos espacios vectoriales V y X y un número natural k , un operador alterno de V ^k a X es una función multilineal

${\displaystyle f:V^{k}\to X}$

de manera que siempre que v ₁ , ..., v _k sean vectores linealmente dependientes en V , entonces

${\displaystyle f(v_{1},\ldots ,v_{k})=0.}$

El mapa

${\displaystyle w:V^{k}\to {\textstyle \bigwedge }^{\!k}(V),}$

que se asocia a vectores de su producto exterior, es decir, su -vector correspondiente, también es alternante. De hecho, esta función es el operador alternante "más general" definido en dado cualquier otro operador alternante existe una única función lineal con Esta propiedad universal caracteriza el espacio de operadores alternantes en y puede servir como su definición.${\displaystyle k}$${\displaystyle V}$${\displaystyle k}$${\displaystyle V^{k};}$${\displaystyle f:V^{k}\rightarrow X,}$ ${\displaystyle \phi :{\textstyle \bigwedge }^{\!k}(V)\rightarrow X}$${\displaystyle f=\phi \circ w.}$${\displaystyle V^{k}}$

La discusión anterior se especializa en el caso cuando ⁠ ⁠${\displaystyle X=K}$ , el campo base. En este caso, una función multilineal alternada

${\displaystyle f:V^{k}\to K}$

se llama forma multilineal alternada . El conjunto de todas las formas multilineales alternadas es un espacio vectorial, ya que la suma de dos de tales mapas, o el producto de tal mapa con un escalar, es nuevamente alternada. Por la propiedad universal de la potencia exterior, el espacio de formas alternadas de grado en es naturalmente isomorfo con el espacio vectorial dual ⁠ ⁠ . Si es de dimensión finita, entonces este último es naturalmente isomorfo ^{[ aclaración necesaria ]} a ⁠ ⁠ . En particular, si es -dimensional, la dimensión del espacio de mapas alternados de a es el coeficiente binomial ⁠ ⁠ .${\displaystyle k}$${\displaystyle V}$ ${\displaystyle {\bigl (}{\textstyle \bigwedge }^{\!k}(V){\bigr )}^{*}}$${\displaystyle V}$${\displaystyle {\textstyle \bigwedge }^{\!k}\left(V^{*}\right)}$${\displaystyle V}$${\displaystyle n}$${\displaystyle V^{k}}$${\displaystyle K}$ ${\displaystyle \textstyle {\binom {n}{k}}}$

En virtud de esta identificación, el producto exterior toma una forma concreta: produce una nueva función antisimétrica a partir de dos funciones dadas. Supóngase que ω  : V ^k → K y η  : V ^m → K son dos funciones antisimétricas. Como en el caso de los productos tensoriales de funciones multilineales, el número de variables de su producto exterior es la suma del número de sus variables. Dependiendo de la elección de la identificación de elementos de potencia exterior con formas multilineales, el producto exterior se define como

${\displaystyle \omega \wedge \eta =\operatorname {Alt} (\omega \otimes \eta )}$

o como

${\displaystyle \omega {\dot {\wedge }}\eta ={\frac {(k+m)!}{k!\,m!}}\operatorname {Alt} (\omega \otimes \eta ),}$

donde, si la característica del campo base es 0, la alternancia Alt de un mapa multilineal se define como el promedio de los valores ajustados por signo sobre todas las permutaciones de sus variables:${\displaystyle K}$

${\displaystyle \operatorname {Alt} (\omega )(x_{1},\ldots ,x_{k})={\frac {1}{k!}}\sum _{\sigma \in S_{k}}\operatorname {sgn} (\sigma )\,\omega (x_{\sigma (1)},\ldots ,x_{\sigma (k)}).}$

Cuando el campo tiene característica finita , una versión equivalente de la segunda expresión sin ningún factorial ni ninguna constante está bien definida:${\displaystyle K}$

${\displaystyle {\omega {\dot {\wedge }}\eta (x_{1},\ldots ,x_{k+m})}=\sum _{\sigma \in \mathrm {Sh} _{k,m}}\operatorname {sgn} (\sigma )\,\omega (x_{\sigma (1)},\ldots ,x_{\sigma (k)})\,\eta (x_{\sigma (k+1)},\ldots ,x_{\sigma (k+m)}),}$

donde aquí Sh _{k , m} ⊂ S _{k + m} es el subconjunto de ( k , m ) baraja : permutaciones σ del conjunto {1, 2, ..., k + m } tales que σ (1) < σ (2) < ⋯ < σ ( k ) , y σ ( k + 1) < σ ( k + 2) < ... < σ ( k + m ) . Como esto puede parecer muy específico y ajustado, una versión cruda equivalente es sumar en la fórmula anterior sobre permutaciones en clases laterales izquierdas de S _{k + m} / ( S _k × S _m ) .

Supongamos que es de dimensión finita. Si denota el espacio dual al espacio vectorial ⁠ ⁠ , entonces para cada ⁠ ⁠ , es posible definir una antiderivación en el álgebra ⁠ ⁠ ,${\displaystyle V}$${\displaystyle V^{*}}$${\displaystyle V}$${\displaystyle \alpha \in V^{*}}$${\displaystyle {\textstyle \bigwedge }(V)}$

${\displaystyle \iota _{\alpha }:{\textstyle \bigwedge }^{\!k}(V)\rightarrow {\textstyle \bigwedge }^{\!k-1}(V).}$

Esta derivación se llama producto interior con ⁠ ⁠${\displaystyle \alpha }$ , o a veces operador de inserción , o contracción por ⁠ ⁠${\displaystyle \alpha }$ .

Supóngase que ⁠ ⁠${\displaystyle w\in {\textstyle \bigwedge }^{\!k}(V)}$ . Entonces es una aplicación multilineal de a ⁠ ⁠ , por lo que se define por sus valores en el producto cartesiano k -fold ⁠ ⁠ . Si u ₁ , u ₂ , ..., u _{k −1} son elementos de ⁠ ⁠ , entonces defina${\displaystyle w}$${\displaystyle V^{*}}$${\displaystyle K}$ ${\displaystyle V^{*}\times V^{*}\times \dots \times V^{*}}$${\displaystyle k-1}$${\displaystyle V^{*}}$

${\displaystyle (\iota _{\alpha }w)(u_{1},u_{2},\ldots ,u_{k-1})=w(\alpha ,u_{1},u_{2},\ldots ,u_{k-1}).}$

Además, sea siempre que sea un escalar puro (es decir, perteneciente a ⁠ ⁠ ).${\displaystyle \iota _{\alpha }f=0}$${\displaystyle f}$${\displaystyle {\textstyle \bigwedge }^{\!0}(V)}$

El producto interior satisface las siguientes propiedades:

1. Para cada ⁠ ⁠${\displaystyle k}$ y cada ⁠ ⁠${\displaystyle \alpha \in V^{*}}$ (donde por convención ),${\displaystyle \Lambda ^{-1}(V)=\{0\}}$

   ${\displaystyle \iota _{\alpha }:{\textstyle \bigwedge }^{\!k}(V)\rightarrow {\textstyle \bigwedge }^{\!k-1}(V).}$

2. Si es un elemento de ( ⁠ ⁠ ), entonces ⁠ ⁠ es el emparejamiento dual entre elementos de y elementos de ⁠ ⁠ .${\displaystyle v}$${\displaystyle V}$${\displaystyle ={\textstyle \bigwedge }^{\!1}(V)}$${\displaystyle \iota _{\alpha }v=\alpha (v)}$${\displaystyle V}$${\displaystyle V^{*}}$
3. Para cada ⁠ ⁠${\displaystyle \alpha \in V^{*}}$ , es una derivación graduada de grado −1:${\displaystyle \iota _{\alpha }}$

   ${\displaystyle \iota _{\alpha }(a\wedge b)=(\iota _{\alpha }a)\wedge b+(-1)^{\deg a}a\wedge (\iota _{\alpha }b).}$

Estas tres propiedades son suficientes para caracterizar el producto interior así como definirlo en el caso general de dimensión infinita.

Otras propiedades del producto interior incluyen:

• ${\displaystyle \iota _{\alpha }\circ \iota _{\alpha }=0.}$
• ${\displaystyle \iota _{\alpha }\circ \iota _{\beta }=-\iota _{\beta }\circ \iota _{\alpha }.}$

Supongamos que tiene dimensión finita ⁠ ⁠ . Entonces el producto interior induce un isomorfismo canónico de espacios vectoriales${\displaystyle V}$${\displaystyle n}$

${\displaystyle {\textstyle \bigwedge }^{\!k}(V^{*})\otimes {\textstyle \bigwedge }^{\!n}(V)\to {\textstyle \bigwedge }^{\!n-k}(V)}$

por la definición recursiva

${\displaystyle \iota _{\alpha \wedge \beta }=\iota _{\beta }\circ \iota _{\alpha }.}$

En el contexto geométrico, un elemento distinto de cero de la potencia exterior superior (que es un espacio vectorial unidimensional) a veces se denomina forma de volumen (o forma de orientación , aunque este término a veces puede generar ambigüedad). El nombre forma de orientación proviene del hecho de que la elección del elemento superior preferido determina una orientación de todo el álgebra exterior, ya que equivale a fijar una base ordenada del espacio vectorial. En relación con la forma de volumen preferida , el isomorfismo se da explícitamente por${\displaystyle {\textstyle \bigwedge }^{\!n}(V)}$${\displaystyle \sigma }$

${\displaystyle {\textstyle \bigwedge }^{\!k}(V^{*})\to {\textstyle \bigwedge }^{\!n-k}(V):\alpha \mapsto \iota _{\alpha }\sigma .}$

Si, además de una forma de volumen, el espacio vectorial V está equipado con un producto interno que se identifica con ⁠ ⁠ , entonces el isomorfismo resultante se llama operador de estrella de Hodge , que asigna un elemento a su dual de Hodge :${\displaystyle V}$${\displaystyle V^{*}}$

${\displaystyle \star :{\textstyle \bigwedge }^{\!k}(V)\rightarrow {\textstyle \bigwedge }^{\!n-k}(V).}$

La composición de consigo misma se aplica a y es siempre un múltiplo escalar de la función identidad. En la mayoría de las aplicaciones, la forma de volumen es compatible con el producto interno en el sentido de que es un producto externo de una base ortonormal de ⁠ ⁠ . En este caso,${\displaystyle \star }$${\displaystyle {\textstyle \bigwedge }^{\!k}(V)\to {\textstyle \bigwedge }^{\!k}(V)}$${\displaystyle V}$

${\displaystyle \star \circ \star :{\textstyle \bigwedge }^{\!k}(V)\to {\textstyle \bigwedge }^{\!k}(V)=(-1)^{k(n-k)+q}\mathrm {id} }$

donde id es la asignación de identidad y el producto interno tiene firma métrica ( p , q ) : p más y q menos.

Para un espacio de dimensión finita, un producto ${\displaystyle V}$interno (o un producto interno pseudoeuclidiano ) en ⁠ ⁠${\displaystyle V}$ define un isomorfismo de con ⁠ ⁠ , y por lo tanto también un isomorfismo de con ⁠ ⁠ . El emparejamiento entre estos dos espacios también toma la forma de un producto interno. En los ⁠ ⁠ -vectores descomponibles,${\displaystyle V}$${\displaystyle V^{*}}$${\displaystyle {\textstyle \bigwedge }^{\!k}(V)}$${\displaystyle {\bigl (}{\textstyle \bigwedge }^{\!k}V{\bigr )}^{*}}$${\displaystyle k}$

${\displaystyle \left\langle v_{1}\wedge \cdots \wedge v_{k},w_{1}\wedge \cdots \wedge w_{k}\right\rangle =\det {\bigl (}\langle v_{i},w_{j}\rangle {\bigr )},}$

el determinante de la matriz de productos internos. En el caso especial v _i = w _i , el producto interno es la norma cuadrada del k -vector, dada por el determinante de la matriz de Gram (⟨ v _i , v _j ⟩) . Esto se extiende luego bilinealmente (o sesquilinealmente en el caso complejo) a un producto interno no degenerado en Si e _i , i = 1, 2, ..., n , forman una base ortonormal de ⁠ ⁠ , entonces los vectores de la forma${\displaystyle {\textstyle \bigwedge }^{\!k}(V).}$${\displaystyle V}$

${\displaystyle e_{i_{1}}\wedge \cdots \wedge e_{i_{k}},\quad i_{1}<\cdots <i_{k},}$

constituyen una base ortonormal para ⁠ ⁠${\displaystyle {\textstyle \bigwedge }^{\!k}(V)}$ , un enunciado equivalente a la fórmula de Cauchy–Binet .

Con respecto al producto interno, la multiplicación externa y el producto interno son mutuamente adjuntos. Específicamente, para ⁠ ⁠${\displaystyle \mathbf {v} \in {\textstyle \bigwedge }^{\!k-1}(V)}$ , ⁠ ⁠${\displaystyle \mathbf {w} \in {\textstyle \bigwedge }^{\!k}(V)}$ , y ⁠ ⁠${\displaystyle x\in V}$ ,

${\displaystyle \langle x\wedge \mathbf {v} ,\mathbf {w} \rangle =\langle \mathbf {v} ,\iota _{x^{\flat }}\mathbf {w} \rangle }$

donde x ^♭ ∈ V ^∗ es el isomorfismo musical , el funcional lineal definido por

${\displaystyle x^{\flat }(y)=\langle x,y\rangle }$

para todos ⁠ ⁠${\displaystyle y\in V}$ . Esta propiedad caracteriza completamente el producto interno en el álgebra externa.

De hecho, de manera más general para ⁠ ⁠${\displaystyle \mathbf {v} \in {\textstyle \bigwedge }^{\!k-l}(V)}$ , ⁠ ⁠${\displaystyle \mathbf {w} \in {\textstyle \bigwedge }^{\!k}(V)}$ , y ⁠ ⁠${\displaystyle \mathbf {x} \in {\textstyle \bigwedge }^{\!l}(V)}$ , la iteración de las propiedades adjuntas anteriores da

${\displaystyle \langle \mathbf {x} \wedge \mathbf {v} ,\mathbf {w} \rangle =\langle \mathbf {v} ,\iota _{\mathbf {x} ^{\flat }}\mathbf {w} \rangle }$

¿Dónde está ahora el dual -vector definido por${\displaystyle \mathbf {x} ^{\flat }\in {\textstyle \bigwedge }^{\!l}\left(V^{*}\right)\simeq {\bigl (}{\textstyle \bigwedge }^{\!l}(V){\bigr )}^{*}}$${\displaystyle l}$

${\displaystyle \mathbf {x} ^{\flat }(\mathbf {y} )=\langle \mathbf {x} ,\mathbf {y} \rangle }$

para todos ⁠ ⁠${\displaystyle \mathbf {y} \in {\textstyle \bigwedge }^{\!l}(V)}$ .

Existe una correspondencia entre el dual graduado del álgebra graduada y las formas multilineales alternas en ⁠ ⁠ . El álgebra exterior (así como el álgebra simétrica ) hereda una estructura de biálgebra y, de hecho, una estructura de álgebra de Hopf , del álgebra tensorial . Consulte el artículo sobre álgebras tensoriales para un tratamiento detallado del tema.${\displaystyle {\textstyle \bigwedge }(V)}$${\displaystyle V}$

El producto exterior de las formas multilineales definidas anteriormente es dual de un coproducto definido en ⁠ ⁠${\displaystyle {\textstyle \bigwedge }(V)}$ , dando la estructura de una coalgebra . El coproducto es una función lineal ⁠ ⁠${\displaystyle \Delta :{\textstyle \bigwedge }(V)\to {\textstyle \bigwedge }(V)\otimes {\textstyle \bigwedge }(V)}$ , que está dada por

${\displaystyle \Delta (v)=1\otimes v+v\otimes 1}$

sobre elementos ⁠ ⁠${\displaystyle v\in V}$ . El símbolo representa el elemento unitario del campo ⁠ ⁠ . Recordemos que ⁠ ⁠ , de modo que lo anterior realmente se encuentra en ⁠ ⁠ . Esta definición del coproducto se eleva al espacio completo mediante el homomorfismo (lineal). La forma correcta de este homomorfismo no es la que uno podría escribir ingenuamente, sino que tiene que ser la que se define cuidadosamente en el artículo sobre la coalgebra . En este caso, se obtiene${\displaystyle 1}$${\displaystyle K}$${\displaystyle K\simeq {\textstyle \bigwedge }^{\!0}(V)\subseteq {\textstyle \bigwedge }(V)}$${\displaystyle {\textstyle \bigwedge }(V)\otimes {\textstyle \bigwedge }(V)}$${\displaystyle {\textstyle \bigwedge }(V)}$

${\displaystyle \Delta (v\wedge w)=1\otimes (v\wedge w)+v\otimes w-w\otimes v+(v\wedge w)\otimes 1.}$

Ampliando esto en detalle, se obtiene la siguiente expresión sobre elementos descomponibles:

${\displaystyle \Delta (x_{1}\wedge \cdots \wedge x_{k})=\sum _{p=0}^{k}\;\sum _{\sigma \in Sh(p,k-p)}\;\operatorname {sgn} (\sigma )(x_{\sigma (1)}\wedge \cdots \wedge x_{\sigma (p)})\otimes (x_{\sigma (p+1)}\wedge \cdots \wedge x_{\sigma (k)}).}$