Dominio estocástico
Orden parcial entre variables aleatorias

El dominio estocástico es un orden parcial entre variables aleatorias . [1] [2] Es una forma de ordenamiento estocástico . El concepto surge en la teoría de decisiones y el análisis de decisiones en situaciones en las que una apuesta (una distribución de probabilidad sobre resultados posibles, también conocidos como perspectivas) puede clasificarse como superior a otra apuesta para una amplia clase de tomadores de decisiones. Se basa en preferencias compartidas con respecto a conjuntos de resultados posibles y sus probabilidades asociadas. Solo se requiere un conocimiento limitado de las preferencias para determinar el dominio. La aversión al riesgo es un factor solo en el dominio estocástico de segundo orden.

El dominio estocástico no da un orden total , sino sólo un orden parcial : para algunos pares de apuestas, ninguna domina estocásticamente a la otra, ya que diferentes miembros de la amplia clase de tomadores de decisiones diferirán respecto de qué apuesta es preferible sin que generalmente se las considere igualmente atractivas.

A lo largo del artículo, las distribuciones de probabilidad se representan en , mientras que las variables aleatorias particulares se representan en . La notación significa que tiene una distribución . ρ , no {\displaystyle \rho ,\nu } R {\displaystyle \mathbb {R}} A , B , incógnita , Y , O {\estilo de visualización A, B, X, Y, Z} R {\displaystyle \mathbb {R}} incógnita ∼ ρ {\displaystyle X\sim \rho } X {\displaystyle X} ρ {\displaystyle \rho }

Hay una secuencia de órdenes de dominancia estocástica, desde el primero , al segundo , hasta órdenes superiores . La secuencia es cada vez más inclusiva. Es decir, si , entonces para todos . Además, existe tal que pero no . ⪰ 1 {\displaystyle \succeq _{1}} ⪰ 2 {\displaystyle \succeq _{2}} ⪰ n {\displaystyle \succeq _{n}} ρ ⪰ n ν {\displaystyle \rho \succeq _{n}\nu } ρ ⪰ k ν {\displaystyle \rho \succeq _{k}\nu } n ≤ k {\displaystyle n\leq k} ρ , ν {\displaystyle \rho ,\nu } ρ ⪰ n + 1 ν {\displaystyle \rho \succeq _{n+1}\nu } ρ ⪰ n ν {\displaystyle \rho \succeq _{n}\nu }

El predominio estocástico se remonta a (Blackwell, 1953), [3] pero no se desarrolló hasta 1969-1970. [4]

Dominio estatal (orden cero)

El caso más simple de dominio estocástico es el dominio estatal (también conocido como dominio estado por estado ), definido de la siguiente manera:

La variable aleatoria A es dominante en cada estado sobre la variable aleatoria B si A da un resultado al menos igual de bueno en cada estado (cada conjunto posible de resultados) y un resultado estrictamente mejor en al menos un estado.

Por ejemplo, si se añade un dólar a uno o más premios de una lotería, la nueva lotería domina a la antigua en todos los estados porque ofrece un mejor pago independientemente de los números específicos obtenidos por la lotería. De manera similar, si una póliza de seguro de riesgo tiene una prima más baja y una mejor cobertura que otra póliza, entonces, con o sin daños, el resultado es mejor. Cualquiera que prefiera más a menos (en la terminología estándar, cualquiera que tenga preferencias que aumentan de manera monótona ) siempre preferirá una apuesta dominante en todos los estados.

Primer orden

F B ∼ N ( 0 , 1 ) ( x ) ≥ F A ∼ N ( 0.75 , 1 ) ( x ) ∀ x {\displaystyle F_{B\sim N(0,1)}(x)\geq F_{A\sim N(0.75,1)}(x)\forall x} ⟹ B ( b l a c k ) ≤ A ( r e d ) {\displaystyle \implies B(black)\leq A(red)}
F X ∼ N ( 0 , 1 ) {\displaystyle F_{X\sim N(0,1)}} y , X e Y no son comparables a través del dominio estocástico de primer orden. F Y ∼ N ( 0.25 , 1.5 ) {\displaystyle F_{Y\sim N(0.25,1.5)}}

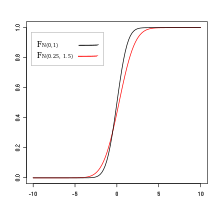
La dominancia estatal implica una dominancia estocástica de primer orden (FSD) , [5] que se define como:

La variable aleatoria A tiene dominio estocástico de primer orden sobre la variable aleatoria B si, para cualquier resultado x , A da al menos una probabilidad tan alta de recibir al menos x como la de B, y para algún x , A da una probabilidad mayor de recibir al menos x . En forma de notación, para todo x , y para algún x , . P [ A ≥ x ] ≥ P [ B ≥ x ] {\displaystyle P[A\geq x]\geq P[B\geq x]} P [ A ≥ x ] > P [ B ≥ x ] {\displaystyle P[A\geq x]>P[B\geq x]}

En términos de las funciones de distribución acumulativa de las dos variables aleatorias, A dominando a B significa que para todo x , con estricta desigualdad en algún  x . F A ( x ) ≤ F B ( x ) {\displaystyle F_{A}(x)\leq F_{B}(x)}

En el caso de funciones de distribución que no se intersecan [ aclaración necesaria ] , la prueba de suma de rangos de Wilcoxon prueba el dominio estocástico de primer orden. [6]

Definiciones equivalentes

Sean dos distribuciones de probabilidad en , tales que ambas son finitas, entonces las siguientes condiciones son equivalentes, por lo tanto todas pueden servir como definición de dominancia estocástica de primer orden: [7] ρ , ν {\displaystyle \rho ,\nu } R {\displaystyle \mathbb {R} } E X ∼ ρ [ | X | ] , E X ∼ ν [ | X | ] {\displaystyle \mathbb {E} _{X\sim \rho }[|X|],\mathbb {E} _{X\sim \nu }[|X|]}

  • Para cualquiera que no sea decreciente, u : R → R {\displaystyle u:\mathbb {R} \to \mathbb {R} } E X ∼ ρ [ u ( X ) ] ≥ E X ∼ ν [ u ( X ) ] {\displaystyle \mathbb {E} _{X\sim \rho }[u(X)]\geq \mathbb {E} _{X\sim \nu }[u(X)]}
  • F ρ ( t ) ≤ F ν ( t ) , ∀ t ∈ R . {\displaystyle F_{\rho }(t)\leq F_{\nu }(t),\quad \forall t\in \mathbb {R} .}
  • Existen dos variables aleatorias , tales que , donde . X ∼ ρ , Y ∼ ν {\displaystyle X\sim \rho ,Y\sim \nu } X = Y + δ {\displaystyle X=Y+\delta } δ ≥ 0 {\displaystyle \delta \geq 0}

La primera definición establece que una apuesta de primer orden domina estocásticamente a una apuesta si y solo si cada maximizador de utilidad esperada con una función de utilidad creciente prefiere una apuesta sobre una apuesta . ρ {\displaystyle \rho } ν {\displaystyle \nu } ρ {\displaystyle \rho } ν {\displaystyle \nu }

La tercera definición establece que podemos construir un par de apuestas con distribuciones , de modo que la apuesta siempre pague al menos tanto como la apuesta . Más concretamente, construya primero una distribuída uniformemente , luego use el muestreo por transformada inversa para obtener , luego para cualquier . X , Y {\displaystyle X,Y} ρ , ν {\displaystyle \rho ,\nu } X {\displaystyle X} Y {\displaystyle Y} Z ∼ U n i f o r m ( 0 , 1 ) {\displaystyle Z\sim \mathrm {Uniform} (0,1)} X = F X − 1 ( Z ) , Y = F Y − 1 ( Z ) {\displaystyle X=F_{X}^{-1}(Z),Y=F_{Y}^{-1}(Z)} X ≥ Y {\displaystyle X\geq Y} Z {\displaystyle Z}

Gráficamente, la segunda y tercera definición son equivalentes, porque podemos pasar de la función de densidad graficada de A a la de B tanto empujándola hacia arriba como empujándola hacia la izquierda.

Ejemplo extendido

Consideremos tres apuestas sobre un único lanzamiento de un dado justo de seis caras:

State (die result) 1 2 3 4 5 6 gamble A wins  $ 1 1 2 2 2 2 gamble B wins  $ 1 1 1 2 2 2 gamble C wins  $ 3 3 3 1 1 1 {\displaystyle {\begin{array}{rcccccc}{\text{State (die result)}}&1&2&3&4&5&6\\\hline {\text{gamble A wins }}\$&1&1&2&2&2&2\\{\text{gamble B wins }}\$&1&1&1&2&2&2\\{\text{gamble C wins }}\$&3&3&3&1&1&1\\\hline \end{array}}}

La apuesta A domina a la apuesta B en términos de estado porque A ofrece un rendimiento al menos igual en todos los estados posibles (resultados de la tirada de dados) y ofrece un rendimiento estrictamente mejor en uno de ellos (estado 3). Como A domina a B en términos de estado, también domina a B en primer orden.

La apuesta C no domina a B por estado porque B da un mejor rendimiento en los estados 4 a 6, pero C domina estocásticamente a B en primer orden porque Pr(B ≥ 1) = Pr(C ≥ 1) = 1, Pr(B ≥ 2) = Pr(C ≥ 2) = 3/6, y Pr(B ≥ 3) = 0 mientras que Pr(C ≥ 3) = 3/6 > Pr(B ≥ 3).

Las apuestas A y C no se pueden ordenar entre sí sobre la base del dominio estocástico de primer orden porque Pr(A ≥ 2) = 4/6 > Pr(C ≥ 2) = 3/6 mientras que, por otro lado, Pr(C ≥ 3) = 3/6 > Pr(A ≥ 3) = 0.

En general, aunque cuando una apuesta domina estocásticamente en primer orden a una segunda apuesta, el valor esperado de la ganancia en la primera será mayor que el valor esperado de la ganancia en la segunda, lo inverso no es cierto: no se pueden ordenar las loterías con respecto a la dominancia estocástica simplemente comparando las medias de sus distribuciones de probabilidad. Por ejemplo, en el ejemplo anterior, C tiene una media más alta (2) que A (5/3), pero C no domina en primer orden a A.

De segundo orden

El otro tipo de dominancia estocástica comúnmente utilizado es la dominancia estocástica de segundo orden . [1] [8] [9] En términos generales, para dos apuestas y , la apuesta tiene dominancia estocástica de segundo orden sobre la apuesta si la primera es más predecible (es decir, implica menos riesgo) y tiene una media al menos tan alta. Todos los maximizadores de utilidad esperada reacios al riesgo (es decir, aquellos con funciones de utilidad crecientes y cóncavas) prefieren una apuesta estocásticamente dominante de segundo orden a una dominada. La dominancia de segundo orden describe las preferencias compartidas de una clase más pequeña de tomadores de decisiones (aquellos para quienes más es mejor y que son reacios al riesgo, en lugar de todos aquellos para quienes más es mejor) que la dominancia de primer orden. ρ {\displaystyle \rho } ν {\displaystyle \nu } ρ {\displaystyle \rho } ν {\displaystyle \nu }

En términos de funciones de distribución acumulativa y , es estocásticamente dominante en segundo orden sobre si y solo si para todos , con desigualdad estricta en algún . De manera equivalente, domina en segundo orden si y solo si para todas las funciones de utilidad no decrecientes y cóncavas . F ρ {\displaystyle F_{\rho }} F ν {\displaystyle F_{\nu }} ρ {\displaystyle \rho } ν {\displaystyle \nu } ∫ − ∞ x [ F ν ( t ) − F ρ ( t ) ] d t ≥ 0 {\displaystyle \int _{-\infty }^{x}[F_{\nu }(t)-F_{\rho }(t)]\,dt\geq 0} x {\displaystyle x} x {\displaystyle x} ρ {\displaystyle \rho } ν {\displaystyle \nu } E X ∼ ρ [ u ( X ) ] ≥ E X ∼ ν [ u ( X ) ] {\displaystyle \mathbb {E} _{X\sim \rho }[u(X)]\geq \mathbb {E} _{X\sim \nu }[u(X)]} u ( x ) {\displaystyle u(x)}

La dominancia estocástica de segundo orden también se puede expresar de la siguiente manera: La apuesta de segundo orden domina estocásticamente si y solo si existen algunas apuestas y tales que , con siempre menor o igual a cero, y con para todos los valores de . Aquí la introducción de la variable aleatoria hace que la de primer orden esté dominada estocásticamente por (haciendo que no guste a quienes tienen una función de utilidad creciente), y la introducción de la variable aleatoria introduce una dispersión que preserva la media en la que no gusta a quienes tienen una utilidad cóncava. Nótese que si y tienen la misma media (de modo que la variable aleatoria degenera al número fijo 0), entonces es una dispersión que preserva la media de . ρ {\displaystyle \rho } ν {\displaystyle \nu } y {\displaystyle y} z {\displaystyle z} x ν = d ( x ρ + y + z ) {\displaystyle x_{\nu }{\overset {d}{=}}(x_{\rho }+y+z)} y {\displaystyle y} E ( z ∣ x ρ + y ) = 0 {\displaystyle \mathbb {E} (z\mid x_{\rho }+y)=0} x ρ + y {\displaystyle x_{\rho }+y} y {\displaystyle y} ν {\displaystyle \nu } ρ {\displaystyle \rho } ν {\displaystyle \nu } z {\displaystyle z} ν {\displaystyle \nu } ρ {\displaystyle \rho } ν {\displaystyle \nu } y {\displaystyle y} ν {\displaystyle \nu } ρ {\displaystyle \rho }

Definiciones equivalentes

Sean dos distribuciones de probabilidad en , tales que ambas son finitas, entonces las siguientes condiciones son equivalentes, por lo que todas pueden servir como definición de dominancia estocástica de segundo orden: [7] ρ , ν {\displaystyle \rho ,\nu } R {\displaystyle \mathbb {R} } E X ∼ ρ [ | X | ] , E X ∼ ν [ | X | ] {\displaystyle \mathbb {E} _{X\sim \rho }[|X|],\mathbb {E} _{X\sim \nu }[|X|]}

  • Para cualquier que no sea decreciente y (no necesariamente estrictamente) cóncava, u : R → R {\displaystyle u:\mathbb {R} \to \mathbb {R} } E X ∼ ρ [ u ( X ) ] ≥ E X ∼ ν [ u ( X ) ] {\displaystyle \mathbb {E} _{X\sim \rho }[u(X)]\geq \mathbb {E} _{X\sim \nu }[u(X)]}
  • ∫ − ∞ t F ρ ( x ) d x ≤ ∫ − ∞ t F ν ( x ) d x , ∀ t ∈ R . {\displaystyle \int _{-\infty }^{t}F_{\rho }(x)dx\leq \int _{-\infty }^{t}F_{\nu }(x)dx,\quad \forall t\in \mathbb {R} .}
  • Existen dos variables aleatorias , tales que , donde y . X ∼ ρ , Y ∼ ν {\displaystyle X\sim \rho ,Y\sim \nu } Y = X − δ + ϵ {\displaystyle Y=X-\delta +\epsilon } δ ≥ 0 {\displaystyle \delta \geq 0} E [ ϵ | X − δ ] = 0 {\displaystyle \mathbb {E} [\epsilon |X-\delta ]=0}

Éstas son análogas a las definiciones equivalentes de dominancia estocástica de primer orden, dadas anteriormente.

Condiciones suficientes

  • El dominio estocástico de primer orden de A sobre B es una condición suficiente para el dominio de segundo orden de A sobre B.
  • Si B es una dispersión que preserva la media de A , entonces A domina estocásticamente a B en segundo orden .

Condiciones necesarias

  • E ρ ( x ) ≥ E ν ( x ) {\displaystyle \mathbb {E} _{\rho }(x)\geq \mathbb {E} _{\nu }(x)} es una condición necesaria para que A domine estocásticamente en segundo orden a B.
  • min ρ ( x ) ≥ min ν ( x ) {\displaystyle \min _{\rho }(x)\geq \min _{\nu }(x)} es una condición necesaria para que A domine en segundo orden a B. La condición implica que la cola izquierda de debe ser más gruesa que la cola izquierda de . F ν {\displaystyle F_{\nu }} F ρ {\displaystyle F_{\rho }}

Tercer orden

Sean y las funciones de distribución acumulativa de dos inversiones distintas y . domina en el tercer orden si y solo si ambas F ρ {\displaystyle F_{\rho }} F ν {\displaystyle F_{\nu }} ρ {\displaystyle \rho } ν {\displaystyle \nu } ρ {\displaystyle \rho } ν {\displaystyle \nu }

  • ∫ − ∞ x ( ∫ − ∞ z [ F ν ( t ) − F ρ ( t ) ] d t ) d z ≥ 0  for all  x , {\displaystyle \int _{-\infty }^{x}\left(\int _{-\infty }^{z}[F_{\nu }(t)-F_{\rho }(t)]\,dt\right)dz\geq 0{\text{ for all }}x,}
  • E ρ ( x ) ≥ E ν ( x ) {\displaystyle \mathbb {E} _{\rho }(x)\geq \mathbb {E} _{\nu }(x)} .

Equivalentemente, domina en el tercer orden si y sólo si para todo . ρ {\displaystyle \rho } ν {\displaystyle \nu } E ρ U ( x ) ≥ E ν U ( x ) {\displaystyle \mathbb {E} _{\rho }U(x)\geq \mathbb {E} _{\nu }U(x)} U ∈ D 3 {\displaystyle U\in D_{3}}

El conjunto tiene dos definiciones equivalentes: D 3 {\displaystyle D_{3}}

  • el conjunto de funciones de utilidad cóncavas y no decrecientes que están sesgadas positivamente (es decir, tienen una tercera derivada no negativa en todas sus partes). [10]
  • el conjunto de funciones de utilidad cóncavas y no decrecientes, tales que para cualquier variable aleatoria , la función de prima de riesgo es una función monótonamente no creciente de . [11] Z {\displaystyle Z} π u ( x , Z ) {\displaystyle \pi _{u}(x,Z)} x {\displaystyle x}

Aquí se define como la solución al problema Ver más detalles en la página de prima de riesgo . π u ( x , Z ) {\displaystyle \pi _{u}(x,Z)} u ( x + E [ Z ] − π ) = E [ u ( x + Z ) ] . {\displaystyle u(x+\mathbb {E} [Z]-\pi )=\mathbb {E} [u(x+Z)].}

Condición suficiente

  • El dominio de segundo orden es una condición suficiente.

Condiciones necesarias[ cita requerida ]

  • E ρ ( log ⁡ ( x ) ) ≥ E ν ( log ⁡ ( x ) ) {\displaystyle \mathbb {E} _{\rho }(\log(x))\geq \mathbb {E} _{\nu }(\log(x))} es una condición necesaria. La condición implica que la media geométrica de debe ser mayor o igual que la media geométrica de . ρ {\displaystyle \rho } ν {\displaystyle \nu }
  • min ρ ( x ) ≥ min ν ( x ) {\displaystyle \min _{\rho }(x)\geq \min _{\nu }(x)} es una condición necesaria. La condición implica que la cola izquierda de debe ser más gruesa que la cola izquierda de . F ν {\displaystyle F_{\nu }} F ρ {\displaystyle F_{\rho }}

De orden superior

También se han analizado órdenes superiores de dominancia estocástica, así como generalizaciones de la relación dual entre los ordenamientos de dominancia estocástica y las clases de funciones de preferencia. [12] Podría decirse que el criterio de dominancia más poderoso se basa en el supuesto económico aceptado de disminución de la aversión absoluta al riesgo . [13] [14] Esto implica varios desafíos analíticos y se está realizando un esfuerzo de investigación para abordarlos. [15]

Formalmente, el dominio estocástico de orden n se define como [16]

  • Para cualquier distribución de probabilidad en , defina las funciones inductivamente: ρ {\displaystyle \rho } [ 0 , ∞ ) {\displaystyle [0,\infty )}

F ρ 1 ( t ) = F ρ ( t ) , F ρ 2 ( t ) = ∫ 0 t F ρ 1 ( x ) d x , ⋯ {\displaystyle F_{\rho }^{1}(t)=F_{\rho }(t),\quad F_{\rho }^{2}(t)=\int _{0}^{t}F_{\rho }^{1}(x)dx,\quad \cdots }

  • Para dos distribuciones de probabilidad cualesquiera en , la dominancia estocástica de orden n estricta y no estricta se define como ρ , ν {\displaystyle \rho ,\nu } [ 0 , ∞ ) {\displaystyle [0,\infty )} ρ ⪰ n ν  iff  F ρ n ≤ F ν n  on  [ 0 , ∞ ) {\displaystyle \rho \succeq _{n}\nu \quad {\text{ iff }}\quad F_{\rho }^{n}\leq F_{\nu }^{n}{\text{ on }}[0,\infty )} ρ ≻ n ν  iff  ρ ⪰ n ν  and  ρ ≠ ν {\displaystyle \rho \succ _{n}\nu \quad {\text{ iff }}\quad \rho \succeq _{n}\nu {\text{ and }}\rho \neq \nu }

Estas relaciones son transitivas y cada vez más inclusivas. Es decir, si , entonces para todo . Además, existe tal que pero no . ρ ⪰ n ν {\displaystyle \rho \succeq _{n}\nu } ρ ⪰ k ν {\displaystyle \rho \succeq _{k}\nu } k ≥ n {\displaystyle k\geq n} ρ , ν {\displaystyle \rho ,\nu } ρ ⪰ n + 1 ν {\displaystyle \rho \succeq _{n+1}\nu } ρ ⪰ n ν {\displaystyle \rho \succeq _{n}\nu }

Defina el momento n-ésimo por , entonces μ k ( ρ ) = E X ∼ ρ [ X k ] = ∫ x k d F ρ ( x ) {\displaystyle \mu _{k}(\rho )=\mathbb {E} _{X\sim \rho }[X^{k}]=\int x^{k}dF_{\rho }(x)}

Teorema  —  Si están en con momentos finitos para todos , entonces . ρ ≻ n ν {\displaystyle \rho \succ _{n}\nu } [ 0 , ∞ ) {\displaystyle [0,\infty )} μ k ( ρ ) , μ k ( ν ) {\displaystyle \mu _{k}(\rho ),\mu _{k}(\nu )} k = 1 , 2 , . . . , n {\displaystyle k=1,2,...,n} ( μ 1 ( ρ ) , . . . , μ n ( ρ ) ) ≻ n ∗ ( μ 1 ( ν ) , μ n ( ν ) ) {\displaystyle (\mu _{1}(\rho ),...,\mu _{n}(\rho ))\succ _{n}^{*}(\mu _{1}(\nu ),\mu _{n}(\nu ))}

Aquí, el ordenamiento parcial se define en por si y solo si , y, siendo el más pequeño tal que , tenemos ≻ n ∗ {\displaystyle \succ _{n}^{*}} R n {\displaystyle \mathbb {R} ^{n}} v ≻ n ∗ w {\displaystyle v\succ _{n}^{*}w} v ≠ w {\displaystyle v\neq w} k {\displaystyle k} v k ≠ w k {\displaystyle v_{k}\neq w_{k}} ( − 1 ) k − 1 v k > ( − 1 ) k − 1 w k {\displaystyle (-1)^{k-1}v_{k}>(-1)^{k-1}w_{k}}

Restricciones

Las relaciones de dominancia estocástica pueden usarse como restricciones en problemas de optimización matemática , en particular programación estocástica . [17] [18] [19] En un problema de maximización de una función real sobre variables aleatorias en un conjunto, podemos requerir adicionalmente que estocásticamente domine un punto de referencia aleatorio fijo . En estos problemas, las funciones de utilidad juegan el papel de multiplicadores de Lagrange asociados con restricciones de dominancia estocástica. Bajo condiciones apropiadas, la solución del problema es también una solución (posiblemente local) del problema para maximizar sobre en , donde es una cierta función de utilidad. Si se emplea la restricción de dominancia estocástica de primer orden, la función de utilidad es no decreciente ; si se utiliza la restricción de dominancia estocástica de segundo orden, es no decreciente y cóncava . Un sistema de ecuaciones lineales puede probar si una solución dada es eficiente para cualquier función de utilidad de este tipo. [20] Las restricciones de dominancia estocástica de tercer orden pueden manejarse usando programación cuadráticamente restringida convexa (QCP). [21] f ( X ) {\displaystyle f(X)} X {\displaystyle X} X 0 {\displaystyle X_{0}} X {\displaystyle X} B {\displaystyle B} f ( X ) + E [ u ( X ) − u ( B ) ] {\displaystyle f(X)+\mathbb {E} [u(X)-u(B)]} X {\displaystyle X} X 0 {\displaystyle X_{0}} u ( x ) {\displaystyle u(x)} u ( x ) {\displaystyle u(x)} u ( x ) {\displaystyle u(x)}

Véase también

Referencias

  1. ^ ab Hadar, J.; Russell, W. (1969). "Reglas para ordenar perspectivas inciertas". American Economic Review . 59 (1): 25–34. JSTOR  1811090.
  2. ^ Bawa, Vijay S. (1975). "Reglas óptimas para ordenar perspectivas inciertas". Revista de economía financiera . 2 (1): 95–121. doi :10.1016/0304-405X(75)90025-2.
  3. ^ Blackwell, David (junio de 1953). "Comparaciones equivalentes de experimentos". Anales de estadística matemática . 24 (2): 265–272. doi : 10.1214/aoms/1177729032 . ISSN  0003-4851.
  4. ^ Levy, Haim (1990), Eatwell, John; Milgate, Murray; Newman, Peter (eds.), "Dominancia estocástica", Utility and Probability , Londres: Palgrave Macmillan UK, págs. 251-254, doi :10.1007/978-1-349-20568-4_34, ISBN 978-1-349-20568-4, consultado el 23 de diciembre de 2022
  5. ^ Quirk, JP; Saposnik, R. (1962). "Admisibilidad y funciones de utilidad mensurables". Review of Economic Studies . 29 (2): 140–146. doi :10.2307/2295819. JSTOR  2295819.
  6. ^ Seifert, S. (2006). Ofertas a precio fijo en los mercados de subastas de Internet. Alemania: Physica-Verlag. Página 85, ISBN 9783540352686, https://books.google.com/books?id=a-ngTxeSLakC&pg=PA85
  7. ^ ab Mas-Colell, Andreu; Whinston, Michael Dennis; Verde, Jerry R. (1995). Teoría microeconómica. Nueva York. Proposición 6.D.1. ISBN 0-19-507340-1.OCLC 32430901  .{{cite book}}: CS1 maint: location missing publisher (link)
  8. ^ Hanoch, G.; Levy, H. (1969). "El análisis de eficiencia de las decisiones que implican riesgo". Review of Economic Studies . 36 (3): 335–346. doi :10.2307/2296431. JSTOR  2296431.
  9. ^ Rothschild, M. ; Stiglitz, JE (1970). "Incremento del riesgo: I. Una definición". Revista de teoría económica . 2 (3): 225–243. doi :10.1016/0022-0531(70)90038-4.
  10. ^ Chan, Raymond H.; Clark, Ephraim; Wong, Wing-Keung (16 de noviembre de 2012). "Sobre la dominancia estocástica de tercer orden para inversores con aversión al riesgo y buscadores de riesgo". mpra.ub.uni-muenchen.de . Consultado el 25 de diciembre de 2022 .
  11. ^ Whitmore, GA (1970). "Dominancia estocástica de tercer grado". The American Economic Review . 60 (3): 457–459. ISSN  0002-8282. JSTOR  1817999.
  12. ^ Ekern, Steinar (1980). "Riesgo creciente de enésimo grado". Cartas de Economía . 6 (4): 329–333. doi :10.1016/0165-1765(80)90005-1.
  13. ^ Vickson, RG (1975). "Pruebas de dominancia estocástica para la disminución de la aversión absoluta al riesgo. I. Variables aleatorias discretas". Management Science . 21 (12): 1438–1446. doi :10.1287/mnsc.21.12.1438.
  14. ^ Vickson, RG (1977). "Pruebas de dominancia estocástica para la disminución de la aversión absoluta al riesgo. II. Variables aleatorias generales". Management Science . 23 (5): 478–489. doi :10.1287/mnsc.23.5.478.
  15. ^ Véase, por ejemplo, Post, Th.; Fang, Y.; Kopa, M. (2015). "Pruebas lineales para la dominancia estocástica DARA". Management Science . 61 (7): 1615–1629. doi :10.1287/mnsc.2014.1960.
  16. ^ Fishburn, Peter C. (1980-02-01). "Dominancia estocástica y momentos de distribuciones". Matemáticas de la investigación de operaciones . 5 (1): 94–100. doi :10.1287/moor.5.1.94. ISSN  0364-765X.
  17. ^ Dentcheva, D. ; Ruszczyński, A. (2003). "Optimización con restricciones de dominancia estocástica". Revista SIAM sobre optimización . 14 (2): 548–566. CiteSeerX 10.1.1.201.7815 . doi :10.1137/S1052623402420528. S2CID  12502544. 
  18. ^ Kuosmanen, T (2004). "Diversificación eficiente según criterios de dominancia estocástica". Management Science . 50 (10): 1390–1406. doi :10.1287/mnsc.1040.0284.
  19. ^ Dentcheva, D. ; Ruszczyński, A. (2004). "Optimización probabilística semiinfinita: restricciones de dominancia estocástica de primer orden". Optimización . 53 (5–6): 583–601. doi :10.1080/02331930412331327148. S2CID  122168294.
  20. ^ Post, Th (2003). "Pruebas empíricas para la eficiencia de dominancia estocástica". Journal of Finance . 58 (5): 1905–1932. doi :10.1111/1540-6261.00592.
  21. ^ Post, Thierry; Kopa, Milos (2016). "Elección de cartera basada en la dominancia estocástica de tercer grado". Management Science . 63 (10): 3381–3392. doi :10.1287/mnsc.2016.2506. SSRN  2687104.
Retrieved from "https://en.wikipedia.org/w/index.php?title=Stochastic_dominance&oldid=1242519681"