Serie de Fourier
| Transformadas de Fourier |
|---|
Una serie de Fourier ( / ˈ f ʊr i eɪ , - i ər / [1] ) es una expansión de una función periódica en una suma de funciones trigonométricas . La serie de Fourier es un ejemplo de una serie trigonométrica , pero no todas las series trigonométricas son series de Fourier. [2] Al expresar una función como una suma de senos y cosenos, muchos problemas que involucran la función se vuelven más fáciles de analizar porque las funciones trigonométricas se entienden bien. Por ejemplo, las series de Fourier fueron utilizadas por primera vez por Joseph Fourier para encontrar soluciones a la ecuación del calor . Esta aplicación es posible porque las derivadas de las funciones trigonométricas caen en patrones simples. Las series de Fourier no se pueden utilizar para aproximar funciones arbitrarias, porque la mayoría de las funciones tienen infinitos términos en su serie de Fourier, y las series no siempre convergen . Las funciones de buen comportamiento, por ejemplo, las funciones suaves , tienen series de Fourier que convergen a la función original. Los coeficientes de la serie de Fourier se determinan mediante integrales de la función multiplicada por funciones trigonométricas, descritas en Formas comunes de la serie de Fourier a continuación.
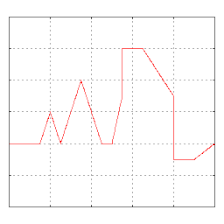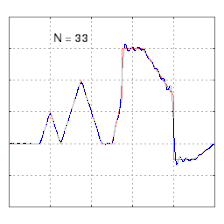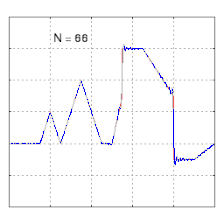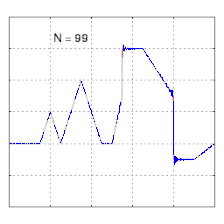
El estudio de la convergencia de las series de Fourier se centra en el comportamiento de las sumas parciales , lo que implica estudiar el comportamiento de la suma a medida que se suman más y más términos de la serie. Las figuras siguientes ilustran algunos resultados de series parciales de Fourier para los componentes de una onda cuadrada .
- Una onda cuadrada (representada como el punto azul) se aproxima mediante su sexta suma parcial (representada como el punto violeta), formada al sumar los primeros seis términos (representados como flechas) de la serie de Fourier de la onda cuadrada. Cada flecha comienza en la suma vertical de todas las flechas a su izquierda (es decir, la suma parcial anterior).
- Las primeras cuatro sumas parciales de la serie de Fourier para una onda cuadrada . A medida que se añaden más armónicos, las sumas parciales convergen (se vuelven cada vez más parecidas) a la onda cuadrada.
- La función (en rojo) es una suma de la serie de Fourier de 6 ondas sinusoidales armónicamente relacionadas (en azul). Su transformada de Fourier es una representación en el dominio de la frecuencia que revela las amplitudes de las ondas sinusoidales sumadas.
Las series de Fourier están estrechamente relacionadas con la transformada de Fourier , una herramienta más general que incluso puede encontrar la información de frecuencia para funciones que no son periódicas. Las funciones periódicas se pueden identificar con funciones en un círculo; por esta razón, las series de Fourier son objeto del análisis de Fourier en un círculo, generalmente denotado como o . La transformada de Fourier también es parte del análisis de Fourier , pero se define para funciones en .
Desde la época de Fourier, se han descubierto muchos enfoques diferentes para definir y comprender el concepto de serie de Fourier, todos ellos coherentes entre sí, pero cada uno de los cuales enfatiza diferentes aspectos del tema. Algunos de los enfoques más potentes y elegantes se basan en ideas y herramientas matemáticas que no estaban disponibles en la época de Fourier. Fourier definió originalmente la serie de Fourier para funciones de valores reales de argumentos reales, y utilizó las funciones seno y coseno en la descomposición. Desde entonces se han definido muchas otras transformadas relacionadas con Fourier , lo que extendió su idea inicial a muchas aplicaciones y dio origen a un área de las matemáticas llamada análisis de Fourier .
Formas comunes de la serie de Fourier
Una serie de Fourier es una función continua y periódica creada por la suma de funciones sinusoidales relacionadas armónicamente. Tiene varias formas diferentes, pero equivalentes, que se muestran aquí como sumas parciales. Pero en teoría, los símbolos con subíndice, llamados coeficientes , y el período, determinan la función de la siguiente manera :

| ( Ec.1 ) |
| ( Ec.2 ) |
| ( Ec.3 ) |
Los armónicos se indexan mediante un número entero, que es también el número de ciclos que dan las sinusoides correspondientes en el intervalo . Por lo tanto, las sinusoides tienen :
- una longitud de onda igual a en las mismas unidades que .
- una frecuencia igual a en las unidades recíprocas de .
Claramente, estas series pueden representar funciones que son simplemente una suma de una o más frecuencias armónicas. Lo notable es que también pueden representar frecuencias intermedias y/o funciones no sinusoidales debido al número infinito de términos. La forma amplitud-fase es particularmente útil por su comprensión de la lógica de los coeficientes de la serie (véase § Derivación). La forma exponencial es más fácil de generalizar para funciones de valores complejos (véase § Funciones de valores complejos).
La equivalencia de estas formas requiere ciertas relaciones entre los coeficientes. Por ejemplo, la identidad trigonométrica :
significa que :
| ( Ec.4.1 ) |
Por lo tanto y son las coordenadas rectangulares de un vector con coordenadas polares y
Los coeficientes pueden darse o suponerse, como en el caso de un sintetizador musical o de muestras de tiempo de una forma de onda. En este último caso, la forma exponencial de la serie de Fourier sintetiza una transformada de Fourier de tiempo discreto donde la variable representa la frecuencia en lugar del tiempo.
Pero normalmente los coeficientes se determinan mediante el análisis de frecuencia/armónico de una función de valor real dada y representan el tiempo :
| ( Ec.5 ) |
El objetivo es converger a como máximo o a todos los valores de en un intervalo de longitud. Para las funciones de buen comportamiento típicas de los procesos físicos, habitualmente se supone la igualdad, y las condiciones de Dirichlet proporcionan condiciones suficientes.
La notación representa la integración sobre el intervalo elegido. Las opciones típicas son y . Algunos autores definen porque simplifica los argumentos de las funciones sinusoidales, a expensas de la generalidad. Y algunos autores suponen que también es -periódica, en cuyo caso se aproxima a la función completa. El factor de escala se explica tomando un caso simple : Solo se necesita el término de la ecuación 2 para la convergencia, con y En consecuencia, la ecuación 5 proporciona :
- según sea necesario.
Coeficientes en forma exponencial
Otra identidad aplicable es la fórmula de Euler :
(Nota : el ∗ denota conjugación compleja ).
Sustituyendo esto en la ecuación 1 y comparándolo con la ecuación 3, finalmente se revela :
| ( Ec.6 ) |
En cambio :
Sustituyendo la ecuación 5 en la ecuación 6 también se revela : [3]
| ( Ec.7 ) |
Funciones de valores complejos
Las ecuaciones 7 y 3 también se aplican cuando es una función de valor complejo. [A] Esto se deduce expresando y como series de Fourier de valores reales separadas, y
Derivación
Los coeficientes y pueden entenderse y derivarse en términos de la correlación cruzada entre y una sinusoide en la frecuencia . Para una frecuencia general y un intervalo de análisis, la función de correlación cruzada :

| ( Ec.8 ) |
es esencialmente un filtro adaptado , con plantilla . El máximo de es una medida de la amplitud de la frecuencia en la función , y el valor de en el máximo determina la fase de esa frecuencia. La figura 2 es un ejemplo, donde es una onda cuadrada (no se muestra) y la frecuencia es el armónico. También es un ejemplo de derivación del máximo a partir de solo dos muestras, en lugar de buscar en toda la función. Al combinar la ecuación 8 con la ecuación 4 se obtiene :
La derivada de es cero en la fase de máxima correlación.
Por lo tanto, al calcular y según la ecuación 5 se crea la fase de máxima correlación del componente . Y la amplitud del componente es :
Otras notaciones comunes
La notación es inadecuada para analizar los coeficientes de Fourier de varias funciones diferentes. Por lo tanto, se suele reemplazar por una forma modificada de la función ( en este caso), como o , y la notación funcional a menudo reemplaza el subíndice :
En ingeniería, en particular cuando la variable representa el tiempo, la secuencia de coeficientes se denomina representación del dominio de frecuencia . Los corchetes se utilizan a menudo para enfatizar que el dominio de esta función es un conjunto discreto de frecuencias.
Otra representación del dominio de frecuencia comúnmente utilizada utiliza los coeficientes de la serie de Fourier para modular un peine de Dirac :
donde representa un dominio de frecuencia continua. Cuando la variable tiene unidades de segundos, tiene unidades de hercios . Los "dientes" del peine están espaciados en múltiplos (es decir, armónicos ) de , lo que se denomina frecuencia fundamental . se puede recuperar a partir de esta representación mediante una transformada de Fourier inversa :
Por lo tanto, la función construida se denomina comúnmente transformada de Fourier , aunque la integral de Fourier de una función periódica no es convergente en las frecuencias armónicas. [B]
Ejemplo de análisis


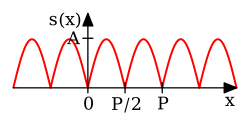
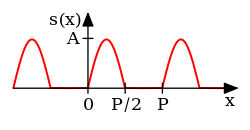
Consideremos una función de diente de sierra :
En este caso, los coeficientes de Fourier vienen dados por
Se puede demostrar que la serie de Fourier converge a en cada punto donde es diferenciable, y por lo tanto :
| ( Ec.9 ) |
Cuando , la serie de Fourier converge a 0, que es la semisuma de los límites izquierdo y derecho de s en . Este es un caso particular del teorema de Dirichlet para la serie de Fourier.
Este ejemplo conduce a una solución del problema de Basilea .
Convergencia
En el § Teorema de Fourier que demuestra la convergencia de las series de Fourier se presenta una prueba de que una serie de Fourier es una representación válida de cualquier función periódica (que satisface las condiciones de Dirichlet ).
En aplicaciones de ingeniería , generalmente se supone que la serie de Fourier converge excepto en discontinuidades de salto, ya que las funciones que se encuentran en ingeniería se comportan mejor que las funciones que se encuentran en otras disciplinas. En particular, si es continua y la derivada de (que puede no existir en todas partes) es integrable al cuadrado, entonces la serie de Fourier de converge de manera absoluta y uniforme a . [4] Si una función es integrable al cuadrado en el intervalo , entonces la serie de Fourier converge a la función en casi todas partes . Es posible definir coeficientes de Fourier para funciones o distribuciones más generales, en cuyo caso la convergencia puntual a menudo falla, y generalmente se estudia la convergencia en la norma o convergencia débil .
- Cuatro sumas parciales (series de Fourier) de longitudes 1, 2, 3 y 4 términos, que muestran cómo la aproximación a una onda cuadrada mejora a medida que aumenta el número de términos (animación)
- Cuatro sumas parciales (series de Fourier) de longitudes 1, 2, 3 y 4 términos, que muestran cómo la aproximación a una onda de diente de sierra mejora a medida que aumenta el número de términos (animación)
- Ejemplo de convergencia hacia una función algo arbitraria. Nótese el desarrollo del "ringing" ( fenómeno de Gibbs ) en las transiciones hacia/desde las secciones verticales.
Historia
La serie de Fourier recibe su nombre en honor a Jean-Baptiste Joseph Fourier (1768-1830), quien realizó importantes contribuciones al estudio de las series trigonométricas , después de las investigaciones preliminares de Leonhard Euler , Jean le Rond d'Alembert y Daniel Bernoulli . [C] Fourier introdujo la serie con el propósito de resolver la ecuación del calor en una placa de metal, publicando sus resultados iniciales en su Mémoire sur la propagation de la chaleur dans les corps solides ( Tratado sobre la propagación del calor en los cuerpos sólidos ) de 1807, y publicando su Théorie analytique de la chaleur ( Teoría analítica del calor ) en 1822. La Mémoire introdujo el análisis de Fourier, específicamente las series de Fourier. A través de la investigación de Fourier se estableció el hecho de que una función arbitraria (al principio, continua [5] y luego generalizada a cualquier sección lisa [6] ) puede representarse mediante una serie trigonométrica. El primer anuncio de este gran descubrimiento fue realizado por Fourier en 1807, ante la Academia Francesa . [7] Las primeras ideas de descomposición de una función periódica en la suma de funciones oscilantes simples se remontan al siglo III a. C., cuando los astrónomos antiguos propusieron un modelo empírico de los movimientos planetarios, basado en deferentes y epiciclos .
La ecuación del calor es una ecuación diferencial parcial . Antes del trabajo de Fourier, no se conocía ninguna solución a la ecuación del calor en el caso general, aunque se conocían soluciones particulares si la fuente de calor se comportaba de una manera simple, en particular, si la fuente de calor era una onda seno o coseno . Estas soluciones simples ahora a veces se denominan soluciones propias . La idea de Fourier era modelar una fuente de calor complicada como una superposición (o combinación lineal ) de ondas seno y coseno simples, y escribir la solución como una superposición de las soluciones propias correspondientes . Esta superposición o combinación lineal se llama serie de Fourier.
Desde un punto de vista moderno, los resultados de Fourier son algo informales, debido a la falta de una noción precisa de función e integral a principios del siglo XIX. Posteriormente, Peter Gustav Lejeune Dirichlet [8] y Bernhard Riemann [9] [10] [11] expresaron los resultados de Fourier con mayor precisión y formalidad.
Aunque la motivación original era resolver la ecuación del calor, más tarde se hizo evidente que las mismas técnicas podrían aplicarse a una amplia gama de problemas matemáticos y físicos, y especialmente a aquellos que involucran ecuaciones diferenciales lineales con coeficientes constantes, para los cuales las soluciones propias son senos paranasales . La serie de Fourier tiene muchas aplicaciones de este tipo en ingeniería eléctrica , análisis de vibraciones , acústica , óptica , procesamiento de señales , procesamiento de imágenes , mecánica cuántica , econometría , [12] teoría de capas , [13] etc.
Principios
Joseph Fourier escribió: [ dudoso – discutir ]
Multiplicando ambos lados por , y luego integrando de a obtenemos:
— Joseph Fourier, Mémoire sur la propagation de la chaleur dans les corps solides . (1807) [14] [D]
Esto da inmediatamente cualquier coeficiente a k de la serie trigonométrica para φ( y ) para cualquier función que tenga dicha expansión. Funciona porque si φ tiene dicha expansión, entonces (bajo supuestos de convergencia adecuados) la integral puede llevarse a cabo término por término. Pero todos los términos que involucran para j ≠ k se anulan cuando se integran de −1 a 1, dejando solo el término.
En estas pocas líneas, que se aproximan al formalismo moderno utilizado en las series de Fourier, Fourier revolucionó tanto las matemáticas como la física. Aunque Euler , d'Alembert , Daniel Bernoulli y Gauss habían utilizado series trigonométricas similares , Fourier creía que dichas series trigonométricas podían representar cualquier función arbitraria. En qué sentido esto es realmente cierto es una cuestión un tanto sutil y los intentos a lo largo de muchos años de aclarar esta idea han conducido a importantes descubrimientos en las teorías de convergencia , espacios de funciones y análisis armónico .
Cuando Fourier presentó un ensayo de competición posterior en 1811, el comité (que incluía a Lagrange , Laplace , Malus y Legendre , entre otros) concluyó: ...la manera en que el autor llega a estas ecuaciones no está exenta de dificultades y... su análisis para integrarlas todavía deja algo que desear en cuanto a generalidad e incluso rigor . [ cita requerida ]
La motivación de Fourier

La expansión de la serie de Fourier de la función diente de sierra (arriba) parece más complicada que la fórmula simple , por lo que no resulta inmediatamente evidente por qué se necesitaría la serie de Fourier. Si bien existen muchas aplicaciones, la motivación de Fourier fue resolver la ecuación del calor . Por ejemplo, considere una placa de metal con forma de cuadrado cuyos lados miden metros, con coordenadas . Si no hay una fuente de calor dentro de la placa, y si tres de los cuatro lados se mantienen a 0 grados Celsius, mientras que el cuarto lado, dado por , se mantiene en el gradiente de temperatura grados Celsius, para en , entonces se puede demostrar que la distribución de calor estacionaria (o la distribución de calor después de que haya transcurrido un largo período de tiempo) está dada por
Aquí, sinh es la función seno hiperbólica . Esta solución de la ecuación del calor se obtiene multiplicando cada término de la ecuación 9 por . Si bien nuestra función de ejemplo parece tener una serie de Fourier innecesariamente complicada, la distribución del calor no es trivial. La función no se puede escribir como una expresión de forma cerrada . Este método de resolver el problema del calor fue posible gracias al trabajo de Fourier.
Otras aplicaciones
Otra aplicación es resolver el problema de Basilea utilizando el teorema de Parseval . El ejemplo se generaliza y se puede calcular ζ (2 n ), para cualquier entero positivo n .
Tabla de series de Fourier comunes
En la siguiente tabla se muestran algunos pares comunes de funciones periódicas y sus coeficientes de series de Fourier.
- designa una función periódica con período .
- designar los coeficientes de la serie de Fourier (forma seno-coseno) de la función periódica .
Tabla de propiedades básicas
Esta tabla muestra algunas operaciones matemáticas en el dominio del tiempo y el efecto correspondiente en los coeficientes de la serie de Fourier. Notación:
- La conjugación compleja se denota con un asterisco.
- designar funciones periódicas o funciones definidas sólo para
- designar los coeficientes de la serie de Fourier (forma exponencial) de y
| Propiedad | Dominio del tiempo | Dominio de frecuencia (forma exponencial) | Observaciones | Referencia |
|---|---|---|---|---|
| Linealidad | ||||
| Inversión de tiempo / Inversión de frecuencia | [16] : pág. 610 | |||
| Conjugación del tiempo | [16] : pág. 610 | |||
| Inversión temporal y conjugación | ||||
| Parte real en el tiempo | ||||
| Parte imaginaria en el tiempo | ||||
| Parte real en frecuencia | ||||
| Parte imaginaria en frecuencia | ||||
| Desplazamiento en el tiempo / Modulación en la frecuencia | [16] : pág. 610 | |||
| Cambio de frecuencia / Modulación en el tiempo | [16] : pág. 610 |
Propiedades de simetría
Cuando las partes reales e imaginarias de una función compleja se descomponen en sus partes pares e impares , hay cuatro componentes, denotados a continuación por los subíndices RE, RO, IE e IO. Y hay una correspondencia biunívoca entre los cuatro componentes de una función de tiempo compleja y los cuatro componentes de su transformada de frecuencia compleja: [17]
De aquí se desprenden diversas relaciones, por ejemplo:
- La transformada de una función de valor real ( s RE + s RO ) es la función simétrica par S RE + i S IO . Por el contrario, una transformada simétrica par implica un dominio temporal de valor real.
- La transformada de una función de valor imaginario ( i s IE + i s IO ) es la función simétrica impar S RO + i S IE , y la inversa es verdadera.
- La transformada de una función par-simétrica ( s RE + i s IO ) es la función de valor real S RE + S RO , y lo inverso es cierto.
- La transformada de una función impar-simétrica ( s RO + i s IE ) es la función de valor imaginario i S IE + i S IO , y lo inverso es cierto.
Otras propiedades
Lema de Riemann-Lebesgue
Si es integrable , , y Este resultado se conoce como el lema de Riemann-Lebesgue .
Teorema de Parseval
Si pertenece a (periódico sobre un intervalo de longitud ) entonces :
Teorema de Plancherel
Si son coeficientes y entonces existe una función única tal que para cada .
Teoremas de convolución
Dadas funciones periódicas y con coeficientes de series de Fourier y
- El producto puntual : también es periódico, y sus coeficientes de serie de Fourier están dados por la convolución discreta de las secuencias y :
- La convolución periódica : también es -periódica, con coeficientes de la serie de Fourier :
- Una secuencia doblemente infinita en es la secuencia de coeficientes de Fourier de una función en si y sólo si es una convolución de dos secuencias en . Véase [18]
Propiedad derivada
Decimos que pertenece a si es una función periódica 2 π en la que es diferenciable 2 veces, y su derivada es continua.
- Si , entonces los coeficientes de Fourier de la derivada se pueden expresar en términos de los coeficientes de Fourier de la función , mediante la fórmula .
- Si , entonces . En particular, dado que para un fijo tenemos como , se deduce que tiende a cero, lo que significa que los coeficientes de Fourier convergen a cero más rápido que la k -ésima potencia de n para cualquier .
Grupos compactos
Una de las propiedades interesantes de la transformada de Fourier que hemos mencionado es que lleva las convoluciones a productos puntuales. Si esa es la propiedad que buscamos preservar, se pueden producir series de Fourier en cualquier grupo compacto . Los ejemplos típicos incluyen aquellos grupos clásicos que son compactos. Esto generaliza la transformada de Fourier a todos los espacios de la forma L 2 ( G ), donde G es un grupo compacto, de tal manera que la transformada de Fourier lleva las convoluciones a productos puntuales. La serie de Fourier existe y converge de manera similar al caso [− π , π ] .
Una extensión alternativa a los grupos compactos es el teorema de Peter-Weyl , que demuestra resultados sobre representaciones de grupos compactos análogos a los de los grupos finitos.

Variedades de Riemann
Si el dominio no es un grupo, entonces no hay una convolución intrínsecamente definida. Sin embargo, si es una variedad compacta de Riemann , tiene un operador de Laplace-Beltrami . El operador de Laplace-Beltrami es el operador diferencial que corresponde al operador de Laplace para la variedad de Riemann . Entonces, por analogía, uno puede considerar ecuaciones de calor en . Dado que Fourier llegó a su base al intentar resolver la ecuación de calor, la generalización natural es usar las soluciones propias del operador de Laplace-Beltrami como base. Esto generaliza las series de Fourier a espacios del tipo , donde es una variedad de Riemann. La serie de Fourier converge de formas similares al caso. Un ejemplo típico es tomar como la esfera con la métrica habitual, en cuyo caso la base de Fourier consiste en armónicos esféricos .
Grupos abelianos localmente compactos
La generalización a grupos compactos que se analizó anteriormente no se puede generalizar a grupos no compactos, no abelianos . Sin embargo, existe una generalización directa a grupos abelianos localmente compactos (LCA) .
Esto generaliza la transformada de Fourier a o , donde es un grupo LCA. Si es compacto, también se obtiene una serie de Fourier, que converge de manera similar al caso, pero si no es compacto, se obtiene en cambio una integral de Fourier . Esta generalización produce la transformada de Fourier habitual cuando el grupo abeliano localmente compacto subyacente es .
Extensiones
Serie de Fourier sobre un cuadrado
También podemos definir la serie de Fourier para funciones de dos variables y en el cuadrado :
Además de ser útil para resolver ecuaciones diferenciales parciales como la ecuación del calor, una aplicación notable de las series de Fourier sobre el cuadrado es la compresión de imágenes . En particular, el estándar de compresión de imágenes JPEG utiliza la transformada de coseno discreta bidimensional , una forma discreta de la transformada de coseno de Fourier , que utiliza solo el coseno como función base.
En el caso de matrices bidimensionales con una apariencia escalonada, la mitad de los coeficientes de la serie de Fourier desaparecen debido a la simetría adicional. [19]
Serie de Fourier de la función periódica de la red de Bravais
Una red de Bravais tridimensional se define como el conjunto de vectores de la forma: donde son números enteros y son tres vectores linealmente independientes. Suponiendo que tenemos alguna función, , tal que obedece la condición de periodicidad para cualquier vector de la red de Bravais , , podríamos hacer una serie de Fourier de ella. Este tipo de función puede ser, por ejemplo, el potencial efectivo que un electrón "siente" dentro de un cristal periódico. Es útil hacer la serie de Fourier del potencial cuando se aplica el teorema de Bloch . Primero, podemos escribir cualquier vector de posición arbitrario en el sistema de coordenadas de la red: donde lo que significa que se define como la magnitud de , por lo que es el vector unitario dirigido a lo largo de .
De esta manera podemos definir una nueva función,
Esta nueva función, , es ahora una función de tres variables, cada una de las cuales tiene periodicidad , , y respectivamente:
Esto nos permite construir un conjunto de coeficientes de Fourier, cada uno de ellos indexado por tres enteros independientes . En lo que sigue, utilizamos la notación de funciones para denotar estos coeficientes, donde antes usábamos subíndices. Si escribimos una serie para en el intervalo para , podemos definir lo siguiente:
Y luego podemos escribir:
Definiciones más detalladas:
Podemos escribir una vez más como:
Finalmente aplicando lo mismo para la tercera coordenada, definimos:
Escribimos como:
Reorganizando:
Ahora bien, cada vector reticular recíproco puede escribirse (pero no significa que sea la única forma de escribirlo) como , donde son números enteros y son vectores reticulares recíprocos que satisfacen ( para , y para ). Entonces, para cualquier vector reticular recíproco arbitrario y cualquier vector de posición arbitrario en el espacio reticular de Bravais original, su producto escalar es:
Por lo tanto, queda claro que en nuestra expansión de , la suma es en realidad sobre vectores reticulares recíprocos:
dónde
Suponiendo que podemos resolver este sistema de tres ecuaciones lineales para , , y en términos de , y para calcular el elemento de volumen en el sistema de coordenadas rectangular original. Una vez que tenemos , , y en términos de , y , podemos calcular el determinante jacobiano : que después de algunos cálculos y de aplicar algunas identidades de productos cruzados no triviales se puede demostrar que es igual a:
(puede ser ventajoso para simplificar los cálculos trabajar en un sistema de coordenadas rectangular en el que resulta que es paralelo al eje x , se encuentra en el plano xy y tiene componentes de los tres ejes). El denominador es exactamente el volumen de la celda unitaria primitiva que está encerrada por los tres vectores primitivos , y . En particular, ahora sabemos que
Podemos escribir ahora como una integral con el sistema de coordenadas tradicional sobre el volumen de la celda unitaria primitiva, en lugar de con las variables , y : escribiendo para el elemento de volumen ; y donde es la celda unitaria primitiva, por lo tanto, es el volumen de la celda unitaria primitiva.
Interpretación del espacio de Hilbert
En el lenguaje de los espacios de Hilbert , el conjunto de funciones es una base ortonormal para el espacio de funciones integrables al cuadrado en . Este espacio es en realidad un espacio de Hilbert con un producto interno dado para dos elementos cualesquiera y por:
- ¿Dónde está el complejo conjugado de?
El resultado básico de la serie de Fourier para los espacios de Hilbert se puede escribir como

Esto corresponde exactamente a la formulación exponencial compleja dada anteriormente. La versión con senos y cosenos también se justifica con la interpretación del espacio de Hilbert. De hecho, los senos y cosenos forman un conjunto ortogonal : (donde δ mn es el delta de Kronecker ), y además, los senos y cosenos son ortogonales a la función constante . Una base ortonormal para que consiste en funciones reales está formada por las funciones y , con n = 1,2,.... La densidad de su amplitud es una consecuencia del teorema de Stone-Weierstrass , pero se desprende también de las propiedades de los núcleos clásicos como el núcleo de Fejér .
Teorema de Fourier que demuestra la convergencia de las series de Fourier
Estos teoremas, y variaciones informales de ellos que no especifican las condiciones de convergencia, a veces se denominan genéricamente teorema de Fourier o teorema de Fourier . [20] [21] [22] [23]
La ecuación anterior 3 :
es un polinomio trigonométrico de grado que generalmente se puede expresar como :
Propiedad de mínimos cuadrados
El teorema de Parseval implica que:
Teorema — El polinomio trigonométrico es el único mejor polinomio trigonométrico de grado que se aproxima a , en el sentido de que, para cualquier polinomio trigonométrico de grado , tenemos: donde la norma del espacio de Hilbert se define como:
Teoremas de convergencia
Debido a la propiedad de mínimos cuadrados y a la completitud de la base de Fourier, obtenemos un resultado de convergencia elemental.
Teorema — Si pertenece a (un intervalo de longitud ), entonces converge a en , es decir, converge a 0 cuando .
Ya hemos mencionado que si es continuamente diferenciable, entonces es el coeficiente de Fourier de la derivada . Como la derivada es continua y, por lo tanto, acotada, es integrable al cuadrado y sus coeficientes de Fourier son sumables al cuadrado . Entonces, por la desigualdad de Cauchy-Schwarz ,
Esto significa que es absolutamente sumable. La suma de esta serie es una función continua, igual a , ya que la serie de Fourier converge en :
Teorema — Si , entonces converge a uniformemente (y por lo tanto también puntualmente ).
Este resultado se puede demostrar fácilmente si se supone además que es , ya que en ese caso tiende a cero cuando . De manera más general, la serie de Fourier es absolutamente sumable, por lo tanto converge uniformemente a , siempre que satisfaga una condición de Hölder de orden . En el caso absolutamente sumable, la desigualdad:
prueba convergencia uniforme
Se conocen muchos otros resultados relativos a la convergencia de las series de Fourier , que van desde el resultado moderadamente simple de que la serie converge en si es diferenciable en , hasta el resultado mucho más sofisticado de Lennart Carleson de que la serie de Fourier de una función en realidad converge casi en todas partes .
Divergencia
Como las series de Fourier tienen propiedades de convergencia tan buenas, muchas personas se sorprenden con frecuencia por algunos de los resultados negativos. Por ejemplo, la serie de Fourier de una función continua T -periódica no necesita converger puntualmente. El principio de acotación uniforme proporciona una prueba simple y no constructiva de este hecho.
En 1922, Andrey Kolmogorov publicó un artículo titulado Une série de Fourier-Lebesgue divergente casi en todas partes , en el que dio un ejemplo de una función integrable de Lebesgue cuya serie de Fourier diverge casi en todas partes. Más tarde construyó un ejemplo de una función integrable cuya serie de Fourier diverge en todas partes. [24]
Es posible dar ejemplos explícitos de una función continua cuya serie de Fourier diverge en 0: por ejemplo, la función par y 2π-periódica f definida para todo x en [0,π] por [25]
Como la función es par, la serie de Fourier contiene sólo cosenos:
Los coeficientes son:
A medida que m aumenta, los coeficientes serán positivos y aumentarán hasta alcanzar un valor de aproximadamente en para algún n y luego se volverán negativos (comenzando con un valor de alrededor de ) y se harán más pequeños, antes de comenzar una nueva onda de este tipo. En la serie de Fourier es simplemente la suma corriente de y esto se acumula hasta aproximadamente
en la onda n antes de volver a alrededor de cero, lo que demuestra que la serie no converge en cero sino que alcanza picos cada vez más altos. Nótese que, aunque la función es continua, no es diferenciable.
Véase también
- Teorema ATS
- Teorema de Carleson
- Núcleo de Dirichlet
- Transformada de Fourier discreta
- Transformada rápida de Fourier
- Teorema de Fejér
- Análisis de Fourier
- Serie de senos y cosenos de Fourier
- Transformada de Fourier
- Fenómeno de Gibbs
- Serie de Fourier de medio rango
- Serie de Laurent : la sustitución q = e ix transforma una serie de Fourier en una serie de Laurent, o viceversa. Se utiliza en la expansión de la serie q del invariante j .
- Análisis espectral de mínimos cuadrados
- Transformación multidimensional
- Transformadas de seno y coseno
- Teoría espectral
- Teoría de Sturm-Liouville
- Teorema de residuos, integrales de f ( z ), singularidades, polos
Notas
- ^ Pero , en general.
- ^ Dado que la integral que define la transformada de Fourier de una función periódica no es convergente, es necesario considerar la función periódica y su transformada como distribuciones . En este sentido , se trata de una función delta de Dirac , que es un ejemplo de distribución.
- ^ Estos tres realizaron algunos trabajos importantes en la ecuación de onda , especialmente D'Alembert. El trabajo de Euler en esta área fue en su mayoría contemporáneo/en colaboración con Bernoulli , aunque este último hizo algunas contribuciones independientes a la teoría de ondas y vibraciones. (Véase Fetter & Walecka 2003, pp. 209-210).
- ^ Estas palabras no son estrictamente de Fourier. Si bien el artículo citado sí menciona a Fourier como autor, una nota al pie indica que el artículo en realidad fue escrito por Poisson (que no fue escrito por Fourier también queda claro por el uso constante de la tercera persona para referirse a él) y que, "por razones de interés histórico", se presenta como si se tratara de las memorias originales de Fourier.
Referencias
- ^ "Fourier". Dictionary.com Unabridged (en línea). nd
- ^ Zygmund, A. (2002). Series trigonométricas (3.ª ed.). Cambridge, Reino Unido: Cambridge University Press. ISBN 0-521-89053-5.
- ^ Pinkus, Allan; Zafrany, Samy (1997). Series de Fourier y transformadas integrales (1.ª ed.). Cambridge, Reino Unido: Cambridge University Press. pp. 42–44. ISBN 0-521-59771-4.
- ^ Tolstov, Georgi P. (1976). Serie Fourier. Courier-Dover. ISBN 0-486-63317-9.
- ^ Stillwell, John (2013). "Lógica y filosofía de las matemáticas en el siglo XIX". En Ten, CL (ed.). Routledge History of Philosophy . Vol. VII: El siglo XIX. Routledge. pág. 204. ISBN 978-1-134-92880-4.
- ^ Fasshauer, Greg (2015). "Problemas de series de Fourier y valores en la frontera" (PDF) . Apuntes del curso de Matemáticas 461, cap. 3 . Departamento de Matemáticas Aplicadas, Instituto Tecnológico de Illinois . Consultado el 6 de noviembre de 2020 .
- ^ Cajori, Florian (1893). Una historia de las matemáticas. Macmillan. pág. 283.
- ^ Lejeune-Dirichlet, Peter Gustav (1829). "Sur la convergence des séries trigonométriques qui servent à représenter une fonction arbitraire entre des limites données" [Sobre la convergencia de series trigonométricas que sirven para representar una función arbitraria entre dos límites dados]. Journal für die reine und angewandte Mathematik (en francés). 4 : 157–169. arXiv : 0806.1294 .
- ^ "Ueber die Darstellbarkeit einer Function durch eine trigonometrische Reihe" [Acerca de la representabilidad de una función mediante una serie trigonométrica]. Habilitationsschrift , Gotinga ; 1854. Abhandlungen der Königlichen Gesellschaft der Wissenschaften zu Göttingen , vol. 13, 1867. Publicado póstumamente para Riemann por Richard Dedekind (en alemán). Archivado desde el original el 20 de mayo de 2008 . Consultado el 19 de mayo de 2008 .
- ^ Mascre, D.; Riemann, Bernhard (1867), "Tesis póstuma sobre la representación de funciones mediante series trigonométricas", en Grattan-Guinness, Ivor (ed.), Landmark Writings in Western Mathematics 1640–1940, Elsevier (publicado en 2005), pág. 49, ISBN 9780080457444
- ^ Remmert, Reinhold (1991). Teoría de funciones complejas: lecturas de matemáticas. Springer. pág. 29. ISBN 9780387971957.
- ^ Nerlove, Marc; Grether, David M.; Carvalho, Jose L. (1995). Análisis de series temporales económicas. Teoría económica, econometría y economía matemática . Elsevier. ISBN 0-12-515751-7.
- ^ Wilhelm Flügge , Tensiones en conchas (1973) 2.ª edición. ISBN 978-3-642-88291-3 . Publicado originalmente en alemán como Statik und Dynamik der Schalen (1937).
- ^ Fourier, Jean-Baptiste-Joseph (1888). Gastón Darboux (ed.). Oeuvres de Fourier [ Las obras de Fourier ] (en francés). París: Gauthier-Villars et Fils. págs. 218-219 - vía Gallica.
- ^ abcde Papula, Lothar (2009). Mathematische Formelsammlung: für Ingenieure und Naturwissenschaftler [ Funciones matemáticas para ingenieros y físicos ] (en alemán). Vieweg+Teubner Verlag. ISBN 978-3834807571.
- ^ abcd Shmaliy, YS (2007). Señales de tiempo continuo . Springer. ISBN 978-1402062711.
- ^ Proakis, John G.; Manolakis, Dimitris G. (1996). Procesamiento de señales digitales: principios, algoritmos y aplicaciones (3.ª ed.). Prentice Hall. pág. 291. ISBN 978-0-13-373762-2.
- ^ "Caracterizaciones de un subespacio lineal asociado a series de Fourier". MathOverflow. 19 de noviembre de 2010. Consultado el 8 de agosto de 2014 .
- ^ Desaparición de la mitad de los coeficientes de Fourier en matrices escalonadas
- ^ Siebert, William McC. (1985). Circuitos, señales y sistemas. MIT Press. pág. 402. ISBN 978-0-262-19229-3.
- ^ Marton, L.; Marton, Claire (1990). Avances en electrónica y física electrónica. Academic Press. pág. 369. ISBN 978-0-12-014650-5.
- ^ Kuzmany, Hans (1998). Espectroscopia de estado sólido. Springer. pág. 14. ISBN 978-3-540-63913-8.
- ^ Pribram, Karl H.; Yasue, Kunio; Jibu, Mari (1991). Cerebro y percepción. Asociados de Lawrence Erlbaum. pag. 26.ISBN 978-0-89859-995-4.
- ^ Katznelson, Yitzhak (1976). Introducción al análisis armónico (2.ª edición corregida). Nueva York, NY: Dover Publications, Inc. ISBN 0-486-63331-4.
- ^ Gourdon, Xavier (2009). Les maths en tête. Analizar (2ème édition) (en francés). Elipses. pag. 264.ISBN 978-2729837594.
Lectura adicional
- William E. Boyce; Richard C. DiPrima (2005). Ecuaciones diferenciales elementales y problemas de valores en la frontera (8.ª ed.). Nueva Jersey: John Wiley & Sons, Inc. ISBN 0-471-43338-1.
- Joseph Fourier, traducido por Alexander Freeman (2003). La teoría analítica del calor . Dover Publications. ISBN 0-486-49531-0.Republicación íntegra de 2003 de la traducción al inglés de 1878 realizada por Alexander Freeman de la obra de Fourier Théorie Analytique de la Chaleur , publicada originalmente en 1822.
- Enrique A. Gonzalez-Velasco (1992). "Conexiones en el análisis matemático: el caso de las series de Fourier". American Mathematical Monthly . 99 (5): 427–441. doi :10.2307/2325087. JSTOR 2325087.
- Fetter, Alexander L.; Walecka, John Dirk (2003). Mecánica teórica de partículas y continuos. Courier. ISBN 978-0-486-43261-8.
- Felix Klein , Desarrollo de las matemáticas en el siglo XIX . Mathsci Press Brookline, Mass, 1979. Traducido por M. Ackerman de Vorlesungen über die Entwicklung der Mathematik im 19 Jahrhundert , Springer, Berlín, 1928.
- Walter Rudin (1976). Principios del análisis matemático (3.ª ed.). Nueva York: McGraw-Hill, Inc. ISBN 0-07-054235-X.
- A. Zygmund (2002). Series trigonométricas (tercera edición). Cambridge: Cambridge University Press. ISBN 0-521-89053-5.La primera edición se publicó en 1935.
Enlaces externos
- "Series de Fourier", Enciclopedia de Matemáticas , EMS Press , 2001 [1994]
- Hobson, Ernest (1911). . Encyclopædia Britannica . Vol. 10 (11.ª ed.). Págs. 753–758.
- Weisstein, Eric W. "Series de Fourier". MathWorld .
- Joseph Fourier – Un sitio sobre la vida de Fourier que se utilizó para la sección histórica de este artículo en Wayback Machine (archivado el 5 de diciembre de 2001)
Este artículo incorpora material del ejemplo de serie de Fourier en PlanetMath , que se encuentra bajo la licencia Creative Commons Attribution/Share-Alike License .































![{\estilo de visualización [-P/2,P/2]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/773e3d42ef176524eeb449749ec2bc0a83b5566a)
![{\estilo de visualización [0, P]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e22a95e69fea5905acab328644408c110eedea0e)







![{\displaystyle {\begin{aligned}\cos \left(2\pi {\tfrac {n}{P}}x-\varphi _{n}\right)&{}\equiv {\tfrac {1}{2}}e^{i\left(2\pi {\tfrac {n}{P}}x-\varphi _{n}\right)}+{\tfrac {1}{2}}e^{-i\left(2\pi {\tfrac {n}{P}}x-\varphi _{n}\right)}\\[6pt]&=\left({\tfrac {1}{2}}e^{-i\varphi _{n}}\right)\cdot e^{i2\pi {\tfrac {+n}{P}}x}+\left({\tfrac {1}{2}}e^{-i\varphi _{n}}\right)^{*}\cdot e^{i2\pi {\tfrac {-n}{P}}x}\end{alineado}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2b4e16273af487d058c192627d139fe8fca55e67)








![{\displaystyle [x_{0},x_{0}+P],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/74358f52e616039efc9b1fcc9568f99f6ae93463)
![{\displaystyle \mathrm {X} _{f}(\tau )={\tfrac {2}{P}}\int _{x_{0}}^{x_{0}+P}s(x)\cdot \cos \left(2\pi f(x-\tau )\right)\,dx;\quad \tau \in \left[0,{\tfrac {1}{f}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0ae1bbd189d0cd0cdc4218a2b78ced49bcc11d89)







![{\displaystyle {\begin{aligned}\mathrm {X} _{n}(\varphi )&={\tfrac {2}{P}}\int _{P}s(x)\cdot \cos \left(2\pi {\tfrac {n}{P}}x-\varphi \right)\,dx;\quad \varphi \in [0,2\pi ]\\&=\cos(\varphi )\cdot \underbrace {{\tfrac {2}{P}}\int _{P}s(x)\cdot \cos \left(2\pi {\tfrac {n}{P}}x\right)\,dx} _{A}+\sin(\varphi )\cdot \underbrace {{\tfrac {2}{P}}\int _{P}s(x)\cdot \sin \left(2\pi {\tfrac {n}{P}}x\right)\,dx} _{B}\\&=\cos(\varphi )\cdot A+\sin(\varphi )\cdot B\end{alineado}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/24287ecc41a76aacf2f640f52674dbcfcee07d21)






![{\displaystyle S[n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0b4222b53917b43f530116997b71049100c95586)
![{\displaystyle {\begin{aligned}s(x)&=\sum _{n=-\infty }^{\infty }{\widehat {s}}(n)\cdot e^{i2\pi {\tfrac {n}{P}}x}&&\scriptstyle {\text{notación matemática común}}\\&=\sum _{n=-\infty }^{\infty }S[n]\cdot e^{i2\pi {\tfrac {n}{P}}x}&&\scriptstyle {\text{notación común de ingeniería}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ab1656144664ad56f8ed36ac280fbf9401ea7da9)
![{\displaystyle S(f)\ \triangleq \ \sum _{n=-\infty }^{\infty }S[n]\cdot \delta \left(f-{\frac {n}{P}}\right),}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e6a4127cd2d8d239076aad35e6b82248554b6036)


![{\displaystyle {\begin{aligned}{\mathcal {F}}^{-1}\{S(f)\}&=\int _{-\infty }^{\infty }\left(\sum _{n=-\infty }^{\infty }S[n]\cdot \delta \left(f-{\frac {n}{P}}\right)\right)e^{i2\pi fx}\,df,\\[6pt]&=\sum _{n=-\infty }^{\infty }S[n]\cdot \int _{-\infty }^{\infty }\delta \left(f-{\frac {n}{P}}\right)e^{i2\pi fx}\,df,\\[6pt]&=\sum _{n=-\infty }^{\infty }S[n]\cdot e^{i2\pi {\tfrac {n}{P}}x}\ \ \triangleq \ s_{\infty }(x).\end{alineado}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/10002996a7c3e5b28df028d7096c4c00efee99c6)

![{\estilo de visualización (-\pi ,\pi ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7fbb1843079a9df3d3bbcce3249bb2599790de9c)


![{\displaystyle {\begin{aligned}A_{n}&={\frac {1}{\pi }}\int _{-\pi }^{\pi }s(x)\cos(nx)\, dx=0,\quad n\geq 0.\\[4pt]B_{n}&={\frac {1}{\pi }}\int _{-\pi }^{\pi }s(x) \sin(nx)\,dx\\[4pt]&=-{\frac {2}{\pi n}}\cos(n\pi )+{\frac {2}{\pi ^{2}n ^{2}}}\sin(n\pi )\\[4pt]&={\frac {2\,(-1)^{n+1}}{\pi n}},\quad n\geq 1.\end{alineado}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/60820ad01df637675beb2c56a9db388cd0539490)

![{\displaystyle {\begin{aligned}s(x)&={\frac {a_{0}}{2}}+\sum _{n=1}^{\infty }\left[A_{n}\cos \left(nx\right)+B_{n}\sin \left(nx\right)\right]\\[4pt]&={\frac {2}{\pi }}\sum _{n=1}^{\infty }{\frac {(-1)^{n+1}}{n}}\sin(nx),\quad \mathrm {para} \ (x-\pi )\ {\text{no es un múltiplo de}}\ 2\pi .\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4b5b85f18c97953fdf678240a1f7d70bc15abbdb)

![{\displaystyle [x_{0},x_{0}+P]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3ef79a1b836ec65eacb0d2c73464996d2b7830ba)










![{\displaystyle (x,y)\en [0,\pi ]\times [0,\pi ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c18734f151b17b5d3e325f79c7000826ab832610)


















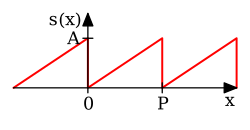








![{\displaystyle x\en [0,P].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/06b058e43f16179590921d9669ac45cec21a975e)
![{\displaystyle S[n],R[n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/320b593144d771f4aac1aae12d9513debbd3b20f)


![{\displaystyle a\cdot S[n]+b\cdot R[n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/23622be4a50d54928d05c273e803240a2cb1e413)


![{\displaystyle S[-n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ab628b28c49c04cab81d0bd30d19ee0797b0587c)

![Estilo de visualización S^{*}[-n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a3f6ea8a947b86f8a31046070359f6b8111a0bae)

![Estilo de visualización S*[n]](https://wikimedia.org/api/rest_v1/media/math/render/svg/3776c67c40997d8044720ef84de7575679cf9638)

![{\displaystyle {\frac {1}{2}}(S[n]+S^{*}[-n])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2eb44dffaae6c85870914249c054e33236b02cc8)

![{\displaystyle {\frac {1}{2i}}(S[n]-S^{*}[-n])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bc039a9c12ae20a4b47337ae55bf8a7bc26d2e11)

![{\displaystyle \operatorname {Re} {(S[n])}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/140ebff319eb8eb7965d0ca86dcaadb21685177a)

![{\displaystyle \operatorname {Im} {(S[n])}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0c726948120015ce0d482f5f7f4af81713342b5c)

![{\displaystyle S[n]\cdot e^{-i2\pi {\tfrac {x_{0}}{P}}n}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7c56731e1382c8189ca81104cbade4d310fd72d8)


![{\displaystyle S[n-n_{0}]\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/07385c0e5fd45d4e07a279a91668cf8894963e0c)



![{\textstyle \lim _{|n|\to \infty }S[n]=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7fc04d857f6462ae29422edcada981c8a798d4b5)



![{\textstyle {\frac {1}{P}}\int _{P}|s(x)|^{2}\,dx=\sum _{n=-\infty }^{\infty }{\Bigl |}S[n]{\Bigr |}^{2}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/90e7f4dd99392022f87674ed1c8ea8306634bc28)



![{\displaystyle S[n]=c_{n}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c4375307afdf29e78a31ef64b699dcb3e2fde140)



![{\displaystyle R[n],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/80d8bbe147f3eb3fb318d09437a3540e054b0289)



![{\displaystyle H[n]=\{S*R\}[n].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b5d3978629d1c2cd954f884509a1bb360f01cac5)

![{\displaystyle H[n]=P\cdot S[n]\cdot R[n].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1804f502413d4e3e5f28f8715c52e2a3d7e7e9a6)


![{\displaystyle L^{1}([0,2\pi ])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bd16426bda528c05e32e97bfba7f51b598c081b8)





![{\displaystyle {\widehat {s'}}[n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a50845d25c79fe9547d0194fce67a390efc1a4ed)

![{\displaystyle {\widehat {s}}[n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/efb5adbeb52d198894dc8f70ec8c434f0e193e6b)
![{\displaystyle {\widehat {s'}}[n]=en{\widehat {s}}[n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d281471757291b705a757faa55af0f1cebf8a0b6)

![{\displaystyle {\widehat {s^{(k)}}}[n]=(en)^{k}{\widehat {s}}[n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b0120eafbcb1c02b4c2f81f5589fdc328c28bd20)

![{\displaystyle {\widehat {s^{(k)}}}[n]\to 0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0ddeff4d322091a8ec85a30a10d584d426d703b1)

![{\displaystyle |n|^{k}{\widehat {s}}[n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/541244c281f9472e99fca9b32f2cd7676434d09c)


![{\estilo de visualización [-\pi ,\pi ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cb064fd6c55820cfa660eabeeda0f6e3c4935ae6)




![{\displaystyle [-\pi,\pi]\times [-\pi,\pi]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/df436805f50de7386abdb2a9d058672ec1b4cebb)
![{\displaystyle {\begin{aligned}f(x,y)&=\sum _{j,k\in \mathbb {Z} }c_{j,k}e^{ijx}e^{iky},\ \[5pt]c_{j,k}&={\frac {1}{4\pi ^{2}}}\int _{-\pi }^{\pi }\int _{-\pi }^ {\pi }f(x,y)e^{-ijx}e^{-iky}\,dx\,dy.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/aec3723d7051701ab4530dce39f1480cef835981)



















![{\displaystyle \left[0,a_{1}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/187cf2c27876a96c668f73266f673002808773ac)



![{\displaystyle {\begin{aligned}h^{\mathrm {dos} }(m_{1},m_{2},x_{3})&\triangleq {\frac {1}{a_{2}}}\int _{0}^{a_{2}}h^{\mathrm {uno} }(m_{1},x_{2},x_{3})\cdot e^{-i2\pi {\tfrac {m_{2}}{a_{2}}}x_{2}}\,dx_{2}\\[12pt]&={\frac {1}{a_{2}}}\int _{0}^{a_{2}}dx_{2}{\frac {1}{a_{1}}}\int _{0}^{a_{1}}dx_{1}g(x_{1},x_{2},x_{3})\cdot e^{-i2\pi \left({\tfrac {m_{1}}{a_{1}}}x_{1}+{\tfrac {m_{2}}{a_{2}}}x_{2}\right)}\end{alineado}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/257f40440f195f996a7a7df57b110f544e8553c6)

![{\displaystyle {\begin{aligned}h^{\mathrm {tres} }(m_{1},m_{2},m_{3})&\triangleq {\frac {1}{a_{3}}}\int _{0}^{a_{3}}h^{\mathrm {dos} }(m_{1},m_{2},x_{3})\cdot e^{-i2\pi {\tfrac {m_{3}}{a_{3}}}x_{3}}\,dx_{3}\\[12pt]&={\frac {1}{a_{3}}}\int _{0}^{a_{3}}dx_{3}{\frac {1}{a_{2}}}\int _{0}^{a_{2}}dx_{2}{\frac {1}{a_{1}}}\int _{0}^{a_{1}}dx_{1}g(x_{1},x_{2},x_{3})\cdot e^{-i2\pi \left({\tfrac {m_{1}}{a_{1}}}x_{1}+{\tfrac {m_{2}}{a_{2}}}x_{2}+{\tfrac {m_{3}}{a_{3}}}x_{3}\right)}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e16c337b17dc4ed299de47b108a2ff7eb060b9f3)



















![{\displaystyle {\begin{vmatrix}{\dfrac {\partial x_{1}}{\partial x}}&{\dfrac {\partial x_{1}}{\partial y}}&{\dfrac {\partial x_{1}}{\partial z}}\\[12pt]{\dfrac {\partial x_{2}}{\partial x}}&{\dfrac {\partial x_{2}}{\partial y}}&{\dfrac {\partial x_{2}}{\partial z}}\\[12pt]{\dfrac {\partial x_{3}}{\partial x}}&{\dfrac {\partial x_{3}}{\partial y}}&{\dfrac {\partial x_{3}}{\partial z}}\end{vmatrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5e5df9134486606d6a55c8ec4a96ee3ca353e924)












![{\displaystyle L^{2}([-\pi ,\pi ])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0f84fea7a212acaf14649b6cdcca282b0646a8b0)












![{\displaystyle s_{_{N}}(x)=\sum _{n=-N}^{N}S[n]\ e^{i2\pi {\tfrac {n}{P}}x} ,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b5a3caa42e24c74a3efb0abdf3eb44ad068f7eb5)

![{\displaystyle p_{_{N}}(x)=\sum _{n=-N}^{N}p[n]\ e^{i2\pi {\tfrac {n}{P}}x} .}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ef1c25f3121bf8a28e6ae0a7d00eef1b2953f1dc)







![{\displaystyle (i\cdot n)S[n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4a89ae55b94c8d25d1f3927c5ba4eb65ac7c4762)

![{\displaystyle \left(\sum _{n\neq 0}|S[n]|\right)^{2}\leq \sum _{n\neq 0}{\frac {1}{n^{2}}}\cdot \sum _{n\neq 0}|nS[n]|^{2}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5d7d56e47f74b571fd1be62f2ec4df2276c825f5)


![Estilo de visualización n^{2}S[n]](https://wikimedia.org/api/rest_v1/media/math/render/svg/340e0b24995005f3669a865a57edb4035b77ca2d)


![{\displaystyle \sup_{x}|s(x)-s_{_{N}}(x)|\leq \sum_{|n|>N}|S[n]|}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d8225d322a5b676b2b1709c2a636dcd092ff11ec)

![{\displaystyle f(x)=\sum _{n=1}^{\infty }{\frac {1}{n^{2}}}\sin \left[\left(2^{n^{3}}+1\right){\frac {x}{2}}\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a8707621c87adf54eadc1389a9b18497c22a437d)









