Expansión de la serie

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed. Find sources: "Series expansion" – news · newspapers · books · scholar · JSTOR (August 2021) (Learn how and when to remove this message)

Some of this article's listed sources may not be reliable. Please help improve this article by looking for better, more reliable sources. Unreliable citations may be challenged and removed. (May 2024) (Learn how and when to remove this message)

En matemáticas , una expansión en serie es una técnica que expresa una función como una suma infinita, o serie , de funciones más simples. Es un método para calcular una función que no puede expresarse únicamente mediante operadores elementales (suma, resta, multiplicación y división). ^[1]

La denominada serie resultante a menudo se puede limitar a un número finito de términos, lo que produce una aproximación de la función. Cuantos menos términos de la secuencia se utilicen, más sencilla será esta aproximación. A menudo, la inexactitud resultante (es decir, la suma parcial de los términos omitidos) se puede describir mediante una ecuación que implica la notación Big O (véase también expansión asintótica ). La expansión de la serie en un intervalo abierto también será una aproximación para funciones no analíticas . ^{[2] [ verificación necesaria ]}

Hay varios tipos de expansiones de series, que se enumeran a continuación.

Una serie de Taylor es una serie de potencias basada en las derivadas de una función en un único punto. ^[3] Más específicamente, si una función es infinitamente diferenciable alrededor de un punto , entonces la serie de Taylor de f alrededor de este punto está dada por${\displaystyle f:U\to \mathbb {R} }$${\displaystyle x_{0}}$

${\displaystyle \sum _{n=0}^{\infty }{\frac {f^{(n)}(x_{0})}{n!}}(x-x_{0})^{n}}$

bajo la convención . ^{[3] [4]} La serie de Maclaurin de f es su serie de Taylor alrededor de . ^{[5] [4]}${\displaystyle 0^{0}:=1}$${\displaystyle x_{0}=0}$

Una serie de Laurent es una generalización de la serie de Taylor, que permite términos con exponentes negativos; toma la forma y converge en un anillo . ^[6] En particular, una serie de Laurent se puede utilizar para examinar el comportamiento de una función compleja cerca de una singularidad considerando la expansión de la serie en un anillo centrado en la singularidad.${\textstyle \sum _{k=-\infty }^{\infty }c_{k}(z-a)^{k}}$

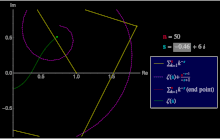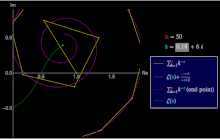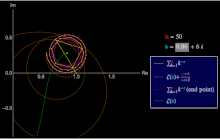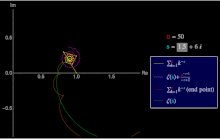
Una serie de Dirichlet general es una serie de la forma Un caso especial importante de esto es la serie de Dirichlet ordinaria ^[7] Utilizada en teoría de números . ^{[ cita requerida ]}${\textstyle \sum _{n=1}^{\infty }a_{n}e^{-\lambda _{n}s}.}$ ${\textstyle \sum _{n=1}^{\infty }{\frac {a_{n}}{n^{s}}}.}$

Una serie de Fourier es una expansión de funciones periódicas como una suma de muchas funciones seno ^{[ ancla rota ]} y coseno ^{[ ancla rota ]} . ^[8] Más específicamente, la serie de Fourier de una función de período está dada por la expresión donde los coeficientes están dados por las fórmulas ^{[8] [9]}${\displaystyle f(x)}$${\displaystyle 2L}$$${\displaystyle a_{0}+\sum _{n=1}^{\infty }\left[a_{n}\cos \left({\frac {n\pi x}{L}}\right)+b_{n}\sin \left({\frac {n\pi x}{L}}\right)\right]}$$$${\displaystyle {\begin{aligned}a_{n}&:={\frac {1}{L}}\int _{-L}^{L}f(x)\cos \left({\frac {n\pi x}{L}}\right)dx,\\b_{n}&:={\frac {1}{L}}\int _{-L}^{L}f(x)\sin \left({\frac {n\pi x}{L}}\right)dx.\end{aligned}}}$$

• En acústica , por ejemplo, el tono fundamental y los armónicos juntos forman un ejemplo de una serie de Fourier. ^{[ cita requerida ]}

• Serie newtoniana ^{[ cita requerida ]}

• Polinomios de Legendre : se utilizan en física para describir un campo eléctrico arbitrario como una superposición de un campo dipolar , un campo cuadrupolar , un campo octupolar , etc. ^{[ cita requerida ]}

• Polinomios de Zernike : se utilizan en óptica para calcular las aberraciones de los sistemas ópticos. Cada término de la serie describe un tipo particular de aberración. ^{[ cita requerida ]}

• La serie de Stirling es una aproximación de la función log-gamma . ^[10]$${\displaystyle {\text{Ln}}\Gamma \left(z\right)\sim \left(z-{\tfrac {1}{2}}\right)\ln z-z+{\tfrac {1}{2}}\ln \left(2\pi \right)+\sum _{k=1}^{\infty }{\frac {B_{2k}}{2k(2k-1)z^{2k-1}}}}$$

La siguiente es la serie de Taylor de : ^{[11] [12]}${\displaystyle e^{x}}$$${\displaystyle e^{x}=\sum _{n=0}^{\infty }{\frac {x^{n}}{n!}}=1+x+{\frac {x^{2}}{2}}+{\frac {x^{3}}{6}}...}$$

La serie de Dirichlet de la función zeta de Riemann es ^[7]$${\displaystyle \zeta (s):=\sum _{n=1}^{\infty }{\frac {1}{n^{s}}}={\frac {1}{1^{s}}}+{\frac {1}{2^{s}}}+\cdots }$$