Teoría del control

La teoría de control es un campo de la ingeniería de control y las matemáticas aplicadas que se ocupa del control de sistemas dinámicos en procesos y máquinas de ingeniería. El objetivo es desarrollar un modelo o algoritmo que rija la aplicación de las entradas del sistema para conducir el sistema a un estado deseado, mientras se minimiza cualquier retraso , sobreimpulso o error de estado estable y se garantiza un nivel de estabilidad de control ; a menudo con el objetivo de lograr un grado de optimalidad .

Para ello, se requiere un controlador con el comportamiento correctivo requerido. Este controlador monitorea la variable de proceso controlada (PV) y la compara con el punto de referencia o punto de ajuste (SP). La diferencia entre el valor real y el deseado de la variable de proceso, llamada señal de error o error SP-PV, se aplica como retroalimentación para generar una acción de control para llevar la variable de proceso controlada al mismo valor que el punto de ajuste. Otros aspectos que también se estudian son la controlabilidad y la observabilidad . La teoría de control se utiliza en la ingeniería de sistemas de control para diseñar la automatización que ha revolucionado la fabricación, la aviación, las comunicaciones y otras industrias, y ha creado nuevos campos como la robótica .

Se suele hacer un uso extensivo de un estilo diagramático conocido como diagrama de bloques . En él, la función de transferencia , también conocida como función del sistema o función de red, es un modelo matemático de la relación entre la entrada y la salida basado en las ecuaciones diferenciales que describen el sistema.

La teoría de control data del siglo XIX, cuando James Clerk Maxwell describió por primera vez la base teórica para el funcionamiento de los reguladores . ^[1] La teoría de control fue desarrollada por Edward Routh en 1874, Charles Sturm y en 1895, Adolf Hurwitz , quienes contribuyeron al establecimiento de criterios de estabilidad de control; y desde 1922 en adelante, el desarrollo de la teoría de control PID por Nicolas Minorsky . ^[2] Aunque una aplicación importante de la teoría de control matemático es en la ingeniería de sistemas de control , que se ocupa del diseño de sistemas de control de procesos para la industria, otras aplicaciones van mucho más allá de esto. Como teoría general de los sistemas de retroalimentación, la teoría de control es útil dondequiera que ocurra la retroalimentación; por lo tanto, la teoría de control también tiene aplicaciones en las ciencias de la vida, la ingeniería informática, la sociología y la investigación de operaciones . ^[3]

Aunque los sistemas de control de varios tipos se remontan a la antigüedad, un análisis más formal del campo comenzó con un análisis dinámico del regulador centrífugo , realizado por el físico James Clerk Maxwell en 1868, titulado On Governors . ^[4] Un regulador centrífugo ya se utilizaba para regular la velocidad de los molinos de viento. ^[5] Maxwell describió y analizó el fenómeno de la autooscilación , en el que los rezagos en el sistema pueden provocar una sobrecompensación y un comportamiento inestable. Esto generó una oleada de interés en el tema, durante el cual el compañero de clase de Maxwell, Edward John Routh , resumió los resultados de Maxwell para la clase general de sistemas lineales. ^[6] Independientemente, Adolf Hurwitz analizó la estabilidad del sistema utilizando ecuaciones diferenciales en 1877, lo que dio como resultado lo que ahora se conoce como el teorema de Routh-Hurwitz . ^{[7] [8]}

Una aplicación notable del control dinámico fue en el área de vuelo tripulado. Los hermanos Wright realizaron sus primeros vuelos de prueba con éxito el 17 de diciembre de 1903 y se distinguieron por su capacidad de controlar sus vuelos durante períodos sustanciales (más que la capacidad de producir sustentación a partir de un perfil aerodinámico, que era conocida). El control continuo y confiable del avión era necesario para vuelos que duraban más de unos pocos segundos.

En la Segunda Guerra Mundial , la teoría del control se estaba convirtiendo en un área importante de investigación. Irmgard Flügge-Lotz desarrolló la teoría de los sistemas de control automático discontinuo y aplicó el principio bang-bang al desarrollo de equipos de control de vuelo automático para aeronaves. ^{[9] [10]} Otras áreas de aplicación de los controles discontinuos incluían los sistemas de control de tiro , los sistemas de guía y la electrónica .

En ocasiones se utilizan métodos mecánicos para mejorar la estabilidad de los sistemas. Por ejemplo, los estabilizadores de los barcos son aletas montadas debajo de la línea de flotación y que emergen lateralmente. En los buques contemporáneos, pueden ser aletas activas controladas giroscópicamente, que tienen la capacidad de cambiar su ángulo de ataque para contrarrestar el balanceo causado por el viento o las olas que actúan sobre el barco.

La carrera espacial también dependía de un control preciso de las naves espaciales, y la teoría del control también ha visto un uso creciente en campos como la economía y la inteligencia artificial. Aquí, se podría decir que el objetivo es encontrar un modelo interno que obedezca el teorema del buen regulador . Así, por ejemplo, en economía, cuanto más exactamente un modelo de negociación (de acciones o materias primas) represente las acciones del mercado, más fácilmente puede controlar ese mercado (y extraer "trabajo útil" (ganancias) de él). En IA, un ejemplo podría ser un chatbot que modele el estado discursivo de los humanos: cuanto más exactamente pueda modelar el estado humano (por ejemplo, en una línea directa de asistencia telefónica), mejor puede manipular al humano (por ejemplo, para que realice las acciones correctivas para resolver el problema que causó la llamada telefónica a la línea de ayuda). Estos dos últimos ejemplos toman la estrecha interpretación histórica de la teoría del control como un conjunto de ecuaciones diferenciales que modelan y regulan el movimiento cinético, y la amplían hasta convertirla en una vasta generalización de un regulador que interactúa con una planta .

Básicamente, existen dos tipos de bucle de control: control de bucle abierto (feedforward) y control de bucle cerrado (feedback).

En el control de bucle abierto, la acción de control del controlador es independiente de la "salida del proceso" (o "variable de proceso controlada"). Un buen ejemplo de esto es una caldera de calefacción central controlada únicamente por un temporizador, de modo que se aplica calor durante un tiempo constante, independientemente de la temperatura del edificio. La acción de control es el encendido y apagado de la caldera, pero la variable controlada debería ser la temperatura del edificio, pero no es así porque se trata de un control de bucle abierto de la caldera, que no proporciona un control de bucle cerrado de la temperatura.

En el control de bucle cerrado, la acción de control del controlador depende de la salida del proceso. En el caso de la analogía de la caldera, esto incluiría un termostato para monitorear la temperatura del edificio y, de ese modo, enviar una señal para garantizar que el controlador mantenga el edificio a la temperatura establecida en el termostato. Por lo tanto, un controlador de bucle cerrado tiene un bucle de retroalimentación que garantiza que el controlador ejerza una acción de control para proporcionar una salida de proceso que sea igual a la "entrada de referencia" o "punto de ajuste". Por este motivo, los controladores de bucle cerrado también se denominan controladores de retroalimentación. ^[11]

La definición de un sistema de control de lazo cerrado según la British Standards Institution es "un sistema de control que posee retroalimentación de monitoreo, siendo la señal de desviación formada como resultado de esta retroalimentación utilizada para controlar la acción de un elemento de control final de tal manera que tienda a reducir la desviación a cero". ^[12]

De igual modo, “Un sistema de control por retroalimentación es un sistema que tiende a mantener una relación prescrita de una variable del sistema con otra comparando funciones de estas variables y utilizando la diferencia como un medio de control”. ^[13]

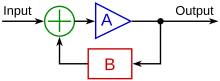
Un controlador de bucle cerrado o controlador con retroalimentación es un bucle de control que incorpora retroalimentación , en contraste con un controlador de bucle abierto o controlador sin retroalimentación . Un controlador de bucle cerrado utiliza la retroalimentación para controlar los estados o las salidas de un sistema dinámico . Su nombre proviene de la ruta de información en el sistema: las entradas del proceso (por ejemplo, el voltaje aplicado a un motor eléctrico ) tienen un efecto en las salidas del proceso (por ejemplo, la velocidad o el par del motor), que se mide con sensores y se procesa por el controlador; el resultado (la señal de control) se "realimenta" como entrada al proceso, cerrando el bucle. ^[14]

En el caso de los sistemas de retroalimentación lineal , se organiza un bucle de control que incluye sensores , algoritmos de control y actuadores en un intento de regular una variable en un punto de ajuste (SP). Un ejemplo cotidiano es el control de crucero en un vehículo de carretera; donde las influencias externas como las colinas causarían cambios de velocidad, y el conductor tiene la capacidad de alterar la velocidad establecida deseada. El algoritmo PID en el controlador restaura la velocidad real a la velocidad deseada de una manera óptima, con un retraso o sobreimpulso mínimo , controlando la salida de potencia del motor del vehículo. Los sistemas de control que incluyen algún tipo de detección de los resultados que intentan lograr hacen uso de la retroalimentación y pueden adaptarse a circunstancias variables hasta cierto punto. Los sistemas de control de bucle abierto no hacen uso de la retroalimentación y funcionan solo de formas preestablecidas.

Los controladores de circuito cerrado tienen las siguientes ventajas sobre los controladores de circuito abierto:

• Rechazo de perturbaciones (como colinas en el ejemplo de control de crucero anterior)
• Rendimiento garantizado incluso con incertidumbres del modelo , cuando la estructura del modelo no coincide perfectamente con el proceso real y los parámetros del modelo no son exactos
• Los procesos inestables pueden estabilizarse
• Sensibilidad reducida a las variaciones de parámetros.
• Rendimiento mejorado del seguimiento de referencias
• Mejora de la rectificación de fluctuaciones aleatorias ^[15]

En algunos sistemas, se utilizan simultáneamente el control de bucle cerrado y el de bucle abierto. En dichos sistemas, el control de bucle abierto se denomina " feedforward" y sirve para mejorar aún más el rendimiento del seguimiento de referencia.

Una arquitectura de controlador de circuito cerrado común es el controlador PID .

El campo de la teoría del control se puede dividir en dos ramas:

• Teoría de control lineal : se aplica a sistemas formados por dispositivos que obedecen al principio de superposición , lo que significa aproximadamente que la salida es proporcional a la entrada. Se rigen por ecuaciones diferenciales lineales . Una subclase importante son los sistemas que, además, tienen parámetros que no cambian con el tiempo, llamados sistemas lineales invariantes en el tiempo (LTI). Estos sistemas son susceptibles de potentes técnicas matemáticas de dominio de frecuencia de gran generalidad, como la transformada de Laplace , la transformada de Fourier , la transformada Z , el diagrama de Bode , el lugar de las raíces y el criterio de estabilidad de Nyquist . Estos conducen a una descripción del sistema utilizando términos como ancho de banda , respuesta de frecuencia , valores propios , ganancia , frecuencias de resonancia , ceros y polos , que dan soluciones para la respuesta del sistema y técnicas de diseño para la mayoría de los sistemas de interés.
• Teoría de control no lineal : cubre una clase más amplia de sistemas que no obedecen al principio de superposición y se aplica a más sistemas del mundo real porque todos los sistemas de control reales son no lineales. Estos sistemas a menudo se rigen por ecuaciones diferenciales no lineales . Las pocas técnicas matemáticas que se han desarrollado para manejarlas son más difíciles y mucho menos generales, y a menudo se aplican solo a categorías estrechas de sistemas. Estas incluyen la teoría del ciclo límite , los mapas de Poincaré , el teorema de estabilidad de Lyapunov y las funciones descriptivas . Los sistemas no lineales a menudo se analizan utilizando métodos numéricos en computadoras, por ejemplo, simulando su funcionamiento utilizando un lenguaje de simulación . Si solo son de interés las soluciones cercanas a un punto estable, los sistemas no lineales a menudo se pueden linealizar aproximándolos mediante un sistema lineal utilizando la teoría de perturbaciones , y se pueden utilizar técnicas lineales. ^[16]

Las técnicas matemáticas para analizar y diseñar sistemas de control se dividen en dos categorías diferentes:

• Dominio de frecuencia – En este tipo, los valores de las variables de estado , las variables matemáticas que representan la entrada, la salida y la retroalimentación del sistema se representan como funciones de frecuencia . La señal de entrada y la función de transferencia del sistema se convierten de funciones de tiempo a funciones de frecuencia mediante una transformada como la transformada de Fourier , la transformada de Laplace o la transformada Z. La ventaja de esta técnica es que da como resultado una simplificación de las matemáticas; las ecuaciones diferenciales que representan el sistema se reemplazan por ecuaciones algebraicas en el dominio de la frecuencia que son mucho más simples de resolver. Sin embargo, las técnicas del dominio de la frecuencia solo se pueden utilizar con sistemas lineales, como se mencionó anteriormente.
• Representación en el espacio de estados en el dominio del tiempo : en este tipo, los valores de las variables de estado se representan como funciones del tiempo. Con este modelo, el sistema que se analiza se representa mediante una o más ecuaciones diferenciales . Dado que las técnicas del dominio de la frecuencia se limitan a los sistemas lineales , el dominio del tiempo se utiliza ampliamente para analizar sistemas no lineales del mundo real. Aunque estos son más difíciles de resolver, las técnicas modernas de simulación por computadora, como los lenguajes de simulación, han hecho que su análisis sea rutinario.

A diferencia del análisis del dominio de frecuencia de la teoría de control clásica, la teoría de control moderna utiliza la representación del espacio de estado del dominio del tiempo , ^{[ cita requerida ]} un modelo matemático de un sistema físico como un conjunto de variables de entrada, salida y estado relacionadas por ecuaciones diferenciales de primer orden. Para abstraerse del número de entradas, salidas y estados, las variables se expresan como vectores y las ecuaciones diferenciales y algebraicas se escriben en forma de matriz (esto último solo es posible cuando el sistema dinámico es lineal). La representación del espacio de estado (también conocida como el "enfoque del dominio del tiempo") proporciona una forma conveniente y compacta de modelar y analizar sistemas con múltiples entradas y salidas. Con entradas y salidas, de lo contrario tendríamos que escribir transformadas de Laplace para codificar toda la información sobre un sistema. A diferencia del enfoque del dominio de frecuencia, el uso de la representación del espacio de estado no se limita a sistemas con componentes lineales y condiciones iniciales cero. "Espacio de estado" se refiere al espacio cuyos ejes son las variables de estado. El estado del sistema se puede representar como un punto dentro de ese espacio. ^{[17] [18]}

Los sistemas de control se pueden dividir en diferentes categorías dependiendo del número de entradas y salidas.

• Entrada única, salida única (SISO): este es el tipo más simple y común, en el que una salida está controlada por una señal de control. Algunos ejemplos son el ejemplo de control de crucero anterior o un sistema de audio , en el que la entrada de control es la señal de audio de entrada y la salida son las ondas de sonido del altavoz.
• Entrada múltiple, salida múltiple (MIMO): se encuentran en sistemas más complejos. Por ejemplo, los grandes telescopios modernos , como el Keck y el MMT, tienen espejos compuestos de muchos segmentos separados, cada uno controlado por un actuador . La forma de todo el espejo se ajusta constantemente mediante un sistema de control de óptica activa MIMO que utiliza la información de varios sensores en el plano focal para compensar los cambios en la forma del espejo debido a la expansión térmica, la contracción, las tensiones a medida que gira y la distorsión del frente de onda debido a la turbulencia en la atmósfera. Los sistemas complicados, como los reactores nucleares y las células humanas , se simulan mediante una computadora como grandes sistemas de control MIMO.

El alcance de la teoría de control clásica se limita al diseño de sistemas de entrada única y salida única (SISO), excepto cuando se analiza el rechazo de perturbaciones utilizando una segunda entrada. El análisis del sistema se lleva a cabo en el dominio del tiempo utilizando ecuaciones diferenciales , en el dominio complejo-s con la transformada de Laplace o en el dominio de la frecuencia mediante la transformación desde el dominio complejo-s. Se puede suponer que muchos sistemas tienen una respuesta del sistema de segundo orden y de una sola variable en el dominio del tiempo. Un controlador diseñado utilizando la teoría clásica a menudo requiere un ajuste in situ debido a aproximaciones de diseño incorrectas. Sin embargo, debido a la implementación física más sencilla de los diseños de controladores clásicos en comparación con los sistemas diseñados utilizando la teoría de control moderna, estos controladores son los preferidos en la mayoría de las aplicaciones industriales. Los controladores más comunes diseñados utilizando la teoría de control clásica son los controladores PID . Una implementación menos común puede incluir un filtro de adelanto o de atraso o ambos. El objetivo final es cumplir con los requisitos que normalmente se proporcionan en el dominio del tiempo llamado respuesta al escalón o, a veces, en el dominio de la frecuencia llamado respuesta de bucle abierto. Las características de respuesta de escalón que se aplican en una especificación son, por lo general, el porcentaje de sobreimpulso, el tiempo de asentamiento, etc. Las características de respuesta de lazo abierto que se aplican en una especificación son, por lo general, el margen de ganancia y fase y el ancho de banda. Estas características se pueden evaluar mediante simulación que incluye un modelo dinámico del sistema bajo control acoplado con el modelo de compensación.

La teoría de control moderna se lleva a cabo en el espacio de estados y puede tratar con sistemas de múltiples entradas y múltiples salidas (MIMO). Esto supera las limitaciones de la teoría de control clásica en problemas de diseño más sofisticados, como el control de aviones de combate, con la limitación de que no es posible un análisis del dominio de frecuencia. En el diseño moderno, un sistema se representa con la mayor ventaja como un conjunto de ecuaciones diferenciales de primer orden desacopladas definidas utilizando variables de estado . Las teorías de control no lineales , multivariables, adaptativas y robustas entran en esta división. Los métodos matriciales son significativamente limitados para los sistemas MIMO donde no se puede asegurar la independencia lineal en la relación entre entradas y salidas. ^{[ cita requerida ]} Al ser bastante nueva, la teoría de control moderna tiene muchas áreas aún por explorar. Académicos como Rudolf E. Kálmán y Aleksandr Lyapunov son bien conocidos entre las personas que han dado forma a la teoría de control moderna.

La estabilidad de un sistema dinámico general sin entrada se puede describir con los criterios de estabilidad de Lyapunov .

• Un sistema lineal se denomina estable con entrada acotada y salida acotada (BIBO) si su salida permanecerá acotada para cualquier entrada acotada.
• La estabilidad de los sistemas no lineales que toman una entrada es la estabilidad de entrada a estado (ISS), que combina la estabilidad de Lyapunov y una noción similar a la estabilidad BIBO.

Para simplificar, las siguientes descripciones se centran en sistemas lineales de tiempo continuo y tiempo discreto .

Matemáticamente, esto significa que para que un sistema lineal causal sea estable, todos los polos de su función de transferencia deben tener valores reales negativos, es decir, la parte real de cada polo debe ser menor que cero. En términos prácticos, la estabilidad requiere que los polos complejos de la función de transferencia residan

• en la mitad izquierda abierta del plano complejo para tiempo continuo, cuando se utiliza la transformada de Laplace para obtener la función de transferencia.
• dentro del círculo unitario para tiempo discreto, cuando se utiliza la transformada Z.

La diferencia entre los dos casos se debe simplemente al método tradicional de representar gráficamente las funciones de transferencia de tiempo continuo frente a tiempo discreto. La transformada de Laplace continua está en coordenadas cartesianas donde el eje es el eje real y la transformada Z discreta está en coordenadas circulares donde el eje es el eje real.${\estilo de visualización x}$${\estilo de visualización \rho}$

Cuando se satisfacen las condiciones apropiadas anteriores, se dice que un sistema es asintóticamente estable ; las variables de un sistema de control asintóticamente estable siempre disminuyen desde su valor inicial y no muestran oscilaciones permanentes. Las oscilaciones permanentes ocurren cuando un polo tiene una parte real exactamente igual a cero (en el caso de tiempo continuo) o un módulo igual a uno (en el caso de tiempo discreto). Si una respuesta de sistema simplemente estable no decae ni crece con el tiempo y no tiene oscilaciones, es marginalmente estable ; en este caso, la función de transferencia del sistema tiene polos no repetidos en el origen del plano complejo (es decir, su componente real y complejo es cero en el caso de tiempo continuo). Las oscilaciones están presentes cuando los polos con parte real igual a cero tienen una parte imaginaria no igual a cero.

Si un sistema en cuestión tiene una respuesta al impulso de

${\displaystyle \ x[n]=0,5^{n}u[n]}$

entonces la transformada Z (ver este ejemplo ), viene dada por

${\displaystyle \ X(z)={\frac {1}{1-0.5z^{-1}}}}$

que tiene un polo en ( parte imaginaria cero ). Este sistema es BIBO (asintóticamente) estable ya que el polo está dentro del círculo unitario.${\displaystyle z=0,5}$

Sin embargo, si la respuesta al impulso fue

${\displaystyle \ x[n]=1.5^{n}u[n]}$

Entonces la transformada Z es

${\displaystyle \ X(z)={\frac {1}{1-1.5z^{-1}}}}$

que tiene un polo en y no es BIBO estable ya que el polo tiene un módulo estrictamente mayor que uno.${\displaystyle z=1.5}$

Existen numerosas herramientas para el análisis de los polos de un sistema, entre ellas sistemas gráficos como el lugar de las raíces , los diagramas de Bode o los diagramas de Nyquist .

Los cambios mecánicos pueden hacer que los equipos (y los sistemas de control) sean más estables. Los marineros añaden lastre para mejorar la estabilidad de los barcos. Los cruceros utilizan aletas antibalanceo que se extienden transversalmente desde el costado del barco durante unos 30 pies (10 m) y giran continuamente sobre sus ejes para desarrollar fuerzas que se oponen al balanceo.

La controlabilidad y la observabilidad son cuestiones principales en el análisis de un sistema antes de decidir la mejor estrategia de control a aplicar, o si es posible controlar o estabilizar el sistema. La controlabilidad está relacionada con la posibilidad de forzar al sistema a un estado particular mediante el uso de una señal de control apropiada. Si un estado no es controlable, entonces ninguna señal podrá controlar el estado. Si un estado no es controlable, pero su dinámica es estable, entonces el estado se denomina estabilizable . La observabilidad, en cambio, está relacionada con la posibilidad de observar , a través de mediciones de salida, el estado de un sistema. Si un estado no es observable, el controlador nunca podrá determinar el comportamiento de un estado no observable y, por lo tanto, no puede usarlo para estabilizar el sistema. Sin embargo, de manera similar a la condición de estabilización anterior, si un estado no se puede observar, aún podría ser detectable.

Desde un punto de vista geométrico, considerando los estados de cada variable del sistema a controlar, cada estado "malo" de estas variables debe ser controlable y observable para asegurar un buen comportamiento en el sistema de lazo cerrado. Es decir, si uno de los valores propios del sistema no es controlable y observable, esta parte de la dinámica permanecerá intacta en el sistema de lazo cerrado. Si dicho valor propio no es estable, la dinámica de este valor propio estará presente en el sistema de lazo cerrado que, por lo tanto, será inestable. Los polos no observables no están presentes en la realización de la función de transferencia de una representación en el espacio de estados, por lo que a veces se prefiere esta última en el análisis de sistemas dinámicos.

Las soluciones a los problemas de un sistema incontrolable o inobservable incluyen la adición de actuadores y sensores.

En los últimos años se han ideado diversas estrategias de control, desde las más generales (controlador PID) hasta otras dedicadas a clases de sistemas muy particulares (especialmente robótica o control de crucero de aeronaves).

Un problema de control puede tener varias especificaciones. La estabilidad, por supuesto, siempre está presente. El controlador debe garantizar que el sistema de lazo cerrado sea estable, independientemente de la estabilidad de lazo abierto. Una mala elección del controlador puede incluso empeorar la estabilidad del sistema de lazo abierto, lo que normalmente debe evitarse. A veces sería deseable obtener una dinámica particular en el lazo cerrado: es decir, que los polos tengan , donde es un valor fijo estrictamente mayor que cero, en lugar de simplemente pedir que .${\displaystyle Re[\lambda ]<-{\overline {\lambda }}}$${\displaystyle {\overline {\lambda}}}$${\displaystyle Re[\lambda ]<0}$

Otra especificación típica es el rechazo de una perturbación escalonada; incluir un integrador en la cadena de bucle abierto (es decir, directamente antes del sistema bajo control) permite lograr esto fácilmente. Otras clases de perturbaciones requieren que se incluyan diferentes tipos de subsistemas.

Otras especificaciones de la teoría de control "clásica" se refieren a la respuesta temporal del sistema de bucle cerrado. Entre ellas se encuentran el tiempo de subida (el tiempo que necesita el sistema de control para alcanzar el valor deseado después de una perturbación), el sobreimpulso máximo (el valor más alto que alcanza la respuesta antes de alcanzar el valor deseado) y otras ( tiempo de asentamiento , decaimiento de un cuarto). Las especificaciones del dominio de frecuencia suelen estar relacionadas con la robustez (véase más adelante).

Las evaluaciones de desempeño modernas utilizan alguna variación del error de seguimiento integrado (IAE, ISA, CQI).

Un sistema de control debe tener siempre alguna propiedad de robustez. Un controlador robusto es aquel cuyas propiedades no cambian mucho si se aplica a un sistema ligeramente diferente del sistema matemático utilizado para su síntesis. Este requisito es importante, ya que ningún sistema físico real se comporta verdaderamente como la serie de ecuaciones diferenciales utilizadas para representarlo matemáticamente. Normalmente se elige un modelo matemático más simple para simplificar los cálculos; de lo contrario, la dinámica real del sistema puede ser tan complicada que un modelo completo es imposible.

Identificación del sistema

El proceso de determinar las ecuaciones que gobiernan la dinámica del modelo se denomina identificación del sistema . Esto se puede hacer fuera de línea: por ejemplo, ejecutando una serie de medidas a partir de las cuales calcular un modelo matemático aproximado, típicamente su función de transferencia o matriz. Sin embargo, dicha identificación a partir de la salida no puede tener en cuenta la dinámica no observable. A veces, el modelo se construye directamente a partir de ecuaciones físicas conocidas; por ejemplo, en el caso de un sistema masa-resorte-amortiguador, sabemos que . Incluso suponiendo que se utilice un modelo "completo" para diseñar el controlador, todos los parámetros incluidos en estas ecuaciones (llamados "parámetros nominales") nunca se conocen con absoluta precisión; el sistema de control tendrá que comportarse correctamente incluso cuando esté conectado a un sistema físico con valores de parámetros verdaderos alejados de los nominales.${\displaystyle m{\ddot {x}}(t)=-Kx(t)-\mathrm {B} {\dot {x}}(t)}$

Algunas técnicas de control avanzadas incluyen un proceso de identificación "on-line" (ver más adelante). Los parámetros del modelo se calculan ("identifican") mientras el propio controlador está en funcionamiento. De esta manera, si se produce una variación drástica de los parámetros, por ejemplo, si el brazo del robot suelta un peso, el controlador se ajustará en consecuencia para garantizar el correcto funcionamiento.

Análisis

El análisis de la robustez de un sistema de control SISO (single input single output) se puede realizar en el dominio de la frecuencia, considerando la función de transferencia del sistema y utilizando diagramas de Nyquist y Bode . Los temas incluyen margen de ganancia y fase y margen de amplitud. Para MIMO (multi-input multi output) y, en general, sistemas de control más complicados, se deben considerar los resultados teóricos ideados para cada técnica de control (ver la siguiente sección). Es decir, si se necesitan cualidades particulares de robustez, el ingeniero debe trasladar su atención a una técnica de control incluyendo estas cualidades en sus propiedades.

Restricciones

Un problema de robustez particular es el requisito de que un sistema de control funcione correctamente en presencia de restricciones de entrada y estado. En el mundo físico, cada señal es limitada. Podría suceder que un controlador envíe señales de control que no puedan ser seguidas por el sistema físico, por ejemplo, al intentar girar una válvula a una velocidad excesiva. Esto puede producir un comportamiento no deseado del sistema de lazo cerrado, o incluso dañar o romper los actuadores u otros subsistemas. Existen técnicas de control específicas para resolver el problema: control predictivo de modelos (ver más adelante) y sistemas anti-wind up . Este último consiste en un bloque de control adicional que garantiza que la señal de control nunca supere un umbral determinado.

En el caso de los sistemas MIMO, la colocación de los polos se puede realizar matemáticamente utilizando una representación del espacio de estados del sistema de bucle abierto y calculando una matriz de retroalimentación que asigne los polos a las posiciones deseadas. En sistemas complicados, esto puede requerir capacidades de cálculo asistidas por computadora y no siempre puede garantizar la solidez. Además, en general no se miden todos los estados del sistema, por lo que se deben incluir observadores e incorporarlos en el diseño de la colocación de los polos.

Los procesos en industrias como la robótica y la industria aeroespacial suelen tener una fuerte dinámica no lineal. En la teoría de control, a veces es posible linealizar estas clases de sistemas y aplicar técnicas lineales, pero en muchos casos puede ser necesario idear desde cero teorías que permitan el control de sistemas no lineales. Estas, por ejemplo, linealización por retroalimentación , retroceso , control de modo deslizante y control de linealización de trayectoria, normalmente aprovechan los resultados basados ​​en la teoría de Lyapunov . La geometría diferencial se ha utilizado ampliamente como una herramienta para generalizar conceptos de control lineal bien conocidos al caso no lineal, así como para mostrar las sutilezas que lo convierten en un problema más desafiante. La teoría de control también se ha utilizado para descifrar el mecanismo neuronal que dirige los estados cognitivos. ^[19]

Cuando el sistema está controlado por múltiples controladores, el problema es el control descentralizado. La descentralización es útil de muchas maneras; por ejemplo, ayuda a que los sistemas de control operen en un área geográfica más amplia. Los agentes en sistemas de control descentralizados pueden interactuar utilizando canales de comunicación y coordinar sus acciones.

Un problema de control estocástico es aquel en el que la evolución de las variables de estado está sujeta a perturbaciones aleatorias externas al sistema. Un problema de control determinista no está sujeto a perturbaciones aleatorias externas.

Todo sistema de control debe garantizar en primer lugar la estabilidad del comportamiento en lazo cerrado. En el caso de los sistemas lineales , esto se puede conseguir colocando directamente los polos. Los sistemas de control no lineales utilizan teorías específicas (normalmente basadas en la teoría de Aleksandr Lyapunov ) para garantizar la estabilidad sin tener en cuenta la dinámica interna del sistema. La posibilidad de cumplir con diferentes especificaciones varía según el modelo considerado y la estrategia de control elegida.

Lista de las principales técnicas de control

• El control óptimo es una técnica de control particular en la que la señal de control optimiza un cierto "índice de costo": por ejemplo, en el caso de un satélite, los empujes del chorro necesarios para llevarlo a la trayectoria deseada que consumen la menor cantidad de combustible. Dos métodos de diseño de control óptimo se han utilizado ampliamente en aplicaciones industriales, ya que se ha demostrado que pueden garantizar la estabilidad de bucle cerrado. Estos son el control predictivo de modelos (MPC) y el control lineal-cuadrático-gaussiano (LQG). El primero puede tener en cuenta de manera más explícita las restricciones de las señales en el sistema, lo que es una característica importante en muchos procesos industriales. Sin embargo, la estructura de "control óptimo" en MPC es solo un medio para lograr tal resultado, ya que no optimiza un verdadero índice de rendimiento del sistema de control de bucle cerrado. Junto con los controladores PID, los sistemas MPC son la técnica de control más utilizada en el control de procesos .
• El control robusto aborda explícitamente la incertidumbre en su enfoque del diseño del controlador. Los controladores diseñados utilizando métodos de control robusto tienden a ser capaces de lidiar con pequeñas diferencias entre el sistema real y el modelo nominal utilizado para el diseño. ^[20] Los primeros métodos de Bode y otros eran bastante robustos; los métodos de espacio de estados inventados en los años 1960 y 1970 a veces resultaron carentes de robustez. Los ejemplos de técnicas modernas de control robusto incluyen la conformación de bucle H-infinito desarrollada por Duncan McFarlane y Keith Glover , el control de modo deslizante (SMC) desarrollado por Vadim Utkin y protocolos seguros diseñados para el control de grandes poblaciones heterogéneas de cargas eléctricas en aplicaciones de redes eléctricas inteligentes. ^[21] Los métodos robustos apuntan a lograr un rendimiento robusto y/o estabilidad en presencia de pequeños errores de modelado.
• El control estocástico se ocupa del diseño de control con incertidumbre en el modelo. En los problemas típicos de control estocástico, se supone que existen ruidos y perturbaciones aleatorias en el modelo y el controlador, y el diseño de control debe tener en cuenta estas desviaciones aleatorias.
• El control adaptativo utiliza la identificación en línea de los parámetros del proceso o la modificación de las ganancias del controlador, obteniendo así propiedades de robustez muy elevadas. Los controles adaptativos se aplicaron por primera vez en la industria aeroespacial en la década de 1950 y han tenido un éxito especial en ese campo.
• Un sistema de control jerárquico es un tipo de sistema de control en el que un conjunto de dispositivos y software de control se organizan en un árbol jerárquico . Cuando los vínculos del árbol se implementan mediante una red informática , entonces ese sistema de control jerárquico también es una forma de sistema de control en red .
• El control inteligente utiliza varios enfoques de computación de IA como redes neuronales artificiales , probabilidad bayesiana , lógica difusa , ^[22] aprendizaje automático , computación evolutiva y algoritmos genéticos o una combinación de estos métodos, como algoritmos neuro-difusos , para controlar un sistema dinámico .
• El control de criticidad autoorganizado puede definirse como los intentos de interferir en los procesos mediante los cuales el sistema autoorganizado disipa energía.

Muchas figuras activas e históricas hicieron contribuciones significativas a la teoría del control, entre ellas:

• Pierre-Simon Laplace inventó la transformada Z en su trabajo sobre teoría de la probabilidad , que ahora se utiliza para resolver problemas de teoría de control en tiempo discreto. La transformada Z es un equivalente en tiempo discreto de la transformada de Laplace que lleva su nombre.
• Irmgard Flugge-Lotz desarrolló la teoría del control automático discontinuo y la aplicó a los sistemas de control automático de aeronaves .
• Alexander Lyapunov en la década de 1890 marca el comienzo de la teoría de la estabilidad .
• Harold S. Black inventó el concepto de amplificadores de retroalimentación negativa en 1927. Logró desarrollar amplificadores de retroalimentación negativa estables en la década de 1930.
• Harry Nyquist desarrolló el criterio de estabilidad de Nyquist para sistemas de retroalimentación en la década de 1930.
• Richard Bellman desarrolló la programación dinámica en la década de 1940. ^[23]
• Warren E. Dixon , teórico del control y profesor
• Kyriakos G. Vamvoudakis desarrolló algoritmos de aprendizaje de refuerzo sincrónico para resolver problemas de control óptimo y teoría de juegos.
• Andrey Kolmogorov co-desarrolló el filtro Wiener-Kolmogorov en 1941.
• Norbert Wiener co-desarrolló el filtro Wiener-Kolmogorov y acuñó el término cibernética en la década de 1940.
• John R. Ragazzini introdujo el control digital y el uso de la transformada Z en la teoría de control (inventada por Laplace) en la década de 1950.
• Lev Pontryagin introdujo el principio de máximo y el principio bang-bang .
• Pierre-Louis Lions desarrolló soluciones de viscosidad en control estocástico y métodos de control óptimo .
• Rudolf E. Kálmán fue pionero en el enfoque de espacio de estados para sistemas y control. Introdujo los conceptos de controlabilidad y observabilidad . Desarrolló el filtro de Kalman para estimación lineal.
• Ali H. Nayfeh , quien fue uno de los principales contribuyentes a la teoría de control no lineal y publicó muchos libros sobre métodos de perturbación.
• Jan C. Willems introdujo el concepto de disipatividad como una generalización de la función de Lyapunov a los sistemas de entrada/estado/salida. La construcción de la función de almacenamiento, como se denomina al análogo de una función de Lyapunov, condujo al estudio de la desigualdad matricial lineal (LMI) en la teoría de control. Fue pionero en el enfoque conductual de la teoría de sistemas matemáticos.

Ejemplos de sistemas de control

Temas de la teoría del control

Otros temas relacionados

• Levine, William S., ed. (1996). The Control Handbook . Nueva York: CRC Press. ISBN 978-0-8493-8570-4.
• Karl J. Åström; Richard M. Murray (2008). Sistemas de retroalimentación: una introducción para científicos e ingenieros (PDF) . Princeton University Press. ISBN 978-0-691-13576-2.
• Christopher Kilian (2005). Tecnología de control moderna . Thompson Delmar Learning. ISBN 978-1-4018-5806-3.
• Vannevar Bush (1929). Análisis de circuitos operacionales . John Wiley and Sons, Inc.
• Robert F. Stengel (1994). Control óptimo y estimación . Publicaciones de Dover. ISBN 978-0-486-68200-6.
• Franklin y col. (2002). Control de retroalimentación de sistemas dinámicos (4.ª ed.). Nueva Jersey: Prentice Hall. ISBN 978-0-13-032393-4.
• Joseph L. Hellerstein; Dawn M. Tilbury ; Sujay Parekh (2004). Control de retroalimentación de sistemas informáticos . John Wiley and Sons. ISBN 978-0-471-26637-2.
• Diederich Hinrichsen y Anthony J. Pritchard (2005). Teoría de sistemas matemáticos I: modelado, análisis del espacio de estados, estabilidad y robustez . Springer. ISBN 978-3-540-44125-0.
• Sontag, Eduardo (1998). Teoría del control matemático: sistemas deterministas de dimensión finita. Segunda edición (PDF) . Springer. ISBN 978-0-387-98489-6.
• Goodwin, Graham (2001). Diseño de sistemas de control . Prentice Hall. ISBN 978-0-13-958653-8.
• Christophe Basso (2012). Diseño de bucles de control para fuentes de alimentación lineales y conmutadas: guía didáctica. Artech House. ISBN 978-1608075577.
• Boris J. Lurie; Paul J. Enright (2019). Control de retroalimentación clásico con sistemas multilazo no lineales (3.ª edición). CRC Press. ISBN 978-1-1385-4114-6.

Para ingeniería química

• Luyben, William (1989). Modelado, simulación y control de procesos para ingenieros químicos . McGraw Hill. ISBN 978-0-07-039159-8.

Wikimedia Commons tiene medios relacionados con Teoría de control .

Wikilibros tiene un libro sobre el tema: Sistemas de control

• Tutoriales de control para Matlab, un conjunto de ejemplos de control resueltos mediante varios métodos diferentes.
• Ajuste de control y mejores prácticas
• Estructuras de control avanzadas, simuladores gratuitos en línea que explican la teoría de control