Ecuación del calor

Este artículo necesita citas adicionales para su verificación . Por favor, ayude a mejorar este artículo añadiendo citas de fuentes fiables . El material sin fuentes puede ser cuestionado y eliminado. Buscar fuentes:  «Ecuación del calor» – noticias  · periódicos  · libros  · académico  · JSTOR ( agosto de 2024 ) ( Aprenda cómo y cuándo eliminar este mensaje )

En matemáticas y física , la ecuación del calor es una ecuación diferencial parcial . Las soluciones de la ecuación del calor se conocen a veces como funciones calóricas . La teoría de la ecuación del calor fue desarrollada por primera vez por Joseph Fourier en 1822 con el propósito de modelar cómo una cantidad como el calor se difunde a través de una región determinada.

Como la ecuación diferencial parcial parabólica prototípica , la ecuación del calor se encuentra entre los temas más estudiados en matemáticas puras , y su análisis se considera fundamental para el campo más amplio de las ecuaciones diferenciales parciales . La ecuación del calor también se puede considerar en variedades de Riemann , lo que lleva a muchas aplicaciones geométricas. Siguiendo el trabajo de Subbaramiah Minakshisundaram y Åke Pleijel , la ecuación del calor está estrechamente relacionada con la geometría espectral . Una variante no lineal seminal de la ecuación del calor fue introducida en la geometría diferencial por James Eells y Joseph Sampson en 1964, inspirando la introducción del flujo de Ricci por Richard Hamilton en 1982 y culminando en la prueba de la conjetura de Poincaré por Grigori Perelman en 2003. Ciertas soluciones de la ecuación del calor conocidas como núcleos de calor proporcionan información sutil sobre la región en la que se definen, como se ejemplifica a través de su aplicación al teorema del índice de Atiyah-Singer . ^[1]

La ecuación del calor, junto con sus variantes, también es importante en muchos campos de la ciencia y las matemáticas aplicadas . En la teoría de la probabilidad , la ecuación del calor está relacionada con el estudio de los paseos aleatorios y el movimiento browniano a través de la ecuación de Fokker-Planck . La ecuación de Black-Scholes de las matemáticas financieras es una pequeña variante de la ecuación del calor, y la ecuación de Schrödinger de la mecánica cuántica puede considerarse una ecuación del calor en tiempo imaginario . En el análisis de imágenes , la ecuación del calor se utiliza a veces para resolver la pixelación y para identificar los bordes . Tras la introducción de los métodos de "viscosidad artificial" por parte de Robert Richtmyer y John von Neumann , las soluciones de las ecuaciones del calor han sido útiles en la formulación matemática de los choques hidrodinámicos . Las soluciones de la ecuación del calor también han recibido mucha atención en la literatura de análisis numérico , a partir de la década de 1950 con el trabajo de Jim Douglas, DW Peaceman y Henry Rachford Jr.

En matemáticas, si se da un subconjunto abierto U de R ⁿ y un subintervalo I de R , se dice que una función u  : U × I → R es una solución de la ecuación del calor si

${\displaystyle {\frac {\parcial u}{\parcial t}}={\frac {\parcial ^{2}u}{\parcial x_{1}^{2}}}+\cdots +{\frac {\parcial ^{2}u}{\parcial x_{n}^{2}}},}$

donde ( x ₁ , …, x _n , t ) denota un punto general del dominio. Es típico referirse a t como "tiempo" y a x ₁ , …, x _n como "variables espaciales", incluso en contextos abstractos donde estas frases no tienen su significado intuitivo. La colección de variables espaciales a menudo se denomina simplemente x . Para cualquier valor dado de t , el lado derecho de la ecuación es el laplaciano de la función u (⋅, t ) : U → R . Como tal, la ecuación del calor a menudo se escribe de manera más compacta como

En contextos de física e ingeniería, especialmente en el contexto de la difusión a través de un medio, es más común fijar un sistema de coordenadas cartesianas y luego considerar el caso específico de una función u ( x , y , z , t ) de tres variables espaciales ( x , y , z ) y la variable temporal t . Se dice entonces que u es una solución de la ecuación del calor si

${\displaystyle {\frac {\partial u}{\partial t}}=\alpha \left({\frac {\partial ^{2}u}{\partial x^{2}}}+{\frac {\partial ^{2}u}{\partial y^{2}}}+{\frac {\partial ^{2}u}{\partial z^{2}}}\right)}$

donde α es un coeficiente positivo llamado difusividad térmica del medio. Además de otros fenómenos físicos, esta ecuación describe el flujo de calor en un medio homogéneo e isótropo, siendo u ( x , y , z , t ) la temperatura en el punto ( x , y , z ) y el tiempo t . Si el medio no es homogéneo e isótropo, entonces α no sería un coeficiente fijo, y en cambio dependería de ( x , y , z ) ; la ecuación también tendría una forma ligeramente diferente. En la literatura de física e ingeniería, es común usar ∇ ² para denotar el laplaciano, en lugar de ∆ .

Tanto en matemáticas como en física e ingeniería, es común utilizar la notación de Newton para las derivadas del tiempo, por lo que se utiliza para denotar ⁠${\displaystyle {\punto {u}}}$∂u/∂t⁠ , por lo que la ecuación se puede escribir

Obsérvese también que la capacidad de utilizar ∆ o ∇ ² para denotar el laplaciano, sin referencia explícita a las variables espaciales, es un reflejo del hecho de que el laplaciano es independiente de la elección del sistema de coordenadas. En términos matemáticos, se podría decir que el laplaciano es "invariante en cuanto a traslación y rotación". De hecho, es (en términos generales) el operador diferencial más simple que tiene estas simetrías. Esto puede tomarse como una justificación significativa (y puramente matemática) del uso del laplaciano y de la ecuación del calor para modelar cualquier fenómeno físico que sea homogéneo e isótropo, de los cuales la difusión del calor es un ejemplo principal.

La "constante de difusividad" α no suele estar presente en los estudios matemáticos de la ecuación del calor, mientras que su valor puede ser muy importante en ingeniería. Esta no es una diferencia importante, por la siguiente razón. Sea u una función con

${\displaystyle {\frac {\parcial u}{\parcial t}}=\alpha \Delta u.}$

Definir una nueva función . Entonces, según la regla de la cadena , se tiene${\displaystyle v(t,x)=u(t/\alpha ,x)}$

${\displaystyle {\frac {\parcial }{\parcial t}}v(t,x)={\frac {\parcial }{\parcial t}}u(t/\alpha ,x)=\alpha ^{-1}{\frac {\parcial u}{\parcial t}}(t/\alpha ,x)=\Delta u(t/\alpha ,x)=\Delta v(t,x)}$

( ⁎ )

Por lo tanto, existe una manera sencilla de traducir entre soluciones de la ecuación del calor con un valor general de α y soluciones de la ecuación del calor con α = 1. Por lo tanto, a los efectos del análisis matemático, a menudo es suficiente considerar solo el caso α = 1 .

Dado que existe otra opción para definir una función satisfactoria como en ( ⁎ ) anterior estableciendo . Nótese que los dos medios posibles para definir la nueva función discutida aquí equivalen, en términos físicos, a cambiar la unidad de medida de tiempo o la unidad de medida de longitud.${\displaystyle \alpha >0}$${\estilo de visualización v}$${\textstyle {\frac {\partial }{\partial t}}v=\Delta v}$${\displaystyle v(t,x)=u(t,\alpha ^{1/2}x)}$${\estilo de visualización v}$

De manera informal, el operador laplaciano ∆ da la diferencia entre el valor promedio de una función en la vecindad de un punto y su valor en ese punto. Por lo tanto, si u es la temperatura, ∆u indica (y en qué medida) que el material que rodea cada punto es más caliente o más frío, en promedio, que el material en ese punto.

Según la segunda ley de la termodinámica , el calor fluirá desde los cuerpos más calientes a los cuerpos adyacentes más fríos, en proporción a la diferencia de temperatura y de la conductividad térmica del material entre ellos. Cuando el calor fluye hacia adentro (o hacia afuera) de un material, su temperatura aumenta (o disminuye) en proporción a la cantidad de calor dividida por la cantidad ( masa ) de material, con un factor de proporcionalidad llamado capacidad calorífica específica del material.

Mediante la combinación de estas observaciones, la ecuación del calor dice que la velocidad a la que el material en un punto se calentará (o se enfriará) es proporcional a cuánto más caliente (o más frío) esté el material circundante. El coeficiente α en la ecuación tiene en cuenta la conductividad térmica, el calor específico y la densidad del material.${\displaystyle {\punto {u}}}$

La primera mitad del razonamiento físico anterior se puede expresar en forma matemática. La clave es que, para cualquier x fijo , se tiene

${\displaystyle {\begin{aligned}u_{(x)}(0)&=u(x)\\u_{(x)}'(0)&=0\\u_{(x)}''(0)&={\frac {1}{n}}\Delta u(x)\end{aligned}}}$

donde u _{( x )} ( r ) es la función de una sola variable que denota el valor promedio de u sobre la superficie de la esfera de radio r centrada en x ; puede definirse por

${\displaystyle u_{(x)}(r)={\frac {1}{\omega _{n-1}r^{n-1}}}\int _{\{y:|x-y|=r\}}u\,d{\mathcal {H}}^{n-1},}$

en la que ω _{n − 1} denota el área de superficie de la bola unitaria en el espacio euclidiano de n dimensiones. Esto formaliza la afirmación anterior de que el valor de ∆ u en un punto x mide la diferencia entre el valor de u ( x ) y el valor de u en puntos cercanos a x , en el sentido de que este último está codificado por los valores de u _{( x )} ( r ) para valores positivos pequeños de r .

Siguiendo esta observación, se puede interpretar la ecuación del calor como la imposición de un promedio infinitesimal de una función. Dada una solución de la ecuación del calor, el valor de u ( x , t + τ) para un valor positivo pequeño de τ se puede aproximar como ⁠1/2 n⁠ veces el valor promedio de la función u (⋅, t ) sobre una esfera de radio muy pequeño centrada en x .

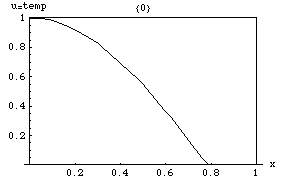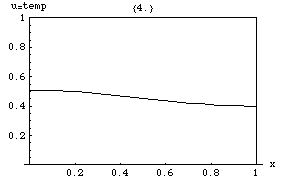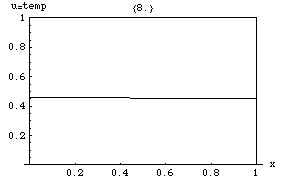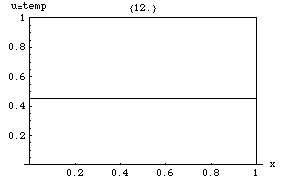
La ecuación del calor implica que los picos ( máximos locales ) de se irán erosionando gradualmente, mientras que las depresiones ( mínimos locales ) se irán rellenando. El valor en un punto determinado permanecerá estable solo mientras sea igual al valor medio en sus alrededores inmediatos. En particular, si los valores en un entorno están muy cerca de una función lineal , entonces el valor en el centro de ese entorno no cambiará en ese momento (es decir, la derivada será cero).${\displaystyle u}$${\displaystyle Ax+By+Cz+D}$${\displaystyle {\dot {u}}}$

Una consecuencia más sutil es el principio del máximo , que dice que el valor máximo de en cualquier región del medio no superará el valor máximo que se produjo previamente en , a menos que esté en el límite de . Es decir, la temperatura máxima en una región puede aumentar solo si el calor proviene del exterior . Esta es una propiedad de las ecuaciones diferenciales parciales parabólicas y no es difícil de demostrar matemáticamente (ver más abajo).${\displaystyle u}$${\displaystyle R}$${\displaystyle R}$${\displaystyle R}$${\displaystyle R}$${\displaystyle R}$

Otra propiedad interesante es que, incluso si inicialmente tiene un salto brusco (discontinuidad) de valor a través de alguna superficie dentro del medio, el salto se suaviza inmediatamente por una tasa momentánea, infinitesimalmente corta pero infinitamente grande de flujo de calor a través de esa superficie. Por ejemplo, si se hace que dos cuerpos aislados, inicialmente a temperaturas uniformes pero diferentes y , se toquen entre sí, la temperatura en el punto de contacto asumirá inmediatamente un valor intermedio y se desarrollará una zona alrededor de ese punto donde variará gradualmente entre y .${\displaystyle u}$${\displaystyle u_{0}}$${\displaystyle u_{1}}$${\displaystyle u}$${\displaystyle u_{0}}$${\displaystyle u_{1}}$

Si se aplica de repente una determinada cantidad de calor a un punto del medio, se propagará en todas direcciones en forma de onda de difusión. A diferencia de las ondas elásticas y electromagnéticas , la velocidad de una onda de difusión disminuye con el tiempo: a medida que se propaga por una región más grande, el gradiente de temperatura disminuye y, por lo tanto, el flujo de calor también disminuye.

Para el flujo de calor, la ecuación de calor se deriva de las leyes físicas de conducción de calor y conservación de energía (Cannon 1984).

Según la ley de Fourier para un medio isótropo, la tasa de flujo de energía térmica por unidad de área a través de una superficie es proporcional al gradiente de temperatura negativo a través de ella:

${\displaystyle \mathbf {q} =-k\,\nabla u}$

donde es la conductividad térmica del material, es la temperatura, y es un campo vectorial que representa la magnitud y dirección del flujo de calor en el punto del espacio y el tiempo .${\displaystyle k}$${\displaystyle u=u(\mathbf {x} ,t)}$${\displaystyle \mathbf {q} =\mathbf {q} (\mathbf {x} ,t)}$${\displaystyle \mathbf {x} }$${\displaystyle t}$

Si el medio es una varilla delgada de sección y material uniformes, la posición x es una coordenada única y el flujo de calor hacia es un campo escalar . La ecuación se convierte en${\displaystyle q=q(t,x)}$${\displaystyle x}$

${\displaystyle q=-k\,{\frac {\partial u}{\partial x}}}$

Sea la energía interna (calor) por unidad de volumen de la barra en cada punto y tiempo. La tasa de cambio de calor por unidad de volumen en el material, , es proporcional a la tasa de cambio de su temperatura, . Es decir,${\displaystyle Q=Q(x,t)}$${\displaystyle \partial Q/\partial t}$${\displaystyle \partial u/\partial t}$

${\displaystyle {\frac {\partial Q}{\partial t}}=c\,\rho \,{\frac {\partial u}{\partial t}}}$

donde es la capacidad calorífica específica (a presión constante, en el caso de un gas) y es la densidad (masa por unidad de volumen) del material. Esta derivación supone que el material tiene una densidad de masa y una capacidad calorífica constantes en el espacio y en el tiempo.${\displaystyle c}$${\displaystyle \rho }$

Aplicando la ley de conservación de la energía a un elemento pequeño del medio centrado en , se concluye que la velocidad a la que cambia el calor en un punto dado es igual a la derivada del flujo de calor en ese punto (la diferencia entre los flujos de calor a ambos lados de la partícula). Es decir,${\displaystyle x}$${\displaystyle x}$

${\displaystyle {\frac {\partial Q}{\partial t}}=-{\frac {\partial q}{\partial x}}}$

De las ecuaciones anteriores se deduce que

${\displaystyle {\frac {\partial u}{\partial t}}\;=\;-{\frac {1}{c\rho }}{\frac {\partial q}{\partial x}}\;=\;-{\frac {1}{c\rho }}{\frac {\partial }{\partial x}}\left(-k\,{\frac {\partial u}{\partial x}}\right)\;=\;{\frac {k}{c\rho }}{\frac {\partial ^{2}u}{\partial x^{2}}}}$

que es la ecuación del calor en una dimensión, con coeficiente de difusividad

${\displaystyle \alpha ={\frac {k}{c\rho }}}$

Esta cantidad se llama difusividad térmica del medio.

Se puede introducir un término adicional en la ecuación para tener en cuenta la pérdida de calor por radiación. Según la ley de Stefan-Boltzmann , este término es , donde es la temperatura del entorno y es un coeficiente que depende de la constante de Stefan-Boltzmann y de la emisividad del material. La tasa de cambio de la energía interna se convierte en${\displaystyle \mu \left(u^{4}-v^{4}\right)}$${\displaystyle v=v(x,t)}$${\displaystyle \mu }$

${\displaystyle {\frac {\partial Q}{\partial t}}=-{\frac {\partial q}{\partial x}}-\mu \left(u^{4}-v^{4}\right)}$

y la ecuación para la evolución de se convierte en${\displaystyle u}$

${\displaystyle {\frac {\partial u}{\partial t}}={\frac {k}{c\rho }}{\frac {\partial ^{2}u}{\partial x^{2}}}-{\frac {\mu }{c\rho }}\left(u^{4}-v^{4}\right).}$

Nótese que la ecuación de estado, dada por la primera ley de la termodinámica (es decir, la conservación de la energía), se escribe en la siguiente forma (suponiendo que no hay transferencia de masa ni radiación). Esta forma es más general y particularmente útil para reconocer qué propiedad (por ejemplo, c _p o ) influye en qué término.${\displaystyle \rho }$

${\displaystyle \rho c_{p}{\frac {\partial T}{\partial t}}-\nabla \cdot \left(k\nabla T\right)={\dot {q}}_{V}}$

¿Dónde está la fuente de calor volumétrica?${\displaystyle {\dot {q}}_{V}}$

En los casos especiales de propagación de calor en un medio isótropo y homogéneo en un espacio tridimensional , esta ecuación es

${\displaystyle {\frac {\partial u}{\partial t}}=\alpha \nabla ^{2}u=\alpha \left({\frac {\partial ^{2}u}{\partial x^{2}}}+{\frac {\partial ^{2}u}{\partial y^{2}}}+{\frac {\partial ^{2}u}{\partial z^{2}}}\right)}$   ${\displaystyle =\alpha \left(u_{xx}+u_{yy}+u_{zz}\right)}$

dónde:

• ${\displaystyle u=u(x,y,z,t)}$¿La temperatura es una función del espacio y del tiempo?
• ${\displaystyle {\tfrac {\partial u}{\partial t}}}$es la tasa de cambio de la temperatura en un punto a lo largo del tiempo;
• ${\displaystyle u_{xx}}$, , y son las segundas derivadas espaciales ( conductivas térmicas ) de la temperatura en las direcciones , , y , respectivamente;${\displaystyle u_{yy}}$${\displaystyle u_{zz}}$${\displaystyle x}$${\displaystyle y}$${\displaystyle z}$
• ${\displaystyle \alpha \equiv {\tfrac {k}{c_{p}\rho }}}$es la difusividad térmica , una cantidad específica del material que depende de la conductividad térmica , la capacidad calorífica específica y la densidad de masa .${\displaystyle k}$ ${\displaystyle c_{p}}$ ${\displaystyle \rho }$

La ecuación del calor es una consecuencia de la ley de conducción de Fourier (ver conducción de calor ).

Si el medio no es todo el espacio, para resolver la ecuación del calor de forma única también necesitamos especificar condiciones de contorno para u . Para determinar la unicidad de las soluciones en todo el espacio es necesario suponer condiciones adicionales, por ejemplo, un límite exponencial en el crecimiento de las soluciones ^[2] o una condición de signo (las soluciones no negativas son únicas por un resultado de David Widder ). ^[3]

Las soluciones de la ecuación del calor se caracterizan por una suavización gradual de la distribución de temperatura inicial por el flujo de calor desde las áreas más cálidas a las más frías de un objeto. En general, muchos estados y condiciones iniciales diferentes tenderán hacia el mismo equilibrio estable . En consecuencia, invertir la solución y sacar conclusiones sobre tiempos anteriores o condiciones iniciales a partir de la distribución de calor actual es muy inexacto, excepto en los períodos de tiempo más cortos.

La ecuación del calor es el ejemplo prototípico de una ecuación diferencial parcial parabólica .

Utilizando el operador de Laplace , la ecuación del calor se puede simplificar y generalizar a ecuaciones similares sobre espacios de un número arbitrario de dimensiones, como

${\displaystyle u_{t}=\alpha \nabla ^{2}u=\alpha \Delta u,}$

donde el operador de Laplace, Δ o ∇ ² , la divergencia del gradiente, se toma en las variables espaciales.

La ecuación del calor regula la difusión del calor, así como otros procesos difusivos, como la difusión de partículas o la propagación del potencial de acción en las células nerviosas. Aunque no son difusivos por naturaleza, algunos problemas de mecánica cuántica también se rigen por un análogo matemático de la ecuación del calor (véase más adelante). También se puede utilizar para modelar algunos fenómenos que surgen en finanzas , como los procesos de Black-Scholes o de Ornstein-Uhlenbeck . La ecuación, y varios análogos no lineales, también se han utilizado en el análisis de imágenes.

La ecuación del calor viola, técnicamente, la relatividad especial , porque sus soluciones implican la propagación instantánea de una perturbación. La parte de la perturbación fuera del cono de luz delantero normalmente se puede ignorar con seguridad, pero si es necesario desarrollar una velocidad razonable para la transmisión de calor, se debe considerar en su lugar un problema hiperbólico , como una ecuación diferencial parcial que involucra una derivada temporal de segundo orden. Algunos modelos de conducción de calor no lineal (que también son ecuaciones parabólicas) tienen soluciones con una velocidad de transmisión de calor finita. ^{[4] [5]}

La función u anterior representa la temperatura de un cuerpo. Alternativamente, a veces es conveniente cambiar las unidades y representar u como la densidad térmica de un medio. Dado que la densidad térmica es proporcional a la temperatura en un medio homogéneo, la ecuación térmica se sigue cumpliendo en las nuevas unidades.

Supongamos que un cuerpo obedece la ecuación del calor y, además, genera su propio calor por unidad de volumen (por ejemplo, en vatios/litro - W/L) a una tasa dada por una función conocida q que varía en el espacio y el tiempo. ^[6] Entonces el calor por unidad de volumen u satisface una ecuación

${\displaystyle {\frac {1}{\alpha }}{\frac {\partial u}{\partial t}}=\left({\frac {\partial ^{2}u}{\partial x^{2}}}+{\frac {\partial ^{2}u}{\partial y^{2}}}+{\frac {\partial ^{2}u}{\partial z^{2}}}\right)+{\frac {1}{k}}q.}$

Por ejemplo, el filamento de una bombilla de tungsteno genera calor, por lo que su valor de q sería positivo y distinto de cero cuando está encendida. Mientras la luz está apagada, el valor de q para el filamento de tungsteno sería cero.

La siguiente técnica de solución para la ecuación del calor fue propuesta por Joseph Fourier en su tratado Théorie analytique de la chaleur , publicado en 1822. Considere la ecuación del calor para una variable espacial. Esto podría usarse para modelar la conducción de calor en una varilla. La ecuación es

${\displaystyle \displaystyle u_{t}=\alpha u_{xx}}$

( 1 )

donde u = u ( x , t ) es una función de dos variables x y t . Aquí

• x es la variable espacial, por lo tanto x ∈ [0, L ], donde L es la longitud de la varilla.
• t es la variable tiempo, por lo tanto t ≥ 0.

Suponemos la condición inicial

${\displaystyle u(x,0)=f(x)\quad \forall x\in [0,L]}$

( 2 )

donde se da la función f y las condiciones de contorno

${\displaystyle u(0,t)=0=u(L,t)\quad \forall t>0}$.

( 3 )

Intentemos encontrar una solución de ( 1 ) que no sea idénticamente cero y que satisfaga las condiciones de contorno ( 3 ) pero que tenga la siguiente propiedad: u es un producto en el que la dependencia de u respecto de x , t está separada, es decir:

${\displaystyle u(x,t)=X(x)T(t).}$

( 4 )

Esta técnica de solución se llama separación de variables . Sustituyendo u en la ecuación ( 1 ),

${\displaystyle {\frac {T'(t)}{\alpha T(t)}}={\frac {X''(x)}{X(x)}}.}$

Como el lado derecho depende solo de x y el lado izquierdo solo de t , ambos lados son iguales a un valor constante − λ . Por lo tanto:

${\displaystyle T'(t)=-\lambda \alpha T(t)}$

( 5 )

y

${\displaystyle X''(x)=-\lambda X(x).}$

( 6 )

Ahora demostraremos que no pueden ocurrir soluciones no triviales para ( 6 ) para valores de λ ≤ 0:

1. Supongamos que λ < 0. Entonces existen números reales B , C tales que De ( 3 ) obtenemos X (0) = 0 = X ( L ) y por lo tanto B = 0 = C lo que implica que u es idénticamente 0.$${\displaystyle X(x)=Be^{{\sqrt {-\lambda }}\,x}+Ce^{-{\sqrt {-\lambda }}\,x}.}$$
2. Supongamos que λ = 0. Entonces existen números reales B , C tales que X ( x ) = Bx + C . De la ecuación ( 3 ) concluimos de la misma manera que en 1 que u es idénticamente 0.
3. Por lo tanto, debe ser el caso que λ > 0. Entonces existen números reales A , B , C tales que y De ( 3 ) obtenemos C = 0 y que para algún entero positivo n ,$${\displaystyle T(t)=Ae^{-\lambda \alpha t}}$$$${\displaystyle X(x)=B\sin \left({\sqrt {\lambda }}\,x\right)+C\cos \left({\sqrt {\lambda }}\,x\right).}$$$${\displaystyle {\sqrt {\lambda }}=n{\frac {\pi }{L}}.}$$

Esto resuelve la ecuación de calor en el caso especial de que la dependencia de u tiene la forma especial ( 4 ).

En general, la suma de soluciones de ( 1 ) que satisfacen las condiciones de contorno ( 3 ) también satisface ( 1 ) y ( 3 ). Podemos demostrar que la solución de ( 1 ), ( 2 ) y ( 3 ) está dada por

${\displaystyle u(x,t)=\sum _{n=1}^{\infty }D_{n}\sin \left({\frac {n\pi x}{L}}\right)e^{-{\frac {n^{2}\pi ^{2}\alpha t}{L^{2}}}}}$

dónde

${\displaystyle D_{n}={\frac {2}{L}}\int _{0}^{L}f(x)\sin \left({\frac {n\pi x}{L}}\right)\,dx.}$

La técnica de solución utilizada anteriormente se puede extender en gran medida a muchos otros tipos de ecuaciones. La idea es que el operador u _xx con las condiciones de contorno cero se puede representar en términos de sus funciones propias . Esto conduce naturalmente a una de las ideas básicas de la teoría espectral de los operadores lineales autoadjuntos .

Consideremos el operador lineal Δ u = u _xx . La secuencia infinita de funciones

${\displaystyle e_{n}(x)={\sqrt {\frac {2}{L}}}\sin \left({\frac {n\pi x}{L}}\right)}$

para n ≥ 1 son funciones propias de Δ. De hecho,

${\displaystyle \Delta e_{n}=-{\frac {n^{2}\pi ^{2}}{L^{2}}}e_{n}.}$

Además, cualquier función propia f de Δ con las condiciones de contorno f (0) = f ( L ) = 0 es de la forma e _n para algún n ≥ 1. Las funciones e _n para n ≥ 1 forman una secuencia ortonormal con respecto a un cierto producto interno en el espacio de funciones de valor real en [0, L ]. Esto significa

${\displaystyle \langle e_{n},e_{m}\rangle =\int _{0}^{L}e_{n}(x)e_{m}^{*}(x)dx=\delta _{mn}}$

Finalmente, la secuencia { e _n } _{n ∈ N} abarca un subespacio lineal denso de L ² ((0, L )). Esto muestra que, en efecto, hemos diagonalizado el operador Δ.

En general, el estudio de la conducción del calor se basa en varios principios. El flujo de calor es una forma de flujo de energía y, como tal, tiene sentido hablar de la velocidad temporal del flujo de calor en una región del espacio.

• La tasa temporal de flujo de calor hacia una región V está dada por una cantidad dependiente del tiempo q _t ( V ). Suponemos que q tiene una densidad Q , de modo que$${\displaystyle q_{t}(V)=\int _{V}Q(x,t)\,dx\quad }$$
• El flujo de calor es una función vectorial dependiente del tiempo H ( x ) caracterizada de la siguiente manera: la tasa temporal de flujo de calor a través de un elemento de superficie infinitesimal con área dS y con vector normal unitario n es Por lo tanto, la tasa de flujo de calor en V también está dada por la integral de superficie donde n ( x ) es el vector normal que apunta hacia afuera en x .$${\displaystyle \mathbf {H} (x)\cdot \mathbf {n} (x)\,dS.}$$$${\displaystyle q_{t}(V)=-\int _{\partial V}\mathbf {H} (x)\cdot \mathbf {n} (x)\,dS}$$
• La ley de Fourier establece que el flujo de energía térmica tiene la siguiente dependencia lineal del gradiente de temperatura , donde A ( x ) es una matriz real de 3 × 3 que es simétrica y definida positiva .$${\displaystyle \mathbf {H} (x)=-\mathbf {A} (x)\cdot \nabla u(x)}$$
• Por el teorema de divergencia , la integral de superficie anterior para el flujo de calor en V se puede transformar en la integral de volumen$${\displaystyle {\begin{aligned}q_{t}(V)&=-\int _{\partial V}\mathbf {H} (x)\cdot \mathbf {n} (x)\,dS\\&=\int _{\partial V}\mathbf {A} (x)\cdot \nabla u(x)\cdot \mathbf {n} (x)\,dS\\&=\int _{V}\sum _{i,j}\partial _{x_{i}}{\bigl (}a_{ij}(x)\partial _{x_{j}}u(x,t){\bigr )}\,dx\end{aligned}}}$$
• La tasa temporal de cambio de temperatura en x es proporcional al calor que fluye hacia un elemento de volumen infinitesimal, donde la constante de proporcionalidad depende de una constante κ $${\displaystyle \partial _{t}u(x,t)=\kappa (x)Q(x,t)}$$

Juntando estas ecuaciones obtenemos la ecuación general del flujo de calor:

${\displaystyle \partial _{t}u(x,t)=\kappa (x)\sum _{i,j}\partial _{x_{i}}{\bigl (}a_{ij}(x)\partial _{x_{j}}u(x,t){\bigr )}}$

Observaciones

• El coeficiente κ ( x ) es el inverso del calor específico de la sustancia en x × densidad de la sustancia en x : .${\displaystyle \kappa =1/(\rho c_{p})}$
• En el caso de un medio isótropo, la matriz A es una matriz escalar igual a la conductividad térmica k .
• En el caso anisotrópico donde la matriz de coeficientes A no es escalar y/o si depende de x , entonces rara vez se puede escribir una fórmula explícita para la solución de la ecuación del calor, aunque normalmente es posible considerar el problema abstracto de Cauchy asociado y demostrar que es un problema bien planteado y/o mostrar algunas propiedades cualitativas (como la preservación de datos iniciales positivos, velocidad infinita de propagación, convergencia hacia un equilibrio, propiedades de suavizado). Esto se hace normalmente mediante la teoría de semigrupos de un parámetro : por ejemplo, si A es una matriz simétrica, entonces el operador elíptico definido por es autoadjunto y disipativo, por lo que mediante el teorema espectral genera un semigrupo de un parámetro .$${\displaystyle Au(x):=\sum _{i,j}\partial _{x_{i}}a_{ij}(x)\partial _{x_{j}}u(x)}$$

Una solución fundamental , también llamada núcleo de calor , es una solución de la ecuación de calor correspondiente a la condición inicial de una fuente puntual de calor inicial en una posición conocida. Estas soluciones se pueden utilizar para encontrar una solución general de la ecuación de calor en ciertos dominios; véase, por ejemplo, (Evans 2010) para un tratamiento introductorio.

En una variable, la función de Green es una solución del problema de valor inicial (por el principio de Duhamel , equivalente a la definición de la función de Green como una con una función delta como solución a la primera ecuación)

${\displaystyle {\begin{cases}u_{t}(x,t)-ku_{xx}(x,t)=0&(x,t)\in \mathbb {R} \times (0,\infty )\\u(x,0)=\delta (x)&\end{cases}}}$

¿Dónde está la función delta de Dirac ? La solución de este problema es la solución fundamental ( núcleo de calor ).${\displaystyle \delta }$

${\displaystyle \Phi (x,t)={\frac {1}{\sqrt {4\pi kt}}}\exp \left(-{\frac {x^{2}}{4kt}}\right).}$

Se puede obtener la solución general de la ecuación de calor de una variable con condición inicial u ( x , 0) = g ( x ) para −∞ < x < ∞ y 0 < t < ∞ aplicando una convolución :

${\displaystyle u(x,t)=\int \Phi (x-y,t)g(y)dy.}$

En varias variables espaciales, la solución fundamental resuelve el problema análogo

${\displaystyle {\begin{cases}u_{t}(\mathbf {x} ,t)-k\sum _{i=1}^{n}u_{x_{i}x_{i}}(\mathbf {x} ,t)=0&(\mathbf {x} ,t)\in \mathbb {R} ^{n}\times (0,\infty )\\u(\mathbf {x} ,0)=\delta (\mathbf {x} )\end{cases}}}$

La solución fundamental de n variables es el producto de las soluciones fundamentales en cada variable; es decir,

${\displaystyle \Phi (\mathbf {x} ,t)=\Phi (x_{1},t)\Phi (x_{2},t)\cdots \Phi (x_{n},t)={\frac {1}{\sqrt {(4\pi kt)^{n}}}}\exp \left(-{\frac {\mathbf {x} \cdot \mathbf {x} }{4kt}}\right).}$

La solución general de la ecuación del calor en R ⁿ se obtiene entonces mediante una convolución, de modo que para resolver el problema de valor inicial con u ( x , 0) = g ( x ), se tiene

${\displaystyle u(\mathbf {x} ,t)=\int _{\mathbb {R} ^{n}}\Phi (\mathbf {x} -\mathbf {y} ,t)g(\mathbf {y} )d\mathbf {y} .}$

El problema general en un dominio Ω en R ⁿ es

${\displaystyle {\begin{cases}u_{t}(\mathbf {x} ,t)-k\sum _{i=1}^{n}u_{x_{i}x_{i}}(\mathbf {x} ,t)=0&(\mathbf {x} ,t)\in \Omega \times (0,\infty )\\u(\mathbf {x} ,0)=g(\mathbf {x} )&\mathbf {x} \in \Omega \end{cases}}}$

con datos de contorno de Dirichlet o Neumann . Siempre existe una función de Green , pero a menos que el dominio Ω pueda descomponerse fácilmente en problemas de una variable (ver más abajo), puede que no sea posible escribirlo explícitamente. Otros métodos para obtener funciones de Green incluyen el método de imágenes , la separación de variables y las transformadas de Laplace (Cole, 2011).

Aquí se registran diversas soluciones de funciones de Green elementales en una dimensión; muchas otras están disponibles en otros lugares. ^[7] En algunas de ellas, el dominio espacial es (−∞,∞). En otras, es el intervalo semiinfinito (0,∞) con condiciones de contorno de Neumann o Dirichlet . Otra variación es que algunas de estas resuelven la ecuación no homogénea.

${\displaystyle u_{t}=ku_{xx}+f.}$

donde f es una función dada de x y t .

Problema de valor inicial en (−∞,∞)

${\displaystyle {\begin{cases}u_{t}=ku_{xx}&(x,t)\in \mathbb {R} \times (0,\infty )\\u(x,0)=g(x)&{\text{Initial condition}}\end{cases}}}$

${\displaystyle u(x,t)={\frac {1}{\sqrt {4\pi kt}}}\int _{-\infty }^{\infty }\exp \left(-{\frac {(x-y)^{2}}{4kt}}\right)g(y)\,dy}$

Comentario . Esta solución es la convolución respecto a la variable x de la solución fundamental.

${\displaystyle \Phi (x,t):={\frac {1}{\sqrt {4\pi kt}}}\exp \left(-{\frac {x^{2}}{4kt}}\right),}$

y la función g ( x ). (El número de función de Green de la solución fundamental es X00.)

Por lo tanto, de acuerdo con las propiedades generales de la convolución con respecto a la diferenciación, u = g ∗ Φ es una solución de la misma ecuación de calor, para

${\displaystyle \left(\partial _{t}-k\partial _{x}^{2}\right)(\Phi *g)=\left[\left(\partial _{t}-k\partial _{x}^{2}\right)\Phi \right]*g=0.}$

Además,

${\displaystyle \Phi (x,t)={\frac {1}{\sqrt {t}}}\,\Phi \left({\frac {x}{\sqrt {t}}},1\right)}$

${\displaystyle \int _{-\infty }^{\infty }\Phi (x,t)\,dx=1,}$

de modo que, por hechos generales sobre aproximación a la identidad , Φ(⋅, t ) ∗ g → g cuando t → 0 en varios sentidos, según la g específica . Por ejemplo, si se supone que g es acotada y continua en R entonces Φ(⋅, t ) ∗ g converge uniformemente a g cuando t → 0, lo que significa que u ( x , t ) es continua en R × [0, ∞) con u ( x , 0) = g ( x ).

Problema de valor inicial en (0,∞) con condiciones de contorno de Dirichlet homogéneas

${\displaystyle {\begin{cases}u_{t}=ku_{xx}&(x,t)\in [0,\infty )\times (0,\infty )\\u(x,0)=g(x)&{\text{IC}}\\u(0,t)=0&{\text{BC}}\end{cases}}}$

${\displaystyle u(x,t)={\frac {1}{\sqrt {4\pi kt}}}\int _{0}^{\infty }\left[\exp \left(-{\frac {(x-y)^{2}}{4kt}}\right)-\exp \left(-{\frac {(x+y)^{2}}{4kt}}\right)\right]g(y)\,dy}$

Comentario. Esta solución se obtiene a partir de la fórmula precedente aplicada a los datos g ( x ) adecuadamente extendida a R , de modo que sea una función impar , es decir, siendo g (− x ) := − g ( x ) para todo x . En consecuencia, la solución del problema de valor inicial en (−∞,∞) es una función impar con respecto a la variable x para todos los valores de t , y en particular satisface las condiciones de contorno homogéneas de Dirichlet u (0, t ) = 0. El número de función de Green de esta solución es X10.

Problema de valor inicial en (0,∞) con condiciones de contorno de Neumann homogéneas

${\displaystyle {\begin{cases}u_{t}=ku_{xx}&(x,t)\in [0,\infty )\times (0,\infty )\\u(x,0)=g(x)&{\text{IC}}\\u_{x}(0,t)=0&{\text{BC}}\end{cases}}}$

${\displaystyle u(x,t)={\frac {1}{\sqrt {4\pi kt}}}\int _{0}^{\infty }\left[\exp \left(-{\frac {(x-y)^{2}}{4kt}}\right)+\exp \left(-{\frac {(x+y)^{2}}{4kt}}\right)\right]g(y)\,dy}$

Comentario. Esta solución se obtiene a partir de la primera fórmula de solución aplicada a los datos g ( x ) adecuadamente extendida a R de modo que sea una función par , es decir, siendo g (− x ) := g ( x ) para todo x . En consecuencia, la solución del problema de valor inicial en R es una función par con respecto a la variable x para todos los valores de t > 0, y en particular, al ser suave, satisface las condiciones de contorno homogéneas de Neumann u _x (0, t ) = 0. El número de función de Green de esta solución es X20.

Problema en (0,∞) con condiciones iniciales homogéneas y condiciones de contorno de Dirichlet no homogéneas

${\displaystyle {\begin{cases}u_{t}=ku_{xx}&(x,t)\in [0,\infty )\times (0,\infty )\\u(x,0)=0&{\text{IC}}\\u(0,t)=h(t)&{\text{BC}}\end{cases}}}$

${\displaystyle u(x,t)=\int _{0}^{t}{\frac {x}{\sqrt {4\pi k(t-s)^{3}}}}\exp \left(-{\frac {x^{2}}{4k(t-s)}}\right)h(s)\,ds,\qquad \forall x>0}$

Comentario . Esta solución es la convolución con respecto a la variable t de

${\displaystyle \psi (x,t):=-2k\partial _{x}\Phi (x,t)={\frac {x}{\sqrt {4\pi kt^{3}}}}\exp \left(-{\frac {x^{2}}{4kt}}\right)}$

y la función h ( t ). Puesto que Φ( x , t ) es la solución fundamental de

${\displaystyle \partial _{t}-k\partial _{x}^{2},}$

la función ψ ( x , t ) es también una solución de la misma ecuación de calor, y por lo tanto lo es u  := ψ ∗ h , gracias a las propiedades generales de la convolución con respecto a la diferenciación. Además,

${\displaystyle \psi (x,t)={\frac {1}{x^{2}}}\,\psi \left(1,{\frac {t}{x^{2}}}\right)}$

${\displaystyle \int _{0}^{\infty }\psi (x,t)\,dt=1,}$

de modo que, por hechos generales sobre aproximación a la identidad , ψ ( x , ⋅) ∗ h → h cuando x → 0 en varios sentidos, según la h específica . Por ejemplo, si se supone que h es continua en R con apoyo en [0, ∞) entonces ψ ( x , ⋅) ∗ h converge uniformemente en compacta a h cuando x → 0, lo que significa que u ( x , t ) es continua en [0, ∞) × [0, ∞) con u (0, t ) = h ( t ).

Problema sobre condiciones iniciales homogéneas (-∞,∞)

Comentario . Esta solución es la convolución en R ² , es decir con respecto a ambas variables x y t , de la solución fundamental

${\displaystyle \Phi (x,t):={\frac {1}{\sqrt {4\pi kt}}}\exp \left(-{\frac {x^{2}}{4kt}}\right)}$

y la función f ( x , t ), ambas entendidas como definidas en todo R ² e idénticamente 0 para todo t → 0. Se verifica que

${\displaystyle \left(\partial _{t}-k\partial _{x}^{2}\right)(\Phi *f)=f,}$

que expresado en el lenguaje de distribuciones se convierte en

${\displaystyle \left(\partial _{t}-k\partial _{x}^{2}\right)\Phi =\delta ,}$

donde la distribución δ es la función delta de Dirac , es decir la evaluación en 0.

Problema en (0,∞) con condiciones de contorno de Dirichlet homogéneas y condiciones iniciales

${\displaystyle {\begin{cases}u_{t}=ku_{xx}+f(x,t)&(x,t)\in [0,\infty )\times (0,\infty )\\u(x,0)=0&{\text{IC}}\\u(0,t)=0&{\text{BC}}\end{cases}}}$

${\displaystyle u(x,t)=\int _{0}^{t}\int _{0}^{\infty }{\frac {1}{\sqrt {4\pi k(t-s)}}}\left(\exp \left(-{\frac {(x-y)^{2}}{4k(t-s)}}\right)-\exp \left(-{\frac {(x+y)^{2}}{4k(t-s)}}\right)\right)f(y,s)\,dy\,ds}$

Comentario . Esta solución se obtiene a partir de la fórmula precedente aplicada a los datos f ( x , t ) adecuadamente extendida a R × [0,∞), de modo que sea una función impar de la variable x , es decir, siendo f (− x , t ) := − f ( x , t ) para todo x y t . En consecuencia, la solución del problema no homogéneo en (−∞,∞) es una función impar con respecto a la variable x para todos los valores de t , y en particular satisface las condiciones de contorno homogéneas de Dirichlet u (0, t ) = 0.

Problema en (0,∞) con condiciones de contorno de Neumann homogéneas y condiciones iniciales

${\displaystyle {\begin{cases}u_{t}=ku_{xx}+f(x,t)&(x,t)\in [0,\infty )\times (0,\infty )\\u(x,0)=0&{\text{IC}}\\u_{x}(0,t)=0&{\text{BC}}\end{cases}}}$

${\displaystyle u(x,t)=\int _{0}^{t}\int _{0}^{\infty }{\frac {1}{\sqrt {4\pi k(t-s)}}}\left(\exp \left(-{\frac {(x-y)^{2}}{4k(t-s)}}\right)+\exp \left(-{\frac {(x+y)^{2}}{4k(t-s)}}\right)\right)f(y,s)\,dy\,ds}$

Comentario . Esta solución se obtiene a partir de la primera fórmula aplicada a los datos f ( x , t ) adecuadamente extendida a R × [0,∞), de modo que sea una función par de la variable x , es decir, siendo f (− x , t ) := f ( x , t ) para todo x y t . En consecuencia, la solución del problema no homogéneo en (−∞,∞) es una función par con respecto a la variable x para todos los valores de t , y en particular, al ser una función suave, satisface las condiciones de contorno homogéneas de Neumann u _x (0, t ) = 0.

Dado que la ecuación de calor es lineal, se pueden encontrar soluciones de otras combinaciones de condiciones de contorno, términos no homogéneos y condiciones iniciales tomando una combinación lineal apropiada de las soluciones de la función de Green anteriores.

Por ejemplo, para resolver

${\displaystyle {\begin{cases}u_{t}=ku_{xx}+f&(x,t)\in \mathbb {R} \times (0,\infty )\\u(x,0)=g(x)&{\text{IC}}\end{cases}}}$

Sea u = w + v donde w y v resuelven los problemas

${\displaystyle {\begin{cases}v_{t}=kv_{xx}+f,\,w_{t}=kw_{xx}\,&(x,t)\in \mathbb {R} \times (0,\infty )\\v(x,0)=0,\,w(x,0)=g(x)\,&{\text{IC}}\end{cases}}}$

De manera similar, para resolver

${\displaystyle {\begin{cases}u_{t}=ku_{xx}+f&(x,t)\in [0,\infty )\times (0,\infty )\\u(x,0)=g(x)&{\text{IC}}\\u(0,t)=h(t)&{\text{BC}}\end{cases}}}$

sea ​​u = w + v + r donde w , v y r resuelven los problemas

${\displaystyle {\begin{cases}v_{t}=kv_{xx}+f,\,w_{t}=kw_{xx},\,r_{t}=kr_{xx}&(x,t)\in [0,\infty )\times (0,\infty )\\v(x,0)=0,\;w(x,0)=g(x),\;r(x,0)=0&{\text{IC}}\\v(0,t)=0,\;w(0,t)=0,\;r(0,t)=h(t)&{\text{BC}}\end{cases}}}$

Soluciones de las ecuaciones del calor

${\displaystyle (\partial _{t}-\Delta )u=0}$

satisfacen una propiedad de valor medio análoga a las propiedades de valor medio de las funciones armónicas , soluciones de

${\displaystyle \Delta u=0,}$

aunque un poco más complicado. Precisamente, si lo resuelves

${\displaystyle (\partial _{t}-\Delta )u=0}$

y

${\displaystyle (x,t)+E_{\lambda }\subset \mathrm {dom} (u)}$

entonces

${\displaystyle u(x,t)={\frac {\lambda }{4}}\int _{E_{\lambda }}u(x-y,t-s){\frac {|y|^{2}}{s^{2}}}ds\,dy,}$

donde E _λ es una "bola de calor", es decir, un conjunto de supernivel de la solución fundamental de la ecuación del calor:

${\displaystyle E_{\lambda }:=\{(y,s):\Phi (y,s)>\lambda \},}$

${\displaystyle \Phi (x,t):=(4t\pi )^{-{\frac {n}{2}}}\exp \left(-{\frac {|x|^{2}}{4t}}\right).}$

Tenga en cuenta que

${\displaystyle \mathrm {diam} (E_{\lambda })=o(1)}$

como λ → ∞ entonces la fórmula anterior es válida para cualquier ( x , t ) en el conjunto (abierto) dom( u ) para λ suficientemente grande. ^[8] Esto se puede demostrar mediante un argumento similar al análogo para las funciones armónicas .

La ecuación del calor en estado estacionario no depende, por definición, del tiempo. En otras palabras, se supone que existen condiciones tales que:

${\displaystyle {\frac {\partial u}{\partial t}}=0}$

Esta condición depende de la constante de tiempo y del tiempo transcurrido desde que se impusieron las condiciones de contorno. Por lo tanto, la condición se cumple en situaciones en las que la constante de equilibrio temporal es lo suficientemente rápida como para que la ecuación de calor dependiente del tiempo más compleja pueda aproximarse mediante el caso de estado estacionario. De manera equivalente, la condición de estado estacionario existe para todos los casos en los que ha transcurrido suficiente tiempo como para que el campo térmico u ya no evolucione en el tiempo.

En el caso del estado estacionario, puede existir (o no) un gradiente térmico espacial, pero si lo hay, no cambia con el tiempo. Por lo tanto, esta ecuación describe el resultado final en todos los problemas térmicos en los que se enciende una fuente (por ejemplo, el motor de un automóvil) y ha pasado suficiente tiempo para que todos los gradientes de temperatura permanentes se establezcan en el espacio, después de lo cual estos gradientes espaciales ya no cambian con el tiempo (como sucede nuevamente con un automóvil en el que el motor ha estado funcionando durante suficiente tiempo). La otra solución (trivial) es que también desaparezcan todos los gradientes de temperatura espaciales, en cuyo caso la temperatura también se vuelve uniforme en el espacio.

La ecuación es mucho más sencilla y puede ayudar a comprender mejor la física de los materiales sin centrarse en la dinámica del proceso de transporte de calor. Se utiliza ampliamente para problemas de ingeniería simples suponiendo que existe un equilibrio de los campos de temperatura y transporte de calor con el tiempo.

Condición de estado estable:

${\displaystyle {\frac {\partial u}{\partial t}}=0}$

La ecuación de calor en estado estacionario para un volumen que contiene una fuente de calor (el caso no homogéneo), es la ecuación de Poisson :

${\displaystyle -k\nabla ^{2}u=q}$

donde u es la temperatura , k es la conductividad térmica y q es la tasa de generación de calor por unidad de volumen.

En electrostática , esto es equivalente al caso en el que el espacio en consideración contiene una carga eléctrica.

La ecuación de calor en estado estacionario sin una fuente de calor dentro del volumen (caso homogéneo) es la ecuación de la electrostática para un volumen de espacio libre que no contiene carga. Se describe mediante la ecuación de Laplace :

${\displaystyle \nabla ^{2}u=0}$

La difusión de partículas se puede modelar mediante una ecuación que involucra:

• la concentración volumétrica de partículas, denotada c , en el caso de difusión colectiva de un gran número de partículas, o
• la función de densidad de probabilidad asociada con la posición de una sola partícula, denotada P .

En cualquier caso, se utiliza la ecuación del calor.

${\displaystyle c_{t}=D\Delta c,}$

o

${\displaystyle P_{t}=D\Delta P.}$

Tanto c como P son funciones de la posición y el tiempo. D es el coeficiente de difusión que controla la velocidad del proceso de difusión y se expresa normalmente en metros al cuadrado por segundo. Si el coeficiente de difusión D no es constante, sino que depende de la concentración c (o P en el segundo caso), entonces se obtiene la ecuación de difusión no lineal .

Sea el proceso estocástico la solución de la ecuación diferencial estocástica${\displaystyle X}$

${\displaystyle {\begin{cases}\mathrm {d} X_{t}={\sqrt {2k}}\;\mathrm {d} B_{t}\\X_{0}=0\end{cases}}}$

donde es el proceso de Wiener (movimiento browniano estándar). La función de densidad de probabilidad de está dada en cualquier momento por${\displaystyle B}$${\displaystyle X}$${\displaystyle t}$

${\displaystyle {\frac {1}{\sqrt {4\pi kt}}}\exp \left(-{\frac {x^{2}}{4kt}}\right)}$

¿Cuál es la solución al problema del valor inicial?

${\displaystyle {\begin{cases}u_{t}(x,t)-ku_{xx}(x,t)=0,&(x,t)\in \mathbb {R} \times (0,+\infty )\\u(x,0)=\delta (x)\end{cases}}}$

¿Dónde está la función delta de Dirac ?${\displaystyle \delta }$

Con una simple división, la ecuación de Schrödinger para una sola partícula de masa m en ausencia de cualquier campo de fuerza aplicado se puede reescribir de la siguiente manera:

${\displaystyle \psi _{t}={\frac {i\hbar }{2m}}\Delta \psi }$,

donde i es la unidad imaginaria , ħ es la constante de Planck reducida y ψ es la función de onda de la partícula.

Esta ecuación es formalmente similar a la ecuación de difusión de partículas, que se obtiene mediante la siguiente transformación:

${\displaystyle {\begin{aligned}c(\mathbf {R} ,t)&\to \psi (\mathbf {R} ,t)\\D&\to {\frac {i\hbar }{2m}}\end{aligned}}}$

Aplicando esta transformación a las expresiones de las funciones de Green determinadas en el caso de la difusión de partículas se obtienen las funciones de Green de la ecuación de Schrödinger , que a su vez pueden utilizarse para obtener la función de onda en cualquier tiempo mediante una integral sobre la función de onda en t = 0:

${\displaystyle \psi (\mathbf {R} ,t)=\int \psi \left(\mathbf {R} ^{0},t=0\right)G\left(\mathbf {R} -\mathbf {R} ^{0},t\right)dR_{x}^{0}\,dR_{y}^{0}\,dR_{z}^{0},}$

con

${\displaystyle G(\mathbf {R} ,t)=\left({\frac {m}{2\pi i\hbar t}}\right)^{3/2}e^{-{\frac {\mathbf {R} ^{2}m}{2i\hbar t}}}.}$

Observación: esta analogía entre la mecánica cuántica y la difusión es puramente formal. Físicamente, la evolución de la función de onda que satisface la ecuación de Schrödinger podría tener un origen distinto a la difusión ^{[ cita requerida ]} .

Una aplicación práctica directa de la ecuación del calor, en conjunción con la teoría de Fourier , en coordenadas esféricas, es la predicción de perfiles de transferencia térmica y la medición de la difusividad térmica en polímeros (Unsworth y Duarte ). Este método dual teórico-experimental es aplicable al caucho, a varios otros materiales poliméricos de interés práctico y a los microfluidos. Estos autores derivaron una expresión para la temperatura en el centro de una esfera T _C

${\displaystyle {\frac {T_{C}-T_{S}}{T_{0}-T_{S}}}=2\sum _{n=1}^{\infty }(-1)^{n+1}\exp \left({-{\frac {n^{2}\pi ^{2}\alpha t}{L^{2}}}}\right)}$

donde T ₀ es la temperatura inicial de la esfera y T _S la temperatura en la superficie de la esfera, de radio L . Esta ecuación también ha encontrado aplicaciones en la transferencia de energía de proteínas y en el modelado térmico en biofísica.

La ecuación del calor surge en el modelado de una serie de fenómenos y se utiliza a menudo en matemáticas financieras en el modelado de opciones . La ecuación diferencial del modelo de fijación de precios de opciones de Black-Scholes se puede transformar en la ecuación del calor, lo que permite soluciones relativamente fáciles a partir de un cuerpo familiar de matemáticas. Muchas de las extensiones de los modelos de opciones simples no tienen soluciones de forma cerrada y, por lo tanto, deben resolverse numéricamente para obtener un precio de opción modelado. La ecuación que describe la difusión de presión en un medio poroso es idéntica en forma a la ecuación del calor. Los problemas de difusión que tratan con condiciones de contorno de Dirichlet , Neumann y Robin tienen soluciones analíticas de forma cerrada (Thambynayagam 2011). La ecuación del calor también se utiliza ampliamente en el análisis de imágenes (Perona y Malik 1990) y en el aprendizaje automático como la teoría impulsora detrás de los métodos de escala-espacio o laplacianos de gráficos . La ecuación del calor se puede resolver numéricamente de manera eficiente utilizando el método implícito de Crank-Nicolson de (Crank y Nicolson 1947). Este método se puede extender a muchos de los modelos que no tienen una solución de forma cerrada, véase por ejemplo (Wilmott, Howison y Dewynne 1995).

Una forma abstracta de la ecuación de calor en variedades proporciona un enfoque importante al teorema del índice de Atiyah-Singer y ha llevado a mucho más trabajo sobre ecuaciones de calor en geometría de Riemann .

• Polinomio calórico
• Flujo que acorta la curva
• Ecuación de difusión
• Conducción de calor relativista
• Ecuación de Schrödinger
• Transformada de Weierstrass

• Cannon, John Rozier (1984), La ecuación unidimensional del calor , Enciclopedia de matemáticas y sus aplicaciones, vol. 23, Reading, MA: Addison-Wesley Publishing Company, Advanced Book Program, ISBN 0-201-13522-1, MR  0747979, Zbl  0567.35001
• Crank, J.; Nicolson, P. (1947), "Un método práctico para la evaluación numérica de soluciones de ecuaciones diferenciales parciales del tipo de conducción de calor", Actas de la Sociedad Filosófica de Cambridge , 43 (1): 50–67, Bibcode :1947PCPS...43...50C, doi :10.1017/S0305004100023197, S2CID  16676040
• Evans, Lawrence C. (2010), Ecuaciones diferenciales parciales, Estudios de posgrado en matemáticas, vol. 19 (2.ª ed.), Providence, RI: American Mathematical Society, ISBN 978-0-8218-4974-3
• Perona, P; Malik, J. (1990), "Detección de bordes y escala espacial mediante difusión anisotrópica" (PDF) , IEEE Transactions on Pattern Analysis and Machine Intelligence , 12 (7): 629–639, doi :10.1109/34.56205, S2CID  14502908
• Thambynayagam, RKM (2011), El manual de difusión: soluciones aplicadas para ingenieros , McGraw-Hill Professional, ISBN 978-0-07-175184-1
• Wilmott, Paul; Howison, Sam; Dewynne, Jeff (1995), Las matemáticas de los derivados financieros. Una introducción para estudiantes , Cambridge: Cambridge University Press, ISBN 0-521-49699-3

• Carslaw, HS ; Jaeger, JC (1988), Conducción de calor en sólidos , Oxford Science Publications (2.ª ed.), Nueva York: The Clarendon Press, Oxford University Press, ISBN 978-0-19-853368-9
• Cole, Kevin D.; Beck, James V.; Haji-Sheikh, A.; Litkouhi, Bahan (2011), Conducción de calor mediante funciones de Green , Serie sobre procesos físicos y computacionales en mecánica y ciencias térmicas (2.ª ed.), Boca Raton, FL: CRC Press, ISBN 978-1-43-981354-6
• Einstein, Albert (1905), "Über die von der molekularkinetischen Theorie der Wärme geforderte Bewegung von in ruhenden Flüssigkeiten suspendierten Teilchen" (PDF) , Annalen der Physik , 322 (8): 549–560, Bibcode :1905AnP...322. .549E, doi : 10.1002/andp.19053220806
• Friedman, Avner (1964), Ecuaciones diferenciales parciales de tipo parabólico , Englewood Cliffs, NJ: Prentice-Hall
• Unsworth, J.; Duarte, FJ (1979), "Difusión de calor en una esfera sólida y teoría de Fourier", Am. J. Phys. , 47 (11): 891–893, Bibcode :1979AmJPh..47..981U, doi :10.1119/1.11601
• Jili, Latif M. (2009), Conducción de calor , Springer (3.ª ed.), Berlín-Heidelberg: Springer-Verlag, ISBN 978-3-642-01266-2
• Widder, DV (1975), La ecuación del calor , Matemáticas puras y aplicadas, vol. 67, Nueva York-Londres: Academic Press [Harcourt Brace Jovanovich, Publishers]

Wikiversidad tiene recursos de aprendizaje sobre la ecuación del calor.

Wikimedia Commons tiene medios relacionados con Ecuación del calor .

• Derivación de la ecuación del calor
• Ecuaciones de calor lineales: Soluciones particulares y problemas con valores de contorno - de EqWorld
• "La ecuación del calor". Serie Infinite de PBS . 17 de noviembre de 2017. Archivado desde el original el 11 de diciembre de 2021 – vía YouTube .