Distribución de arroz

Función de densidad de probabilidad
Función de distribución acumulativa
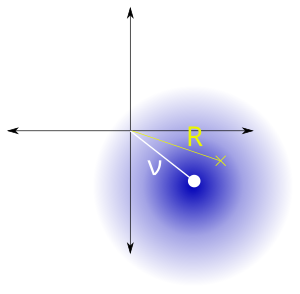
Parámetros	${\displaystyle \nu \geq 0}$, distancia entre el punto de referencia y el centro de la distribución bivariada, , escala ${\displaystyle \sigma \geq 0}$
Apoyo	${\displaystyle x\in [0,\infty )}$
PDF	${\displaystyle {\frac {x}{\sigma ^{2}}}\exp \left({\frac {-(x^{2}+\nu ^{2})}{2\sigma ^{2}}}\right)I_{0}\left({\frac {x\nu }{\sigma ^{2}}}\right)}$
CDF	${\displaystyle 1-Q_{1}\left({\frac {\nu }{\sigma }},{\frac {x}{\sigma }}\right)}$ donde Q 1 es la función Q de Marcum
Significar	${\displaystyle \sigma {\sqrt {\pi /2}}\,\,L_{1/2}(-\nu ^{2}/2\sigma ^{2})}$
Diferencia	${\displaystyle 2\sigma ^{2}+\nu ^{2}-{\frac {\pi \sigma ^{2}}{2}}L_{1/2}^{2}\left({\frac {-\nu ^{2}}{2\sigma ^{2}}}\right)}$
Oblicuidad	(complicado)
Exceso de curtosis	(complicado)

En teoría de la probabilidad , la distribución de Rice o distribución riciana (o, con menos frecuencia, distribución riceana ) es la distribución de probabilidad de la magnitud de una variable aleatoria normal bivariada simétrica circularmente , posiblemente con media distinta de cero (no central). Recibe su nombre en honor a Stephen O. Rice (1907–1986).

La función de densidad de probabilidad es

${\displaystyle f(x\mid \nu ,\sigma )={\frac {x}{\sigma ^{2}}}\exp \left({\frac {-(x^{2}+\nu ^{2})}{2\sigma ^{2}}}\right)I_{0}\left({\frac {x\nu }{\sigma ^{2}}}\right),}$

donde I ₀ ( z ) es la función de Bessel modificada de primer tipo con orden cero.

En el contexto del desvanecimiento de Rician , la distribución a menudo también se reescribe utilizando el parámetro de forma , definido como la relación entre las contribuciones de potencia por ruta de línea de visión y los trayectos múltiples restantes, y el parámetro de escala , definido como la potencia total recibida en todas las rutas. ^[1]${\displaystyle K={\frac {\nu ^{2}}{2\sigma ^{2}}}}$ ${\displaystyle \Omega =\nu ^{2}+2\sigma ^{2}}$

La función característica de la distribución de Rice se da como: ^{[2] [3]}

${\displaystyle {\begin{aligned}\chi _{X}(t\mid \nu ,\sigma )=\exp \left(-{\frac {\nu ^{2}}{2\sigma ^{2}}}\right)&\left[\Psi _{2}\left(1;1,{\frac {1}{2}};{\frac {\nu ^{2}}{2\sigma ^{2}}},-{\frac {1}{2}}\sigma ^{2}t^{2}\right)\right.\\[8pt]&\left.{}+i{\sqrt {2}}\sigma t\Psi _{2}\left({\frac {3}{2}};1,{\frac {3}{2}};{\frac {\nu ^{2}}{2\sigma ^{2}}},-{\frac {1}{2}}\sigma ^{2}t^{2}\right)\right],\end{aligned}}}$

donde es una de las funciones hipergeométricas confluentes de Horn con dos variables y convergente para todos los valores finitos de y . Está dada por: ^{[4] [5]}${\displaystyle \Psi _{2}\left(\alpha ;\gamma ,\gamma ';x,y\right)}$${\displaystyle x}$${\displaystyle y}$

${\displaystyle \Psi _{2}\left(\alpha ;\gamma ,\gamma ';x,y\right)=\sum _{n=0}^{\infty }\sum _{m=0}^{\infty }{\frac {(\alpha )_{m+n}}{(\gamma )_{m}(\gamma ')_{n}}}{\frac {x^{m}y^{n}}{m!n!}},}$

dónde

${\displaystyle (x)_{n}=x(x+1)\cdots (x+n-1)={\frac {\Gamma (x+n)}{\Gamma (x)}}}$

es el factorial ascendente .

Los primeros momentos crudos son:

${\displaystyle {\begin{aligned}\mu _{1}^{'}&=\sigma {\sqrt {\pi /2}}\,\,L_{1/2}(-\nu ^{2}/2\sigma ^{2})\\\mu _{2}^{'}&=2\sigma ^{2}+\nu ^{2}\,\\\mu _{3}^{'}&=3\sigma ^{3}{\sqrt {\pi /2}}\,\,L_{3/2}(-\nu ^{2}/2\sigma ^{2})\\\mu _{4}^{'}&=8\sigma ^{4}+8\sigma ^{2}\nu ^{2}+\nu ^{4}\,\\\mu _{5}^{'}&=15\sigma ^{5}{\sqrt {\pi /2}}\,\,L_{5/2}(-\nu ^{2}/2\sigma ^{2})\\\mu _{6}^{'}&=48\sigma ^{6}+72\sigma ^{4}\nu ^{2}+18\sigma ^{2}\nu ^{4}+\nu ^{6}\end{aligned}}}$

y, en general, los momentos crudos vienen dados por

${\displaystyle \mu _{k}^{'}=\sigma ^{k}2^{k/2}\,\Gamma (1\!+\!k/2)\,L_{k/2}(-\nu ^{2}/2\sigma ^{2}).\,}$

Aquí L _q ( x ) denota un polinomio de Laguerre :

${\displaystyle L_{q}(x)=L_{q}^{(0)}(x)=M(-q,1,x)=\,_{1}F_{1}(-q;1;x)}$

donde es la función hipergeométrica confluente de primera especie. Cuando k es par, los momentos en bruto se convierten en polinomios simples en σ y ν , como en los ejemplos anteriores.${\displaystyle M(a,b,z)=_{1}F_{1}(a;b;z)}$

Para el caso q = 1/2:

${\displaystyle {\begin{aligned}L_{1/2}(x)&=\,_{1}F_{1}\left(-{\frac {1}{2}};1;x\right)\\&=e^{x/2}\left[\left(1-x\right)I_{0}\left(-{\frac {x}{2}}\right)-xI_{1}\left(-{\frac {x}{2}}\right)\right].\end{aligned}}}$

El segundo momento central , la varianza , es

${\displaystyle \mu _{2}=2\sigma ^{2}+\nu ^{2}-(\pi \sigma ^{2}/2)\,L_{1/2}^{2}(-\nu ^{2}/2\sigma ^{2}).}$

Tenga en cuenta que indica el cuadrado del polinomio de Laguerre , no el polinomio de Laguerre generalizado.${\displaystyle L_{1/2}^{2}(\cdot )}$${\displaystyle L_{1/2}(\cdot )}$${\displaystyle L_{1/2}^{(2)}(\cdot ).}$

• ${\displaystyle R\sim \mathrm {Rice} \left(|\nu |,\sigma \right)}$si donde y son variables aleatorias normales estadísticamente independientes y es cualquier número real.${\displaystyle R={\sqrt {X^{2}+Y^{2}}}}$${\displaystyle X\sim N\left(\nu \cos \theta ,\sigma ^{2}\right)}$${\displaystyle Y\sim N\left(\nu \sin \theta ,\sigma ^{2}\right)}$${\displaystyle \theta }$
• Otro caso que surge de los siguientes pasos:${\displaystyle R\sim \mathrm {Rice} \left(\nu ,\sigma \right)}$
  1. Generar teniendo una distribución de Poisson con parámetro (también media, para una Poisson)${\displaystyle P}$${\displaystyle \lambda ={\frac {\nu ^{2}}{2\sigma ^{2}}}.}$
  2. Generar teniendo una distribución chi-cuadrado con 2 P + 2 grados de libertad.${\displaystyle X}$
  3. Colocar${\displaystyle R=\sigma {\sqrt {X}}.}$
• Si entonces tiene una distribución chi-cuadrado no central con dos grados de libertad y parámetro de no centralidad .${\displaystyle R\sim \operatorname {Rice} (\nu ,1)}$${\displaystyle R^{2}}$${\displaystyle \nu ^{2}}$
• Si entonces tiene una distribución chi no central con dos grados de libertad y parámetro de no centralidad .${\displaystyle R\sim \operatorname {Rice} (\nu ,1)}$${\displaystyle R}$${\displaystyle \nu }$
• Si entonces , es decir, para el caso especial de la distribución de Rice dada por , la distribución se convierte en la distribución de Rayleigh , para la cual la varianza es .${\displaystyle R\sim \operatorname {Rice} (0,\sigma )}$${\displaystyle R\sim \operatorname {Rayleigh} (\sigma )}$${\displaystyle \nu =0}$${\displaystyle \mu _{2}={\frac {4-\pi }{2}}\sigma ^{2}}$
• Si entonces tiene una distribución exponencial . ^[6]${\displaystyle R\sim \operatorname {Rice} (0,\sigma )}$${\displaystyle R^{2}}$
• Si entonces tiene una distribución Rician inversa. ^[7]${\displaystyle R\sim \operatorname {Rice} \left(\nu ,\sigma \right)}$${\displaystyle 1/R}$
• La distribución normal plegada es el caso especial univariante de la distribución de Rice.

Para valores grandes del argumento, el polinomio de Laguerre se convierte en ^[8]

${\displaystyle \lim _{x\to -\infty }L_{\nu }(x)={\frac {|x|^{\nu }}{\Gamma (1+\nu )}}.}$

Se observa que a medida que ν se vuelve grande o σ se vuelve pequeño, la media se convierte en ν y la varianza se convierte en σ ² .

La transición a una aproximación gaussiana se realiza de la siguiente manera. De la teoría de funciones de Bessel tenemos

${\displaystyle I_{\alpha }(z)\to {\frac {e^{z}}{\sqrt {2\pi z}}}\left(1-{\frac {4\alpha ^{2}-1}{8z}}+\cdots \right){\text{ as }}z\rightarrow \infty }$

Así, en la región grande, una expansión asintótica de la distribución riciana:${\displaystyle x\nu /\sigma ^{2}}$

${\displaystyle {\begin{aligned}f(x,\nu ,\sigma )={}&{\frac {x}{\sigma ^{2}}}\exp \left({\frac {-(x^{2}+\nu ^{2})}{2\sigma ^{2}}}\right)I_{0}\left({\frac {x\nu }{\sigma ^{2}}}\right)\\{\text{ is }}\\&{\frac {x}{\sigma ^{2}}}\exp \left({\frac {-(x^{2}+\nu ^{2})}{2\sigma ^{2}}}\right){\sqrt {\frac {\sigma ^{2}}{2\pi x\nu }}}\exp \left({\frac {2x\nu }{2\sigma ^{2}}}\right)\left(1+{\frac {\sigma ^{2}}{8x\nu }}+\cdots \right)\\\rightarrow {}&{\frac {1}{\sigma {\sqrt {2\pi }}}}\exp \left(-{\frac {(x-\nu )^{2}}{2\sigma ^{2}}}\right){\sqrt {\frac {x}{\nu }}},\;\;\;{\text{ as }}{\frac {x\nu }{\sigma ^{2}}}\rightarrow \infty \end{aligned}}}$

Además, cuando la densidad se concentra alrededor y debido al exponente gaussiano, también podemos escribir y finalmente obtener la aproximación Normal${\textstyle \nu }$${\textstyle |x-\nu |\ll \sigma }$${\textstyle {\sqrt {{x}/{\nu }}}\approx 1}$

${\displaystyle f(x,\nu ,\sigma )\approx {\frac {1}{\sigma {\sqrt {2\pi }}}}\exp \left(-{\frac {(x-\nu )^{2}}{2\sigma ^{2}}}\right),\;\;\;{\frac {\nu }{\sigma }}\gg 1}$

La aproximación se vuelve utilizable para${\displaystyle {\frac {\nu }{\sigma }}>3}$

Existen tres métodos diferentes para estimar los parámetros de la distribución de Rice, (1) método de momentos , ^{[9] [10] [11] [12]} (2) método de máxima verosimilitud , ^{[9] [10] [11] [13]} y (3) método de mínimos cuadrados. ^{[ cita requerida ]} En los dos primeros métodos el interés está en estimar los parámetros de la distribución, ν y σ, a partir de una muestra de datos. Esto se puede hacer utilizando el método de momentos, por ejemplo, la media de la muestra y la desviación estándar de la muestra. La media de la muestra es una estimación de μ ₁ ^' y la desviación estándar de la muestra es una estimación de μ ₂ ^1/2 .

El siguiente es un método eficiente, conocido como la "técnica de inversión de Koay". ^[14] para resolver las ecuaciones de estimación , basadas en la media de la muestra y la desviación estándar de la muestra, simultáneamente. Esta técnica de inversión también se conoce como la fórmula de punto fijo de SNR . Los trabajos anteriores ^{[9] [15]} sobre el método de momentos generalmente utilizan un método de búsqueda de raíces para resolver el problema, que no es eficiente.

En primer lugar, la relación entre la media de la muestra y la desviación estándar de la muestra se define como r , es decir, . La fórmula de punto fijo de la relación señal-ruido se expresa como${\displaystyle r=\mu _{1}^{'}/\mu _{2}^{1/2}}$

${\displaystyle g(\theta )={\sqrt {\xi {(\theta )}\left[1+r^{2}\right]-2}},}$

donde es la relación de los parámetros, es decir , y viene dada por:${\displaystyle \theta }$${\displaystyle \theta ={\nu }/{\sigma }}$${\displaystyle \xi {\left(\theta \right)}}$

${\displaystyle \xi {\left(\theta \right)}=2+\theta ^{2}-{\frac {\pi }{8}}\exp {(-\theta ^{2}/2)}\left[(2+\theta ^{2})I_{0}(\theta ^{2}/4)+\theta ^{2}I_{1}(\theta ^{2}/4)\right]^{2},}$

donde y son funciones de Bessel modificadas del primer tipo .${\displaystyle I_{0}}$${\displaystyle I_{1}}$

Tenga en cuenta que es un factor de escala de y está relacionado con:${\displaystyle \xi {\left(\theta \right)}}$${\displaystyle \sigma }$${\displaystyle \mu _{2}}$

${\displaystyle \mu _{2}=\xi {\left(\theta \right)}\sigma ^{2}.}$

Para encontrar el punto fijo, , de , se selecciona una solución inicial, , que es mayor que el límite inferior, que es y ocurre cuando ^[14] (Observe que este es el de una distribución de Rayleigh). Esto proporciona un punto de partida para la iteración, que utiliza la composición funcional, ^{[ aclaración necesaria ]} y esto continúa hasta que es menor que algún pequeño valor positivo. Aquí, denota la composición de la misma función, , veces. En la práctica, asociamos el final para algún entero como el punto fijo, , es decir, .${\displaystyle \theta ^{*}}$${\displaystyle g}$${\displaystyle {\theta }_{0}}$${\displaystyle {\theta }_{\text{lower bound}}=0}$${\textstyle r={\sqrt {\pi /(4-\pi )}}}$${\displaystyle r=\mu _{1}^{'}/\mu _{2}^{1/2}}$${\displaystyle \left|g^{i}\left(\theta _{0}\right)-\theta _{i-1}\right|}$${\displaystyle g^{i}}$${\displaystyle g}$${\displaystyle i}$${\displaystyle \theta _{n}}$${\displaystyle n}$${\displaystyle \theta ^{*}}$${\displaystyle \theta ^{*}=g\left(\theta ^{*}\right)}$

Una vez encontrado el punto fijo, las estimaciones y se encuentran a través de la función de escala, , de la siguiente manera:${\displaystyle \nu }$${\displaystyle \sigma }$${\displaystyle \xi {\left(\theta \right)}}$

${\displaystyle \sigma ={\frac {\mu _{2}^{1/2}}{\sqrt {\xi \left(\theta ^{*}\right)}}},}$

y

${\displaystyle \nu ={\sqrt {\left(\mu _{1}^{'~2}+\left(\xi \left(\theta ^{*}\right)-2\right)\sigma ^{2}\right)}}.}$

Para acelerar aún más la iteración, se puede utilizar el método de Newton para encontrar raíces. ^[14] Este enfoque particular es muy eficiente.

• La norma euclidiana de un vector aleatorio normalmente distribuido, simétrico circularmente y bivariado .
• Desvanecimiento de Rician (para interferencias por trayectos múltiples )
• Efecto del error de puntería en el tiro al blanco. ^[16]
• Análisis de la diversidad de receptores en comunicaciones por radio. ^{[17] [18]}
• Distribución de excentricidades para modelos del Sistema Solar interior después de la integración numérica a largo plazo . ^[19]

• Distribución de Hoyt
• Distribución de Rayleigh

• Abramowitz, M. y Stegun, IA (ed.), Handbook of Mathematical Functions , Oficina Nacional de Normas, 1964; reimpreso en Dover Publications, 1965. ISBN 0-486-61272-4 
• Rice, SO , Análisis matemático del ruido aleatorio. Bell System Technical Journal 24 (1945) 46–156.
• I. Soltani Bozchalooi; Ming Liang (20 de noviembre de 2007). "Un enfoque guiado por índice de suavidad para la selección de parámetros wavelet en la eliminación de ruido de la señal y la detección de fallas". Journal of Sound and Vibration . 308 (1–2): 253–254. Bibcode :2007JSV...308..246B. doi :10.1016/j.jsv.2007.07.038.
• Wang, Dong; Zhou, Qiang; Tsui, Kwok-Leung (2017). "Sobre la distribución del módulo de los coeficientes wavelet de Gabor y el límite superior del índice de suavidad adimensional en el caso de ruidos gaussianos aditivos: revisitado". Journal of Sound and Vibration . 395 : 393–400. doi :10.1016/j.jsv.2017.02.013.
• Liu, X. y Hanzo, L., Un análisis unificado del rendimiento BER exacto de sistemas DS-CDMA asíncronos utilizando modulación BPSK sobre canales con desvanecimiento, IEEE Transactions on Wireless Communications, Volumen 6, Número 10, octubre de 2007, págs. 3504–3509.
• Annamalai, A., Tellambura, C. y Bhargava, VK, Rendimiento del receptor de diversidad de igual ganancia en canales inalámbricos, IEEE Transactions on Communications, Volumen 48, octubre de 2000, págs. 1732–1745.
• Erdelyi, A., Magnus, W., Oberhettinger, F. y Tricomi, FG, Funciones trascendentales superiores, Volumen 1. Archivado el 11 de agosto de 2011 en Wayback Machine . McGraw-Hill Book Company Inc., 1953.
• Srivastava, HM y Karlsson, PW, Series hipergeométricas gaussianas múltiples. Ellis Horwood Ltd., 1985.
• Sijbers J., den Dekker AJ, Scheunders P. y Van Dyck D., "Estimación de máxima verosimilitud de los parámetros de distribución de Rician", Archivado el 19 de octubre de 2011 en Wayback Machine , IEEE Transactions on Medical Imaging, vol. 17, n.º 3, págs. 357–361, (1998)
• Varadarajan D. y Haldar JP, "Un marco de trabajo de minimización y mayorización para imágenes de resonancia magnética de Chi no central y de Rician", IEEE Transactions on Medical Imaging, vol. 34, n.º 10, págs. 2191–2202, (2015)
• den Dekker, AJ; Sijbers, J (diciembre de 2014). "Distribuciones de datos en imágenes de resonancia magnética: una revisión". Physica Medica . 30 (7): 725–741. doi :10.1016/j.ejmp.2014.05.002. PMID  25059432.
• Koay, CG y Basser, PJ, Esquema de corrección analíticamente exacto para la extracción de señales de RM de magnitud ruidosa, Journal of Magnetic Resonance, Volumen 179, Número = 2, págs. 317–322, (2006)
• Abdi, A., Tepedelenlioglu, C., Kaveh, M. y Giannakis, G. Sobre la estimación del parámetro K para la distribución de desvanecimiento de Rice, IEEE Communications Letters, Volumen 5, Número 3, marzo de 2001, págs. 92–94.
• Talukdar, KK; Lawing, William D. (marzo de 1991). "Estimación de los parámetros de la distribución de Rice". Revista de la Sociedad Acústica de América . 89 (3): 1193–1197. Código Bibliográfico :1991ASAJ...89.1193T. doi :10.1121/1.400532.
• Bonny, JM; Renou, JP; Zanca, M. (noviembre de 1996). "Medición óptima de magnitud y fase a partir de datos de RM". Journal of Magnetic Resonance, Serie B . 113 (2): 136–144. Bibcode :1996JMRB..113..136B. doi :10.1006/jmrb.1996.0166. PMID  8954899.

• Código MATLAB para la distribución Rice/Rician (PDF, media y varianza, y generación de muestras aleatorias)