Distribución normal multivariante

Normal multivariante

Función de densidad de probabilidad 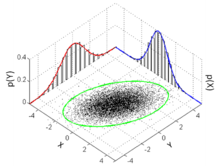Muchos puntos de muestra de una distribución normal multivariada con y , que se muestran junto con la elipse de 3 sigma, las dos distribuciones marginales y los dos histogramas 1-d.${\displaystyle {\boldsymbol {\mu }}=\left[{\begin{smallmatrix}0\\0\end{smallmatrix}}\right]}$${\displaystyle {\boldsymbol {\Sigma }}=\left[{\begin{smallmatrix}1&3/5\\3/5&2\end{smallmatrix}}\right]}$
Notación	${\displaystyle {\mathcal {N}}({\boldsymbol {\mu }},\,{\boldsymbol {\Sigma }})}$
Parámetros	μ ∈ R k — ubicación Σ ∈ R k  ×  k — covarianza ( matriz semidefinida positiva )
Apoyo	x ∈ μ + span( Σ ) ⊆ R k
PDF	${\displaystyle (2\pi )^{-k/2}\det({\boldsymbol {\Sigma }})^{-1/2}\,\exp \left(-{\frac {1}{2}}(\mathbf {x} -{\boldsymbol {\mu }})^{\mathrm {T} }{\boldsymbol {\Sigma }}^{-1}(\mathbf {x} -{\boldsymbol {\mu }})\right),}$ existe solo cuando Σ es definida positiva
Significar	micras
Modo	micras
Diferencia	Σ
Entropía	${\displaystyle {\frac {k}{2}}\log {\mathord {\left(2\pi \mathrm {e} \right)}}+{\frac {1}{2}}\log \det {\mathord {\left({\boldsymbol {\Sigma }}\right)}}}$
MGF	${\displaystyle \exp \!{\Big (}{\boldsymbol {\mu }}^{\mathrm {T} }\mathbf {t} +{\tfrac {1}{2}}\mathbf {t} ^{\mathrm {T} }{\boldsymbol {\Sigma }}\mathbf {t} {\Big )}}$
CF	${\displaystyle \exp \!{\Big (}i{\boldsymbol {\mu }}^{\mathrm {T} }\mathbf {t} -{\tfrac {1}{2}}\mathbf {t} ^{\mathrm {T} }{\boldsymbol {\Sigma }}\mathbf {t} {\Big )}}$
Divergencia de Kullback-Leibler	Véase § Divergencia de Kullback–Leibler

En teoría de probabilidad y estadística , la distribución normal multivariada , distribución gaussiana multivariada o distribución normal conjunta es una generalización de la distribución normal unidimensional ( univariada ) a dimensiones superiores . Una definición es que se dice que un vector aleatorio tiene una distribución normal de k -variadas si cada combinación lineal de sus k componentes tiene una distribución normal univariante. Su importancia deriva principalmente del teorema del límite central multivariado . La distribución normal multivariada se utiliza a menudo para describir, al menos aproximadamente, cualquier conjunto de variables aleatorias de valor real (posiblemente) correlacionadas , cada una de las cuales se agrupa alrededor de un valor medio.

La distribución normal multivariada de un vector aleatorio de dimensión k se puede escribir en la siguiente notación:${\displaystyle \mathbf {X} =(X_{1},\ldots ,X_{k})^{\mathrm {T} }}$

${\displaystyle \mathbf {X} \ \sim \ {\mathcal {N}}({\boldsymbol {\mu }},\,{\boldsymbol {\Sigma }}),}$

o para hacer saber explícitamente que X es k -dimensional,

${\displaystyle \mathbf {X} \ \sim \ {\mathcal {N}}_{k}({\boldsymbol {\mu }},\,{\boldsymbol {\Sigma }}),}$

con vector medio de dimensión k

${\displaystyle {\boldsymbol {\mu }}=\nombredeloperador {E} [\mathbf {X} ]=(\nombredeloperador {E} [X_{1}],\nombredeloperador {E} [X_{2}],\ldots ,\nombredeloperador {E} [X_{k}])^{\mathrm {T} },}$

y matriz de covarianza${\displaystyle k\veces k}$

${\displaystyle \Sigma _{i,j}=\operatorname {E} [(X_{i}-\mu _{i})(X_{j}-\mu _{j})]=\operatorname {Cov } [X_ {i}, X_ {j}]}$

tal que y . La inversa de la matriz de covarianza se llama matriz de precisión , denotada por .${\displaystyle 1\leq i\leq k}$${\displaystyle 1\leq j\leq k}$${\displaystyle {\boldsymbol {Q}}={\boldsymbol {\Sigma }}^{-1}}$

Un vector aleatorio real se denomina vector aleatorio normal estándar si todos sus componentes son independientes y cada uno es una variable aleatoria distribuida normalmente con varianza unitaria de media cero, es decir, si para todos . ^{[1] : p. 454}${\displaystyle \mathbf {X} =(X_{1},\ldots ,X_{k})^{\mathrm {T} }}$$Estilo de visualización X_{i}}$${\displaystyle X_{i}\sim \ {\mathcal {N}}(0,1)}$${\displaystyle i=1\lpuntos k}$

Un vector aleatorio real se denomina vector aleatorio normal centrado si existe una matriz determinista que tiene la misma distribución que donde es un vector aleatorio normal estándar con componentes. ^{[1] : p. 454}${\displaystyle \mathbf {X} =(X_{1},\ldots ,X_{k})^{\mathrm {T} }}$${\displaystyle k\times \ell }$${\displaystyle {\boldsymbol {A}}}$${\displaystyle {\boldsymbol {A}}\mathbf {Z} }$${\displaystyle \mathbf {X} }$${\displaystyle \mathbf {Z} }$${\displaystyle \ell }$

Un vector aleatorio real se denomina vector aleatorio normal si existe un -vector aleatorio , que es un vector aleatorio normal estándar, un -vector y una matriz , tales que . ^{[2] : p. 454  [1] : p. 455}${\displaystyle \mathbf {X} =(X_{1},\ldots ,X_{k})^{\mathrm {T} }}$${\displaystyle \ell }$${\displaystyle \mathbf {Z} }$${\displaystyle k}$${\displaystyle \mathbf {\mu } }$${\displaystyle k\times \ell }$${\displaystyle {\boldsymbol {A}}}$${\displaystyle \mathbf {X} ={\boldsymbol {A}}\mathbf {Z} +\mathbf {\mu } }$

Formalmente:

Aquí la matriz de covarianza es .${\displaystyle {\boldsymbol {\Sigma }}={\boldsymbol {A}}{\boldsymbol {A}}^{\mathrm {T} }}$

En el caso degenerado en el que la matriz de covarianza es singular , la distribución correspondiente no tiene densidad; consulte la sección siguiente para obtener más detalles. Este caso surge con frecuencia en estadística ; por ejemplo, en la distribución del vector de residuos en la regresión de mínimos cuadrados ordinarios . En general , no son independientes; pueden verse como el resultado de aplicar la matriz a una colección de variables gaussianas independientes .${\displaystyle X_{i}}$${\displaystyle {\boldsymbol {A}}}$${\displaystyle \mathbf {Z} }$

Las siguientes definiciones son equivalentes a la definición dada anteriormente. Un vector aleatorio tiene una distribución normal multivariada si satisface una de las siguientes condiciones equivalentes.${\displaystyle \mathbf {X} =(X_{1},\ldots ,X_{k})^{\mathrm {T} }}$

• Toda combinación lineal de sus componentes se distribuye normalmente . Es decir, para cualquier vector constante , la variable aleatoria tiene una distribución normal univariante, donde una distribución normal univariante con varianza cero es una masa puntual sobre su media.${\displaystyle Y=a_{1}X_{1}+\cdots +a_{k}X_{k}}$${\displaystyle \mathbf {a} \in \mathbb {R} ^{k}}$${\displaystyle Y=\mathbf {a} ^{\mathrm {T} }\mathbf {X} }$
• Hay un vector k y una matriz semidefinida positiva simétrica , tal que la función característica de es${\displaystyle \mathbf {\mu } }$ ${\displaystyle k\times k}$${\displaystyle {\boldsymbol {\Sigma }}}$${\displaystyle \mathbf {X} }$$${\displaystyle \varphi _{\mathbf {X} }(\mathbf {u} )=\exp {\Big (}i\mathbf {u} ^{\mathrm {T} }{\boldsymbol {\mu }}-{\tfrac {1}{2}}\mathbf {u} ^{\mathrm {T} }{\boldsymbol {\Sigma }}\mathbf {u} {\Big )}.}$$

La distribución normal esférica se puede caracterizar como la única distribución donde los componentes son independientes en cualquier sistema de coordenadas ortogonales. ^{[3] [4]}

Se dice que la distribución normal multivariante es "no degenerada" cuando la matriz de covarianza simétrica es definida positiva . En este caso, la distribución tiene densidad ^[5]${\displaystyle {\boldsymbol {\Sigma }}}$

donde es un vector columna real de dimensión k y es el determinante de , también conocido como varianza generalizada . La ecuación anterior se reduce a la de la distribución normal univariante si es una matriz (es decir, un solo número real).${\displaystyle {\mathbf {x} }}$${\displaystyle |{\boldsymbol {\Sigma }}|\equiv \det {\boldsymbol {\Sigma }}}$${\displaystyle {\boldsymbol {\Sigma }}}$${\displaystyle {\boldsymbol {\Sigma }}}$${\displaystyle 1\times 1}$

La versión circularmente simétrica de la distribución normal compleja tiene una forma ligeramente diferente.

Cada lugar geométrico de isodensidad (el lugar geométrico de los puntos en el espacio k -dimensional, cada uno de los cuales da el mismo valor particular de la densidad) es una elipse o su generalización de dimensión superior; por lo tanto, la normal multivariada es un caso especial de las distribuciones elípticas .

La cantidad se conoce como la distancia de Mahalanobis , que representa la distancia del punto de prueba desde la media . La distancia de Mahalanobis al cuadrado se descompone en una suma de k términos, siendo cada término un producto de tres componentes significativos. ^[6] Nótese que en el caso cuando , la distribución se reduce a una distribución normal univariante y la distancia de Mahalanobis se reduce al valor absoluto de la puntuación estándar . Véase también Intervalo a continuación.${\displaystyle {\sqrt {({\mathbf {x} }-{\boldsymbol {\mu }})^{\mathrm {T} }{\boldsymbol {\Sigma }}^{-1}({\mathbf {x} }-{\boldsymbol {\mu }})}}}$${\displaystyle {\mathbf {x} }}$${\displaystyle {\boldsymbol {\mu }}}$${\displaystyle ({\mathbf {x} }-{\boldsymbol {\mu }})^{\mathrm {T} }{\boldsymbol {\Sigma }}^{-1}({\mathbf {x} }-{\boldsymbol {\mu }})}$${\displaystyle k=1}$

En el caso no singular bidimensional ( ), la función de densidad de probabilidad de un vector es: donde es la correlación entre y y donde y . En este caso,${\displaystyle k=\operatorname {rank} \left(\Sigma \right)=2}$${\displaystyle {\text{[XY]}}\prime }$$${\displaystyle f(x,y)={\frac {1}{2\pi \sigma _{X}\sigma _{Y}{\sqrt {1-\rho ^{2}}}}}\exp \left(-{\frac {1}{2\left[1-\rho ^{2}\right]}}\left[\left({\frac {x-\mu _{X}}{\sigma _{X}}}\right)^{2}-2\rho \left({\frac {x-\mu _{X}}{\sigma _{X}}}\right)\left({\frac {y-\mu _{Y}}{\sigma _{Y}}}\right)+\left({\frac {y-\mu _{Y}}{\sigma _{Y}}}\right)^{2}\right]\right)}$$${\displaystyle \rho }$${\displaystyle X}$${\displaystyle Y}$${\displaystyle \sigma _{X}>0}$${\displaystyle \sigma _{Y}>0}$

${\displaystyle {\boldsymbol {\mu }}={\begin{pmatrix}\mu _{X}\\\mu _{Y}\end{pmatrix}},\quad {\boldsymbol {\Sigma }}={\begin{pmatrix}\sigma _{X}^{2}&\rho \sigma _{X}\sigma _{Y}\\\rho \sigma _{X}\sigma _{Y}&\sigma _{Y}^{2}\end{pmatrix}}.}$

En el caso bivariado, la primera condición equivalente para la reconstrucción multivariada de la normalidad puede hacerse menos restrictiva, ya que es suficiente verificar que un conjunto infinito numerable de combinaciones lineales distintas de y son normales para concluir que el vector de es normal bivariado. ^[7]${\displaystyle X}$${\displaystyle Y}$${\displaystyle {\text{[XY]}}\prime }$

Los lugares de isodensidad bivariados representados en el plano son elipses , cuyos ejes principales están definidos por los vectores propios de la matriz de covarianza (los semidiámetros mayor y menor de la elipse son iguales a la raíz cuadrada de los valores propios ordenados).${\displaystyle x,y}$${\displaystyle {\boldsymbol {\Sigma }}}$

A medida que aumenta el valor absoluto del parámetro de correlación , estos loci se comprimen hacia la siguiente línea:${\displaystyle \rho }$

${\displaystyle y(x)=\operatorname {sgn}(\rho ){\frac {\sigma _{Y}}{\sigma _{X}}}(x-\mu _{X})+\mu _{Y}.}$

Esto se debe a que esta expresión, con (donde sgn es la función Signo ) reemplazada por , es la mejor predicción lineal imparcial de dado un valor de . ^[8]${\displaystyle \operatorname {sgn}(\rho )}$${\displaystyle \rho }$${\displaystyle Y}$${\displaystyle X}$

Si la matriz de covarianza no es de rango completo, entonces la distribución normal multivariante es degenerada y no tiene densidad. Más precisamente, no tiene densidad con respecto a la medida de Lebesgue de dimensión k (que es la medida habitual que se asume en los cursos de probabilidad a nivel de cálculo). Sólo los vectores aleatorios cuyas distribuciones son absolutamente continuas con respecto a una medida se dice que tienen densidades (con respecto a esa medida). Para hablar de densidades pero evitar lidiar con complicaciones de teoría de la medida, puede ser más simple restringir la atención a un subconjunto de las coordenadas de tal que la matriz de covarianza para este subconjunto sea definida positiva; entonces las otras coordenadas pueden considerarse como una función afín de estas coordenadas seleccionadas. ^[9]${\displaystyle {\boldsymbol {\Sigma }}}$${\displaystyle \operatorname {rank} ({\boldsymbol {\Sigma }})}$${\displaystyle \mathbf {x} }$

Para hablar de densidades de manera significativa en casos singulares, entonces, debemos seleccionar una medida base diferente. Usando el teorema de desintegración podemos definir una restricción de la medida de Lebesgue al subespacio afín de dimensión α de donde se sustenta la distribución gaussiana, es decir . Con respecto a esta medida, la distribución tiene la densidad del siguiente motivo:${\displaystyle \operatorname {rank} ({\boldsymbol {\Sigma }})}$${\displaystyle \mathbb {R} ^{k}}$${\displaystyle \left\{{\boldsymbol {\mu }}+{\boldsymbol {\Sigma ^{1/2}}}\mathbf {v} :\mathbf {v} \in \mathbb {R} ^{k}\right\}}$

${\displaystyle f(\mathbf {x} )={\frac {\exp \left(-{\frac {1}{2}}\left(\mathbf {x} -{\boldsymbol {\mu }}\right)^{\mathrm {T} }{\boldsymbol {\Sigma }}^{+}\left(\mathbf {x} -{\boldsymbol {\mu }}\right)\right)}{\sqrt {\det \nolimits ^{*}(2\pi {\boldsymbol {\Sigma }})}}}}$

donde es la inversa generalizada y es el pseudodeterminante . ^[10]${\displaystyle {\boldsymbol {\Sigma }}^{+}}$${\displaystyle \det \nolimits ^{*}}$

La noción de función de distribución acumulativa (cdf) en dimensión 1 se puede extender de dos maneras al caso multidimensional, basado en regiones rectangulares y elipsoidales.

La primera forma es definir la función de distribución de un vector aleatorio como la probabilidad de que todos los componentes sean menores o iguales a los valores correspondientes en el vector : ^[11]${\displaystyle F(\mathbf {x} )}$${\displaystyle \mathbf {X} }$${\displaystyle \mathbf {X} }$${\displaystyle \mathbf {x} }$

${\displaystyle F(\mathbf {x} )=\mathbb {P} (\mathbf {X} \leq \mathbf {x} ),\quad {\text{where }}\mathbf {X} \sim {\mathcal {N}}({\boldsymbol {\mu }},\,{\boldsymbol {\Sigma }}).}$

Aunque no existe una forma cerrada para , hay varios algoritmos que la estiman numéricamente. ^{[11] [12]}${\displaystyle F(\mathbf {x} )}$

Otra forma es definir la cdf como la probabilidad de que una muestra se encuentre dentro del elipsoide determinado por su distancia de Mahalanobis desde la gaussiana, una generalización directa de la desviación estándar. ^[13] Para calcular los valores de esta función, existe una fórmula analítica cerrada, ^[13] como sigue.${\displaystyle F(r)}$ ${\displaystyle r}$

El intervalo para la distribución normal multivariada produce una región que consiste en aquellos vectores x que satisfacen

${\displaystyle ({\mathbf {x} }-{\boldsymbol {\mu }})^{\mathrm {T} }{\boldsymbol {\Sigma }}^{-1}({\mathbf {x} }-{\boldsymbol {\mu }})\leq \chi _{k}^{2}(p).}$

Aquí hay un vector -dimensional, es el vector medio -dimensional conocido , es la matriz de covarianza conocida y es la función cuantil para la probabilidad de la distribución de chi-cuadrado con grados de libertad. ^[14] Cuando la expresión define el interior de una elipse y la distribución de chi-cuadrado se simplifica a una distribución exponencial con media igual a dos (tasa igual a la mitad).${\displaystyle {\mathbf {x} }}$${\displaystyle k}$${\displaystyle {\boldsymbol {\mu }}}$${\displaystyle k}$${\displaystyle {\boldsymbol {\Sigma }}}$${\displaystyle \chi _{k}^{2}(p)}$${\displaystyle p}$${\displaystyle k}$${\displaystyle k=2,}$

La función de distribución acumulativa complementaria (ccdf) o distribución de cola se define como . Cuando , entonces la ccdf se puede escribir como una probabilidad máxima de las variables gaussianas dependientes: ^[15]${\displaystyle {\overline {F}}(\mathbf {x} )=1-\mathbb {P} \left(\mathbf {X} \leq \mathbf {x} \right)}$${\displaystyle \mathbf {X} \sim {\mathcal {N}}({\boldsymbol {\mu }},\,{\boldsymbol {\Sigma }})}$

${\displaystyle {\overline {F}}(\mathbf {x} )=\mathbb {P} \left(\bigcup _{i}\{X_{i}\geq x_{i}\}\right)=\mathbb {P} \left(\max _{i}Y_{i}\geq 0\right),\quad {\text{where }}\mathbf {Y} \sim {\mathcal {N}}\left({\boldsymbol {\mu }}-\mathbf {x} ,\,{\boldsymbol {\Sigma }}\right).}$

Si bien no existe una fórmula cerrada simple para calcular la ccdf, el máximo de variables gaussianas dependientes se puede estimar con precisión a través del método de Monte Carlo . ^{[15] [16]}

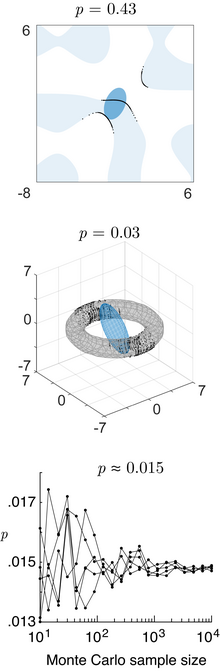
El contenido de probabilidad de la normal multivariada en un dominio cuadrático definido por (donde es una matriz, es un vector y es un escalar), que es relevante para la teoría de clasificación/decisión bayesiana utilizando el análisis discriminante gaussiano, está dado por la distribución chi-cuadrado generalizada . ^[17] El contenido de probabilidad dentro de cualquier dominio general definido por (donde es una función general) se puede calcular utilizando el método numérico de trazado de rayos ^[17] (código Matlab).${\displaystyle q({\boldsymbol {x}})={\boldsymbol {x}}'\mathbf {Q_{2}} {\boldsymbol {x}}+{\boldsymbol {q_{1}}}'{\boldsymbol {x}}+q_{0}>0}$${\displaystyle \mathbf {Q_{2}} }$${\displaystyle {\boldsymbol {q_{1}}}}$${\displaystyle q_{0}}$${\displaystyle f({\boldsymbol {x}})>0}$${\displaystyle f({\boldsymbol {x}})}$

Los momentos de orden k de x están dados por

${\displaystyle \mu _{1,\ldots ,N}(\mathbf {x} )\mathrel {\stackrel {\mathrm {def} }{=}} \mu _{r_{1},\ldots ,r_{N}}(\mathbf {x} )\mathrel {\stackrel {\mathrm {def} }{=}} \operatorname {E} \left[\prod _{j=1}^{N}X_{j}^{r_{j}}\right]}$

donde r ₁ + r ₂ + ⋯ + r _N = k .

Los momentos centrales de orden k son los siguientes

donde la suma se toma sobre todas las asignaciones del conjunto en pares λ (no ordenados). Es decir, para un momento central k (= 2 λ = 6) , se suman los productos de λ = 3 covarianzas (el valor esperado μ se toma como 0 en aras de la parsimonia):${\displaystyle \left\{1,\ldots ,2\lambda \right\}}$

${\displaystyle {\begin{aligned}&\operatorname {E} [X_{1}X_{2}X_{3}X_{4}X_{5}X_{6}]\\[8pt]={}&\operatorname {E} [X_{1}X_{2}]\operatorname {E} [X_{3}X_{4}]\operatorname {E} [X_{5}X_{6}]+\operatorname {E} [X_{1}X_{2}]\operatorname {E} [X_{3}X_{5}]\operatorname {E} [X_{4}X_{6}]+\operatorname {E} [X_{1}X_{2}]\operatorname {E} [X_{3}X_{6}]\operatorname {E} [X_{4}X_{5}]\\[4pt]&{}+\operatorname {E} [X_{1}X_{3}]\operatorname {E} [X_{2}X_{4}]\operatorname {E} [X_{5}X_{6}]+\operatorname {E} [X_{1}X_{3}]\operatorname {E} [X_{2}X_{5}]\operatorname {E} [X_{4}X_{6}]+\operatorname {E} [X_{1}X_{3}]\operatorname {E} [X_{2}X_{6}]\operatorname {E} [X_{4}X_{5}]\\[4pt]&{}+\operatorname {E} [X_{1}X_{4}]\operatorname {E} [X_{2}X_{3}]\operatorname {E} [X_{5}X_{6}]+\operatorname {E} [X_{1}X_{4}]\operatorname {E} [X_{2}X_{5}]\operatorname {E} [X_{3}X_{6}]+\operatorname {E} [X_{1}X_{4}]\operatorname {E} [X_{2}X_{6}]\operatorname {E} [X_{3}X_{5}]\\[4pt]&{}+\operatorname {E} [X_{1}X_{5}]\operatorname {E} [X_{2}X_{3}]\operatorname {E} [X_{4}X_{6}]+\operatorname {E} [X_{1}X_{5}]\operatorname {E} [X_{2}X_{4}]\operatorname {E} [X_{3}X_{6}]+\operatorname {E} [X_{1}X_{5}]\operatorname {E} [X_{2}X_{6}]\operatorname {E} [X_{3}X_{4}]\\[4pt]&{}+\operatorname {E} [X_{1}X_{6}]\operatorname {E} [X_{2}X_{3}]\operatorname {E} [X_{4}X_{5}]+\operatorname {E} [X_{1}X_{6}]\operatorname {E} [X_{2}X_{4}]\operatorname {E} [X_{3}X_{5}]+\operatorname {E} [X_{1}X_{6}]\operatorname {E} [X_{2}X_{5}]\operatorname {E} [X_{3}X_{4}].\end{aligned}}}$

Esto produce términos en la suma (15 en el caso anterior), cada uno de los cuales es el producto de λ (en este caso 3) covarianzas. Para los momentos de cuarto orden (cuatro variables) hay tres términos. Para los momentos de sexto orden hay 3 × 5 = 15 términos, y para los momentos de octavo orden hay 3 × 5 × 7 = 105 términos.${\displaystyle {\tfrac {(2\lambda -1)!}{2^{\lambda -1}(\lambda -1)!}}}$

Las covarianzas se determinan entonces reemplazando los términos de la lista por los términos correspondientes de la lista que consiste en r ₁ unos, luego r ₂ dos, etc. Para ilustrar esto, examine el siguiente caso de momento central de cuarto orden:${\displaystyle [1,\ldots ,2\lambda ]}$

${\displaystyle {\begin{aligned}\operatorname {E} \left[X_{i}^{4}\right]&=3\sigma _{ii}^{2}\\[4pt]\operatorname {E} \left[X_{i}^{3}X_{j}\right]&=3\sigma _{ii}\sigma _{ij}\\[4pt]\operatorname {E} \left[X_{i}^{2}X_{j}^{2}\right]&=\sigma _{ii}\sigma _{jj}+2\sigma _{ij}^{2}\\[4pt]\operatorname {E} \left[X_{i}^{2}X_{j}X_{k}\right]&=\sigma _{ii}\sigma _{jk}+2\sigma _{ij}\sigma _{ik}\\[4pt]\operatorname {E} \left[X_{i}X_{j}X_{k}X_{n}\right]&=\sigma _{ij}\sigma _{kn}+\sigma _{ik}\sigma _{jn}+\sigma _{in}\sigma _{jk}.\end{aligned}}}$

donde es la covarianza de X _i y X _j . Con el método anterior, primero se encuentra el caso general para un k- ésimo momento con k variables X diferentes , , y luego se simplifica en consecuencia. Por ejemplo, para , se deja X _i = X _j y se usa el hecho de que .${\displaystyle \sigma _{ij}}$${\displaystyle E\left[X_{i}X_{j}X_{k}X_{n}\right]}$${\displaystyle \operatorname {E} [X_{i}^{2}X_{k}X_{n}]}$${\displaystyle \sigma _{ii}=\sigma _{i}^{2}}$

Una forma cuadrática de un vector normal , (donde es una matriz, es un vector y es un escalar), es una variable chi-cuadrado generalizada . ^[17] La ​​dirección de un vector normal sigue una distribución normal proyectada . ^[18]${\displaystyle {\boldsymbol {x}}}$${\displaystyle q({\boldsymbol {x}})={\boldsymbol {x}}'\mathbf {Q_{2}} {\boldsymbol {x}}+{\boldsymbol {q_{1}}}'{\boldsymbol {x}}+q_{0}}$${\displaystyle \mathbf {Q_{2}} }$${\displaystyle {\boldsymbol {q_{1}}}}$${\displaystyle q_{0}}$

Si es una función escalar general de un vector normal, su función de densidad de probabilidad , su función de distribución acumulativa y su función de distribución acumulativa inversa se pueden calcular con el método numérico de trazado de rayos (código Matlab). ^[17]${\displaystyle f({\boldsymbol {x}})}$

Si se conocen la media y la matriz de covarianza, la probabilidad logarítmica de un vector observado es simplemente el logaritmo de la función de densidad de probabilidad :${\displaystyle {\boldsymbol {x}}}$

${\displaystyle \ln L({\boldsymbol {x}})=-{\frac {1}{2}}\left[\ln(|{\boldsymbol {\Sigma }}|\,)+({\boldsymbol {x}}-{\boldsymbol {\mu }})'{\boldsymbol {\Sigma }}^{-1}({\boldsymbol {x}}-{\boldsymbol {\mu }})+k\ln(2\pi )\right]}$,

La versión circularmente simétrica del caso complejo no central, donde es un vector de números complejos, sería${\displaystyle {\boldsymbol {z}}}$

${\displaystyle \ln L({\boldsymbol {z}})=-\ln(|{\boldsymbol {\Sigma }}|\,)-({\boldsymbol {z}}-{\boldsymbol {\mu }})^{\dagger }{\boldsymbol {\Sigma }}^{-1}({\boldsymbol {z}}-{\boldsymbol {\mu }})-k\ln(\pi )}$

es decir, con la transpuesta conjugada (indicada por ) reemplazando a la transpuesta normal (indicada por ). Esto es ligeramente diferente que en el caso real, porque la versión circularmente simétrica de la distribución normal compleja tiene una forma ligeramente diferente para la constante de normalización .${\displaystyle \dagger }$${\displaystyle '}$

Se utiliza una notación similar para la regresión lineal múltiple . ^[19]

Dado que la verosimilitud logarítmica de un vector normal es una forma cuadrática del vector normal, se distribuye como una variable chi-cuadrado generalizada . ^[17]

La entropía diferencial de la distribución normal multivariada es ^[20]

${\displaystyle {\begin{aligned}h\left(f\right)&=-\int _{-\infty }^{\infty }\int _{-\infty }^{\infty }\cdots \int _{-\infty }^{\infty }f(\mathbf {x} )\ln f(\mathbf {x} )\,d\mathbf {x} \\&={\frac {1}{2}}\ln {}\left|2\pi e{\boldsymbol {\Sigma }}\right|={\frac {k}{2}}+{\frac {k}{2}}\ln {}2\pi +{\frac {1}{2}}\ln {}\left|{\boldsymbol {\Sigma }}\right|\\\end{aligned}}}$,

donde las barras denotan el determinante de la matriz , k es la dimensionalidad del espacio vectorial y el resultado tiene unidades de nats .

La divergencia de Kullback–Leibler de a , para matrices no singulares Σ ₁ y Σ ₀ , es: ^[21]${\displaystyle {\mathcal {N}}_{1}({\boldsymbol {\mu }}_{1},{\boldsymbol {\Sigma }}_{1})}$${\displaystyle {\mathcal {N}}_{0}({\boldsymbol {\mu }}_{0},{\boldsymbol {\Sigma }}_{0})}$

${\displaystyle D_{\text{KL}}({\mathcal {N}}_{0}\parallel {\mathcal {N}}_{1})={1 \over 2}\left\{\operatorname {tr} \left({\boldsymbol {\Sigma }}_{1}^{-1}{\boldsymbol {\Sigma }}_{0}\right)+\left({\boldsymbol {\mu }}_{1}-{\boldsymbol {\mu }}_{0}\right)^{\rm {T}}{\boldsymbol {\Sigma }}_{1}^{-1}({\boldsymbol {\mu }}_{1}-{\boldsymbol {\mu }}_{0})-k+\ln {|{\boldsymbol {\Sigma }}_{1}| \over |{\boldsymbol {\Sigma }}_{0}|}\right\},}$

donde denota el determinante de la matriz , es la traza , es el logaritmo natural y es la dimensión del espacio vectorial.${\displaystyle |\cdot |}$${\displaystyle tr(\cdot )}$${\displaystyle ln(\cdot )}$${\displaystyle k}$

El logaritmo debe tomarse en base e, ya que los dos términos que siguen al logaritmo son en sí mismos logaritmos en base e de expresiones que son factores de la función de densidad o surgen de manera natural. Por lo tanto, la ecuación da un resultado medido en nats . Dividiendo toda la expresión anterior por log _e  2 se obtiene la divergencia en bits .

Cuando ,${\displaystyle {\boldsymbol {\mu }}_{1}={\boldsymbol {\mu }}_{0}}$

${\displaystyle D_{\text{KL}}({\mathcal {N}}_{0}\parallel {\mathcal {N}}_{1})={1 \over 2}\left\{\operatorname {tr} \left({\boldsymbol {\Sigma }}_{1}^{-1}{\boldsymbol {\Sigma }}_{0}\right)-k+\ln {|{\boldsymbol {\Sigma }}_{1}| \over |{\boldsymbol {\Sigma }}_{0}|}\right\}.}$

La información mutua de una distribución es un caso especial de la divergencia de Kullback-Leibler en la que es la distribución multivariante completa y es el producto de las distribuciones marginales unidimensionales. En la notación de la sección de divergencia de Kullback-Leibler de este artículo, es una matriz diagonal con las entradas diagonales de , y . La fórmula resultante para la información mutua es:${\displaystyle P}$${\displaystyle Q}$${\displaystyle {\boldsymbol {\Sigma }}_{1}}$${\displaystyle {\boldsymbol {\Sigma }}_{0}}$${\displaystyle {\boldsymbol {\mu }}_{1}={\boldsymbol {\mu }}_{0}}$

${\displaystyle I({\boldsymbol {X}})=-{1 \over 2}\ln |{\boldsymbol {\rho }}_{0}|,}$

donde es la matriz de correlación construida a partir de . ^[22]${\displaystyle {\boldsymbol {\rho }}_{0}}$${\displaystyle {\boldsymbol {\Sigma }}_{0}}$

En el caso bivariado la expresión para la información mutua es:

${\displaystyle I(x;y)=-{1 \over 2}\ln(1-\rho ^{2}).}$

Si y se distribuyen normalmente y son independientes , esto implica que están "distribuidas normalmente de manera conjunta", es decir, el par debe tener una distribución normal multivariante. Sin embargo, un par de variables distribuidas normalmente de manera conjunta no necesita ser independiente (solo lo sería si no estuviera correlacionada, ).${\displaystyle X}$${\displaystyle Y}$${\displaystyle (X,Y)}$${\displaystyle \rho =0}$

El hecho de que dos variables aleatorias tengan una distribución normal no implica que el par tenga una distribución normal conjunta. Un ejemplo sencillo es aquel en el que X tiene una distribución normal con un valor esperado de 0 y una varianza de 1, y si y si , donde . Existen contraejemplos similares para más de dos variables aleatorias. En general, suman un modelo mixto . ^{[ cita requerida ]}${\displaystyle X}$${\displaystyle Y}$${\displaystyle (X,Y)}$${\displaystyle Y=X}$${\displaystyle |X|>c}$${\displaystyle Y=-X}$${\displaystyle |X|<c}$${\displaystyle c>0}$

En general, las variables aleatorias pueden no estar correlacionadas pero ser estadísticamente dependientes. Pero si un vector aleatorio tiene una distribución normal multivariante, entonces dos o más de sus componentes que no están correlacionados son independientes . Esto implica que dos o más de sus componentes que son independientes por pares son independientes. Pero, como se señaló anteriormente, no es cierto que dos variables aleatorias que están ( por separado , marginalmente) distribuidas normalmente y no correlacionadas sean independientes.

Si x N -dimensional se particiona de la siguiente manera

${\displaystyle \mathbf {x} ={\begin{bmatrix}\mathbf {x} _{1}\\\mathbf {x} _{2}\end{bmatrix}}{\text{ with sizes }}{\begin{bmatrix}q\times 1\\(N-q)\times 1\end{bmatrix}}}$

y en consecuencia μ y Σ se dividen de la siguiente manera

${\displaystyle {\boldsymbol {\mu }}={\begin{bmatrix}{\boldsymbol {\mu }}_{1}\\{\boldsymbol {\mu }}_{2}\end{bmatrix}}{\text{ with sizes }}{\begin{bmatrix}q\times 1\\(N-q)\times 1\end{bmatrix}}}$

${\displaystyle {\boldsymbol {\Sigma }}={\begin{bmatrix}{\boldsymbol {\Sigma }}_{11}&{\boldsymbol {\Sigma }}_{12}\\{\boldsymbol {\Sigma }}_{21}&{\boldsymbol {\Sigma }}_{22}\end{bmatrix}}{\text{ with sizes }}{\begin{bmatrix}q\times q&q\times (N-q)\\(N-q)\times q&(N-q)\times (N-q)\end{bmatrix}}}$

entonces la distribución de x ₁ condicional a x ₂ = a es normal multivariada ^[23] ( x ₁  |  x ₂ = a ) ~ N ( μ , Σ ) donde

${\displaystyle {\bar {\boldsymbol {\mu }}}={\boldsymbol {\mu }}_{1}+{\boldsymbol {\Sigma }}_{12}{\boldsymbol {\Sigma }}_{22}^{-1}\left(\mathbf {a} -{\boldsymbol {\mu }}_{2}\right)}$

y matriz de covarianza

${\displaystyle {\overline {\boldsymbol {\Sigma }}}={\boldsymbol {\Sigma }}_{11}-{\boldsymbol {\Sigma }}_{12}{\boldsymbol {\Sigma }}_{22}^{-1}{\boldsymbol {\Sigma }}_{21}.}$^[24]

Aquí está la inversa generalizada de . La matriz es el complemento de Schur de Σ ₂₂ en Σ . Es decir, la ecuación anterior es equivalente a invertir la matriz de covarianza general, eliminar las filas y columnas correspondientes a las variables que se condicionan y volver a invertir para obtener la matriz de covarianza condicional.${\displaystyle {\boldsymbol {\Sigma }}_{22}^{-1}}$${\displaystyle {\boldsymbol {\Sigma }}_{22}}$${\displaystyle {\overline {\boldsymbol {\Sigma }}}}$

Nótese que saber que x ₂ = a altera la varianza, aunque la nueva varianza no depende del valor específico de a ; quizás más sorprendente aún, la media se desplaza en ; compare esto con la situación de no conocer el valor de a , en cuyo caso x ₁ tendría una distribución .${\displaystyle {\boldsymbol {\Sigma }}_{12}{\boldsymbol {\Sigma }}_{22}^{-1}\left(\mathbf {a} -{\boldsymbol {\mu }}_{2}\right)}$${\displaystyle {\mathcal {N}}_{q}\left({\boldsymbol {\mu }}_{1},{\boldsymbol {\Sigma }}_{11}\right)}$

Un hecho interesante derivado para probar este resultado es que los vectores aleatorios y son independientes.${\displaystyle \mathbf {x} _{2}}$${\displaystyle \mathbf {y} _{1}=\mathbf {x} _{1}-{\boldsymbol {\Sigma }}_{12}{\boldsymbol {\Sigma }}_{22}^{-1}\mathbf {x} _{2}}$

La matriz Σ ₁₂ Σ ₂₂ ⁻¹ se conoce como la matriz de coeficientes de regresión .

En el caso bivariado donde x se divide en y , la distribución condicional de dado es ^[25]${\displaystyle X_{1}}$${\displaystyle X_{2}}$${\displaystyle X_{1}}$${\displaystyle X_{2}}$

${\displaystyle X_{1}\mid X_{2}=a\ \sim \ {\mathcal {N}}\left(\mu _{1}+{\frac {\sigma _{1}}{\sigma _{2}}}\rho (a-\mu _{2}),\,(1-\rho ^{2})\sigma _{1}^{2}\right)}$

¿Dónde está el coeficiente de correlación entre y ?${\displaystyle \rho }$${\displaystyle X_{1}}$${\displaystyle X_{2}}$

${\displaystyle {\begin{pmatrix}X_{1}\\X_{2}\end{pmatrix}}\sim {\mathcal {N}}\left({\begin{pmatrix}\mu _{1}\\\mu _{2}\end{pmatrix}},{\begin{pmatrix}\sigma _{1}^{2}&\rho \sigma _{1}\sigma _{2}\\\rho \sigma _{1}\sigma _{2}&\sigma _{2}^{2}\end{pmatrix}}\right)}$

La esperanza condicional de X ₁ dado X ₂ es:

${\displaystyle \operatorname {E} (X_{1}\mid X_{2}=x_{2})=\mu _{1}+\rho {\frac {\sigma _{1}}{\sigma _{2}}}(x_{2}-\mu _{2})}$

Demostración: el resultado se obtiene tomando la esperanza de la distribución condicional anterior.${\displaystyle X_{1}\mid X_{2}}$

${\displaystyle {\begin{pmatrix}X_{1}\\X_{2}\end{pmatrix}}\sim {\mathcal {N}}\left({\begin{pmatrix}0\\0\end{pmatrix}},{\begin{pmatrix}1&\rho \\\rho &1\end{pmatrix}}\right)}$

La esperanza condicional de X ₁ dado X ₂ es

${\displaystyle \operatorname {E} (X_{1}\mid X_{2}=x_{2})=\rho x_{2}}$

y la varianza condicional es

${\displaystyle \operatorname {var} (X_{1}\mid X_{2}=x_{2})=1-\rho ^{2};}$

Por lo tanto, la varianza condicional no depende de x ₂ .

La expectativa condicional de X ₁ dado que X ₂ es menor/mayor que z es: ^{[26] : 367}

${\displaystyle \operatorname {E} (X_{1}\mid X_{2}<z)=-\rho {\varphi (z) \over \Phi (z)},}$

${\displaystyle \operatorname {E} (X_{1}\mid X_{2}>z)=\rho {\varphi (z) \over (1-\Phi (z))},}$

donde la relación final aquí se llama relación de Mills inversa .

Demostración: los dos últimos resultados se obtienen utilizando el resultado , de modo que${\displaystyle \operatorname {E} (X_{1}\mid X_{2}=x_{2})=\rho x_{2}}$

${\displaystyle \operatorname {E} (X_{1}\mid X_{2}<z)=\rho E(X_{2}\mid X_{2}<z)}$y luego utilizando las propiedades de la expectativa de una distribución normal truncada .

Para obtener la distribución marginal sobre un subconjunto de variables aleatorias normales multivariadas, sólo es necesario eliminar las variables irrelevantes (las variables que se quieren marginar) del vector de medias y de la matriz de covarianza. La prueba de esto se desprende de las definiciones de distribuciones normales multivariadas y del álgebra lineal. ^[27]

Ejemplo

Sean X = [ X ₁ , X ₂ , X ₃ ] variables aleatorias normales multivariadas con vector medio μ = [ μ ₁ , μ ₂ , μ ₃ ] y matriz de covarianza Σ (parametrización estándar para distribuciones normales multivariadas). Entonces la distribución conjunta de X ′ = [ X ₁ , X ₃ ] es normal multivariada con vector medio μ ′ = [ μ ₁ , μ ₃ ] y matriz de covarianza .${\displaystyle {\boldsymbol {\Sigma }}'={\begin{bmatrix}{\boldsymbol {\Sigma }}_{11}&{\boldsymbol {\Sigma }}_{13}\\{\boldsymbol {\Sigma }}_{31}&{\boldsymbol {\Sigma }}_{33}\end{bmatrix}}}$

Si Y = c + BX es una transformación afín de donde c es un vector de constantes y B es una matriz constante , entonces Y tiene una distribución normal multivariada con valor esperado c + Bμ y varianza BΣB ^T es decir, . En particular, cualquier subconjunto de X _i tiene una distribución marginal que también es normal multivariada. Para ver esto, considere el siguiente ejemplo: para extraer el subconjunto ( X ₁ , X ₂ , X ₄ ) ^T , use${\displaystyle \mathbf {X} \ \sim {\mathcal {N}}({\boldsymbol {\mu }},{\boldsymbol {\Sigma }}),}$${\displaystyle M\times 1}$${\displaystyle M\times N}$${\displaystyle \mathbf {Y} \sim {\mathcal {N}}\left(\mathbf {c} +\mathbf {B} {\boldsymbol {\mu }},\mathbf {B} {\boldsymbol {\Sigma }}\mathbf {B} ^{\rm {T}}\right)}$

${\displaystyle \mathbf {B} ={\begin{bmatrix}1&0&0&0&0&\ldots &0\\0&1&0&0&0&\ldots &0\\0&0&0&1&0&\ldots &0\end{bmatrix}}}$

que extrae directamente los elementos deseados.

Otro corolario es que la distribución de Z = b · X , donde b es un vector constante con el mismo número de elementos que X y el punto indica el producto escalar , es gaussiana univariante con . Este resultado se deduce utilizando${\displaystyle Z\sim {\mathcal {N}}\left(\mathbf {b} \cdot {\boldsymbol {\mu }},\mathbf {b} ^{\rm {T}}{\boldsymbol {\Sigma }}\mathbf {b} \right)}$

${\displaystyle \mathbf {B} ={\begin{bmatrix}b_{1}&b_{2}&\ldots &b_{n}\end{bmatrix}}=\mathbf {b} ^{\rm {T}}.}$

Observe cómo la definición positiva de Σ implica que la varianza del producto escalar debe ser positiva.

Una transformación afín de X como 2 X no es lo mismo que la suma de dos realizaciones independientes de X.

Los contornos de equidensidad de una distribución normal multivariada no singular son elipsoides (es decir, transformaciones afines de hiperesferas ) centrados en la media. ^[28] Por lo tanto, la distribución normal multivariada es un ejemplo de la clase de distribuciones elípticas . Las direcciones de los ejes principales de los elipsoides están dadas por los vectores propios de la matriz de covarianza . Las longitudes relativas al cuadrado de los ejes principales están dadas por los valores propios correspondientes.${\displaystyle {\boldsymbol {\Sigma }}}$

Si Σ = UΛU ^T = UΛ ^1/2 ( UΛ ^1/2 ) ^T es una descomposición propia donde las columnas de U son vectores propios unitarios y Λ es una matriz diagonal de los valores propios, entonces tenemos

${\displaystyle \mathbf {X} \ \sim {\mathcal {N}}({\boldsymbol {\mu }},{\boldsymbol {\Sigma }})\iff \mathbf {X} \ \sim {\boldsymbol {\mu }}+\mathbf {U} {\boldsymbol {\Lambda }}^{1/2}{\mathcal {N}}(0,\mathbf {I} )\iff \mathbf {X} \ \sim {\boldsymbol {\mu }}+\mathbf {U} {\mathcal {N}}(0,{\boldsymbol {\Lambda }}).}$

Además, U puede elegirse como una matriz de rotación , ya que invertir un eje no tiene ningún efecto sobre N (0, Λ ), pero invertir una columna cambia el signo del determinante de U. La distribución N ( μ , Σ ) es en efecto N (0, I ) escalada por Λ ^1/2 , rotada por U y trasladada por μ .

Por el contrario, cualquier elección de μ , matriz de rango completo U y entradas diagonales positivas Λ _i produce una distribución normal multivariante no singular. Si cualquier Λ _i es cero y U es cuadrado, la matriz de covarianza resultante UΛU ^T es singular . Geométricamente, esto significa que cada elipsoide de contorno es infinitamente delgado y tiene volumen cero en el espacio n -dimensional, ya que al menos uno de los ejes principales tiene una longitud de cero; este es el caso degenerado .

"El radio alrededor de la media verdadera en una variable aleatoria normal bivariada, reescrita en coordenadas polares (radio y ángulo), sigue una distribución de Hoyt ". ^[29]

En una dimensión, la probabilidad de encontrar una muestra de la distribución normal en el intervalo es aproximadamente 68,27%, pero en dimensiones superiores la probabilidad de encontrar una muestra en la región de la elipse de desviación estándar es menor. ^[30]${\displaystyle \mu \pm \sigma }$

La derivación del estimador de máxima verosimilitud de la matriz de covarianza de una distribución normal multivariada es sencilla.

En resumen, la función de densidad de probabilidad (pdf) de una normal multivariada es

${\displaystyle f(\mathbf {x} )={\frac {1}{\sqrt {(2\pi )^{k}|{\boldsymbol {\Sigma }}|}}}\exp \left(-{1 \over 2}(\mathbf {x} -{\boldsymbol {\mu }})^{\rm {T}}{\boldsymbol {\Sigma }}^{-1}({\mathbf {x} }-{\boldsymbol {\mu }})\right)}$

y el estimador ML de la matriz de covarianza de una muestra de n observaciones es ^[31]

${\displaystyle {\widehat {\boldsymbol {\Sigma }}}={1 \over n}\sum _{i=1}^{n}({\mathbf {x} }_{i}-{\overline {\mathbf {x} }})({\mathbf {x} }_{i}-{\overline {\mathbf {x} }})^{\mathrm {T} }}$

que es simplemente la matriz de covarianza de la muestra . Este es un estimador sesgado cuya expectativa es

${\displaystyle E\left[{\widehat {\boldsymbol {\Sigma }}}\right]={\frac {n-1}{n}}{\boldsymbol {\Sigma }}.}$

Una covarianza de muestra imparcial es

${\displaystyle {\widehat {\boldsymbol {\Sigma }}}={\frac {1}{n-1}}\sum _{i=1}^{n}(\mathbf {x} _{i}-{\overline {\mathbf {x} }})(\mathbf {x} _{i}-{\overline {\mathbf {x} }})^{\rm {T}}={\frac {1}{n-1}}\left[X'\left(I-{\frac {1}{n}}\cdot J\right)X\right]}$ (forma matricial; es la matriz identidad, J es una matriz de unos; el término entre paréntesis es por tanto la matriz de centrado)${\displaystyle I}$${\displaystyle K\times K}$${\displaystyle K\times K}$${\displaystyle K\times K}$

La matriz de información de Fisher para estimar los parámetros de una distribución normal multivariante tiene una expresión en forma cerrada. Esta se puede utilizar, por ejemplo, para calcular el límite de Cramér-Rao para la estimación de parámetros en este contexto. Consulte la información de Fisher para obtener más detalles.

En estadística bayesiana , la distribución conjugada a priori del vector de media es otra distribución normal multivariante, y la distribución conjugada a priori de la matriz de covarianza es una distribución Wishart inversa . Supongamos entonces que se han realizado n observaciones.${\displaystyle {\mathcal {W}}^{-1}}$

${\displaystyle \mathbf {X} =\{\mathbf {x} _{1},\dots ,\mathbf {x} _{n}\}\sim {\mathcal {N}}({\boldsymbol {\mu }},{\boldsymbol {\Sigma }})}$

y que se ha asignado un conjugado anterior, donde

${\displaystyle p({\boldsymbol {\mu }},{\boldsymbol {\Sigma }})=p({\boldsymbol {\mu }}\mid {\boldsymbol {\Sigma }})\ p({\boldsymbol {\Sigma }}),}$

dónde

${\displaystyle p({\boldsymbol {\mu }}\mid {\boldsymbol {\Sigma }})\sim {\mathcal {N}}({\boldsymbol {\mu }}_{0},m^{-1}{\boldsymbol {\Sigma }}),}$

y

${\displaystyle p({\boldsymbol {\Sigma }})\sim {\mathcal {W}}^{-1}({\boldsymbol {\Psi }},n_{0}).}$

Entonces ^[31]

${\displaystyle {\begin{array}{rcl}p({\boldsymbol {\mu }}\mid {\boldsymbol {\Sigma }},\mathbf {X} )&\sim &{\mathcal {N}}\left({\frac {n{\bar {\mathbf {x} }}+m{\boldsymbol {\mu }}_{0}}{n+m}},{\frac {1}{n+m}}{\boldsymbol {\Sigma }}\right),\\p({\boldsymbol {\Sigma }}\mid \mathbf {X} )&\sim &{\mathcal {W}}^{-1}\left({\boldsymbol {\Psi }}+n\mathbf {S} +{\frac {nm}{n+m}}({\bar {\mathbf {x} }}-{\boldsymbol {\mu }}_{0})({\bar {\mathbf {x} }}-{\boldsymbol {\mu }}_{0})',n+n_{0}\right),\end{array}}}$

dónde

${\displaystyle {\begin{aligned}{\bar {\mathbf {x} }}&={\frac {1}{n}}\sum _{i=1}^{n}\mathbf {x} _{i},\\\mathbf {S} &={\frac {1}{n}}\sum _{i=1}^{n}(\mathbf {x} _{i}-{\bar {\mathbf {x} }})(\mathbf {x} _{i}-{\bar {\mathbf {x} }})'.\end{aligned}}}$

Las pruebas de normalidad multivariante comprueban la similitud de un conjunto de datos con la distribución normal multivariante . La hipótesis nula es que el conjunto de datos es similar a la distribución normal, por lo tanto, un valor p suficientemente pequeño indica datos no normales. Las pruebas de normalidad multivariante incluyen la prueba de Cox-Small ^[32] y la adaptación de Smith y Jain ^[33] de la prueba de Friedman-Rafsky creada por Larry Rafsky y Jerome Friedman . ^[34]

La prueba de Mardia ^[35] se basa en extensiones multivariadas de medidas de asimetría y curtosis . Para una muestra { x ₁ , ..., x _n } de vectores k -dimensionales calculamos

${\displaystyle {\begin{aligned}&{\widehat {\boldsymbol {\Sigma }}}={1 \over n}\sum _{j=1}^{n}\left(\mathbf {x} _{j}-{\bar {\mathbf {x} }}\right)\left(\mathbf {x} _{j}-{\bar {\mathbf {x} }}\right)^{\mathrm {T} }\\&A={1 \over 6n}\sum _{i=1}^{n}\sum _{j=1}^{n}\left[(\mathbf {x} _{i}-{\bar {\mathbf {x} }})^{\mathrm {T} }\;{\widehat {\boldsymbol {\Sigma }}}^{-1}(\mathbf {x} _{j}-{\bar {\mathbf {x} }})\right]^{3}\\&B={\sqrt {\frac {n}{8k(k+2)}}}\left\{{1 \over n}\sum _{i=1}^{n}\left[(\mathbf {x} _{i}-{\bar {\mathbf {x} }})^{\mathrm {T} }\;{\widehat {\boldsymbol {\Sigma }}}^{-1}(\mathbf {x} _{i}-{\bar {\mathbf {x} }})\right]^{2}-k(k+2)\right\}\end{aligned}}}$

Bajo la hipótesis nula de normalidad multivariada, el estadístico A tendrá aproximadamente una distribución de chi-cuadrado con ⁠1/6⁠ ⋅ k ( k + 1)( k + 2) grados de libertad, y B será aproximadamente la normal estándar N (0,1).

La estadística de curtosis de Mardia está sesgada y converge muy lentamente a la distribución normal límite. Para muestras de tamaño medio , se modifican los parámetros de la distribución asintótica de la estadística de curtosis ^[36] . Para pruebas de muestras pequeñas ( ) se utilizan valores críticos empíricos. Rencher ^[37] proporciona tablas de valores críticos para ambas estadísticas para k  = 2, 3, 4.${\displaystyle (50\leq n<400)}$${\displaystyle n<50}$

Las pruebas de Mardia son invariantes afines pero no consistentes. Por ejemplo, la prueba de asimetría multivariante no es consistente frente a alternativas no normales simétricas. ^[38]

La prueba BHEP ^[39] calcula la norma de la diferencia entre la función característica empírica y la función característica teórica de la distribución normal. El cálculo de la norma se realiza en el espacio L ² ( μ ) de funciones integrables al cuadrado con respecto a la función de ponderación gaussiana . La estadística de prueba es${\displaystyle \mu _{\beta }(\mathbf {t} )=(2\pi \beta ^{2})^{-k/2}e^{-|\mathbf {t} |^{2}/(2\beta ^{2})}}$