Antena dipolo

En radio y telecomunicaciones, una antena dipolo o doblete ^{[1] es uno de los dos} tipos de antena más simples y más utilizados ; el otro es el monopolo . ^{[2] [3] [ cita completa requerida ]} El dipolo es cualquiera de una clase de antenas que producen un patrón de radiación que se aproxima al de un dipolo eléctrico elemental con una estructura radiante que soporta una corriente de línea tan energizada que la corriente tiene solo un nodo en cada extremo lejano. ^[a] Una antena dipolo comúnmente consta de dos elementos conductores idénticos ^[5] como alambres o varillas de metal. ^{[2] [6] [7] (p 3)} La corriente de conducción del transmisor se aplica, o para antenas receptoras se toma la señal de salida al receptor , entre las dos mitades de la antena. Cada lado de la línea de alimentación al transmisor o receptor está conectado a uno de los conductores. Esto contrasta con una antena monopolo , que consta de una sola varilla o conductor con un lado de la línea de alimentación conectado a él y el otro lado conectado a algún tipo de tierra. ^[7] Un ejemplo común de dipolo es la antena de televisión en forma de orejas de conejo que se encuentra en los televisores de transmisión. Todos los dipolos son eléctricamente equivalentes a dos monopolos montados uno al lado del otro y alimentados con fases opuestas, con el plano de tierra entre ellos hecho virtual por el monopolo opuesto.

El dipolo es el tipo de antena más simple desde un punto de vista teórico. ^[1] Lo más común es que conste de dos conductores de igual longitud orientados de extremo a extremo con la línea de alimentación conectada entre ellos. ^{[8] [9]} Los dipolos se utilizan con frecuencia como antenas resonantes . Si el punto de alimentación de una antena de este tipo está en cortocircuito, podrá resonar a una frecuencia particular, como una cuerda de guitarra que se pulsa. El uso de la antena en torno a esa frecuencia es ventajoso en términos de impedancia del punto de alimentación (y, por lo tanto, relación de onda estacionaria ), por lo que su longitud está determinada por la longitud de onda (o frecuencia) prevista de funcionamiento. ^[2] El más utilizado es el dipolo de media onda alimentado por el centro, que tiene una longitud de poco menos de media longitud de onda. El patrón de radiación del dipolo de media onda es máximo perpendicular al conductor, cayendo a cero en la dirección axial, implementando así una antena omnidireccional si se instala verticalmente, o (más comúnmente) una antena débilmente direccional si se instala horizontalmente. ^[10]

Aunque pueden utilizarse como antenas independientes de baja ganancia , los dipolos también se emplean como elementos excitados en diseños de antenas más complejos ^{[2] [5]} como la antena Yagi y los conjuntos excitados . Las antenas dipolo (o diseños derivados de ellas, incluido el monopolo) se utilizan para alimentar antenas direccionales más elaboradas, como una antena de bocina , un reflector parabólico o un reflector de esquina . Los ingenieros analizan las antenas verticales (u otras antenas monopolares ) basándose en las antenas dipolo de las que son la mitad.

El físico alemán Heinrich Hertz demostró por primera vez la existencia de ondas de radio en 1887 utilizando lo que ahora conocemos como una antena dipolo (con carga final capacitiva). Por otro lado, Guglielmo Marconi descubrió empíricamente que podía simplemente conectar a tierra el transmisor (o un lado de una línea de transmisión, si se usaba) prescindiendo de la mitad de la antena, logrando así la antena vertical o monopolar . ^{[7] (p. 3)} Para las frecuencias bajas que Marconi empleó para lograr comunicaciones de larga distancia, esta forma era más práctica; cuando la radio pasó a frecuencias más altas (especialmente transmisiones VHF para radio FM y TV) fue ventajoso que estas antenas mucho más pequeñas estuvieran completamente sobre una torre, por lo que se requirió una antena dipolo o una de sus variaciones.

En los primeros tiempos de la radio, la denominada antena Marconi (monopolo) y el doblete (dipolo) se consideraban inventos distintos. Sin embargo, hoy en día, la antena monopolar se entiende como un caso especial de dipolo que tiene un elemento virtual bajo tierra.

Un dipolo corto es un dipolo formado por dos conductores con una longitud total ℓ sustancialmente menor que la mitad de la longitud de onda ( ⁠1/ 2 ⁠ λ ). Los dipolos cortos se utilizan a veces en aplicaciones en las que un dipolo de media onda completo sería demasiado grande. Se pueden analizar fácilmente utilizando los resultados obtenidos a continuación para el dipolo hertziano, una entidad ficticia. Al ser más corto que una antena resonante (media longitud de onda de longitud), su impedancia de punto de alimentación incluye una reactancia capacitiva grande que requiere una bobina de carga u otra red de adaptación para ser práctico, especialmente como antena de transmisión.

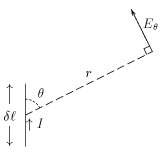
Para encontrar los campos eléctricos y magnéticos de campo lejano generados por un dipolo corto, utilizamos el resultado que se muestra a continuación para el dipolo hertziano (un elemento de corriente infinitesimal) a una distancia r de la corriente y en un ángulo θ con respecto a la dirección de la corriente, como siendo: ^{[11] (p132)}

${\displaystyle {\begin{aligned}H_{\phi }&=j\ {\frac {\ I_{h}\ \ell \ k\ }{4\pi \ r}}\ e^{\ j\ \left(\omega t\ -\ kr\right)}\ \sin(\theta )\\E_{\theta }&=\zeta _{0}\ H_{\phi }=j\ {\frac {\ \zeta _{0}\ I_{h}\ \ell \ k\ }{4\pi \ r}}\ e^{\ j\ \left(\omega t\ -\ kr\right)}\ \sin(\theta )~.\end{aligned}}}$

donde el radiador consiste en una corriente de una longitud corta ℓ y en electrónica reemplaza el símbolo matemático habitual i para la raíz cuadrada de −1 . ω es la frecuencia en radianes ( ) y k es el número de onda ( ). ζ ₀ es la impedancia del espacio libre ( ), que es la relación entre la intensidad del campo eléctrico y magnético de una onda plana del espacio libre.${\displaystyle \ I_{h}\ e^{\ j\ \omega \ t}\ }$${\displaystyle \ j^{2}\equiv -1\ }$${\displaystyle \omega \equiv 2\pi f\ }$${\displaystyle \ k\equiv 2\pi /\lambda \ }$${\displaystyle \zeta _{0}\approx 377{\text{ Ω}}}$

El punto de alimentación suele estar en el centro del dipolo, como se muestra en el diagrama. La corriente a lo largo de los brazos del dipolo se describe aproximadamente como proporcional a donde z es la distancia hasta el extremo del brazo. En el caso de un dipolo corto, se trata esencialmente de una caída lineal desde el punto de alimentación hasta cero en el extremo. Por lo tanto, esto es comparable a un dipolo hertziano con una corriente efectiva I _h igual a la corriente promedio sobre el conductor, por lo que con esa sustitución, las ecuaciones anteriores se aproximan estrechamente a los campos generados por un dipolo corto alimentado por corriente${\displaystyle \ \sin(\ k\ z\ )\ }$${\displaystyle \ I_{0}\ }$${\textstyle \ I_{h}={\frac {1}{2}}I_{0}\ .}$${\displaystyle \ I_{0}~.}$

A partir de los campos calculados anteriormente, se puede encontrar el flujo radiado (potencia por unidad de área) en cualquier punto como la magnitud de la parte real del vector de Poynting , S , que se da por Con E y H en ángulos rectos y en fase, no hay parte imaginaria y es simplemente igual a con los factores de fase (los exponenciales) cancelándose dejando:${\textstyle \ {\frac {1}{2}}\mathbf {E} \times \mathbf {H} ^{*}~.}$${\textstyle \ {\frac {1}{2}}E_{\theta }H_{\phi }^{*}\ }$

${\displaystyle S={\frac {1}{2}}E_{\theta }H_{\phi }^{*}={\frac {1}{2}}\ {\frac {\ \zeta _{0}\ I_{h}^{2}\ \ell ^{2}\ k^{2}\ }{(4\pi r)^{2}}}\ \sin ^{2}(\theta )={\frac {\zeta _{0}}{32}}\ I_{0}^{2}\ \left({\frac {\ell }{\lambda }}\right)^{2}\ {\frac {1}{r^{2}}}\ \sin ^{2}(\theta )~.}$

Ahora hemos expresado el flujo en términos de la corriente del punto de alimentación I ₀ y la relación entre la longitud del dipolo corto ℓ y la longitud de onda de la radiación λ . El patrón de radiación dado por se ve similar y solo ligeramente menos direccional que el del dipolo de media onda.${\displaystyle \ \sin ^{2}(\theta )\ }$

Utilizando la expresión anterior para la radiación en el campo lejano para una corriente de punto de alimentación dada, podemos integrar sobre todos los ángulos sólidos para obtener la potencia radiada total.

${\displaystyle P_{\text{total}}={\frac {\pi }{12}}\ \zeta _{0}\ I_{0}^{2}\ \left({\frac {\ell }{\lambda }}\right)^{2}~.}$

De ahí, es posible inferir la resistencia de radiación , igual a la parte resistiva (real) de la impedancia del punto de alimentación, despreciando un componente debido a las pérdidas óhmicas. Al establecer P _total como la potencia suministrada en el punto de alimentación, obtenemos:${\textstyle \ {\tfrac {1}{2}}\ I_{0}^{2}\ R_{\text{radiation}}\ }$

${\displaystyle \ R_{\text{radiation}}={\frac {\pi }{6}}\ \zeta _{0}\ \left({\frac {\ell }{\lambda }}\right)^{2}\approx \left({\frac {\ell }{\lambda }}\right)^{2}(197\ \Omega )~.}$

Nuevamente, estas aproximaciones se vuelven bastante precisas para ℓ ≪ ⁠ 1/ 2 ⁠ λ . Ajuste ℓ = ⁠ 1/ 2 ⁠ λ a pesar de que su uso no es del todo válido para una fracción tan grande de la longitud de onda, la fórmula predeciría una resistencia de radiación de 49 Ω, en lugar del valor real de 73 Ω producido por un dipolo de media onda cuando se utilizan corrientes sinusoidales de cuarto de onda más correctas.

La resonancia fundamental de un conductor lineal delgado ocurre a una frecuencia cuya longitud de onda en el espacio libre es el doble de la longitud del cable; es decir, donde el conductor está 1 /2⁠ longitud de onda larga. Las antenas dipolo se utilizan con frecuencia en torno a esa frecuencia y, por lo tanto, se denominan antenas dipolo de media onda . Este importante caso se trata en la siguiente sección.

Los conductores lineales delgados de longitud son de hecho resonantes en cualquier múltiplo entero de media longitud de onda:${\displaystyle \ \ell \ }$

${\displaystyle \ \ell =n\times {\frac {\ \lambda \ }{2}}\ }$

donde n es un número entero, es la longitud de onda y c es la velocidad reducida de las ondas de radio en el conductor radiante ( c ≈ 97%× c _o , la velocidad de la luz ). Sin embargo, para un dipolo alimentado centralmente, existe una gran disimilitud entre que n sea impar o par. Los dipolos que tienen una longitud de un número impar de medias longitudes de onda tienen impedancias de punto de excitación razonablemente bajas (que son puramente resistivas a esa frecuencia de resonancia). Sin embargo, los que tienen una longitud de un número par de medias longitudes de onda, es decir, un número entero de longitudes de onda, tienen una impedancia de punto de excitación alta (aunque puramente resistiva a esa frecuencia de resonancia).${\displaystyle \ \lambda ={\frac {\ c\ }{f}}\ }$

Por ejemplo, una antena dipolo de onda completa se puede fabricar con dos conductores de media longitud de onda colocados de extremo a extremo para una longitud total de aproximadamente Esto da como resultado una ganancia adicional sobre un dipolo de media onda de aproximadamente 2 dB. Los dipolos de onda completa se pueden utilizar en la radiodifusión de onda corta solo haciendo que el diámetro efectivo sea muy grande y alimentando desde una línea balanceada de alta impedancia. Los dipolos de jaula se utilizan a menudo para obtener el gran diámetro.${\displaystyle \ \ell \approx \lambda \ .}$

A ⁠ 5 /4La antena dipolo de media onda tiene una impedancia de punto de alimentación mucho menor, pero no puramente resistiva, lo que requiere una red adaptada a la impedancia de la línea de transmisión. Su ganancia es aproximadamente 3 dB mayor que la de un dipolo de media onda, la ganancia más alta de cualquier dipolo de longitud similar.

Ganancia de antenas dipolo ^[11]

Longitud, en longitudes de onda ${\displaystyle \ \ell \ }$	Ganancia directiva (dBi)	Notas
≪ 0,5	1,76	Pobre eficiencia
0,5	2.15	Más común
1.0	4.0	Sólo con dipolos de grasa
1.25	5.2	Mayor ganancia
1.5	3.5	Tercer armónico
2.0	4.3	No utilizado

Otras longitudes razonables de dipolo no ofrecen ventajas y rara vez se utilizan. Sin embargo, a veces se aprovechan las resonancias de sobretonos de una antena dipolo de media onda en múltiplos impares de su frecuencia fundamental. Por ejemplo, las antenas de radioaficionado diseñadas como dipolos de media onda a 7 MHz también se pueden utilizar como ⁠ 3 /2-dipolos de ondas métricas a 21 MHz; de igual modo, las antenas de televisión VHF resonantes en la banda baja de televisión VHF (centrada alrededor de 65 MHz) también son resonantes en la banda alta de televisión VHF (alrededor de 195 MHz).

Una antena dipolo de media onda consta de dos conductores de un cuarto de longitud de onda colocados de extremo a extremo para una longitud total de aproximadamente ℓ = ⁠1/2⁠ λ .La distribución de corriente es la de unaonda estacionaria, aproximadamente sinusoidal a lo largo del dipolo, con un nodo en cada extremo y un antinodo (corriente pico) en el centro (punto de alimentación):^{[12] (pp 98–99)}

${\displaystyle I(z)=I_{0}\cos(\omega t)\cos(kz)\ ,}$

donde k = ⁠ 2π​/la⁠ yzva desde ⁠−+1/2⁠ ℓ a ⁠++1/2⁠ ℓ .

En el campo lejano, esto produce un patrón de radiación cuyo campo eléctrico está dado por ^{[12] (pp 98-99).}

${\displaystyle \ E_{\theta }={\frac {\ \zeta _{0}I_{0}\ }{2\pi r}}\ {\frac {\ \cos \left({\frac {\pi }{2}}\ \cos \theta \right)\ }{\sin \theta }}\ \sin {(\omega t-kr)}~.}$

El factor direccional es casi el mismo que sen  θ aplicado al dipolo corto, lo que da como resultado un patrón de radiación muy similar al señalado anteriormente. ^{[12] (pp 98–99)}${\textstyle \ {\frac {\cos \left[\ {\tfrac {\pi }{2}}\ \cos \theta \ \right]}{\sin \theta }}\ }$

Una integración numérica de la potencia radiada sobre todo el ángulo sólido, como hicimos para el dipolo corto, obtiene un valor para la potencia total P _total radiada por el dipolo con una corriente que tiene un valor pico de I ₀ como en la forma especificada anteriormente. Dividiendo P _total por proporciona el flujo a una gran distancia, promediado en todas las direcciones. Dividiendo el flujo en la dirección θ = 0 (donde está en su pico) a esa gran distancia por el flujo promedio, encontramos que la ganancia directiva es 1,64. Esto también se puede calcular directamente utilizando la integral del coseno :${\textstyle \ {\frac {\ |E_{\theta }|^{2}\ }{2\zeta _{0}}}\ }$${\textstyle 4\pi r^{2}}$

${\displaystyle G={\frac {4}{\ \operatorname {Cin} (2\pi )\ }}\approx 1.64~}$(2,15 dBi)

(  La forma Cin( x ) de la integral del coseno no es la misma que la forma Ci( x ) ; se diferencian en un logaritmo. Tanto MATLAB como Mathematica tienen funciones integradas que calculan Ci( x ) , pero no Cin( x ) . Consulte la página de Wikipedia sobre la integral del coseno para conocer la relación entre estas funciones  ) .

Ahora también podemos encontrar la resistencia a la radiación como lo hicimos para el dipolo corto resolviendo:

${\displaystyle P_{\mathsf {total}}={\frac {1}{2}}I_{0}^{2}R_{\mathsf {radiation}}\ }$

Para obtener:

${\displaystyle R_{\mathsf {radiation}}\approx 73.1\ {\mathsf {\Omega }}~.}$

Utilizando el método EMF inducido, ^{[11] (p 224)} la parte real de la impedancia del punto de excitación también se puede escribir en términos de la integral del coseno, obteniendo el mismo resultado:

${\displaystyle R_{\mathsf {radiation}}={\frac {\zeta _{0}}{\ 4\pi \ }}\operatorname {Cin} (2\pi )={\frac {\zeta _{0}}{\ 4\pi \ }}\int _{0}^{2\pi }{\frac {\ 1-\cos \theta \ }{\theta }}\ \mathrm {d} \theta \ \approx \ 73.1\ {\mathsf {\Omega }}~.}$

Si un dipolo de media onda se activa en un punto distinto del centro, la resistencia del punto de alimentación será mayor. La resistencia de radiación se expresa normalmente en relación con la corriente máxima presente a lo largo de un elemento de antena, que para el dipolo de media onda (y la mayoría de las demás antenas) es también la corriente en el punto de alimentación. Sin embargo, si el dipolo se alimenta en un punto diferente a una distancia x de un máximo de corriente (el centro en el caso de un dipolo de media onda), entonces la corriente allí no es I ₀ sino solo I ₀ cos( kx ) .

Para suministrar la misma potencia, el voltaje en el punto de alimentación debe aumentarse de manera similar por el factor sec( kx ) . En consecuencia, la parte resistiva de la impedancia del punto de alimentación aumenta ^{[11] (pág. 227)} por el factor sec ² ( k x )  : ${\displaystyle \ \operatorname {\mathcal {R_{e}}} \left[{\tfrac {V}{\ I\ }}\right]\ }$

${\displaystyle \ R_{\mathsf {feedpoint}}={\frac {\ R_{\mathsf {radiation}}\ }{\cos ^{2}(kx)}}\approx {\frac {73.1\ {\mathsf {\Omega }}}{\ \cos ^{2}(kx)\ }}\ }$

Esta ecuación también se puede utilizar para antenas dipolares de cualquier longitud, siempre que _{la radiación} R se haya calculado en relación con el máximo de corriente, que generalmente no es el mismo que la corriente del punto de alimentación para dipolos de más de media onda. Nótese que esta ecuación falla cuando se alimenta una antena cerca de un nodo de corriente, donde cos( kx ) se acerca a cero. La impedancia del punto de excitación aumenta de hecho en gran medida, pero sin embargo está limitada debido a los componentes de orden superior de la corriente no exactamente sinusoidal de los elementos, que se han ignorado anteriormente en el modelo para la distribución de corriente. ^{[11] (p. 228)}

This section needs additional citations for verification. Please help improve this article by adding citations to reliable sources in this section. Unsourced material may be challenged and removed. Find sources: "Dipole antenna" – news · newspapers · books · scholar · JSTOR (March 2018) (Learn how and when to remove this message)

Un dipolo plegado es un dipolo de media onda con un cable paralelo adicional que conecta sus dos extremos. Si el cable adicional tiene el mismo diámetro y sección transversal que el dipolo, se generan dos corrientes de radiación casi idénticas. El patrón de emisión de campo lejano resultante es casi idéntico al del dipolo de un solo cable descrito anteriormente, pero en resonancia su impedancia en el punto de alimentación es cuatro veces la resistencia de radiación de un dipolo de un solo cable.${\displaystyle \ R_{\mathsf {f.d.}}\ }$

Un dipolo plegado es, técnicamente, una antena de bucle de onda completa plegada , donde el bucle se ha doblado en extremos opuestos y se ha aplastado en dos cables paralelos en una línea plana. Aunque el ancho de banda amplio, la alta impedancia del punto de alimentación y la alta eficiencia son características más similares a una antena de bucle completo, el patrón de radiación del dipolo plegado es más parecido a un dipolo común. Dado que el funcionamiento de un solo dipolo de media onda es más fácil de entender, tanto los bucles completos como los dipolos plegados se describen a menudo como dos dipolos de media onda en paralelo, conectados en los extremos.

La alta impedancia del punto de alimentación en resonancia se debe a que, para una cantidad fija de potencia, la corriente radiante total es igual al doble de la corriente en cada cable por separado y, por lo tanto, igual al doble de la corriente en el punto de alimentación. Igualamos la potencia radiada promedio con la potencia promedio entregada en el punto de alimentación, podemos escribir${\displaystyle \ R_{\mathsf {f.d.}}\ }$${\displaystyle \ I_{0}\ }$

${\displaystyle \ {\frac {\ 1\ }{2}}\ R_{\mathsf {h.w.}}\ I_{0}^{2}={\frac {1}{2}}\ R_{\mathsf {f.d.}}\ \left({\frac {\ 1\ }{2}}\ I_{0}\right)^{2}\ ,}$

donde es la impedancia del punto de alimentación inferior del dipolo de media onda resonante. De ello se deduce que${\displaystyle \ R_{\mathsf {h.w.}}\ }$

${\displaystyle \ R_{\mathsf {f.d.}}=4R_{\mathsf {h.w.}}\approx 292\ {\mathsf {\Omega }}~.}$

Los dipolos plegados de media onda se utilizan a menudo para antenas de radio FM ; las versiones fabricadas con dos conductores que se pueden colgar en una pared interior suelen venir con sintonizadores de FM. También se utilizan ampliamente como elementos accionados para antenas de televisión Yagi en tejados . La antena T²FD es un dipolo plegado con una resistencia añadida en el segundo conductor, opuesto al punto de alimentación.

Por lo tanto, el dipolo plegado se adapta bien a las líneas de transmisión balanceadas de 300  Ω , como los cables planos de doble alimentación. El dipolo plegado tiene un ancho de banda mayor que un dipolo simple. Se pueden utilizar para transformar el valor de la impedancia de entrada del dipolo en un amplio rango de relaciones de aumento modificando el espesor de los conductores de cable para los lados plegado y alimentado. ^[13]

En lugar de alterar el grosor o el espaciado, se puede agregar un tercer cable paralelo para aumentar la impedancia de la antena a 9 veces la de un dipolo de un solo cable, lo que aumenta la impedancia a 658 Ω, lo que hace que sea una buena opción para el cable de alimentación de cable abierto y amplía aún más la banda de frecuencia resonante de la antena. Se pueden agregar más cables paralelos adicionales: se puede unir cualquier cantidad de cables paralelos adicionales a la antena, con la resistencia de radiación (y la impedancia del punto de alimentación) dada por

${\displaystyle \ R_{\mathsf {rad}}\approx n^{2}\ \times \ 73{\mathsf {\ \Omega \ ,}}}$

donde es el número de cables paralelos de media onda de longitud colocados uno al lado del otro en la antena y conectados en sus extremos. También es posible modificar el llamado diseño de bucle aplanado y obtener un rendimiento casi tan bueno, haciendo que cada cable paralelo sea demasiado corto en la misma cantidad, pero conectando un solo cable de carga capacitiva (que sale en casi cualquier dirección, la mayoría de las veces colgando) en cada uno de los extremos de la antena. La longitud del cable de carga es igual a la longitud única faltante de uno de los cables paralelos.${\displaystyle \ n\ }$

Existen numerosas modificaciones en la forma de una antena dipolo que son útiles de una manera u otra, pero que dan como resultado características de radiación similares (ganancia baja). Esto sin mencionar las numerosas antenas direccionales que incluyen uno o más elementos dipolo en su diseño como elementos accionados , muchas de las cuales están vinculadas en el cuadro de información al final de esta página.

• La antena de pajarita es un dipolo con brazos triangulares ensanchados. Su forma le otorga un ancho de banda mucho mayor que el de un dipolo común. Se utiliza ampliamente en antenas de televisión UHF .

• El dipolo de jaula es una modificación similar en la que se aumenta el ancho de banda mediante el uso de elementos dipolares cilíndricos gruesos hechos de una jaula de cables (ver foto). Estos se utilizan en algunas antenas de banda ancha en las bandas de onda media y onda corta para aplicaciones como radares y radiotelescopios sobre el horizonte .
• Una antena de halo es un dipolo de media onda doblado en forma de círculo para generar un patrón de radiación casi uniforme en el plano del círculo. Cuando el círculo del halo es horizontal, produce radiación polarizada horizontalmente en un patrón casi omnidireccional con solo un poco de energía desperdiciada hacia el cenit, en comparación con un dipolo horizontal recto. En la práctica, se clasifica como un dipolo doblado o como una antena de bucle, según la preferencia del autor. ^[b]
• Una antena de torniquete consta de dos dipolos cruzados en ángulo recto y un sistema de alimentación que introduce una diferencia de fase de un cuarto de onda entre las corrientes a lo largo de los dos. Con esa geometría, los dos dipolos no interactúan eléctricamente, pero sus campos se suman en el campo lejano produciendo un patrón de radiación neta que es bastante cercano a isótropo , con polarización horizontal en el plano de los elementos y polarización circular o elíptica en otros ángulos. Las antenas de torniquete se pueden apilar y alimentar en fase para realizar una matriz de banda ancha omnidireccional o en fase para una matriz de disparo final con polarización circular.
• La antena de ala de murciélago es una antena de torniquete con sus elementos lineales ensanchados como una antena de pajarita, nuevamente con el propósito de ampliar su frecuencia de resonancia y, por lo tanto, utilizarla en un ancho de banda mayor, sin resintonización. Cuando se apilan para formar una matriz, la radiación es omnidireccional, polarizada horizontalmente y con mayor ganancia a bajas elevaciones, lo que la hace ideal para la transmisión de televisión.
• Una antena V es un dipolo con una curva en el medio, por lo que sus brazos forman un ángulo en lugar de ser colineales.
• Una antena cuadrante es una antena en "V" con una longitud total inusual de una longitud de onda completa , con dos elementos horizontales de media onda que se encuentran en un ángulo recto donde se alimenta. ^[14] Las antenas cuadrantes producen principalmente polarización horizontal en ángulos de elevación bajos a intermedios y tienen patrones de radiación casi omnidireccionales . ^[15]

Una implementación utiliza elementos de jaula (ver arriba); el espesor de los elementos resultantes reduce la impedancia del punto de excitación alto de un dipolo de onda completa a un valor que permite una adaptación razonable a líneas de cable abiertas y aumenta el ancho de banda (en términos de ROE) a una octava completa. Se utilizan para transmisiones de banda de alta frecuencia .

• La antena G5RV es una antena dipolo alimentada indirectamente, a través de un cable doble de 300 Ω o 450 Ω de longitud cuidadosamente elegida , que actúa como una red de adaptación de impedancia para conectarse (a través de un balun ) a una línea de transmisión coaxial estándar de 50 Ω.
• La antena inclinada es una antena dipolar vertical inclinada que se fija a la parte superior de una sola torre. El elemento puede estar alimentado por el centro o por el extremo como una antena monopolar desequilibrada desde una línea de transmisión en la parte superior de la torre, en cuyo caso la conexión a tierra del monopolar puede considerarse mejor como un segundo elemento que comprende la torre o el blindaje de la línea de transmisión.
• La antena en "V" invertida también se apoya sobre una única torre, pero es una antena balanceada con dos elementos simétricos en ángulo hacia el suelo. Por lo tanto, es un dipolo de media onda con una curva en el medio. Al igual que la antena inclinada , tiene la ventaja práctica de elevar la antena, pero requiere solo una única torre.
• La antena AS-2259 es una antena dipolo en forma de "V" invertida que se utiliza para comunicaciones locales a través de ondas ionosféricas de incidencia casi vertical (NVIS).

La antena vertical , Marconi o monopolo es una antena de un solo elemento que normalmente se alimenta por la parte inferior (con el lado blindado de su línea de transmisión desequilibrada conectado a tierra). Se comporta esencialmente igual que la mitad de una antena dipolo. La tierra (o plano de tierra ) se considera una superficie conductora que funciona como reflector (véase efecto de tierra ). Las corrientes verticales en la imagen reflejada tienen la misma dirección (por lo tanto, no se reflejan sobre el suelo) y fase que la corriente en la antena real. ^{[7] (p. 164)} El conductor y su imagen juntos actúan como un dipolo en la mitad superior del espacio. Al igual que un dipolo, para lograr resonancia (impedancia resistiva del punto de alimentación), el conductor debe tener una altura cercana a un cuarto de longitud de onda (como cada conductor en un dipolo de media onda).

En este lado superior del espacio, el campo emitido tiene la misma amplitud del campo radiado por un dipolo similar alimentado con la misma corriente. Por lo tanto, la potencia emitida total es la mitad de la potencia emitida de un dipolo alimentado con la misma corriente. Como la corriente es la misma, la resistencia de radiación (parte real de la impedancia en serie) será la mitad de la impedancia en serie del dipolo comparable. Un monopolo de cuarto de onda, entonces, tiene una impedancia ^{[7] (p. 173)} de Otra forma de ver esto, es que un dipolo verdadero que recibe una corriente I tiene voltajes en sus terminales de +V y −V , para una impedancia a través de los terminales de ⁠2${\textstyle \ {\frac {\ 73\ +\ j\ 43\ }{2}}=36\ +\ j\ 21\ {\mathsf {\Omega }}~.}$+V/ I ⁠ , mientras que la antena vertical comparable tiene la corriente I pero un voltaje aplicado de solo V .

Dado que los campos sobre el suelo son los mismos que para el dipolo, pero solo se aplica la mitad de la potencia, la ganancia se duplica a 5,14 dBi. Esto no es una ventaja de rendimiento real per se , ya que en la práctica un dipolo también refleja la mitad de su potencia desde el suelo, lo que (dependiendo de la altura de la antena y el ángulo del cielo) puede aumentar (o cancelar) la señal directa. La polarización vertical del monopolo (como para un dipolo orientado verticalmente) es ventajosa en ángulos de elevación bajos donde la reflexión del suelo se combina con la onda directa aproximadamente en fase.

La tierra actúa como un plano de tierra, pero puede ser un mal conductor que produzca pérdidas. Su conductividad se puede mejorar (a un coste) colocando una malla de cobre. Cuando no se dispone de una tierra real (como en un vehículo), otras superficies metálicas pueden servir como plano de tierra (normalmente el techo del vehículo). Alternativamente, los cables radiales colocados en la base de la antena pueden formar un plano de tierra. Para las bandas VHF y UHF, los elementos de plano de tierra y radiante se pueden construir a partir de varillas o tubos rígidos. El uso de un plano de tierra artificial de este tipo permite montar toda la antena y la tierra a una altura arbitraria. Una modificación habitual es la de inclinar hacia abajo los radiales que forman el plano de tierra, lo que tiene el efecto de aumentar la impedancia del punto de alimentación a unos 50 Ω, lo que coincide con el cable coaxial común. Al dejar de ser una verdadera tierra, se recomienda un balun (como un simple balun de estrangulamiento).

La impedancia del punto de alimentación de una antena dipolo es sensible a su longitud eléctrica y a la posición del punto de alimentación. ^{[8] [9]} Por lo tanto, un dipolo generalmente solo funcionará de manera óptima en un ancho de banda bastante estrecho, más allá del cual su impedancia se convertirá en una mala adaptación para el transmisor o receptor (y la línea de transmisión). Los componentes reales (resistivos) e imaginarios (reactivos) de esa impedancia, en función de la longitud eléctrica, se muestran en el gráfico adjunto. El cálculo detallado de estos números se describe a continuación. Tenga en cuenta que el valor de la reactancia depende en gran medida del diámetro de los conductores; este gráfico es para conductores con un diámetro de 0,001 longitudes de onda.

Los dipolos que son mucho más pequeños que la mitad de la longitud de onda de la señal se denominan dipolos cortos . Tienen una resistencia a la radiación muy baja (y una reactancia capacitiva alta ), lo que los convierte en antenas ineficientes. Una mayor parte de la corriente de un transmisor se disipa en forma de calor debido a la resistencia finita de los conductores, que es mayor que la resistencia a la radiación. Sin embargo, pueden ser antenas receptoras prácticas para longitudes de onda más largas. ^[c]

Los dipolos cuya longitud es aproximadamente la mitad de la longitud de onda de la señal se denominan dipolos de media onda y se utilizan ampliamente como tales o como base para diseños de antenas derivadas. Estos tienen una resistencia a la radiación mucho mayor, más cercana a las impedancias características de las líneas de transmisión disponibles , y normalmente mucho mayor que la resistencia de los conductores, de modo que su eficiencia se acerca al 100%. En ingeniería de radio en general, el término dipolo , si no se califica más, se entiende como un dipolo de media onda alimentado por el centro.

Un verdadero dipolo de media onda tiene la mitad de la longitud de onda λ , donde λ = ⁠ do / F ⁠ en el espacio libre. Un dipolo de este tipo tiene una impedancia en el punto de alimentación que consta de una resistencia de 73 Ω y una reactancia de +43 Ω, por lo que presenta una reactancia ligeramente inductiva. Para cancelar esa reactancia y presentar una resistencia pura a la línea de alimentación, el elemento se acorta por el factorkpara una longitud netade:${\displaystyle \ \ell \ }$

${\displaystyle \ \ell ={\frac {\ 1\ }{2}}\ k\ \lambda ={\frac {\ 1\ }{2}}\ k\ {\frac {\ c\ }{f}}\ }$

donde λ es la longitud de onda en el espacio libre, c es la velocidad de la luz en el espacio libre y f es la frecuencia. El factor de ajuste k que hace que se elimine la reactancia del punto de alimentación depende del diámetro del conductor, ^[17] como se representa en el gráfico adjunto. El tamaño de escala relativo k varía de aproximadamente 0,98 para cables delgados (diámetro,  onda 0,00001 ) a aproximadamente 0,94 para conductores gruesos (diámetro,  onda 0,008 ). Esto se debe a que el efecto de la longitud de la antena en la reactancia (gráfico superior) es mucho mayor para conductores más delgados, de modo que se requiere una desviación menor de la mitad exacta de la longitud de onda para cancelar la reactancia inductiva de 43 Ω que tiene cuando exactamente ⁠ 1 /2⁠ λ .Por la misma razón, las antenas con conductores más gruesos tienen un ancho de banda operativo más amplio en el que alcanzan unarelación de onda estacionariaque se degrada por cualquier reactancia restante.

Para un k típico de aproximadamente 0,95, la fórmula anterior para la longitud de antena corregida se puede escribir, para una longitud en metros, como 143 / F ⁠ , o una longitud en pies como ⁠ 468 / F ⁠ donde f es la frecuencia en megahercios. ^[18]

Antenas dipolo de longitudes aproximadamente iguales a cualquier múltiplo impar de ⁠ 1 /2⁠ λ también son resonantes y presentan poca o ningunareactancia(que se puede eliminar haciendo un pequeño ajuste de longitud). Sin embargo, rara vez se utilizan. Un tamaño que es un radiador mucho más eficiente tanto en términos devatiossalientes como en dirección radiada es un dipolo con una longitud de ⁠ 5 /4⁠ ola .No estar cerca de ⁠ 3 /2⁠ onda ,la impedancia de esta antena tiene una reactancia grande (negativa) y solo se puede usar con unared deadaptación de impedanciabobina de cargao un llamadosintonizador de antena). Es una longitud deseable porque una antena de este tipo tiene la mayor ganancia para cualquier dipolo que no sea mucho más largo.

Un dipolo es omnidireccional en el plano perpendicular al eje del cable, y la radiación cae hasta cero en el eje (en los extremos de la antena). En un dipolo de media onda, la radiación es máxima perpendicular a la antena y declina hasta cero en el eje. Su patrón de radiación en tres dimensiones (ver figura) se representaría aproximadamente como un toroide (forma de rosquilla) simétrico respecto del conductor. Cuando se monta verticalmente, esto da como resultado una radiación máxima en direcciones horizontales. Cuando se monta horizontalmente, la radiación alcanza su punto máximo en ángulos rectos (90°) respecto del conductor, con nulos en la dirección del dipolo.${\displaystyle \ (\ \sin \theta \ )^{2}\ }$

Si se ignora la ineficiencia eléctrica, la ganancia de la antena es igual a la ganancia directiva , que es 1,50 (1,76 dBi o -0,39 dBd ) para un dipolo corto, aumentando a 1,64 (2,15 dBi o 0 dBd) para un dipolo de media onda.  5 /4⁠ dipolo de media ondala ganancia aumenta aún más hasta aproximadamente 5,2 dBi, lo que hace que esta longitud sea deseable por esa razón, incluso aunque la antena esté entonces fuera de resonancia. Los dipolos más largos que ese tienen patrones de radiación que son multilobulados, con peor ganancia (a menos que seanmuchoSe pueden considerarotras mejoras al dipolo (como incluir unreflector de esquinauna directividad. Dichos diseños de antena, aunque se basan en el dipolo de media onda, generalmente adquieren sus propios nombres.

Idealmente, un dipolo de media onda debería ser alimentado usando una línea de transmisión balanceada que coincida con su impedancia de entrada típica de 65–70 Ω. Hay disponible un cable doble con una impedancia similar, pero rara vez se usa y no coincide con los terminales de antena balanceados de la mayoría de los receptores de radio y televisión. Mucho más común es el uso de un cable doble común de 300 Ω junto con un dipolo plegado . La impedancia del punto de excitación de un dipolo plegado de media onda es 4 veces la de un dipolo de media onda simple, por lo que coincide estrechamente con esa impedancia característica de 300 Ω . ^{[19] [ cita completa requerida ]} La mayoría de los sintonizadores de banda de transmisión FM y televisores analógicos más antiguos incluyen terminales de entrada de antena balanceados de 300 Ω. Sin embargo, el cable doble tiene el inconveniente de que se ve perturbado eléctricamente por cualquier otro conductor cercano (incluida la tierra); cuando se usa para transmitir, se debe tener cuidado de no colocarlo cerca de otros conductores.

Muchos tipos de cable coaxial (o coax) tienen una impedancia característica de 75 Ω, que de otro modo sería una buena opción para un dipolo de media onda. Sin embargo, el cable coaxial es una línea de un solo extremo , mientras que un dipolo con alimentación central espera una línea balanceada (como un cable doble). Por simetría, se puede ver que los terminales del dipolo tienen un voltaje igual pero opuesto, mientras que el cable coaxial tiene un conductor conectado a tierra. El uso del cable coaxial independientemente de esto da como resultado una línea desequilibrada, en la que las corrientes a lo largo de los dos conductores de la línea de transmisión ya no son iguales y opuestas. Dado que entonces hay una corriente neta a lo largo de la línea de transmisión, la línea de transmisión se convierte en una antena en sí misma, con resultados impredecibles (ya que depende de la trayectoria de la línea de transmisión). ^[20] Esto generalmente alterará el patrón de radiación previsto de la antena y cambiará la impedancia observada en el transmisor o receptor.

Se requiere un balun para utilizar un cable coaxial con una antena dipolo. El balun transfiere energía entre el cable coaxial de un solo extremo y la antena balanceada, a veces con un cambio adicional en la impedancia. Un balun se puede implementar como un transformador que también permite una transformación de impedancia. Este generalmente se enrolla en un núcleo toroidal de ferrita . El material del núcleo toroidal debe ser adecuado para la frecuencia de uso y, en una antena transmisora, debe ser de un tamaño suficiente para evitar la saturación . ^[21] A continuación se mencionan otros diseños de balun. ^{[22] [23]}

Un balun de corriente utiliza un transformador enrollado en un toroide o varilla de material magnético como la ferrita . Toda la corriente que se ve en la entrada va a un terminal de la antena balanceada. Forma un balun al estrangular la corriente de modo común. El material no es crítico para 1:1 porque no se aplica ninguna acción de transformador a la corriente diferencial deseada. ^{[24] [25]} Un diseño relacionado implica dos transformadores e incluye una transformación de impedancia 1:4. ^{[20] [24]}

Un balun coaxial es un método rentable para eliminar la radiación del alimentador, pero está limitado a un conjunto estrecho de frecuencias operativas.

Una forma sencilla de fabricar un balun es utilizar una longitud de cable coaxial igual a la mitad de una longitud de onda. El núcleo interno del cable está conectado en cada extremo a una de las conexiones balanceadas para un alimentador o dipolo. Uno de estos terminales debe estar conectado al núcleo interno del alimentador coaxial. Las tres trenzas deben estar conectadas entre sí. Esto forma un balun 4:1, que funciona correctamente solo en una banda estrecha de frecuencias.

En frecuencias VHF , también se puede construir un balun de manguito para eliminar la radiación del alimentador. ^[26]

Otro diseño de banda estrecha es utilizar un ⁠  1 /4⁠ λ longitud de tubo metálico. El cable coaxial se coloca dentro del tubo; en un extremo la trenza está conectada al tubo mientras que en el otro extremo no se realiza ninguna conexión al tubo. El extremo equilibrado de este balun está en el extremo donde no se realiza ninguna conexión al tubo.  1 /4 El conductor λ actúa como un transformador, convirtiendo la impedancia cero en el cortocircuito a la trenza en una impedancia infinita en el extremo abierto. Esta impedancia infinita en el extremo abierto del tubo evita que la corriente fluya hacia el cable coaxial externo formado por el exterior del blindaje del cable coaxial interno y el tubo, lo que obliga a la corriente a permanecer en el cable coaxial interno. Este diseño de balun no es práctico para frecuencias bajas debido a la gran longitud de tubo que se necesitará.

Una de las aplicaciones más comunes de la antena dipolo es la antena de televisión con orejas de conejo , que se encuentra en la parte superior de los receptores de televisión por radiodifusión . Se utiliza para recibir las bandas de televisión terrestre VHF, que en los EE. UU. consisten en 54-88 MHz ( banda I ) y 174-216 MHz ( banda III ), con longitudes de onda de 5,5-1,4 m. Dado que este rango de frecuencia es mucho más amplio que el que puede cubrir una sola antena dipolo fija, se fabrica con varios grados de ajuste. Está construida con dos varillas telescópicas que se pueden extender cada una hasta aproximadamente 1 m de longitud (un cuarto de longitud de onda a 75 MHz). Con el control sobre la longitud de los segmentos, el ángulo con respecto a la vertical y el ángulo de la brújula, uno tiene mucha más flexibilidad para optimizar la recepción que la disponible con una antena de techo, incluso si está equipada con un rotor de antena .

A diferencia de las amplias bandas de frecuencia de televisión, la banda de transmisión FM (88-108 MHz) es lo suficientemente estrecha como para que una antena dipolo pueda cubrirla. Para uso fijo en hogares, los sintonizadores de alta fidelidad se suministran típicamente con dipolos plegados simples resonantes cerca del centro de esa banda. La impedancia del punto de alimentación de un dipolo plegado, que es el cuádruple de la impedancia de un dipolo simple, es una buena combinación para un cable doble de 300 Ω , por lo que generalmente se usa para la línea de transmisión al sintonizador. Una construcción común es hacer los brazos del dipolo plegado también con cables gemelos, cortocircuitados en sus extremos. Esta antena flexible se puede pegar o clavar cómodamente a las paredes, siguiendo los contornos de las molduras.

Las antenas dipolo de alambre horizontal son populares para su uso en las bandas de onda corta de HF , tanto para transmisión como para escucha de onda corta . Por lo general, se construyen con dos tramos de alambre unidos por un aislador de tensión en el centro, que es el punto de alimentación. Los extremos se pueden unir a edificios, estructuras o árboles existentes, aprovechando sus alturas. Si se utilizan para transmisión, es esencial que los extremos de la antena se unan a soportes a través de aisladores de tensión con un voltaje de descarga disruptiva suficientemente alto, ya que los antinodos de alto voltaje de la antena se producen allí. Al ser una antena balanceada, se alimentan mejor con un balun entre la línea de transmisión (coaxial) y el punto de alimentación.

Son fáciles de instalar para uso temporal o en el campo, pero también son ampliamente utilizadas por radioaficionados y oyentes de ondas cortas en ubicaciones fijas debido a su construcción simple (y económica), al tiempo que permiten realizar una antena resonante en frecuencias en las que los elementos de antena resonante deben ser de un tamaño considerable. Son una solución atractiva para estas frecuencias, cuando no se desea una direccionalidad significativa, y el costo de varias antenas resonantes de este tipo para diferentes bandas de frecuencia, construidas en casa, puede ser mucho menor que una sola antena producida comercialmente.

Las antenas para estaciones de radio de frecuencias medias y bajas suelen construirse como radiadores de mástil , en los que el propio mástil vertical forma la antena. Aunque los radiadores de mástil suelen ser monopolos , algunos son dipolos. La estructura metálica del mástil se divide en su punto medio en dos secciones aisladas ^{[ cita requerida ]} para formar un dipolo vertical, que se activa en el punto medio.

Muchos tipos de antenas de matriz se construyen utilizando múltiples dipolos, generalmente dipolos de media onda. El propósito de utilizar múltiples dipolos es aumentar la ganancia direccional de la antena sobre la ganancia de un solo dipolo; la radiación de los dipolos separados interfiere para mejorar la potencia radiada en las direcciones deseadas. En matrices con múltiples elementos accionados por dipolos , la línea de alimentación se divide utilizando una red eléctrica para proporcionar energía a los elementos, prestando especial atención a los retrasos de fase relativos debido a la transmisión entre el punto común y cada elemento.

Para aumentar la ganancia de la antena en direcciones horizontales (a expensas de la radiación hacia el cielo o hacia el suelo) se pueden apilar antenas en la dirección vertical en un arreglo de banda ancha donde las antenas se alimentan en fase. Al hacerlo con antenas dipolo horizontales se conserva la direccionalidad de esos dipolos y el nulo en la dirección de sus elementos. Sin embargo, si cada dipolo está orientado verticalmente, en un llamado arreglo de antena colineal (ver gráfico), esa dirección nula se vuelve vertical y el arreglo adquiere un patrón de radiación omnidireccional (en el plano horizontal) como se desea típicamente. Los arreglos colineales verticales se utilizan en las bandas de frecuencia VHF y UHF en las que las longitudes de onda del tamaño de los elementos son lo suficientemente pequeñas como para apilar prácticamente varios en un mástil. Son una alternativa de mayor ganancia a las antenas de plano de tierra de cuarto de onda utilizadas en estaciones base fijas para radios bidireccionales móviles , como policía, bomberos y despachadores de taxis.

Por otra parte, para una antena giratoria (o una que se utiliza sólo hacia una dirección particular) se puede desear una mayor ganancia y directividad en una dirección horizontal particular. Si el conjunto de antenas laterales discutido anteriormente (ya sea colineal o no) se gira horizontalmente, entonces se obtiene una mayor ganancia en la dirección horizontal perpendicular a las antenas, a expensas de la mayoría de las otras direcciones. Desafortunadamente, eso también significa que la dirección opuesta a la dirección deseada también tiene una ganancia alta, mientras que generalmente se desea una ganancia alta en una sola dirección. Sin embargo, la potencia que se desperdicia en la dirección inversa se puede redirigir, por ejemplo, utilizando un reflector plano grande, como se logra en la antena de conjunto reflectante , aumentando la ganancia en la dirección deseada en otros 3 dB.

Una realización alternativa de una antena unidireccional es la matriz de onda de emisión en el extremo . En este caso, los dipolos están nuevamente uno al lado del otro (pero no colineales), pero se alimentan en fases progresivas, dispuestos de modo que sus ondas se suman coherentemente en una dirección pero se cancelan en la dirección opuesta. Por lo tanto, ahora, en lugar de ser perpendiculares a la dirección de la matriz como en una matriz de onda de emisión lateral, la directividad está en la dirección de la matriz (es decir, la dirección de la línea que conecta sus puntos de alimentación) pero con una de las direcciones opuestas suprimida.

Las antenas descritas anteriormente con múltiples elementos excitados requieren un sistema de alimentación complejo de división de señal, ajuste de fase, distribución a los elementos y adaptación de impedancia. Un tipo diferente de matriz de disparo final que se utiliza con mucha más frecuencia se basa en el uso de los denominados elementos parásitos . En la popular antena Yagi de alta ganancia , solo uno de los dipolos está realmente conectado eléctricamente, pero los otros reciben y reirradian la potencia suministrada por el elemento excitado. Esta vez, el ajuste de fase se logra mediante una elección cuidadosa de las longitudes y las posiciones de los elementos parásitos, con el fin de concentrar la ganancia en una dirección y cancelar en gran medida la radiación en la dirección opuesta (así como en todas las demás direcciones). Aunque la ganancia obtenida es menor que la de una matriz excitada con el mismo número de elementos, la simplicidad de las conexiones eléctricas hace que la Yagi sea más práctica para aplicaciones de consumo.

La ganancia de la antena se mide frecuentemente en decibeles en relación con un dipolo de media onda. Una razón es que las mediciones prácticas de antenas necesitan una intensidad de referencia para comparar la intensidad de campo de una antena bajo prueba a una distancia particular. Si bien no existe nada parecido a un radiador isotrópico, el dipolo de media onda es bien conocido y se comporta bien, y se puede construir para que sea casi 100% eficiente. También es una comparación más justa, ya que la ganancia obtenida por el propio dipolo es esencialmente "gratuita", dado que casi ningún diseño de antena tiene una ganancia directiva menor.

Para una ganancia medida en relación con un dipolo, se dice que la antena tiene una ganancia de " x dBd" (ver Decibel ). Más a menudo, las ganancias se expresan en relación con un radiador isotrópico , lo que hace que la ganancia parezca mayor. Teniendo en cuenta la ganancia conocida de un dipolo de media onda, 0 dBd se define como 2,15 dBi; todas las ganancias en "dBi" se desplazan 2,15 veces más que las ganancias en "dBd".

El dipolo hertziano o doblete elemental se refiere a una construcción teórica, más que a un diseño de antena física: es un pequeño segmento idealizado de conductor que transporta una corriente de RF con amplitud y dirección constantes a lo largo de toda su longitud (corta); una antena real se puede modelar como la combinación de muchos dipolos hertzianos dispuestos de extremo a extremo.

El dipolo hertziano puede definirse como una corriente oscilante finita (en una dirección específica) de una longitud diminuta o infinitesimal en una posición específica. La solución de los campos de un dipolo hertziano puede utilizarse como base para el cálculo analítico o numérico de la radiación de geometrías de antena más complejas (como dipolos prácticos) mediante la formación de la superposición de campos de un gran número de dipolos hertzianos que comprenden el patrón de corriente de la antena real. Como función de la posición, al tomar los elementos de corriente elementales multiplicados por longitudes infinitesimales, el patrón de campo resultante se reduce a una integral sobre la trayectoria de un conductor de antena (modelado como un cable delgado).${\displaystyle \ I\ e^{i\omega t}\ }$${\displaystyle \ \delta \ell \ }$${\displaystyle \ I\!\left(\mathbf {r} \right)\ ,}$${\displaystyle \ \delta \ell \ ,}$

Para la siguiente derivación, tomaremos la corriente en la dirección, centrada en el origen donde con la dependencia temporal sinusoidal para todas las cantidades entendidas. El enfoque más simple es utilizar el cálculo del potencial vectorial utilizando la fórmula para el potencial retardado . Aunque el valor de no es único, lo restringiremos adoptando el calibre de Lorenz y suponiendo que la corriente sinusoidal a la frecuencia en radianes, el retardo del campo se convierte solo en un factor de fase donde el número de onda en el espacio libre y es la distancia lineal entre el punto que se está considerando y el origen (donde asumimos que está la fuente de corriente), por lo que Esto da como resultado ^[27] un potencial vectorial en la posición debido solo a ese elemento de corriente, que encontramos que está puramente en la dirección (la dirección de la corriente):${\displaystyle \ z\ }$${\displaystyle \ x=y=z=0\ ,}$${\displaystyle \ e^{i\omega t}\ }$ ${\displaystyle \ \mathbf {A} \!\left(\mathbf {r} \right)\ }$${\displaystyle \ \mathbf {A} \ }$${\displaystyle \ \omega \ }$${\displaystyle \ e^{-ikr}\ ,}$${\textstyle \ k={\frac {\omega }{\ c\ }}\ }$${\displaystyle \ r\ }$${\displaystyle \ r\equiv \left|\ \mathbf {r} \ \right|~.}$${\displaystyle \ \mathbf {A} \ }$${\displaystyle \ \mathbf {r} \ }$${\displaystyle \ z\ }$

${\displaystyle \mathbf {A} \!\left(\mathbf {r} \right)=I\ \delta \ell \ {\frac {\mu _{0}}{\ 4\pi r\ }}\ e^{-ikr}\ {\hat {\mathbf {z} }}\ }$

donde es la permeabilidad del espacio libre . Entonces usando${\displaystyle \ \mu _{0}\ }$

${\displaystyle \ \mu \mathbf {H} =\mathbf {B} =\nabla \times \mathbf {A} \ }$

Podemos resolver el campo magnético y a partir de ahí (dependiendo de que hayamos elegido el calibre de Lorenz) el campo eléctrico usando${\displaystyle \ \mathbf {H} \ ,}$${\displaystyle \ \mathbf {E} \ }$

${\displaystyle \mathbf {E} ={\frac {\ \nabla \times \mathbf {H} \ }{i\omega \epsilon }}}$

En coordenadas esféricas encontramos ^{[12] (pp 92–94)} que el campo magnético sólo tiene un componente en la dirección:${\displaystyle \ \mathbf {H} \ }$${\displaystyle \ \phi \ }$

${\displaystyle \mathbf {H} =H_{\phi }\ {\hat {\boldsymbol {\phi }}}}$

dónde

${\displaystyle H_{\phi }=i{\frac {\ I\ \delta \ell \ }{4\pi }}\left({\frac {\ k\ }{r}}-{\frac {i}{\ r^{2}}}\right)\ e^{-ikr}\ \sin \theta \ ,}$

mientras que el campo eléctrico tiene componentes tanto en la dirección como en la dirección:${\displaystyle \ \theta \ }$${\displaystyle \ r\ }$

${\displaystyle \mathbf {E} =E_{\theta }\ {\hat {\boldsymbol {\theta }}}+E_{r}\ {\hat {\mathbf {r} }}}$

dónde

${\displaystyle {\begin{aligned}E_{\theta }&=i{\frac {\ \zeta _{0}\ I\ \delta \ell \ }{4\pi }}\left({\frac {\ k\ }{r}}-{\frac {i}{\ r^{2}}}-{\frac {1}{\ k\ r^{3}}}\right)\ e^{-ikr}\ \sin \theta \ ,\\[2pt]E_{r}&={\frac {\ \zeta _{0}\ I\ \delta \ell \ }{2\pi }}\left({\frac {1}{\ r^{2}\ }}-{\frac {i}{\ kr^{3}}}\right)\ e^{-ikr}\ \cos \theta \ ,\end{aligned}}}$

con es la impedancia del espacio libre .${\displaystyle \ \zeta _{0}\equiv {\sqrt {{\frac {\ \mu _{0}\ }{\epsilon _{0}}}\;}}\ }$

Esta solución incluye términos de campo cercano que son muy fuertes cerca de la fuente pero que no se irradian . Como se ve en la animación adjunta, los campos y muy cercanos a la fuente están desfasados ​​casi 90°, por lo que contribuyen muy poco al vector de Poynting con el que se calcula el flujo irradiado. La solución de campo cercano para un elemento de antena (a partir de la integral que utiliza esta fórmula sobre la longitud de ese elemento) es el campo que se puede utilizar para calcular la impedancia mutua entre este y otro elemento cercano.${\displaystyle \ \mathbf {E} \ }$${\displaystyle \ \mathbf {H} \ }$

Para calcular el patrón de radiación del campo lejano , las ecuaciones anteriores se simplifican ya que solo los términos siguen siendo significativos: ^{[12] (pp 92–94)}${\textstyle \ {\frac {\ 1\ }{r}}\ }$

${\displaystyle {\begin{aligned}H_{\phi }&=i{\frac {\ I\ \delta \ell \ k\ }{4\pi r}}\ e^{-ikr}\ \sin \theta \ ,\\[2pt]E_{\theta }&=i{\frac {\ \zeta _{0}\ I\ \delta \ell \ k\ }{4\pi r}}\ e^{-ikr}\ \sin \theta ~.\end{aligned}}}$

El patrón de campo lejano se ve así que consiste en una onda electromagnética transversal (TEM), con campos eléctricos y magnéticos en ángulos rectos entre sí y en ángulos rectos a la dirección de propagación (la dirección de , ya que asumimos que la fuente está en el origen). La polarización eléctrica, en la dirección, es coplanar con la corriente de la fuente (en la dirección), mientras que el campo magnético está en ángulos rectos con esta, en la dirección. Se puede ver a partir de estas ecuaciones, y también en la animación, que los campos a estas distancias están exactamente en fase . Ambos campos caen de acuerdo con con la potencia cayendo así de acuerdo con como dicta la ley del cuadrado inverso .${\displaystyle \ \mathbf {r} \ }$${\displaystyle \theta }$${\displaystyle \ z\ }$${\displaystyle \ \phi \ }$${\textstyle \ {\frac {\ 1\ }{r}}\ ,}$${\textstyle \ {\frac {1}{\ r^{2}}}\ }$

Si se conoce el patrón de radiación de campo lejano debido a una corriente de antena dada, entonces es posible calcular la resistencia de radiación directamente. Para los campos anteriores debidos al dipolo hertziano, podemos calcular el flujo de potencia de acuerdo con el vector de Poynting , lo que da como resultado una potencia (promediada durante un ciclo) de:

${\displaystyle \langle \mathbf {S} \rangle ={\frac {\ 1\ }{2}}{\mathcal {R_{e}}}\left\{\ \mathbf {E} \times \mathbf {H} ^{*}\ \right\}=\langle S_{\mathsf {r}}\rangle \ {\hat {\mathbf {r} }}+\langle S_{\mathsf {\phi }}\rangle \ {\hat {\boldsymbol {\phi }}}~.}$

A medida que aumenta, se vuelve insignificantemente pequeño en comparación con el componente. Aunque no es obligatorio, es más fácil trabajar solo con el valor asintótico que se acerca a un valor grande utilizando las expresiones de campo lejano más simples para y Considere una esfera grande que rodea la fuente con un radio. Hallamos la potencia por unidad de área que cruza la superficie de esa esfera en la dirección es:${\displaystyle \ r\ }$${\displaystyle \ \langle S_{\mathsf {\phi }}\rangle \ }$${\displaystyle \ \langle S_{\mathsf {r}}\rangle \ }$${\displaystyle \ \langle S_{\mathsf {r}}\rangle \ }$${\displaystyle \ r\ }$${\displaystyle \ \mathbf {E} \ }$${\displaystyle \ \mathbf {H} ~.}$${\displaystyle \ r~.}$${\displaystyle \ {\hat {\mathbf {r} }}\ }$

${\displaystyle \left\langle S_{\mathsf {r}}\right\rangle ={\frac {\ \zeta _{0}\ }{2}}\ \left({\frac {\ \left|I\right|\ k\ \delta \ell \ }{4\pi r}}\ \sin \theta \right)^{2}\ }$

La integración de este flujo sobre toda la esfera da como resultado:

${\displaystyle {\begin{aligned}P_{\mathsf {net}}&=\int _{0}^{2\pi }\!\!\int _{0}^{\pi }\left|\langle S_{\mathsf {r}}\rangle \right|\ r^{2}\sin \theta \ \mathrm {d} {\phi }\ \mathrm {d} \theta ={\tfrac {\ 1\ }{2}}\zeta _{0}\ \left({\frac {\ \left|I\right|\ k\ \delta \ell \ }{4\pi }}\right)^{2}\int _{0}^{2\pi }\!\!\int _{0}^{\pi }\sin ^{3}\theta \ \mathrm {d} {\phi }\ \mathrm {d} \theta \\&={\frac {\zeta _{0}}{\ 12\pi \ }}\left(\left|I\right|\ k\ \delta \ell \right)^{2}={\frac {\ \pi \ }{3}}\zeta _{0}\ \left(\left|I\right|{\frac {\ \delta \ell \ }{\lambda }}\right)^{2}\end{aligned}}}$

donde es la longitud de onda del espacio libre correspondiente a la frecuencia en radianes Por definición, la resistencia de radiación multiplicada por el promedio del cuadrado de la corriente es la potencia neta radiada debido a esa corriente, por lo que al equiparar lo anterior a encontramos:${\displaystyle \ \lambda =2\pi /k\ }$${\displaystyle \ \omega ~.}$${\displaystyle R_{\text{rad}}}$${\textstyle \ {\tfrac {\ 1\ }{2}}\left|\ I\ \right|^{2}\ }$${\textstyle \ {\tfrac {\ 1\ }{2}}\left|I\right|^{2}R_{\text{rad}}\ }$

${\displaystyle R_{\text{rad}}={\tfrac {\ 2\ \pi \ }{3}}\zeta _{0}\ \left({\frac {\ \delta \ell \ }{\lambda }}\right)^{2}~.}$

Este método se puede utilizar para calcular la resistencia de radiación de cualquier antena cuyo patrón de radiación de campo lejano se haya determinado en términos de una corriente de antena específica. Si se descuidan las pérdidas óhmicas en los conductores, la resistencia de radiación (considerada en relación con el punto de alimentación) es idéntica al componente resistivo (real) de la impedancia del punto de alimentación. Desafortunadamente, este ejercicio no nos dice nada sobre el componente reactivo (imaginario) de la impedancia del punto de alimentación, cuyo cálculo se considera a continuación.

Utilizando la expresión anterior para el flujo radiado dado por el vector de Poynting, también es posible calcular la ganancia directiva del dipolo hertziano. Dividiendo la potencia total calculada anteriormente por podemos encontrar el flujo promediado en todas las direcciones como${\displaystyle 4\pi r^{2}}$${\displaystyle \ P_{\text{avg}}\ }$

${\displaystyle \ P_{\text{avg}}={\frac {P_{\text{net}}}{\ 4\pi \ r^{2}}}={\frac {\zeta _{0}}{\ 48\pi ^{2}\ r^{2}}}k^{2}\ \left|I\right|^{2}\ \left(\delta \ell \right)^{2}~.}$

Dividiendo el flujo irradiado en una dirección particular por obtenemos la ganancia directiva${\displaystyle \ P_{\text{avg}}\ }$ ${\displaystyle \ \operatorname {\mathsf {G}} \left(\theta \right)\ :}$

${\displaystyle \ \operatorname {\mathsf {G}} \left(\theta \right)={\frac {\ \left\langle \mathbf {S} _{\mathsf {r}}\right\rangle \ }{P_{\text{avg}}}}={\tfrac {\ 3\ }{2}}\sin ^{2}\theta \ }$

Se ha descubierto que la "ganancia" de antena comúnmente citada, es decir, el valor máximo del patrón de ganancia (patrón de radiación), es de 1,5~1,76 dBi, inferior a prácticamente cualquier otra configuración de antena.

El dipolo hertziano es similar al dipolo corto, del que hablamos anteriormente, pero difiere de él. En ambos casos, el conductor es muy corto en comparación con una longitud de onda, por lo que el patrón de onda estacionaria presente en un dipolo de media onda (por ejemplo) está ausente. Sin embargo, con el dipolo hertziano especificamos que la corriente a lo largo de ese conductor es constante a lo largo de su corta longitud. Esto hace que el dipolo hertziano sea útil para el análisis de configuraciones de antena más complejas, donde cada sección infinitesimal del conductor de esa antena real se puede modelar como un dipolo hertziano y se descubre que la corriente fluye en esa antena real.

Sin embargo, un conductor corto alimentado con un voltaje de RF no tendrá una corriente uniforme ni siquiera a lo largo de ese corto rango. En cambio, un dipolo corto en la vida real tiene una corriente igual a la corriente del punto de alimentación en el punto de alimentación, pero que cae linealmente hasta cero a lo largo de ese conductor corto. Al colocar un sombrero capacitivo , como una bola metálica, en el extremo del conductor, es posible que su propia capacitancia absorba la corriente del conductor y se aproxime mejor a la corriente constante supuesta para el dipolo hertziano. Pero nuevamente, el dipolo hertziano está pensado solo como una construcción teórica para el análisis de antenas.

El dipolo corto, con una corriente en el punto de alimentación de tiene una corriente promedio sobre cada conductor de solo Las ecuaciones de campo anteriores para el dipolo hertziano de longitud predecirían entonces los campos reales para un dipolo corto usando esa corriente efectiva. Esto daría como resultado una potencia medida en el campo lejano de un cuarto de la dada por la ecuación anterior para la magnitud del vector de Poynting si hubiéramos asumido una corriente de elemento de En consecuencia, se puede ver que la resistencia de radiación calculada para el dipolo corto es un cuarto de la calculada anteriormente para el dipolo hertziano. Pero sus patrones de radiación (y ganancias) son idénticos.${\displaystyle \ I_{0}\ ,}$${\textstyle \ {\tfrac {\ 1\ }{2}}\ I_{0}~.}$${\displaystyle \ \delta \ell \ }$${\textstyle \ I={\tfrac {\ 1\ }{2}}\ I_{0}~.}$${\displaystyle \ \langle S_{\mathsf {r}}\rangle \ }$${\displaystyle \ I_{0}~.}$

La impedancia observada en el punto de alimentación de un dipolo de varias longitudes se ha representado gráficamente anteriormente, en términos del componente real (resistivo) R _dipolo y el componente imaginario ( reactivo ) j X _dipolo de esa impedancia. Para el caso de una antena con conductores perfectos (sin pérdida óhmica), R _dipolo es idéntico a la resistencia de radiación , que se puede calcular más fácilmente a partir de la potencia total en el patrón de radiación de campo lejano para una corriente aplicada dada, como mostramos para el dipolo corto. El cálculo de X _dipolo es más difícil.

Utilizando el método de la FEM inducida se obtienen expresiones de forma cerrada para ambos componentes de la impedancia del punto de alimentación; dichos resultados se representan gráficamente arriba. La solución depende de una suposición para la forma de la distribución de corriente a lo largo de los conductores de la antena. Para relaciones de longitud de onda a diámetro del elemento mayores que aproximadamente 60, la distribución de corriente a lo largo de cada elemento de antena de longitud ⁠ 1 /2⁠ L se aproxima muy bien^[27]al tener la forma de la función seno en puntos a lo largo de la antenaz, con la corriente llegando a cero en los extremos de los elementos, donde z = ⁠± + 1 /2⁠ L , de la siguiente manera:

${\displaystyle \ I(z)=A\sin {\Bigl (}\ k\left({\tfrac {\ 1\ }{2}}\ L-\left|z\right|\right)\ {\Bigr )}\ ,}$

donde k es el número de onda dado por k = ⁠  2π ​ / la ⁠ = ⁠ 2πf ​ / do ⁠ ,y la amplitudAse establece para que coincida con una corriente de punto de activación especificada en z = 0 .

En los casos en los que se puede suponer una distribución de corriente aproximadamente sinusoidal, este método resuelve la impedancia del punto de excitación en forma cerrada utilizando las funciones integrales de coseno y seno  Si( x )  y  Ci( x )  . Para un dipolo de longitud total  L  , los componentes resistivos y reactivos de la impedancia del punto de excitación se pueden expresar como: ^{[28] [d]}

${\displaystyle {\begin{aligned}R_{\mathsf {dipole}}={\frac {\zeta _{0}}{\ 2\pi \sin ^{2}\left({\tfrac {1}{2}}kL\right)\ }}{\Biggl \{}\ \gamma _{e}+\ln(kL)-\operatorname {Ci} (kL)+{}&{\tfrac {1}{2}}\sin(kL)\,{\Bigl [}+\operatorname {Si} (2kL)-2\operatorname {Si} (kL)\ {\Bigr ]}\\{}+{}&{\tfrac {1}{2}}\cos(kL)\,{\Big [}+\operatorname {Ci} (2kL)-2\operatorname {Ci} (kL)+\gamma _{e}+\ln \left({\tfrac {1}{2}}kL\right)\ {\Bigr ]}\ {\Bigg \}}\ ,\\X_{\mathsf {dipole}}={\frac {\zeta _{0}}{\ 2\pi \sin ^{2}\left({\tfrac {1}{2}}kL\right)\ }}{\Biggl \{}{}+\operatorname {Si} (kL)+{}&{\tfrac {1}{2}}\cos(kL)\,{\Bigl [}-\operatorname {Si} (2kL)+2\operatorname {Si} (kL)\ {\Bigr ]}\\{}+{}&{\tfrac {1}{2}}\sin(kL)\,{\Bigl [}+\operatorname {Ci} (2kL)-2\operatorname {Ci} (kL)+\operatorname {Ci} \left({\tfrac {\;2ka^{2}\ }{L}}\right)\ {\Bigr ]}\ {\Biggr \}}\ ,\end{aligned}}}$

donde a es el radio de los conductores, k es nuevamente el número de onda como se definió anteriormente, ζ ₀ es la impedancia del espacio vacío , que es casi la misma que la impedancia del aire: ζ ₀ ≈ 377 Ω, y es la constante de Euler . Existe una forma alternativa equivalente favorecida por algunos autores que utiliza una función diferente, Cin  . ^[e] ${\displaystyle \ \gamma _{e}=0.57721566\ \ldots \ }$

El método de la FEM inducida depende de la suposición de una distribución de corriente sinusoidal, y ofrece una precisión mejor que aproximadamente el 10% siempre que la relación entre la longitud de onda y el diámetro del elemento sea mayor que aproximadamente 60. ^[27] Sin embargo, para conductores aún más grandes se requieren soluciones numéricas que resuelvan la distribución de corriente del conductor (en lugar de suponer un patrón sinusoidal). Esto puede basarse en soluciones aproximadas para la ecuación integrodiferencial de Pocklington o la ecuación integral de Hallén . ^[7] Estos enfoques también tienen una mayor generalidad, ya que no se limitan a los conductores lineales.

La solución numérica de cualquiera de ellos se realiza utilizando la solución del método de momento que requiere la expansión de esa corriente en un conjunto de funciones base ; una opción simple (pero no la mejor), por ejemplo, es dividir el conductor en N segmentos con una corriente constante asumida a lo largo de cada uno. Después de establecer una función de ponderación adecuada, el costo se puede minimizar mediante la inversión de una matriz N × N. La determinación de cada elemento de la matriz requiere al menos una doble integración que involucra las funciones de ponderación, que puede volverse computacionalmente intensiva. Estas se simplifican si las funciones de ponderación son simplemente funciones delta , que corresponden a ajustar las condiciones de contorno para la corriente a lo largo del conductor en solo N puntos discretos. Luego, la matriz N × N debe invertirse, lo que también es computacionalmente intensivo a medida que N aumenta. En un ejemplo simple, Balanis (2011) realiza este cálculo para encontrar la impedancia de la antena con diferentes N utilizando el método de Pocklington, y encuentra que con N > 60 las soluciones se acercan a sus valores límite con una diferencia de unos pocos porcentajes. ^[7]

• Dinkins, Rodney R., AC6V ( SK ); Dinkins, Jeff A., AC6V . "Enlaces". ac6v.com . Antenas caseras.{{cite web}}: CS1 maint: multiple names: authors list (link) CS1 maint: numeric names: authors list (link)

• "Tu primer dipolo HF". eham.net .— tutorial simple y completo

• "Artículos sobre dipolos". Antenas y propagación. electronics-notes.com .— índice de una serie de artículos sobre el dipolo en sus diversas formas