Densidad
| Densidad | |
|---|---|
 Un tubo de ensayo que contiene cuatro líquidos coloreados no miscibles con diferentes densidades. | |
Símbolos comunes | ρ , D |
| Unidad SI | kg/ m3 |
| ¿ Extenso ? | No |
| Intensivo ? | Sí |
| ¿ Conservado ? | No |
Derivaciones de otras magnitudes | |
| Dimensión | |
La densidad ( densidad de masa volumétrica o masa específica ) es la masa de una sustancia por unidad de volumen . El símbolo más utilizado para la densidad es ρ (la letra griega minúscula rho ), aunque también se puede utilizar la letra latina D. Matemáticamente, la densidad se define como la masa dividida por el volumen: [1] donde ρ es la densidad, m es la masa y V es el volumen. En algunos casos (por ejemplo, en la industria del petróleo y el gas de los Estados Unidos), la densidad se define vagamente como su peso por unidad de volumen , [2] aunque esto es científicamente inexacto: esta cantidad se llama más específicamente peso específico .
En el caso de una sustancia pura, la densidad tiene el mismo valor numérico que su concentración másica . Los distintos materiales suelen tener densidades diferentes, y la densidad puede ser relevante para la flotabilidad , la pureza y el empaquetamiento . El osmio es el elemento más denso conocido en condiciones estándar de temperatura y presión .
Para simplificar las comparaciones de densidad entre diferentes sistemas de unidades, a veces se la reemplaza por la cantidad adimensional " densidad relativa " o " gravedad específica ", es decir, la relación entre la densidad del material y la de un material estándar, generalmente agua. Por lo tanto, una densidad relativa menor que uno en relación con el agua significa que la sustancia flota en el agua.
La densidad de un material varía con la temperatura y la presión. Esta variación suele ser pequeña para los sólidos y líquidos, pero mucho mayor para los gases. Al aumentar la presión sobre un objeto, disminuye el volumen del mismo y, por lo tanto, aumenta su densidad. Al aumentar la temperatura de una sustancia (con algunas excepciones), disminuye su densidad al aumentar su volumen. En la mayoría de los materiales, calentar la parte inferior de un fluido produce convección del calor desde abajo hacia arriba, debido a la disminución de la densidad del fluido calentado, lo que hace que suba en relación con el material más denso sin calentar.
El recíproco de la densidad de una sustancia se denomina a veces volumen específico , un término que se utiliza a veces en termodinámica . La densidad es una propiedad intensiva en el sentido de que aumentar la cantidad de una sustancia no aumenta su densidad, sino su masa.
Otras cantidades o proporciones conceptualmente comparables incluyen la densidad específica , la densidad relativa (gravedad específica) y el peso específico .
Historia
Densidad, flotación y hundimiento
La comprensión de que los distintos materiales tienen densidades diferentes y de la relación entre densidad, flotación y hundimiento debe remontarse a tiempos prehistóricos. Mucho más tarde se puso por escrito. Aristóteles , por ejemplo, escribió: [3]
Hay una diferencia tan grande de densidad entre el agua salada y el agua dulce que los barcos cargados con cargas del mismo peso casi se hunden en los ríos, pero navegan con bastante facilidad en el mar y son perfectamente aptos para navegar. Y la ignorancia de esto a veces le ha costado caro a la gente que carga sus barcos en los ríos. La siguiente es una prueba de que la densidad de un fluido es mayor cuando se mezcla una sustancia con él. Si haces que el agua sea muy salada mezclándola con sal, los huevos flotarán en ella. ... Si hubiera algo de verdad en las historias que cuentan sobre el lago en Palestina, confirmarían aún más lo que digo. Porque dicen que si atas a un hombre o a un animal y lo arrojas al lago, flota y no se hunde debajo de la superficie.
— Aristóteles, Meteorología , Libro II, Capítulo III
Volumen vs. densidad; volumen de una forma irregular
En un relato muy conocido, aunque probablemente apócrifo , se le encomendó a Arquímedes la tarea de determinar si el orfebre del rey Hierón estaba malversando oro durante la fabricación de una corona de oro dedicada a los dioses y reemplazándolo por otra aleación más barata . [4] Arquímedes sabía que la corona de forma irregular podía aplastarse hasta formar un cubo cuyo volumen podía calcularse fácilmente y compararse con la masa; pero el rey no aprobó esto. Desconcertado, se dice que Arquímedes se dio un baño de inmersión y observó por la subida del agua al entrar que podía calcular el volumen de la corona de oro a través del desplazamiento del agua. Ante este descubrimiento, saltó de su baño y corrió desnudo por las calles gritando: "¡Eureka! ¡Eureka!" ( griego antiguo : Εύρηκα!, lit. ' Lo he encontrado'). Como resultado, el término eureka entró en el lenguaje común y se usa hoy para indicar un momento de iluminación.
La historia apareció por primera vez en forma escrita en los libros de arquitectura de Vitruvio , dos siglos después de que supuestamente tuvo lugar. [5] Algunos eruditos han dudado de la exactitud de este relato, diciendo entre otras cosas que el método habría requerido mediciones precisas que habrían sido difíciles de hacer en ese momento. [6] [7]
Sin embargo, en 1586, Galileo Galilei , en uno de sus primeros experimentos, hizo una posible reconstrucción de cómo se podría haber realizado el experimento con recursos de la antigua Grecia [8]
Unidades
De la ecuación de densidad ( ρ = m / V ), la densidad de masa tiene cualquier unidad que sea masa dividida por volumen . Como hay muchas unidades de masa y volumen que cubren muchas magnitudes diferentes, hay una gran cantidad de unidades para la densidad de masa en uso. La unidad SI de kilogramo por metro cúbico (kg/m 3 ) y la unidad cgs de gramo por centímetro cúbico (g/cm 3 ) son probablemente las unidades más comúnmente utilizadas para la densidad. Un g/cm 3 es igual a 1000 kg/m 3 . Un centímetro cúbico (abreviatura cc) es igual a un mililitro. En la industria, otras unidades más grandes o más pequeñas de masa y/o volumen suelen ser más prácticas y se pueden utilizar las unidades habituales de EE. UU . Vea a continuación una lista de algunas de las unidades de densidad más comunes.
El litro y la tonelada no forman parte del SI, pero su uso es aceptable, dando lugar a las siguientes unidades:
Las densidades que utilizan las siguientes unidades métricas tienen exactamente el mismo valor numérico, una milésima parte del valor en (kg/m 3 ). El agua líquida tiene una densidad de aproximadamente 1 kg/dm 3 , lo que hace que cualquiera de estas unidades del SI sea numéricamente conveniente de usar, ya que la mayoría de los sólidos y líquidos tienen densidades entre 0,1 y 20 kg/dm 3 .
- kilogramo por decímetro cúbico (kg/dm 3 )
- gramo por centímetro cúbico (g/cm 3 )
- 1 g/cm3 = 1000 kg/ m3
- megagramo (tonelada métrica) por metro cúbico (Mg/m 3 )
En las unidades habituales de EE. UU., la densidad se puede expresar en:
- Onza de Avoirdupois por pulgada cúbica (1 g/cm3 ≈ 0,578036672 oz/cu in)
- Onza avoirdupois por onza fluida (1 g/cm3 ≈ 1,04317556 oz/oz líquida estadounidense = 1,04317556 lb/pinta líquida estadounidense)
- Libra por pulgada cúbica (1 g/cm3 ≈ 0,036127292 lb/cu in)
- libra por pie cúbico (1 g/cm3 ≈ 62,427961 lb/cu ft)
- libra por yarda cúbica (1 g/cm3 ≈ 1685,5549 lb/cu yd)
- libra por galón líquido estadounidense (1 g/cm3 ≈ 8,34540445 lb/gal estadounidense)
- Libra por bushel estadounidense (1 g/cm3 ≈ 77,6888513 lb/bu)
- babosa por pie cúbico
En la práctica, rara vez se utilizan unidades imperiales que difieren de las anteriores (como el galón y el bushel imperiales, que difieren de las unidades estadounidenses), aunque se encuentran en documentos más antiguos. El galón imperial se basaba en el concepto de que una onza líquida imperial de agua tendría una masa de una onza Avoirdupois y, de hecho, 1 g/cm 3 ≈ 1,00224129 onzas por onza líquida imperial = 10,0224129 libras por galón imperial. La densidad de los metales preciosos podría basarse en onzas troy y libras, lo que podría causar confusión.
Conociendo el volumen de la celda unitaria de un material cristalino y su peso fórmula (en daltons ), se puede calcular la densidad. Un dalton por ångström cúbico equivale a una densidad de 1,660 539 066 60 g/cm 3 .
Medición
Existen varias técnicas y normas para medir la densidad de los materiales. Entre estas técnicas se incluyen el uso de un hidrómetro (un método de flotabilidad para líquidos), la balanza hidrostática (un método de flotabilidad para líquidos y sólidos), el método del cuerpo sumergido (un método de flotabilidad para líquidos), el picnómetro (líquidos y sólidos), el picnómetro de comparación de aire (sólidos), el densitómetro oscilante (líquidos) y el método de vertido y vaciado (sólidos). [9] Sin embargo, cada método o técnica individual mide diferentes tipos de densidad (por ejemplo, densidad aparente, densidad esquelética, etc.) y, por lo tanto, es necesario comprender el tipo de densidad que se mide, así como el tipo de material en cuestión.
Materiales homogéneos
La densidad en todos los puntos de un objeto homogéneo es igual a su masa total dividida por su volumen total. La masa se mide normalmente con una báscula o balanza ; el volumen puede medirse directamente (a partir de la geometría del objeto) o por el desplazamiento de un fluido. Para determinar la densidad de un líquido o un gas, se puede utilizar un hidrómetro , un dasimetro o un caudalímetro Coriolis , respectivamente. De manera similar, el pesaje hidrostático utiliza el desplazamiento de agua debido a un objeto sumergido para determinar la densidad del objeto.
Materiales heterogéneos
Si el cuerpo no es homogéneo, entonces su densidad varía entre las diferentes regiones del objeto. En ese caso, la densidad alrededor de cualquier ubicación dada se determina calculando la densidad de un pequeño volumen alrededor de esa ubicación. En el límite de un volumen infinitesimal, la densidad de un objeto no homogéneo en un punto se convierte en: , donde es un volumen elemental en la posición . La masa del cuerpo puede entonces expresarse como
Materiales no compactos
En la práctica, los materiales a granel, como el azúcar, la arena o la nieve, contienen huecos. Muchos materiales existen en la naturaleza en forma de copos, pellets o gránulos.
Los vacíos son regiones que contienen algo distinto del material considerado. Normalmente, el vacío es aire, pero también puede ser vacío, líquido, sólido o cualquier otro gas o mezcla gaseosa.
El volumen aparente de un material, incluida la fracción de espacio vacío , a menudo se obtiene mediante una medición simple (por ejemplo, con una taza medidora calibrada) o geométricamente a partir de dimensiones conocidas.
La masa dividida por el volumen a granel determina la densidad a granel . Esto no es lo mismo que la densidad de masa volumétrica del material. Para determinar la densidad de masa volumétrica del material, primero se debe descontar el volumen de la fracción de huecos. A veces, esto se puede determinar mediante un razonamiento geométrico. Para el empaquetamiento compacto de esferas iguales, la fracción de no huecos puede ser como máximo de alrededor del 74%. También se puede determinar empíricamente. Sin embargo, algunos materiales a granel, como la arena, tienen una fracción de huecos variable que depende de cómo se agite o se vierta el material. Puede ser suelto o compacto, con más o menos espacio de aire según la manipulación.
En la práctica, la fracción de huecos no es necesariamente aire, ni siquiera gaseosa. En el caso de la arena, podría ser agua, lo que puede resultar ventajoso para la medición, ya que la fracción de huecos de la arena saturada en agua (una vez que se han eliminado por completo las burbujas de aire) es potencialmente más consistente que la de la arena seca medida con un hueco de aire.
En el caso de materiales no compactos, también hay que tener cuidado al determinar la masa de la muestra de material. Si el material está bajo presión (normalmente la presión del aire ambiente en la superficie de la Tierra), la determinación de la masa a partir del peso de la muestra medida puede tener que tener en cuenta los efectos de flotabilidad debido a la densidad del componente vacío, según cómo se haya realizado la medición. En el caso de la arena seca, la arena es mucho más densa que el aire, por lo que el efecto de flotabilidad suele ignorarse (menos de una parte en mil).
El cambio de masa al desplazar un material vacío por otro mientras se mantiene un volumen constante se puede utilizar para estimar la fracción de vacío, si se conoce de manera confiable la diferencia de densidad de los dos materiales vacíos.
Cambios de densidad
En general, la densidad se puede modificar modificando la presión o la temperatura . Aumentar la presión siempre aumenta la densidad de un material. Aumentar la temperatura generalmente disminuye la densidad, pero hay excepciones notables a esta generalización. Por ejemplo, la densidad del agua aumenta entre su punto de fusión a 0 °C y 4 °C; se observa un comportamiento similar en el silicio a bajas temperaturas.
El efecto de la presión y la temperatura sobre las densidades de líquidos y sólidos es pequeño. La compresibilidad de un líquido o sólido típico es de 10 −6 bar −1 (1 bar = 0,1 MPa) y una expansividad térmica típica es de 10 −5 K −1 . Esto se traduce aproximadamente en la necesidad de unas diez mil veces la presión atmosférica para reducir el volumen de una sustancia en un uno por ciento. (Aunque las presiones necesarias pueden ser unas mil veces menores para suelos arenosos y algunas arcillas). Una expansión del volumen del uno por ciento normalmente requiere un aumento de la temperatura del orden de miles de grados Celsius .
Por el contrario, la densidad de los gases se ve fuertemente afectada por la presión. La densidad de un gas ideal es
donde M es la masa molar , P es la presión, R es la constante universal de los gases y T es la temperatura absoluta . Esto significa que la densidad de un gas ideal se puede duplicar duplicando la presión o dividiendo a la mitad la temperatura absoluta.
En el caso de expansión térmica volumétrica a presión constante y pequeños intervalos de temperatura, la dependencia de la temperatura de la densidad es
donde es la densidad a una temperatura de referencia, es el coeficiente de expansión térmica del material a temperaturas cercanas a .
Densidad de soluciones
La densidad de una solución es la suma de las concentraciones másicas de los componentes de esa solución.
La concentración másica de cada componente dado en una solución se suma a la densidad de la solución.
Expresada en función de las densidades de los componentes puros de la mezcla y su participación volumétrica , permite determinar volúmenes molares excedentes : siempre que no haya interacción entre los componentes.
Conociendo la relación entre los volúmenes excedentes y los coeficientes de actividad de los componentes, se pueden determinar los coeficientes de actividad:
Lista de densidades
Varios materiales
| Material | ρ (kg/m 3 ) [nota 1] | Notas |
|---|---|---|
| Hidrógeno | 0,0898 | |
| Helio | 0,179 | |
| Aerografito | 0,2 | [nota 2] [10] [11] |
| Microenrejado metálico | 0.9 | [nota 2] |
| Aerogel | 1.0 | [nota 2] |
| Aire | 1.2 | A nivel del mar |
| Hexafluoruro de tungsteno | 12.4 | Uno de los gases más pesados conocidos en condiciones estándar. |
| Hidrógeno líquido | 70 | A aproximadamente -255 °C |
| Espuma de poliestireno | 75 | Aproximado [12] |
| Corcho | 240 | Aproximado [12] |
| Pino | 373 | [13] |
| Litio | 535 | Metal menos denso |
| Madera | 700 | Sazonado, típico [14] [15] |
| Roble | 710 | [13] |
| Potasio | 860 | [16] |
| Hielo | 916.7 | A temperatura < 0 °C |
| Aceite de cocina | 910–930 | |
| Sodio | 970 | |
| Agua (fresca) | 1.000 | A 4 °C, la temperatura de su máxima densidad |
| Agua (sal) | 1.030 | 3% |
| Oxígeno líquido | 1.141 | A aproximadamente -219 °C |
| Nylon | 1.150 | |
| Plástica | 1,175 | Aproximado; para polipropileno y PETE / PVC |
| Glicerol | 1.261 | [17] |
| Tetracloroeteno | 1.622 | |
| Arena | 1.600 | Entre 1.600 y 2.000 [18] |
| Magnesio | 1.740 | |
| Berilio | 1.850 | |
| Silicio | 2.330 | |
| Concreto | 2.400 | [19] [20] |
| Vaso | 2.500 | [21] |
| Cuarcita | 2.600 | [18] |
| Granito | 2.700 | [18] |
| Gneis | 2.700 | [18] |
| Aluminio | 2.700 | |
| Caliza | 2.750 | Compacto [18] |
| Basalto | 3.000 | [18] |
| diyodometano | 3.325 | Líquido a temperatura ambiente |
| Diamante | 3.500 | |
| Titanio | 4.540 | |
| Selenio | 4.800 | |
| Vanadio | 6.100 | |
| Antimonio | 6.690 | |
| Zinc | 7.000 | |
| Cromo | 7.200 | |
| Estaño | 7.310 | |
| Manganeso | 7,325 | Aproximado |
| Acero dulce | 7.850 | |
| Hierro | 7.870 | |
| Niobio | 8,570 | |
| Latón | 8.600 | [20] |
| Cadmio | 8.650 | |
| Cobalto | 8.900 | |
| Níquel | 8.900 | |
| Cobre | 8,940 | |
| Bismuto | 9.750 | |
| Molibdeno | 10,220 | |
| Plata | 10.500 | |
| Dirigir | 11.340 | |
| Torio | 11.700 | |
| Rodio | 12.410 | |
| Mercurio | 13.546 | |
| Tantalio | 16.600 | |
| Uranio | 19.100 | |
| Tungsteno | 19.300 | |
| Oro | 19.320 | |
| Plutonio | 19.840 | |
| Renio | 21.020 | |
| Platino | 21.450 | |
| Iridio | 22.420 | |
| Osmio | 22.570 | El elemento natural más denso de la Tierra |
- ^ A menos que se indique lo contrario, todas las densidades dadas corresponden a condiciones estándar de temperatura y presión ,
es decir, 273,15 K (0,00 °C) y 100 kPa (0,987 atm). - ^ abc El aire contenido en el material se excluye al calcular la densidad
Otros
| Entidad | ρ (kg/ m3 ) | Notas |
|---|---|---|
| Medio interestelar | 1,7 × 10 −26 | Basado en 10 −5 átomos de hidrógeno por centímetro cúbico [22] |
| Nube interestelar local | 5 × 10 −22 | Basado en 0,3 átomos de hidrógeno por centímetro cúbico [22] |
| Medio interestelar | 1,7 × 10 −16 | Basado en 10 5 átomos de hidrógeno por centímetro cúbico [22] |
| La Tierra | 5,515 | Densidad media. [23] |
| El núcleo interno de la Tierra | 13.000 | Aprox., según aparece en Earth . [24] |
| El núcleo del Sol | 33.000–160.000 | Aprox. [25] |
| Estrella enana blanca | 2,1 × 10 9 | Aprox. [26] |
| Núcleos atómicos | 2,3 × 10 17 | No depende en gran medida del tamaño del núcleo [27] |
| Estrella de neutrones | 1 × 10 18 |
Agua
| Temperatura (°C) [nota 1] | Densidad (kg/ m3 ) |
|---|---|
| -30 | 983.854 |
| -20 | 993.547 |
| -10 | 998.117 |
| 0 | 999.8395 |
| 4 | 999.9720 |
| 10 | 999.7026 |
| 15 | 999.1026 |
| 20 | 998.2071 |
| 22 | 997.7735 |
| 25 | 997.0479 |
| 30 | 995.6502 |
| 40 | 992.2 |
| 60 | 983.2 |
| 80 | 971.8 |
| 100 | 958.4 |
Notas:
| |
Aire
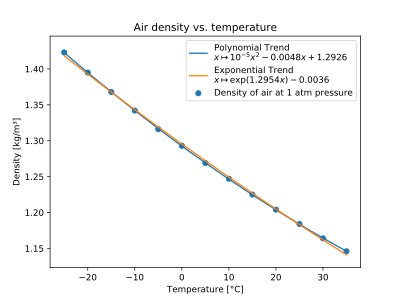
| Temperatura (°C) | ρ (kg/ m3 ) |
|---|---|
| -25 | 1.423 |
| -20 | 1.395 |
| -15 | 1.368 |
| -10 | 1.342 |
| -5 | 1.316 |
| 0 | 1.293 |
| 5 | 1.269 |
| 10 | 1.247 |
| 15 | 1.225 |
| 20 | 1.204 |
| 25 | 1.184 |
| 30 | 1.164 |
| 35 | 1.146 |
Volúmenes molares de elementos en fase líquida y sólida

Véase también
- Densidades de los elementos (página de datos)
- Lista de elementos por densidad
- Densidad del aire
- Densidad de área
- Densidad aparente
- Flotabilidad
- Densidad de carga
- Corriente de densidad
- Predicción de densidad por el método de Girolami
- Dord
- Densidad de energía
- Más ligero que el aire
- Densidad lineal
- Densidad numérica
- Densidad ortobarica
- Densidad del papel
- Peso específico
- Especias (oceanografía)
- Temperatura y presión estándar
- Cantidad volumétrica
Referencias
- ^ "Densidad de gas". Centro de Investigación Glenn . Administración Nacional de Aeronáutica y del Espacio . Archivado desde el original el 14 de abril de 2013. Consultado el 9 de abril de 2013 .
- ^ "Definición de densidad". Glosario de petróleo y gas. Archivado desde el original el 5 de agosto de 2010. Consultado el 14 de septiembre de 2010 .
- ^ Aristóteles (1952) [c. 340 a. C.]. Meteorologica (en griego antiguo e inglés). Traducido por Lee, HDP Harvard University Press. pp. 2.3, 359a.
- ^ Arquímedes, un ladrón de oro y la flotabilidad Archivado el 27 de agosto de 2007 en Wayback Machine – por Larry "Harris" Taylor, Ph.D.
- ^ Vitruvio sobre la arquitectura, Libro IX, párrafos 9-12, traducido al inglés y al latín original.
- ^ "EXPOSICIÓN: El primer momento Eureka". Science . 305 (5688): 1219e. 2004. doi : 10.1126/science.305.5688.1219e .
- ^ Biello, David (8 de diciembre de 2006). "¿Realidad o ficción?: Arquímedes acuñó el término "¡Eureka!" en el baño". Scientific American .
- ^ La Bilancetta, Texto completo del tratado de Galileo en el original italiano junto con una traducción moderna al inglés [1]
- ^ "Ensayo n.º 109: densidad de líquidos y sólidos". Directrices de la OCDE para el ensayo de sustancias químicas, sección 1 : 6. 2 de octubre de 2012. doi :10.1787/9789264123298-en. ISBN 9789264123298. ISSN 2074-5753.
- ^ El nuevo aerografito, una estructura de nanotubos de carbono, es el material más ligero Archivado el 17 de octubre de 2013 en Wayback Machine . Phys.org (13 de julio de 2012). Consultado el 14 de julio de 2012.
- ↑ Aerographit: Leichtestes Material der Welt entwickelt – SPIEGEL ONLINE Archivado el 17 de octubre de 2013 en Wayback Machine . Spiegel.de (11 de julio de 2012). Recuperado el 14 de julio de 2012.
- ^ ab "Re: ¿Cuál es más flotante, el poliestireno o el corcho?". Madsci.org. Archivado desde el original el 14 de febrero de 2011. Consultado el 14 de septiembre de 2010 .
- ^ ab Serway, Raymond; Jewett, John (2005), Principios de física: un texto basado en cálculo, Cengage Learning, pág. 467, ISBN 0-534-49143-X, archivado desde el original el 17 de mayo de 2016
- ^ "Densidades de la madera". www.engineeringtoolbox.com . Archivado desde el original el 20 de octubre de 2012. Consultado el 15 de octubre de 2012 .
- ^ "Densidad de la madera". www.simetric.co.uk . Archivado desde el original el 26 de octubre de 2012 . Consultado el 15 de octubre de 2012 .
- ^ Bolz, Ray E.; Tuve, George L., eds. (1970). "§1.3 Sólidos—Metales: Tabla 1-59 Metales y aleaciones—Propiedades diversas". Manual de tablas para la ciencia de la ingeniería aplicada del CRC (2.ª ed.). CRC Press. pág. 117. ISBN 9781315214092.
- ^ Composición del glicerol en Archivado el 28 de febrero de 2013 en Wayback Machine . Physics.nist.gov. Recuperado el 14 de julio de 2012.
- ^ abcdef Sharma, PV (1997), Geofísica ambiental e ingeniería , Cambridge University Press, pág. 17, doi :10.1017/CBO9781139171168, ISBN 9781139171168
- ^ "Densidad del hormigón - The Physics Factbook". hypertextbook.com .
- ^ ab Young, Hugh D.; Freedman, Roger A. (2012). Física universitaria con física moderna . Addison-Wesley. pág. 374. ISBN 978-0-321-69686-1.
- ^ "Densidad del vidrio - The Physics Factbook". hypertextbook.com .
- ^ abc «Nuestro vecindario galáctico local». Proyecto de sonda interestelar. NASA. 2000. Archivado desde el original el 21 de noviembre de 2013. Consultado el 8 de agosto de 2012 .
- ^ Densidad de la Tierra, wolframalpha.com, archivado desde el original el 17 de octubre de 2013
- ^ Densidad del núcleo de la Tierra, wolframalpha.com, archivado desde el original el 17 de octubre de 2013
- ^ Densidad del núcleo del Sol, wolframalpha.com, archivado desde el original el 17 de octubre de 2013
- ^ Johnson, Jennifer. "Estrellas extremas: enanas blancas y estrellas de neutrones" (PDF) . Notas de clase, Astronomía 162. Universidad Estatal de Ohio . Archivado desde el original (PDF) el 25 de septiembre de 2007.
- ^ "Tamaño y densidad nuclear". HyperPhysics . Universidad Estatal de Georgia. Archivado desde el original el 6 de julio de 2009.
Enlaces externos
- . Encyclopædia Britannica . Vol. 8 (11.ª ed.). 1911.
- . . 1914.
- Vídeo: Experimento de densidad con aceite y alcohol
- Vídeo: Experimento de densidad con whisky y agua
- Cálculo de la densidad del vidrio: cálculo de la densidad del vidrio a temperatura ambiente y del vidrio fundido a 1000 – 1400 °C
- Lista de elementos de la tabla periódica ordenados por densidad
- Cálculo de densidades de líquidos saturados para algunos componentes
- Prueba de densidad de campo Archivado el 15 de diciembre de 2010 en Wayback Machine .
- Agua – Densidad y peso específico
- Dependencia de la temperatura de la densidad del agua – Conversiones de unidades de densidad
- Un delicioso experimento de densidad Archivado el 18 de julio de 2015 en Wayback Machine .
- Calculadora de densidad del agua Archivado el 13 de julio de 2011 en Wayback Machine . Densidad del agua para una salinidad y temperatura determinadas.
- Calculadora de densidad de líquidos [ enlace muerto permanente ] Seleccione un líquido de la lista y calcule la densidad en función de la temperatura.
- Calculadora de densidad de gas [ enlace muerto permanente ] Calcule la densidad de un gas en función de la temperatura y la presión.
- Densidades de varios materiales.
- Determinación de la densidad de un sólido, instrucciones para realizar el experimento en clase.
- Lam EJ, Alvarez MN, Galvez ME, Alvarez EB (2008). "Un modelo para calcular la densidad de soluciones electrolíticas acuosas multicomponentes". Revista de la Sociedad Química de Chile . 53 (1): 1393–8. doi : 10.4067/S0717-97072008000100015 .
- Radović IR, Kijevčanin ML, Tasić AŽ, Djordjević BD, Šerbanović SP (2010). "Propiedades termodinámicas derivadas de mezclas de alcohol + ciclohexilamina". Revista de la Sociedad Química Serbia . 75 (2): 283–293. CiteSeerX 10.1.1.424.3486 . doi :10.2298/JSC1002283R.















