Densidad relativa
| Peso específico | |
|---|---|
Símbolos comunes | es |
| Unidad SI | Sin unidad |
Derivaciones de otras magnitudes | |
_3rd_Class_Rolando_Calilung_tests_for_a_specific_gravity_test_on_JP-5_fuel.jpg/440px-US_Navy_111005-N-ZN781-031_Aviation_Boatswain's_Mate_(Fuel)_3rd_Class_Rolando_Calilung_tests_for_a_specific_gravity_test_on_JP-5_fuel.jpg)
La densidad relativa , también llamada gravedad específica , [1] [2] es una cantidad adimensional definida como la relación entre la densidad (masa de una unidad de volumen) de una sustancia y la densidad de un material de referencia dado. La gravedad específica de los sólidos y líquidos casi siempre se mide con respecto al agua en su punto más denso (a 4 °C o 39,2 °F); para los gases, la referencia es el aire a temperatura ambiente (20 °C o 68 °F). El término "densidad relativa" (abreviado rd o RD ) se prefiere en el SI , mientras que el término "gravedad específica" se está abandonando gradualmente. [3]
Si la densidad relativa de una sustancia es menor que 1, entonces es menos densa que la de referencia; si es mayor que 1, entonces es más densa que la de referencia. Si la densidad relativa es exactamente 1, entonces las densidades son iguales; es decir, volúmenes iguales de las dos sustancias tienen la misma masa. Si el material de referencia es agua, entonces una sustancia con una densidad relativa (o gravedad específica) menor que 1 flotará en el agua. Por ejemplo, un cubo de hielo, con una densidad relativa de aproximadamente 0,91, flotará. Una sustancia con una densidad relativa mayor que 1 se hundirá.
La temperatura y la presión deben especificarse tanto para la muestra como para la referencia. La presión es casi siempre 1 atm (101,325 kPa ). Cuando no lo es, es más habitual especificar la densidad directamente. Las temperaturas tanto para la muestra como para la referencia varían de una industria a otra. En la práctica cervecera británica, la gravedad específica, como se especifica anteriormente, se multiplica por 1000. [4] La gravedad específica se utiliza comúnmente en la industria como un medio simple para obtener información sobre la concentración de soluciones de varios materiales como salmueras , peso del mosto ( jarabes , jugos, mieles, mosto de cerveza , mosto , etc.) y ácidos.
Cálculo básico
La densidad relativa ( ) o gravedad específica ( ) es una cantidad adimensional , ya que es la relación entre densidades o pesos , donde es la densidad relativa, es la densidad de la sustancia que se mide y es la densidad de la referencia. (Por convención , la letra griega rho denota densidad).
El material de referencia se puede indicar mediante subíndices: que significa "la densidad relativa de la sustancia con respecto a la referencia ". Si la referencia no se indica explícitamente, normalmente se supone que es agua a 4 ° C (o, más precisamente, 3,98 °C, que es la temperatura a la que el agua alcanza su densidad máxima). En unidades del SI , la densidad del agua es (aproximadamente) 1000 kg / m3 o 1 g / cm3 , lo que hace que los cálculos de densidad relativa sean particularmente convenientes: la densidad del objeto solo necesita dividirse por 1000 o 1, según las unidades .
La densidad relativa de los gases se mide a menudo con respecto al aire seco a una temperatura de 20 °C y una presión absoluta de 101,325 kPa, que tiene una densidad de 1,205 kg/m 3 . La densidad relativa con respecto al aire se puede obtener mediante donde es la masa molar y se utiliza el signo aproximadamente igual porque la igualdad solo se aplica si 1 mol del gas y 1 mol de aire ocupan el mismo volumen a una temperatura y presión dadas, es decir, ambos son gases ideales . El comportamiento ideal generalmente solo se ve a presiones muy bajas. Por ejemplo, un mol de un gas ideal ocupa 22,414 L a 0 °C y 1 atmósfera, mientras que el dióxido de carbono tiene un volumen molar de 22,259 L en esas mismas condiciones.
Los que tienen una gravedad específica mayor que 1 son más densos que el agua y, sin tener en cuenta los efectos de la tensión superficial , se hundirán en ella. Los que tienen una gravedad específica menor que 1 son menos densos que el agua y flotarán en ella. En el trabajo científico, la relación entre masa y volumen suele expresarse directamente en términos de la densidad (masa por unidad de volumen) de la sustancia en estudio. Es en la industria donde la gravedad específica encuentra una amplia aplicación, a menudo por razones históricas.
La gravedad específica verdadera de un líquido se puede expresar matemáticamente como: donde es la densidad de la muestra y es la densidad del agua.
La gravedad específica aparente es simplemente la relación de los pesos de volúmenes iguales de muestra y agua en el aire: donde representa el peso de la muestra medida en el aire y el peso de un volumen igual de agua medido en el aire.
Se puede demostrar que la gravedad específica verdadera se puede calcular a partir de diferentes propiedades:
donde g es la aceleración local debida a la gravedad, V es el volumen de la muestra y del agua (el mismo para ambos), ρ muestra es la densidad de la muestra, ρ H 2 O es la densidad del agua, W V representa un peso obtenido en el vacío, es la masa de la muestra y es la masa de un volumen igual de agua.
La densidad del agua y de la muestra varía con la temperatura y la presión, por lo que es necesario especificar las temperaturas y presiones a las que se determinaron las densidades o pesos. Las mediciones casi siempre se realizan a 1 atmósfera nominal (101,325 kPa ± variaciones de los patrones climáticos cambiantes), pero como la gravedad específica generalmente se refiere a soluciones acuosas altamente incompresibles u otras sustancias incompresibles (como productos derivados del petróleo), las variaciones en la densidad causadas por la presión generalmente se descuidan al menos cuando se mide la gravedad específica aparente. Para los cálculos de gravedad específica verdaderos ( en vacío ), se debe considerar la presión del aire (ver a continuación). Las temperaturas se especifican mediante la notación ( T s / T r ), donde T s representa la temperatura a la que se determinó la densidad de la muestra y T r la temperatura a la que se especifica la densidad de referencia (agua). Por ejemplo, se entendería que SG (20 °C/4 °C) significa que la densidad de la muestra se determinó a 20 °C y la del agua a 4 °C. Teniendo en cuenta diferentes temperaturas de muestra y de referencia, mientras que SG H 2 O =1.000 000 (20 °C/20 °C), también es el caso que SG H 2 O =0,998 2008 ⁄0,999 9720 =0,998 2288 (20 °C/4 °C). Aquí, la temperatura se especifica utilizando la escala ITS-90 actual y las densidades [5] utilizadas aquí y en el resto de este artículo se basan en esa escala. En la escala IPTS-68 anterior, las densidades a 20 °C y 4 °C son0,998 2041 y0,999 9720 respectivamente, [6] resultando en un valor de SG (20 °C/4 °C) para agua de0,998 232 .
Como el uso principal de las mediciones de gravedad específica en la industria es la determinación de las concentraciones de sustancias en soluciones acuosas y como estas se encuentran en tablas de gravedad específica versus concentración, es extremadamente importante que el analista ingrese la tabla con la forma correcta de gravedad específica. Por ejemplo, en la industria cervecera, la tabla de Platón enumera la concentración de sacarosa en peso contra la gravedad específica real, y originalmente era (20 °C/4 °C) [7], es decir, se basaba en mediciones de la densidad de soluciones de sacarosa realizadas a temperatura de laboratorio (20 °C) pero referenciadas a la densidad del agua a 4 °C, que es muy cercana a la temperatura a la que el agua tiene su densidad máxima, ρ H 2 O igual a 999,972 kg/m 3 en unidades del SI (0,999 972 g/cm 3 en unidades cgs o 62,43 lb/cu ft en unidades habituales de los Estados Unidos ). La tabla ASBC [8] que se utiliza actualmente en Norteamérica para mediciones de gravedad específica aparente a (20 °C/20 °C) se deriva de la tabla Plato original utilizando el valor de Plato et al. para SG(20 °C/4 °C) =0,998 2343 . En las industrias del azúcar, los refrescos, la miel, los jugos de frutas y las relacionadas, la concentración de sacarosa en peso se toma de una tabla preparada por A. Brix , que utiliza SG (17,5 °C/17,5 °C). Como ejemplo final, las unidades de SG británicas se basan en temperaturas de referencia y de muestra de 60 °F y, por lo tanto, son (15,56 °C/15,56 °C).
Dada la gravedad específica de una sustancia, su densidad real se puede calcular reorganizando la fórmula anterior:
Ocasionalmente se especifica una sustancia de referencia distinta del agua (por ejemplo, aire), en cuyo caso la gravedad específica significa densidad relativa a esa referencia.
Dependencia de la temperatura
- Consulte Densidad para ver una tabla de las densidades medidas del agua a distintas temperaturas.
La densidad de las sustancias varía con la temperatura y la presión, por lo que es necesario especificar las temperaturas y presiones a las que se determinaron las densidades o masas. Casi siempre se da el caso de que las mediciones se realizan a una presión nominal de 1 atmósfera (101,325 kPa, ignorando las variaciones causadas por los patrones climáticos cambiantes), pero como la densidad relativa generalmente se refiere a soluciones acuosas altamente incompresibles u otras sustancias incompresibles (como productos derivados del petróleo), las variaciones de densidad causadas por la presión generalmente se ignoran, al menos cuando se mide la densidad relativa aparente. Para los cálculos de densidad relativa verdaderos ( en vacío ), se debe considerar la presión del aire (ver a continuación). Las temperaturas se especifican mediante la notación ( T s / T r ), donde T s representa la temperatura a la que se determinó la densidad de la muestra y T r la temperatura a la que se especifica la densidad de referencia (agua). Por ejemplo, se entendería que SG (20 °C/4 °C) significa que la densidad de la muestra se determinó a 20 °C y la del agua a 4 °C. Teniendo en cuenta las diferentes temperaturas de muestra y de referencia, mientras que SG H 2 O = 1,000000 (20 °C/20 °C) también es el caso que RD H 2 O = 0,9982008/0,9999720 = 0,9982288 (20 °C/4 °C). Aquí se especifica la temperatura utilizando la escala ITS-90 actual y las densidades [5] utilizadas aquí y en el resto de este artículo se basan en esa escala. En la escala IPTS-68 anterior, las densidades [6] a 20 °C y 4 °C son, respectivamente, 0,9982041 y 0,9999720, lo que da como resultado un valor RD (20 °C/4 °C) para el agua de 0,99823205.
Las temperaturas de los dos materiales pueden indicarse explícitamente en los símbolos de densidad; por ejemplo:
- densidad relativa: 8,1520 °C
4 °C; o gravedad específica: 2,43215
0
donde el superíndice indica la temperatura a la que se mide la densidad del material y el subíndice indica la temperatura de la sustancia de referencia con la que se compara.
Usos
La densidad relativa también puede ayudar a cuantificar la flotabilidad de una sustancia en un fluido o gas, o determinar la densidad de una sustancia desconocida a partir de la densidad conocida de otra. Los geólogos y mineralogistas suelen utilizar la densidad relativa para determinar el contenido mineral de una roca u otra muestra. Los gemólogos la utilizan como ayuda para la identificación de piedras preciosas . Se prefiere el agua como referencia porque las mediciones son fáciles de realizar en el campo (consulte a continuación ejemplos de métodos de medición).
Como el uso principal de las mediciones de densidad relativa en la industria es la determinación de las concentraciones de sustancias en soluciones acuosas y estas se encuentran en tablas de RD vs concentración, es extremadamente importante que el analista ingrese la tabla con la forma correcta de densidad relativa. Por ejemplo, en la industria cervecera, la tabla de Platón , que enumera la concentración de sacarosa por masa contra la RD verdadera, originalmente era (20 °C/4 °C) [7] que se basa en mediciones de la densidad de soluciones de sacarosa realizadas a temperatura de laboratorio (20 °C) pero referenciadas a la densidad del agua a 4 °C que es muy cercana a la temperatura a la que el agua tiene su densidad máxima de ρ ( H
2O ) igual a 0,999972 g/cm 3 (o 62,43 lb·ft −3 ). La tabla ASBC [8] que se utiliza actualmente en Norteamérica, si bien se deriva de la tabla Platón original, es para mediciones de densidad relativa aparente a (20 °C/20 °C) en la escala IPTS-68 donde la densidad del agua es 0,9982071 g/cm 3 . En las industrias del azúcar, refrescos, miel, jugos de frutas y relacionadas, la concentración de sacarosa en masa se toma de este trabajo [4] que utiliza SG (17,5 °C/17,5 °C). Como ejemplo final, las unidades RD británicas se basan en temperaturas de referencia y de muestra de 60 °F y, por lo tanto, son (15,56 °C/15,56 °C). [4]
Medición
La densidad relativa se puede calcular directamente midiendo la densidad de una muestra y dividiéndola por la densidad (conocida) de la sustancia de referencia. La densidad de la muestra es simplemente su masa dividida por su volumen. Aunque la masa es fácil de medir, el volumen de una muestra de forma irregular puede ser más difícil de determinar. Un método consiste en colocar la muestra en un cilindro graduado lleno de agua y leer la cantidad de agua que desplaza. Otra opción es llenar el recipiente hasta el borde, sumergir la muestra y medir el volumen de desbordamiento. La tensión superficial del agua puede evitar que se desborde una cantidad significativa de agua, lo que es especialmente problemático para muestras pequeñas. Por este motivo, es conveniente utilizar un recipiente de agua con una boca lo más pequeña posible.
Para cada sustancia, la densidad, ρ , viene dada por
Cuando se dividen estas densidades, las referencias a la constante del resorte, la gravedad y el área de la sección transversal simplemente se cancelan, quedando
Pesaje hidrostático
La densidad relativa se mide con mayor facilidad y quizás con mayor precisión sin medir el volumen. Utilizando una báscula de resorte, la muestra se pesa primero en el aire y luego en el agua. La densidad relativa (con respecto al agua) se puede calcular utilizando la siguiente fórmula: donde
- W air es el peso de la muestra en el aire (medido en newtons , libras-fuerza o alguna otra unidad de fuerza)
- W agua es el peso de la muestra en agua (medido en las mismas unidades).
Esta técnica no se puede utilizar fácilmente para medir densidades relativas inferiores a uno, porque la muestra flotaría. W agua se convierte en una cantidad negativa, que representa la fuerza necesaria para mantener la muestra bajo el agua.
Otro método práctico utiliza tres medidas. La muestra se pesa en seco. A continuación, se pesa un recipiente lleno hasta el borde con agua y se vuelve a pesar con la muestra sumergida, una vez que el agua desplazada se ha desbordado y se ha eliminado. Restando la última lectura de la suma de las dos primeras lecturas se obtiene el peso del agua desplazada. El resultado de la densidad relativa es el peso de la muestra en seco dividido por el del agua desplazada. Este método permite el uso de básculas que no pueden manipular una muestra suspendida. También se puede manipular una muestra menos densa que el agua, pero hay que sujetarla y tener en cuenta el error introducido por el material de fijación.
Hidrómetro
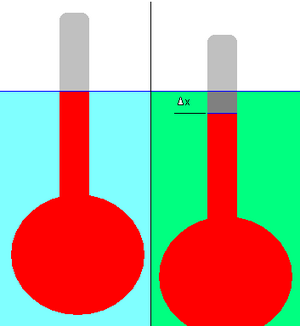
La densidad relativa de un líquido se puede medir con un hidrómetro, que consiste en un bulbo unido a un vástago de sección transversal constante, como se muestra en el diagrama adjunto.
En primer lugar, se hace flotar el hidrómetro en el líquido de referencia (mostrado en azul claro) y se marca el desplazamiento (el nivel del líquido en el vástago) (línea azul). El líquido de referencia puede ser cualquier líquido, pero en la práctica suele ser agua.
A continuación, el hidrómetro se deja flotar en un líquido de densidad desconocida (mostrado en verde). Se anota el cambio en el desplazamiento, Δ x . En el ejemplo representado, el hidrómetro ha descendido ligeramente en el líquido verde; por lo tanto, su densidad es menor que la del líquido de referencia. Es necesario que el hidrómetro flote en ambos líquidos.
La aplicación de principios físicos simples permite calcular la densidad relativa del líquido desconocido a partir del cambio de desplazamiento. (En la práctica, el vástago del hidrómetro está marcado previamente con graduaciones para facilitar esta medición).
En la explicación que sigue,
- ρ ref es la densidad conocida ( masa por unidad de volumen ) del líquido de referencia (normalmente agua).
- ρ nuevo es la densidad desconocida del nuevo líquido (verde).
- RD nuevo/ref es la densidad relativa del nuevo líquido con respecto a la referencia.
- V es el volumen del líquido de referencia desplazado, es decir, el volumen rojo en el diagrama.
- m es la masa de todo el hidrómetro.
- g es la constante gravitacional local .
- Δ x es el cambio de desplazamiento. De acuerdo con la forma en que se suelen graduar los hidrómetros, Δ x se considera aquí negativo si la línea de desplazamiento asciende en el vástago del hidrómetro, y positivo si desciende. En el ejemplo representado, Δ x es negativo.
- A es el área de la sección transversal del eje.
Como el hidrómetro flotante está en equilibrio estático , la fuerza gravitacional descendente que actúa sobre él debe equilibrar exactamente la fuerza de flotabilidad ascendente. La fuerza gravitacional que actúa sobre el hidrómetro es simplemente su peso, mg . Según el principio de flotabilidad de Arquímedes , la fuerza de flotabilidad que actúa sobre el hidrómetro es igual al peso del líquido desplazado. Este peso es igual a la masa del líquido desplazado multiplicada por g , que en el caso del líquido de referencia es ρ ref Vg . Al igualarlos, tenemos
o simplemente
| ( 1 ) |
Se aplica exactamente la misma ecuación cuando el hidrómetro está flotando en el líquido que se está midiendo, excepto que el nuevo volumen es V − A Δ x (ver nota anterior sobre el signo de Δ x ). Por lo tanto,
| ( 2 ) |
Combinando ( 1 ) y ( 2 ) se obtiene
| ( 3 ) |
Pero de ( 1 ) tenemos V = m / ρ ref . Sustituyendo en ( 3 ) obtenemos
| ( 4 ) |
Esta ecuación permite calcular la densidad relativa a partir del cambio de desplazamiento, la densidad conocida del líquido de referencia y las propiedades conocidas del hidrómetro. Si Δ x es pequeño, entonces, como aproximación de primer orden de la ecuación de la serie geométrica ( 4 ) se puede escribir como:
Esto demuestra que, para Δ x pequeños , los cambios en el desplazamiento son aproximadamente proporcionales a los cambios en la densidad relativa.
Picnómetro


Un picnómetro (del griego antiguo πυκνός , romanizado : puknos , lit. ' denso'), también llamado picnómetro o botella de gravedad específica , es un dispositivo utilizado para determinar la densidad de un líquido. Un picnómetro suele estar hecho de vidrio , con un tapón de vidrio esmerilado ajustado con un tubo capilar a través de él, de modo que las burbujas de aire puedan escapar del aparato. Este dispositivo permite medir la densidad de un líquido con precisión en referencia a un fluido de trabajo apropiado, como agua o mercurio , utilizando una balanza analítica . [ cita requerida ]
Si se pesa el matraz vacío, lleno de agua y lleno de un líquido cuya densidad relativa se desea, se puede calcular fácilmente la densidad relativa del líquido. La densidad de partículas de un polvo, al que no se puede aplicar el método habitual de pesaje, también se puede determinar con un picnómetro. El polvo se añade al picnómetro, que luego se pesa, dando el peso de la muestra de polvo. A continuación, el picnómetro se llena con un líquido de densidad conocida, en el que el polvo es completamente insoluble. A continuación, se puede determinar el peso del líquido desplazado y, por lo tanto, la densidad relativa del polvo.
Un picnómetro de gas , la manifestación basada en gas de un picnómetro, compara el cambio de presión causado por un cambio medido en un volumen cerrado que contiene una referencia (normalmente una esfera de acero de volumen conocido) con el cambio de presión causado por la muestra en las mismas condiciones. La diferencia en el cambio de presión representa el volumen de la muestra en comparación con la esfera de referencia y se utiliza normalmente para partículas sólidas que pueden disolverse en el medio líquido del diseño del picnómetro descrito anteriormente o para materiales porosos en los que el líquido no penetraría por completo.
Cuando se llena un picnómetro hasta un volumen específico, pero no necesariamente conocido con precisión, V , y se coloca sobre una balanza, ejercerá una fuerza donde m b es la masa de la botella y g la aceleración gravitacional en el lugar en el que se están realizando las mediciones. ρ a es la densidad del aire a la presión ambiente y ρ b es la densidad del material del que está hecha la botella (normalmente vidrio), de modo que el segundo término es la masa de aire desplazada por el vidrio de la botella, cuyo peso, por el principio de Arquímedes, debe restarse. La botella está llena de aire, pero como ese aire desplaza una cantidad igual de aire, el peso de ese aire se cancela por el peso del aire desplazado. Ahora llenamos la botella con el fluido de referencia, por ejemplo, agua pura. La fuerza ejercida sobre el platillo de la balanza se convierte en:
Si restamos de esto la fuerza medida sobre la botella vacía (o taramos la balanza antes de realizar la medición del agua), obtenemos. donde el subíndice n indica que esta fuerza es neta de la fuerza de la botella vacía. Ahora la botella está vacía, secada completamente y rellenada con la muestra. La fuerza, neta de la botella vacía, es ahora: donde ρ s es la densidad de la muestra. La relación entre las fuerzas de la muestra y del agua es:
A esto se le llama densidad relativa aparente , denotada por el subíndice A, porque es lo que obtendríamos si tomáramos la relación de las pesadas netas en el aire de una balanza analítica o usáramos un hidrómetro (el vástago desplaza el aire). Nótese que el resultado no depende de la calibración de la balanza. El único requisito es que la lectura sea lineal con la fuerza. RD A tampoco depende del volumen real del picnómetro.
Una manipulación adicional y finalmente la sustitución de RD V , la densidad relativa verdadera (se utiliza el subíndice V porque a menudo se hace referencia a ella como la densidad relativa en el vacío ), por ρ s / ρ w da la relación entre la densidad relativa aparente y la verdadera:
En el caso habitual, habremos medido pesos y querremos conocer la densidad relativa real. Esta se obtiene a partir de
Puesto que la densidad del aire seco a 101,325 kPa a 20 °C es [9] 0,001205 g/cm 3 y la del agua es 0,998203 g/cm 3, vemos que la diferencia entre las densidades relativas verdaderas y aparentes para una sustancia con una densidad relativa (20 °C/20 °C) de aproximadamente 1,100 sería 0,000120. Cuando la densidad relativa de la muestra es cercana a la del agua (por ejemplo, soluciones de etanol diluidas), la corrección es incluso menor.
El picnómetro se utiliza en la norma ISO: ISO 1183-1:2004, ISO 1014–1985 y en la norma ASTM : ASTM D854.
Tipos
- Gay-Lussac , en forma de pera, con tapón perforado, ajustado, capacidad 1, 2, 5, 10, 25, 50 y 100 mL
- Como arriba, con termómetro esmerilado , ajustado, tubo lateral con tapa
- Hubbard, para betún y crudos pesados , tipo cilíndrico, ASTM D 70, 24 mL
- Como arriba, tipo cónico, ASTM D 115 y D 234, 25 mL
- Bota, con camisa de vacío y termómetro, capacidad 5, 10, 25 y 50 mL
Densímetros digitales
Instrumentos basados en presión hidrostática : esta tecnología se basa en el principio de Pascal, que establece que la diferencia de presión entre dos puntos dentro de una columna vertical de fluido depende de la distancia vertical entre los dos puntos, la densidad del fluido y la fuerza gravitacional. Esta tecnología se utiliza a menudo para aplicaciones de medición de tanques como un medio conveniente para medir el nivel y la densidad del líquido.
Transductores de elementos vibratorios : este tipo de instrumento requiere que se coloque un elemento vibratorio en contacto con el fluido de interés. Se mide la frecuencia de resonancia del elemento y se relaciona con la densidad del fluido mediante una caracterización que depende del diseño del elemento. En los laboratorios modernos, se realizan mediciones precisas de densidad relativa utilizando medidores de tubo en U oscilantes . Estos pueden medir hasta 5 o 6 lugares más allá del punto decimal y se utilizan en las industrias cervecera, de destilación, farmacéutica, petrolera y otras. Los instrumentos miden la masa real de fluido contenido en un volumen fijo a temperaturas entre 0 y 80 °C, pero como están basados en microprocesadores, pueden calcular la densidad relativa aparente o verdadera y contienen tablas que relacionan estas con las concentraciones de ácidos comunes, soluciones de azúcar, etc.
Transductor ultrasónico : las ondas ultrasónicas pasan desde una fuente a través del fluido de interés y llegan a un detector que mide la espectroscopia acústica de las ondas. Las propiedades del fluido, como la densidad y la viscosidad, se pueden inferir a partir del espectro.
Medidor basado en radiación : la radiación pasa desde una fuente, a través del fluido de interés, hasta un detector de centelleo o contador. A medida que aumenta la densidad del fluido, los "conteos" de radiación detectados disminuirán. La fuente es típicamente el isótopo radiactivo cesio-137 , con una vida media de aproximadamente 30 años. Una ventaja clave de esta tecnología es que no se requiere que el instrumento esté en contacto con el fluido; por lo general, la fuente y el detector se montan en el exterior de los tanques o tuberías. [10]
Transductor de fuerza de flotación : la fuerza de flotación producida por un flotador en un líquido homogéneo es igual al peso del líquido que es desplazado por el flotador. Dado que la fuerza de flotación es lineal con respecto a la densidad del líquido dentro del cual está sumergido el flotador, la medida de la fuerza de flotación produce una medida de la densidad del líquido. Una unidad disponible comercialmente afirma que el instrumento es capaz de medir la densidad relativa con una precisión de ± 0,005 unidades RD. El cabezal de la sonda sumergible contiene un sistema de flotador-resorte caracterizado matemáticamente. Cuando el cabezal se sumerge verticalmente en el líquido, el flotador se mueve verticalmente y la posición del flotador controla la posición de un imán permanente cuyo desplazamiento es detectado por una matriz concéntrica de sensores de desplazamiento lineal de efecto Hall. Las señales de salida de los sensores se mezclan en un módulo electrónico dedicado que proporciona un único voltaje de salida cuya magnitud es una medida lineal directa de la cantidad que se va a medir. [11]
La densidad relativa en la mecánica de suelos
La densidad relativa es una medida de la relación de huecos actual en relación con las relaciones de huecos máxima y mínima, y la tensión efectiva aplicada controla el comportamiento mecánico del suelo sin cohesión. La densidad relativa se define por donde , y son las relaciones de huecos máxima, mínima y real.
Limitaciones
La gravedad específica (GE) es un concepto útil, pero tiene varias limitaciones. Un problema importante es su sensibilidad a la temperatura, ya que la densidad tanto de la sustancia que se mide como de la referencia cambia con la temperatura, lo que afecta la precisión. [12] También supone que los materiales son incompresibles, lo que no es cierto para los gases o algunos líquidos bajo presiones variables. [13] No proporciona información detallada sobre la composición o las propiedades de un material más allá de la densidad. [14] También pueden producirse errores debido a impurezas, mezcla incompleta o burbujas de aire en líquidos, que pueden distorsionar los resultados. [15]
Ejemplos
| Material | Peso específico |
|---|---|
| Madera de balsa | 0,2 |
| Madera de roble | 0,75 |
| Etanol | 0,78 |
| Aceite de oliva | 0,91 |
| Agua | 1 |
| Palo de hierro | 1.5 |
| Grafito | 1.9–2.3 |
| Sal de mesa | 2.17 |
| Aluminio | 2.7 |
| Cemento | 3.15 |
| Hierro | 7.87 |
| Cobre | 8,96 |
| Dirigir | 11.35 |
| Mercurio | 13.56 |
| Uranio empobrecido | 19.1 |
| Oro | 19.3 |
| Osmio | 22,59 |
(Las muestras pueden variar y estas cifras son aproximadas).
Las sustancias con una densidad relativa de 1 son neutralmente flotantes, aquellas con una RD mayor que uno son más densas que el agua y, por lo tanto (ignorando los efectos de la tensión superficial ) se hundirán en ella, y aquellas con una RD menor que uno son menos densas que el agua y, por lo tanto, flotarán.
Ejemplo:
El gas helio tiene una densidad de 0,164 g/L; [16] es 0,139 veces más denso que el aire , que tiene una densidad de 1,18 g/L. [16]
- La orina normalmente tiene una gravedad específica entre 1,003 y 1,030. La prueba diagnóstica de gravedad específica de la orina se utiliza para evaluar la capacidad de concentración renal para la evaluación del sistema urinario. [17] Una concentración baja puede indicar diabetes insípida , mientras que una concentración alta puede indicar albuminuria o glucosuria . [17]
- La sangre normalmente tiene una gravedad específica de aproximadamente 1,060. [18]
- El vodka de 80° proof (40% v/v) tiene una gravedad específica de 0,9498. [19]
Véase también
Referencias
- ^ Dana, Edward Salisbury (1922). Un libro de texto de mineralogía: con un tratado extenso sobre cristalografía... Nueva York, Londres (Chapman Hall): John Wiley and Sons. pp. 195–200, 316.
- ^ Schetz, José A.; Allen E. Fuhs (5 de febrero de 1999). Fundamentos de la mecánica de fluidos. Wiley, John & Sons, incorporada. págs.111, 142, 144, 147, 109, 155, 157, 160, 175. ISBN 0-471-34856-2.
- ^ Oficina de Recuperación de los Estados Unidos (1978). Manual métrico. Departamento del Interior de los Estados Unidos, Oficina de Recuperación. pág. 37.
- ^ abc Hough, JS, Briggs, DE, Stevens, R y Young, TW Malting and Brewing Science, Vol. II Hopped Wort and Beer, Chapman and Hall, Londres, 1997, pág. 881 ISBN 0-412-16590-2
- ^ ab Bettin, H.; Spiewek, F. (1990). "Die Dichte des Wassers als Funktion der Temperatur nach Einführung des Internationalen Temperaturskala von 1990". PTB-Mitteilungen (en alemán). 100 : 195-196.
- ^ ab Kell, George S. "Densidad, expansividad térmica y compresibilidad del agua líquida de 0 a 150 °C: correlaciones y tablas para la presión atmosférica y la saturación revisadas y expresadas en la escala de temperatura de 1968". Journal of Chemical and Engineering Data . 20 : 97–105. doi :10.1021/je60064a005.
- ^ ab Métodos de análisis de la ASBC Prefacio a la Tabla 1: Extracto en mosto y cerveza, Sociedad Estadounidense de Químicos Cerveceros, St Paul, 2009
- ^ ab Métodos de análisis de la ASBC, op. cit. Tabla 1: Extracto en mosto y cerveza
- ^ DIN51 757 (04.1994): Ensayo de aceites minerales y materiales relacionados; determinación de la densidad
- ^ Densidad – VEGA Americas, Inc. Ohmartvega.com. Consultado el 30 de septiembre de 2011.
- ^ Hidrómetro electrónico digital para control de procesos. Gardco. Recuperado el 30 de septiembre de 2011.
- ^ Shaw, PE (1916). "La constante newtoniana de gravitación en función de la temperatura". Philosophical Transactions of the Royal Society of London . 216 (538–548): 349–392. doi : 10.1098/rsta.1916.0007 .
- ^ "Capítulo 3: Gravedad específica". Manual de diseño de ingeniería: fluidos hidráulicos . Comando de Material del Ejército de EE. UU. 1971. pág. 3-38 . Consultado el 15 de septiembre de 2024 .
- ^ Trento, Chin (5 de enero de 2024). "Gravedad específica: líquidos, gases y sólidos". Stanford Advanced Materials . Consultado el 15 de septiembre de 2024 .
- ^ Patente WO 1992005422A1
- ^ ab "Demostraciones de conferencias". physics.ucsb.edu .
- ^ ab Lewis, Sharon Mantik; Dirksen, Shannon Ruff; Heitkemper, Margaret M.; Bucher, Linda; Harding, Mariann (5 de diciembre de 2013). Enfermería médico-quirúrgica: evaluación y gestión de problemas clínicos (novena edición). St. Louis, Missouri. ISBN 978-0-323-10089-2.OCLC 228373703 .
{{cite book}}: CS1 maint: location missing publisher (link) - ^ Shmukler, Michael (2004). Elert, Glenn (ed.). "Densidad de la sangre". The Physics Factbook . Consultado el 23 de enero de 2022 .
- ^ "Gravedad específica de los licores". Good Cocktails.com .
Lectura adicional
- Fundamentos de mecánica de fluidos Wiley, BR Munson, DF Young y TH Okishi
- Introducción a la mecánica de fluidos , cuarta edición, Wiley, versión SI, RW Fox y AT McDonald
- Termodinámica: un enfoque de ingeniería, segunda edición, McGraw-Hill, edición internacional, YA Cengel y MA Boles
- Munson, BR; DF Young; TH Okishi (2001). Fundamentos de mecánica de fluidos (4.ª ed.). Wiley. ISBN 978-0-471-44250-9.
- Fox, RW; McDonald, AT (2003). Introducción a la mecánica de fluidos (4.ª ed.). Wiley. ISBN 0-471-20231-2.
Enlaces externos
- Pesos de gravedad específica de los materiales (archivado el 22 de mayo de 2006)








































