Teorema de Bayes

Parte de una serie sobre
Estadísticas bayesianas
Posterior = Probabilidad × Anterior ÷ Evidencia
Fondo
Inferencia bayesiana Probabilidad bayesiana Teorema de Bayes Teorema de Bernstein-von Mises Coherencia Teorema de Cox El gobierno de Cromwell Principio de verosimilitud Principio de indiferencia Principio de máxima entropía
Construcción de modelos
Conjugado anterior Regresión lineal Bayes empírico Modelo jerárquico
Aproximación posterior
Cadena de Markov Monte Carlo Aproximación de Laplace Aproximaciones de Laplace anidadas integradas Inferencia variacional Cálculo bayesiano aproximado
Estimadores
Estimador bayesiano Intervalo creíble Estimación máxima a posteriori
Aproximación de evidencia
Límite inferior de evidencia Muestreo anidado
Evaluación del modelo
Factor de Bayes Promedio del modelo Predicción posterior
Portal de matemáticas
en a mi

El teorema de Bayes (también conocido como ley de Bayes o regla de Bayes , en honor a Thomas Bayes ) proporciona una regla matemática para invertir las probabilidades condicionales , lo que nos permite hallar la probabilidad de una causa dado su efecto. ^[1] Por ejemplo, si se sabe que el riesgo de desarrollar problemas de salud aumenta con la edad, el teorema de Bayes permite evaluar con mayor precisión el riesgo de un individuo de una edad conocida condicionándolo en relación con su edad, en lugar de asumir que el individuo es típico de la población en su conjunto. Según la ley de Bayes, se deben tener en cuenta tanto la prevalencia de una enfermedad en una población dada como la tasa de error de una prueba de enfermedad infecciosa para evaluar correctamente el significado de un resultado positivo de la prueba y evitar la falacia de la tasa base .

Una de las muchas aplicaciones del teorema de Bayes es la inferencia bayesiana , un enfoque particular de la inferencia estadística , donde se utiliza para invertir la probabilidad de las observaciones dada una configuración del modelo (es decir, la función de verosimilitud ) para obtener la probabilidad de la configuración del modelo dadas las observaciones (es decir, la probabilidad posterior ).

El teorema de Bayes recibe su nombre del reverendo Thomas Bayes ( / b eɪ z / ), también estadístico y filósofo. Bayes utilizó la probabilidad condicional para proporcionar un algoritmo (su Proposición 9) que utiliza evidencia para calcular límites sobre un parámetro desconocido. Su trabajo fue publicado en 1763 como Un ensayo para resolver un problema en la doctrina de las probabilidades . Bayes estudió cómo calcular una distribución para el parámetro de probabilidad de una distribución binomial (en terminología moderna). A la muerte de Bayes, su familia transfirió sus documentos a un amigo, el ministro, filósofo y matemático Richard Price .

Durante dos años, Richard Price editó en profundidad el manuscrito inédito, antes de enviárselo a un amigo que lo leyó en voz alta en la Royal Society el 23 de diciembre de 1763. ^[2] Price editó ^[3] la obra principal de Bayes "An Essay Towards Solving a Problem in the Doctrine of Chances" (1763), que apareció en Philosophical Transactions , ^[4] y que contiene el teorema de Bayes. Price escribió una introducción al artículo que proporciona algunas de las bases filosóficas de las estadísticas bayesianas y eligió una de las dos soluciones ofrecidas por Bayes. En 1765, Price fue elegido miembro de la Royal Society en reconocimiento a su trabajo sobre el legado de Bayes. ^{[5] [6]} El 27 de abril se leyó en la Royal Society una carta enviada a su amigo Benjamin Franklin , que luego se publicó, en la que Price aplica este trabajo a la población y al cálculo de "anualidades vitalicias". ^[7]

Independientemente de Bayes, Pierre-Simon Laplace en 1774, y más tarde en su Théorie analytique des probabilités de 1812 , utilizó la probabilidad condicional para formular la relación de una probabilidad posterior actualizada a partir de una probabilidad previa, dada la evidencia. Reprodujo y amplió los resultados de Bayes en 1774, aparentemente sin conocer el trabajo de Bayes. ^{[nota 1] [8]} La interpretación bayesiana de la probabilidad fue desarrollada principalmente por Laplace. ^[9]

Unos 200 años después, Sir Harold Jeffreys puso el algoritmo de Bayes y la formulación de Laplace sobre una base axiomática , escribiendo en un libro de 1973 que el teorema de Bayes "es a la teoría de la probabilidad lo que el teorema de Pitágoras es a la geometría". ^[10]

Stephen Stigler utilizó un argumento bayesiano para concluir que el teorema de Bayes fue descubierto por Nicholas Saunderson , un matemático inglés ciego, algún tiempo antes que Bayes; ^{[11] [12]} sin embargo, esa interpretación ha sido cuestionada. ^[13] Martyn Hooper ^[14] y Sharon McGrayne ^[15] han argumentado que la contribución de Richard Price fue sustancial:

Según los estándares modernos, deberíamos referirnos a la regla de Bayes-Price. Price descubrió el trabajo de Bayes, reconoció su importancia, lo corrigió, contribuyó al artículo y encontró un uso para él. La convención moderna de emplear solo el nombre de Bayes es injusta, pero está tan arraigada que cualquier otra cosa tiene poco sentido. ^[15]

El teorema de Bayes se enuncia matemáticamente como la siguiente ecuación: ^[16]

donde y son eventos y .${\estilo de visualización A}$${\estilo de visualización B}$${\displaystyle P(B)\neq 0}$

• ${\displaystyle P(A\vert B)}$es una probabilidad condicional : la probabilidad de que ocurra un evento dado que es verdadero. También se denomina probabilidad posterior de un evento dado .${\estilo de visualización A}$${\estilo de visualización B}$${\estilo de visualización A}$${\estilo de visualización B}$
• ${\displaystyle P(B\vert A)}$También es una probabilidad condicional: la probabilidad de que ocurra un evento dado que es cierto. También se puede interpretar como la probabilidad de que se dé un evento fijo porque .${\estilo de visualización B}$${\estilo de visualización A}$${\estilo de visualización A}$${\estilo de visualización B}$${\displaystyle P(B\vert A)=L(A\vert B)}$
• ${\estilo de visualización P(A)}$y son las probabilidades de observar y respectivamente sin ninguna condición dada; se conocen como probabilidad previa y probabilidad marginal .${\estilo de visualización P(B)}$${\estilo de visualización A}$${\estilo de visualización B}$

El teorema de Bayes puede derivarse de la definición de probabilidad condicional :

${\displaystyle P(A\vert B)={\frac {P(A\cap B)}{P(B)}},{\text{ if }}P(B)\neq 0,}$

donde es la probabilidad de que tanto A como B sean verdaderas. De manera similar,${\displaystyle P(A\cap B)}$

${\displaystyle P(B\vert A)={\frac {P(A\cap B)}{P(A)}},{\text{ if }}P(A)\neq 0.}$

Resolviendo y sustituyendo en la expresión anterior se obtiene el teorema de Bayes:${\displaystyle P(A\cap B)}$${\displaystyle P(A\vert B)}$

${\displaystyle P(A\vert B)={\frac {P(B\vert A)P(A)}{P(B)}},{\text{ if }}P(B)\neq 0.}$

Para dos variables aleatorias continuas X e Y , el teorema de Bayes puede derivarse análogamente de la definición de densidad condicional :

${\displaystyle f_{X\vert Y=y}(x)={\frac {f_{X,Y}(x,y)}{f_{Y}(y)}}}$

${\displaystyle f_{Y\vert X=x}(y)={\frac {f_{X,Y}(x,y)}{f_{X}(x)}}}$

Por lo tanto,

${\displaystyle f_{X\vert Y=y}(x)={\frac {f_{Y\vert X=x}(y)f_{X}(x)}{f_{Y}(y)}}.}$

Sea la distribución condicional de dados y sea la distribución de . La distribución conjunta es entonces . La distribución condicional de dados se determina entonces por${\displaystyle P_{Y}^{x}}$${\displaystyle Y}$${\displaystyle X=x}$${\displaystyle P_{X}}$${\displaystyle X}$${\displaystyle P_{X,Y}(dx,dy)=P_{Y}^{x}(dy)P_{X}(dx)}$${\displaystyle P_{X}^{y}}$${\displaystyle X}$${\displaystyle Y=y}$

$${\displaystyle P_{X}^{y}(A)=E(1_{A}(X)|Y=y)}$$

La existencia y unicidad de la expectativa condicional necesaria es una consecuencia del teorema de Radon-Nikodym . Este fue formulado por Kolmogorov en su famoso libro de 1933. Kolmogorov subraya la importancia de la probabilidad condicional al escribir "Deseo llamar la atención sobre... y especialmente la teoría de probabilidades condicionales y expectativas condicionales..." en el Prefacio. ^[17] El teorema de Bayes determina la distribución posterior a partir de la distribución anterior. La unicidad requiere suposiciones de continuidad. ^[18] El teorema de Bayes se puede generalizar para incluir distribuciones anteriores impropias, como la distribución uniforme en la línea real. ^[19] Los métodos modernos de Monte Carlo de cadena de Markov han impulsado la importancia del teorema de Bayes, incluidos los casos con anteriores impropias. ^[20]

La regla de Bayes y el cálculo de probabilidades condicionales proporcionan un método de solución para una serie de problemas populares, como el problema de los tres prisioneros , el problema de Monty Hall , el problema de los dos niños y el problema de los dos sobres .

Supongamos que una prueba particular para determinar si alguien ha consumido cannabis tiene una sensibilidad del 90 % , es decir, una tasa de verdaderos positivos (TPR) de 0,90. Por lo tanto, arroja un 90 % de resultados verdaderos positivos (identificación correcta del consumo de drogas) para los consumidores de cannabis.

La prueba también tiene una especificidad del 80 % , lo que significa que la tasa de verdaderos negativos (TNR) es de 0,80. Por lo tanto, la prueba identifica correctamente el 80 % de no uso en el caso de los no usuarios, pero también genera un 20 % de falsos positivos, o una tasa de falsos positivos (FPR) de 0,20 en el caso de los no usuarios.

Suponiendo una prevalencia de 0,05 , es decir, que el 5% de las personas consumen cannabis, ¿cuál es la probabilidad de que una persona al azar que dé positivo sea realmente un consumidor de cannabis?

El valor predictivo positivo (VPP) de una prueba es la proporción de personas que realmente dan positivo de todas las que dan positivo, y se puede calcular a partir de una muestra como:

PPV = Verdadero positivo / Probado positivo

Si se conocen la sensibilidad, la especificidad y la prevalencia, el VPP se puede calcular utilizando el teorema de Bayes. Sea "la probabilidad de que alguien sea consumidor de cannabis dado que dé positivo en la prueba", que es lo que se entiende por VPP. Podemos escribir:${\displaystyle P({\text{User}}\vert {\text{Positive}})}$

${\displaystyle {\begin{aligned}P({\text{User}}\vert {\text{Positive}})&={\frac {P({\text{Positive}}\vert {\text{User}})P({\text{User}})}{P({\text{Positive}})}}\\&={\frac {P({\text{Positive}}\vert {\text{User}})P({\text{User}})}{P({\text{Positive}}\vert {\text{User}})P({\text{User}})+P({\text{Positive}}\vert {\text{Non-user}})P({\text{Non-user}})}}\\[8pt]&={\frac {0.90\times 0.05}{0.90\times 0.05+0.20\times 0.95}}={\frac {0.045}{0.045+0.19}}\approx 19\%\end{aligned}}}$

El denominador es una aplicación directa de la Ley de Probabilidad Total . En este caso, dice que la probabilidad de que alguien dé positivo es la probabilidad de que un usuario dé positivo multiplicada por la probabilidad de ser un usuario, más la probabilidad de que un no usuario dé positivo multiplicada por la probabilidad de ser un no usuario. Esto es cierto porque las clasificaciones usuario y no usuario forman una partición de un conjunto , es decir, el conjunto de personas que se someten a la prueba de drogas. Esto, combinado con la definición de probabilidad condicional , da como resultado la afirmación anterior.${\displaystyle P({\text{Positive}})=P({\text{Positive}}\vert {\text{User}})P({\text{User}})+P({\text{Positive}}\vert {\text{Non-user}})P({\text{Non-user}})}$

En otras palabras, incluso si alguien da positivo, la probabilidad de que sea consumidor de cannabis es solo del 19%; esto se debe a que en este grupo, solo el 5% de las personas son consumidores y la mayoría de los positivos son falsos positivos provenientes del 95% restante.

Si se hicieran la prueba a 1.000 personas:

• 950 son no usuarios y 190 de ellos dan falso positivo (0,20 × 950)
• 50 de ellos son usuarios y 45 de ellos dan verdaderos positivos (0,90 × 50)

De las 1.000 personas analizadas se obtienen 235 pruebas positivas, de las que sólo 45 son auténticos consumidores de drogas, aproximadamente el 19%.

La importancia de la especificidad se puede ver al mostrar que incluso si la sensibilidad se eleva al 100% y la especificidad se mantiene en el 80%, la probabilidad de que alguien que dé positivo sea realmente un consumidor de cannabis solo aumenta del 19% al 21%, pero si la sensibilidad se mantiene en el 90% y la especificidad se incrementa al 95%, la probabilidad aumenta al 49%.

Aunque el 100% de los pacientes con cáncer de páncreas presenten un determinado síntoma, el hecho de que alguien presente el mismo síntoma no significa que esa persona tenga un 100% de posibilidades de padecer cáncer de páncreas. Suponiendo que la tasa de incidencia del cáncer de páncreas sea de 1/100000, mientras que 10/99999 individuos sanos presentan los mismos síntomas en todo el mundo, la probabilidad de padecer cáncer de páncreas dados los síntomas es de tan solo el 9,1%, y el otro 90,9% podría ser "falso positivo" (es decir, que se diga falsamente que se padece cáncer; "positivo" es un término confuso cuando, como en este caso, la prueba da malas noticias).

Según la tasa de incidencia, la siguiente tabla presenta los números correspondientes por cada 100.000 personas.

Que luego se puede utilizar para calcular la probabilidad de tener cáncer cuando se presentan los síntomas:

${\displaystyle {\begin{aligned}P({\text{Cancer}}|{\text{Symptoms}})&={\frac {P({\text{Symptoms}}|{\text{Cancer}})P({\text{Cancer}})}{P({\text{Symptoms}})}}\\&={\frac {P({\text{Symptoms}}|{\text{Cancer}})P({\text{Cancer}})}{P({\text{Symptoms}}|{\text{Cancer}})P({\text{Cancer}})+P({\text{Symptoms}}|{\text{Non-Cancer}})P({\text{Non-Cancer}})}}\\[8pt]&={\frac {1\times 0.00001}{1\times 0.00001+(10/99999)\times 0.99999}}={\frac {1}{11}}\approx 9.1\%\end{aligned}}}$

Una fábrica produce artículos utilizando tres máquinas (A, B y C), que representan el 20%, el 30% y el 50% de su producción respectivamente. De los artículos producidos por la máquina A, el 5% son defectuosos; de manera similar, el 3% de los artículos de la máquina B y el 1% de los de la máquina C son defectuosos. Si un artículo seleccionado al azar es defectuoso, ¿cuál es la probabilidad de que haya sido producido por la máquina C?

Una vez más, se puede llegar a la respuesta sin utilizar la fórmula aplicando las condiciones a un número hipotético de casos. Por ejemplo, si la fábrica produce 1.000 artículos, 200 serán producidos por la máquina A, 300 por la máquina B y 500 por la máquina C. La máquina A producirá el 5% × 200 = 10 artículos defectuosos, la máquina B el 3% × 300 = 9 y la máquina C el 1% × 500 = 5, para un total de 24. Por lo tanto, la probabilidad de que un artículo defectuoso seleccionado al azar haya sido producido por la máquina C es 5/24 (~20,83%).

Este problema también se puede resolver utilizando el teorema de Bayes: Sea X _i el evento de que un artículo elegido al azar haya sido fabricado por la i ^-ésima máquina (para i  = A, B, C). Sea Y el evento de que un artículo elegido al azar sea defectuoso. Entonces, tenemos la siguiente información:

${\displaystyle P(X_{A})=0.2,\quad P(X_{B})=0.3,\quad P(X_{C})=0.5.}$

Si el artículo fue fabricado por la primera máquina, entonces la probabilidad de que esté defectuoso es 0,05; es decir, P ( Y  |  X _A ) = 0,05. En general, tenemos

${\displaystyle P(Y|X_{A})=0.05,\quad P(Y|X_{B})=0.03,\quad P(Y|X_{C})=0.01.}$

Para responder a la pregunta original, primero hallamos P (Y). Esto se puede hacer de la siguiente manera:

${\displaystyle P(Y)=\sum _{i}P(Y|X_{i})P(X_{i})=(0.05)(0.2)+(0.03)(0.3)+(0.01)(0.5)=0.024.}$

Por lo tanto, el 2,4% de la producción total es defectuosa.

Se nos da que Y ha ocurrido y queremos calcular la probabilidad condicional de X _C . Por el teorema de Bayes,

${\displaystyle P(X_{C}|Y)={\frac {P(Y|X_{C})P(X_{C})}{P(Y)}}={\frac {0.01\cdot 0.50}{0.024}}={\frac {5}{24}}}$

Dado que el artículo es defectuoso, la probabilidad de que haya sido fabricado por la máquina C es 5/24. Aunque la máquina C produce la mitad de la producción total, produce una fracción mucho menor de los artículos defectuosos. Por lo tanto, el conocimiento de que el artículo seleccionado era defectuoso nos permite reemplazar la probabilidad previa P ( X _C ) = 1/2 por la probabilidad posterior más pequeña P ( X _C  |  Y ) = 5/24.

La interpretación de la regla de Bayes depende de la interpretación de la probabilidad que se le asigne a los términos. A continuación se describen las dos interpretaciones predominantes.

En la interpretación bayesiana (o epistemológica) , la probabilidad mide un "grado de creencia". El teorema de Bayes vincula el grado de creencia en una proposición antes y después de tener en cuenta la evidencia. Por ejemplo, supongamos que se cree con un 50% de certeza que una moneda tiene el doble de probabilidades de caer cara que cruz. Si se lanza la moneda varias veces y se observan los resultados, ese grado de creencia probablemente aumentará o disminuirá, pero incluso podría permanecer igual, dependiendo de los resultados. Para la proposición A y la evidencia B ,

• P  ( A ), el anterior , es el grado inicial de creencia en A .
• P  ( A  |  B ), la posterior , es el grado de creencia después de incorporar la noticia de que B es verdadera.
• el cocienteP ( B  |  A )/P ( B )⁠ representa el apoyo que B proporciona a A.

Para más información sobre la aplicación del teorema de Bayes bajo la interpretación bayesiana de la probabilidad, véase Inferencia bayesiana .

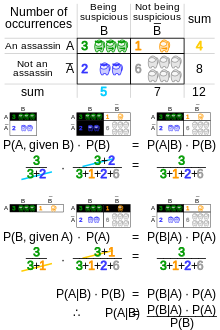
En la interpretación frecuentista , la probabilidad mide una "proporción de resultados". Por ejemplo, supongamos que un experimento se realiza muchas veces. P ( A ) es la proporción de resultados con la propiedad A (la anterior) y P ( B ) es la proporción con la propiedad B . P ( B  |  A ) es la proporción de resultados con la propiedad B de los resultados con la propiedad A , y P ( A  |  B ) es la proporción de aquellos con A de aquellos con  B (la posterior).

El papel del teorema de Bayes se visualiza mejor con diagramas de árbol. Los dos diagramas dividen los mismos resultados entre A y B en órdenes opuestos, para obtener las probabilidades inversas. El teorema de Bayes vincula las diferentes divisiones.

Un entomólogo descubre lo que podría ser, debido al patrón en su espalda, una subespecie rara de escarabajo . Un 98% de los miembros de la subespecie rara tienen el patrón, por lo que P (Patrón | Raro) = 98%. Solo el 5% de los miembros de la subespecie común tienen el patrón. La subespecie rara es el 0,1% de la población total. ¿Qué probabilidad hay de que el escarabajo que tiene el patrón sea raro? ¿Qué es P (Raro | Patrón)?

De la forma extendida del teorema de Bayes (ya que cualquier escarabajo es raro o común),

$${\displaystyle {\begin{aligned}P({\text{Rare}}\vert {\text{Pattern}})&={\frac {P({\text{Pattern}}\vert {\text{Rare}})P({\text{Rare}})}{P({\text{Pattern}})}}\\[8pt]&={\frac {P({\text{Pattern}}\vert {\text{Rare}})P({\text{Rare}})}{P({\text{Pattern}}\vert {\text{Rare}})P({\text{Rare}})+P({\text{Pattern}}\vert {\text{Common}})P({\text{Common}})}}\\[8pt]&={\frac {0.98\times 0.001}{0.98\times 0.001+0.05\times 0.999}}\\[8pt]&\approx 1.9\%\end{aligned}}}$$

Para los eventos A y B , siempre que P ( B ) ≠ 0,

${\displaystyle P(A|B)={\frac {P(B|A)P(A)}{P(B)}}.}$

En muchas aplicaciones, por ejemplo en la inferencia bayesiana , el evento B está fijado en la discusión, y deseamos considerar el impacto de haber sido observado en nuestra creencia en varios eventos posibles A. En tal situación, el denominador de la última expresión, la probabilidad de la evidencia dada B , está fijado; lo que queremos variar es A. El teorema de Bayes muestra entonces que las probabilidades posteriores son proporcionales al numerador, por lo que la última ecuación se convierte en:

${\displaystyle P(A|B)\propto P(A)\cdot P(B|A).}$

En palabras, el posterior es proporcional al anterior multiplicado por la probabilidad. ^[21]

Si los eventos A ₁ , A ₂ , ..., son mutuamente excluyentes y exhaustivos, es decir, uno de ellos es seguro que ocurrirá pero no pueden ocurrir dos juntos, podemos determinar la constante de proporcionalidad utilizando el hecho de que sus probabilidades deben sumar uno. Por ejemplo, para un evento dado A , el evento A mismo y su complemento ¬ A son excluyentes y exhaustivos. Denotando la constante de proporcionalidad por c tenemos

${\displaystyle P(A|B)=c\cdot P(A)\cdot P(B|A){\text{ and }}P(\neg A|B)=c\cdot P(\neg A)\cdot P(B|\neg A).}$

Sumando estas dos fórmulas deducimos que

${\displaystyle 1=c\cdot (P(B|A)\cdot P(A)+P(B|\neg A)\cdot P(\neg A)),}$

o

${\displaystyle c={\frac {1}{P(B|A)\cdot P(A)+P(B|\neg A)\cdot P(\neg A)}}={\frac {1}{P(B)}}.}$

Otra forma del teorema de Bayes para dos afirmaciones o hipótesis en competencia es:

${\displaystyle P(A|B)={\frac {P(B|A)P(A)}{P(B|A)P(A)+P(B|\neg A)P(\neg A)}}.}$

Para una interpretación epistemológica:

Para la proposición A y la evidencia o antecedentes B , ^[22]

• ${\displaystyle P(A)}$es la probabilidad previa , el grado inicial de creencia en A.
• ${\displaystyle P(\neg A)}$es el grado inicial correspondiente de creencia en no-A , que A es falso, donde${\displaystyle P(\neg A)=1-P(A)}$
• ${\displaystyle P(B|A)}$es la probabilidad o verosimilitud condicional, el grado de creencia en B dado que la proposición A es verdadera.
• ${\displaystyle P(B|\neg A)}$es la probabilidad o verosimilitud condicional, el grado de creencia en B dado que la proposición A es falsa.
• ${\displaystyle P(A|B)}$es la probabilidad posterior , la probabilidad de A después de tomar en cuenta B.

A menudo, para alguna partición { A _j } del espacio muestral , el espacio de eventos se da en términos de P ( A _j ) y P ( B  |  A _j ). Entonces resulta útil calcular P ( B ) utilizando la ley de probabilidad total :

${\displaystyle P(B)=\sum _{j}P(B\cap A_{j}),}$

O (utilizando la regla de multiplicación para la probabilidad condicional), ^[23]

${\displaystyle P(B)={\sum _{j}P(B|A_{j})P(A_{j})},}$

${\displaystyle \Rightarrow P(A_{i}|B)={\frac {P(B|A_{i})P(A_{i})}{\sum \limits _{j}P(B|A_{j})P(A_{j})}}\cdot }$

En el caso especial donde A es una variable binaria :

${\displaystyle P(A|B)={\frac {P(B|A)P(A)}{P(B|A)P(A)+P(B|\neg A)P(\neg A)}}\cdot }$

Consideremos un espacio muestral Ω generado por dos variables aleatorias X e Y con distribuciones de probabilidad conocidas. En principio, el teorema de Bayes se aplica a los eventos A  = { X  =  x } y B  = { Y  =  y }.

${\displaystyle P(X{=}x|Y{=}y)={\frac {P(Y{=}y|X{=}x)P(X{=}x)}{P(Y{=}y)}}}$

Sin embargo, los términos se vuelven 0 en los puntos donde cualquiera de las variables tiene una densidad de probabilidad finita . Para que siga siendo útil, el teorema de Bayes se puede formular en términos de las densidades relevantes (ver Derivación).

Si X es continua e Y es discreta,

${\displaystyle f_{X|Y{=}y}(x)={\frac {P(Y{=}y|X{=}x)f_{X}(x)}{P(Y{=}y)}}}$

donde cada uno es una función de densidad.${\displaystyle f}$

Si X es discreto e Y es continuo,

${\displaystyle P(X{=}x|Y{=}y)={\frac {f_{Y|X{=}x}(y)P(X{=}x)}{f_{Y}(y)}}.}$

Si tanto X como Y son continuas,

${\displaystyle f_{X|Y{=}y}(x)={\frac {f_{Y|X{=}x}(y)f_{X}(x)}{f_{Y}(y)}}.}$

Un espacio de eventos continuos suele conceptualizarse en términos de los términos del numerador. En ese caso, resulta útil eliminar el denominador utilizando la ley de probabilidad total . Para f _Y ( y ), esto se convierte en una integral:

${\displaystyle f_{Y}(y)=\int _{-\infty }^{\infty }f_{Y|X=\xi }(y)f_{X}(\xi )\,d\xi .}$

El teorema de Bayes en forma de probabilidades es:

${\displaystyle O(A_{1}:A_{2}\vert B)=O(A_{1}:A_{2})\cdot \Lambda (A_{1}:A_{2}\vert B)}$

dónde

${\displaystyle \Lambda (A_{1}:A_{2}\vert B)={\frac {P(B\vert A_{1})}{P(B\vert A_{2})}}}$

se llama factor de Bayes o razón de verosimilitud . Las probabilidades entre dos eventos son simplemente la razón de las probabilidades de los dos eventos. Por lo tanto

${\displaystyle O(A_{1}:A_{2})={\frac {P(A_{1})}{P(A_{2})}},}$

${\displaystyle O(A_{1}:A_{2}\vert B)={\frac {P(A_{1}\vert B)}{P(A_{2}\vert B)}},}$

Por lo tanto, la regla dice que las probabilidades posteriores son las probabilidades anteriores multiplicadas por el factor de Bayes , o en otras palabras, la probabilidad posterior es proporcional a la probabilidad anterior multiplicada por la probabilidad.

En el caso especial de que y , se escribe , y se utiliza una abreviatura similar para el factor de Bayes y para las probabilidades condicionales. Las probabilidades de son por definición las probabilidades a favor y en contra de . La regla de Bayes se puede escribir entonces en la forma abreviada${\displaystyle A_{1}=A}$${\displaystyle A_{2}=\neg A}$${\displaystyle O(A)=O(A:\neg A)=P(A)/(1-P(A))}$${\displaystyle A}$${\displaystyle A}$

${\displaystyle O(A\vert B)=O(A)\cdot \Lambda (A\vert B),}$

o, en palabras, las probabilidades posteriores son iguales a las probabilidades previas multiplicadas por la razón de verosimilitud para una información dada . En resumen, las probabilidades posteriores son iguales a las probabilidades previas multiplicadas por la razón de verosimilitud .${\displaystyle A}$${\displaystyle A}$${\displaystyle A}$${\displaystyle B}$

Por ejemplo, si una prueba médica tiene una sensibilidad del 90% y una especificidad del 91%, entonces el factor Bayes positivo es . Ahora bien, si la prevalencia de esta enfermedad es del 9,09%, y si tomamos eso como la probabilidad previa, entonces las probabilidades previas son de aproximadamente 1:10. Entonces, después de recibir un resultado positivo en la prueba, las probabilidades posteriores de tener realmente la enfermedad se convierten en 1:1, lo que significa que la probabilidad posterior de tener la enfermedad es del 50%. Si se realiza una segunda prueba en pruebas seriadas, y esta también resulta ser positiva, entonces las probabilidades posteriores de tener realmente la enfermedad se convierten en 10:1, lo que significa una probabilidad posterior de aproximadamente el 90,91%. El factor Bayes negativo se puede calcular como 91%/(100%-90%)=9,1, por lo que si la segunda prueba resulta ser negativa, entonces las probabilidades posteriores de tener realmente la enfermedad son 1:9,1, lo que significa una probabilidad posterior de aproximadamente el 9,9%.${\displaystyle \Lambda _{+}=P({\text{True Positive}})/P({\text{False Positive}})=90\%/(100\%-91\%)=10}$

El ejemplo anterior también se puede entender con números más sólidos: supongamos que el paciente que se realiza la prueba pertenece a un grupo de 1000 personas, donde 91 de ellas tienen realmente la enfermedad (prevalencia del 9,1%). Si todas estas 1000 personas se realizan la prueba médica, 82 de las que tienen la enfermedad obtendrán un resultado positivo verdadero (sensibilidad del 90,1%), 9 de las que tienen la enfermedad obtendrán un resultado negativo falso ( tasa de falsos negativos del 9,9%), 827 de las que no tienen la enfermedad obtendrán un resultado negativo verdadero (especificidad del 91,0%) y 82 de las que no tienen la enfermedad obtendrán un resultado positivo falso (tasa de falsos positivos del 9,0%). Antes de realizar cualquier prueba, las probabilidades del paciente de tener la enfermedad son de 91:909. Después de recibir un resultado positivo, las probabilidades del paciente de tener la enfermedad son

${\displaystyle {\frac {91}{909}}\times {\frac {90.1\%}{9.0\%}}={\frac {91\times 90.1\%}{909\times 9.0\%}}=1:1}$

lo cual es consistente con el hecho de que hay 82 verdaderos positivos y 82 falsos positivos en el grupo de 1000 personas.

Usando dos veces, se puede usar el teorema de Bayes para expresar también en términos de y sin negaciones:${\displaystyle P(\neg B\vert A)=1-P(B\vert A)}$${\displaystyle P(\neg B\vert \neg A)}$${\displaystyle P(A\vert B)}$

${\displaystyle P(\neg B\vert \neg A)=1-\left(1-P(A\vert B)\right){\frac {P(B)}{P(\neg A)}},}$

cuando . De esto podemos leer la inferencia${\displaystyle P(\neg A)=1-P(A)\neq 0}$

${\displaystyle P(A\vert B)=1\implies P(\neg B\vert \neg A)=1}$.

En palabras: Si ciertamente implica , inferimos que ciertamente implica . Donde , siendo ciertas las dos implicaciones, son afirmaciones equivalentes. En las fórmulas de probabilidad, la probabilidad condicional generaliza la implicación lógica , donde ahora, además de asignar verdadero o falso, asignamos valores de probabilidad a las afirmaciones. La afirmación de es capturada por la certeza del condicional, la afirmación de . Relacionando las direcciones de la implicación, el teorema de Bayes representa una generalización de la ley de contraposición , que en la lógica proposicional clásica puede expresarse como:${\displaystyle B}$${\displaystyle A}$${\displaystyle \neg A}$${\displaystyle \neg B}$${\displaystyle P(B)\neq 0}$ ${\displaystyle P(A\vert B)}$${\displaystyle B\implies A}$${\displaystyle B\implies A}$${\displaystyle P(A\vert B)=1}$

${\displaystyle (B\implies A)\iff (\neg A\implies \neg B)}$.

En esta relación entre implicaciones, las posiciones de resp. se invierten.${\displaystyle A}$${\displaystyle B}$

La fórmula correspondiente en términos de cálculo de probabilidad es el teorema de Bayes, que en su forma expandida que involucra la probabilidad previa / tasa base de solo , se expresa como: ^[1]${\displaystyle a}$${\displaystyle A}$

${\displaystyle P(A\vert B)=P(B\vert A){\frac {a(A)}{P(B\vert A)\,a(A)+P(B\vert \neg A)\,a(\neg A)}}.}$

El teorema de Bayes representa un caso especial de derivación de opiniones condicionales invertidas en lógica subjetiva expresada como:

${\displaystyle (\omega _{A{\tilde {|}}B}^{S},\omega _{A{\tilde {|}}\lnot B}^{S})=(\omega _{B\vert A}^{S},\omega _{B\vert \lnot A}^{S}){\widetilde {\phi }}a_{A},}$

donde denota el operador para invertir opiniones condicionales. El argumento denota un par de opiniones condicionales binomiales dadas por source , y el argumento denota la probabilidad previa (también conocida como la tasa base ) de . El par de opiniones condicionales invertidas derivadas se denota . La opinión condicional generaliza la condicional probabilística , es decir, además de asignar una probabilidad, la source puede asignar cualquier opinión subjetiva al enunciado condicional . Una opinión subjetiva binomial es la creencia en la verdad de un enunciado con grados de incertidumbre epistémica, tal como lo expresa source . Cada opinión subjetiva tiene una probabilidad proyectada correspondiente . La aplicación del teorema de Bayes a las probabilidades proyectadas de las opiniones es un homomorfismo , lo que significa que el teorema de Bayes se puede expresar en términos de probabilidades proyectadas de las opiniones:${\displaystyle {\widetilde {\phi }}}$${\displaystyle (\omega _{B\vert A}^{S},\omega _{B\vert \lnot A}^{S})}$${\displaystyle S}$${\displaystyle a_{A}}$${\displaystyle A}$${\displaystyle (\omega _{A{\tilde {|}}B}^{S},\omega _{A{\tilde {|}}\lnot B}^{S})}$${\displaystyle \omega _{A\vert B}^{S}}$${\displaystyle P(A\vert B)}$${\displaystyle S}$${\displaystyle (A\vert B)}$${\displaystyle \omega _{A}^{S}}$${\displaystyle A}$${\displaystyle S}$${\displaystyle P(\omega _{A}^{S})}$

${\displaystyle P(\omega _{A{\tilde {|}}B}^{S})={\frac {P(\omega _{B\vert A}^{S})a(A)}{P(\omega _{B\vert A}^{S})a(A)+P(\omega _{B\vert \lnot A}^{S})a(\lnot A)}}.}$

Por lo tanto, el teorema de Bayes subjetivo representa una generalización del teorema de Bayes. ^[24]

Una versión del teorema de Bayes para 3 eventos ^[25] resulta de la adición de un tercer evento , con el que se condicionan todas las probabilidades:${\displaystyle C}$${\displaystyle P(C)>0,}$

${\displaystyle P(A\vert B\cap C)={\frac {P(B\vert A\cap C)\,P(A\vert C)}{P(B\vert C)}}}$

Usando la regla de la cadena

${\displaystyle P(A\cap B\cap C)=P(A\vert B\cap C)\,P(B\vert C)\,P(C)}$

Y, por otro lado

${\displaystyle P(A\cap B\cap C)=P(B\cap A\cap C)=P(B\vert A\cap C)\,P(A\vert C)\,P(C)}$

El resultado deseado se obtiene identificando ambas expresiones y resolviendo para .${\displaystyle P(A\vert B\cap C)}$

En genética, la regla de Bayes se puede utilizar para estimar la probabilidad de que un individuo tenga un genotipo específico. Muchas personas intentan aproximarse a sus posibilidades de verse afectadas por una enfermedad genética o su probabilidad de ser portadores de un gen recesivo de interés. Se puede realizar un análisis bayesiano basándose en los antecedentes familiares o en pruebas genéticas , con el fin de predecir si un individuo desarrollará una enfermedad o la transmitirá a sus hijos. Las pruebas y predicciones genéticas son una práctica común entre las parejas que planean tener hijos pero les preocupa que ambos puedan ser portadores de una enfermedad, especialmente dentro de comunidades con baja varianza genética. ^[26]

Ejemplo de una tabla de análisis bayesiano para el riesgo de una mujer de padecer una enfermedad basándose en el conocimiento de que la enfermedad está presente en sus hermanos pero no en sus padres o en ninguno de sus cuatro hijos. Basándose únicamente en el estado de los hermanos y padres de la mujer, es igualmente probable que sea portadora que no lo sea (esta probabilidad se denota por la Hipótesis previa). Sin embargo, la probabilidad de que los cuatro hijos de la mujer no se vean afectados es 1/16 ( 1 ⁄ 2 ⋅ 1 ⁄ 2 ⋅ 1 ⁄ 2 ⋅ 1 ⁄ 2 ) si es portadora, aproximadamente 1 si no es portadora (esta es la Probabilidad Condicional). La Probabilidad Conjunta reconcilia estas dos predicciones multiplicándolas entre sí. La última línea (la Probabilidad Posterior) se calcula dividiendo la Probabilidad Conjunta para cada hipótesis por la suma de ambas probabilidades conjuntas. ^[27]

Las pruebas genéticas parentales pueden detectar alrededor del 90% de los alelos de enfermedades conocidas en los padres que pueden dar lugar a un estado de portador o afectado en su hijo. La fibrosis quística es una enfermedad hereditaria causada por una mutación autosómica recesiva en el gen CFTR, ^[28] ubicado en el brazo q del cromosoma 7. ^[29]

Análisis bayesiano de una paciente con antecedentes familiares de fibrosis quística (FQ) que dio negativo en la prueba de FQ, que demuestra cómo se utilizó este método para determinar su riesgo de tener un hijo nacido con FQ:

Como la paciente no está afectada, es homocigótica para el alelo de tipo salvaje o heterocigótica. Para establecer probabilidades previas, se utiliza un cuadro de Punnett, basado en el conocimiento de que ninguno de los padres estaba afectado por la enfermedad, pero ambos podrían haber sido portadores:

Dado que el paciente no está afectado, solo hay tres posibilidades. Dentro de estas tres, hay dos escenarios en los que el paciente es portador del alelo mutante. Por lo tanto, las probabilidades previas son 2 ⁄ 3 y 1 ⁄ 3 .

A continuación, el paciente se somete a una prueba genética que da negativo en el test de fibrosis quística. Esta prueba tiene una tasa de detección del 90%, por lo que las probabilidades condicionales de un test negativo son 1/10 y 1. Por último, se calculan las probabilidades conjuntas y posteriores como antes.

Después de realizar el mismo análisis en la pareja masculina del paciente (con un resultado negativo en la prueba), las probabilidades de que su hijo esté afectado son iguales al producto de las respectivas probabilidades posteriores de los padres de ser portadores por las probabilidades de que dos portadores produzcan una descendencia afectada ( 1 ⁄ 4 ).

El análisis bayesiano se puede realizar utilizando información fenotípica asociada con una condición genética, y cuando se combina con pruebas genéticas este análisis se vuelve mucho más complicado. La fibrosis quística, por ejemplo, se puede identificar en un feto a través de una ecografía que busque un intestino ecogénico, es decir, uno que aparezca más brillante de lo normal en una exploración. Esta no es una prueba infalible, ya que un intestino ecogénico puede estar presente en un feto perfectamente sano. Las pruebas genéticas parentales son muy influyentes en este caso, donde una faceta fenotípica puede ser demasiado influyente en el cálculo de probabilidad. En el caso de un feto con un intestino ecogénico, con una madre que se ha sometido a pruebas y se sabe que es portadora de fibrosis quística, la probabilidad posterior de que el feto realmente tenga la enfermedad es muy alta (0,64). Sin embargo, una vez que el padre ha dado negativo en la prueba de fibrosis quística, la probabilidad posterior disminuye significativamente (a 0,16). ^[27]

El cálculo de los factores de riesgo es una herramienta poderosa en el asesoramiento genético y la planificación reproductiva, pero no puede ser considerado como el único factor importante a tener en cuenta. Como se mencionó anteriormente, las pruebas incompletas pueden arrojar una probabilidad falsamente alta de estado de portador, y las pruebas pueden ser económicamente inaccesibles o inviables cuando uno de los padres no está presente.

• Epistemología bayesiana
• Probabilidad inductiva
• Bayesianismo cuántico
• Por qué la mayoría de los resultados de las investigaciones publicadas son falsos , un ensayo de 2005 sobre metaciencia de John Ioannidis
• Probabilidad condicional regular
• Persuasión bayesiana

•  Este artículo incorpora texto de una publicación que ahora es de dominio público :  Mitchell, John Malcolm (1911). "Price, Richard". En Chisholm, Hugh (ed.). Encyclopædia Britannica . Vol. 22 (11.ª ed.). Cambridge University Press. págs. 314–315.

• Bolstad, William M.; Curran, James M. (2017). "Lógica, probabilidad e incertidumbre". Introducción a la estadística bayesiana (3.ª ed.). Nueva York: Wiley. págs. 59–82. ISBN 978-1-118-09156-2.
• Lee, Peter M. (2012). Estadística bayesiana: una introducción (4.ª ed.). Wiley. ISBN 978-1-118-33257-3.
• Schmitt, Samuel A. (1969). "Acumulación de evidencia". Medición de la incertidumbre: una introducción elemental a la estadística bayesiana . Lectura: Addison-Wesley. págs. 61–99. OCLC  5013.
• Stigler, Stephen M. (agosto de 1986). "Memorias de Laplace de 1774 sobre probabilidad inversa". Ciencia estadística . 1 (3): 359–363. doi : 10.1214/ss/1177013620 .

• "La trampa bayesiana". Veritasium . 5 de abril de 2017 – vía YouTube .