Espectroscopia Doppler

.jpg/440px-The_radial_velocity_method_(artist’s_impression).jpg)
La espectroscopia Doppler (también conocida como método de velocidad radial o, coloquialmente, método de bamboleo ) es un método indirecto para encontrar planetas extrasolares y enanas marrones a partir de mediciones de velocidad radial mediante la observación de los cambios Doppler en el espectro de la estrella madre del planeta . A fecha de noviembre de 2022, aproximadamente el 19,5 % de los planetas extrasolares conocidos (1018 del total) se han descubierto mediante espectroscopia Doppler. [2]
Historia

Otto Struve propuso en 1952 el uso de potentes espectrógrafos para detectar planetas distantes. Describió cómo un planeta muy grande, tan grande como Júpiter , por ejemplo, haría que su estrella madre se tambaleara ligeramente mientras los dos objetos orbitan alrededor de su centro de masas. [3] Predijo que los pequeños desplazamientos Doppler de la luz emitida por la estrella, causados por su velocidad radial que varía continuamente, serían detectables por los espectrógrafos más sensibles como pequeños desplazamientos al rojo y al azul en la emisión de la estrella. Sin embargo, la tecnología de la época producía mediciones de velocidad radial con errores de 1.000 m/s o más, lo que las hacía inútiles para la detección de planetas en órbita. [4] Los cambios esperados en la velocidad radial son muy pequeños (Júpiter hace que el Sol cambie la velocidad en unos 12,4 m/s durante un período de 12 años, y el efecto de la Tierra es de solo 0,1 m/s durante un período de 1 año), por lo que se requieren observaciones a largo plazo con instrumentos con una resolución muy alta . [4] [5]
Los avances en la tecnología de los espectrómetros y las técnicas de observación en los años 1980 y 1990 produjeron instrumentos capaces de detectar el primero de muchos nuevos planetas extrasolares. El espectrógrafo ELODIE , instalado en el Observatorio de Haute-Provence en el sur de Francia en 1993, podía medir cambios de velocidad radial tan bajos como 7 m/s, lo suficientemente bajos para que un observador extraterrestre detectara la influencia de Júpiter en el Sol. [6] Utilizando este instrumento, los astrónomos Michel Mayor y Didier Queloz identificaron 51 Pegasi b , un " Júpiter caliente " en la constelación de Pegaso. [7] Aunque anteriormente se habían detectado planetas orbitando púlsares , 51 Pegasi b fue el primer planeta que se confirmó que orbitaba una estrella de secuencia principal , y el primero detectado utilizando espectroscopia Doppler. [8]
En noviembre de 1995, los científicos publicaron sus hallazgos en la revista Nature ; desde entonces, el artículo ha sido citado más de 1000 veces. Desde esa fecha, se han identificado más de 1000 candidatos a exoplanetas, muchos de los cuales han sido detectados por programas de búsqueda Doppler con sede en los Observatorios Keck , Lick y Anglo-Australian (respectivamente, las búsquedas de planetas de California, Carnegie y Anglo-Australian), y equipos con sede en Geneva Extrasolar Planet Search . [9]
A principios de la década de 2000, una segunda generación de espectrógrafos para la búsqueda de planetas permitió realizar mediciones mucho más precisas. El espectrógrafo HARPS , instalado en el Observatorio La Silla en Chile en 2003, puede identificar cambios de velocidad radial de tan solo 0,3 m/s, suficientes para localizar muchos planetas posiblemente rocosos similares a la Tierra. [10] Se espera que una tercera generación de espectrógrafos entre en funcionamiento en 2017. [ necesita actualización ] Con errores de medición estimados por debajo de 0,1 m/s, estos nuevos instrumentos permitirían a un observador extraterrestre detectar incluso la Tierra. [11]
Procedimiento

Se realizan una serie de observaciones del espectro de luz emitido por una estrella. Se pueden detectar variaciones periódicas en el espectro de la estrella, con la longitud de onda de las líneas espectrales características del espectro aumentando y disminuyendo regularmente durante un período de tiempo. Luego se aplican filtros estadísticos al conjunto de datos para cancelar los efectos del espectro de otras fuentes. Mediante técnicas matemáticas de ajuste óptimo , los astrónomos pueden aislar la onda sinusoidal periódica reveladora que indica un planeta en órbita. [7]
Si se detecta un planeta extrasolar, se puede determinar una masa mínima del planeta a partir de los cambios en la velocidad radial de la estrella. Para encontrar una medida más precisa de la masa se requiere conocer la inclinación de la órbita del planeta. Un gráfico de la velocidad radial medida en función del tiempo dará una curva característica ( curva sinusoidal en el caso de una órbita circular), y la amplitud de la curva permitirá calcular la masa mínima del planeta utilizando la función de masa binaria .
El periodograma bayesiano de Kepler es un algoritmo matemático que se utiliza para detectar uno o varios planetas extrasolares a partir de mediciones sucesivas de la velocidad radial de la estrella que orbitan. Implica un análisis estadístico bayesiano de los datos de velocidad radial, utilizando una distribución de probabilidad previa sobre el espacio determinada por uno o más conjuntos de parámetros orbitales keplerianos. Este análisis se puede implementar utilizando el método de Monte Carlo de cadena de Markov (MCMC).
El método se ha aplicado al sistema HD 208487 , dando como resultado una aparente detección de un segundo planeta con un período de aproximadamente 1000 días. Sin embargo, esto puede ser un artefacto de la actividad estelar. [12] [13] El método también se aplica al sistema HD 11964 , donde se encontró un aparente planeta con un período de aproximadamente 1 año. Sin embargo, este planeta no se encontró en los datos re-reducidos, [14] [15] lo que sugiere que esta detección fue un artefacto del movimiento orbital de la Tierra alrededor del Sol. [ cita requerida ]
Aunque la velocidad radial de la estrella solo proporciona la masa mínima de un planeta, si las líneas espectrales del planeta se pueden distinguir de las líneas espectrales de la estrella, se puede encontrar la velocidad radial del propio planeta y esto proporciona la inclinación de la órbita del planeta y, por lo tanto, se puede determinar la masa real del planeta. El primer planeta no en tránsito cuya masa se determinó de esta manera fue Tau Boötis b en 2012, cuando se detectó monóxido de carbono en la parte infrarroja del espectro. [16]
Ejemplo
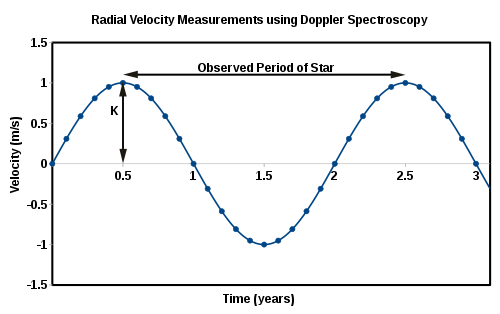
El gráfico de la derecha ilustra la curva sinusoidal obtenida mediante espectroscopia Doppler para observar la velocidad radial de una estrella imaginaria que orbita un planeta en una órbita circular. Las observaciones de una estrella real producirían un gráfico similar, aunque la excentricidad de la órbita distorsionará la curva y complicará los cálculos que se indican a continuación.
La velocidad de esta estrella teórica muestra una variación periódica de ±1 m/s, lo que sugiere una masa en órbita que está creando una atracción gravitatoria sobre esta estrella. Utilizando la tercera ley de Kepler del movimiento planetario , el período observado de la órbita del planeta alrededor de la estrella (igual al período de las variaciones observadas en el espectro de la estrella) se puede utilizar para determinar la distancia del planeta a la estrella ( ) utilizando la siguiente ecuación:
dónde:
- r es la distancia del planeta a la estrella
- G es la constante gravitacional
- M estrella es la masa de la estrella
- P estrella es el período observado de la estrella.
Una vez determinada la velocidad del planeta alrededor de la estrella, se puede calcular utilizando la ley de gravitación de Newton y la ecuación de la órbita :
¿Dónde está la velocidad del planeta?
La masa del planeta se puede encontrar a partir de la velocidad calculada del planeta:
donde es la velocidad de la estrella madre. La velocidad Doppler observada, , donde i es la inclinación de la órbita del planeta con respecto a la línea perpendicular a la línea de visión .
Así, asumiendo un valor para la inclinación de la órbita del planeta y para la masa de la estrella, los cambios observados en la velocidad radial de la estrella pueden utilizarse para calcular la masa del planeta extrasolar.
Tablas de comparación de velocidad radial
| Masa del planeta | Distancia AU | Velocidad radial de la estrella debido al planeta ( v radial ) | Aviso |
|---|---|---|---|
| Júpiter | 5 | 12,7 m/s | |
| Neptuno | 0,1 | 4,8 m/s | |
| Neptuno | 1 | 1,5 m/s | |
| Súper-Tierra (5 M 🜨 ) | 0,1 | 1,4 m/s | |
| L 98-59b (0,4 millones 🜨 ) | 0,02 | 0,46 m/s | [17] |
| Súper-Tierra (5 M 🜨 ) | 1 | 0,45 m/s | |
| Tierra | 0,09 | 0,30 m/s | |
| Tierra | 1 | 0,09 m/s |
Referencia: [18]
| Planeta | Tipo de planeta | Semieje mayor ( UA ) | Periodo orbital | Velocidad radial de la estrella debido al planeta (m/s) | Detectable por: |
|---|---|---|---|---|---|
| 51 Pegasos b | Júpiter caliente | 0,05 | 4,23 días | 55.9 [19] | Espectrógrafo de primera generación |
| 55 cáncer d | Gigante gaseoso | 5.77 | 14,29 años | 45.2 [20] | Espectrógrafo de primera generación |
| Júpiter | Gigante gaseoso | 5.20 | 11,86 años | 12.4 [21] | Espectrógrafo de primera generación |
| Gliese 581c | Super-Tierra | 0,07 | 12,92 días | 3.18 [22] | Espectrógrafo de segunda generación |
| Saturno | Gigante gaseoso | 9.58 | 29,46 años | 2,75 | Espectrógrafo de segunda generación |
| L 98-59b | Planeta terrestre | 0,02 | 2,25 días | 0,46 [17] | Espectrógrafo de tercera generación |
| Neptuno | Gigante de hielo | 30.10 | 164,79 años | 0,281 | Espectrógrafo de tercera generación |
| Tierra | Planeta habitable | 1.00 | 365,26 días | 0,089 | Espectrógrafo de tercera generación (probable) |
| Plutón | Planeta enano | 39,26 | 246,04 años | 0,00003 | No detectable |
Para estrellas de tipo MK con planetas en la zona habitable
| Masa estelar ( M ☉ ) | Masa planetaria ( M E ) | Lum. (L 0 ) | Tipo | RHAB ( AU ) | Velocidad del viento (cm/s) | Periodo (días) |
|---|---|---|---|---|---|---|
| 0,10 | 1.0 | 8 × 10-4 | M8 | 0,028 | 168 | 6 |
| 0,21 | 1.0 | 7,9 × 10-3 | M5 | 0,089 | 65 | 21 |
| 0,47 | 1.0 | 6,3 × 10-2 | M0 | 0,25 | 26 | 67 |
| 0,65 | 1.0 | 1,6 × 10-1 | K5 | 0,40 | 18 | 115 |
| 0,78 | 2.0 | 4.0 × 10-1 | K0 | 0,63 | 25 | 209 |
Limitaciones
La principal limitación de la espectroscopia Doppler es que sólo puede medir el movimiento a lo largo de la línea de visión, por lo que depende de una medición (o estimación) de la inclinación de la órbita del planeta para determinar la masa del planeta. Si el plano orbital del planeta coincide con la línea de visión del observador, la variación medida en la velocidad radial de la estrella es el valor verdadero. Sin embargo, si el plano orbital está inclinado en dirección opuesta a la línea de visión, el efecto verdadero del planeta en el movimiento de la estrella será mayor que la variación medida en la velocidad radial de la estrella, que es sólo el componente a lo largo de la línea de visión. Como resultado, la masa verdadera del planeta será mayor que la medida.
Para corregir este efecto y determinar así la verdadera masa de un planeta extrasolar, las mediciones de velocidad radial se pueden combinar con observaciones astrométricas , que rastrean el movimiento de la estrella a través del plano del cielo, perpendicular a la línea de visión. Las mediciones astrométricas permiten a los investigadores verificar si los objetos que parecen planetas de gran masa tienen más probabilidades de ser enanas marrones . [4]
Otra desventaja es que la envoltura de gas que rodea a ciertos tipos de estrellas puede expandirse y contraerse, y algunas estrellas son variables . Este método no es adecuado para encontrar planetas alrededor de este tipo de estrellas, ya que los cambios en el espectro de emisión estelar causados por la variabilidad intrínseca de la estrella pueden eclipsar el pequeño efecto causado por un planeta.
El método es más eficaz para detectar objetos muy masivos cercanos a la estrella madre (los llamados " Júpiter calientes "), que tienen el mayor efecto gravitacional sobre la estrella madre y, por lo tanto, causan los mayores cambios en su velocidad radial. Los Júpiter calientes tienen el mayor efecto gravitacional sobre sus estrellas anfitrionas porque tienen órbitas relativamente pequeñas y masas grandes. La observación de muchas líneas espectrales separadas y muchos períodos orbitales permite aumentar la relación señal-ruido de las observaciones, lo que aumenta la posibilidad de observar planetas más pequeños y más distantes, pero los planetas como la Tierra siguen siendo indetectables con los instrumentos actuales.
Derecha : En este caso, ningún movimiento de la estrella se produce a lo largo de la línea de visión del observador y el método de espectroscopia Doppler no detectará el planeta en absoluto.
Véase también
- Métodos de detección de exoplanetas
- Sistémico (proyecto amateur de búsqueda de planetas extrasolares)
Referencias
- ^ Wenz, John (10 de octubre de 2019). "Lecciones de planetas extraños y abrasadores". Revista Knowable . Reseñas anuales. doi : 10.1146/knowable-101019-2 . Consultado el 4 de abril de 2022 .
- ^ "Estadísticas de exoplanetas y candidatos". Archivo de exoplanetas de la NASA . Instituto de Ciencia de Exoplanetas de la NASA . Consultado el 27 de noviembre de 2022 .
- ^ O. Struve (1952). "Propuesta para un proyecto de trabajo de velocidad radial estelar de alta precisión". El Observatorio . 72 (870): 199–200. Código Bibliográfico :1952Obs....72..199S.
- ^ abc "Método de velocidad radial". The Internet Encyclopedia of Science . Consultado el 27 de abril de 2007 .
- ^ A. Wolszczan (primavera de 2006). «Espectroscopia Doppler y astrometría: teoría y práctica de las mediciones de órbitas planetarias» (PDF) . ASTRO 497: notas de la clase «Astronomía de planetas extrasolares» . Universidad Estatal de Pensilvania . Archivado desde el original (PDF) el 17 de diciembre de 2008. Consultado el 19 de abril de 2009 .
- ^ "Guía del usuario de los productos de datos del archivo Elodie". Observatorio de la Alta Provenza. Mayo de 2009. Consultado el 26 de octubre de 2012 .
- ^ ab Mayor, Michel; Queloz, Didier (1995). "Un compañero de masa de Júpiter para una estrella de tipo solar". Nature . 378 (6555): 355–359. Bibcode :1995Natur.378..355M. doi :10.1038/378355a0. ISSN 1476-4687. OCLC 01586310. S2CID 4339201.
- ^ Brennan, Pat (7 de julio de 2015). "¿Podría ponerse de pie el verdadero 'primer exoplaneta'?". Exploración de exoplanetas: planetas más allá de nuestro sistema solar . Consultado el 28 de febrero de 2022 .
- ^ RP Butler ; et al. (2006). "Catálogo de exoplanetas cercanos" (PDF) . Astrophysical Journal . 646 (2–3): 25–33. arXiv : astro-ph/0607493 . Bibcode :2006ApJ...646..505B. doi :10.1086/504701. S2CID 119067572. Archivado desde el original (PDF) el 2007-07-07.
- ^ Mayor; et al. (2003). "Establecer nuevos estándares con HARPS" (PDF) . ESO Messenger . 114 : 20. Bibcode :2003Msngr.114...20M.
- ^ "ESPRESSO - Buscando otros mundos". Centro de Astrofísica de la Universidade do Porto. 2009-12-16. Archivado desde el original el 17 de octubre de 2010 . Consultado el 26 de octubre de 2010 .
- ^ PC Gregory (2007). "Un periodograma bayesiano de Kepler detecta un segundo planeta en HD 208487". Monthly Notices of the Royal Astronomical Society . 374 (4): 1321–1333. arXiv : astro-ph/0609229 . Código Bibliográfico :2007MNRAS.374.1321G. doi : 10.1111/j.1365-2966.2006.11240.x . S2CID 8220838.
- ^ Wright, JT; Marcy, GW; Fischer, D. A; Butler, RP; Vogt, SS; Tinney, CG; Jones, HRA; Carter, BD; et al. (2007). "Cuatro nuevos exoplanetas y pistas de compañeros subestelares adicionales para las estrellas anfitrionas de exoplanetas". The Astrophysical Journal . 657 (1): 533–545. arXiv : astro-ph/0611658 . Código Bibliográfico :2007ApJ...657..533W. doi :10.1086/510553. S2CID 35682784.
- ^ PC Gregory (2007). "Un periodograma bayesiano encuentra evidencia de tres planetas en HD 11964". Monthly Notices of the Royal Astronomical Society . 381 (4): 1607–1616. arXiv : 0709.0970 . Bibcode :2007MNRAS.381.1607G. doi : 10.1111/j.1365-2966.2007.12361.x . S2CID 16796923.
- ^ Wright, JT; Upadhyay, S.; Marcy, GW; Fischer, DA; Ford, Eric B.; Johnson, John Asher (2009). "Diez sistemas multiplanetarios nuevos y actualizados, y un estudio de sistemas exoplanetarios". The Astrophysical Journal . 693 (2): 1084–1099. arXiv : 0812.1582 . Código Bibliográfico :2009ApJ...693.1084W. doi :10.1088/0004-637X/693/2/1084. S2CID 18169921.
- ^ Pesando el Júpiter caliente no transitante Tau BOO b, Florian Rodler, Mercedes López-Morales, Ignasi Ribas, 27 de junio de 2012
- ^ ab Demangeon, Oliver DS; Zapatero Osorio, MR; Alibert, Y.; Barros, SCC; Adibekyan, V.; Tabernero, HM; et al. (julio de 2021). "Un planeta terrestre cálido con la mitad de la masa de Venus transitando una estrella cercana" (PDF) . Astronomía y Astrofísica . 653 : 38. arXiv : 2108.03323 . Bibcode :2021A&A...653A..41D. doi :10.1051/0004-6361/202140728. S2CID 236957385.
- ^ ab "ESPRESSO y CODEX, la próxima generación de cazadores de planetas RV en ESO". Academia China de Ciencias . 2010-10-16. Archivado desde el original el 2011-07-04 . Consultado el 2010-10-16 .
- ^ "51 Peg b". Explorador de datos de exoplanetas.
- ^ "55 Cnc d". Explorador de datos de exoplanetas.
- ^ Endl, Michael. "El método Doppler o detección de planetas por velocidad radial". Universidad de Texas en Austin . Consultado el 26 de octubre de 2012 .[ enlace muerto permanente ]
- ^ "GJ 581 c". Explorador de datos de exoplanetas.
- ^ "Un peine de frecuencia láser NIR para sondeos de planetas Doppler de alta precisión". Academia China de Ciencias . 2010-10-16 . Consultado el 2010-10-16 .[ enlace muerto ]
Enlaces externos
- Búsqueda de planetas extrasolares en California y Carnegie
- La ecuación de velocidad radial en la búsqueda de exoplanetas (método de espectroscopia Doppler o Wobble)






