Ola

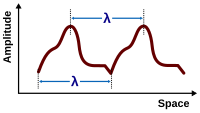
En física , matemáticas , ingeniería y campos relacionados, una onda es una perturbación dinámica que se propaga (cambio del equilibrio ) de una o más cantidades . Las ondas periódicas oscilan repetidamente alrededor de un valor de equilibrio (reposo) a cierta frecuencia . Cuando toda la forma de onda se mueve en una dirección, se dice que es una onda viajera ; por el contrario, un par de ondas periódicas superpuestas que viajan en direcciones opuestas forman una onda estacionaria . En una onda estacionaria, la amplitud de vibración tiene nulos en algunas posiciones donde la amplitud de la onda parece menor o incluso cero.
Existen dos tipos de ondas que se estudian con mayor frecuencia en la física clásica : las ondas mecánicas y las ondas electromagnéticas . En una onda mecánica, los campos de tensión y deformación oscilan alrededor de un equilibrio mecánico. Una onda mecánica es una deformación local (deformación) en algún medio físico que se propaga de partícula a partícula creando tensiones locales que también causan tensión en las partículas vecinas. Por ejemplo, las ondas sonoras son variaciones de la presión local y el movimiento de partículas que se propagan a través del medio. Otros ejemplos de ondas mecánicas son las ondas sísmicas , las ondas de gravedad , las ondas superficiales y las vibraciones de cuerdas . En una onda electromagnética (como la luz), el acoplamiento entre los campos eléctrico y magnético sostiene la propagación de ondas que involucran estos campos de acuerdo con las ecuaciones de Maxwell . Las ondas electromagnéticas pueden viajar a través del vacío y a través de algunos medios dieléctricos (en longitudes de onda donde se consideran transparentes ). Las ondas electromagnéticas, determinadas por sus frecuencias (o longitudes de onda ), tienen designaciones más específicas que incluyen ondas de radio , radiación infrarroja , ondas de terahercios , luz visible , radiación ultravioleta , rayos X y rayos gamma .
Otros tipos de ondas incluyen las ondas gravitacionales , que son perturbaciones en el espacio-tiempo que se propagan de acuerdo con la relatividad general ; ondas de difusión de calor ; ondas de plasma que combinan deformaciones mecánicas y campos electromagnéticos; ondas de reacción-difusión , como en la reacción de Belousov-Zhabotinsky ; y muchas más. Las ondas mecánicas y electromagnéticas transfieren energía , [1] momento e información , pero no transfieren partículas en el medio. En matemáticas y electrónica, las ondas se estudian como señales . [2] Por otro lado, algunas ondas tienen envolturas que no se mueven en absoluto, como las ondas estacionarias (que son fundamentales para la música) y los saltos hidráulicos .
Un campo de ondas físicas casi siempre está confinado a alguna región finita del espacio, llamada su dominio . Por ejemplo, las ondas sísmicas generadas por terremotos son significativas solo en el interior y la superficie del planeta, por lo que pueden ignorarse fuera de él. Sin embargo, las ondas con dominio infinito, que se extienden por todo el espacio, se estudian comúnmente en matemáticas y son herramientas muy valiosas para comprender las ondas físicas en dominios finitos.
Una onda plana es una idealización matemática importante donde la perturbación es idéntica a lo largo de cualquier plano (infinito) normal a una dirección específica de viaje. Matemáticamente, la onda más simple es una onda plana sinusoidal en la que en cualquier punto el campo experimenta un movimiento armónico simple a una frecuencia. En medios lineales, las ondas complicadas generalmente se pueden descomponer como la suma de muchas ondas planas sinusoidales que tienen diferentes direcciones de propagación y/o diferentes frecuencias . Una onda plana se clasifica como onda transversal si la perturbación del campo en cada punto se describe mediante un vector perpendicular a la dirección de propagación (también la dirección de transferencia de energía); o onda longitudinal si esos vectores están alineados con la dirección de propagación. Las ondas mecánicas incluyen ondas transversales y longitudinales; por otro lado, las ondas planas electromagnéticas son estrictamente transversales, mientras que las ondas sonoras en fluidos (como el aire) solo pueden ser longitudinales. Esa dirección física de un campo oscilante en relación con la dirección de propagación también se conoce como polarización de la onda , que puede ser un atributo importante.
| Física moderna |
|---|
| |
Descripción matemática
Ondas individuales
Una onda puede describirse como un campo, es decir, como una función donde es una posición y es un tiempo.
El valor de es un punto del espacio, específicamente en la región donde se define la onda. En términos matemáticos, suele ser un vector en el espacio tridimensional cartesiano . Sin embargo, en muchos casos se puede ignorar una dimensión y dejar que sea un punto del plano cartesiano . Este es el caso, por ejemplo, cuando se estudian las vibraciones de la piel de un tambor. Incluso se puede restringir a un punto de la línea cartesiana , es decir, el conjunto de números reales . Este es el caso, por ejemplo, cuando se estudian las vibraciones de una cuerda de violín o de una flauta dulce . El tiempo , por otro lado, siempre se supone que es un escalar ; es decir, un número real.
El valor de puede ser cualquier cantidad física de interés asignada al punto que puede variar con el tiempo. Por ejemplo, si representa las vibraciones dentro de un sólido elástico, el valor de suele ser un vector que da el desplazamiento actual desde de las partículas materiales que estarían en el punto en ausencia de vibración. Para una onda electromagnética, el valor de puede ser el vector de campo eléctrico , o el vector de campo magnético , o cualquier cantidad relacionada, como el vector de Poynting . En dinámica de fluidos , el valor de podría ser el vector de velocidad del fluido en el punto , o cualquier propiedad escalar como presión , temperatura o densidad . En una reacción química, podría ser la concentración de alguna sustancia en la vecindad de punto del medio de reacción.
Para cualquier dimensión (1, 2 o 3), el dominio de la onda es entonces un subconjunto de , de modo que el valor de la función está definido para cualquier punto en . Por ejemplo, al describir el movimiento de la piel de un tambor , se puede considerar que es un disco (círculo) en el plano con centro en el origen , y sea el desplazamiento vertical de la piel en el punto de y en el tiempo .
Superposición
Las ondas del mismo tipo suelen superponerse y encontrarse simultáneamente en un punto determinado del espacio y del tiempo. Las propiedades en ese punto son la suma de las propiedades de cada onda componente en ese punto. En general, las velocidades no son las mismas, por lo que la forma de onda cambiará con el tiempo y el espacio.
Espectro de ondas
![[icon]](http://upload.wikimedia.org/wikipedia/commons/thumb/1/1c/Wiki_letter_w_cropped.svg/20px-Wiki_letter_w_cropped.svg.png) | This section needs expansion with: concept summary. You can help by adding to it. (May 2023) |
Familias de ondas
A veces, nos interesa una onda específica, pero con más frecuencia es necesario comprender un conjunto más amplio de ondas posibles, como todas las formas en que la piel de un tambor puede vibrar después de ser golpeada una vez con una baqueta o todos los posibles ecos de radar que se pueden obtener de un avión que se está acercando a un aeropuerto .
En algunas de esas situaciones, se puede describir esa familia de ondas mediante una función que depende de ciertos parámetros , además de y . Luego se pueden obtener ondas diferentes (es decir, funciones diferentes de y ) eligiendo valores diferentes para esos parámetros.
Por ejemplo, la presión sonora dentro de una grabadora que reproduce una nota "pura" es típicamente una onda estacionaria , que se puede escribir como
El parámetro define la amplitud de la onda (es decir, la presión sonora máxima en el orificio, que está relacionada con la sonoridad de la nota); es la velocidad del sonido; es la longitud del orificio; y es un entero positivo (1,2,3,...) que especifica el número de nodos en la onda estacionaria. (La posición debe medirse desde la boquilla , y el tiempo desde cualquier momento en el que la presión en la boquilla sea máxima. La cantidad es la longitud de onda de la nota emitida, y es su frecuencia .) Muchas propiedades generales de estas ondas se pueden inferir de esta ecuación general, sin elegir valores específicos para los parámetros.
Como otro ejemplo, puede ser que las vibraciones de la piel de un tambor después de un solo golpe dependan únicamente de la distancia desde el centro de la piel hasta el punto de golpe y de la fuerza del golpe. En ese caso, la vibración para todos los golpes posibles se puede describir mediante una función .
A veces, la familia de ondas de interés tiene infinitos parámetros. Por ejemplo, se puede querer describir lo que le sucede a la temperatura en una barra de metal cuando se calienta inicialmente a varias temperaturas en diferentes puntos a lo largo de su longitud y luego se deja enfriar por sí sola en el vacío. En ese caso, en lugar de un escalar o un vector, el parámetro tendría que ser una función tal que sea la temperatura inicial en cada punto de la barra. Entonces, las temperaturas en momentos posteriores se pueden expresar mediante una función que depende de la función (es decir, un operador funcional ), de modo que la temperatura en un momento posterior sea
Ecuaciones de ondas diferenciales
Otra forma de describir y estudiar una familia de ondas es dar una ecuación matemática que, en lugar de dar explícitamente el valor de , solo limite cómo pueden cambiar esos valores con el tiempo. Entonces, la familia de ondas en cuestión consta de todas las funciones que satisfacen esas restricciones, es decir, todas las soluciones de la ecuación.
Este enfoque es extremadamente importante en física, porque las restricciones suelen ser consecuencia de los procesos físicos que hacen que la onda evolucione. Por ejemplo, si es la temperatura dentro de un bloque de algún material sólido homogéneo e isótropo , su evolución está limitada por la ecuación diferencial parcial
donde es el calor que se genera por unidad de volumen y tiempo en la vecindad de en un momento (por ejemplo, por reacciones químicas que ocurren allí); son las coordenadas cartesianas del punto ; es la (primera) derivada de con respecto a ; y es la segunda derivada de con respecto a . (El símbolo " " significa que, en la derivada con respecto a alguna variable, todas las demás variables deben considerarse fijas).
Esta ecuación se puede derivar de las leyes de la física que rigen la difusión del calor en medios sólidos. Por ese motivo, en matemáticas se la denomina ecuación del calor , aunque se aplica a muchas otras magnitudes físicas además de las temperaturas.
Otro ejemplo: podemos describir todos los sonidos posibles que resuenan dentro de un recipiente de gas mediante una función que da la presión en un punto y tiempo dentro de ese recipiente. Si el gas inicialmente tenía una temperatura y composición uniformes, la evolución de está limitada por la fórmula
Aquí hay una fuerza de compresión adicional que se aplica al gas cerca mediante algún proceso externo, como un altavoz o un pistón justo al lado .
Esta misma ecuación diferencial describe el comportamiento de las vibraciones mecánicas y los campos electromagnéticos en un sólido isótropo homogéneo no conductor. Nótese que esta ecuación difiere de la del flujo de calor solo en que el lado izquierdo es , la segunda derivada de con respecto al tiempo, en lugar de la primera derivada . Sin embargo, este pequeño cambio hace una gran diferencia en el conjunto de soluciones . Esta ecuación diferencial se llama "la" ecuación de onda en matemáticas, aunque describe solo un tipo muy especial de ondas.
Onda en medio elástico
Considere una onda transversal que viaja (que puede ser un pulso ) sobre una cuerda (el medio). Considere que la cuerda tiene una única dimensión espacial. Considere que esta onda viaja
- en la dirección en el espacio. Por ejemplo, supongamos que la dirección positiva es hacia la derecha y la dirección negativa hacia la izquierda.
- con amplitud constante
- con velocidad constante , donde es
- independiente de la longitud de onda (sin dispersión )
- independiente de la amplitud ( medio lineal , no no lineal ). [4] [5]
- con forma de onda constante , o forma
Esta onda puede entonces describirse mediante las funciones bidimensionales
- (forma de onda que viaja hacia la derecha)
- (forma de onda que viaja hacia la izquierda)
o, de manera más general, por la fórmula de d'Alembert : [6] que representa dos formas de onda componentes y que viajan a través del medio en direcciones opuestas. Una representación generalizada de esta onda se puede obtener [7] como la ecuación diferencial parcial
Las soluciones generales se basan en el principio de Duhamel . [8]
Formas de onda
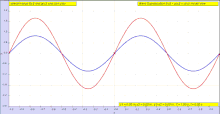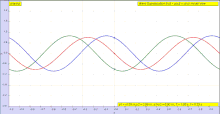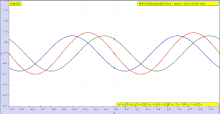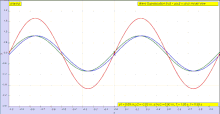
La forma de F en la fórmula de d'Alembert implica el argumento x − vt . Los valores constantes de este argumento corresponden a valores constantes de F , y estos valores constantes se dan si x aumenta al mismo ritmo que vt . Es decir, la onda con forma de la función F se moverá en la dirección x positiva a la velocidad v (y G se propagará a la misma velocidad en la dirección x negativa ). [9]
En el caso de una función periódica F con período λ , es decir, F ( x + λ − vt ) = F ( x − vt ), la periodicidad de F en el espacio significa que una instantánea de la onda en un tiempo dado t encuentra que la onda varía periódicamente en el espacio con período λ (la longitud de onda de la onda). De manera similar, esta periodicidad de F implica también una periodicidad en el tiempo: F ( x − v ( t + T )) = F ( x − vt ) siempre que vT = λ , por lo que una observación de la onda en una ubicación fija x encuentra que la onda ondula periódicamente en el tiempo con período T = λ / v . [10]
Amplitud y modulación


La amplitud de una onda puede ser constante (en cuyo caso la onda es una onda continua o de onda continua ), o puede ser modulada de modo que varíe con el tiempo y/o la posición. El contorno de la variación en amplitud se llama envolvente de la onda. Matemáticamente, la onda modulada puede escribirse en la forma: [11] [12] [13] donde es la envolvente de amplitud de la onda, es el número de onda y es la fase . Si la velocidad de grupo (ver abajo) es independiente de la longitud de onda, esta ecuación puede simplificarse como: [14] mostrando que la envolvente se mueve con la velocidad de grupo y retiene su forma. De lo contrario, en los casos donde la velocidad de grupo varía con la longitud de onda, la forma del pulso cambia de una manera que a menudo se describe usando una ecuación de envolvente . [14] [15]
Velocidad de fase y velocidad de grupo

Hay dos velocidades asociadas con las ondas, la velocidad de fase y la velocidad de grupo .
La velocidad de fase es la velocidad a la que la fase de la onda se propaga en el espacio : cualquier fase dada de la onda (por ejemplo, la cresta ) parecerá viajar a la velocidad de fase. La velocidad de fase se da en términos de la longitud de onda λ (lambda) y el período T como

La velocidad de grupo es una propiedad de las ondas que tienen una envolvente definida, que mide la propagación a través del espacio (es decir, la velocidad de fase) de la forma general de las amplitudes de las ondas: modulación o envolvente de la onda.
Ondas especiales
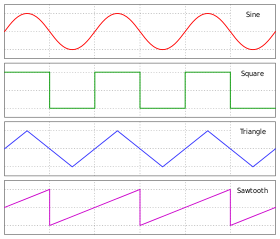
Ondas sinusoidales

Una onda sinusoidal , onda sinusoidal o senoide (símbolo: ∿) es una onda periódica cuya forma de onda (figura) es la función seno trigonométrica . En mecánica , como movimiento lineal en el tiempo, se trata de un movimiento armónico simple ; como rotación , corresponde a un movimiento circular uniforme . Las ondas sinusoidales se producen a menudo en física , incluidas las ondas de viento , las ondas sonoras y las ondas de luz , como la radiación monocromática . En ingeniería , procesamiento de señales y matemáticas , el análisis de Fourier descompone las funciones generales en una suma de ondas sinusoidales de varias frecuencias, fases relativas y magnitudes.
Cuando se combinan linealmente dos ondas sinusoidales cualesquiera de la misma frecuencia (pero con una fase arbitraria ) , el resultado es otra onda sinusoidal de la misma frecuencia; esta propiedad es única entre las ondas periódicas. Por el contrario, si se elige una fase como referencia cero, una onda sinusoidal de fase arbitraria se puede escribir como la combinación lineal de dos ondas sinusoidales con fases de cero y un cuarto de ciclo, los componentes seno y coseno , respectivamente.Ondas planas
Una onda plana es un tipo de onda cuyo valor varía solo en una dirección espacial. Es decir, su valor es constante en un plano que es perpendicular a esa dirección. Las ondas planas se pueden especificar mediante un vector de longitud unitaria que indica la dirección en la que varía la onda y un perfil de onda que describe cómo varía la onda en función del desplazamiento a lo largo de esa dirección ( ) y el tiempo ( ). Dado que el perfil de onda solo depende de la posición en la combinación , cualquier desplazamiento en direcciones perpendiculares a no puede afectar el valor del campo.
Las ondas planas se utilizan a menudo para modelar ondas electromagnéticas alejadas de una fuente. En el caso de las ondas planas electromagnéticas, los campos eléctricos y magnéticos son transversales a la dirección de propagación y también perpendiculares entre sí.
Ondas estacionarias

Una onda estacionaria, también conocida como onda estacionaria , es una onda cuya envolvente permanece en una posición constante. Este fenómeno surge como resultado de la interferencia entre dos ondas que viajan en direcciones opuestas.
La suma de dos ondas que se propagan en sentido contrario (de igual amplitud y frecuencia) crea una onda estacionaria . Las ondas estacionarias suelen surgir cuando un límite impide que la onda se propague más, lo que provoca la reflexión de la onda y, por lo tanto, la introducción de una onda que se propaga en sentido contrario. Por ejemplo, cuando se desplaza la cuerda de un violín , las ondas transversales se propagan hasta el punto en el que la cuerda se mantiene en su lugar en el puente y la cejuela , donde las ondas se reflejan de vuelta. En el puente y la cejuela, las dos ondas opuestas están en antifase y se cancelan entre sí, lo que produce un nodo . A medio camino entre dos nodos hay un antinodo , donde las dos ondas que se propagan en sentido contrario se potencian mutuamente al máximo. No hay propagación neta de energía a lo largo del tiempo.
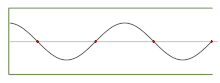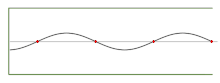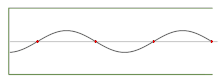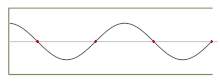
- Ondas estacionarias unidimensionales; el modo fundamental y los primeros 5 armónicos
- Una onda estacionaria bidimensional en un disco ; este es el modo fundamental.
- Una onda estacionaria en un disco con dos líneas nodales que se cruzan en el centro; esto es un armónico.
Ondas solitarias

Un solitón u onda solitaria es un paquete de ondas que se refuerza a sí mismo y que mantiene su forma mientras se propaga a una velocidad constante. Los solitones son causados por una cancelación de efectos no lineales y dispersivos en el medio. (Los efectos dispersivos son una propiedad de ciertos sistemas en los que la velocidad de una onda depende de su frecuencia). Los solitones son las soluciones de una clase generalizada de ecuaciones diferenciales parciales dispersivas débilmente no lineales que describen sistemas físicos.
Propiedades físicas
Propagación
La propagación de ondas es cualquiera de las formas en que viajan las ondas. Con respecto a la dirección de la oscilación con respecto a la dirección de propagación, podemos distinguir entre ondas longitudinales y ondas transversales .
Las ondas electromagnéticas se propagan tanto en el vacío como en medios materiales. La propagación de otros tipos de ondas, como el sonido, sólo puede producirse en un medio de transmisión .
Reflexión de ondas planas en un semiespacio
La propagación y reflexión de ondas planas, por ejemplo, ondas de presión ( ondas P ) u ondas transversales (ondas SH o SV), son fenómenos que se caracterizaron por primera vez en el campo de la sismología clásica y ahora se consideran conceptos fundamentales en la tomografía sísmica moderna . La solución analítica a este problema existe y es bien conocida. La solución del dominio de frecuencia se puede obtener encontrando primero la descomposición de Helmholtz del campo de desplazamiento, que luego se sustituye en la ecuación de onda . A partir de aquí, se pueden calcular los modos propios de la onda plana . [ cita requerida ] [ aclaración necesaria ]
Propagación de ondas SV

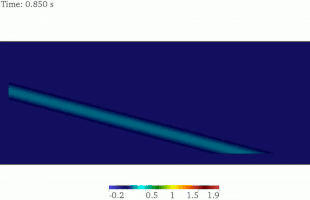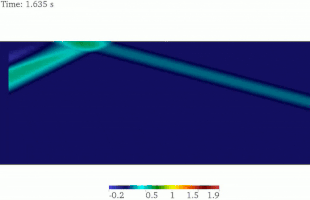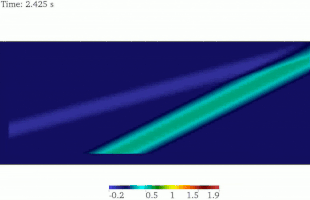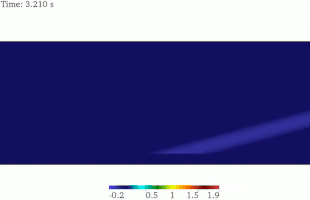
La solución analítica de la onda SV en un semiespacio indica que la onda SV plana se refleja de vuelta al dominio como ondas P y SV, dejando de lado los casos especiales. El ángulo de la onda SV reflejada es idéntico al de la onda de incidencia, mientras que el ángulo de la onda P reflejada es mayor que el de la onda SV. Para la misma frecuencia de onda, la longitud de onda SV es menor que la longitud de onda P. Este hecho se ha representado en esta imagen animada. [16]
Propagación de ondas P
De manera similar a la onda SV, la incidencia P, en general, se refleja como la onda P y SV. Hay algunos casos especiales en los que el régimen es diferente. [ Aclaración necesaria ]
Velocidad de onda

La velocidad de onda es un concepto general que abarca varios tipos de velocidades de onda, para la fase y la velocidad de una onda en relación con la propagación de energía (e información). La velocidad de fase se expresa como: donde:
- v p es la velocidad de fase (con unidad SI m/s),
- ω es la frecuencia angular (con unidad SI rad/s),
- k es el número de onda (con unidad SI rad/m).
La velocidad de fase nos indica la velocidad a la que viajará un punto de fase constante de la onda para una frecuencia discreta. La frecuencia angular ω no se puede elegir independientemente del número de onda k , sino que ambas están relacionadas a través de la relación de dispersión :
En el caso especial Ω( k ) = ck , con c constante, las ondas se denominan no dispersivas, ya que todas las frecuencias viajan a la misma velocidad de fase c . Por ejemplo, las ondas electromagnéticas en el vacío no son dispersivas. En el caso de otras formas de la relación de dispersión, tenemos ondas dispersivas. La relación de dispersión depende del medio a través del cual se propagan las ondas y del tipo de ondas (por ejemplo, ondas electromagnéticas , sonoras o acuáticas ).
La velocidad a la que viajará un paquete de ondas resultante de un rango estrecho de frecuencias se denomina velocidad de grupo y se determina a partir del gradiente de la relación de dispersión :
En casi todos los casos, una onda es principalmente un movimiento de energía a través de un medio. En la mayoría de los casos, la velocidad de grupo es la velocidad a la que se mueve la energía a través de este medio.

Las ondas exhiben comportamientos comunes en una serie de situaciones estándar, por ejemplo:
Transmisión y medios
Las ondas se desplazan normalmente en línea recta (es decir, de forma rectilínea) a través de un medio de transmisión . Dichos medios pueden clasificarse en una o más de las siguientes categorías:
- Un medio limitado si es finito en extensión, de lo contrario un medio ilimitado
- Un medio lineal si se pueden sumar las amplitudes de diferentes ondas en cualquier punto particular del medio.
- Un medio uniforme o medio homogéneo si sus propiedades físicas no cambian en diferentes lugares del espacio.
- Un medio anisotrópico si una o más de sus propiedades físicas difieren en una o más direcciones
- Un medio isótropo si sus propiedades físicas son las mismas en todas las direcciones.
Absorción
Las ondas se definen generalmente en medios que permiten que la mayor parte o la totalidad de la energía de una onda se propague sin pérdida . Sin embargo, los materiales pueden caracterizarse como "con pérdida" si eliminan energía de una onda, generalmente convirtiéndola en calor. Esto se denomina "absorción". Un material que absorbe la energía de una onda, ya sea en transmisión o reflexión, se caracteriza por un índice de refracción que es complejo . La cantidad de absorción generalmente dependerá de la frecuencia (longitud de onda) de la onda, lo que, por ejemplo, explica por qué los objetos pueden parecer coloreados.
Reflexión
Cuando una onda golpea una superficie reflectante, cambia de dirección, de modo que el ángulo formado por la onda incidente y la línea normal a la superficie es igual al ángulo formado por la onda reflejada y la misma línea normal.
Refracción

La refracción es el fenómeno por el cual una onda cambia su velocidad. Matemáticamente, esto significa que cambia el tamaño de la velocidad de fase . Normalmente, la refracción ocurre cuando una onda pasa de un medio a otro. La cantidad en que una onda es refractada por un material está dada por el índice de refracción del material. Las direcciones de incidencia y refracción están relacionadas con los índices de refracción de los dos materiales por la ley de Snell .
Difracción
Una onda presenta difracción cuando encuentra un obstáculo que la curva o cuando se propaga tras emerger de una abertura. Los efectos de difracción son más pronunciados cuando el tamaño del obstáculo o la abertura es comparable a la longitud de onda de la onda.
Interferencia

Cuando las ondas en un medio lineal (el caso habitual) se cruzan entre sí en una región del espacio, en realidad no interactúan entre sí, sino que continúan como si la otra no estuviera presente. Sin embargo, en cualquier punto de esa región, las magnitudes de campo que describen esas ondas se suman de acuerdo con el principio de superposición . Si las ondas son de la misma frecuencia en una relación de fase fija , entonces generalmente habrá posiciones en las que las dos ondas estén en fase y sus amplitudes se sumen , y otras posiciones en las que estén desfasadas y sus amplitudes se cancelen (parcial o totalmente) . Esto se llama patrón de interferencia .
Polarización

El fenómeno de la polarización surge cuando el movimiento de las ondas puede ocurrir simultáneamente en dos direcciones ortogonales . Las ondas transversales pueden ser polarizadas, por ejemplo. Cuando la polarización se utiliza como descriptor sin calificación, generalmente se refiere al caso especial y simple de polarización lineal . Una onda transversal está polarizada linealmente si oscila en una sola dirección o plano. En el caso de la polarización lineal, a menudo es útil agregar la orientación relativa de ese plano, perpendicular a la dirección de viaje, en el que ocurre la oscilación, como "horizontal", por ejemplo, si el plano de polarización es paralelo al suelo. Las ondas electromagnéticas que se propagan en el espacio libre, por ejemplo, son transversales; pueden polarizarse mediante el uso de un filtro polarizador .
Las ondas longitudinales, como las ondas sonoras, no presentan polarización. Para estas ondas existe una única dirección de oscilación, es decir, a lo largo de la dirección de propagación.
Dispersión
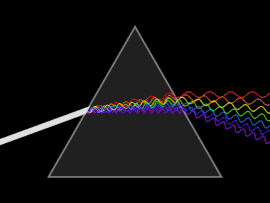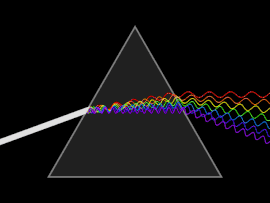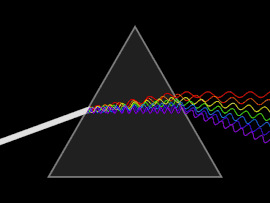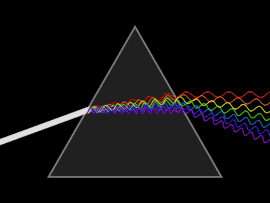
Una onda sufre dispersión cuando la velocidad de fase o la velocidad de grupo dependen de la frecuencia de la onda. La dispersión se observa más fácilmente al dejar pasar la luz blanca a través de un prisma , cuyo resultado es producir el espectro de colores del arco iris. Isaac Newton realizó experimentos con luz y prismas, presentando sus hallazgos en la Opticks (1704) de que la luz blanca consta de varios colores y que estos colores no se pueden descomponer más. [17]
Efecto Doppler
El efecto Doppler o desplazamiento Doppler es el cambio en la frecuencia de una onda en relación con un observador que se mueve en relación con la fuente de la onda. [18] Recibe su nombre en honor al físico austríaco Christian Doppler , quien describió el fenómeno en 1842.
Ondas mecánicas
Una onda mecánica es una oscilación de materia y, por lo tanto, transfiere energía a través de un medio . [19] Si bien las ondas pueden moverse a grandes distancias, el movimiento del medio de transmisión (el material) es limitado. Por lo tanto, el material oscilante no se mueve mucho de su posición inicial. Las ondas mecánicas solo se pueden producir en medios que poseen elasticidad e inercia . Hay tres tipos de ondas mecánicas: ondas transversales , ondas longitudinales y ondas superficiales .
Ondas en cuerdas
La vibración transversal de una cuerda es una función de la tensión y la inercia, y está limitada por la longitud de la cuerda, ya que los extremos están fijos. Esta restricción limita los modos de estado estable que son posibles y, por lo tanto, las frecuencias. La velocidad de una onda transversal que viaja a lo largo de una cuerda vibrante ( v ) es directamente proporcional a la raíz cuadrada de la tensión de la cuerda ( T ) sobre la densidad de masa lineal ( μ ):
donde la densidad lineal μ es la masa por unidad de longitud de la cuerda.
Ondas acústicas
Las ondas acústicas o sonoras son ondas de compresión que viajan como ondas corporales a la velocidad dada por:
o la raíz cuadrada del módulo volumétrico adiabático dividido por la densidad ambiental del medio (ver velocidad del sonido ).
Ondas de agua

- Las ondas en la superficie de un estanque son en realidad una combinación de ondas transversales y longitudinales; por lo tanto, los puntos de la superficie siguen trayectorias orbitales.
- Sonido : onda mecánica que se propaga a través de gases, líquidos, sólidos y plasmas;
- Ondas inerciales , que se producen en fluidos rotatorios y se restauran por el efecto Coriolis ;
- Ondas superficiales del océano , que son perturbaciones que se propagan a través del agua.
Ondas corporales
Las ondas de cuerpo viajan a través del interior del medio a lo largo de trayectorias controladas por las propiedades del material en términos de densidad y módulo (rigidez). La densidad y el módulo, a su vez, varían según la temperatura, la composición y la fase del material. Este efecto se asemeja a la refracción de las ondas de luz. Dos tipos de movimiento de partículas dan como resultado dos tipos de ondas de cuerpo: ondas primarias y secundarias.
Ondas sísmicas
Las ondas sísmicas son ondas de energía que viajan a través de las capas de la Tierra y son resultado de terremotos, erupciones volcánicas, movimiento de magma, grandes deslizamientos de tierra y grandes explosiones provocadas por el hombre que emiten energía acústica de baja frecuencia. Incluyen ondas corporales (ondas primarias ( ondas P ) y ondas secundarias ( ondas S )) y ondas superficiales, como las ondas de Rayleigh , las ondas de Love y las ondas de Stoneley .
Ondas de choque

Una onda de choque es un tipo de perturbación que se propaga. Cuando una onda se mueve más rápido que la velocidad local del sonido en un fluido , se trata de una onda de choque. Al igual que una onda ordinaria, una onda de choque transporta energía y puede propagarse a través de un medio; sin embargo, se caracteriza por un cambio abrupto, casi discontinuo, en la presión , la temperatura y la densidad del medio. [20]
Ondas transversales
Las ondas transversales son ondas de volumen debidas a la rigidez e inercia de las fuerzas de corte. Solo pueden transmitirse a través de sólidos y, en menor medida, a través de líquidos con una viscosidad suficientemente alta.
Otro
- Ondas de tráfico , es decir, propagación de diferentes densidades de vehículos de motor, etc., que pueden modelarse como ondas cinemáticas [21] [22]
- La onda metacrónica se refiere a la aparición de una onda viajera producida por acciones secuenciales coordinadas.
Ondas electromagnéticas

Una onda electromagnética consiste en dos ondas que son oscilaciones de los campos eléctrico y magnético . Una onda electromagnética viaja en una dirección que forma ángulos rectos con la dirección de oscilación de ambos campos. En el siglo XIX, James Clerk Maxwell demostró que, en el vacío , los campos eléctrico y magnético satisfacen la ecuación de onda ambos con velocidad igual a la de la luz . De esto surgió la idea de que la luz es una onda electromagnética. La unificación de la luz y las ondas electromagnéticas fue confirmada experimentalmente por Hertz a finales de la década de 1880. Las ondas electromagnéticas pueden tener diferentes frecuencias (y por lo tanto longitudes de onda), y se clasifican en consecuencia en bandas de ondas, como ondas de radio , microondas , infrarrojos , luz visible , ultravioleta , rayos X y rayos gamma . El rango de frecuencias en cada una de estas bandas es continuo, y los límites de cada banda son en su mayoría arbitrarios, con la excepción de la luz visible, que debe ser visible para el ojo humano normal.
Ondas mecánicas cuánticas
Ecuación de Schrödinger
La ecuación de Schrödinger describe el comportamiento ondulatorio de las partículas en mecánica cuántica . Las soluciones de esta ecuación son funciones de onda que se pueden utilizar para describir la densidad de probabilidad de una partícula.
Ecuación de Dirac
La ecuación de Dirac es una ecuación de onda relativista que detalla las interacciones electromagnéticas. Las ondas de Dirac explicaban los detalles finos del espectro del hidrógeno de una manera completamente rigurosa. La ecuación de onda también implicaba la existencia de una nueva forma de materia, la antimateria, previamente insospechada e inobservada y que fue confirmada experimentalmente. En el contexto de la teoría cuántica de campos, la ecuación de Dirac se reinterpreta para describir los campos cuánticos correspondientes a partículas de espín 1 ⁄ 2 .

olas de de Broglie
Louis de Broglie postuló que todas las partículas con momento tienen una longitud de onda
donde h es la constante de Planck y p es la magnitud del momento de la partícula. Esta hipótesis fue la base de la mecánica cuántica . Hoy en día, esta longitud de onda se denomina longitud de onda de De Broglie . Por ejemplo, los electrones en una pantalla CRT tienen una longitud de onda de De Broglie de aproximadamente 10 −13 m.
Una onda que representa una partícula que viaja en la dirección k se expresa mediante la función de onda de la siguiente manera:
donde la longitud de onda está determinada por el vector de onda k como:
y el impulso por:
Sin embargo, una onda como esta con una longitud de onda definida no está localizada en el espacio, y por lo tanto no puede representar una partícula localizada en el espacio. Para localizar una partícula, de Broglie propuso una superposición de diferentes longitudes de onda que oscilan alrededor de un valor central en un paquete de ondas , [24] una forma de onda que se utiliza a menudo en mecánica cuántica para describir la función de onda de una partícula. En un paquete de ondas, la longitud de onda de la partícula no es precisa, y la longitud de onda local se desvía a ambos lados del valor de longitud de onda principal.
Al representar la función de onda de una partícula localizada, el paquete de ondas a menudo se considera que tiene una forma gaussiana y se denomina paquete de ondas gaussianas . [25] [26] [27] Los paquetes de ondas gaussianas también se utilizan para analizar ondas de agua. [28]
Por ejemplo, una función de onda gaussiana ψ podría tomar la forma: [29]
en algún tiempo inicial t = 0, donde la longitud de onda central está relacionada con el vector de onda central k 0 como λ 0 = 2π / k 0 . Es bien conocido por la teoría del análisis de Fourier , [30] o por el principio de incertidumbre de Heisenberg (en el caso de la mecánica cuántica) que es necesario un rango estrecho de longitudes de onda para producir un paquete de ondas localizado, y cuanto más localizada sea la envoltura, mayor será la dispersión en las longitudes de onda requeridas. La transformada de Fourier de una gaussiana es en sí misma una gaussiana. [31] Dado el gaussiano:
La transformada de Fourier es:
Por tanto, la gaussiana en el espacio está formada por ondas:
es decir, un número de ondas de longitudes de onda λ tales que kλ = 2 π.
El parámetro σ decide la dispersión espacial de la gaussiana a lo largo del eje x , mientras que la transformada de Fourier muestra una dispersión en el vector de onda k determinada por 1/ σ . Es decir, cuanto menor sea la extensión en el espacio, mayor será la extensión en k , y por lo tanto en λ = 2π/ k .

Ondas de gravedad
Las ondas de gravedad son ondas generadas en un medio fluido o en la interfaz entre dos medios cuando la fuerza de la gravedad o la flotabilidad actúan para restablecer el equilibrio. Las ondas superficiales en el agua son el ejemplo más conocido.
Ondas gravitacionales
Las ondas gravitacionales también viajan a través del espacio. La primera observación de ondas gravitacionales se anunció el 11 de febrero de 2016. [32] Las ondas gravitacionales son perturbaciones en la curvatura del espacio-tiempo , predichas por la teoría de la relatividad general de Einstein .
Véase también
Ondas en general
- Onda mecánica , en transmisión de medios
- Ecuación de onda , general
- Interferencia de ondas , fenómeno en el que dos ondas se superponen para formar una onda resultante.
- Wave Motion (revista) , una revista científica
- Frente de onda , una superficie de avance de propagación de ondas.
Parámetros
- Frecuencia
- Fase (ondas) , desplazamiento o ángulo de una función de onda sinusoidal en su origen
- Relación de ondas estacionarias en telecomunicaciones
- Longitud de onda
- Número de onda
Formas de onda
- Onda progresiva , una onda difractada alrededor de una esfera.
- Campo evanescente
- Onda longitudinal
- Onda viajera periódica
- Onda sinusoidal
- Onda cuadrada
- Onda estacionaria
- Onda transversal
Ondas electromagnéticas
- Onda superficial de Dyakonov
- Onda de Dyakonov-Voigt
- Guía de ondas Tierra-ionosfera , en transmisión de radio
- Radiación electromagnética
- La ecuación de onda electromagnética describe la propagación de ondas electromagnéticas.
- Microondas , una forma de radiación electromagnética.
En fluidos
- Teoría de ondas de Airy , en dinámica de fluidos
- Onda capilar , en dinámica de fluidos
- Onda cnoidal , en dinámica de fluidos
- Onda de borde , una onda de gravedad superficial fijada por refracción contra un límite rígido.
- Onda de Faraday , un tipo de onda en líquidos
- Onda de gravedad , en dinámica de fluidos
- Onda interna , una onda dentro de un medio fluido.
- Onda de choque , en aerodinámica
- Onda sonora, una onda de sonido a través de un medio como el aire o el agua.
- Maremoto, un nombre científicamente incorrecto para un tsunami
- Onda de Tollmien-Schlichting , en dinámica de fluidos
- Onda de viento
En mecánica cuántica
En relatividad
- Onda gravitacional , en la teoría de la relatividad
- Ecuaciones de onda relativistas , ecuaciones de onda que consideran la relatividad especial
- espacio-tiempo de ondas pp , un conjunto de soluciones exactas a la ecuación de campo de Einstein
Otros tipos específicos de ondas
- Onda de Alfvén , en física del plasma
- Onda atmosférica , una perturbación periódica en los campos de variables atmosféricas.
- Onda de abeto , una configuración de bosque
- Ondas de cordero , en materiales sólidos
- Onda de Rayleigh , ondas acústicas superficiales que viajan en sólidos.
- Onda de espín , en magnetismo
- Onda de densidad de espín en materiales sólidos
- Paquete de ondas troyanas en la ciencia de partículas
- Ondas en plasmas , en física del plasma
Temas relacionados
- Absorción (radiación electromagnética)
- Antena (radio)
- Ritmo (acústica)
- Flujo ramificado
- Cimática
- Difracción
- Dispersión (ondas de agua)
- Efecto Doppler
- Detector de sobres
- Transformada de Fourier para calcular la periodicidad en datos espaciados uniformemente
- Velocidad de grupo
- Armónico
- Principio de Huygens-Fresnel
- Índice de artículos sobre olas
- Onda inercial
- Análisis espectral de mínimos cuadrados para calcular la periodicidad en datos espaciados de forma desigual
- Lista de olas que llevan nombres de personas
- Velocidad de fase
- Fotón
- Polarización (física)
- Constante de propagación
- Propagación de radio
- Rayo (óptica)
- Sistema de reacción-difusión
- Reflexión (física)
- Refracción
- Resonancia
- Tanque de ondulación
- Ola rebelde
- Dispersión
- Ecuaciones de aguas poco profundas
- Maquina de ondas Shive
- Sonido
- Onda estacionaria
- Medio de transmisión
- Factor de velocidad
- Ecuación de onda
- Energía de las olas
- Turbulencia de las olas
- Onda de viento
- Onda de viento#Formación
Referencias
- ^ (Hall 1980, pág. 8)
- ^ Pragnan Chakravorty, "¿Qué es una señal? [Notas de clase]", IEEE Signal Processing Magazine , vol. 35, núm. 5, págs. 175-177, septiembre de 2018. doi :10.1109/MSP.2018.2832195
- ^ Santos, Edgar; Schöll, Michael; Sánchez-Porras, Renán; Dahlem, Markus A.; Silos, Humberto; Unterberg, Andreas; Dickhaus, Hartmut; Sakowitz, Oliver W. (1 de octubre de 2014). "Ondas radiales, espirales y reverberantes de despolarización propagada ocurren en el cerebro girencefálico". NeuroImage . 99 : 244–255. doi :10.1016/j.neuroimage.2014.05.021. ISSN 1095-9572. PMID 24852458. S2CID 1347927.
- ^ Michael A. Slawinski (2003). "Ecuaciones de onda". Ondas y rayos sísmicos en medios elásticos . Elsevier. pp. 131 y siguientes . ISBN 978-0-08-043930-3.
- ^ Lev A. Ostrovsky y Alexander I. Potapov (2001). Ondas moduladas: teoría y aplicación. Prensa de la Universidad Johns Hopkins. ISBN 978-0-8018-7325-6.
- ^ Graaf, Karl F (1991). Movimiento ondulatorio en sólidos elásticos (Reimpresión de la edición de Oxford de 1975). Dover. Págs. 13-14. ISBN 978-0-486-66745-4.
- ^ Para un ejemplo de derivación, véanse los pasos que conducen a la ecuación (17) en Redfern, Francis. "Kinematic Derivation of the Wave Equation". Physics Journal . Archivado desde el original el 24 de julio de 2013. Consultado el 11 de diciembre de 2012 .
- ^ Jalal M. Ihsan Shatah; Michael Struwe (2000). "La ecuación de onda lineal". Ecuaciones de onda geométricas . Librería de la American Mathematical Society. pp. 37 y siguientes . ISBN 978-0-8218-2749-9.
- ^ Louis Lyons (1998). Todo lo que querías saber sobre matemáticas pero temías preguntar. Cambridge University Press. pp. 128 y siguientes . ISBN 978-0-521-43601-4.
- ^ McPherson, Alexander (2009). "Ondas y sus propiedades". Introducción a la cristalografía macromolecular (2.ª ed.). Wiley. pág. 77. ISBN 978-0-470-18590-2.
- ^ Christian Jirauschek (2005). Dinámica láser de ciclo FEW y detección de fase de envolvente portadora. Cuvillier Verlag. p. 9. ISBN 978-3-86537-419-6.
- ^ Fritz Kurt Kneubühl (1997). Oscilaciones y ondas. Springer. Pág. 365. ISBN. 978-3-540-62001-3.
- ^ Mark Lundstrom (2000). Fundamentos del transporte de portadores. Cambridge University Press. p. 33. ISBN 978-0-521-63134-1.
- ^ ab Chin-Lin Chen (2006). "§13.7.3 Envolvente de pulso en medios no dispersivos". Fundamentos de la óptica de ondas guiadas . Wiley. pág. 363. ISBN 978-0-471-75687-3.
- ^ Longhi, Stefano; Janner, Davide (2008). "Localización y paquetes de ondas de Wannier en cristales fotónicos". En Hugo E. Hernández-Figueroa; Michel Zamboni-Rached; Erasmo Recami (eds.). Ondas localizadas . Wiley-Interscience. pág. 329. ISBN 978-0-470-10885-7.
- ^ Las animaciones están tomadas de Poursartip, Babak (2015). "Amplificación topográfica de ondas sísmicas". UT Austin. Archivado desde el original el 9 de enero de 2017. Consultado el 24 de febrero de 2023 .
- ^ Newton, Isaac (1704). "Proposición VII Teoría V". Opticks: o tratado de las reflexiones, refracciones, inflexiones y colores de la luz. También dos tratados de las especies y magnitud de las figuras curvilíneas . Vol. 1. Londres. pág. 118.
Todos los colores del universo que son creados por la luz... son o bien los colores de luces homogéneas, o bien compuestos de éstas...
- ^ Giordano, Nicholas (2009). Física universitaria: razonamiento y relaciones. Cengage Learning. págs. 421–424. ISBN 978-0534424718.
- ^ Giancoli, DC (2009) Física para científicos e ingenieros con física moderna (4.ª ed.). Upper Saddle River, NJ: Pearson Prentice Hall.
- ^ Anderson, John D. Jr. (enero de 2001) [1984], Fundamentos de aerodinámica (3.ª ed.), McGraw-Hill Science/Engineering/Math , ISBN 978-0-07-237335-6
- ^ MJ Lighthill ; GB Whitham (1955). "Sobre las ondas cinemáticas. II. Una teoría del flujo de tráfico en carreteras largas y concurridas". Actas de la Royal Society de Londres. Serie A . 229 (1178): 281–345. Bibcode :1955RSPSA.229..281L. CiteSeerX 10.1.1.205.4573 . doi :10.1098/rspa.1955.0088. S2CID 18301080.
- ^ PI Richards (1956). "Ondas de choque en la autopista". Investigación de operaciones . 4 (1): 42–51. doi :10.1287/opre.4.1.42.
- ^ AT Fromhold (1991). "Soluciones de paquetes de ondas". Mecánica cuántica para la física aplicada y la ingeniería (reimpresión de Academic Press, edición de 1981). Courier Dover Publications. pp. 59 y siguientes . ISBN 978-0-486-66741-6.
(p. 61) ...las ondas individuales se mueven más lentamente que el paquete y, por lo tanto, pasan de nuevo a través del paquete a medida que avanza.
- ^ Ming Chiang Li (1980). "Interferencia electrónica". En L. Marton; Claire Marton (eds.). Avances en electrónica y física electrónica . Vol. 53. Academic Press. pág. 271. ISBN 978-0-12-014653-6.
- ^ Walter Greiner; D. Allan Bromley (2007). Mecánica cuántica (2.ª ed.). Springer. pág. 60. ISBN 978-3-540-67458-0.
- ^ John Joseph Gilman (2003). Base electrónica de la resistencia de los materiales. Cambridge University Press. pág. 57. ISBN 978-0-521-62005-5.
- ^ Donald D. Fitts (1999). Principios de la mecánica cuántica. Cambridge University Press. pág. 17. ISBN 978-0-521-65841-6.
- ^ Chiang C. Mei (1989). Dinámica aplicada de las olas de la superficie oceánica (2.ª ed.). World Scientific. pág. 47. ISBN 978-9971-5-0789-3.
- ^ Greiner, Walter; Bromley, D. Allan (2007). Mecánica cuántica (2.ª ed.). Springer. pág. 60. ISBN 978-3-540-67458-0.
- ^ Siegmundo Brandt; Hans Dieter Dahmen (2001). El libro ilustrado de la mecánica cuántica (3ª ed.). Saltador. pag. 23.ISBN 978-0-387-95141-6.
- ^ Cyrus D. Cantrell (2000). Métodos matemáticos modernos para físicos e ingenieros . Cambridge University Press. pág. 677. ISBN 978-0-521-59827-9.
- ^ "Las ondas gravitacionales detectadas por primera vez 'abren una nueva ventana al universo'". Canadian Broadcasting Corporation. 11 de febrero de 2016.
Fuentes
- Fleisch, D.; Kinnaman, L. (2015). Una guía para estudiantes sobre las olas . Cambridge: Prensa de la Universidad de Cambridge. Bibcode : 2015sgw..libro.....F. ISBN 978-1107643260.
- Campbell, Murray; Greated, Clive (2001). Guía acústica para músicos (edición revisada). Oxford: Oxford University Press. ISBN 978-0198165057.
- French, AP (1971). Vibraciones y ondas (Serie de introducción a la física del MIT) . Nelson Thornes. ISBN 978-0-393-09936-2.OCLC 163810889 .
- Hall, DE (1980). Acústica musical: una introducción . Belmont, CA: Wadsworth Publishing Company. ISBN 978-0-534-00758-4..
- Hunt, Frederick Vinton (1978). Orígenes de la acústica . Woodbury, NY: Publicado para la Sociedad Acústica de Estados Unidos a través del Instituto Americano de Física. ISBN 978-0300022209.
- Ostrovsky, LA; Potapov, AS (1999). Ondas moduladas, teoría y aplicaciones . Baltimore: The Johns Hopkins University Press. ISBN 978-0-8018-5870-3..
- Griffiths, G.; Schiesser, WE (2010). Análisis de ondas viajeras de ecuaciones diferenciales parciales: métodos numéricos y analíticos con Matlab y Maple . Academic Press. ISBN 9780123846532.
- Crawford Jr., Frank S. (1968). Ondas (Berkeley Physics Course, Vol. 3) , McGraw-Hill, ISBN 978-0070048607 Versión gratuita en línea
- AEH Love (1944). Tratado sobre la teoría matemática de la elasticidad . Nueva York: Dover .
- EW Weisstein. "Velocidad de onda". ScienceWorld . Consultado el 30 de mayo de 2009 .
Enlaces externos
- Las conferencias Feynman sobre física: ondas
- Ondas lineales y no lineales
- Science Aid: Propiedades de las ondas: guía concisa dirigida a adolescentes
- "Archivos AT&T: similitudes en el comportamiento de las ondas", demostrado por JN Shive de Bell Labs (video en YouTube )













































































