Difusión

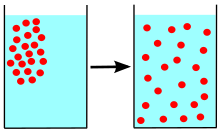
La difusión es el movimiento neto de cualquier cosa (por ejemplo, átomos, iones, moléculas, energía) generalmente desde una región de mayor concentración a una región de menor concentración. La difusión es impulsada por un gradiente en la energía libre de Gibbs o potencial químico . Es posible difundir "cuesta arriba" desde una región de menor concentración a una región de mayor concentración, como en la descomposición espinodal . La difusión es un proceso estocástico debido a la aleatoriedad inherente de la entidad que se difunde y se puede utilizar para modelar muchos escenarios estocásticos de la vida real. Por lo tanto, la difusión y los modelos matemáticos correspondientes se utilizan en varios campos más allá de la física, como la estadística , la teoría de la probabilidad , la teoría de la información , las redes neuronales , las finanzas y el marketing .

El concepto de difusión se utiliza ampliamente en muchos campos, entre ellos la física ( difusión de partículas ), la química , la biología , la sociología , la economía , la estadística , la ciencia de datos y las finanzas (difusión de personas, ideas, datos y valores de precios). Sin embargo, la idea central de la difusión es común a todos ellos: una sustancia o conjunto que experimenta difusión se extiende desde un punto o ubicación en el que hay una mayor concentración de esa sustancia o conjunto.

Un gradiente es el cambio en el valor de una cantidad; por ejemplo, concentración, presión o temperatura, con el cambio en otra variable, generalmente la distancia . Un cambio en la concentración a lo largo de una distancia se denomina gradiente de concentración , un cambio en la presión a lo largo de una distancia se denomina gradiente de presión y un cambio en la temperatura a lo largo de una distancia se denomina gradiente de temperatura .

La palabra difusión deriva del latín diffundere , que significa "difundir".

Una característica distintiva de la difusión es que depende del recorrido aleatorio de las partículas y da como resultado la mezcla o el transporte de masa sin requerir un movimiento masivo dirigido. El movimiento masivo, o flujo masivo, es la característica de la advección . ^[1] El término convección se utiliza para describir la combinación de ambos fenómenos de transporte .

Si un proceso de difusión puede describirse mediante las leyes de Fick , se denomina difusión normal (o difusión fickiana); de lo contrario, se denomina difusión anómala (o difusión no fickiana).

Cuando se habla de la extensión de la difusión, se utilizan dos escalas de longitud en dos escenarios diferentes:

1. Movimiento browniano de una fuente puntual impulsiva (por ejemplo, una sola pulverización de perfume): la raíz cuadrada del desplazamiento cuadrático medio desde este punto. En la difusión fickiana, esto es , donde es la dimensión de este movimiento browniano;${\displaystyle {\sqrt {2nDt}}}$${\displaystyle n}$
2. Fuente de concentración constante en una dimensión: la longitud de difusión. En la difusión fickiana, esta es .${\displaystyle 2{\sqrt {Dt}}}$

El "flujo en masa" es el movimiento/flujo de un cuerpo entero debido a un gradiente de presión (por ejemplo, el agua que sale de un grifo). La "difusión" es el movimiento/dispersión gradual de la concentración dentro de un cuerpo sin movimiento neto de materia. Un ejemplo de un proceso en el que se producen tanto el movimiento en masa como la difusión es la respiración humana. ^[2]

En primer lugar, se produce un proceso de "flujo masivo". Los pulmones se encuentran en la cavidad torácica , que se expande como primer paso de la respiración externa. Esta expansión conduce a un aumento del volumen de los alvéolos en los pulmones, lo que provoca una disminución de la presión en los alvéolos. Esto crea un gradiente de presión entre el aire fuera del cuerpo a una presión relativamente alta y los alvéolos a una presión relativamente baja. El aire se mueve a favor del gradiente de presión a través de las vías respiratorias de los pulmones y hacia los alvéolos hasta que la presión del aire y la de los alvéolos se igualan, es decir, el movimiento del aire por flujo masivo se detiene una vez que ya no hay gradiente de presión.

En segundo lugar, se produce un proceso de "difusión". El aire que llega a los alvéolos tiene una concentración de oxígeno mayor que el aire "viciado" de los alvéolos. El aumento de la concentración de oxígeno crea un gradiente de concentración de oxígeno entre el aire de los alvéolos y la sangre de los capilares que rodean los alvéolos. El oxígeno se desplaza entonces por difusión, siguiendo el gradiente de concentración, hacia la sangre. La otra consecuencia de la llegada del aire a los alvéolos es que la concentración de dióxido de carbono en los alvéolos disminuye. Esto crea un gradiente de concentración para que el dióxido de carbono se difunda desde la sangre hacia los alvéolos, ya que el aire fresco tiene una concentración muy baja de dióxido de carbono en comparación con la sangre del cuerpo.

En tercer lugar, existe otro proceso de "flujo masivo". La acción de bombeo del corazón transporta la sangre por todo el cuerpo. A medida que el ventrículo izquierdo del corazón se contrae, el volumen disminuye, lo que aumenta la presión en el ventrículo. Esto crea un gradiente de presión entre el corazón y los capilares, y la sangre se mueve a través de los vasos sanguíneos mediante un flujo masivo a favor del gradiente de presión.

Hay dos maneras de introducir la noción de difusión : un enfoque fenomenológico que comienza con las leyes de difusión de Fick y sus consecuencias matemáticas, o un enfoque físico y atomístico, considerando el recorrido aleatorio de las partículas en difusión . ^[3]

En el enfoque fenomenológico, la difusión es el movimiento de una sustancia desde una región de alta concentración a una región de baja concentración sin movimiento de masa . Según las leyes de Fick, el flujo de difusión es proporcional al gradiente negativo de concentraciones. Va desde regiones de mayor concentración a regiones de menor concentración. Tiempo después, se desarrollaron varias generalizaciones de las leyes de Fick en el marco de la termodinámica y la termodinámica del no equilibrio . ^[4]

Desde el punto de vista atomístico , la difusión se considera como el resultado del recorrido aleatorio de las partículas que se difunden. En la difusión molecular , las moléculas en movimiento en un gas, líquido o sólido se autopropulsan mediante energía cinética. El recorrido aleatorio de pequeñas partículas en suspensión en un fluido fue descubierto en 1827 por Robert Brown , quien descubrió que las partículas diminutas suspendidas en un medio líquido y lo suficientemente grandes como para ser visibles bajo un microscopio óptico exhiben un movimiento rápido y continuamente irregular de partículas conocido como movimiento browniano. La teoría del movimiento browniano y los antecedentes atomísticos de la difusión fueron desarrollados por Albert Einstein . ^[5] El concepto de difusión se aplica típicamente a cualquier tema que involucre recorridos aleatorios en conjuntos de individuos.

En química y ciencia de los materiales , la difusión también se refiere al movimiento de moléculas de fluido en sólidos porosos. ^[6] Se distinguen diferentes tipos de difusión en sólidos porosos. La difusión molecular ocurre cuando la colisión con otra molécula es más probable que la colisión con las paredes del poro. En tales condiciones, la difusividad es similar a la de un espacio no confinado y es proporcional al camino libre medio. La difusión de Knudsen ocurre cuando el diámetro del poro es comparable o menor que el camino libre medio de la molécula que se difunde a través del poro. En esta condición, la colisión con las paredes del poro se vuelve gradualmente más probable y la difusividad es menor. Finalmente, existe la difusión configuracional, que ocurre si las moléculas tienen un tamaño comparable al del poro. En esta condición, la difusividad es mucho menor en comparación con la difusión molecular y pequeñas diferencias en el diámetro cinético de la molécula causan grandes diferencias en la difusividad .

Los biólogos suelen utilizar los términos "movimiento neto" o "difusión neta" para describir el movimiento de iones o moléculas por difusión. Por ejemplo, el oxígeno puede difundirse a través de las membranas celulares siempre que haya una mayor concentración de oxígeno fuera de la célula. Sin embargo, como el movimiento de las moléculas es aleatorio, en ocasiones las moléculas de oxígeno salen de la célula (en contra del gradiente de concentración). Como hay más moléculas de oxígeno fuera de la célula, la probabilidad de que entren en la célula es mayor que la probabilidad de que salgan de ella. Por lo tanto, el movimiento "neto" de las moléculas de oxígeno (la diferencia entre el número de moléculas que entran o salen de la célula) es hacia el interior de la célula. En otras palabras, hay un movimiento neto de moléculas de oxígeno a favor del gradiente de concentración.

En el ámbito de la época, la difusión en sólidos se utilizó mucho antes de que se creara la teoría de la difusión. Por ejemplo, Plinio el Viejo había descrito anteriormente el proceso de cementación , que produce acero a partir del elemento hierro (Fe) mediante difusión de carbono. Otro ejemplo es bien conocido desde hace muchos siglos, la difusión de colores de las vidrieras o la loza y la cerámica china .

En la ciencia moderna, el primer estudio sistemático experimental de la difusión lo realizó Thomas Graham . Estudió la difusión en gases y describió el fenómeno principal entre 1831 y 1833: ^[7]

"...los gases de diferente naturaleza, al ponerse en contacto, no se ordenan según su densidad, el más pesado abajo y el más ligero arriba, sino que se difunden espontáneamente, mutua e igualmente, unos a través de otros, y permanecen así en un estado íntimo de mezcla durante cualquier período de tiempo."

Las mediciones de Graham contribuyeron a que James Clerk Maxwell dedujera, en 1867, el coeficiente de difusión del CO2 _en el aire. El margen de error es inferior al 5%.

En 1855, Adolf Fick , un joven de 26 años que se dedicaba a la demostración de anatomía en Zúrich, propuso su ley de difusión . Utilizó la investigación de Graham y afirmó que su objetivo era "el desarrollo de una ley fundamental para el funcionamiento de la difusión en un único elemento del espacio". Afirmó que existía una profunda analogía entre la difusión y la conducción de calor o electricidad, creando un formalismo similar a la ley de Fourier para la conducción de calor (1822) y la ley de Ohm para la corriente eléctrica (1827).

Robert Boyle demostró la difusión en sólidos en el siglo XVII ^[8] mediante la penetración de zinc en una moneda de cobre. Sin embargo, la difusión en sólidos no se estudió sistemáticamente hasta la segunda mitad del siglo XIX. William Chandler Roberts-Austen , el conocido metalúrgico británico y ex asistente de Thomas Graham, estudió sistemáticamente la difusión en estado sólido utilizando el ejemplo del oro en plomo en 1896. : ^[9]

"... Mi larga conexión con las investigaciones de Graham hizo que fuera casi un deber intentar extender su trabajo sobre la difusión de líquidos a los metales".

En 1858, Rudolf Clausius introdujo el concepto de trayectoria libre media . Ese mismo año, James Clerk Maxwell desarrolló la primera teoría atomística de los procesos de transporte en gases. La teoría atomística moderna de la difusión y el movimiento browniano fue desarrollada por Albert Einstein , Marian Smoluchowski y Jean-Baptiste Perrin . Ludwig Boltzmann , en el desarrollo de los antecedentes atomísticos de los procesos de transporte macroscópicos , introdujo la ecuación de Boltzmann , que ha servido a las matemáticas y a la física como fuente de ideas y preocupaciones sobre los procesos de transporte durante más de 140 años. ^[10]

Entre 1920 y 1921, George de Hevesy midió la autodifusión utilizando radioisótopos . Estudió la autodifusión de isótopos radiactivos del plomo en el plomo líquido y sólido.

Yakov Frenkel (a veces Jakov/Jacob Frenkel) propuso y elaboró ​​en 1926 la idea de la difusión en cristales a través de defectos locales (vacantes y átomos intersticiales ). Concluyó que el proceso de difusión en materia condensada es un conjunto de saltos elementales e interacciones cuasiquímicas de partículas y defectos. Introdujo varios mecanismos de difusión y halló constantes de velocidad a partir de datos experimentales.

Más tarde, Carl Wagner y Walter H. Schottky desarrollaron aún más las ideas de Frenkel sobre los mecanismos de difusión. En la actualidad, se reconoce universalmente que los defectos atómicos son necesarios para mediar la difusión en los cristales. ^[9]

Henry Eyring , junto con otros autores, aplicó su teoría de las velocidades de reacción absolutas al modelo cuasidiquímico de difusión de Frenkel. ^[11] La analogía entre la cinética de reacción y la difusión conduce a varias versiones no lineales de la ley de Fick. ^[12]

Cada modelo de difusión expresa el flujo de difusión con el uso de concentraciones, densidades y sus derivadas. El flujo es un vector que representa la cantidad y la dirección de transferencia. Dada una pequeña área con normal , la transferencia de una cantidad física a través del área por tiempo es${\displaystyle \mathbf {J} }$ ${\displaystyle \Delta S}$${\displaystyle {\boldsymbol {\nu }}}$ ${\displaystyle N}$${\displaystyle \Delta S}$${\displaystyle \Delta t}$

${\displaystyle \Delta N=(\mathbf {J} ,{\boldsymbol {\nu }})\,\Delta S\,\Delta t+o(\Delta S\,\Delta t)\,,}$

donde es el producto interno y es la notación de o minúscula . Si usamos la notación del área vectorial entonces${\displaystyle (\mathbf {J} ,{\boldsymbol {\nu }})}$${\displaystyle o(\cdots )}$ ${\displaystyle \Delta \mathbf {S} ={\boldsymbol {\nu }}\,\Delta S}$

${\displaystyle \Delta N=(\mathbf {J} ,\Delta \mathbf {S} )\,\Delta t+o(\Delta \mathbf {S} \,\Delta t)\,.}$

La dimensión del flujo de difusión es [flujo] = [cantidad]/([tiempo]·[área]). La cantidad física que se difunde puede ser el número de partículas, masa, energía, carga eléctrica o cualquier otra cantidad extensiva escalar . Para su densidad, , la ecuación de difusión tiene la forma${\displaystyle N}$${\displaystyle n}$

${\displaystyle {\frac {\partial n}{\partial t}}=-\nabla \cdot \mathbf {J} +W\,,}$

donde es la intensidad de cualquier fuente local de esta cantidad (por ejemplo, la velocidad de una reacción química). Para la ecuación de difusión, las condiciones de contorno sin flujo se pueden formular como en el límite, donde es la normal al límite en el punto .${\displaystyle W}$${\displaystyle (\mathbf {J} (x),{\boldsymbol {\nu }}(x))=0}$${\displaystyle {\boldsymbol {\nu }}}$${\displaystyle x}$

Primera ley de Fick: El flujo de difusión, , es proporcional al gradiente negativo de concentración espacial, :${\displaystyle \mathbf {J} }$${\displaystyle n(x,t)}$

${\displaystyle \mathbf {J} =-D(x)\,\nabla n(x,t),}$

donde D es el coeficiente de difusión . La ecuación de difusión correspondiente (segunda ley de Fick) es

${\displaystyle {\frac {\partial n(x,t)}{\partial t}}=\nabla \cdot (D(x)\,\nabla n(x,t))\,.}$

En caso de que el coeficiente de difusión sea independiente de , la segunda ley de Fick se puede simplificar a${\displaystyle x}$

${\displaystyle {\frac {\partial n(x,t)}{\partial t}}=D\,\Delta n(x,t)\ ,}$

¿Dónde está el operador de Laplace ?${\displaystyle \Delta }$

${\displaystyle \Delta n(x,t)=\sum _{i}{\frac {\partial ^{2}n(x,t)}{\partial x_{i}^{2}}}\ .}$

La ley de Fick describe la difusión de una mezcla en un medio. La concentración de esta mezcla debe ser pequeña y el gradiente de esta concentración también debe ser pequeño. La fuerza impulsora de la difusión en la ley de Fick es el antigradiente de concentración, .${\displaystyle -\nabla n}$

En 1931, Lars Onsager ^[13] incluyó los procesos de transporte multicomponente en el contexto general de la termodinámica lineal de no equilibrio. Para el transporte multicomponente,

${\displaystyle \mathbf {J} _{i}=\sum _{j}L_{ij}X_{j}\,,}$

donde es el flujo de la magnitud física (componente) y es la fuerza termodinámica .${\displaystyle \mathbf {J} _{i}}$${\displaystyle i}$${\displaystyle X_{j}}$${\displaystyle j}$

Las fuerzas termodinámicas para los procesos de transporte fueron introducidas por Onsager como gradientes espaciales de las derivadas de la densidad de entropía (utilizó el término "fuerza" entre comillas o "fuerza impulsora"):${\displaystyle s}$

${\displaystyle X_{i}=\nabla {\frac {\partial s(n)}{\partial n_{i}}}\,,}$

donde son las "coordenadas termodinámicas". Para la transferencia de calor y masa se puede tomar (la densidad de energía interna) y es la concentración del componente th. Las fuerzas impulsoras correspondientes son los vectores espaciales${\displaystyle n_{i}}$${\displaystyle n_{0}=u}$${\displaystyle n_{i}}$${\displaystyle i}$

${\displaystyle X_{0}=\nabla {\frac {1}{T}}\ ,\;\;\;X_{i}=-\nabla {\frac {\mu _{i}}{T}}\;(i>0),}$porque${\displaystyle \mathrm {d} s={\frac {1}{T}}\,\mathrm {d} u-\sum _{i\geq 1}{\frac {\mu _{i}}{T}}\,{\rm {d}}n_{i}}$

donde T es la temperatura absoluta y es el potencial químico del componente th. Cabe destacar que las ecuaciones de difusión separadas describen la mezcla o el transporte de masa sin movimiento en masa. Por lo tanto, se descuidan los términos con variación de la presión total. Es posible para la difusión de pequeñas mezclas y para gradientes pequeños.${\displaystyle \mu _{i}}$${\displaystyle i}$

Para las ecuaciones lineales de Onsager, debemos tomar las fuerzas termodinámicas en la aproximación lineal cerca del equilibrio:

${\displaystyle X_{i}=\sum _{k\geq 0}\left.{\frac {\partial ^{2}s(n)}{\partial n_{i}\,\partial n_{k}}}\right|_{n=n^{*}}\nabla n_{k}\ ,}$

donde las derivadas de se calculan en el equilibrio . La matriz de los coeficientes cinéticos debe ser simétrica ( relaciones recíprocas de Onsager ) y definida positiva ( para el crecimiento de la entropía ).${\displaystyle s}$${\displaystyle n^{*}}$ ${\displaystyle L_{ij}}$

Las ecuaciones de transporte son

${\displaystyle {\frac {\partial n_{i}}{\partial t}}=-\operatorname {div} \mathbf {J} _{i}=-\sum _{j\geq 0}L_{ij}\operatorname {div} X_{j}=\sum _{k\geq 0}\left[-\sum _{j\geq 0}L_{ij}\left.{\frac {\partial ^{2}s(n)}{\partial n_{j}\,\partial n_{k}}}\right|_{n=n^{*}}\right]\,\Delta n_{k}\ .}$

Aquí, todos los índices i , j , k = 0, 1, 2, ... están relacionados con la energía interna (0) y varios componentes. La expresión entre corchetes es la matriz de los coeficientes de difusión ( i , k  > 0), termodifusión ( i  > 0, k  = 0 o k  > 0, i  = 0) y conductividad térmica ( i = k = 0 ).${\displaystyle D_{ik}}$

En condiciones isotérmicas, T  = constante. El potencial termodinámico relevante es la energía libre (o la entropía libre ). Las fuerzas impulsoras termodinámicas para la difusión isotérmica son antigradientes de potenciales químicos, , y la matriz de coeficientes de difusión es${\displaystyle -(1/T)\,\nabla \mu _{j}}$

${\displaystyle D_{ik}={\frac {1}{T}}\sum _{j\geq 1}L_{ij}\left.{\frac {\partial \mu _{j}(n,T)}{\partial n_{k}}}\right|_{n=n^{*}}}$

( i,k  > 0).

Existe una arbitrariedad intrínseca en la definición de las fuerzas termodinámicas y los coeficientes cinéticos porque no se pueden medir por separado y solo se pueden medir sus combinaciones. Por ejemplo, en el trabajo original de Onsager ^[13] las fuerzas termodinámicas incluyen un multiplicador adicional T , mientras que en el Curso de física teórica ^[14] se omite este multiplicador pero el signo de las fuerzas termodinámicas es opuesto. Todos estos cambios se complementan con los cambios correspondientes en los coeficientes y no afectan a las cantidades mensurables.${\textstyle \sum _{j}L_{ij}X_{j}}$

El formalismo de la termodinámica lineal irreversible (Onsager) genera los sistemas de ecuaciones de difusión lineal en la forma

${\displaystyle {\frac {\partial c_{i}}{\partial t}}=\sum _{j}D_{ij}\,\Delta c_{j}.}$

Si la matriz de coeficientes de difusión es diagonal, entonces este sistema de ecuaciones es simplemente una colección de ecuaciones de Fick desacopladas para varios componentes. Supongamos que la difusión no es diagonal, por ejemplo, y consideremos el estado con . En este estado, . Si en algunos puntos, entonces se vuelve negativo en estos puntos en un corto tiempo. Por lo tanto, la difusión no diagonal lineal no preserva la positividad de las concentraciones. Las ecuaciones no diagonales de difusión multicomponente deben ser no lineales. ^[12]${\displaystyle D_{12}\neq 0}$${\displaystyle c_{2}=\cdots =c_{n}=0}$${\displaystyle \partial c_{2}/\partial t=D_{12}\,\Delta c_{1}}$${\displaystyle D_{12}\,\Delta c_{1}(x)<0}$${\displaystyle c_{2}(x)}$

La relación de Einstein (teoría cinética) conecta el coeficiente de difusión y la movilidad (la relación entre la velocidad de deriva terminal de la partícula y una fuerza aplicada ). ^[15] Para partículas cargadas:

${\displaystyle D={\frac {\mu \,k_{\text{B}}T}{q}},}$

donde D es la constante de difusión , μ es la "movilidad", k _B es la constante de Boltzmann , T es la temperatura absoluta y q es la carga elemental , es decir, la carga de un electrón.

A continuación, para combinar en una misma fórmula el potencial químico μ y la movilidad, utilizamos para la movilidad la notación .${\displaystyle {\mathfrak {m}}}$

El enfoque basado en la movilidad fue aplicado posteriormente por T. Teorell. ^[16] En 1935, estudió la difusión de iones a través de una membrana. Formuló la esencia de su enfoque en la fórmula:

El flujo es igual a la movilidad × concentración × fuerza por gramo-ion .

Esta es la llamada fórmula de Teorell . ^{[ cita requerida ]} El término "ion-gramo" ("partícula-gramo") se utiliza para una cantidad de una sustancia que contiene el número de Avogadro de iones (partículas). El término moderno común es mol .

La fuerza en condiciones isotérmicas consta de dos partes:

1. Fuerza de difusión causada por el gradiente de concentración: .${\displaystyle -RT{\frac {1}{n}}\,\nabla n=-RT\,\nabla (\ln(n/n^{\text{eq}}))}$
2. Fuerza electrostática causada por gradiente de potencial eléctrico: .${\displaystyle q\,\nabla \varphi }$

Aquí R es la constante del gas, T es la temperatura absoluta, n es la concentración, la concentración de equilibrio está marcada por un superíndice "eq", q es la carga y φ es el potencial eléctrico.

La diferencia simple pero crucial entre la fórmula de Teorell y las leyes de Onsager es el factor de concentración en la expresión de Teorell para el flujo. En el enfoque de Einstein-Teorell, si para la fuerza finita la concentración tiende a cero, entonces el flujo también tiende a cero, mientras que las ecuaciones de Onsager violan esta regla simple y físicamente obvia.

La formulación general de la fórmula de Teorell para sistemas no perfectos en condiciones isotérmicas es ^[12]

${\displaystyle \mathbf {J} ={\mathfrak {m}}\exp \left({\frac {\mu -\mu _{0}}{RT}}\right)(-\nabla \mu +({\text{external force per mole}})),}$

donde μ es el potencial químico , μ ₀ es el valor estándar del potencial químico. La expresión es la denominada actividad . Mide la "concentración efectiva" de una especie en una mezcla no ideal. En esta notación, la fórmula de Teorell para el flujo tiene una forma muy simple ^[12]${\displaystyle a=\exp \left({\frac {\mu -\mu _{0}}{RT}}\right)}$

${\displaystyle \mathbf {J} ={\mathfrak {m}}a(-\nabla \mu +({\text{external force per mole}})).}$

La derivación estándar de la actividad incluye un factor de normalización y para concentraciones pequeñas , donde es la concentración estándar. Por lo tanto, esta fórmula para el flujo describe el flujo de la cantidad adimensional normalizada :${\displaystyle a=n/n^{\ominus }+o(n/n^{\ominus })}$${\displaystyle n^{\ominus }}$${\displaystyle n/n^{\ominus }}$

${\displaystyle {\frac {\partial (n/n^{\ominus })}{\partial t}}=\nabla \cdot [{\mathfrak {m}}a(\nabla \mu -({\text{external force per mole}}))].}$

El modelo de Einstein ignora la inercia de la partícula que se difunde. La ecuación alternativa de Langevin comienza con la segunda ley del movimiento de Newton: ^[17]

${\displaystyle m{\frac {d^{2}x}{dt^{2}}}=-{\frac {1}{\mu }}{\frac {dx}{dt}}+F(t)}$

dónde

• x es la posición.
• μ es la movilidad de la partícula en el fluido o gas, que puede calcularse utilizando la relación de Einstein (teoría cinética) .
• m es la masa de la partícula.
• F es la fuerza aleatoria aplicada a la partícula.
• Es el momento.

Resolviendo esta ecuación, se obtiene la constante de difusión dependiente del tiempo en el límite de tiempo largo y cuando la partícula es significativamente más densa que el fluido circundante, ^[17]

${\displaystyle D(t)=\mu \,k_{\rm {B}}T(1-e^{-t/(m\mu )})}$

dónde

• k _B es la constante de Boltzmann ;
• T es la temperatura absoluta .
• μ es la movilidad de la partícula en el fluido o gas, que puede calcularse utilizando la relación de Einstein (teoría cinética) .
• m es la masa de la partícula.
• Es el momento.

En escalas de tiempo largas, se recupera el resultado de Einstein, pero en escalas de tiempo cortas, también se explica el régimen balístico . Además, a diferencia del enfoque de Einstein, se puede definir una velocidad, lo que conduce al teorema de fluctuación-disipación , que conecta la competencia entre la fricción y las fuerzas aleatorias en la definición de la temperatura. ^{[17] : 3.2}

La difusión de reactivos en la superficie de un catalizador puede desempeñar un papel importante en la catálisis heterogénea. El modelo de difusión en la monocapa ideal se basa en los saltos de los reactivos en los lugares libres más próximos. Este modelo se utilizó para la oxidación de CO sobre Pt a baja presión de gas.

El sistema incluye varios reactivos en la superficie. Sus concentraciones superficiales son La superficie es una red de lugares de adsorción. Cada molécula de reactivo llena un lugar en la superficie. Algunos de los lugares están libres. La concentración de los lugares libres es . La suma de todos (incluidos los lugares libres) es constante, la densidad de lugares de adsorción b .${\displaystyle A_{1},A_{2},\ldots ,A_{m}}$${\displaystyle c_{1},c_{2},\ldots ,c_{m}.}$${\displaystyle z=c_{0}}$${\displaystyle c_{i}}$

El modelo de salto da para el flujo de difusión de ( i  = 1, ...,  n ):${\displaystyle A_{i}}$

${\displaystyle \mathbf {J} _{i}=-D_{i}[z\,\nabla c_{i}-c_{i}\nabla z]\,.}$

La ecuación de difusión correspondiente es: ^[12]

${\displaystyle {\frac {\partial c_{i}}{\partial t}}=-\operatorname {div} \mathbf {J} _{i}=D_{i}[z\,\Delta c_{i}-c_{i}\,\Delta z]\,.}$

Debido a la ley de conservación, tenemos el sistema de m ecuaciones de difusión. Para un componente obtenemos la ley de Fick y ecuaciones lineales porque . Para dos o más componentes las ecuaciones son no lineales.${\displaystyle z=b-\sum _{i=1}^{n}c_{i}\,,}$${\displaystyle (b-c)\,\nabla c-c\,\nabla (b-c)=b\,\nabla c}$

Si todas las partículas pueden intercambiar sus posiciones con sus vecinas más cercanas, entonces una generalización simple da

${\displaystyle \mathbf {J} _{i}=-\sum _{j}D_{ij}[c_{j}\,\nabla c_{i}-c_{i}\,\nabla c_{j}]}$

${\displaystyle {\frac {\partial c_{i}}{\partial t}}=\sum _{j}D_{ij}[c_{j}\,\Delta c_{i}-c_{i}\,\Delta c_{j}]}$

donde es una matriz simétrica de coeficientes que caracterizan las intensidades de los saltos. Los lugares libres (vacantes) deben considerarse como "partículas" especiales con concentración .${\displaystyle D_{ij}=D_{ji}\geq 0}$${\displaystyle c_{0}}$

Varias versiones de estos modelos de salto también son adecuadas para mecanismos de difusión simples en sólidos.

Para la difusión en medios porosos las ecuaciones básicas son (si Φ es constante): ^[18]

${\displaystyle \mathbf {J} =-\phi D\,\nabla n^{m}}$

${\displaystyle {\frac {\partial n}{\partial t}}=D\,\Delta n^{m}\,,}$

donde D es el coeficiente de difusión, Φ es la porosidad, n es la concentración, m  > 0 (normalmente m  > 1, el caso m  = 1 corresponde a la ley de Fick).

Se debe tener cuidado de tener en cuenta adecuadamente la porosidad (Φ) del medio poroso tanto en los términos de flujo como en los términos de acumulación. ^[19] Por ejemplo, a medida que la porosidad tiende a cero, el flujo molar en el medio poroso tiende a cero para un gradiente de concentración dado. Al aplicar la divergencia del flujo, los términos de porosidad se cancelan y se forma la segunda ecuación anterior.

Para la difusión de gases en medios porosos esta ecuación es la formalización de la ley de Darcy : el flujo volumétrico de un gas en un medio poroso es

${\displaystyle q=-{\frac {k}{\mu }}\,\nabla p}$

donde k es la permeabilidad del medio, μ es la viscosidad y p es la presión.

El flujo molar advectivo se da como

J  =  nq

y para la ley de Darcy da la ecuación de difusión en medios porosos con m  =  γ  + 1.${\displaystyle p\sim n^{\gamma }}$

En medios porosos, la velocidad lineal promedio (ν), está relacionada con el flujo volumétrico como:

${\displaystyle \upsilon =q/\phi }$

Combinando el flujo molar advectivo con el flujo difusivo se obtiene la ecuación de dispersión por advección.

${\displaystyle {\frac {\partial n}{\partial t}}=D\,\Delta n^{m}\ -\nu \cdot \nabla n^{m},}$

Para la infiltración de agua subterránea, la aproximación de Boussinesq da la misma ecuación con  m  = 2.

Para el plasma con alto nivel de radiación, la ecuación de Zeldovich -Raizer da m  > 4 para la transferencia de calor.

El coeficiente de difusión es el coeficiente de la primera ley de Fick , donde J es el flujo de difusión ( cantidad de sustancia ) por unidad de área por unidad de tiempo, n (para mezclas ideales) es la concentración, x es la posición [longitud].${\displaystyle D}$ ${\displaystyle J=-D\,\partial n/\partial x}$

Consideremos dos gases con moléculas del mismo diámetro d y masa m ( autodifusión ). En este caso, la teoría elemental de la difusión por camino libre medio da como resultado el coeficiente de difusión

${\displaystyle D={\frac {1}{3}}\ell v_{T}={\frac {2}{3}}{\sqrt {\frac {k_{\rm {B}}^{3}}{\pi ^{3}m}}}{\frac {T^{3/2}}{Pd^{2}}}\,,}$

donde k _B es la constante de Boltzmann , T es la temperatura , P es la presión , es el recorrido libre medio y v _T es la velocidad térmica media:${\displaystyle \ell }$

${\displaystyle \ell ={\frac {k_{\rm {B}}T}{{\sqrt {2}}\pi d^{2}P}}\,,\;\;\;v_{T}={\sqrt {\frac {8k_{\rm {B}}T}{\pi m}}}\,.}$

Podemos ver que el coeficiente de difusión en la aproximación del camino libre medio crece con T como T ^3/2 y disminuye con P como 1/ P . Si usamos para P la ley de los gases ideales P  =  RnT con la concentración total n , entonces podemos ver que para una concentración dada n el coeficiente de difusión crece con T como T ^1/2 y para una temperatura dada disminuye con la concentración total como 1/ n .

Para dos gases diferentes, A y B, con masas moleculares m _A , m _B y diámetros moleculares d _A , d _B , la estimación del recorrido libre medio del coeficiente de difusión de A en B y B en A es:

${\displaystyle D_{\rm {AB}}={\frac {2}{3}}{\sqrt {\frac {k_{\rm {B}}^{3}}{\pi ^{3}}}}{\sqrt {{\frac {1}{2m_{\rm {A}}}}+{\frac {1}{2m_{\rm {B}}}}}}{\frac {4T^{3/2}}{P(d_{\rm {A}}+d_{\rm {B}})^{2}}}\,,}$

En la cinética de Boltzmann de la mezcla de gases, cada gas tiene su propia función de distribución, , donde t es el instante de tiempo, x es la posición y c es la velocidad de la molécula del i -ésimo componente de la mezcla. Cada componente tiene su velocidad media . Si las velocidades no coinciden entonces existe difusión .${\displaystyle f_{i}(x,c,t)}$${\textstyle C_{i}(x,t)={\frac {1}{n_{i}}}\int _{c}cf(x,c,t)\,dc}$${\displaystyle C_{i}(x,t)}$

En la aproximación de Chapman-Enskog , todas las funciones de distribución se expresan a través de las densidades de las cantidades conservadas: ^[10]

• concentraciones individuales de partículas (partículas por volumen),${\textstyle n_{i}(x,t)=\int _{c}f_{i}(x,c,t)\,dc}$
• densidad de momento ( m _i es la masa de la partícula i ),${\textstyle \sum _{i}m_{i}n_{i}C_{i}(x,t)}$
• densidad de energía cinética$${\displaystyle \sum _{i}\left(n_{i}{\frac {m_{i}C_{i}^{2}(x,t)}{2}}+\int _{c}{\frac {m_{i}(c_{i}-C_{i}(x,t))^{2}}{2}}f_{i}(x,c,t)\,dc\right).}$$

La temperatura cinética T y la presión P se definen en el espacio 3D como

${\displaystyle {\frac {3}{2}}k_{\rm {B}}T={\frac {1}{n}}\int _{c}{\frac {m_{i}(c_{i}-C_{i}(x,t))^{2}}{2}}f_{i}(x,c,t)\,dc;\quad P=k_{\rm {B}}nT,}$

¿Dónde está la densidad total?${\textstyle n=\sum _{i}n_{i}}$

Para dos gases, la diferencia entre velocidades, viene dada por la expresión: ^[10]${\displaystyle C_{1}-C_{2}}$

${\displaystyle C_{1}-C_{2}=-{\frac {n^{2}}{n_{1}n_{2}}}D_{12}\left\{\nabla \left({\frac {n_{1}}{n}}\right)+{\frac {n_{1}n_{2}(m_{2}-m_{1})}{Pn(m_{1}n_{1}+m_{2}n_{2})}}\nabla P-{\frac {m_{1}n_{1}m_{2}n_{2}}{P(m_{1}n_{1}+m_{2}n_{2})}}(F_{1}-F_{2})+k_{T}{\frac {1}{T}}\nabla T\right\},}$

donde es la fuerza aplicada a las moléculas del i -ésimo componente y es la relación de termodifusión.${\displaystyle F_{i}}$${\displaystyle k_{T}}$

El coeficiente D ₁₂ es positivo. Se trata del coeficiente de difusión. Cuatro términos de la fórmula C ₁ − C ₂ describen cuatro efectos principales en la difusión de gases:

1. ${\displaystyle \nabla \,\left({\frac {n_{1}}{n}}\right)}$describe el flujo del primer componente desde las áreas con la alta relación n ₁ / n a las áreas con valores más bajos de esta relación (y, análogamente, el flujo del segundo componente desde n ₂ / n alto a n ₂ / n bajo porque n ₂ / n  = 1 –  n ₁ / n );
2. ${\displaystyle {\frac {n_{1}n_{2}(m_{2}-m_{1})}{n(m_{1}n_{1}+m_{2}n_{2})}}\nabla P}$describe el flujo de las moléculas más pesadas hacia las zonas con mayor presión y de las moléculas más ligeras hacia las zonas con menor presión, esto es barodifusión;
3. ${\displaystyle {\frac {m_{1}n_{1}m_{2}n_{2}}{P(m_{1}n_{1}+m_{2}n_{2})}}(F_{1}-F_{2})}$describe la difusión causada por la diferencia de fuerzas aplicadas a moléculas de distintos tipos. Por ejemplo, en el campo gravitatorio de la Tierra, las moléculas más pesadas deberían descender, o en el campo eléctrico, las moléculas cargadas deberían moverse, hasta que este efecto no se equilibre con la suma de otros términos. Este efecto no debe confundirse con la barodifusión causada por el gradiente de presión.
4. ${\displaystyle k_{T}{\frac {1}{T}}\nabla T}$describe la termodifusión , el flujo de difusión causado por el gradiente de temperatura.

Todos estos efectos se denominan difusión porque describen las diferencias entre las velocidades de los distintos componentes de la mezcla. Por lo tanto, estos efectos no pueden describirse como un transporte masivo y difieren de la advección o la convección.

En una primera aproximación, ^[10]

• $${\displaystyle D_{12}={\frac {3}{2n(d_{1}+d_{2})^{2}}}\left[{\frac {kT(m_{1}+m_{2})}{2\pi m_{1}m_{2}}}\right]^{1/2}}$$para esferas rígidas;
• $${\displaystyle D_{12}={\frac {3}{8nA_{1}({\nu })\Gamma (3-{\frac {2}{\nu -1}})}}\left[{\frac {kT(m_{1}+m_{2})}{2\pi m_{1}m_{2}}}\right]^{1/2}\left({\frac {2kT}{\kappa _{12}}}\right)^{\frac {2}{\nu -1}}}$$para repeler la fuerza${\displaystyle \kappa _{12}r^{-\nu }.}$

El número se define mediante cuadraturas (fórmulas (3.7), (3.9), cap. 10 del libro clásico de Chapman y Cowling ^[10] )${\displaystyle A_{1}({\nu })}$

Podemos ver que la dependencia de T para las esferas rígidas es la misma que para la teoría simple del camino libre medio, pero para las leyes de repulsión de potencia el exponente es diferente. La dependencia de una concentración total n para una temperatura dada tiene siempre el mismo carácter, 1/ n .

En aplicaciones de dinámica de gases, el flujo de difusión y el flujo volumétrico deben unirse en un sistema de ecuaciones de transporte. El flujo volumétrico describe la transferencia de masa. Su velocidad V es la velocidad media de masa. Se define a través de la densidad de momento y las concentraciones de masa:

${\displaystyle V={\frac {\sum _{i}\rho _{i}C_{i}}{\rho }}\,.}$

donde es la concentración de masa de la i -ésima especie, es la densidad de masa.${\displaystyle \rho _{i}=m_{i}n_{i}}$${\textstyle \rho =\sum _{i}\rho _{i}}$

Por definición, la velocidad de difusión del i -ésimo componente es , . La transferencia de masa del i -ésimo componente se describe mediante la ecuación de continuidad${\displaystyle v_{i}=C_{i}-V}$${\textstyle \sum _{i}\rho _{i}v_{i}=0}$

${\displaystyle {\frac {\partial \rho _{i}}{\partial t}}+\nabla (\rho _{i}V)+\nabla (\rho _{i}v_{i})=W_{i}\,,}$

¿Dónde está la tasa de producción de masa neta en reacciones químicas, .${\displaystyle W_{i}}$${\textstyle \sum _{i}W_{i}=0}$

En estas ecuaciones, el término describe la advección del componente i y el término representa la difusión de este componente.${\displaystyle \nabla (\rho _{i}V)}$${\displaystyle \nabla (\rho _{i}v_{i})}$

En 1948, Wendell H. Furry propuso utilizar la forma de las velocidades de difusión encontradas en la teoría cinética como marco para el nuevo enfoque fenomenológico de la difusión en gases. Este enfoque fue desarrollado posteriormente por FA Williams y SH Lam. ^[20] Para las velocidades de difusión en gases multicomponentes ( N componentes) utilizaron

${\displaystyle v_{i}=-\left(\sum _{j=1}^{N}D_{ij}\mathbf {d} _{j}+D_{i}^{(T)}\,\nabla (\ln T)\right)\,;}$

${\displaystyle \mathbf {d} _{j}=\nabla X_{j}+(X_{j}-Y_{j})\,\nabla (\ln P)+\mathbf {g} _{j}\,;}$

${\displaystyle \mathbf {g} _{j}={\frac {\rho }{P}}\left(Y_{j}\sum _{k=1}^{N}Y_{k}(f_{k}-f_{j})\right)\,.}$

Aquí, es la matriz de coeficientes de difusión, es el coeficiente de difusión térmica, es la fuerza corporal por unidad de masa que actúa sobre la i- ésima especie, es la fracción de presión parcial de la i- ésima especie (y es la presión parcial), es la fracción de masa de la i- ésima especie, y${\displaystyle D_{ij}}$${\displaystyle D_{i}^{(T)}}$${\displaystyle f_{i}}$${\displaystyle X_{i}=P_{i}/P}$${\displaystyle P_{i}}$${\displaystyle Y_{i}=\rho _{i}/\rho }$${\textstyle \sum _{i}X_{i}=\sum _{i}Y_{i}=1.}$

Cuando la densidad de electrones en los sólidos no está en equilibrio, se produce la difusión de electrones. Por ejemplo, cuando se aplica una polarización a dos extremos de un trozo de semiconductor, o una luz brilla en un extremo (ver figura de la derecha), los electrones se difunden desde las regiones de alta densidad (centro) a las regiones de baja densidad (dos extremos), formando un gradiente de densidad de electrones. Este proceso genera corriente, denominada corriente de difusión .

La corriente de difusión también se puede describir mediante la primera ley de Fick.

${\displaystyle J=-D\,\partial n/\partial x\,,}$

donde J es la densidad de corriente de difusión ( cantidad de sustancia ) por unidad de área por unidad de tiempo, n (para mezclas ideales) es la densidad electrónica, x es la posición [longitud].

Los modelos analíticos y numéricos que resuelven la ecuación de difusión para diferentes condiciones iniciales y de contorno han sido populares para estudiar una amplia variedad de cambios en la superficie de la Tierra. La difusión se ha utilizado ampliamente en estudios de erosión de retroceso de laderas, erosión de acantilados, degradación de escarpes de fallas, retroceso de terrazas/costas cortadas por olas, incisión de canales aluviales, retroceso de la plataforma costera y progradación de deltas. ^[21] Aunque la superficie de la Tierra no se difunde literalmente en muchos de estos casos, el proceso de difusión imita de manera efectiva los cambios holísticos que ocurren a lo largo de décadas a milenios. Los modelos de difusión también se pueden utilizar para resolver problemas de valor límite inverso en los que se conoce cierta información sobre el entorno deposicional a partir de la reconstrucción paleoambiental y se utiliza la ecuación de difusión para determinar la afluencia de sedimentos y las series temporales de cambios en la forma del relieve. ^[22]

La diálisis funciona según los principios de la difusión de solutos y la ultrafiltración de fluidos a través de una membrana semipermeable . La difusión es una propiedad de las sustancias en el agua; las sustancias en el agua tienden a moverse desde un área de alta concentración a un área de baja concentración. ^[23] La sangre fluye por un lado de una membrana semipermeable, y un dializado, o fluido de diálisis especial, fluye por el lado opuesto. Una membrana semipermeable es una capa delgada de material que contiene agujeros de varios tamaños, o poros. Los solutos y fluidos más pequeños pasan a través de la membrana, pero la membrana bloquea el paso de sustancias más grandes (por ejemplo, glóbulos rojos y proteínas grandes). Esto replica el proceso de filtrado que tiene lugar en los riñones cuando la sangre ingresa a los riñones y las sustancias más grandes se separan de las más pequeñas en el glomérulo . ^[23]

Un error muy común es creer que los átomos, iones o moléculas individuales se mueven aleatoriamente, lo cual no es así. En la animación de la derecha, el ion del panel izquierdo parece tener un movimiento "aleatorio" en ausencia de otros iones. Sin embargo, como muestra el panel derecho, este movimiento no es aleatorio, sino que es el resultado de "colisiones" con otros iones. Por lo tanto, el movimiento de un solo átomo, ion o molécula dentro de una mezcla parece aleatorio cuando se observa de forma aislada. El movimiento de una sustancia dentro de una mezcla por "caminata aleatoria" está regido por la energía cinética dentro del sistema, que puede verse afectada por cambios en la concentración, la presión o la temperatura. (Esta es una descripción clásica. A escalas más pequeñas, los efectos cuánticos no serán despreciables, en general. Por lo tanto, el estudio del movimiento de un solo átomo se vuelve más sutil, ya que las partículas a escalas tan pequeñas se describen mediante amplitudes de probabilidad en lugar de medidas deterministas de posición y velocidad).

Si bien el movimiento browniano de partículas mesoscópicas multimoleculares (como los granos de polen estudiados por Brown) se puede observar con un microscopio óptico, la difusión molecular solo se puede estudiar en condiciones experimentales cuidadosamente controladas. Desde los experimentos de Graham, es bien sabido que es necesario evitar la convección y que esto puede ser una tarea nada trivial.

En condiciones normales, la difusión molecular predomina sólo en longitudes comprendidas entre nanómetros y milímetros. En escalas de longitud mayores, el transporte en líquidos y gases se debe normalmente a otro fenómeno de transporte , la convección . Para separar la difusión en estos casos, se necesitan esfuerzos especiales.

En cambio, la conducción de calor a través de medios sólidos es algo cotidiano (por ejemplo, una cuchara de metal parcialmente sumergida en un líquido caliente). Esto explica por qué la difusión del calor se explicó matemáticamente antes que la difusión de la masa.

• La difusión anisotrópica , también conocida como ecuación de Perona-Malik, mejora los gradientes altos
• Difusión atómica , en sólidos
• Difusión de Bohm , propagación del plasma a través de campos magnéticos.
• Difusión de remolinos , en la descripción de grano grueso del flujo turbulento
• Efusión de un gas a través de pequeños orificios
• Difusión electrónica , que da lugar a una corriente eléctrica denominada corriente de difusión.
• Difusión facilitada , presente en algunos organismos
• Difusión gaseosa , utilizada para la separación de isótopos.
• Ecuación del calor , difusión de la energía térmica.
• Difusión de Itō , matematización del movimiento browniano, proceso estocástico continuo.
• Difusión de gas de Knudsen en poros largos con frecuentes colisiones de paredes
• Vuelo de Lévy
• Difusión molecular , difusión de moléculas desde zonas más densas a zonas menos densas.
• Difusión del momento , por ejemplo, la difusión del campo de velocidad hidrodinámico.
• Difusión de fotones
• Difusión de plasma
• Paseo aleatorio , ^[24] modelo para difusión
• Difusión inversa , contra el gradiente de concentración, en separación de fases
• Difusión rotacional , reorientación aleatoria de moléculas.
• Difusión de espín , difusión de momentos magnéticos de espín en sólidos
• Difusión superficial , difusión de partículas adheridas sobre una superficie.
• Los taxis son la actividad de movimiento direccional de un animal en respuesta a un estímulo.
  • La kinesis es la actividad de movimiento no direccional de un animal en respuesta a un estímulo.
• Difusión transcultural , difusión de rasgos culturales a través del área geográfica.
• Difusión turbulenta , transporte de masa, calor o momento dentro de un fluido turbulento.