Índice de refracción

En óptica , el índice de refracción (o índice de refracción ) de un medio óptico es un número adimensional que da la indicación de la capacidad de ese medio para curvar la luz .

El índice de refracción determina cuánto se dobla, o refracta , el camino de la luz al entrar en un material. Esto se describe mediante la ley de refracción de Snell , n 1 sen θ 1 = n 2 sen θ 2 , donde θ 1 y θ 2 son el ángulo de incidencia y el ángulo de refracción, respectivamente, de un rayo que cruza la interfaz entre dos medios con índices de refracción n 1 y n 2 . Los índices de refracción también determinan la cantidad de luz que se refleja al llegar a la interfaz, así como el ángulo crítico para la reflexión interna total , su intensidad ( ecuaciones de Fresnel ) y el ángulo de Brewster . [1]
El índice de refracción, , puede considerarse como el factor por el cual la velocidad y la longitud de onda de la radiación se reducen con respecto a sus valores en el vacío: la velocidad de la luz en un medio es v = c/ n , y de manera similar la longitud de onda en ese medio es λ = λ 0 / n , donde λ 0 es la longitud de onda de esa luz en el vacío. Esto implica que el vacío tiene un índice de refracción de 1, y supone que la frecuencia ( f = v / λ ) de la onda no se ve afectada por el índice de refracción.
El índice de refracción puede variar con la longitud de onda. Esto hace que la luz blanca se divida en los colores que la constituyen cuando se refracta. Esto se llama dispersión . Este efecto se puede observar en prismas y arcoíris , y como aberración cromática en lentes. La propagación de la luz en materiales absorbentes se puede describir utilizando un índice de refracción de valor complejo . [2] La parte imaginaria maneja la atenuación , mientras que la parte real da cuenta de la refracción. Para la mayoría de los materiales, el índice de refracción cambia con la longitud de onda en varios porcentajes a lo largo del espectro visible. En consecuencia, los índices de refracción para materiales informados utilizando un solo valor para n deben especificar la longitud de onda utilizada en la medición.
El concepto de índice de refracción se aplica a todo el espectro electromagnético , desde los rayos X hasta las ondas de radio . También se puede aplicar a fenómenos ondulatorios como el sonido . En este caso, se utiliza la velocidad del sonido en lugar de la de la luz, y se debe elegir un medio de referencia distinto del vacío. [3]
En el caso de las lentes (como las gafas ), una lente fabricada con un material con un índice de refracción alto será más delgada y, por lo tanto, más liviana que una lente convencional con un índice de refracción más bajo. Estas lentes suelen ser más caras de fabricar que las convencionales.
Definición
El índice de refracción relativo de un medio óptico 2 con respecto a otro medio de referencia 1 ( n 21 ) viene dado por la relación entre la velocidad de la luz en el medio 1 y la del medio 2. Esto se puede expresar de la siguiente manera: Si el medio de referencia 1 es el vacío , entonces el índice de refracción del medio 2 se considera con respecto al vacío. Se representa simplemente como n 2 y se denomina índice de refracción absoluto del medio 2.
El índice de refracción absoluto n de un medio óptico se define como la relación entre la velocidad de la luz en el vacío, c =299 792 458 m/s , y la velocidad de fase v de la luz en el medio, Como c es constante, n es inversamente proporcional a v : La velocidad de fase es la velocidad a la que se mueven las crestas o la fase de la onda , que puede ser diferente de la velocidad de grupo , la velocidad a la que se mueve el pulso de luz o la envolvente de la onda. [1] Históricamente, el aire a una presión y temperatura estandarizadas ha sido común como medio de referencia.
Historia
.jpg/440px-Thomas_Young_(scientist).jpg)
Se presume que Thomas Young fue la primera persona que utilizó e inventó el nombre de "índice de refracción", en 1807. [4] Al mismo tiempo, cambió este valor de poder refractivo a un solo número, en lugar de la relación tradicional de dos números. La relación tenía la desventaja de tener diferentes apariencias. Newton , que la llamó la "proporción de los senos de incidencia y refracción", la escribió como una relación de dos números, como "529 a 396" (o "casi 4 a 3"; para el agua). [5] Hauksbee , que la llamó la "relación de refracción", la escribió como una relación con un numerador fijo, como "10000 a 7451,9" (para la orina). [6] Hutton la escribió como una relación con un denominador fijo, como 1,3358 a 1 (agua). [7]
En 1807, Young no utilizó un símbolo para el índice de refracción. En años posteriores, otros comenzaron a utilizar símbolos diferentes: n , m y µ . [8] [9] [10] El símbolo n prevaleció gradualmente.
Valores típicos

El índice de refracción también varía con la longitud de onda de la luz, como se indica en la ecuación de Cauchy . La forma más general de esta ecuación es donde n es el índice de refracción, λ es la longitud de onda y A , B , C , etc., son coeficientes que se pueden determinar para un material ajustando la ecuación a los índices de refracción medidos en longitudes de onda conocidas. Los coeficientes se expresan generalmente para λ como la longitud de onda del vacío en micrómetros .
Por lo general, es suficiente utilizar una forma de dos términos de la ecuación: donde los coeficientes A y B se determinan específicamente para esta forma de la ecuación.
| Material | norte |
|---|---|
| Vacío | 1 |
| Gases a 0 °C y 1 atm | |
| Aire | 1.000 293 |
| Helio | 1.000 036 |
| Hidrógeno | 1.000 132 |
| Dióxido de carbono | 1.000 45 |
| Líquidos a 20 °C | |
| Agua | 1.333 |
| Etanol | 1.36 |
| Aceite de oliva | 1.47 |
| Sólidos | |
| Hielo | 1.31 |
| Sílice fundida (cuarzo) | 1.46 [11] |
| PMMA (acrílico, plexiglás, lucita, perspex) | 1.49 |
| Vidrio de ventana | 1.52 [12] |
| Policarbonato (Lexan™) | 1.58 [13] |
| Vidrio de sílex (típico) | 1.69 |
| Zafiro | 1.77 [14] |
| Circonita cúbica | 2.15 |
| Diamante | 2.417 |
| Moissanita | 2.65 |
Para la luz visible, la mayoría de los medios transparentes tienen índices de refracción entre 1 y 2. En la tabla adyacente se dan algunos ejemplos. Estos valores se miden en la línea D del doblete amarillo del sodio , con una longitud de onda de 589 nanómetros , como se hace convencionalmente. [15] Los gases a presión atmosférica tienen índices de refracción cercanos a 1 debido a su baja densidad. Casi todos los sólidos y líquidos tienen índices de refracción superiores a 1,3, con el aerogel como clara excepción. El aerogel es un sólido de muy baja densidad que se puede producir con un índice de refracción en el rango de 1,002 a 1,265. [16] La moissanita se encuentra en el otro extremo del rango con un índice de refracción tan alto como 2,65. La mayoría de los plásticos tienen índices de refracción en el rango de 1,3 a 1,7, pero algunos polímeros de alto índice de refracción pueden tener valores tan altos como 1,76. [17]
En el caso de la luz infrarroja , los índices de refracción pueden ser considerablemente más altos. El germanio es transparente en la región de longitud de onda deEl material tiene un espesor de entre 2 y 14 μm y un índice de refracción de aproximadamente 4. [18] Recientemente se ha descubierto un tipo de nuevos materiales denominados " aislantes topológicos ", que tienen un índice de refracción elevado de hasta 6 en el rango de frecuencias de infrarrojo cercano a medio. Además, los aislantes topológicos son transparentes cuando tienen un espesor a escala nanométrica. Estas propiedades son potencialmente importantes para aplicaciones en óptica infrarroja. [19]
Índice de refracción por debajo de la unidad
Según la teoría de la relatividad , ninguna información puede viajar más rápido que la velocidad de la luz en el vacío, pero esto no significa que el índice de refracción no pueda ser menor que 1. El índice de refracción mide la velocidad de fase de la luz, que no transporta información . [20] [a] La velocidad de fase es la velocidad a la que se mueven las crestas de la onda y puede ser más rápida que la velocidad de la luz en el vacío, y por lo tanto dar un índice de refracción por debajo de 1. Esto puede ocurrir cerca de frecuencias de resonancia , para medios absorbentes, en plasmas y para rayos X. En el régimen de rayos X, los índices de refracción son inferiores pero muy cercanos a 1 (excepciones cerca de algunas frecuencias de resonancia). [21] Como ejemplo, el agua tiene un índice de refracción de0,999 999 74 = 1 −2,6 × 10 −7 para la radiación de rayos X a una energía de fotón de30 keV (Longitud de onda de 0,04 nm ). [21]
Un ejemplo de plasma con un índice de refracción menor que la unidad es la ionosfera terrestre . Dado que el índice de refracción de la ionosfera (un plasma ) es menor que la unidad, las ondas electromagnéticas que se propagan a través del plasma se desvían "fuera de la normal" (véase Óptica geométrica ), lo que permite que la onda de radio se refracte de vuelta hacia la Tierra, lo que permite las comunicaciones por radio a larga distancia. Véase también Propagación de radio y Onda celeste . [22]
Índice de refracción negativo

Investigaciones recientes han demostrado también la "existencia" de materiales con un índice de refracción negativo, lo que puede ocurrir si la permitividad y la permeabilidad tienen valores negativos simultáneos. [23] Esto se puede lograr con metamateriales construidos periódicamente . La refracción negativa resultante (es decir, una inversión de la ley de Snell ) ofrece la posibilidad de que las superlentes y otros fenómenos nuevos se desarrollen activamente por medio de metamateriales . [24] [25]
Explicación microscópica

A escala atómica, la velocidad de fase de una onda electromagnética se reduce en un material porque el campo eléctrico crea una perturbación en las cargas de cada átomo (principalmente los electrones ) proporcional a la susceptibilidad eléctrica del medio. (De manera similar, el campo magnético crea una perturbación proporcional a la susceptibilidad magnética ). A medida que los campos electromagnéticos oscilan en la onda, las cargas en el material se "sacuden" de un lado a otro a la misma frecuencia. [1] : 67 Las cargas irradian así su propia onda electromagnética que está a la misma frecuencia, pero normalmente con un retraso de fase , ya que las cargas pueden desfasarse con respecto a la fuerza que las impulsa (véase oscilador armónico impulsado sinusoidalmente ). La onda de luz que viaja en el medio es la superposición macroscópica (suma) de todas esas contribuciones en el material: la onda original más las ondas radiadas por todas las cargas en movimiento. Esta onda es típicamente una onda con la misma frecuencia pero una longitud de onda más corta que la original, lo que lleva a una ralentización de la velocidad de fase de la onda. La mayor parte de la radiación de las cargas materiales oscilantes modificará la onda entrante, cambiando su velocidad. Sin embargo, una parte de la energía neta se irradiará en otras direcciones o incluso a otras frecuencias (véase dispersión ).
Dependiendo de la fase relativa de la onda impulsora original y de las ondas irradiadas por el movimiento de la carga, existen varias posibilidades:
- Si los electrones emiten una onda luminosa que está desfasada 90° con respecto a la onda luminosa que los sacude, esto hará que la onda luminosa total se propague más lentamente. Esta es la refracción normal de los materiales transparentes, como el vidrio o el agua, y corresponde a un índice de refracción real y mayor que 1. [26] [ página necesaria ]
- Si los electrones emiten una onda de luz que está desfasada 270° con respecto a la onda de luz que los sacude, la onda viajará más rápido. Esto se llama "refracción anómala" y se observa cerca de las líneas de absorción (normalmente en los espectros infrarrojos), con rayos X en materiales ordinarios y con ondas de radio en la ionosfera de la Tierra . Corresponde a una permitividad menor que 1, lo que hace que el índice de refracción sea también menor que la unidad y la velocidad de fase de la luz mayor que la velocidad de la luz en el vacío c (nótese que la velocidad de la señal sigue siendo menor que c , como se ha comentado anteriormente). Si la respuesta es suficientemente fuerte y desfasada, el resultado es un valor negativo de permitividad e índice de refracción imaginario, como se observa en metales o plasma. [26] [ página necesaria ]
- Si los electrones emiten una onda luminosa que está desfasada 180° con respecto a la onda luminosa que los sacude, interferirá destructivamente con la luz original y reducirá la intensidad luminosa total. Esto es absorción de luz en materiales opacos y corresponde a un índice de refracción imaginario .
- Si los electrones emiten una onda luminosa que está en fase con la onda luminosa que los sacude, ésta se amplificará. Esto es poco frecuente, pero ocurre en los láseres debido a la emisión estimulada . Corresponde a un índice de refracción imaginario, de signo opuesto al de absorción.
Para la mayoría de los materiales en frecuencias de luz visible, la fase está entre 90° y 180°, lo que corresponde a una combinación de refracción y absorción.
Dispersión

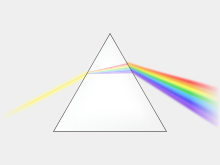
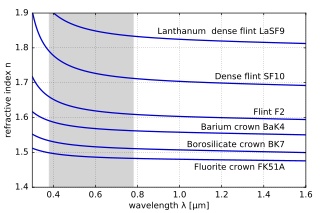
El índice de refracción de los materiales varía con la longitud de onda (y la frecuencia ) de la luz. [27] Esto se llama dispersión y hace que los prismas y los arcoíris dividan la luz blanca en sus colores espectrales constituyentes . [28] Como el índice de refracción varía con la longitud de onda, también lo hará el ángulo de refracción cuando la luz pase de un material a otro. La dispersión también hace que la longitud focal de las lentes dependa de la longitud de onda. Este es un tipo de aberración cromática , que a menudo necesita ser corregida en los sistemas de imágenes. En las regiones del espectro donde el material no absorbe la luz, el índice de refracción tiende a disminuir con el aumento de la longitud de onda y, por lo tanto, aumenta con la frecuencia. Esto se llama "dispersión normal", en contraste con la "dispersión anómala", donde el índice de refracción aumenta con la longitud de onda. [27] Para la luz visible, la dispersión normal significa que el índice de refracción es más alto para la luz azul que para la roja.
En el campo de la óptica, la cantidad de dispersión de un material de lente se cuantifica a menudo mediante el número de Abbe : [28] Para una descripción más precisa de la dependencia de la longitud de onda del índice de refracción, se puede utilizar la ecuación de Sellmeier . [29] Es una fórmula empírica que funciona bien para describir la dispersión. Los coeficientes de Sellmeier se citan a menudo en lugar del índice de refracción en las tablas.
Ambigüedad de la longitud de onda del índice de refracción principal
Debido a la dispersión, suele ser importante especificar la longitud de onda de la luz en el vacío para la que se mide el índice de refracción. Normalmente, las mediciones se realizan en varias líneas de emisión espectral bien definidas .
Los fabricantes de vidrio óptico en general definen el índice principal de refracción en la línea espectral amarilla del helio (587,56 nm ) y alternativamente en una línea espectral verde de mercurio (546,07 nm ), llamadas líneas d y e respectivamente. El número de Abbe se define para ambos y se denota V d y V e . Los datos espectrales proporcionados por los fabricantes de vidrio también suelen ser más precisos para estas dos longitudes de onda. [30] [31] [32] [33]
Tanto las líneas espectrales d como e son singletes y, por lo tanto, son adecuadas para realizar mediciones muy precisas, como el método goniométrico espectral. [34] [35]
En aplicaciones prácticas, las mediciones del índice de refracción se realizan en varios refractómetros, como el refractómetro Abbe . La precisión de la medición de estos dispositivos comerciales típicos es del orden de 0,0002. [36] [37] Los refractómetros suelen medir el índice de refracción n D , definido para el doblete de sodio D (589,29 nm ), que en realidad es un punto medio entre dos líneas espectrales amarillas adyacentes del sodio. Las líneas espectrales amarillas del helio ( d ) y el sodio ( D ) son1,73 nm de distancia, lo que puede considerarse insignificante para los refractómetros típicos, pero puede causar confusión y provocar errores si la precisión es fundamental.
Las tres definiciones típicas de índices de refracción principales se pueden encontrar dependiendo de la aplicación y la región, [38] por lo que se debe utilizar un subíndice adecuado para evitar ambigüedades.
Índice de refracción complejo
Cuando la luz pasa a través de un medio, siempre se absorberá una parte de ella . Esto se puede tener en cuenta fácilmente definiendo un índice de refracción complejo,
Aquí, la parte real n es el índice de refracción e indica la velocidad de fase , mientras que la parte imaginaria κ se llama coeficiente de extinción [39] : 36 indica la cantidad de atenuación cuando la onda electromagnética se propaga a través del material. [1] : 128 Está relacionado con el coeficiente de absorción , , a través de: [39] : 41 Estos valores dependen de la frecuencia de la luz utilizada en la medición.
El hecho de que κ corresponda a la absorción se puede ver insertando este índice de refracción en la expresión para el campo eléctrico de una onda electromagnética plana que viaja en la dirección x . Esto se puede hacer relacionando el número de onda complejo k con el índice de refracción complejo n mediante k = 2π n / λ 0 , donde λ 0 es la longitud de onda del vacío; esto se puede insertar en la expresión de onda plana para una onda que viaja en la dirección x como:
Aquí vemos que κ da una desintegración exponencial, como se esperaba de la ley de Beer-Lambert . Dado que la intensidad es proporcional al cuadrado del campo eléctrico, la intensidad dependerá de la profundidad en el material como
y por lo tanto el coeficiente de absorción es α = 4π κ / λ 0 , [1] : 128 y la profundidad de penetración (la distancia después de la cual la intensidad se reduce en un factor de 1/ e ) es δ p = 1/ α = λ 0 /4π κ .
Tanto n como κ dependen de la frecuencia. En la mayoría de las circunstancias, κ > 0 (la luz se absorbe) o κ = 0 (la luz viaja indefinidamente sin pérdidas). En situaciones especiales, especialmente en el medio de ganancia de los láseres , también es posible que κ < 0 , lo que corresponde a una amplificación de la luz.
Una convención alternativa utiliza n = n + iκ en lugar de n = n − iκ , pero donde κ > 0 todavía corresponde a pérdida. Por lo tanto, estas dos convenciones son inconsistentes y no deben confundirse. La diferencia está relacionada con la definición de dependencia temporal sinusoidal como Re[exp(− iωt )] versus Re[exp(+ iωt )] . Consulte Descripciones matemáticas de la opacidad .
La pérdida dieléctrica y la conductividad de CC distinta de cero en los materiales provocan absorción. Los buenos materiales dieléctricos, como el vidrio, tienen una conductividad de CC extremadamente baja y, a frecuencias bajas, la pérdida dieléctrica también es insignificante, lo que da como resultado una absorción casi nula. Sin embargo, a frecuencias más altas (como la luz visible), la pérdida dieléctrica puede aumentar la absorción significativamente, lo que reduce la transparencia del material a estas frecuencias.
Las partes reales n e imaginarias κ del índice de refracción complejo están relacionadas a través de las relaciones de Kramers-Kronig . En 1986, AR Forouhi e I. Bloomer dedujeron una ecuación que describe κ como una función de la energía del fotón, E , aplicable a materiales amorfos. Forouhi y Bloomer aplicaron luego la relación de Kramers-Kronig para derivar la ecuación correspondiente para n como una función de E. Forouhi y Bloomer aplicaron el mismo formalismo a los materiales cristalinos en 1988.
El índice de refracción y el coeficiente de extinción, n y κ , se miden típicamente a partir de cantidades que dependen de ellos, como la reflectancia, R , o la transmitancia, T , o los parámetros elipsométricos, ψ y δ . La determinación de n y κ a partir de dichas cantidades medidas implicará el desarrollo de una expresión teórica para R o T , o ψ y δ en términos de un modelo físico válido para n y κ . Al ajustar el modelo teórico a la R o T medida , o ψ y δ utilizando el análisis de regresión, se pueden deducir n y κ .
Rayos X y UV extremos
Para los rayos X y la radiación ultravioleta extrema , el índice de refracción complejo se desvía solo ligeramente de la unidad y generalmente tiene una parte real menor que 1. Por lo tanto, normalmente se escribe como n = 1 − δ + iβ (o n = 1 − δ − iβ con la convención alternativa mencionada anteriormente). [2] Muy por encima de la frecuencia de resonancia atómica, delta se puede dar por donde r 0 es el radio electrónico clásico , λ es la longitud de onda de los rayos X y n e es la densidad electrónica. Se puede suponer que la densidad electrónica es simplemente el número de electrones por átomo Z multiplicado por la densidad atómica, pero un cálculo más preciso del índice de refracción requiere reemplazar Z con el factor de forma atómica complejo . De ello se deduce que con δ y β típicamente del orden de 10 −5 y10 −6 .
Relaciones con otras magnitudes
Longitud del recorrido óptico

La longitud del camino óptico (OPL) es el producto de la longitud geométrica d del camino que sigue la luz a través de un sistema y el índice de refracción del medio a través del cual se propaga. [40] Este es un concepto importante en óptica porque determina la fase de la luz y gobierna la interferencia y la difracción de la luz a medida que se propaga. Según el principio de Fermat , los rayos de luz se pueden caracterizar como aquellas curvas que optimizan la longitud del camino óptico. [1] : 68–69
Refracción

Cuando la luz se mueve de un medio a otro, cambia de dirección, es decir, se refracta . Si se mueve de un medio con índice de refracción n 1 a uno con índice de refracción n 2 , con un ángulo de incidencia a la normal de la superficie de θ 1 , el ángulo de refracción θ 2 se puede calcular a partir de la ley de Snell : [41]
Cuando la luz entra en un material con un índice de refracción más alto, el ángulo de refracción será menor que el ángulo de incidencia y la luz se refractará hacia la normal de la superficie. Cuanto más alto sea el índice de refracción, más cerca de la dirección normal viajará la luz. Al pasar a un medio con un índice de refracción más bajo, la luz se refractará en dirección contraria a la normal, hacia la superficie.
Reflexión interna total

Si no existe un ángulo θ 2 que cumpla la ley de Snell, es decir, la luz no puede transmitirse y en su lugar experimentará una reflexión interna total . [42] : 49–50 Esto ocurre solo cuando se pasa a un material ópticamente menos denso, es decir, uno con un índice de refracción más bajo. Para obtener una reflexión interna total, los ángulos de incidencia θ 1 deben ser mayores que el ángulo crítico [43]
Reflectividad
Además de la luz transmitida, también hay una parte reflejada . El ángulo de reflexión es igual al ángulo de incidencia y la cantidad de luz que se refleja está determinada por la reflectividad de la superficie. La reflectividad se puede calcular a partir del índice de refracción y el ángulo de incidencia con las ecuaciones de Fresnel , que para la incidencia normal se reduce a [42] : 44
Para el vidrio común en el aire, n 1 = 1 y n 2 = 1,5 , y por lo tanto se refleja aproximadamente el 4% de la potencia incidente. [44] En otros ángulos de incidencia, la reflectividad también dependerá de la polarización de la luz entrante. En un cierto ángulo llamado ángulo de Brewster , la luz p -polarizada (luz con el campo eléctrico en el plano de incidencia ) se transmitirá totalmente. El ángulo de Brewster se puede calcular a partir de los dos índices de refracción de la interfaz como [1] : 245
Lentes

La distancia focal de una lente está determinada por su índice de refracción n y los radios de curvatura R 1 y R 2 de sus superficies. La potencia de una lente delgada en el aire se obtiene mediante la versión simplificada de la fórmula de Lensmaker : [45] donde f es la distancia focal de la lente.
Resolución del microscopio
La resolución de un buen microscopio óptico está determinada principalmente por la apertura numérica ( A Num ) de su lente objetivo . La apertura numérica a su vez está determinada por el índice de refracción n del medio que llena el espacio entre la muestra y la lente y el ángulo medio de recolección de luz θ según Carlsson (2007): [46] : 6
Por esta razón, la inmersión en aceite se utiliza comúnmente para obtener una alta resolución en microscopía. En esta técnica, el objetivo se sumerge en una gota de aceite de inmersión de alto índice de refracción sobre la muestra en estudio. [46] : 14
Permitividad relativa y permeabilidad
El índice de refracción de la radiación electromagnética es igual a donde ε r es la permitividad relativa del material y μ r es su permeabilidad relativa . [47] : 229 El índice de refracción se utiliza para la óptica en las ecuaciones de Fresnel y la ley de Snell ; mientras que la permitividad relativa y la permeabilidad se utilizan en las ecuaciones de Maxwell y la electrónica. La mayoría de los materiales naturales no son magnéticos a frecuencias ópticas, es decir, μ r es muy cercano a 1, por lo tanto , n es aproximadamente √ ε r . [48] En este caso particular, la permitividad relativa compleja ε r , con partes reales e imaginarias ε r y ɛ̃ r , y el índice de refracción complejo n , con partes reales e imaginarias n y κ (este último llamado "coeficiente de extinción"), siguen la relación
y sus componentes están relacionados por: [49]
y:
¿Dónde está el módulo complejo ?
Impedancia de onda
La impedancia de onda de una onda electromagnética plana en un medio no conductor viene dada por
donde Z 0 es la impedancia de la onda de vacío, μ y ε son la permeabilidad y permitividad absolutas del medio, ε r es la permitividad relativa del material y μ r es su permeabilidad relativa .
En medios no magnéticos (es decir, en materiales con μ r = 1 ), y
Por lo tanto, el índice de refracción en un medio no magnético es la relación entre la impedancia de la onda de vacío y la impedancia de onda del medio.
La reflectividad R 0 entre dos medios puede así expresarse tanto por las impedancias de onda como por los índices de refracción como
Densidad
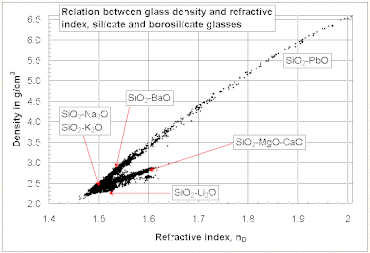
En general, se supone que el índice de refracción de un vidrio aumenta con su densidad . Sin embargo, no existe una relación lineal general entre el índice de refracción y la densidad para todos los vidrios de silicato y borosilicato. Se puede obtener un índice de refracción relativamente alto y una densidad baja con vidrios que contienen óxidos metálicos ligeros como Li2O y MgO , mientras que se observa la tendencia opuesta con vidrios que contienen PbO y BaO, como se ve en el diagrama de la derecha.
Muchos aceites (como el aceite de oliva ) y el etanol son ejemplos de líquidos que son más refractivos, pero menos densos, que el agua, contrariamente a la correlación general entre densidad e índice de refracción.
Para el aire, n - 1 es proporcional a la densidad del gas siempre que la composición química no cambie. [51] Esto significa que también es proporcional a la presión e inversamente proporcional a la temperatura para los gases ideales . Para los líquidos se puede hacer la misma observación que para los gases, por ejemplo, el índice de refracción en los alcanos aumenta casi perfectamente lineal con la densidad. Por otro lado, para los ácidos carboxílicos, la densidad disminuye con el aumento del número de átomos de C dentro de la serie homóloga. La explicación simple de este hallazgo es que no es la densidad, sino la concentración molar del cromóforo lo que cuenta. En las series homólogas, esta es la excitación del enlace CH. August Beer debe haberlo sabido intuitivamente cuando le dio a Hans H. Landolt en 1862 el consejo de investigar el índice de refracción de los compuestos de series homólogas. [52] Aunque Landolt no encontró esta relación, ya que en ese momento la teoría de la dispersión estaba en sus inicios, tuvo la idea de la refractividad molar que incluso puede asignarse a átomos individuales. [53] Con base en este concepto, se pueden calcular los índices de refracción de los materiales orgánicos.
Índice de grupos
A veces, se define un "índice de refracción de velocidad de grupo", normalmente llamado índice de grupo : [ cita requerida ] donde v g es la velocidad de grupo . Este valor no debe confundirse con n , que siempre se define con respecto a la velocidad de fase . Cuando la dispersión es pequeña, la velocidad de grupo se puede vincular a la velocidad de fase mediante la relación [42] : 22 donde λ es la longitud de onda en el medio. En este caso, el índice de grupo se puede escribir en términos de la dependencia de la longitud de onda del índice de refracción como
Cuando el índice de refracción de un medio se conoce como una función de la longitud de onda del vacío (en lugar de la longitud de onda en el medio), las expresiones correspondientes para la velocidad y el índice de grupo son (para todos los valores de dispersión) [54] donde λ 0 es la longitud de onda en el vacío.
Velocidad, momento y polarizabilidad
Como se muestra en el experimento de Fizeau , cuando la luz se transmite a través de un medio en movimiento, su velocidad relativa a un observador que viaja con velocidad v en la misma dirección que la luz es:
El momento de los fotones en un medio de índice de refracción n es un tema complejo y controvertido con dos valores diferentes que tienen diferentes interpretaciones físicas. [55]
El índice de refracción de una sustancia puede relacionarse con su polarizabilidad mediante la ecuación de Lorentz-Lorenz o con las refractividades molares de sus constituyentes mediante la relación de Gladstone-Dale .
Refracción
En aplicaciones atmosféricas, la refractividad se define como N = n – 1 , a menudo reescalada como [56] N = 10 6 ( n – 1)[57][58]o N = 108 ( n – 1);[59]los factores de multiplicación se utilizan porque el índice de refracción del aire,n,se desvía de la unidad como máximo en unas pocas partes por diez mil.
La refractividad molar , por otro lado, es una medida de la polarizabilidad total de un mol de una sustancia y se puede calcular a partir del índice de refracción como donde ρ es la densidad y M es la masa molar . [42] : 93
Refracción no escalar, no lineal o no homogénea
Hasta ahora, hemos supuesto que la refracción se da mediante ecuaciones lineales que implican un índice de refracción escalar y espacialmente constante. Estas suposiciones pueden descomponerse de diferentes maneras, que se describirán en las siguientes subsecciones.
Birrefringencia


En algunos materiales, el índice de refracción depende de la polarización y la dirección de propagación de la luz. [60] Esto se llama birrefringencia o anisotropía óptica .
En la forma más simple, la birrefringencia uniaxial, solo hay una dirección especial en el material. Este eje se conoce como el eje óptico del material. [1] : 230 La luz con polarización lineal perpendicular a este eje experimentará un índice de refracción ordinario n o mientras que la luz polarizada en paralelo experimentará un índice de refracción extraordinario n e . [1] : 236 La birrefringencia del material es la diferencia entre estos índices de refracción, Δ n = n e − n o . [1] : 237 La luz que se propaga en la dirección del eje óptico no se verá afectada por la birrefringencia ya que el índice de refracción será n o independiente de la polarización. Para otras direcciones de propagación, la luz se dividirá en dos haces polarizados linealmente. Para la luz que viaja perpendicularmente al eje óptico, los haces tendrán la misma dirección. [1] : 233 Esto se puede utilizar para cambiar la dirección de polarización de la luz polarizada linealmente o para convertir entre polarizaciones lineales, circulares y elípticas con placas de onda . [1] : 237
Muchos cristales son naturalmente birrefringentes, pero los materiales isótropos como los plásticos y el vidrio también pueden volverse birrefringentes introduciendo una dirección preferida a través de, por ejemplo, una fuerza externa o un campo eléctrico. Este efecto se llama fotoelasticidad y puede usarse para revelar tensiones en las estructuras. El material birrefringente se coloca entre polarizadores cruzados . Un cambio en la birrefringencia altera la polarización y, por lo tanto, la fracción de luz que se transmite a través del segundo polarizador.
En el caso más general de los materiales trirrefringentes descritos por el campo de la óptica de cristales , la constante dieléctrica es un tensor de rango 2 (una matriz de 3 por 3). En este caso, la propagación de la luz no se puede describir simplemente mediante índices de refracción, excepto en el caso de polarizaciones a lo largo de ejes principales.
No linealidad
El fuerte campo eléctrico de luz de alta intensidad (como la salida de un láser ) puede hacer que el índice de refracción de un medio varíe a medida que la luz pasa a través de él, dando lugar a la óptica no lineal . [1] : 502 Si el índice varía cuadráticamente con el campo (linealmente con la intensidad), se denomina efecto Kerr óptico y causa fenómenos como el autoenfoque y la automodulación de fase . [1] : 264 Si el índice varía linealmente con el campo (un coeficiente lineal no trivial solo es posible en materiales que no poseen simetría de inversión ), se conoce como efecto Pockels . [1] : 265
Inhomogeneidad
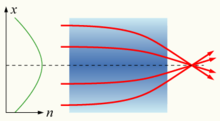
Si el índice de refracción de un medio no es constante sino que varía gradualmente con la posición, el material se conoce como medio de índice de gradiente (GRIN) y se describe mediante óptica de índice de gradiente . [1] : 273 La luz que viaja a través de un medio de este tipo se puede doblar o enfocar, y este efecto se puede explotar para producir lentes , algunas fibras ópticas y otros dispositivos. La introducción de elementos GRIN en el diseño de un sistema óptico puede simplificar enormemente el sistema, reduciendo el número de elementos hasta en un tercio manteniendo el rendimiento general. [1] : 276 El cristalino del ojo humano es un ejemplo de lente GRIN con un índice de refracción que varía de aproximadamente 1,406 en el núcleo interno a aproximadamente 1,386 en la corteza menos densa. [1] : 203 Algunos espejismos comunes son causados por un índice de refracción del aire que varía espacialmente .
Medición del índice de refracción
Medios homogéneos
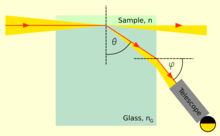
El índice de refracción de líquidos o sólidos se puede medir con refractómetros . Por lo general, miden algún ángulo de refracción o el ángulo crítico para la reflexión interna total. Los primeros refractómetros de laboratorio vendidos comercialmente fueron desarrollados por Ernst Abbe a fines del siglo XIX. [61] Los mismos principios todavía se utilizan hoy en día. En este instrumento, se coloca una capa delgada del líquido que se va a medir entre dos prismas. La luz brilla a través del líquido en ángulos de incidencia de hasta 90°, es decir, rayos de luz paralelos a la superficie. El segundo prisma debe tener un índice de refracción más alto que el del líquido, de modo que la luz solo ingrese al prisma en ángulos menores que el ángulo crítico para la reflexión total. Este ángulo se puede medir luego mirando a través de un telescopio , [ aclaración necesaria ] o con un fotodetector digital colocado en el plano focal de una lente. El índice de refracción n del líquido se puede calcular a partir del ángulo de transmisión máximo θ como n = n G sen θ , donde n G es el índice de refracción del prisma. [62]

Este tipo de dispositivo se utiliza habitualmente en laboratorios químicos para la identificación de sustancias y para el control de calidad . Las variantes portátiles se utilizan en agricultura , por ejemplo, por los productores de vino para determinar el contenido de azúcar en el jugo de uva , y los refractómetros de proceso en línea se utilizan, por ejemplo, en la industria química y farmacéutica para el control de procesos .
En gemología , se utiliza un tipo diferente de refractómetro para medir el índice de refracción y la birrefringencia de las piedras preciosas . La gema se coloca sobre un prisma de alto índice de refracción y se ilumina desde abajo. Se utiliza un líquido de contacto de alto índice de refracción para lograr el contacto óptico entre la gema y el prisma. En ángulos de incidencia pequeños, la mayor parte de la luz se transmitirá a la gema, pero en ángulos altos se producirá una reflexión interna total en el prisma. El ángulo crítico normalmente se mide mirando a través de un telescopio. [63]
Variaciones del índice de refracción

Las estructuras biológicas no teñidas aparecen en su mayoría transparentes bajo microscopio de campo claro , ya que la mayoría de las estructuras celulares no atenúan cantidades apreciables de luz. Sin embargo, la variación en los materiales que constituyen estas estructuras también corresponde a una variación en el índice de refracción. Las siguientes técnicas convierten dicha variación en diferencias de amplitud mensurables:
Para medir la variación espacial del índice de refracción en una muestra se utilizan métodos de imagen de contraste de fase . Estos métodos miden las variaciones en la fase de la onda de luz que sale de la muestra. La fase es proporcional a la longitud del camino óptico que ha recorrido el rayo de luz y, por lo tanto, proporciona una medida de la integral del índice de refracción a lo largo del camino del rayo. La fase no se puede medir directamente a frecuencias ópticas o más altas y, por lo tanto, debe convertirse en intensidad mediante la interferencia con un haz de referencia. En el espectro visual, esto se hace utilizando microscopía de contraste de fase de Zernike , microscopía de contraste de interferencia diferencial (DIC) o interferometría .
La microscopía de contraste de fase de Zernike introduce un cambio de fase en los componentes de baja frecuencia espacial de la imagen con un anillo de cambio de fase en el plano de Fourier de la muestra, de modo que las partes de alta frecuencia espacial de la imagen pueden interferir con el haz de referencia de baja frecuencia. En DIC, la iluminación se divide en dos haces que reciben polarizaciones diferentes, se desplazan de fase de manera diferente y se desplazan transversalmente con cantidades ligeramente diferentes. Después de la muestra, se hace que las dos partes interfieran, dando una imagen de la derivada de la longitud del camino óptico en la dirección de la diferencia en el desplazamiento transversal. [46] En interferometría, la iluminación se divide en dos haces mediante un espejo parcialmente reflectante . Uno de los haces pasa a través de la muestra antes de que se combinen para interferir y dar una imagen directa de los cambios de fase. Si las variaciones de la longitud del camino óptico son mayores que una longitud de onda, la imagen contendrá franjas.
Existen varias técnicas de imágenes de rayos X de contraste de fase para determinar la distribución espacial 2D o 3D del índice de refracción de las muestras en el régimen de rayos X. [64]
Aplicaciones
El índice de refracción es una propiedad importante de los componentes de cualquier instrumento óptico . Determina el poder de enfoque de las lentes, el poder dispersivo de los prismas, la reflectividad de los recubrimientos de las lentes y la naturaleza de guía de luz de la fibra óptica . Dado que el índice de refracción es una propiedad física fundamental de una sustancia, a menudo se utiliza para identificar una sustancia en particular, confirmar su pureza o medir su concentración. El índice de refracción se utiliza para medir sólidos, líquidos y gases. Lo más común es que se utilice para medir la concentración de un soluto en una solución acuosa . También se puede utilizar como una herramienta útil para diferenciar entre diferentes tipos de piedras preciosas, debido a la chatoyancia única que muestra cada piedra individual. Un refractómetro es el instrumento utilizado para medir el índice de refracción. Para una solución de azúcar, el índice de refracción se puede utilizar para determinar el contenido de azúcar (ver Brix ).
Véase también
- Cálculo de propiedades del vidrio
- Relación Clausius-Mossotti
- Elipsometría
- Principio de Fermat
- Elipsoide índice
- Material de coincidencia de índices
- Deflectometría láser Schlieren
- Propiedades ópticas del agua y el hielo.
- Imágenes de rayos X con contraste de fase
- Refractometría de acoplamiento de prismas
- Factor de velocidad
Notas al pie
- ^ Una consecuencia de que la parte real de n sea menor que la unidad es que implica que la velocidad de fase dentro del material, do/norte , es mayor que la velocidad de la luz, c . Sin embargo, esto no viola la ley de la relatividad, que requiere que sólo las señales que transportan información no viajen más rápido que c . Tales señales se mueven con la velocidad de grupo, no con la velocidad de fase, y se puede demostrar que la velocidad de grupo es de hecho menor que c . [20]
Referencias
- ^ abcdefghijklmnopqr Hecht, Eugene (2002). Óptica . Addison-Wesley. ISBN 978-0-321-18878-6.
- ^ ab Attwood, David (1999). Rayos X suaves y radiación ultravioleta extrema: principios y aplicaciones . Cambridge University Press. pág. 60. ISBN 978-0-521-02997-1.
- ^ Kinsler, Lawrence E. (2000). Fundamentos de acústica . John Wiley. pág. 136. ISBN 978-0-471-84789-2.
- ^ Young, Thomas (1807). Un curso de conferencias sobre filosofía natural y artes mecánicas. J. Johnson. pág. 413.
- ^ Newton, Isaac (1730). Opticks: o tratado sobre los reflejos, refracciones, inflexiones y colores de la luz. William Innys en el West-End de St. Paul's. pág. 247.
- ^ Hauksbee, Francis (1710). "Una descripción del aparato para hacer experimentos sobre las refracciones de fluidos". Philosophical Transactions of the Royal Society of London . 27 (325–336): 207. doi :10.1098/rstl.1710.0015. S2CID 186208526.
- ^ Hutton, Charles (1795). Diccionario filosófico y matemático. p. 299. Archivado desde el original el 22 de febrero de 2017.
- ^ von Fraunhofer, José (1817). "Bestimmung des Brechungs und Farbenzerstreuungs Vermogens verschiedener Glasarten" [Determinación del poder de refracción y dispersión del color de diferentes tipos de vidrio]. Denkschriften der Königlichen Akademie der Wissenschaften zu München [ Revista de la Real Academia de Ciencias de Múnich ] (en alemán). 5 : 208. Archivado desde el original el 22 de febrero de 2017. Exponente des Brechungsverhältnisses es índice de refracción
- ^ Brewster, David (1815). "Sobre la estructura de los cristales doblemente refractantes". Philosophical Magazine . 45 (202): 126. doi :10.1080/14786441508638398. Archivado desde el original el 22 de febrero de 2017.
- ^ Herschel, John FW (1828). Sobre la teoría de la luz. p. 368. Archivado desde el original el 24 de noviembre de 2015.
- ^ Malitson (1965). «Base de datos del índice de refracción». refractiveindex.info . Consultado el 20 de junio de 2018 .
- ^ Faick, CA; Finn, AN (julio de 1931). "El índice de refracción de algunos vidrios de sílice-soda-cal como función de la composición" (PDF) . Instituto Nacional de Estándares y Tecnología. Archivado (PDF) del original el 30 de diciembre de 2016. Consultado el 11 de diciembre de 2016 .
- ^ Sultanova, N.; Kasarova, S.; Nikolov, I. (octubre de 2009). "Propiedades de dispersión de polímeros ópticos". Acta Physica Polonica A . 116 (4): 585–587. Código Bibliográfico :2009AcPPA.116..585S. doi : 10.12693/APhysPolA.116.585 .
- ^ Tapping, J.; Reilly, ML (1 de mayo de 1986). "Índice de refracción del zafiro entre 24 y 1060 °C para longitudes de onda de 633 y 799 nm". Journal of the Optical Society of America A . 3 (5): 610. Bibcode :1986JOSAA...3..610T. doi :10.1364/JOSAA.3.000610.
- ^ "Comunicaciones científicas forenses, determinación del índice de refracción del vidrio". Servicios de laboratorio del FBI. Archivado desde el original el 10 de septiembre de 2014. Consultado el 8 de septiembre de 2014 .
- ^ Tabata, M.; et al. (2005). Desarrollo de aerogel de sílice con cualquier densidad (PDF) . Acta de la conferencia del simposio sobre ciencia nuclear del IEEE. Vol. 2. págs. 816–818. doi :10.1109/NSSMIC.2005.1596380. ISBN . 978-0-7803-9221-2. S2CID 18187536. Archivado desde el original (PDF) el 18 de mayo de 2013.
- ^ Sadayori, Naoki; Hotta, Yuji (2004). "Policarbodiimida con alto índice de refracción y método de producción de la misma". Oficina de Patentes de EE. UU. Patente de EE. UU. 2004/0158021 A1 – vía Google Patents.
- ^ Tosi, Jeffrey L., artículo sobre materiales ópticos infrarrojos comunes en el Manual de fotónica, consultado el 10 de septiembre de 2014
- ^ Yue, Zengji; Cai, Boyuan; Wang, Lan; Wang, Xiaolin; Gu, Min (1 de marzo de 2016). "Nanoestructuras dieléctricas plasmónicas intrínsecamente núcleo-capa con índice de refracción ultraalto". Science Advances . 2 (3): e1501536. Bibcode :2016SciA....2E1536Y. doi :10.1126/sciadv.1501536. ISSN 2375-2548. PMC 4820380 . PMID 27051869.
- ^ de Als-Nielsen, J.; McMorrow, D. (2011). Elementos de la física moderna de rayos X. Wiley-VCH. pág. 25. ISBN 978-0-470-97395-0.
- ^ ab Gullikson, Eric. "Interacciones de rayos X con la materia". Constantes ópticas. Centro de Óptica de Rayos X. Laboratorio Lawrence Berkeley . Archivado desde el original el 27 de agosto de 2011. Consultado el 30 de agosto de 2011 .
- ^ Lied, Finn (1967). Comunicaciones por radio de alta frecuencia con énfasis en problemas polares . Grupo asesor para la investigación y el desarrollo aeroespacial. págs. 1–7.
- ^ Veselago, VG (1968). "La electrodinámica de sustancias con valores simultáneamente negativos de ε y μ". Física soviética Uspekhi . 10 (4): 509–514. Código Bibliográfico :1968SvPhU..10..509V. doi :10.1070/PU2003v046n07ABEH001614. S2CID 250862458.
- ^ Pendry, JB; Schurig, D.; Smith, DR (8 de diciembre de 2009). "Aparatos, métodos y sistemas de compresión electromagnética". Oficina de Patentes de EE. UU. Patente de EE. UU. 7629941 – a través de Google Patents.
- ^ Shalaev, VM (2007). "Metamateriales ópticos de índice negativo". Nature Photonics . 1 (1): 41–48. Código Bibliográfico :2007NaPho...1...41S. doi :10.1038/nphoton.2006.49. S2CID 170678.
- ^ ab Feynman, Richard P. (2011). Principalmente mecánica, radiación y calor . Feynman Lectures on Physics. Vol. 1 (edición del nuevo milenio). Basic Books. ISBN 978-0-465-02493-3.
- ^ ab Paschotta, Rüdiger. «Dispersión cromática». RP Photonics Encyclopedia . Archivado desde el original el 2015-06-29 . Consultado el 2023-08-13 .
- ^ ab Nave, Carl R. (2000). "Dispersión". HyperPhysics . Departamento de Física y Astronomía, Universidad Estatal de Georgia. Archivado desde el original el 24 de septiembre de 2014 . Consultado el 13 de agosto de 2023 .
- ^ Paschotta, Rüdiger. «Fórmula de Sellmeier». RP Photonics Encyclopedia . Archivado desde el original el 2015-03-19 . Consultado el 2014-09-08 .
- ^ Schott Company. "Diagrama de Abbe interactivo". Schott.com . Consultado el 13 de agosto de 2023 .
- ^ Ohara Corporation. "Propiedades ópticas". Oharacorp.com . Consultado el 15 de agosto de 2022 .
- ^ Hoya Group. «Propiedades ópticas». División de Óptica de Hoya Group . Consultado el 13 de agosto de 2023 .
- ^ Lentes, Frank-Thomas; Clement, Marc K. Th.; Neuroth, Norbert; Hoffmann, Hans-Jürgen; Hayden, Yuiko T.; Hayden, Joseph S.; Kolberg, Uwe; Wolff, Silke (1998). "Propiedades ópticas". En Bach, Hans; Neuroth, Norbert (eds.). Las propiedades del vidrio óptico . Serie Schott sobre vidrio y cerámica de vidrio. p. 30. doi :10.1007/978-3-642-57769-7. ISBN 978-3-642-63349-2.
- ^ Krey, Stefan; Off, Dennis; Ruprecht, Aiko (8 de marzo de 2014). "Medición del índice de refracción con goniómetros de precisión: un estudio comparativo". En Soskind, Yakov G.; Olson, Craig (eds.). Proc. SPIE 8992, Ingeniería de instrumentación fotónica . SPIE OPTO, 2014. Vol. 8992. San Francisco, California: SPIE. págs. 56–65. Código Bibliográfico :2014SPIE.8992E..0DK. doi :10.1117/12.2041760. S2CID 120544352.
- ^ Rupp, Fabian; Jedamzik, Ralf; Bartelmess, Lothar; Petzold, Uwe (12 de septiembre de 2021). "La forma moderna de medición del índice de refracción del vidrio óptico en SCHOTT". En Völkel, Reinhard; Geyl, Roland; Otaduy, Deitze (eds.). Fabricación óptica, pruebas y metrología VII . Vol. 11873. SPIE. págs. 15–22. Código Bibliográfico :2021SPIE11873E..08R. doi :10.1117/12.2597023. ISBN 9781510645905.S2CID240561530 .
{{cite book}}:|journal=ignorado ( ayuda ) - ^ "Refractómetro Abbe | ATAGO CO., LTD". www.atago.net . Consultado el 15 de agosto de 2022 .
- ^ "Refractómetro de longitud de onda múltiple Abbe". Nova-Tech International . Consultado el 15 de agosto de 2022 .
- ^ Bach, Hans; Neuroth, Norbert, eds. (1998). Las propiedades del vidrio óptico. Serie Schott sobre vidrio y cerámica de vidrio. p. 267. doi :10.1007/978-3-642-57769-7. ISBN 978-3-642-63349-2.
- ^ ab Dresselhaus, MS (1999). "Solid State Physics Part II Optical Properties of Solids" (PDF) . Curso 6.732 Física del Estado Sólido . MIT. Archivado (PDF) desde el original el 24 de julio de 2015. Consultado el 5 de enero de 2015 .
- ^ R. Paschotta, artículo sobre espesor óptico Archivado el 22 de marzo de 2015 en Wayback Machine en la Enciclopedia de Física y Tecnología Láser Archivado el 13 de agosto de 2015 en Wayback Machine , consultado el 8 de septiembre de 2014
- ^ R. Paschotta, artículo sobre refracción Archivado el 28 de junio de 2015 en Wayback Machine en la Enciclopedia de Física y Tecnología Láser Archivado el 13 de agosto de 2015 en Wayback Machine , consultado el 8 de septiembre de 2014
- ^ abcd Born, Max ; Wolf, Emil (1999). Principios de óptica (7.ª edición ampliada). Archivo CUP. p. 22. ISBN 978-0-521-78449-8.
- ^ Paschotta, R. "Reflexión interna total". RP Photonics Encyclopedia . Archivado desde el original el 28 de junio de 2015. Consultado el 16 de agosto de 2015 .
- ^ Swenson, Jim (10 de noviembre de 2009). "Índice de refracción de minerales". Newton BBS / Laboratorio Nacional Argonne. Departamento de Energía de EE. UU. Archivado desde el original el 28 de mayo de 2010. Consultado el 28 de julio de 2010.
Incorpora material de dominio público del
Departamento de Energía de EE. UU
. - ^ Nave, Carl R. "La fórmula de los fabricantes de lentes". HyperPhysics . Departamento de Física y Astronomía. Universidad Estatal de Georgia. Archivado desde el original el 26 de septiembre de 2014 . Consultado el 8 de septiembre de 2014 .
- ^ abc Carlsson, Kjell (2007). Microscopía óptica (PDF) (Informe). Archivado (PDF) desde el original el 2 de abril de 2015. Consultado el 2 de enero de 2015 .
- ^ Bleaney, B. ; Bleaney, BI (1976). Electricidad y magnetismo (tercera edición). Oxford University Press . ISBN 978-0-19-851141-0.
- ^ Andrews, David L. (24 de febrero de 2015). Photonics, Volume 2: Nanophotonic Structures and Materials. John Wiley & Sons. pág. 54. ISBN 978-1-118-22551-6.
- ^ Wooten, Frederick (1972). Propiedades ópticas de los sólidos . Nueva York: Academic Press . pág. 49. ISBN. 978-0-12-763450-0.(pdf en línea) Archivado el 3 de octubre de 2011 en Wayback Machine.
- ^ "Cálculo del índice de refracción de los vidrios". Cálculo estadístico y desarrollo de propiedades de los vidrios . Archivado desde el original el 15 de octubre de 2007.
- ^ Stone, Jack A.; Zimmerman, Jay H. (28 de diciembre de 2011). "Índice de refracción del aire". Caja de herramientas de metrología de ingeniería . Instituto Nacional de Estándares y Tecnología (NIST). Archivado desde el original el 11 de enero de 2014. Consultado el 11 de enero de 2014 .
- ^ Landolt, H. (enero de 1862). "Ueber die Brechungsexponenten flüssiger homologer Verbindungen". Annalen der Physik . 193 (11): 353–385. doi : 10.1002/andp.18621931102. ISSN 0003-3804.
- ^ Landolt, H. (enero de 1864). "Ueber den Einfluss der atomistischen Zusammensetzung C, H und O-haltiger flüssiger Verbindungen auf die Fortpflanzung des Lichtes". Annalen der Physik . 199 (12): 595–628. doi : 10.1002/andp.18641991206. ISSN 0003-3804.
- ^ Bor, Z.; Osvay, K.; Rácz, B.; Szabó, G. (1990). "Medición del índice de refracción de grupo mediante interferómetro de Michelson". Optics Communications . 78 (2): 109–112. Bibcode :1990OptCo..78..109B. doi :10.1016/0030-4018(90)90104-2.
- ^ Milonni, Peter W.; Boyd, Robert W. (31 de diciembre de 2010). "Momento de la luz en un medio dieléctrico". Avances en óptica y fotónica . 2 (4): 519. Bibcode :2010AdOP....2..519M. doi :10.1364/AOP.2.000519. ISSN 1943-8206.
- ^ Young, AT (2011). «Refractividad del aire». Archivado desde el original el 10 de enero de 2015. Consultado el 31 de julio de 2014 .
- ^ Barrell, H.; Sears, JE (1939). "La refracción y dispersión del aire para el espectro visible". Philosophical Transactions of the Royal Society of London . A, Ciencias Físicas y Matemáticas. 238 (786): 1–64. Bibcode :1939RSPTA.238....1B. doi : 10.1098/rsta.1939.0004 . JSTOR 91351.
- ^ Aparicio, Josep M.; Laroche, Stéphane (2 de junio de 2011). "Una evaluación de la expresión de la refractividad atmosférica para señales GPS". Journal of Geophysical Research . 116 (D11): D11104. Bibcode :2011JGRD..11611104A. doi : 10.1029/2010JD015214 .
- ^ Ciddor, PE (1996). "Índice de refracción del aire: Nuevas ecuaciones para el visible y el infrarrojo cercano". Óptica Aplicada . 35 (9): 1566–1573. Bibcode :1996ApOpt..35.1566C. doi :10.1364/ao.35.001566. PMID 21085275.
- ^ R. Paschotta, artículo sobre birrefringencia Archivado el 3 de julio de 2015 en Wayback Machine en la Enciclopedia de Física y Tecnología Láser Archivado el 13 de agosto de 2015 en Wayback Machine , consultado el 9 de septiembre de 2014
- ^ "La evolución del refractómetro de Abbe". Universidad Estatal de Humboldt, Richard A. Paselk. 1998. Archivado desde el original el 12 de junio de 2011. Consultado el 3 de septiembre de 2011 .
- ^ "Refractómetros y refractometría". Refractometer.pl. 2011. Archivado desde el original el 20 de octubre de 2011. Consultado el 3 de septiembre de 2011 .
- ^ "Refractómetro". Proyecto Gemología. Archivado desde el original el 10 de septiembre de 2011. Consultado el 3 de septiembre de 2011 .
- ^ Fitzgerald, Richard (julio de 2000). "Imágenes de rayos X sensibles a la fase". Physics Today . 53 (7): 23. Bibcode :2000PhT....53g..23F. doi : 10.1063/1.1292471 . S2CID 121322301.
Enlaces externos
- Calculadora NIST para determinar el índice de refracción del aire
- Materiales dieléctricos
- Mundo de la ciencia
- Base de datos en línea de Filmetrics Base de datos gratuita de información sobre índices de refracción y coeficientes de absorción
- RefractiveIndex.INFO Base de datos del índice de refracción con representación gráfica y parametrización de datos en línea
- LUXPOP Archivado el 7 de septiembre de 2013 en Wayback Machine Cálculos de fotónica y de índices de refracción en película delgada y en masa
- Las conferencias de física de Feynman, vol. II, cap. 32: Índice de refracción de materiales densos










![{\displaystyle {\begin{aligned}\mathbf {E} (x,t)&=\operatorname {Re} \!\left[\mathbf {E} _{0}e^{i({\underline {k }}x-\omega t)}\right]\\&=\operatorname {Re} \!\left[\mathbf {E} _{0}e^{i(2\pi (n+i\kappa ) x/\lambda _{0}-\omega t)}\right]\\&=e^{-2\pi \kappa x/\lambda _{0}}\operatorname {Re} \!\left[\ mathbf {E} _{0}e^{i(kx-\omega t)}\right].\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5e3936daed1b1eca2f8adf0bc77d7e57269bb7cd)










![{\displaystyle {\frac {1}{f}}=(n-1)\left[{\frac {1}{R_{1}}}-{\frac {1}{R_{2}}}\right]\ ,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2f04247634ee3ba3bcbf081cf902a4412900e571)






















