Cuaternio
| ↓×→ | 1 | i | yo | a |
|---|---|---|---|---|
| 1 | 1 | i | yo | a |
| i | i | -1 | a | - yo |
| yo | yo | - k | -1 | i |
| a | a | yo | - yo | -1 |
| La columna de la izquierda muestra el factor izquierdo y la fila superior muestra el factor derecho. Además, y para , . | ||||

En matemáticas , el sistema de numeración de cuaterniones extiende los números complejos . Los cuaterniones fueron descritos por primera vez por el matemático irlandés William Rowan Hamilton en 1843 [1] [2] y aplicados a la mecánica en el espacio tridimensional . El álgebra de cuaterniones a menudo se denota por H (por Hamilton ), o en negrita de pizarra por Los cuaterniones no son un cuerpo , porque la multiplicación de cuaterniones no es, en general, conmutativa . Los cuaterniones proporcionan una definición del cociente de dos vectores en un espacio tridimensional. [3] [4] Los cuaterniones generalmente se representan en la forma
donde los coeficientes a , b , c , d son números reales , y 1, i , j , k son los vectores base o elementos base . [5]
Los cuaterniones se utilizan en matemáticas puras , pero también tienen usos prácticos en matemáticas aplicadas , particularmente para cálculos que involucran rotaciones tridimensionales , como en gráficos de computadora tridimensionales , visión por computadora , robótica, imágenes por resonancia magnética [6] y análisis de textura cristalográfica . [7] Se pueden utilizar junto con otros métodos de rotación, como ángulos de Euler y matrices de rotación , o como una alternativa a ellos, dependiendo de la aplicación.
En términos modernos, los cuaterniones forman un álgebra de división normada asociativa de cuatro dimensiones sobre los números reales, y por lo tanto un anillo, también un anillo de división y un dominio . Es un caso especial de un álgebra de Clifford , clasificada como Fue la primera álgebra de división no conmutativa en ser descubierta.
Según el teorema de Frobenius , el álgebra es uno de los dos únicos anillos de división de dimensión finita que contienen un subanillo propio isomorfo a los números reales; el otro son los números complejos. Estos anillos también son álgebras euclidianas de Hurwitz , de las cuales los cuaterniones son la álgebra asociativa más grande (y, por lo tanto, el anillo más grande). Extendiendo aún más los cuaterniones se obtienen los octoniones no asociativos , que es la última álgebra de división normada sobre los números reales. La siguiente extensión da los sedeniones , que tienen divisores de cero y, por lo tanto, no pueden ser un álgebra de división normada. [8]
Los cuaterniones unitarios dan una estructura de grupo en la 3-esfera S 3 isomorfa a los grupos Spin(3) y SU(2) , es decir, el grupo de cobertura universal de SO(3) . Los vectores de base positivos y negativos forman el grupo de cuaterniones de ocho elementos .

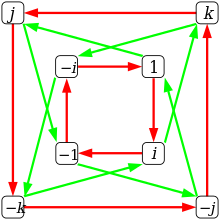
- En azul :
- 1 ⋅ i = i ( plano 1/ i )
- i ⋅ j = k (plano i / k )
- En rojo :
- 1 ⋅ j = j (1/ j plano)
- j ⋅ i = − k (plano j / k )
Historia
_regarding_the_discovery_of_Quaternions_multiplication_by_Sir_William_Rowan_Hamilton.jpg/440px-Inscription_on_Broom_Bridge_(Dublin)_regarding_the_discovery_of_Quaternions_multiplication_by_Sir_William_Rowan_Hamilton.jpg)
Aquí, mientras pasaba
el 16 de octubre de 1843,
Sir William Rowan Hamilton,
en un destello de genialidad, descubrió
la fórmula fundamental para
la multiplicación de cuaterniones
i 2 = j 2 = k 2 = i j k = −1
y la grabó en una piedra de este puente.
Los cuaterniones fueron introducidos por Hamilton en 1843. [9] Los precursores importantes de este trabajo incluyeron la identidad de cuatro cuadrados de Euler (1748) y la parametrización de rotaciones generales por cuatro parámetros de Olinde Rodrigues (1840), pero ninguno de estos escritores trató las rotaciones de cuatro parámetros como un álgebra. [10] [11] Carl Friedrich Gauss había descubierto los cuaterniones en 1819, pero este trabajo no se publicó hasta 1900. [12] [13]
Hamilton sabía que los números complejos podían interpretarse como puntos en un plano , y estaba buscando una forma de hacer lo mismo para los puntos en el espacio tridimensional . Los puntos en el espacio pueden representarse por sus coordenadas, que son triples de números, y durante muchos años había sabido cómo sumar y restar triples de números. Sin embargo, durante mucho tiempo, había estado atascado en el problema de la multiplicación y la división. No podía descubrir cómo calcular el cociente de las coordenadas de dos puntos en el espacio. De hecho, Ferdinand Georg Frobenius demostró más tarde en 1877 que para que un álgebra de división sobre los números reales sea de dimensión finita y asociativa, no puede ser tridimensional, y solo hay tres álgebras de división de este tipo: (números complejos) y (cuaterniones) que tienen dimensión 1, 2 y 4 respectivamente.
El gran avance en los cuaterniones finalmente llegó el lunes 16 de octubre de 1843 en Dublín , cuando Hamilton se dirigía a la Real Academia Irlandesa para presidir una reunión del consejo. Mientras caminaba por el camino de sirga del Canal Real con su esposa, los conceptos detrás de los cuaterniones iban tomando forma en su mente. Cuando la respuesta se le ocurrió, Hamilton no pudo resistir la tentación de escribir la fórmula para los cuaterniones.
En la piedra del puente Brougham , donde se detuvo, se clavó la piedra. Aunque la talla desapareció, desde 1989 se celebra una peregrinación anual llamada Hamilton Walk para científicos y matemáticos que caminan desde el Observatorio Dunsink hasta el puente Royal Canal en recuerdo del descubrimiento de Hamilton.
Al día siguiente, Hamilton escribió una carta a su amigo y colega matemático, John T. Graves , en la que describía la línea de pensamiento que lo había llevado a su descubrimiento. Esta carta se publicó más tarde en una carta a la revista Philosophical Magazine and Journal of Science de Londres, Edimburgo y Dublín ; [14] Hamilton afirma:
Y aquí se me ocurrió la idea de que debemos admitir, en algún sentido, una cuarta dimensión del espacio con el propósito de calcular con triples... Un circuito eléctrico pareció cerrarse y surgió una chispa. [14]
Hamilton denominó cuaternión a un cuádruple con estas reglas de multiplicación y dedicó la mayor parte del resto de su vida a estudiarlas y enseñarlas. El tratamiento de Hamilton es más geométrico que el enfoque moderno, que enfatiza las propiedades algebraicas de los cuaterniones . Fundó una escuela de "cuaternionistas" e intentó popularizar los cuaterniones en varios libros. El último y más largo de sus libros, Elements of Quaternions , [15] tenía 800 páginas; fue editado por su hijo y publicado poco después de su muerte.
Tras la muerte de Hamilton, el físico matemático escocés Peter Tait se convirtió en el principal exponente de los cuaterniones. En esa época, los cuaterniones eran un tema de examen obligatorio en Dublín. Los temas de física y geometría que ahora se describirían utilizando vectores, como la cinemática en el espacio y las ecuaciones de Maxwell , se describían completamente en términos de cuaterniones. Incluso existía una asociación de investigación profesional, la Quaternion Society , dedicada al estudio de los cuaterniones y otros sistemas numéricos hipercomplejos .
A partir de mediados de la década de 1880, los cuaterniones comenzaron a ser desplazados por el análisis vectorial , que había sido desarrollado por Josiah Willard Gibbs , Oliver Heaviside y Hermann von Helmholtz . El análisis vectorial describía los mismos fenómenos que los cuaterniones, por lo que tomó prestadas algunas ideas y terminología generosamente de la literatura sobre cuaterniones. Sin embargo, el análisis vectorial era conceptualmente más simple y notacionalmente más claro, y finalmente los cuaterniones fueron relegados a un papel menor en las matemáticas y la física . Un efecto secundario de esta transición es que el trabajo de Hamilton es difícil de comprender para muchos lectores modernos. Las definiciones originales de Hamilton son desconocidas y su estilo de escritura era prolijo y difícil de seguir.
Sin embargo, los cuaterniones han tenido un resurgimiento desde finales del siglo XX, principalmente debido a su utilidad para describir rotaciones espaciales . Las representaciones de rotaciones por cuaterniones son más compactas y más rápidas de calcular que las representaciones por matrices . Además, a diferencia de los ángulos de Euler, no son susceptibles al " bloqueo de cardán ". Por esta razón, los cuaterniones se utilizan en gráficos por computadora , [16] [17] visión por computadora , robótica , [18] muestreo de imágenes por resonancia magnética nuclear , [6] teoría de control , procesamiento de señales , control de actitud , física , bioinformática , dinámica molecular , simulaciones por computadora y mecánica orbital . Por ejemplo, es común que los sistemas de control de actitud de las naves espaciales se comanden en términos de cuaterniones. Los cuaterniones han recibido otro impulso de la teoría de números debido a sus relaciones con las formas cuadráticas . [19]
Cuaterniones en física
El descubrimiento de 1924 de que en mecánica cuántica el giro de un electrón y otras partículas de materia (conocidas como espinores ) se puede describir usando cuaterniones (en la forma de las famosas matrices de espín de Pauli) fomentó su interés; los cuaterniones ayudaron a comprender cómo las rotaciones de electrones de 360° se pueden discernir de aquellas de 720° (el " truco de la placa "). [20] [21] A partir de 2018 [actualizar], su uso no ha superado a los grupos de rotación . [a]
Definición
Un cuaternión es una expresión de la forma
donde a , b , c , d , son números reales, e i , j , k , son símbolos que pueden interpretarse como vectores unitarios que apuntan a lo largo de los tres ejes espaciales. En la práctica, si uno de a , b , c , d es 0, se omite el término correspondiente; si a , b , c , d son todos cero, el cuaternión es el cuaternión cero , denotado 0; si uno de b , c , d es igual a 1, el término correspondiente se escribe simplemente i , j o k .
Hamilton describe un cuaternión como compuesto de una parte escalar y una parte vectorial. El cuaternión se denomina parte vectorial (a veces parte imaginaria ) de q , y a es la parte escalar (a veces parte real ) de q . Un cuaternión que es igual a su parte real (es decir, su parte vectorial es cero) se denomina cuaternión escalar o real , y se identifica con el número real correspondiente. Es decir, los números reales están incrustados en los cuaterniones. (Más apropiadamente, el campo de los números reales es isomorfo a un subconjunto de los cuaterniones. El campo de los números complejos también es isomorfo a tres subconjuntos de cuaterniones). [22] Un cuaternión que es igual a su parte vectorial se denomina cuaternión vectorial .
El conjunto de cuaterniones es un espacio vectorial de 4 dimensiones sobre los números reales, con como base , por la adición de componentes
y la multiplicación escalar componente por componente
Una estructura de grupo multiplicativa, llamada producto de Hamilton , denotada por yuxtaposición, se puede definir en los cuaterniones de la siguiente manera:
- El cuaternión real 1 es el elemento identidad .
- Los cuaterniones reales conmutan con todos los demás cuaterniones, es decir, aq = qa para cada cuaternión q y cada cuaternión real a . En terminología algebraica, esto quiere decir que el campo de cuaterniones reales es el centro de esta álgebra de cuaterniones.
- El producto se da primero para los elementos base (ver la siguiente subsección), y luego se extiende a todos los cuaterniones utilizando la propiedad distributiva y la propiedad central de los cuaterniones reales. El producto de Hamilton no es conmutativo , sino asociativo , por lo que los cuaterniones forman un álgebra asociativa sobre los números reales.
- Además, cada cuaternión distinto de cero tiene un inverso con respecto al producto de Hamilton:
Así, los cuaterniones forman un álgebra de división.
Multiplicación de elementos base
| × | 1 | i | yo | a |
|---|---|---|---|---|
| 1 | 1 | i | yo | a |
| i | i | -1 | a | - yo |
| yo | yo | - k | -1 | i |
| a | a | yo | - yo | -1 |
La multiplicación por 1 de los elementos base i , j y k se define por el hecho de que 1 es una identidad multiplicativa , es decir,
Los productos de otros elementos básicos son
Combinando estas reglas,
Centro
El centro de un anillo no conmutativo es el subanillo de elementos c tales que cx = xc para cada x . El centro del álgebra de cuaterniones es el subcuerpo de cuaterniones reales. De hecho, es parte de la definición que los cuaterniones reales pertenecen al centro. Por el contrario, si q = a + b i + c j + d k pertenece al centro, entonces
y c = d = 0. Un cálculo similar con j en lugar de i muestra que también se tiene b = 0. Por lo tanto, q = a es un cuaternión real .
Los cuaterniones forman un álgebra de división. Esto significa que la no conmutatividad de la multiplicación es la única propiedad que hace que los cuaterniones sean diferentes de un cuerpo. Esta no conmutatividad tiene algunas consecuencias inesperadas, entre ellas que una ecuación polinómica sobre los cuaterniones puede tener más soluciones distintas que el grado del polinomio. Por ejemplo, la ecuación z 2 + 1 = 0 , tiene infinitas soluciones de cuaterniones, que son los cuaterniones z = b i + c j + d k tales que b 2 + c 2 + d 2 = 1 . Por lo tanto, estas "raíces de –1" forman una esfera unitaria en el espacio tridimensional de los cuaterniones vectoriales.
Producto Hamilton
Para dos elementos a 1 + b 1 i + c 1 j + d 1 k y a 2 + b 2 i + c 2 j + d 2 k , su producto, llamado producto de Hamilton ( a 1 + b 1 i + c 1 j + d 1 k ) ( a 2 + b 2 i + c 2 j + d 2 k ), está determinado por los productos de los elementos base y la ley distributiva . La ley distributiva permite desarrollar el producto de modo que sea una suma de productos de elementos base. Esto da la siguiente expresión:
Ahora los elementos base se pueden multiplicar utilizando las reglas dadas anteriormente para obtener: [9]
Partes escalares y vectoriales
Un cuaternión de la forma a + 0 i + 0 j + 0 k , donde a es un número real, se llama escalar , y un cuaternión de la forma 0 + b i + c j + d k , donde b , c y d son números reales, y al menos uno de b , c o d es distinto de cero, se llama cuaternión vectorial . Si a + b i + c j + d k es cualquier cuaternión, entonces a se llama su parte escalar y b i + c j + d k se llama su parte vectorial . Aunque cada cuaternión puede verse como un vector en un espacio vectorial de cuatro dimensiones, es común referirse a la parte vectorial como vectores en el espacio tridimensional. Con esta convención, un vector es lo mismo que un elemento del espacio vectorial [b]
Hamilton también llamó a los cuaterniones vectoriales cuaterniones rectos [24] [25] y a los números reales (considerados como cuaterniones con parte vectorial cero) cuaterniones escalares .
Si un cuaternión se divide en una parte escalar y una parte vectorial, es decir,
Entonces las fórmulas para la suma, la multiplicación y el inverso multiplicativo son
donde " " y " " denotan respectivamente el producto escalar y el producto vectorial .
Conjugación, norma y reciprocidad
La conjugación de cuaterniones es análoga a la conjugación de números complejos y a la transposición (también conocida como inversión) de elementos de las álgebras de Clifford. Para definirla, sea un cuaternión. El conjugado de q es el cuaternión . Se denota por q ∗ , q t , , o q . [9] La conjugación es una involución , lo que significa que es su propia inversa , por lo que conjugar un elemento dos veces devuelve el elemento original. El conjugado de un producto de dos cuaterniones es el producto de los conjugados en el orden inverso . Es decir, si p y q son cuaterniones, entonces ( pq ) ∗ = q ∗ p ∗ , no p ∗ q ∗ .
La conjugación de un cuaternión, en marcado contraste con la configuración compleja, se puede expresar con la multiplicación y la suma de cuaterniones:
La conjugación se puede utilizar para extraer las partes escalares y vectoriales de un cuaternión. La parte escalar de p es 1/2 ( p + p ∗ ) , y la parte vectorial de p es 1/2 ( p − p ∗ ) .
La raíz cuadrada del producto de un cuaternión por su conjugado se denomina norma y se denota por ‖ q ‖ (Hamilton llamó a esta cantidad el tensor de q , pero esto entra en conflicto con el significado moderno de " tensor "). En fórmulas, esto se expresa de la siguiente manera:
Este es siempre un número real no negativo, y es el mismo que la norma euclidiana en considerado como el espacio vectorial . Al multiplicar un cuaternión por un número real, se escala su norma por el valor absoluto del número. Es decir, si α es real, entonces
Este es un caso especial del hecho de que la norma es multiplicativa , lo que significa que
para dos cuaterniones cualesquiera p y q . La multiplicatividad es una consecuencia de la fórmula para el conjugado de un producto. Alternativamente, se sigue de la identidad
(donde i denota la unidad imaginaria habitual ) y por tanto de la propiedad multiplicativa de los determinantes de matrices cuadradas.
Esta norma permite definir la distancia d ( p , q ) entre p y q como la norma de su diferencia:
Esto crea un espacio métrico . La suma y la multiplicación son continuas en relación con la topología métrica asociada . Esto se deduce exactamente de la misma prueba que para los números reales a partir del hecho de que es un álgebra normada.
Unidad cuaternión
Un cuaternión unidad es un cuaternión de norma uno. Dividir un cuaternión distinto de cero q por su norma produce un cuaternión unidad U q llamado versor de q :
Cada cuaternión distinto de cero tiene una descomposición polar única , mientras que el cuaternión cero puede formarse a partir de cualquier cuaternión unidad.
El uso de la conjugación y la norma permite definir el recíproco de un cuaternión distinto de cero. El producto de un cuaternión por su recíproco debe ser igual a 1, y las consideraciones anteriores implican que el producto de y es 1 (para cualquier orden de multiplicación). Por lo tanto, el recíproco de q se define como
Como la multiplicación no es conmutativa, las cantidades cociente p q −1 o q −1 p son diferentes (excepto si p y q son múltiplos escalares entre sí o si uno es un escalar): la notación pag/q es ambiguo y no debe utilizarse.
Propiedades algebraicas
El conjunto de todos los cuaterniones es un espacio vectorial sobre los números reales con dimensión 4. [c] La multiplicación de cuaterniones es asociativa y se distribuye sobre la suma de vectores, pero con la excepción del subconjunto escalar, no es conmutativa. Por lo tanto, los cuaterniones son un álgebra asociativa no conmutativa sobre los números reales. Aunque contiene copias de los números complejos, no es un álgebra asociativa sobre los números complejos.
Debido a que es posible dividir los cuaterniones, forman un álgebra de división. Esta es una estructura similar a un cuerpo excepto por la no conmutatividad de la multiplicación. Las álgebras de división asociativas de dimensión finita sobre los números reales son muy raras. El teorema de Frobenius establece que hay exactamente tres: , , y . La norma convierte a los cuaterniones en un álgebra normada , y las álgebras de división normadas sobre los números reales también son muy raras: el teorema de Hurwitz dice que solo hay cuatro: , , , y (los octoniones). Los cuaterniones también son un ejemplo de un álgebra de composición y de un álgebra de Banach unital .
Como el producto de dos vectores base cualesquiera es más o menos otro vector base, el conjunto {±1, ± i , ± j , ± k } forma un grupo bajo la multiplicación. Este grupo no abeliano se llama grupo de cuaterniones y se denota Q 8 . [26] El anillo de grupo real de Q 8 es un anillo que también es un espacio vectorial de ocho dimensiones sobre Tiene un vector base para cada elemento de Los cuaterniones son isomorfos al anillo cociente de por el ideal generado por los elementos 1 + (−1) , i + (− i ) , j + (− j ) y k + (− k ) . Aquí el primer término en cada una de las diferencias es uno de los elementos base 1, i , j y k , y el segundo término es uno de los elementos base −1, − i , − j y − k , no los inversos aditivos de 1, i , j y k .
Cuaterniones y geometría tridimensional
La parte vectorial de un cuaternión se puede interpretar como un vector de coordenadas en por lo tanto, las operaciones algebraicas de los cuaterniones reflejan la geometría de Operaciones como los productos punto y vectorial se pueden definir en términos de cuaterniones, y esto hace posible aplicar técnicas de cuaterniones dondequiera que surjan vectores espaciales. Una aplicación útil de los cuaterniones ha sido la interpolación de las orientaciones de fotogramas clave en gráficos de computadora. [16]
En el resto de esta sección, i , j y k denotarán los tres vectores base imaginarios [27] de y una base para Reemplazar i por − i , j por − j y k por − k envía un vector a su inverso aditivo , por lo que el inverso aditivo de un vector es el mismo que su conjugado como cuaternión. Por esta razón, la conjugación a veces se denomina inverso espacial .
Para dos cuaterniones vectoriales p = b 1 i + c 1 j + d 1 k y q = b 2 i + c 2 j + d 2 k su producto escalar , por analogía con los vectores en es
También se puede expresar de manera libre de componentes como
Esto es igual a las partes escalares de los productos pq ∗ , qp ∗ , p ∗ q y q ∗ p . Nótese que sus partes vectoriales son diferentes.
El producto vectorial de p y q con respecto a la orientación determinada por la base ordenada i , j y k es
(Recuerde que la orientación es necesaria para determinar el signo). Esto es igual a la parte vectorial del producto pq (como cuaterniones), así como a la parte vectorial de − q ∗ p ∗ . También tiene la fórmula
Para el conmutador , [ p , q ] = pq − qp , de dos cuaterniones vectoriales se obtiene
En general, sean p y q cuaterniones y escriba
donde p s y q s son las partes escalares, y p v y q v son las partes vectoriales de p y q . Entonces tenemos la fórmula
Esto demuestra que la no conmutatividad de la multiplicación de cuaterniones proviene de la multiplicación de cuaterniones vectoriales. También demuestra que dos cuaterniones conmutan si y solo si sus partes vectoriales son colineales. Hamilton [28] demostró que este producto calcula el tercer vértice de un triángulo esférico a partir de dos vértices dados y sus longitudes de arco asociadas, lo que también es un álgebra de puntos en geometría elíptica .
Los cuaterniones unitarios se pueden identificar con rotaciones en y fueron llamados versores por Hamilton. [28] Consulte también Cuaterniones y rotación espacial para obtener más información sobre el modelado de rotaciones tridimensionales utilizando cuaterniones.
Consulte Hanson (2005) [29] para la visualización de cuaterniones.
Representaciones matriciales
Así como los números complejos pueden representarse como matrices , también lo pueden hacer los cuaterniones. Hay al menos dos formas de representar cuaterniones como matrices de tal manera que la adición y multiplicación de cuaterniones correspondan a la adición y multiplicación de matrices . Una es usar matrices complejas de 2 × 2 y la otra es usar matrices reales de 4 × 4. En cada caso, la representación dada es una de una familia de representaciones relacionadas linealmente. Estas son homomorfismos inyectivos de a los anillos de matrices M(2, C ) y M(4, R ) , respectivamente.
El cuaternión a + b i + c j + d k se puede representar utilizando una matriz compleja de 2 × 2 como
Esta representación tiene las siguientes propiedades:
- Restringir a cero dos de b , c y d produce una representación de números complejos. Por ejemplo, establecer c = d = 0 produce una representación de matriz compleja diagonal de números complejos, y establecer b = d = 0 produce una representación de matriz real.
- La norma de un cuaternión (la raíz cuadrada del producto por su conjugado, como en los números complejos) es la raíz cuadrada del determinante de la matriz correspondiente. [30]
- La parte escalar de un cuaternión es la mitad de la traza de la matriz .
- El conjugado de un cuaternión corresponde a la transpuesta conjugada de la matriz.
- Por restricción, esta representación produce un isomorfismo entre el subgrupo de cuaterniones unitarios y su imagen SU(2) . Topológicamente, los cuaterniones unitarios son la 3-esfera, por lo que el espacio subyacente de SU(2) también es una 3-esfera. El grupo SU(2) es importante para describir el espín en mecánica cuántica; véase Matrices de Pauli .
- Existe una fuerte relación entre las unidades de cuaternión y las matrices de Pauli. La matriz compleja 2 × 2 anterior se puede escribir como , por lo que en esta representación las unidades de cuaternión {±1, ± i , ± j , ± k } corresponden a {± I , , , } = {± I , , , } , por lo que multiplicar dos matrices de Pauli cualesquiera siempre produce una matriz de unidades de cuaternión, todas ellas excepto −1. Se obtiene −1 mediante i 2 = j 2 = k 2 = ijk = −1 ; por ejemplo, la última igualdad es
- La representación en M(2, C ) no es única. Una convención diferente, que preserva la dirección del ordenamiento cíclico entre los cuaterniones y las matrices de Pauli, es elegir Esto da una representación alternativa, [31]
Usando matrices reales de 4 × 4, ese mismo cuaternión se puede escribir como
Sin embargo, la representación de los cuaterniones en M(4, R ) no es única. Por ejemplo, el mismo cuaternión también puede representarse como
Existen 48 representaciones matriciales distintas de esta forma en las que una de las matrices representa la parte escalar y las otras tres son todas antisimétricas. Más precisamente, hay 48 conjuntos de cuádruples de matrices con estas restricciones de simetría tales que una función que envía 1, i , j y k a las matrices en el cuádruple es un homomorfismo, es decir, envía sumas y productos de cuaterniones a sumas y productos de matrices. [32] En esta representación, el conjugado de un cuaternión corresponde a la transpuesta de la matriz. La cuarta potencia de la norma de un cuaternión es el determinante de la matriz correspondiente. La parte escalar de un cuaternión es un cuarto de la traza de la matriz. Al igual que con la representación compleja 2 × 2 anterior, los números complejos se pueden producir nuevamente restringiendo los coeficientes adecuadamente; por ejemplo, como matrices diagonales de bloques con dos bloques 2 × 2 estableciendo c = d = 0 .
Cada representación matricial de cuaterniones de 4×4 corresponde a una tabla de multiplicación de cuaterniones unitarios. Por ejemplo, la última representación matricial dada anteriormente corresponde a la tabla de multiplicación
| × | a | d | -b | - c |
|---|---|---|---|---|
| a | a | d | -b | -c |
| -d | -d | a | do | -b |
| b | b | - c | a | - el |
| do | do | b | d | a |
que es isomorfo —a través de— a
| × | 1 | a | - yo | - yo |
|---|---|---|---|---|
| 1 | 1 | a | - yo | - yo |
| - k | - k | 1 | yo | - yo |
| i | i | - yo | 1 | - k |
| yo | yo | i | a | 1 |
Si restringimos cualquier tabla de multiplicación de este tipo para que tenga la identidad en la primera fila y columna y para que los signos de los encabezados de fila sean opuestos a los de los encabezados de columna, entonces hay 3 opciones posibles para la segunda columna (ignorando el signo), 2 opciones posibles para la tercera columna (ignorando el signo) y 1 opción posible para la cuarta columna (ignorando el signo); eso da 6 posibilidades. Entonces, la segunda columna puede elegirse para que sea positiva o negativa, la tercera columna puede elegirse para que sea positiva o negativa, y la cuarta columna puede elegirse para que sea positiva o negativa, lo que da 8 posibilidades para el signo. Multiplicando las posibilidades para las posiciones de las letras y para sus signos, obtenemos 48. Luego, reemplazando 1 con a , i con b , j con c y k con d y eliminando los encabezados de fila y columna, obtenemos una representación matricial de a + b i + c j + d k .
Teorema de los cuatro cuadrados de Lagrange
Los cuaterniones también se utilizan en una de las demostraciones del teorema de los cuatro cuadrados de Lagrange en la teoría de números , que establece que todo entero no negativo es la suma de cuatro cuadrados enteros. Además de ser un teorema elegante por derecho propio, el teorema de los cuatro cuadrados de Lagrange tiene aplicaciones útiles en áreas de las matemáticas fuera de la teoría de números, como la teoría del diseño combinatorio . La demostración basada en cuaterniones utiliza cuaterniones de Hurwitz , un subanillo del anillo de todos los cuaterniones para el que existe un análogo del algoritmo euclidiano .
Cuaterniones como pares de números complejos
Los cuaterniones pueden representarse como pares de números complejos. Desde esta perspectiva, los cuaterniones son el resultado de aplicar la construcción de Cayley-Dickson a los números complejos. Se trata de una generalización de la construcción de los números complejos como pares de números reales.
Sea un espacio vectorial bidimensional sobre los números complejos. Elija una base que conste de dos elementos 1 y j . Un vector en se puede escribir en términos de los elementos de la base 1 y j como
Si definimos j 2 = −1 e i j = − j i , entonces podemos multiplicar dos vectores usando la ley distributiva. El uso de k como notación abreviada para el producto i j conduce a las mismas reglas de multiplicación que los cuaterniones habituales. Por lo tanto, el vector anterior de números complejos corresponde al cuaternión a + bi + c j + d k . Si escribimos los elementos de como pares ordenados y los cuaterniones como cuádruples, entonces la correspondencia es
Raíces cuadradas
Raíces cuadradas de −1
En los números complejos, hay exactamente dos números, i y − i , que dan −1 cuando se elevan al cuadrado. En hay infinitas raíces cuadradas de menos uno: la solución cuaternial para la raíz cuadrada de −1 es la esfera unitaria en Para ver esto, sea q = a + b i + c j + d k un cuaternial y supongamos que su cuadrado es −1. En términos de a , b , c y d , esto significa
Para satisfacer las tres últimas ecuaciones, a = 0 o b , c y d son todos 0. Esto último es imposible porque a es un número real y la primera ecuación implicaría que a 2 = −1 . Por lo tanto, a = 0 y b 2 + c 2 + d 2 = 1 . En otras palabras: un cuaternión eleva al cuadrado −1 si y solo si es un cuaternión vectorial con norma 1. Por definición, el conjunto de todos esos vectores forma la esfera unitaria.
Sólo los cuaterniones reales negativos tienen infinitas raíces cuadradas. Todos los demás tienen sólo dos (o una en el caso del 0). [ cita requerida ] [d]
Como unión de planos complejos
Cada par antípoda de raíces cuadradas de −1 crea una copia distinta de los números complejos dentro de los cuaterniones. Si q 2 = −1 , entonces la copia es la imagen de la función
Se trata de un homomorfismo de anillo inyectivo de a que define un isomorfismo de campo de sobre su imagen . Las imágenes de las incrustaciones correspondientes a q y − q son idénticas.
Cada cuaternión no real genera un subálgebra de los cuaterniones que es isomorfa a y, por lo tanto, es un subespacio planar de escrito q como la suma de su parte escalar y su parte vectorial:
Descomponga aún más la parte vectorial como el producto de su norma por su versor :
(Esto no es lo mismo que .) El versor de la parte vectorial de q , , es un versor derecho con –1 como su cuadrado. Una verificación sencilla muestra que define un homomorfismo inyectivo de álgebras normadas de en los cuaterniones. Bajo este homomorfismo, q es la imagen del número complejo .
Como la unión de las imágenes de todos estos homomorfismos permite ver los cuaterniones como un lápiz de planos que se cortan en la recta real . Cada uno de estos planos complejos contiene exactamente un par de puntos antípodas de la esfera de raíces cuadradas de menos uno.
Subanillos conmutativos
La relación de los cuaterniones entre sí dentro de los subplanos complejos de también se puede identificar y expresar en términos de subanillos conmutativos . Específicamente, dado que dos cuaterniones p y q conmutan (es decir, pq = qp ) solo si se encuentran en el mismo subplano complejo de , el perfil de como una unión de planos complejos surge cuando uno busca encontrar todos los subanillos conmutativos del anillo de cuaterniones .
Raíces cuadradas de cuaterniones arbitrarios
Cualquier cuaternión (representado aquí en representación escalar-vectorial) tiene al menos una raíz cuadrada que resuelve la ecuación . Al observar las partes escalares y vectoriales de esta ecuación por separado, se obtienen dos ecuaciones que, al resolverlas, dan las soluciones
donde es la norma de y es la norma de . Para cualquier cuaternión escalar , esta ecuación proporciona las raíces cuadradas correctas si se interpreta como un vector unitario arbitrario.
Por lo tanto, los cuaterniones no escalares distintos de cero, o cuaterniones escalares positivos, tienen exactamente dos raíces, mientras que 0 tiene exactamente una raíz (0), y los cuaterniones escalares negativos tienen infinitas raíces, que son los cuaterniones vectoriales ubicados en , es decir, donde la parte escalar es cero y la parte vectorial está ubicada en la 2-esfera con radio .
Funciones de una variable cuaternión

Al igual que las funciones de una variable compleja , las funciones de una variable cuaternial sugieren modelos físicos útiles. Por ejemplo, los campos eléctricos y magnéticos originales descritos por Maxwell eran funciones de una variable cuaternial. Otros ejemplos de funciones incluyen la extensión del conjunto de Mandelbrot y los conjuntos de Julia al espacio de cuatro dimensiones. [36]
Funciones exponenciales, logarítmicas y de potencia
Dado un cuaternión,
La exponencial se calcula como [37]
y el logaritmo es [37]
De ello se deduce que la descomposición polar de un cuaternión puede escribirse
donde el ángulo [e]
y el vector unitario se define por:
Cualquier cuaternión unitario puede expresarse en forma polar como:
La potencia de un cuaternión elevada a un exponente arbitrario (real) x viene dada por:
Norma geodésica
La distancia geodésica d g ( p , q ) entre los cuaterniones unitarios p y q se define como: [39]
y equivale al valor absoluto de la mitad del ángulo subtendido por p y q a lo largo de un gran arco de la esfera S 3 . Este ángulo también se puede calcular a partir del producto escalar del cuaternión sin el logaritmo como:
Grupos de rotación tridimensionales y cuatridimensionales
La palabra " conjugación ", además del significado dado anteriormente, también puede significar tomar un elemento a en r a r −1 donde r es algún cuaternión distinto de cero. Todos los elementos que son conjugados con un elemento dado (en este sentido de la palabra conjugado) tienen la misma parte real y la misma norma de la parte vectorial. (Por lo tanto, el conjugado en el otro sentido es uno de los conjugados en este sentido.) [40]
Así, el grupo multiplicativo de cuaterniones distintos de cero actúa por conjugación sobre la copia de que consiste en cuaterniones con parte real igual a cero. La conjugación por un cuaternión unitario (un cuaternión de valor absoluto 1) con parte real cos( φ ) es una rotación de un ángulo 2 φ , siendo el eje de la rotación la dirección de la parte vectorial. Las ventajas de los cuaterniones son: [41]
- Evitar el bloqueo del cardán , un problema con sistemas como los ángulos de Euler.
- Más rápido y más compacto que las matrices.
- Representación no singular (en comparación con los ángulos de Euler, por ejemplo).
- Los pares de cuaterniones unitarios representan una rotación en el espacio 4D (ver Rotaciones en el espacio euclidiano de 4 dimensiones: Álgebra de rotaciones 4D ).
El conjunto de todos los cuaterniones unitarios ( versores ) forma una 3-esfera S 3 y un grupo (un grupo de Lie ) bajo la multiplicación, cubriendo por partida doble el grupo de matrices reales ortogonales 3×3 de determinante 1, ya que a cada rotación bajo la correspondencia anterior corresponden dos cuaterniones unitarios. Véase el truco de las placas .
La imagen de un subgrupo de versores es un grupo puntual y, a la inversa, la preimagen de un grupo puntual es un subgrupo de versores. La preimagen de un grupo puntual finito se denomina con el mismo nombre, con el prefijo binario . Por ejemplo, la preimagen del grupo icosaédrico es el grupo icosaédrico binario .
El grupo de los versores es isomorfo a SU(2) , el grupo de matrices unitarias complejas 2×2 de determinante 1.
Sea A el conjunto de cuaterniones de la forma a + b i + c j + d k donde a, b, c y d son todos enteros o todos semienteros . El conjunto A es un anillo (de hecho, un dominio ) y una red y se llama anillo de cuaterniones de Hurwitz. Hay 24 cuaterniones unidad en este anillo, y son los vértices de una celda regular de 24 con símbolo de Schläfli {3,4,3}. Corresponden a la doble cobertura del grupo de simetría rotacional del tetraedro regular . De manera similar, los vértices de una celda regular de 600 con símbolo de Schläfli {3,3,5 } pueden tomarse como los icosianos unidad , correspondientes a la doble cobertura del grupo de simetría rotacional del icosaedro regular . La doble cubierta del grupo de simetría rotacional del octaedro regular corresponde a los cuaterniones que representan los vértices de la celda diesfenoidal de 288 . [42]
Álgebras de cuaterniones
Los cuaterniones se pueden generalizar en otras álgebras llamadas álgebras de cuaterniones . Tome F como cualquier cuerpo con característica diferente de 2, y a y b como elementos de F ; se puede definir un álgebra asociativa unitaria de cuatro dimensiones sobre F con base 1, i , j y ij , donde i 2 = a , j 2 = b e ij = − ji (por lo que ( ij ) 2 = − ab ).
Las álgebras de cuaterniones son isomorfas al álgebra de matrices 2×2 sobre F o forman álgebras de división sobre F , dependiendo de la elección de a y b .
Cuaterniones como parte par deCl3,0 ( R )
La utilidad de los cuaterniones para los cálculos geométricos se puede generalizar a otras dimensiones identificando los cuaterniones como la parte par del álgebra de Clifford. Esta es un álgebra asociativa multivectorial construida a partir de elementos básicos fundamentales σ 1 , σ 2 , σ 3 utilizando las reglas del producto.
Si tomamos estos elementos básicos fundamentales para representar vectores en el espacio 3D, entonces resulta que la reflexión de un vector r en un plano perpendicular a un vector unitario w se puede escribir:
Dos reflexiones realizan una rotación en un ángulo dos veces el ángulo entre los dos planos de reflexión, por lo que
corresponde a una rotación de 180° en el plano que contiene σ 1 y σ 2 . Esto es muy similar a la fórmula del cuaternión correspondiente,
De hecho, las dos estructuras y son isomorfas . Una identificación natural es
y es fácil confirmar que esto preserva las relaciones de Hamilton.
En esta imagen, los llamados "cuaterniones vectoriales" (es decir, cuaterniones imaginarios puros) no corresponden a vectores sino a bivectores , es decir, cantidades con magnitudes y orientaciones asociadas a planos 2D particulares en lugar de direcciones 1D . La relación con los números complejos también se vuelve más clara: en 2D, con dos direcciones vectoriales σ 1 y σ 2 , solo hay un elemento base bivectorial σ 1 σ 2 , por lo que solo hay un imaginario. Pero en 3D, con tres direcciones vectoriales, hay tres elementos base bivectoriales σ 2 σ 3 , σ 3 σ 1 , σ 1 σ 2 , por lo que hay tres imaginarios.
Este razonamiento se extiende más allá. En el álgebra de Clifford hay seis elementos base bivectoriales, ya que con cuatro direcciones básicas de vector diferentes, se pueden definir seis pares diferentes y, por lo tanto, seis planos linealmente independientes diferentes. Las rotaciones en tales espacios que utilizan estas generalizaciones de cuaterniones, llamadas rotores , pueden ser muy útiles para aplicaciones que involucran coordenadas homogéneas . Pero es solo en 3D que el número de bivectores base es igual al número de vectores base, y cada bivector puede identificarse como un pseudovector .
Existen varias ventajas en colocar cuaterniones en este entorno más amplio: [43]
- Los rotores son una parte natural del álgebra geométrica y se entienden fácilmente como la codificación de una doble reflexión.
- En álgebra geométrica, un rotor y los objetos sobre los que actúa viven en el mismo espacio. Esto elimina la necesidad de cambiar las representaciones y codificar nuevas estructuras y métodos de datos, algo que tradicionalmente se requiere cuando se amplía el álgebra lineal con cuaterniones.
- Los rotores son universalmente aplicables a cualquier elemento del álgebra, no sólo vectores y otros cuaterniones, sino también líneas, planos, círculos, esferas, rayos, etc.
- En el modelo conforme de la geometría euclidiana, los rotores permiten codificar la rotación, la traslación y el escalamiento en un único elemento del álgebra, actuando de forma universal sobre cualquier elemento. En particular, esto significa que los rotores pueden representar rotaciones alrededor de un eje arbitrario, mientras que los cuaterniones están limitados a un eje que pasa por el origen.
- Las transformaciones codificadas por rotor hacen que la interpolación sea particularmente sencilla.
- Los rotores se trasladan naturalmente a espacios pseudoeuclidianos , por ejemplo, el espacio de Minkowski de la relatividad especial . En tales espacios, los rotores se pueden utilizar para representar eficientemente los impulsos de Lorentz y para interpretar fórmulas que involucran las matrices gamma . [ cita requerida ]
Para más detalles sobre los usos geométricos de las álgebras de Clifford, véase Álgebra geométrica .
Grupo Brauer
Los cuaterniones son "esencialmente" la única álgebra central simple (CSA) (no trivial) sobre los números reales, en el sentido de que cada CSA sobre los números reales es equivalente de Brauer a los números reales o a los cuaterniones. Explícitamente, el grupo de Brauer de los números reales consta de dos clases, representadas por los números reales y los cuaterniones, donde el grupo de Brauer es el conjunto de todas las CSA, hasta la relación de equivalencia de una CSA que es un anillo de matrices sobre otro. Por el teorema de Artin-Wedderburn (específicamente, la parte de Wedderburn), las CSA son todas álgebras matriciales sobre un álgebra de división y, por lo tanto, los cuaterniones son la única álgebra de división no trivial sobre los números reales.
Los anillos de dimensión finita sobre un cuerpo, que son álgebras simples (no tienen ideales bilaterales no triviales, al igual que los cuerpos) cuyo centro es exactamente el cuerpo, son un análogo no conmutativo de los cuerpos de extensión y son más restrictivos que las extensiones de anillo generales. El hecho de que los cuaterniones sean el único anillo de dimensión finita no trivial sobre los números reales (hasta la equivalencia) puede compararse con el hecho de que los números complejos son la única extensión de cuerpo finito no trivial de los números reales.
Citas
Lo considero una inelegancia o imperfección en los cuaterniones, o más bien en el estado en el que se ha desarrollado hasta ahora, siempre que se hace o parece hacerse necesario recurrir a x, y, z, etc.
— William Rowan Hamilton ( c. 1848 ) [44]
Se dice que el tiempo tiene sólo una dimensión y el espacio tiene tres dimensiones. ... El cuaternión matemático participa de ambos elementos; en lenguaje técnico se puede decir que es "tiempo más espacio", o "espacio más tiempo": Y en este sentido tiene, o al menos implica una referencia a, cuatro dimensiones. ... Y cómo el Uno del Tiempo, el Tres del Espacio, Podrían estar rodeados en la Cadena de Símbolos .
— William Rowan Hamilton ( c. 1853 ) [45]
Los cuaterniones surgieron de Hamilton después de que se realizó su muy buen trabajo; y, aunque son maravillosamente ingeniosos, han sido un mal absoluto para aquellos que los han tocado de alguna manera, incluido Clerk Maxwell .
— W. Thompson, Lord Kelvin (1892) [46]
Hubo un tiempo, de hecho, en que yo, aunque reconocía la idoneidad del análisis vectorial en la teoría electromagnética (y en la física matemática en general), pensaba que era más difícil de entender y de trabajar que el análisis cartesiano. Pero eso fue antes de que me hubiera quitado de encima al viejo marino cuaterniónico que se me pegaba a los hombros cuando leía el único tratado accesible sobre el tema: Quaternions del profesor Tait . Pero más tarde llegué a ver que, en lo que respecta al análisis vectorial que necesitaba, el cuaternión no sólo no era necesario, sino que era un mal positivo de una magnitud nada desdeñable; y que al evitarlo se hizo bastante simple el establecimiento del análisis vectorial y también se simplificó su funcionamiento, y que podía armonizarse convenientemente con el trabajo cartesiano ordinario. No hay ni un rastro de cuaternión en ninguno de mis artículos (excepto en uno, para un propósito especial). El análisis vectorial que utilizo puede describirse como una abreviatura conveniente y sistemática del análisis cartesiano; o bien, como cuaterniones sin los cuaterniones, ... . "Cuaternión" fue, creo, definido por una colegiala americana como "una antigua ceremonia religiosa" . Sin embargo, esto fue un completo error: los antiguos -a diferencia del profesor Tait- no conocían ni adoraban los cuaterniones.
—Oliver Heaviside (1893) [47]
Ni las matrices, ni los cuaterniones, ni los vectores ordinarios fueron desterrados de estos diez capítulos [adicionales]. Porque, a pesar del poder indiscutible del cálculo tensorial moderno, esos lenguajes matemáticos más antiguos continúan, en mi opinión, ofreciendo ventajas notables en el campo restringido de la relatividad especial. Además, tanto en la ciencia como en la vida cotidiana, el dominio de más de un lenguaje también es valioso, ya que amplía nuestras perspectivas, conduce a la crítica con respecto a la materia expresada por palabras o símbolos matemáticos y nos protege contra la hipostasis [fundamento débil] de la misma.
— Ludwik Silberstein (1924) [48]
... los cuaterniones parecen exudar un aire de decadencia del siglo XIX, como una especie bastante fracasada en la lucha por la supervivencia de las ideas matemáticas. Es cierto que los matemáticos aún guardan un cálido lugar en sus corazones para las notables propiedades algebraicas de los cuaterniones, pero, por desgracia, tal entusiasmo significa poco para los científicos físicos más testarudos.
— Simon L. Altmann (1986) [49]
Véase también
- Conversión entre cuaterniones y ángulos de Euler – Estrategia matemática
- Cuaternión dual : álgebra de ocho dimensiones sobre los números reales
- Números complejos duales : álgebra de cuatro dimensiones sobre los números realesPages displaying short descriptions of redirect targets
- Álgebra exterior – Álgebra de productos exteriores/cuñas
- Orden de cuaterniones de Hurwitz : concepto en matemáticas
- Cuaternión hiperbólico : mutación de cuaterniones donde los vectores unitarios se elevan al cuadrado a +1
- Esfera de Lénárt : esfera transparente de borrado en seco que se utiliza para enseñar geometría esférica
- Matrices de Pauli : matrices importantes en la mecánica cuántica y el estudio del espín
- Variedad cuaterniónica : concepto en geometría
- Matriz cuaterniónica : concepto de álgebra lineal
- Politopo cuaterniónico : concepto en geometría
- Espacio proyectivo cuaterniónico – Concepto en matemáticas
- Rotaciones en el espacio euclidiano de cuatro dimensiones – Grupo ortogonal especial
- Slerp – Interpolación lineal esférica en gráficos por computadora
- Cuaternión dividido : álgebra asociativa de cuatro dimensiones sobre los números reales
- Tesseract : análogo cuatridimensional del cubo
Notas
- ^ Joachim Lambek escribió en 1995 una visión más personal de los cuaterniones. En su ensayo If Hamilton had prevalenced: Quaternions in physics (Si Hamilton hubiera prevalecido: los cuaterniones en la física) , escribió : "Mi propio interés como estudiante de posgrado se vio despertado por el inspirador libro de Silberstein". Concluyó afirmando: "Creo firmemente que los cuaterniones pueden proporcionar un atajo para los matemáticos puros que deseen familiarizarse con ciertos aspectos de la física teórica". Lambek, J. (1995). "If Hamilton had prevalenced: Quaternions in physics" (Si Hamilton hubiera prevalecido: los cuaterniones en la física). Math. Intelligencer . Vol. 17, no. 4. págs. 7–15. doi :10.1007/BF03024783.
- ^ La parte vectorial de un cuaternión es un vector "axial" o " pseudovector ", no un vector ordinario o "polar", como demostró formalmente Altmann (1986). [23] Un vector polar puede representarse en cálculos (por ejemplo, para la rotación mediante una "transformación de similitud" de cuaternión) mediante un cuaternión imaginario puro, sin pérdida de información, pero no deben confundirse los dos. El eje de un cuaternión de rotación "binario" (180°) corresponde a la dirección del vector polar representado en tal caso.
- ^ En comparación, los números reales tienen dimensión 1, los números complejos tienen dimensión 2 y los octoniones tienen dimensión 8.
- ^ La identificación de las raíces cuadradas de menos uno en fue dada por Hamilton [33] pero fue omitida frecuentemente en otros textos. En 1971, la esfera fue incluida por Sam Perlis en su exposición de tres páginas incluida en Historical Topics in Algebra publicado por el National Council of Teachers of Mathematics . [34] Más recientemente, la esfera de raíces cuadradas de menos uno se describe en el libro de Ian R. Porteous Clifford Algebras and the Classical Groups (Cambridge, 1995) en la proposición 8.13. [35]
- ^ Los libros sobre matemáticas aplicadas, como Corke (2017) [38], a menudo utilizan una notación diferente con φ := 1/2 θ — es decir, otra variable θ = 2 φ .
Referencias
- ^ "Sobre los cuaterniones; o sobre un nuevo sistema de imaginarios en álgebra". Carta a John T. Graves . 17 de octubre de 1843.
- ^ Rozenfelʹd, Boris Abramovich (1988). Historia de la geometría no euclidiana: evolución del concepto de espacio geométrico. Springer. pág. 385. ISBN 9780387964584.
- ^ Hamilton. Hodges y Smith. 1853. p. 60.
líneas de cociente de cuaterniones espacio-tiempo tridimensional
- ^ Hardy 1881. Ginn, Heath y compañía. 1881. pág. 32.ISBN 9781429701860.
- ^ Curtis, Morton L. (1984), Matrix Groups (2ª ed.), Nueva York: Springer-Verlag , p. 10, ISBN 978-0-387-96074-6
- ^ ab Mamone, Salvatore; Pileio, Giuseppe; Levitt, Malcolm H. (2010). "Esquemas de muestreo orientacional basados en politopos de cuatro dimensiones". Symmetry . 2 (3): 1423–1449. Bibcode :2010Symm....2.1423M. doi : 10.3390/sym2031423 .
- ^ Kunze, Karsten; Schaeben, Helmut (noviembre de 2004). "La distribución de Bingham de cuaterniones y su transformación esférica de radón en el análisis de textura". Geología matemática . 36 (8): 917–943. Bibcode :2004MatGe..36..917K. doi :10.1023/B:MATG.0000048799.56445.59. S2CID 55009081.
- ^ Smith, Frank (Tony). "¿Por qué no sedenion?" . Consultado el 8 de junio de 2018 .
- ^ abc Véase Hazewinkel, Gubareni y Kirichenko 2004, p. 12
- ^ Conway y Smith 2003, pág. 9
- ^ Bradley, Robert E.; Sandifer, Charles Edward (2007). Leonhard Euler: vida, obra y legado. Elsevier. pág. 193. ISBN 978-0-444-52728-8.Mencionan la afirmación de Wilhelm Blaschke en 1959 de que "los cuaterniones fueron identificados por primera vez por L. Euler en una carta a Goldbach escrita el 4 de mayo de 1748", y comentan que "no tiene ningún sentido decir que Euler "identificó" los cuaterniones en esta carta... esta afirmación es absurda".
- ^ Pujol, J., "Hamilton, Rodrigues, Gauss, cuaterniones y rotaciones: una reevaluación histórica" Communications in Mathematical Analysis (2012), 13(2), 1–14
- ^ Gauss, CF (1900). "Mutationen des Raumes [Transformaciones del espacio] (c. 1819)". En Martín Brendel (ed.). Carl Friedrich Gauss Werke [ Las obras de Carl Friedrich Gauss ]. vol. 8. artículo editado por el Prof. Stäckel de Kiel, Alemania. Göttingen, DE: Königlichen Gesellschaft der Wissenschaften [Real Sociedad de Ciencias]. págs. 357–361.
- ^ ab Hamilton, WR (1844). "Carta". Revista filosófica y revista científica de Londres, Edimburgo y Dublín . Vol. xxv. págs. 489–495.
- ^ Hamilton, Sir WR (1866). Hamilton, WE (ed.). Elementos de los cuaterniones. Londres: Longmans, Green, & Co.
- ^ ab Shoemake, Ken (1985). "Animación de rotación con curvas de cuaternión" (PDF) . Gráficos por ordenador . 19 (3): 245–254. doi :10.1145/325165.325242.Presentado en SIGGRAPH '85.
- ^ Tomb Raider (1996) suele citarse como el primer juego de ordenador de gran consumo que utilizó cuaterniones para lograr rotaciones tridimensionales suaves. Véase, por ejemplo, Nick Bobick (julio de 1998). "Rotación de objetos mediante cuaterniones". Game Developer .
- ^ McCarthy, JM (1990). Introducción a la cinemática teórica. MIT Press. ISBN 978-0-262-13252-7.
- ^ Hurwitz, A. (1919), Vorlesungen über die Zahlentheorie der Quaternionen , Berlín: J. Springer, JFM 47.0106.01, sobre los cuaterniones de Hurwitz
- ^ Huerta, John (27 de septiembre de 2010). "Introducing The Quaternions" (PDF) . Archivado (PDF) desde el original el 21 de octubre de 2014. Consultado el 8 de junio de 2018 .
- ^ Wood, Charlie (6 de septiembre de 2018). "Los números extraños que dieron origen al álgebra moderna". Blog de abstracciones . Revista Quanta.
- ^ Evas (1976, pág. 391)
- ^ Altmann, SL Rotaciones, cuaterniones y grupos dobles . Cap. 12.
- ^ Hamilton, Sir William Rowan (1866). "Artículo 285". Elementos de los cuaterniones. Longmans, Green, & Company. pág. 310.
- ^ Hardy (1881). "Elementos de los cuaterniones". Science . 2 (75). library.cornell.edu: 65. doi :10.1126/science.os-2.75.564. PMID 17819877.
- ^ "grupo de cuaterniones". Wolframalpha.com .
- ^ Gibbs, J. Willard; Wilson, Edwin Bidwell (1901). Análisis vectorial. Yale University Press. pág. 428.
Tensor derecho diádico
- ^ ab Hamilton, WR (1844–1850). "Sobre los cuaterniones o un nuevo sistema de imaginarios en álgebra". Colección de David R. Wilkins. Philosophical Magazine . Trinity College Dublin .
- ^ "Visualización de cuaterniones". Morgan-Kaufmann/Elsevier. 2005.
- ^ "[sin título citado; evaluación determinante]". Wolframalpha.com .
- ^ p. ej. Altmann (1986), Rotaciones, cuaterniones y grupos dobles , pág. 212, ecuación 5
- ^ Hermano lejano, Richard William; Groß, Jürgen; Troschke, Sven-Oliver (2003). "Representación matricial de cuaterniones". Álgebra lineal y sus aplicaciones . 362 : 251–255. doi : 10.1016/s0024-3795(02)00535-9 .
- ^ Hamilton, WR (1899). Elementos de cuaterniones (2.ª ed.). Cambridge University Press. pág. 244. ISBN 1-108-00171-8.
- ^ Perlis, Sam (1971). "Cápsula 77: Cuaterniones" . Temas históricos en álgebra . Temas históricos para el aula de matemáticas. Vol. 31. Reston, VA: Consejo Nacional de Profesores de Matemáticas . pág. 39. ISBN. 9780873530583.OCLC 195566 .
- ^ Porteous, Ian R. (1995). "Capítulo 8: Cuaterniones". Álgebras de Clifford y grupos clásicos (PDF) . Cambridge Studies in Advanced Mathematics. Vol. 50. Cambridge: Cambridge University Press . pág. 60. doi :10.1017/CBO9780511470912.009. ISBN . 9780521551779. Sr. 1369094. OCLC 32348823.
- ^ "[sin título citado]" (PDF) . bridgesmathart.org . archive . Consultado el 19 de agosto de 2018 .
- ^ ab Särkkä, Simo (28 de junio de 2007). «Notes on Quaternions» (PDF) . Lce.hut.fi . Archivado desde el original (PDF) el 5 de julio de 2017.
- ^ Corke, Peter (2017). Robótica, visión y control: algoritmos fundamentales en MATLAB . Springer . ISBN. 978-3-319-54413-7.
- ^ Park, FC; Ravani, Bahram (1997). "Interpolación invariante suave de rotaciones". ACM Transactions on Graphics . 16 (3): 277–295. doi : 10.1145/256157.256160 . S2CID 6192031.
- ^ Hanson, Jason (2011). "Rotaciones en tres, cuatro y cinco dimensiones". arXiv : 1103.5263 [math.MG].
- ^ Günaşti, Gökmen (2016). Álgebra de cuaterniones, sus aplicaciones en rotaciones y más allá de los cuaterniones (BS). Universidad Linnaeus.
- ^ "Grupos de puntos tridimensionales". www.classe.cornell.edu . Consultado el 9 de diciembre de 2022 .
- ^ "Cuaterniones y álgebra geométrica". geometryalgebra.net . Consultado el 12 de septiembre de 2008 .Véanse también: Dorst, Leo; Fontijne, Daniel; Mann, Stephen (2007). Álgebra geométrica para informática. Morgan Kaufman . ISBN 978-0-12-369465-2.
- ^ Hamilton, WR (1853). Lecciones sobre cuaterniones. Dublin, IE: Hodges & Smith. p. 522.
- ^ Graves, RP Vida de Sir William Rowan Hamilton. Dublin Hodges, Figgis. págs. 635–636.
- ^ Thompson, Silvanus Phillips (1910). La vida de William Thomson. Vol. 2. Londres, Reino Unido: Macmillan. pág. 1138.
- ^ Heaviside, Oliver (1893). Teoría electromagnética. Vol. I. Londres, Reino Unido: The Electrician Printing and Publishing Company. págs. 134-135.
- ^ Silberstein, Ludwik (1924). "Prefacio a la segunda edición". La teoría de la relatividad (2.ª ed.).
- ^ Altmann, Simon L. (1986). Rotaciones, cuaterniones y grupos dobles . Clarendon Press. ISBN 0-19-855372-2. Número de LCCN : 85013615.
Lectura adicional
Libros y publicaciones
- Hamilton, William Rowan (1844). "Sobre los cuaterniones, o sobre un nuevo sistema de imaginarios en álgebra". Revista filosófica . 25 (3): 489–495. doi :10.1080/14786444408645047.
- Hamilton, William Rowan (1853), " Conferencias sobre cuaterniones ". Real Academia Irlandesa.
- Hamilton (1866) Elements of Quaternions (Elementos de cuaterniones) , University of Dublin Press, editado por William Edwin Hamilton, hijo del autor fallecido.
- Hamilton (1899) Elements of Quaternions volumen I, (1901) volumen II. Editado por Charles Jasper Joly ; publicado por Longmans, Green & Co.
- Tait, Peter Guthrie (1873), " Un tratado elemental sobre cuaterniones ". 2a ed., Cambridge, [Eng.] : The University Press.
- Maxwell, James Clerk (1873), " Un tratado sobre electricidad y magnetismo ". Clarendon Press, Oxford.
- Tait, Peter Guthrie (1886), " "Copia archivada". Archivado desde el original el 8 de agosto de 2014 . Consultado el 26 de junio de 2005 .
{{cite web}}: CS1 maint: archived copy as title (link) CS1 maint: unfit URL (link)". MA Sec. RSE Encyclopædia Britannica , Novena edición, 1886, vol. XX, págs. 160-164. ( archivo PostScript comprimido) - Joly, Charles Jasper (1905). Un manual de cuaterniones . Macmillan. LCCN 05036137.
- Macfarlane, Alexander (1906). Análisis vectorial y cuaterniones (4.ª ed.). Wiley. LCCN 16000048.
- Chisholm, Hugh , ed. (1911). . Encyclopædia Britannica (11.ª ed.). Cambridge University Press.( Ver sección sobre cuaterniones ) .
- Finkelstein, David; Jauch, Josef M.; Schiminovich, Samuel; Speiser, David (1962). "Fundamentos de la mecánica cuántica de cuaterniones". J. Math. Phys . 3 (2): 207–220. Bibcode :1962JMP.....3..207F. doi :10.1063/1.1703794. S2CID 121453456.
- Du Val, Patrick (1964). Homografías, cuaterniones y rotaciones . Monografías matemáticas de Oxford. Clarendon Press. LCCN 64056979.
- Michael J. Crowe (1967), A History of Vector Analysis : The Evolution of the Idea of a Vectorial System , University of Notre Dame Press. Examina los sistemas vectoriales mayores y menores del siglo XIX (Hamilton, Möbius, Bellavitis, Clifford, Grassmann, Tait, Peirce, Maxwell, Macfarlane, MacAuley, Gibbs, Heaviside).
- Altmann, Simon L. (1989). "Hamilton, Rodrigues y el escándalo de los cuaterniones". Revista de Matemáticas . 62 (5): 291–308. doi :10.1080/0025570X.1989.11977459.
- Pujol, Jose (2014). "Sobre el trabajo temprano casi olvidado de Hamilton sobre la relación entre rotaciones y cuaterniones y sobre la composición de rotaciones". The American Mathematical Monthly . 121 (6): 515–522. doi :10.4169/amer.math.monthly.121.06.515. S2CID 1543951.
- Adler, Stephen L. (1995). Mecánica cuántica cuaterniónica y campos cuánticos . Serie internacional de monografías sobre física. Vol. 88. Oxford University Press. ISBN 0-19-506643-X. Número de serie LCCN 94006306.
- Ward, JP (1997). Cuaterniones y números de Cayley: álgebra y aplicaciones . Kluwer Academic. ISBN 0-7923-4513-4.
- Kantor, IL; Solodnikov, AS (1989). Números hipercomplejos, una introducción elemental a las álgebras . Springer-Verlag. ISBN 0-387-96980-2.
- Gürlebeck, Klaus; Sprössig, Wolfgang (1997). Cálculo cuaterniónico y de Clifford para físicos e ingenieros . Métodos matemáticos en la práctica. Vol. 1. Wiley. ISBN 0-471-96200-7. Número de serie LCCN 98169958.
- Kuipers, Jack (2002). Cuaterniones y secuencias de rotación: una introducción con aplicaciones a las órbitas, la industria aeroespacial y la realidad virtual . Princeton University Press . ISBN 0-691-10298-8.
- Conway, John Horton ; Smith, Derek A. (2003). Sobre cuaterniones y octoniones: su geometría, aritmética y simetría . AK Peters. ISBN 1-56881-134-9.(revisar).
- Jack, PM (2003). "El espacio físico como estructura de cuaterniones, I: ecuaciones de Maxwell. Una breve nota". arXiv : math-ph/0307038 .
- Kravchenko, Vladislav (2003). Análisis cuaterniónico aplicado . Heldermann Verlag. ISBN 3-88538-228-8.
- Hazewinkel, Michiel ; Gubareni, Nadiya; Kirichenko, Vladimir V. (2004). Álgebras, anillos y módulos. vol. 1. Saltador. ISBN 1-4020-2690-0.
- Hanson, Andrew J. (2006). Visualización de cuaterniones. Elsevier. ISBN 0-12-088400-3.
- Binz, Ernst; Pods, Sonja (2008). "1. El campo sesgado de los cuaterniones". Geometría de los grupos de Heisenberg . American Mathematical Society . ISBN 978-0-8218-4495-3.
- Doran, Chris JL ; Lasenby, Anthony N. (2003). Álgebra geométrica para físicos . Cambridge University Press. ISBN 978-0-521-48022-2.
- Vince, John A. (2008). Álgebra geométrica para gráficos por computadora . Springer. ISBN 978-1-84628-996-5.
- Para las moléculas que pueden considerarse cuerpos rígidos clásicos, la simulación por ordenador de dinámica molecular emplea cuaterniones. Fueron introducidos por primera vez con este fin por Evans, DJ (1977). "Sobre la representación del espacio de orientación". Mol. Phys . 34 (2): 317–325. Bibcode :1977MolPh..34..317E. doi :10.1080/00268977700101751.
- Zhang, Fuzhen (1997). "Cuaterniones y matrices de cuaterniones". Álgebra lineal y sus aplicaciones . 251 : 21–57. doi : 10.1016/0024-3795(95)00543-9 .
- Ron Goldman (2010). Replanteamiento de los cuaterniones: teoría y computación . Morgan & Claypool. ISBN 978-1-60845-420-4.
- Eves, Howard (1976), Introducción a la historia de las matemáticas (4.ª ed.), Nueva York: Holt, Rinehart y Winston , ISBN 0-03-089539-1
- Voight, John (2021). Álgebras de cuaterniones . Textos de posgrado en matemáticas. Vol. 288. Springer. doi : 10.1007/978-3-030-56694-4 . ISBN. 978-3-030-57467-3.
Enlaces y monografías
- "Avisos de cuaternión".Avisos y materiales relacionados con las presentaciones de la conferencia Quaternion
- "Cuaternión", Enciclopedia de Matemáticas , EMS Press , 2001 [1994]
- "Preguntas frecuentes". Matriz y cuaternión . 1.21.
- Sweetser, Doug. "Hacer física con cuaterniones".
- Cuaterniones para gráficos y mecánica de computadoras (Gernot Hoffman)
- Gsponer, Andre; Hurni, Jean-Pierre (2002). "El patrimonio físico de Sir WR Hamilton". arXiv : math-ph/0201058 .
- Wilkins, DR "La investigación de Hamilton sobre los cuaterniones".
- Grossman, David J. "Fractales de Julia del cuaternión".Fractales de Julia de cuaternión con trazado de rayos en 3D
- "Matemáticas y conversiones de cuaterniones".Excelente página que explica matemáticas básicas con enlaces a fórmulas de conversión de rotación directa.
- Mathews, John H. "Bibliografía sobre cuaterniones". Archivado desde el original el 2 de septiembre de 2006.
- "Poderes del cuaternión". GameDev.net.
- Hanson, Andrew. "Visualizing Quaternions home page". Archivado desde el original el 5 de noviembre de 2006.
- Karney, Charles FF (enero de 2007). "Cuaterniones en modelado molecular". J. Mol. Graph. Mod . 25 (5): 595–604. arXiv : physics/0506177 . doi :10.1016/j.jmgm.2006.04.002. PMID 16777449. S2CID 6690718.
- Mebius, Johan E. (2005). "Una prueba basada en matrices del teorema de representación de cuaterniones para rotaciones de cuatro dimensiones". arXiv : math/0501249 .
- Mebius, Johan E. (2007). "Derivación de la fórmula de Euler-Rodrigues para rotaciones tridimensionales a partir de la fórmula general para rotaciones tetradimensionales". arXiv : math/0701759 .
- "Hamilton Walk". Departamento de Matemáticas, NUI Maynooth .
- "Uso de cuaterniones para representar la rotación". OpenGL:Tutorials . Archivado desde el original el 15 de diciembre de 2007.
- David Erickson, Investigación y Desarrollo de Defensa de Canadá (DRDC), Derivación completa de la matriz de rotación a partir de la representación de cuaternión unitario en el artículo DRDC TR 2005-228.
- Martínez, Alberto. "Matemáticas negativas: cómo las reglas matemáticas pueden modificarse positivamente". Departamento de Historia, Universidad de Texas. Archivado desde el original el 24 de septiembre de 2011.
- Stahlke, D. "Cuaterniones en la mecánica clásica" (PDF) .
- Morier-Genoud, Sophie; Ovsienko, Valentin (2008). "Bueno, papá, ¿puedes multiplicar tripletes?". arXiv : 0810.5562 [math.AC].describe cómo los cuaterniones pueden convertirse en un álgebra conmutativa anticuada graduada por Z /2 × Z /2 × Z /2 .
- Joyce, Helen (noviembre de 2004). "Cuaterniones curiosos". Presentado por John Baez .
- Ibanez, Luis. "Tutorial sobre cuaterniones. Parte I" (PDF) . Archivado desde el original (PDF) el 2012-02-04 . Consultado el 2011-12-05 .Parte II (PDF; utilizando la terminología de Hamilton, que difiere del uso moderno)
- Ghiloni, R.; Moretti, V.; Perotti, A. (2013). "Cálculo funcional de rebanadas continuas en espacios de Hilbert cuaterniónicos". Rev. Math. Phys . 25 (4): 1350006–126. arXiv : 1207.0666 . Código Bibliográfico : 2013RvMaP..2550006G. doi : 10.1142/S0129055X13500062. S2CID 119651315.
Ghiloni, R.; Moretti, V.; Perotti, A. (2017). "Representaciones espectrales de operadores normales mediante medidas de proyección cuaterniónica entrelazadas". Rev. Math. Phys . 29 : 1750034. arXiv : 1602.02661 . doi :10.1142/S0129055X17500349. S2CID 124709652.Dos artículos expositivos sobre cálculo funcional continuo y teoría espectral en espacios de Hilbert cuaterniónicos útiles en mecánica cuántica cuaterniónica rigurosa. - Cuaterniones La aplicación de Android muestra el cuaternión correspondiente a la orientación del dispositivo.
- Artículo sobre rotación de objetos mediante cuaterniones que habla sobre el uso de cuaterniones para la rotación en videojuegos y gráficos de computadora.
Enlaces externos
 Medios relacionados con los cuaterniones en Wikimedia Commons
Medios relacionados con los cuaterniones en Wikimedia Commons- Paulson, Lawrence C. Quaternions (Desarrollo de pruebas formales en Isabelle/HOL, Archive of Formal Proofs)
- Cuaterniones – Visualización













![{\displaystyle {\begin{alineado}&(a_{1}+b_{1}\mathbf {i} +c_{1}\mathbf {j} +d_{1}\mathbf {k} )+(a_{ 2}+b_{2}\mathbf {i} +c_{2}\mathbf {j} +d_{2}\mathbf {k} )\\[3mu]&\qquad =(a_{1}+a_{ 2})+(b_{1}+b_{2})\mathbf {i} +(c_{1}+c_{2})\mathbf {j} +(d_{1}+d_{2})\ mathbf {k},\end{alineado}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1e0eaf2c87bb1c97099a2140d0bb051a5d4a5604)



![{\displaystyle {\begin{aligned}\mathbf {i} ^{2}&=\mathbf {j} ^{2}=\mathbf {k} ^{2}=-1,\\[5mu]\mathbf {i\,j} &=-\mathbf {j\,i} =\mathbf {k} ,\qquad \mathbf {j\,k} =-\mathbf {k\,j} =\mathbf {i} ,\qquad \mathbf {k\,i} =-\mathbf {i\,k} =\mathbf {j}.\end{alineado}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/557dac211aa259b3cde6c0aa76d0125562a01c40)






(r_{2},\,{\vec {v}}_{2})&=(r_{1}r_{2}-{\vec {v}}_{1}\cdot {\vec {v}}_{2},\,r_{1}{\vec {v}}_{2}+r_{2}{\vec {v} }_{1}+{\vec {v}}_{1}\veces {\vec {v}}_{2}),\\[5mu](r,\,{\vec {v}})^{-1}&=\left({\frac {r}{r^{2} +{\vec {v}}\cdot {\vec {v}}}},\ {\frac {-{\vec {v}}}{r^{2}+{\vec {v}}\cdot {\vec {v}}}}\derecha),\end{alineado}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/af3b95c2bc8ca03f3f3eba649fd30351e7d69a19)



















![{\displaystyle \mathbb {R} [\mathrm {Q} _ {8}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/95e3ca1ed22f8ae5680236bb417a05d2e38886ae)








![{\displaystyle [p,q]=2p\times q.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c45178772ffab33a9936c42a9df2be320f5d22b8)
![{\displaystyle {\begin{aligned}p&=p_{\text{s}}+p_{\text{v}},\\[5mu]q&=q_{\text{s}}+q_{\text{v}},\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1ab7ef853cfa04d68fc3cd8add199f463e3eb1c8)













![{\displaystyle {\begin{aligned}\left[{\begin{array}{rrrr}a&-b&-c&-d\\b&a&-d&c\\c&d&a&-b\\d&-c&b&a\end{array}}\right]&=a\left[{\begin{array}{rrrr}1&0&0&0\\0&1&0&0\\0&0&1&0\\0&0&0&1\end{array}}\right]+b\left[{\begin{array}{rrrr}0&-1&0&0\\1&0&0&0\\0&0&0&-1\\0&0&1&0\end{array}}\right]\\[10mu]&\qquad +c\left[{\begin{array}{rrrr}0&0&-1&0\\0&0&0&1\\1&0&0&0\\0&-1&0&0\end{array}}\right]+d\left[{\begin{array}{rrrr}0&0&0&-1\\0&0&-1&0\\0&1&0&0\\1&0&0&0\end{array}}\right].\end{alineado}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e0f963faf6a3e52166e4f4421c4cbb7f5b111699)
![{\displaystyle {\begin{aligned}\left[{\begin{array}{rrrr}a&d&-b&-c\\-d&a&c&-b\\b&-c&a&-d\\c&b&d&a\end{array}}\right]&=a\left[{\begin{array}{rrrr}1&0&0&0\\0&1&0&0\\0&0&1&0\\0&0&0&1\end{array}}\right]+b\left[{\begin{array}{rrrr}0&0&-1&0\\0&0&0&-1\\1&0&0&0\\0&1&0&0\end{array}}\right]\\[10mu]&\qquad +c\left[{\begin{array}{rrrr}0&0&0&-1\\0&0&1&0\\0&-1&0&0\\1&0&0&0\end{array}}\right]+d\left[{\begin{array}{rrrr}0&1&0&0\\-1&0&0&0\\0&0&0&-1\\0&0&1&0\end{array}}\right].\end{alineado}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5cdb3a03c5a1b9df69d9244469a9344df49978ad)





![{\displaystyle {\begin{aligned}a^{2}-b^{2}-c^{2}-d^{2}&=-1,{\vphantom {x^{|}}}\\[3mu]2ab&=0,\\[3mu]2ac&=0,\\[3mu]2ad&=0.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2fff161699a746d453fc9110f35c86a9fbcb4164)














































