Covarianza y contravarianza de vectores

En física , especialmente en álgebra multilineal y análisis tensorial , la covarianza y la contravarianza describen cómo cambia la descripción cuantitativa de ciertas entidades geométricas o físicas con un cambio de base . ^[2] Brevemente, un vector contravariante es una lista de números que se transforma de manera opuesta a un cambio de base, y un vector covariante es una lista de números que se transforma de la misma manera. Los vectores contravariantes a menudo se denominan simplemente vectores y los vectores covariantes se denominan covectores o vectores duales . Los términos covariante y contravariante fueron introducidos por James Joseph Sylvester en 1851. ^{[3] [4]}

Los sistemas de coordenadas curvilíneas , como las coordenadas cilíndricas o esféricas , se utilizan a menudo en problemas físicos y geométricos. Asociada a cualquier sistema de coordenadas hay una elección natural de la base de coordenadas para los vectores basados ​​en cada punto del espacio, y la covarianza y la contravarianza son particularmente importantes para comprender cómo cambia la descripción de coordenadas de un vector al pasar de un sistema de coordenadas a otro. Los tensores son objetos del álgebra multilineal que pueden tener aspectos tanto de covarianza como de contravarianza.

En física, un vector normalmente surge como resultado de una medición o una serie de mediciones, y se representa como una lista (o tupla ) de números como

${\displaystyle (v_{1},v_{2},v_{3}).}$

Los números de la lista dependen del sistema de coordenadas elegido . Por ejemplo, si el vector representa la posición con respecto a un observador ( vector de posición ), entonces el sistema de coordenadas puede obtenerse a partir de un sistema de varillas rígidas, o ejes de referencia, a lo largo de los cuales se miden los componentes v ₁ , v ₂ y v ₃ . Para que un vector represente un objeto geométrico, debe ser posible describir cómo se ve en cualquier otro sistema de coordenadas. Es decir, los componentes de los vectores se transformarán de una determinada manera al pasar de un sistema de coordenadas a otro.

Un ejemplo sencillo es el de un vector euclidiano . Una vez que se ha definido un conjunto de vectores base para un vector, los componentes de ese vector siempre variarán en sentido opuesto al de los vectores base. Por lo tanto, ese vector se define como un tensor contravariante . Tomemos como ejemplo un vector de posición estándar. Al cambiar la escala de los ejes de referencia de metros a centímetros (es decir, dividiendo la escala de los ejes de referencia por 100, de modo que los vectores base ahora tengan una longitud de metros), los componentes del vector de posición medido se multiplican por 100. Los componentes de un vector cambian de escala de manera inversa a los cambios de escala de los ejes de referencia y, en consecuencia, un vector se denomina tensor contravariante . ${\estilo de visualización .01}$

Un vector , que es un ejemplo de un tensor contravariante , tiene componentes que se transforman inversamente a la transformación de los ejes de referencia (con transformaciones de ejemplo que incluyen rotación y dilatación ). El vector en sí no cambia bajo estas operaciones ; en cambio, los componentes del vector cambian de una manera que cancela el cambio en los ejes espaciales. En otras palabras, si los ejes de referencia se rotaran en una dirección, la representación del componente del vector rotaría exactamente en la dirección opuesta. De manera similar, si los ejes de referencia se estiraran en una dirección, los componentes del vector se reducirían de una manera exactamente compensatoria. Matemáticamente, si el sistema de coordenadas sufre una transformación descrita por una matriz invertible M , de modo que los vectores base se transforman de acuerdo con , entonces los componentes de un vector v en la base original ( ) deben transformarse de manera similar mediante . Los componentes de un vector a menudo se representan dispuestos en una columna. ${\displaystyle n\veces n}$ ${\displaystyle {\begin{bmatrix}\mathbf {e} _{1}^{\prime }\ \mathbf {e} _{2}^{\prime }\ ...\ \mathbf {e} _{ n}^{\prime }\end{bmatrix}}={\begin{bmatrix}\mathbf {e} _{1}\ \mathbf {e} _{2}\ ...\ \mathbf {e} _ {n}\end{bmatrix}}M}$${\displaystyle v^{i}}$${\displaystyle {\begin{bmatrix}v^{1}{^{\prime }}\\v^{2}{^{\prime }}\\...\\v^{n}{^{ \prime }}\end{bmatrix}}=M^{-1}{\begin{bmatrix}v^{1}\\v^{2}\\...\\v^{n}\end{ matrizb}}}$

Por el contrario, un covector tiene componentes que se transforman como los ejes de referencia. Vive en el espacio vectorial dual y representa una función lineal de vectores a escalares. El operador de producto escalar que involucra vectores es un buen ejemplo de un covector. Para ilustrarlo, supongamos que tenemos un covector definido como , donde es un vector. Los componentes de este covector en alguna base arbitraria son , siendo los vectores base en el espacio vectorial correspondiente. (Esto se puede derivar notando que queremos obtener la respuesta correcta para la operación de producto escalar al multiplicar por un vector arbitrario , con componentes ). La covarianza de estos componentes del covector se ve entonces notando que si una transformación descrita por una matriz invertible M se aplicara a los vectores base en el espacio vectorial correspondiente, , entonces los componentes del covector se transformarán con la misma matriz , es decir, . Los componentes de un covector a menudo se representan dispuestos en una fila. ${\displaystyle \mathbf {v} \ \cdot }$${\displaystyle \mathbf {v}}$${\displaystyle {\begin{bmatrix}\mathbf {v} \cdot \mathbf {e} _{1}&\mathbf {v} \cdot \mathbf {e} _{2}&...&\mathbf { v} \cdot \mathbf {e} _ {n}\end{bmatrix}}}$${\displaystyle {\begin{bmatrix}\mathbf {e} _{1}\ \mathbf {e} _{2}\ ...\ \mathbf {e} _{n}\end{bmatrix}}}$${\displaystyle \mathbf {w} }$${\displaystyle {\begin{bmatrix}w^{1}\\w^{2}\\...\\w^{n}\end{bmatrix}}}$${\displaystyle n\times n}$ ${\displaystyle {\begin{bmatrix}\mathbf {e} _{1}^{\prime }\ \mathbf {e} _{2}^{\prime }\ ...\ \mathbf {e} _{n}^{\prime }\end{bmatrix}}={\begin{bmatrix}\mathbf {e} _{1}\ \mathbf {e} _{2}\ ...\ \mathbf {e} _{n}\end{bmatrix}}M}$${\displaystyle \mathbf {v} \ \cdot }$${\displaystyle M}$${\displaystyle {\begin{bmatrix}\mathbf {v} \cdot \mathbf {e} _{1}^{\prime }&\mathbf {v} \cdot \mathbf {e} _{2}^{\prime }&...&\mathbf {v} \cdot \mathbf {e} _{n}^{\prime }\end{bmatrix}}={\begin{bmatrix}\mathbf {v} \cdot \mathbf {e} _{1}&\mathbf {v} \cdot \mathbf {e} _{2}&...&\mathbf {v} \cdot \mathbf {e} _{n}\end{bmatrix}}M}$

Un tercer concepto relacionado con la covarianza y la contravarianza es la invariancia . Un escalar (también llamado tensor de tipo 0 o de rango 0) es un objeto que no varía con el cambio de base. Un ejemplo de un observable físico que es un escalar es la masa de una partícula. El valor único escalar de la masa es independiente de los cambios en los vectores de base y, en consecuencia, se denomina invariante . La magnitud de un vector (como la distancia ) es otro ejemplo de invariante, porque permanece fija incluso si varían los componentes geométricos del vector. (Por ejemplo, para un vector de posición de longitud metros, si todos los vectores de base cartesianos cambian de longitud metros a metros, la longitud del vector de posición permanece sin cambios en metros, aunque los componentes del vector aumentarán todos en un factor de ). El producto escalar de un vector y un covector es invariante, porque uno tiene componentes que varían con el cambio de base y el otro tiene componentes que varían de manera opuesta, y los dos efectos se cancelan. Por lo tanto, se dice que los covectores son duales a los vectores.${\displaystyle 3}$${\displaystyle 1}$${\displaystyle .01}$${\displaystyle 3}$${\displaystyle 100}$

Así pues, para resumir:

• Un vector o vector tangente tiene componentes que contravarían con un cambio de base para compensar. Es decir, la matriz que transforma los componentes del vector debe ser la inversa de la matriz que transforma los vectores de base. Se dice que los componentes de los vectores (a diferencia de los de los covectores) son contravariantes . En la notación de Einstein (suma implícita sobre índice repetido), los componentes contravariantes se denotan con índices superiores como en

  ${\displaystyle \mathbf {v} =v^{i}\mathbf {e} _{i}}$

• Un covector o vector cotangente tiene componentes que covarían con un cambio de base en el espacio vectorial (inicial) correspondiente. Es decir, los componentes deben ser transformados por la misma matriz que la matriz de cambio de base en el espacio vectorial (inicial) correspondiente. Se dice que los componentes de los covectores (a diferencia de los de los vectores) son covariantes . En la notación de Einstein , los componentes covariantes se denotan con índices más bajos como en

  ${\displaystyle \mathbf {w} =w_{i}\mathbf {e} ^{i}.}$

• El producto escalar de un vector y un covector es el escalar , que es invariante. Es el emparejamiento dual de vectores y covectores.${\displaystyle v^{i}w_{i}}$

La formulación general de covarianza y contravarianza se refiere a cómo los componentes de un vector de coordenadas se transforman bajo un cambio de base ( transformación pasiva ). Por lo tanto, sea V un espacio vectorial de dimensión n sobre un cuerpo de escalares S , y sea cada uno de f = ( X ₁ , ..., X _n ) y f ′ = ( Y ₁ , ..., Y _n ) una base de V. ^{[nota 1]} Además, sea que el cambio de base de f a f ′ esté dado por

${\displaystyle \mathbf {f} \mapsto \mathbf {f} '={\biggl (}\sum _{i}a_{1}^{i}X_{i},\dots ,\sum _{i}a_{n}^{i}X_{i}{\biggr )}=\mathbf {f} A}$

( 1 )

para una matriz A invertible de n × n con entradas . Aquí, cada vector Y _j de la base f ′ es una combinación lineal de los vectores X _i de la base f , de modo que${\displaystyle a_{j}^{i}}$

${\displaystyle Y_{j}=\sum _{i}a_{j}^{i}X_{i}.}$

Un vector en V se expresa únicamente como una combinación lineal de los elementos de la base f como${\displaystyle v}$${\displaystyle X_{i}}$

${\displaystyle v=\sum _{i}v^{i}[\mathbf {f} ]X_{i},}$

( 2 )

donde v ⁱ [ f ] son ​​elementos del campo S conocidos como los componentes de v en la base f . Denotemos el vector columna de componentes de v por v [ f ]:

${\displaystyle \mathbf {v} [\mathbf {f} ]={\begin{bmatrix}v^{1}[\mathbf {f} ]\\v^{2}[\mathbf {f} ]\\\vdots \\v^{n}[\mathbf {f} ]\end{bmatrix}}}$

de modo que ( 2 ) puede reescribirse como un producto matricial

${\displaystyle v=\mathbf {f} \,\mathbf {v} [\mathbf {f} ].}$

El vector v también puede expresarse en términos de la base f ′, de modo que

${\displaystyle v=\mathbf {f'} \,\mathbf {v} [\mathbf {f'} ].}$

Sin embargo, dado que el vector v en sí mismo es invariante bajo la elección de la base,

${\displaystyle \mathbf {f} \,\mathbf {v} [\mathbf {f} ]=v=\mathbf {f'} \,\mathbf {v} [\mathbf {f'} ].}$

La invariancia de v combinada con la relación ( 1 ) entre f y f ′ implica que

${\displaystyle \mathbf {f} \,\mathbf {v} [\mathbf {f} ]=\mathbf {f} A\,\mathbf {v} [\mathbf {f} A],}$

dando la regla de transformación

${\displaystyle \mathbf {v} [\mathbf {f'} ]=\mathbf {v} [\mathbf {f} A]=A^{-1}\mathbf {v} [\mathbf {f} ].}$

En términos de componentes,

${\displaystyle v^{i}[\mathbf {f} A]=\sum _{j}{\tilde {a}}_{j}^{i}v^{j}[\mathbf {f} ]}$

donde los coeficientes son las entradas de la matriz inversa de A .${\displaystyle {\tilde {a}}_{j}^{i}}$

Debido a que los componentes del vector v se transforman con la inversa de la matriz A , se dice que estos componentes se transforman contravariantemente bajo un cambio de base.

La forma en que A relaciona los dos pares se representa en el siguiente diagrama informal mediante una flecha. La inversión de la flecha indica un cambio contravariante:

${\displaystyle {\begin{aligned}\mathbf {f} &\longrightarrow \mathbf {f'} \\v[\mathbf {f} ]&\longleftarrow v[\mathbf {f'} ]\end{aligned}}}$

Un funcional lineal α en V se expresa únicamente en términos de sus componentes (elementos en S ) en la base f como

${\displaystyle \alpha (X_{i})=\alpha _{i}[\mathbf {f} ],\quad i=1,2,\dots ,n.}$

Estos componentes son la acción de α _sobre los vectores base Xi de la base f .

Bajo el cambio de base de f a f ′ (a través de 1 ), los componentes se transforman de manera que

${\displaystyle {\begin{aligned}\alpha _{i}[\mathbf {f} A]&=\alpha (Y_{i})\\&=\alpha {\biggl (}\sum _{j}a_{i}^{j}X_{j}{\biggr )}\\&=\sum _{j}a_{i}^{j}\alpha (X_{j})\\&=\sum _{j}a_{i}^{j}\alpha _{j}[\mathbf {f} ].\end{aligned}}}$

( 3 )

Denotemos el vector fila de componentes de α por α [ f ]:

${\displaystyle \mathbf {\alpha } [\mathbf {f} ]={\begin{bmatrix}\alpha _{1}[\mathbf {f} ],\alpha _{2}[\mathbf {f} ],\dots ,\alpha _{n}[\mathbf {f} ]\end{bmatrix}}}$

de modo que ( 3 ) puede reescribirse como el producto matricial

${\displaystyle \alpha [\mathbf {f} A]=\alpha [\mathbf {f} ]A.}$

Debido a que los componentes de la función lineal α se transforman con la matriz A , se dice que estos componentes se transforman covariantemente bajo un cambio de base.

La forma en que A relaciona los dos pares se representa en el siguiente diagrama informal mediante una flecha. Se indica una relación covariante ya que las flechas viajan en la misma dirección:

${\displaystyle {\begin{aligned}\mathbf {f} &\longrightarrow \mathbf {f'} \\\alpha [\mathbf {f} ]&\longrightarrow \alpha [\mathbf {f'} ]\end{aligned}}}$

Si se hubiera utilizado en su lugar una representación de vector de columna, la ley de transformación sería la transpuesta

${\displaystyle \alpha ^{\mathrm {T} }[\mathbf {f} A]=A^{\mathrm {T} }\alpha ^{\mathrm {T} }[\mathbf {f} ].}$

La elección de la base f en el espacio vectorial V define de forma única un conjunto de funciones de coordenadas en V , por medio de

${\displaystyle x^{i}[\mathbf {f} ](v)=v^{i}[\mathbf {f} ].}$

Las coordenadas de V son por lo tanto contravariantes en el sentido de que

${\displaystyle x^{i}[\mathbf {f} A]=\sum _{k=1}^{n}{\tilde {a}}_{k}^{i}x^{k}[\mathbf {f} ].}$

Por el contrario, un sistema de n magnitudes vi que ^se transforman como las coordenadas x ⁱ en V define un vector contravariante (o simplemente vector). Un sistema de n magnitudes que se transforman en sentido opuesto a las coordenadas es entonces un vector covariante (o covector).

Esta formulación de contravarianza y covarianza es a menudo más natural en aplicaciones en las que hay un espacio de coordenadas (una variedad ) en el que los vectores viven como vectores tangentes o vectores cotangentes . Dado un sistema de coordenadas local x ⁱ en la variedad, los ejes de referencia para el sistema de coordenadas son los campos vectoriales

${\displaystyle X_{1}={\frac {\partial }{\partial x^{1}}},\dots ,X_{n}={\frac {\partial }{\partial x^{n}}}.}$

Esto da lugar al marco f = ( X ₁ , ..., X _n ) en cada punto del parche de coordenadas.

Si y ⁱ es un sistema de coordenadas diferente y

${\displaystyle Y_{1}={\frac {\partial }{\partial y^{1}}},\dots ,Y_{n}={\frac {\partial }{\partial y^{n}}},}$

entonces el marco f' está relacionado con el marco f por la inversa de la matriz jacobiana de la transición de coordenadas:

${\displaystyle \mathbf {f} '=\mathbf {f} J^{-1},\quad J=\left({\frac {\partial y^{i}}{\partial x^{j}}}\right)_{i,j=1}^{n}.}$

O, en índices,

${\displaystyle {\frac {\partial }{\partial y^{i}}}=\sum _{j=1}^{n}{\frac {\partial x^{j}}{\partial y^{i}}}{\frac {\partial }{\partial x^{j}}}.}$

Un vector tangente es por definición un vector que es una combinación lineal de las coordenadas parciales . Por lo tanto, un vector tangente se define por${\displaystyle \partial /\partial x^{i}}$

${\displaystyle v=\sum _{i=1}^{n}v^{i}[\mathbf {f} ]X_{i}=\mathbf {f} \ \mathbf {v} [\mathbf {f} ].}$

Un vector de este tipo es contravariante con respecto al cambio de sistema de coordenadas. En caso de cambios en el sistema de coordenadas, se tiene

${\displaystyle \mathbf {v} \left[\mathbf {f} '\right]=\mathbf {v} \left[\mathbf {f} J^{-1}\right]=J\,\mathbf {v} [\mathbf {f} ].}$

Por lo tanto, los componentes de un vector tangente se transforman mediante

${\displaystyle v^{i}\left[\mathbf {f} '\right]=\sum _{j=1}^{n}{\frac {\partial y^{i}}{\partial x^{j}}}v^{j}[\mathbf {f} ].}$

Por tanto, un sistema de n magnitudes vi ^en función de las coordenadas que se transforman de esta manera al pasar de un sistema de coordenadas a otro se denomina vector contravariante.

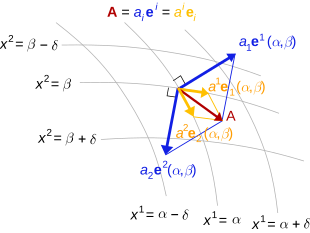
En un espacio vectorial de dimensión finita V sobre un cuerpo K con una forma bilineal simétrica g  : V × V → K (que puede denominarse tensor métrico ), hay poca distinción entre vectores covariantes y contravariantes, porque la forma bilineal permite identificar covectores con vectores. Es decir, un vector v determina de manera única un covector α mediante

${\displaystyle \alpha (w)=g(v,w)}$

para todos los vectores w . A la inversa, cada covector α determina un único vector v mediante esta ecuación. Debido a esta identificación de vectores con covectores, se puede hablar de componentes covariantes o componentes contravariantes de un vector, es decir, son simplemente representaciones del mismo vector utilizando la base recíproca .

Dada una base f = ( X ₁ , ..., X _n ) de V , existe una base recíproca única f ^# = ( Y ¹ , ..., Y ⁿ ) de V determinada al requerir que

${\displaystyle g(Y^{i},X_{j})=\delta _{j}^{i},}$

El delta de Kronecker . En función de estas bases, cualquier vector v puede escribirse de dos maneras:

${\displaystyle {\begin{aligned}v&=\sum _{i}v^{i}[\mathbf {f} ]X_{i}=\mathbf {f} \,\mathbf {v} [\mathbf {f} ]\\&=\sum _{i}v_{i}[\mathbf {f} ]Y^{i}=\mathbf {f} ^{\sharp }\mathbf {v} ^{\sharp }[\mathbf {f} ].\end{aligned}}}$

Las componentes v ⁱ [ f ] son ​​las componentes contravariantes del vector v en la base f , y las componentes v _i [ f ] son ​​las componentes covariantes de v en la base f . La terminología está justificada porque bajo un cambio de base,

${\displaystyle \mathbf {v} [\mathbf {f} A]=A^{-1}\mathbf {v} [\mathbf {f} ],\quad \mathbf {v} ^{\sharp }[\mathbf {f} A]=A^{T}\mathbf {v} ^{\sharp }[\mathbf {f} ].}$

En el plano euclidiano, el producto escalar permite identificar vectores con covectores. Si es una base, entonces la base dual satisface${\displaystyle \mathbf {e} _{1},\mathbf {e} _{2}}$${\displaystyle \mathbf {e} ^{1},\mathbf {e} ^{2}}$

${\displaystyle {\begin{aligned}\mathbf {e} ^{1}\cdot \mathbf {e} _{1}=1,&\quad \mathbf {e} ^{1}\cdot \mathbf {e} _{2}=0\\\mathbf {e} ^{2}\cdot \mathbf {e} _{1}=0,&\quad \mathbf {e} ^{2}\cdot \mathbf {e} _{2}=1.\end{aligned}}}$

Por lo tanto, e ¹ y e ₂ son perpendiculares entre sí, al igual que e ² y e ₁ , y las longitudes de e ¹ y e ² están normalizadas frente a e ₁ y e ₂ , respectivamente.

Por ejemplo, ^[5] supongamos que se nos da una base e ₁ , e ₂ que consiste en un par de vectores que forman un ángulo de 45° entre sí, de modo que e ₁ tiene una longitud de 2 y e ₂ tiene una longitud de 1. Entonces los vectores de base duales se dan de la siguiente manera:

• e ² es el resultado de rotar e ₁ a través de un ángulo de 90° (donde el sentido se mide asumiendo que el par e ₁ , e ₂ está orientado positivamente) y luego reescalar de modo que e ² ⋅ e ₂ = 1 se mantenga.
• e ¹ es el resultado de rotar e ₂ en un ángulo de 90° y luego reescalar de modo que e ¹ ⋅ e ₁ = 1 se mantenga.

Aplicando estas reglas, encontramos

${\displaystyle \mathbf {e} ^{1}={\frac {1}{2}}\mathbf {e} _{1}-{\frac {1}{\sqrt {2}}}\mathbf {e} _{2}}$

y

${\displaystyle \mathbf {e} ^{2}=-{\frac {1}{\sqrt {2}}}\mathbf {e} _{1}+2\mathbf {e} _{2}.}$

Por lo tanto, la matriz de cambio de base al pasar de la base original a la base recíproca es

${\displaystyle R={\begin{bmatrix}{\frac {1}{2}}&-{\frac {1}{\sqrt {2}}}\\-{\frac {1}{\sqrt {2}}}&2\end{bmatrix}},}$

desde

${\displaystyle [\mathbf {e} ^{1}\ \mathbf {e} ^{2}]=[\mathbf {e} _{1}\ \mathbf {e} _{2}]{\begin{bmatrix}{\frac {1}{2}}&-{\frac {1}{\sqrt {2}}}\\-{\frac {1}{\sqrt {2}}}&2\end{bmatrix}}.}$

Por ejemplo, el vector

${\displaystyle v={\frac {3}{2}}\mathbf {e} _{1}+2\mathbf {e} _{2}}$

es un vector con componentes contravariantes

${\displaystyle v^{1}={\frac {3}{2}},\quad v^{2}=2.}$

Los componentes covariantes se obtienen igualando las dos expresiones para el vector v :

${\displaystyle v=v_{1}\mathbf {e} ^{1}+v_{2}\mathbf {e} ^{2}=v^{1}\mathbf {e} _{1}+v^{2}\mathbf {e} _{2}}$

entonces

${\displaystyle {\begin{aligned}{\begin{bmatrix}v_{1}\\v_{2}\end{bmatrix}}&=R^{-1}{\begin{bmatrix}v^{1}\\v^{2}\end{bmatrix}}\\&={\begin{bmatrix}4&{\sqrt {2}}\\{\sqrt {2}}&1\end{bmatrix}}{\begin{bmatrix}v^{1}\\v^{2}\end{bmatrix}}\\&={\begin{bmatrix}6+2{\sqrt {2}}\\2+{\frac {3}{\sqrt {2}}}\end{bmatrix}}\end{aligned}}.}$

En el espacio euclidiano tridimensional , también se puede determinar explícitamente la base dual de un conjunto dado de vectores base e ₁ , e ₂ , e ₃ de E ₃ que no se suponen necesariamente ortogonales ni de norma unitaria. Los vectores base duales son:

${\displaystyle \mathbf {e} ^{1}={\frac {\mathbf {e} _{2}\times \mathbf {e} _{3}}{\mathbf {e} _{1}\cdot (\mathbf {e} _{2}\times \mathbf {e} _{3})}};\qquad \mathbf {e} ^{2}={\frac {\mathbf {e} _{3}\times \mathbf {e} _{1}}{\mathbf {e} _{2}\cdot (\mathbf {e} _{3}\times \mathbf {e} _{1})}};\qquad \mathbf {e} ^{3}={\frac {\mathbf {e} _{1}\times \mathbf {e} _{2}}{\mathbf {e} _{3}\cdot (\mathbf {e} _{1}\times \mathbf {e} _{2})}}.}$

Incluso cuando e _i y e ⁱ no son ortonormales , siguen siendo mutuamente recíprocas:

${\displaystyle \mathbf {e} ^{i}\cdot \mathbf {e} _{j}=\delta _{j}^{i},}$

Entonces los componentes contravariantes de cualquier vector v se pueden obtener mediante el producto escalar de v con los vectores base duales:

${\displaystyle q^{1}=\mathbf {v} \cdot \mathbf {e} ^{1};\qquad q^{2}=\mathbf {v} \cdot \mathbf {e} ^{2};\qquad q^{3}=\mathbf {v} \cdot \mathbf {e} ^{3}.}$

De la misma manera, los componentes covariantes de v se pueden obtener a partir del producto escalar de v con los vectores base, a saber:

${\displaystyle q_{1}=\mathbf {v} \cdot \mathbf {e} _{1};\qquad q_{2}=\mathbf {v} \cdot \mathbf {e} _{2};\qquad q_{3}=\mathbf {v} \cdot \mathbf {e} _{3}.}$

Entonces v puede expresarse de dos maneras (recíprocas), a saber:

${\displaystyle \mathbf {v} =q^{i}\mathbf {e} _{i}=q^{1}\mathbf {e} _{1}+q^{2}\mathbf {e} _{2}+q^{3}\mathbf {e} _{3}.}$

o

${\displaystyle \mathbf {v} =q_{i}\mathbf {e} ^{i}=q_{1}\mathbf {e} ^{1}+q_{2}\mathbf {e} ^{2}+q_{3}\mathbf {e} ^{3}}$

Combinando las relaciones anteriores, tenemos

${\displaystyle \mathbf {v} =(\mathbf {v} \cdot \mathbf {e} ^{i})\mathbf {e} _{i}=(\mathbf {v} \cdot \mathbf {e} _{i})\mathbf {e} ^{i}}$

y podemos convertir entre la base y la base dual con

${\displaystyle q_{i}=\mathbf {v} \cdot \mathbf {e} _{i}=(q^{j}\mathbf {e} _{j})\cdot \mathbf {e} _{i}=(\mathbf {e} _{j}\cdot \mathbf {e} _{i})q^{j}}$

y

${\displaystyle q^{i}=\mathbf {v} \cdot \mathbf {e} ^{i}=(q_{j}\mathbf {e} ^{j})\cdot \mathbf {e} ^{i}=(\mathbf {e} ^{j}\cdot \mathbf {e} ^{i})q_{j}.}$

Si los vectores base son ortonormales , entonces son los mismos que los vectores base duales.

De manera más general, en un espacio euclidiano n -dimensional V , si una base es

${\displaystyle \mathbf {e} _{1},\dots ,\mathbf {e} _{n},}$

La base recíproca está dada por (los índices dobles se suman),

${\displaystyle \mathbf {e} ^{i}=g^{ij}\mathbf {e} _{j}}$

donde los coeficientes g ^ij son las entradas de la matriz inversa de

${\displaystyle g_{ij}=\mathbf {e} _{i}\cdot \mathbf {e} _{j}.}$

De hecho, entonces tenemos

${\displaystyle \mathbf {e} ^{i}\cdot \mathbf {e} _{k}=g^{ij}\mathbf {e} _{j}\cdot \mathbf {e} _{k}=g^{ij}g_{jk}=\delta _{k}^{i}.}$

Los componentes covariantes y contravariantes de cualquier vector

${\displaystyle \mathbf {v} =q_{i}\mathbf {e} ^{i}=q^{i}\mathbf {e} _{i}\,}$

están relacionados como se indicó anteriormente por

${\displaystyle q_{i}=\mathbf {v} \cdot \mathbf {e} _{i}=(q^{j}\mathbf {e} _{j})\cdot \mathbf {e} _{i}=q^{j}g_{ji}}$

y

${\displaystyle q^{i}=\mathbf {v} \cdot \mathbf {e} ^{i}=(q_{j}\mathbf {e} ^{j})\cdot \mathbf {e} ^{i}=q_{j}g^{ji}.}$

La distinción entre covarianza y contravarianza es particularmente importante para los cálculos con tensores , que a menudo tienen varianza mixta . Esto significa que tienen componentes tanto covariantes como contravariantes, o tanto componentes vectoriales como covectoriales. La valencia de un tensor es el número de términos covariantes y contravariantes, y en la notación de Einstein , los componentes covariantes tienen índices más bajos, mientras que los componentes contravariantes tienen índices más altos. La dualidad entre covarianza y contravarianza interviene siempre que una cantidad vectorial o tensorial se representa por sus componentes, aunque la geometría diferencial moderna utiliza métodos sin índice más sofisticados para representar tensores .

En el análisis tensorial , un vector covariante varía más o menos recíprocamente con respecto a un vector contravariante correspondiente. Las expresiones para longitudes, áreas y volúmenes de objetos en el espacio vectorial pueden entonces darse en términos de tensores con índices covariantes y contravariantes. Bajo expansiones y contracciones simples de las coordenadas, la reciprocidad es exacta; bajo transformaciones afines, los componentes de un vector se entremezclan al pasar de una expresión covariante a una contravariante.

En una variedad , un campo tensorial normalmente tendrá múltiples índices superiores e inferiores, donde la notación de Einstein se usa ampliamente. Cuando la variedad está equipada con una métrica , los índices covariantes y contravariantes se vuelven muy relacionados entre sí. Los índices contravariantes se pueden convertir en índices covariantes contrayéndose con el tensor métrico. Lo inverso es posible contrayéndose con la matriz inversa del tensor métrico. Nótese que, en general, no existe tal relación en espacios que no estén dotados de un tensor métrico. Además, desde un punto de vista más abstracto, un tensor simplemente está "ahí" y sus componentes de cualquier tipo son solo artefactos de cálculo cuyos valores dependen de las coordenadas elegidas.

La explicación en términos geométricos es que un tensor general tendrá índices contravariantes así como índices covariantes, porque tiene partes que viven en el fibrado tangente así como en el fibrado cotangente .

Un vector contravariante es aquel que se transforma como , donde son las coordenadas de una partícula en su tiempo propio . Un vector covariante es aquel que se transforma como , donde es un campo escalar.${\displaystyle {\frac {dx^{\mu }}{d\tau }}}$${\displaystyle x^{\mu }\!}$ ${\displaystyle \tau }$${\displaystyle {\frac {\partial \varphi }{\partial x^{\mu }}}}$${\displaystyle \varphi }$

En la teoría de categorías , hay funtores covariantes y funtores contravariantes . La asignación del espacio dual a un espacio vectorial es un ejemplo estándar de un funtor contravariante. Los vectores contravariantes (o covariantes) son funtores contravariantes (o covariantes) desde un - torsor hasta la representación fundamental de . De manera similar, los tensores de grado superior son funtores con valores en otras representaciones de . Sin embargo, algunas construcciones de álgebra multilineal tienen varianza "mixta", lo que les impide ser funtores.${\displaystyle {\text{GL}}(n)}$${\displaystyle {\text{GL}}(n)}$${\displaystyle {\text{GL}}(n)}$

En geometría diferencial , los componentes de un vector relativos a una base del fibrado tangente son covariantes si cambian con la misma transformación lineal que un cambio de base. Son contravariantes si cambian por la transformación inversa. Esto a veces es una fuente de confusión por dos razones distintas pero relacionadas. La primera es que los vectores cuyos componentes son covariantes (llamados covectores o 1-formas ) en realidad retroceden bajo funciones suaves, lo que significa que la operación que asigna el espacio de covectores a una variedad suave es en realidad un funtor contravariante . Del mismo modo, los vectores cuyos componentes son contravariantes avanzan bajo aplicaciones suaves, por lo que la operación que asigna el espacio de vectores (contravariantes) a una variedad suave es un funtor covariante . En segundo lugar, en el enfoque clásico de la geometría diferencial, no son las bases del fibrado tangente el objeto más primitivo, sino más bien los cambios en el sistema de coordenadas. Los vectores con componentes contravariantes se transforman de la misma manera que los cambios en las coordenadas (porque estos en realidad cambian de manera opuesta al cambio de base inducido). Del mismo modo, los vectores con componentes covariantes se transforman en sentido opuesto a medida que cambian las coordenadas.

• Transformación activa y pasiva
• Tensor mixto
• Tensor de dos puntos , una generalización que permite que los índices hagan referencia a múltiples bases vectoriales

• "Tensor covariante", Enciclopedia de Matemáticas , EMS Press , 2001 [1994]
• "Tensor contravariante", Enciclopedia de Matemáticas , EMS Press , 2001 [1994]
• Weisstein, Eric W. "Tensor covariante". MathWorld .
• Weisstein, Eric W. "Tensor contravariante". MathWorld .
• Invariancia, contravariancia y covariancia
• Dullemond, Kees; Peeters, Kasper (2010). «Introducción al cálculo tensorial» (PDF) .