Convertidor analógico a digital





En electrónica , un convertidor analógico a digital ( ADC , A/D o A a D ) es un sistema que convierte una señal analógica , como un sonido captado por un micrófono o la luz que entra en una cámara digital , en una señal digital . Un ADC también puede proporcionar una medición aislada, como un dispositivo electrónico que convierte un voltaje o corriente de entrada analógica en un número digital que representa la magnitud del voltaje o la corriente. Normalmente, la salida digital es un número binario de complemento a dos que es proporcional a la entrada, pero existen otras posibilidades.
Existen varias arquitecturas de ADC . Debido a la complejidad y la necesidad de componentes que combinen con precisión , todos los ADC, excepto los más especializados, se implementan como circuitos integrados (CI). Estos suelen adoptar la forma de chips de circuitos integrados de señal mixta de metal-óxido-semiconductor (MOS) que integran circuitos analógicos y digitales .
Un convertidor digital a analógico (DAC) realiza la función inversa: convierte una señal digital en una señal analógica.
Explicación
Un ADC convierte una señal analógica de amplitud y tiempo continuos en una señal digital de amplitud y tiempo discretos . La conversión implica la cuantificación de la entrada, por lo que necesariamente introduce una pequeña cantidad de error de cuantificación . Además, en lugar de realizar la conversión de forma continua, un ADC la realiza de forma periódica, muestreando la entrada y limitando el ancho de banda permitido de la señal de entrada.
El rendimiento de un ADC se caracteriza principalmente por su ancho de banda y la relación señal-ruido (SNR). El ancho de banda de un ADC se caracteriza principalmente por su frecuencia de muestreo . La SNR de un ADC está influenciada por muchos factores, incluyendo la resolución , linealidad y precisión (qué tan bien los niveles de cuantificación coinciden con la señal analógica verdadera), aliasing y jitter . La SNR de un ADC a menudo se resume en términos de su número efectivo de bits (ENOB), el número de bits de cada medida que devuelve que en promedio no son ruido . Un ADC ideal tiene un ENOB igual a su resolución. Los ADC se eligen para que coincidan con el ancho de banda y la SNR requerida de la señal a digitalizar. Si un ADC opera a una frecuencia de muestreo mayor que el doble del ancho de banda de la señal, entonces, según el teorema de muestreo de Nyquist-Shannon , es posible una reconstrucción casi perfecta. La presencia de error de cuantificación limita la SNR incluso de un ADC ideal. Sin embargo, si la relación señal-ruido del ADC excede la de la señal de entrada, entonces se pueden descuidar los efectos del error de cuantificación, lo que da como resultado una representación digital esencialmente perfecta de la señal de entrada analógica de banda limitada .
Resolución

La resolución del convertidor indica el número de valores diferentes, es decir, discretos, que puede producir en el rango permitido de valores de entrada analógicos. Por lo tanto, una resolución particular determina la magnitud del error de cuantificación y, por lo tanto, determina la relación señal-ruido máxima posible para un ADC ideal sin el uso de sobremuestreo . Las muestras de entrada generalmente se almacenan electrónicamente en forma binaria dentro del ADC, por lo que la resolución generalmente se expresa como la profundidad de bits de audio . En consecuencia, el número de valores discretos disponibles suele ser una potencia de dos. Por ejemplo, un ADC con una resolución de 8 bits puede codificar una entrada analógica en uno en 256 niveles diferentes (2 8 = 256). Los valores pueden representar los rangos de 0 a 255 (es decir, como números enteros sin signo) o de −128 a 127 (es decir, como números enteros con signo), según la aplicación.
La resolución también se puede definir eléctricamente y expresar en voltios . El cambio de voltaje necesario para garantizar un cambio en el nivel de código de salida se denomina voltaje del bit menos significativo (LSB). La resolución Q del ADC es igual al voltaje del LSB. La resolución de voltaje de un ADC es igual a su rango de medición de voltaje general dividido por el número de intervalos:
donde M es la resolución del ADC en bits y E FSR es el rango de voltaje de escala completa (también llamado "span"). E FSR está dado por
donde V RefHi y V RefLow son los extremos superior e inferior, respectivamente, de los voltajes que se pueden codificar.
Normalmente, el número de intervalos de voltaje viene dado por
donde M es la resolución del ADC en bits. [1]
Es decir, se asigna un intervalo de voltaje entre dos niveles de código consecutivos.
Ejemplo:
- Esquema de codificación como en la figura 1
- Rango de medición de escala completa = 0 a 1 voltio
- La resolución del ADC es de 3 bits: 2 3 = 8 niveles de cuantificación (códigos)
- Resolución de voltaje del ADC, Q = 1 V / ( 2 3 - 1 ) = 0,143 V (intervalos)
En muchos casos, la resolución útil de un convertidor está limitada por la relación señal-ruido (SNR) y otros errores en el sistema general expresados como ENOB.
Error de cuantificación

El error de cuantificación se introduce por la cuantificación inherente a un ADC ideal. Es un error de redondeo entre el voltaje de entrada analógico al ADC y el valor digitalizado de salida. El error no es lineal y depende de la señal. En un ADC ideal, donde el error de cuantificación se distribuye uniformemente entre − 1 ⁄ 2 LSB y + 1 ⁄ 2 LSB, y la señal tiene una distribución uniforme que cubre todos los niveles de cuantificación, la relación señal-ruido de cuantificación (SQNR) viene dada por
- [2]
donde Q es el número de bits de cuantificación. Por ejemplo, para un conversor analógico -digital de 16 bits , el error de cuantificación es 96,3 dB por debajo del nivel máximo.
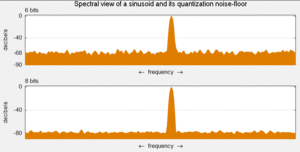
El error de cuantificación se distribuye desde la CC hasta la frecuencia de Nyquist . En consecuencia, si no se utiliza parte del ancho de banda del ADC, como es el caso del sobremuestreo , parte del error de cuantificación se producirá fuera de banda , lo que mejora de manera efectiva la SQNR para el ancho de banda en uso. En un sistema sobremuestreado, se puede utilizar la modelación de ruido para aumentar aún más la SQNR al forzar que haya más error de cuantificación fuera de banda.
Vacilar
En los ADC, el rendimiento se puede mejorar generalmente utilizando dither . Se trata de una cantidad muy pequeña de ruido aleatorio (por ejemplo, ruido blanco ), que se añade a la entrada antes de la conversión. Su efecto es aleatorizar el estado del LSB en función de la señal. En lugar de que la señal simplemente se corte por completo en niveles bajos, amplía el rango efectivo de señales que el ADC puede convertir, a expensas de un ligero aumento del ruido. El dither solo puede aumentar la resolución de un muestreador. No puede mejorar la linealidad y, por lo tanto, la precisión no mejora necesariamente.
La distorsión de cuantificación en una señal de audio de nivel muy bajo con respecto a la profundidad de bits del ADC se correlaciona con la señal y suena distorsionada y desagradable. Con el dithering, la distorsión se transforma en ruido. La señal no distorsionada se puede recuperar con precisión promediando en el tiempo. El dithering también se utiliza en sistemas de integración como los medidores de electricidad . Dado que los valores se suman, el dithering produce resultados que son más exactos que el LSB del convertidor analógico a digital.
El tramado se aplica a menudo cuando se cuantifican imágenes fotográficas a una menor cantidad de bits por píxel: la imagen se vuelve más ruidosa, pero a simple vista parece mucho más realista que la imagen cuantificada, que de otro modo se vuelve con bandas . Este proceso análogo puede ayudar a visualizar el efecto del tramado en una señal de audio analógica que se convierte a digital.
Exactitud
Un ADC tiene varias fuentes de errores. El error de cuantificación y (suponiendo que el ADC esté pensado para ser lineal) la no linealidad son intrínsecos a cualquier conversión de analógico a digital. Estos errores se miden en una unidad llamada bit menos significativo (LSB). En el ejemplo anterior de un ADC de ocho bits, un error de un LSB es 1 ⁄ 256 del rango completo de la señal, o aproximadamente el 0,4 %.
No linealidad
Todos los ADC sufren errores de no linealidad causados por sus imperfecciones físicas, lo que hace que su salida se desvíe de una función lineal (o alguna otra función, en el caso de un ADC deliberadamente no lineal) de su entrada. [ dudoso – discutir ] Estos errores a veces se pueden mitigar mediante calibración o prevenir mediante pruebas. Los parámetros importantes para la linealidad son la no linealidad integral y la no linealidad diferencial . Estas no linealidades introducen distorsión que puede reducir el rendimiento de la relación señal-ruido del ADC y, por lo tanto, reducir su resolución efectiva.
Estar nervioso
Al digitalizar una onda sinusoidal , el uso de un reloj de muestreo no ideal generará cierta incertidumbre en cuanto al momento en que se registran las muestras. Siempre que la incertidumbre del tiempo de muestreo real debido a la fluctuación del reloj sea , el error causado por este fenómeno se puede estimar como . Esto generará un ruido registrado adicional que reducirá el número efectivo de bits (ENOB) por debajo del predicho únicamente por el error de cuantificación . El error es cero para CC, pequeño a bajas frecuencias, pero significativo con señales de alta amplitud y alta frecuencia. El efecto de la fluctuación en el rendimiento se puede comparar con el error de cuantificación: , donde q es el número de bits del ADC. [ cita requerida ]
| Tamaño de salida (bits) | Frecuencia de señal | ||||||
|---|---|---|---|---|---|---|---|
| 1 Hz | 1 kHz | 10 kHz | 1 MHz | 10 MHz | 100 MHz | 1 GHz | |
| 8 | 1.243 microsegundos | 1,24 microsegundos | 124 ns | 1,24 ns | 124 ps | 12,4 ps | 1,24 ps |
| 10 | 311 microsegundos | 311 ns | 31,1 ns | 311 ps | 31,1 ps | 3,11 ps | 0,31 ps |
| 12 | 77,7 microsegundos | 77,7 ns | 7,77 ns | 77,7 ps | 7,77 ps | 0,78 ps | 0,08 ps (77,7 fs) |
| 14 | 19,4 microsegundos | 19,4 ns | 1,94 ns | 19,4 ps | 1,94 ps | 0,19 ps | 0,02 ps (19,4 fs) |
| 16 | 4,86 microsegundos | 4,86 ns | 486 ps | 4,86 ps | 0,49 ps | 0,05 ps (48,5 fs) | – |
| 18 | 1,21 μs | 1,21 ns | 121 ps | 1,21 ps | 0,12 ps | – | – |
| 20 | 304 ns | 304 ps | 30,4 ps | 0,30 ps (303,56 fs) | 0,03 ps (30,3 fs) | – | – |
| 24 | 18,9 ns | 18,9 ps | 1,89 ps | 0,019 ps (18,9 fs) | - | – | – |
La fluctuación del reloj es causada por el ruido de fase . [3] [4] La resolución de los ADC con un ancho de banda de digitalización entre 1 MHz y 1 GHz está limitada por la fluctuación. [5] Para conversiones de ancho de banda más bajo, como cuando se muestrean señales de audio a 44,1 kHz, la fluctuación del reloj tiene un impacto menos significativo en el rendimiento. [6]
Frecuencia de muestreo
Una señal analógica es continua en el tiempo y es necesario convertirla en un flujo de valores digitales. Por lo tanto, es necesario definir la velocidad a la que se muestrean los nuevos valores digitales de la señal analógica. La velocidad de los nuevos valores se denomina frecuencia de muestreo o frecuencia de muestreo del convertidor. Se puede muestrear una señal limitada en banda que varía continuamente y luego se puede reproducir la señal original a partir de los valores de tiempo discreto mediante un filtro de reconstrucción . El teorema de muestreo de Nyquist-Shannon implica que solo es posible una reproducción fiel de la señal original si la frecuencia de muestreo es mayor que el doble de la frecuencia más alta de la señal.
Dado que un convertidor analógico-digital (ADC) práctico no puede realizar una conversión instantánea, el valor de entrada debe mantenerse necesariamente constante durante el tiempo que el convertidor realiza una conversión (denominado tiempo de conversión ). Un circuito de entrada llamado de muestreo y retención realiza esta tarea, en la mayoría de los casos mediante el uso de un condensador para almacenar el voltaje analógico en la entrada y mediante un interruptor o compuerta electrónica para desconectar el condensador de la entrada. Muchos circuitos integrados de ADC incluyen el subsistema de muestreo y retención internamente.
Alias
Un ADC funciona muestreando el valor de la entrada a intervalos discretos en el tiempo. Siempre que la entrada se muestree por encima de la frecuencia de Nyquist , definida como el doble de la frecuencia más alta de interés, entonces se pueden reconstruir todas las frecuencias en la señal. Si se muestrean frecuencias por encima de la mitad de la frecuencia de Nyquist, se detectan incorrectamente como frecuencias más bajas, un proceso conocido como aliasing. El aliasing ocurre porque muestrear instantáneamente una función dos veces o menos por ciclo da como resultado ciclos perdidos y, por lo tanto, la aparición de una frecuencia incorrectamente más baja. Por ejemplo, una onda sinusoidal de 2 kHz muestreada a 1,5 kHz se reconstruiría como una onda sinusoidal de 500 Hz.
Para evitar el aliasing, la entrada de un ADC debe ser filtrada con un filtro de paso bajo para eliminar las frecuencias superiores a la mitad de la frecuencia de muestreo. Este filtro se denomina filtro anti-aliasing y es esencial para un sistema ADC práctico que se aplica a señales analógicas con un contenido de frecuencia más alto. En aplicaciones donde la protección contra el aliasing es esencial, se puede utilizar el sobremuestreo para reducirlo en gran medida o incluso eliminarlo.
Aunque el aliasing no es deseado en la mayoría de los sistemas, se puede aprovechar para proporcionar una mezcla descendente simultánea de una señal de alta frecuencia de banda limitada (consulte submuestreo y mezclador de frecuencia ). El alias es efectivamente el heterodino inferior de la frecuencia de la señal y la frecuencia de muestreo. [7]
Sobremuestreo
Por razones de economía, las señales se muestrean a menudo a la frecuencia mínima requerida, con el resultado de que el error de cuantificación introducido es ruido blanco que se extiende por toda la banda de paso del conversor. Si se muestrea una señal a una frecuencia mucho mayor que la frecuencia de Nyquist y luego se filtra digitalmente para limitarla al ancho de banda de la señal, se obtienen las siguientes ventajas:
- El sobremuestreo puede facilitar la realización de filtros anti-aliasing analógicos
- Profundidad de bits de audio mejorada
- Ruido reducido, especialmente cuando se emplea modelado de ruido además del sobremuestreo.
El sobremuestreo se utiliza normalmente en los convertidores analógico-digitales de frecuencia de audio en los que la frecuencia de muestreo requerida (normalmente 44,1 o 48 kHz) es muy baja en comparación con la velocidad de reloj de los circuitos de transistores típicos (>1 MHz). En este caso, el rendimiento del convertidor analógico-digital se puede aumentar considerablemente con poco o ningún coste. Además, como las señales con alias también suelen estar fuera de banda, el alias se puede eliminar a menudo utilizando filtros de muy bajo coste.
Velocidad relativa y precisión
La velocidad de un ADC varía según el tipo. El ADC Wilkinson está limitado por la frecuencia de reloj que pueden procesar los circuitos digitales actuales. En el caso de un ADC de aproximación sucesiva , el tiempo de conversión se escala con el logaritmo de la resolución, es decir, el número de bits. Los ADC Flash son sin duda el tipo más rápido de los tres; la conversión se realiza básicamente en un solo paso paralelo.
Existe una posible disyuntiva entre velocidad y precisión. Los ADC Flash tienen desviaciones e incertidumbres asociadas con los niveles del comparador, lo que da como resultado una linealidad deficiente. En menor medida, la linealidad deficiente también puede ser un problema para los ADC de aproximación sucesiva. En este caso, la no linealidad surge de la acumulación de errores de los procesos de sustracción. Los ADC Wilkinson tienen la mejor linealidad de los tres. [8] [9]
Principio de escala móvil
El método de escala móvil o aleatorización se puede emplear para mejorar en gran medida la linealidad de cualquier tipo de ADC, pero especialmente de los tipos de aproximaciones sucesivas y de flash. Para cualquier ADC, la asignación del voltaje de entrada al valor de salida digital no es exactamente una función de piso o techo como debería ser. En condiciones normales, un pulso de una amplitud particular siempre se convierte al mismo valor digital. El problema radica en que los rangos de valores analógicos para los valores digitalizados no tienen todos el mismo ancho, y la linealidad diferencial disminuye proporcionalmente con la divergencia del ancho promedio. El principio de escala móvil utiliza un efecto de promediado para superar este fenómeno. Un voltaje analógico aleatorio, pero conocido, se agrega al voltaje de entrada muestreado. Luego se convierte a forma digital y se resta la cantidad digital equivalente, restableciéndolo así a su valor original. La ventaja es que la conversión se ha realizado en un punto aleatorio. La distribución estadística de los niveles finales se decide por un promedio ponderado sobre una región del rango del ADC. Esto a su vez lo desensibiliza al ancho de cualquier nivel específico. [10] [11]
Tipos
Estas son varias formas comunes de implementar un ADC electrónico.
Tiempo de carga del RC
Los circuitos resistor-capacitor (RC) tienen una curva de carga y descarga de voltaje conocida que puede usarse para resolver un valor analógico desconocido.
Wilkinson
El convertidor analógico-digital Wilkinson fue diseñado por Denys Wilkinson en 1950. El convertidor analógico-digital Wilkinson se basa en la comparación de un voltaje de entrada con el producido por un condensador en carga. Se permite que el condensador se cargue hasta que un comparador determine que coincide con el voltaje de entrada. Luego, el condensador se descarga linealmente utilizando una fuente de corriente constante . El tiempo necesario para descargar el condensador es proporcional a la amplitud del voltaje de entrada. Mientras el condensador se descarga, los pulsos de un reloj oscilador de alta frecuencia se cuentan mediante un registro. El número de pulsos de reloj registrados en el registro también es proporcional al voltaje de entrada. [12] [13]
Medición de resistencia o capacitancia analógica
Si el valor analógico a medir está representado por una resistencia o capacitancia, entonces al incluir ese elemento en un circuito RC (con otras resistencias o capacitancias fijas) y medir el tiempo para cargar la capacitancia desde un voltaje inicial conocido a otro voltaje final conocido a través de la resistencia de una fuente de voltaje conocida, el valor de la resistencia o capacitancia desconocida se puede determinar utilizando la ecuación de carga del capacitor:
y resolver la resistencia o capacitancia desconocidas usando esos puntos de datos iniciales y finales. Esto es similar pero contrasta con el ADC de Wilkinson que mide un voltaje desconocido con una resistencia y capacitancia conocidas, midiendo en cambio una resistencia o capacitancia desconocidas con un voltaje conocido.
Por ejemplo, el ancho de pulso positivo (y/o negativo) de un temporizador IC 555 en modo monoestable o astable representa el tiempo que tarda en cargar (y/o descargar) su capacitor desde una fuente de 1 ⁄ 3 V a una fuente de 2 ⁄ 3 V. Al enviar este pulso a un microcontrolador con un reloj preciso, se puede medir la duración del pulso y convertirla utilizando la ecuación de carga del capacitor para producir el valor de la resistencia o capacitancia desconocida.
Las resistencias y capacitancias mayores tardarán más tiempo en medirse que las menores. Y la precisión está limitada por la precisión del reloj del microcontrolador y la cantidad de tiempo disponible para medir el valor, que potencialmente podría incluso cambiar durante la medición o verse afectado por parásitos externos .
Conversión directa
Un convertidor analógico-digital de conversión directa o flash tiene un banco de comparadores que muestrean la señal de entrada en paralelo, y cada uno de ellos se activa para un rango de voltaje específico. El banco de comparadores alimenta un circuito lógico codificador digital que genera un número binario en las líneas de salida para cada rango de voltaje.
Los convertidores analógicos a digitales de este tipo tienen un tamaño de chip grande y una alta disipación de potencia. Se utilizan a menudo para vídeo , comunicaciones de banda ancha u otras señales rápidas en almacenamiento óptico y magnético .
El circuito consta de una red divisora resistiva, un conjunto de comparadores de amplificadores operacionales y un codificador de prioridad. Se incorpora una pequeña cantidad de histéresis en el comparador para resolver cualquier problema en los límites de voltaje. En cada nodo del divisor resistivo, hay disponible un voltaje de comparación. El propósito del circuito es comparar el voltaje de entrada analógico con cada uno de los voltajes de los nodos.
El circuito tiene la ventaja de ser rápido, ya que la conversión se realiza de manera simultánea en lugar de secuencial. El tiempo de conversión típico es de 100 ns o menos. El tiempo de conversión está limitado únicamente por la velocidad del comparador y del codificador de prioridad. Este tipo de ADC tiene la desventaja de que la cantidad de comparadores necesarios casi se duplica por cada bit agregado. Además, cuanto mayor sea el valor de n, más complejo será el codificador de prioridad.
Aproximación sucesiva
Un convertidor analógico-digital de aproximación sucesiva utiliza un comparador y una búsqueda binaria para reducir sucesivamente un rango que contiene el voltaje de entrada. En cada paso sucesivo, el convertidor compara el voltaje de entrada con la salida de un convertidor digital-analógico (DAC) interno que inicialmente representa el punto medio del rango de voltaje de entrada permitido. En cada paso de este proceso, la aproximación se almacena en un registro de aproximación sucesiva (SAR) y la salida del convertidor digital-analógico se actualiza para realizar una comparación en un rango más estrecho.
Comparación de rampas
Un ADC de comparación de rampa produce una señal de dientes de sierra que aumenta o disminuye y luego vuelve rápidamente a cero. [14] Cuando comienza la rampa, un temporizador comienza a contar. Cuando el voltaje de rampa coincide con la entrada, se activa un comparador y se registra el valor del temporizador. Los convertidores de rampa temporizada se pueden implementar de manera económica, [a] sin embargo, el tiempo de rampa puede ser sensible a la temperatura porque el circuito que genera la rampa es a menudo un integrador analógico simple . Un convertidor más preciso utiliza un contador sincronizado que controla un DAC. Una ventaja especial del sistema de comparación de rampa es que convertir una segunda señal solo requiere otro comparador y otro registro para almacenar el valor del temporizador. Para reducir la sensibilidad a los cambios de entrada durante la conversión, un muestreo y retención puede cargar un capacitor con el voltaje de entrada instantáneo y el convertidor puede cronometrar el tiempo requerido para descargar con una corriente constante .
Integrando
Un ADC integrador (también ADC de pendiente doble o pendiente múltiple ) aplica el voltaje de entrada desconocido a la entrada de un integrador y permite que el voltaje aumente durante un período de tiempo fijo (el período de aceleración). Luego, se aplica un voltaje de referencia conocido de polaridad opuesta al integrador y se permite que aumente hasta que la salida del integrador vuelva a cero (el período de desaceleración). El voltaje de entrada se calcula como una función del voltaje de referencia, el período de aceleración constante y el período de desaceleración medido. La medición del tiempo de desaceleración generalmente se realiza en unidades del reloj del convertidor, por lo que los tiempos de integración más largos permiten resoluciones más altas. Asimismo, la velocidad del convertidor se puede mejorar sacrificando la resolución. Los convertidores de este tipo (o variaciones del concepto) se utilizan en la mayoría de los voltímetros digitales por su linealidad y flexibilidad.
- Convertidor analógico-digital de equilibrio de carga
- El principio del ADC de equilibrio de carga es convertir primero la señal de entrada a una frecuencia utilizando un convertidor de voltaje a frecuencia . Luego, esta frecuencia se mide mediante un contador y se convierte en un código de salida proporcional a la entrada analógica. La principal ventaja de estos convertidores es que es posible transmitir frecuencia incluso en un entorno ruidoso o de forma aislada. Sin embargo, la limitación de este circuito es que la salida del convertidor de voltaje a frecuencia depende de un producto RC cuyo valor no se puede mantener con precisión a lo largo de la temperatura y el tiempo.
- Convertidor analógico-digital de doble pendiente
- La parte analógica del circuito consta de un buffer de alta impedancia de entrada, un integrador de precisión y un comparador de tensión. El convertidor primero integra la señal de entrada analógica durante una duración fija y luego integra una tensión de referencia interna de polaridad opuesta hasta que la salida del integrador es cero. La principal desventaja de este circuito es el largo tiempo de duración. Son especialmente adecuados para la medición precisa de señales que varían lentamente, como termopares y básculas .
Codificado delta
Un conversor de analógico a digital (ADC) codificado en delta o de rampa de contrarreloj tiene un contador ascendente y descendente que alimenta un conversor de analógico a digital. La señal de entrada y el conversor de analógico a digital van a un comparador. El comparador controla el contador. El circuito utiliza la retroalimentación negativa del comparador para ajustar el contador hasta que la salida del conversor de analógico a digital coincida con la señal de entrada y se lea el número del contador. Los conversores delta tienen rangos muy amplios y una alta resolución, pero el tiempo de conversión depende del comportamiento de la señal de entrada, aunque siempre tendrá un peor caso garantizado. Los conversores delta suelen ser muy buenas opciones para leer señales del mundo real, ya que la mayoría de las señales de los sistemas físicos no cambian abruptamente. Algunos conversores combinan los enfoques de aproximación delta y sucesiva; esto funciona especialmente bien cuando se sabe que los componentes de alta frecuencia de la señal de entrada son de pequeña magnitud.
Canalizado
Un conversor analógico-digital ( ADC) segmentado (también llamado cuantificador de subrango ) utiliza dos o más pasos de conversión. Primero, se realiza una conversión aproximada. En un segundo paso, se determina la diferencia con la señal de entrada con un DAC. Luego, esta diferencia se convierte de manera más precisa y los resultados se combinan en el último paso. Esto puede considerarse un refinamiento del conversor analógico-digital de aproximación sucesiva, en el que la señal de referencia de retroalimentación consiste en la conversión provisional de un rango completo de bits (por ejemplo, cuatro bits) en lugar de solo el siguiente bit más significativo. Al combinar las ventajas de los conversores analógico-digitales de aproximación sucesiva y flash, este tipo es rápido, tiene una alta resolución y se puede implementar de manera eficiente.
Delta-sigma
Un ADC delta-sigma (también conocido como ADC sigma-delta ) se basa en un bucle de retroalimentación negativa con un filtro analógico y un ADC y DAC de baja resolución (a menudo 1 bit) pero de alta frecuencia de muestreo . El bucle de retroalimentación corrige continuamente los errores de cuantificación acumulados y realiza la modelación del ruido : el ruido de cuantificación se reduce en las frecuencias bajas de interés, pero aumenta en frecuencias más altas. Esas frecuencias más altas pueden luego eliminarse mediante un filtro digital de submuestreo , que también convierte el flujo de datos de esa alta frecuencia de muestreo con baja profundidad de bits a una frecuencia más baja con mayor profundidad de bits.
Intercalado en el tiempo
Un ADC intercalado en el tiempo utiliza M ADC paralelos donde cada ADC muestrea datos cada M:ésimo ciclo del reloj de muestreo efectivo. El resultado es que la frecuencia de muestreo aumenta M veces en comparación con lo que cada ADC individual puede gestionar. En la práctica, las diferencias individuales entre los M ADC degradan el rendimiento general, lo que reduce el rango dinámico libre de espurios (SFDR). [16] Sin embargo, existen técnicas para corregir estos errores de desajuste en el intercalado en el tiempo. [17]
Etapa intermedia de FM
Un ADC con una etapa intermedia de FM utiliza primero un convertidor de voltaje a frecuencia para producir una señal oscilante con una frecuencia proporcional al voltaje de la señal de entrada, y luego utiliza un contador de frecuencia para convertir esa frecuencia en un conteo digital proporcional al voltaje de señal deseado. Los tiempos de integración más largos permiten resoluciones más altas. Asimismo, la velocidad del convertidor se puede mejorar sacrificando la resolución. Las dos partes del ADC pueden estar muy separadas, con la señal de frecuencia pasando a través de un optoaislador o transmitiéndose de forma inalámbrica. Algunos de estos ADC utilizan modulación de frecuencia de onda sinusoidal o de onda cuadrada ; otros utilizan modulación de frecuencia de pulso . Estos ADC alguna vez fueron la forma más popular de mostrar una pantalla digital del estado de un sensor analógico remoto. [18] [19] [20] [21] [22]
Estiramiento temporal
Un convertidor analógico-digital con estiramiento temporal (TS-ADC) digitaliza una señal analógica de ancho de banda muy amplio, que no puede digitalizarse con un ADC electrónico convencional, al estirar temporalmente la señal antes de la digitalización. Generalmente, utiliza un preprocesador fotónico para estirar temporalmente la señal, lo que efectivamente la ralentiza en el tiempo y comprime su ancho de banda. Como resultado, un ADC electrónico, que habría sido demasiado lento para capturar la señal original, ahora puede capturar esta señal ralentizada. Para la captura continua de la señal, el extremo frontal también divide la señal en múltiples segmentos además del estiramiento temporal. Cada segmento se digitaliza individualmente mediante un ADC electrónico independiente. Finalmente, un procesador de señal digital reorganiza las muestras y elimina cualquier distorsión agregada por el preprocesador para producir los datos binarios que son la representación digital de la señal analógica original.
Medición de valores físicos distintos del voltaje
Aunque el término ADC suele asociarse con la medición de un voltaje analógico, algunos dispositivos parcialmente electrónicos que convierten alguna cantidad analógica física medible en un número digital también pueden considerarse ADC, por ejemplo:
- Los codificadores rotatorios convierten una cantidad física analógica que produce mecánicamente una cantidad de rotación en un flujo de código Gray digital que un microcontrolador puede interpretar digitalmente para derivar la dirección de rotación, la posición angular y la velocidad de rotación. [23]
- La detección capacitiva convierte la cantidad física analógica de una capacitancia . Esa capacitancia podría ser un indicador de alguna otra cantidad física, como la distancia entre un objeto metálico y una placa de detección metálica, la cantidad de agua en un tanque o la permitividad de un material dieléctrico .
- Los convertidores capacitivos a digitales (CDC) determinan la capacitancia aplicando una excitación conocida a una placa de un capacitor y midiendo su carga. [24]
- Los calibradores digitales convierten la cantidad física analógica en una cantidad de desplazamiento entre dos reglas deslizantes.
- Los convertidores inductivos a digitales miden un cambio de inductancia producido por un objetivo conductor que se mueve en el campo magnético de CA de un inductor . [25]
- Los convertidores de tiempo a formato digital reconocen eventos y proporcionan una representación digital del tiempo analógico en el que ocurrieron.
- Las mediciones del tiempo de vuelo , por ejemplo, pueden convertirse a partir de alguna cantidad analógica que afecta el retraso de propagación de un evento.
- Los sensores en general que no producen directamente un voltaje pueden producirlo indirectamente o, a través de otras formas, convertirse en un valor digital.
- La salida resistiva (por ejemplo, de un potenciómetro o una resistencia de detección de fuerza ) se puede convertir en un voltaje enviando una corriente conocida a través de él, o se puede convertir en una medición del tiempo de carga RC , para producir un resultado digital.
Comercial
En muchos casos, la parte más cara de un circuito integrado son los pines, porque hacen que el encapsulado sea más grande y cada pin debe estar conectado al silicio del circuito integrado. Para ahorrar pines, es común que los ADC envíen sus datos un bit a la vez a través de una interfaz serial al ordenador, y cada bit sale cuando una señal de reloj cambia de estado. Esto ahorra bastantes pines en el encapsulado del ADC y, en muchos casos, no hace que el diseño general sea más complejo.
Los ADC comerciales suelen tener varias entradas que alimentan el mismo convertidor, normalmente a través de un multiplexor analógico . Los distintos modelos de ADC pueden incluir circuitos de muestreo y retención , amplificadores de instrumentación o entradas diferenciales , donde la cantidad medida es la diferencia entre dos entradas.
Aplicaciones
Grabación de música
Los convertidores analógico-digitales son parte integral de la tecnología de reproducción de música moderna y de la grabación de sonido basada en estaciones de trabajo de audio digital . La música se puede producir en computadoras utilizando una grabación analógica y, por lo tanto, se necesitan convertidores analógico-digitales para crear los flujos de datos de modulación por código de pulsos (PCM) que se almacenan en discos compactos y archivos de música digital. La generación actual de convertidores analógico-digitales utilizados en música puede muestrear a velocidades de hasta 192 kilohercios . Muchos estudios de grabación graban en formato de modulación por código de pulsos (PCM) de 24 bits a 96 kHz y luego reducen la resolución y traman la señal para la producción de audio digital en discos compactos (44,1 kHz) o a 48 kHz para aplicaciones de transmisión de radio y televisión.
Procesamiento de señales digitales
Los ADC son necesarios en los sistemas de procesamiento de señales digitales que procesan, almacenan o transportan prácticamente cualquier señal analógica en formato digital. Las tarjetas sintonizadoras de TV , por ejemplo, utilizan convertidores de analógico a digital de vídeo rápidos. Los convertidores de analógico a digital lentos en chip de 8, 10, 12 o 16 bits son comunes en los microcontroladores . Los osciloscopios de almacenamiento digital necesitan convertidores de analógico a digital muy rápidos, también cruciales para la radio definida por software y sus nuevas aplicaciones.
Instrumentos científicos
Los sistemas de imágenes digitales suelen utilizar convertidores analógicos a digitales para digitalizar píxeles . Algunos sistemas de radar utilizan convertidores analógicos a digitales para convertir la intensidad de la señal en valores digitales para su posterior procesamiento . Muchos otros sistemas de detección in situ y remota suelen utilizar tecnología análoga.
Muchos sensores en instrumentos científicos producen una señal analógica: temperatura , presión , pH , intensidad de luz , etc. Todas estas señales se pueden amplificar y enviar a un ADC para producir una representación digital.
Muestra
Las pantallas planas son inherentemente digitales y necesitan un ADC para procesar una señal analógica, como compuesta o VGA .
Símbolo eléctrico
Pruebas
Para probar un convertidor analógico a digital se necesita una fuente de entrada analógica y hardware para enviar señales de control y capturar la salida de datos digitales. Algunos ADC también requieren una fuente precisa de señal de referencia.
Los parámetros clave para probar un ADC son:
- Error de compensación de CC
- Error de ganancia de CC
- relación señal-ruido (SNR)
- Distorsión armónica total (THD)
- No linealidad integral (INL)
- No linealidad diferencial (DNL)
- Rango dinámico libre espurio
- Disipación de potencia
Véase también
- Codificación predictiva adaptativa , un tipo de ADC en el que el valor de la señal se predice mediante una función lineal
- Códec de audio
- Codificador beta
- Linealidad integral
- Módem
Notas
- ^ Se puede implementar un convertidor de rampa muy simple (no lineal) con un microcontrolador y una resistencia y un condensador. [15]
Referencias
- ^ "Principios de adquisición y conversión de datos" (PDF) . Texas Instruments. Abril de 2015. Archivado (PDF) del original el 9 de octubre de 2022 . Consultado el 18 de octubre de 2016 .
- ^ Lathi, BP (1998). Sistemas de comunicación analógicos y digitales modernos (3.ª ed.). Oxford University Press.
- ^ "Maxim App 800: Diseño de un reloj de baja fluctuación para convertidores de datos de alta velocidad", maxim-ic.com , 17 de julio de 2002
- ^ "Efectos de fluctuación en convertidores analógico-digitales y digitales-analógicos" (PDF) . Consultado el 19 de agosto de 2012 .
- ^ Löhning, Michael; Fettweis, Gerhard (2007). "Los efectos de la fluctuación de apertura y de reloj en los ADC de banda ancha". Archivo de estándares e interfaces de computadoras . 29 (1): 11–18. CiteSeerX 10.1.1.3.9217 . doi :10.1016/j.csi.2005.12.005.
- ^ Redmayne, Derek; Steer, Alison (8 de diciembre de 2008), "Entender el efecto de la fluctuación del reloj en los ADC de alta velocidad", eetimes.com
- ^ "Conversores analógicos de GSPS y muestreo de RF: los conversores analógicos innovadores revolucionan las arquitecturas de radio" (PDF) . Texas Instruments. Archivado (PDF) del original el 9 de octubre de 2022 . Consultado el 4 de noviembre de 2013 .
- ^ Knoll (1989, págs. 664-665)
- ^ Nicholson (1974, págs. 313-315)
- ^ Knoll (1989, págs. 665-666)
- ^ Nicholson (1974, págs. 315-316)
- ^ Knoll (1989, págs. 663-664)
- ^ Nicholson (1974, págs. 309-310)
- ^ Couch - 2001 - Sistemas de comunicación digitales y analógicos - Prentice Hall - Nueva Jersey, EE.UU.
- ^ "Nota de aplicación Atmel AVR400: convertidor A/D de bajo costo" (PDF) . atmel.com . Archivado (PDF) del original el 9 de octubre de 2022.
- ^ Vogel, Christian (2005). "El impacto de los efectos de desajuste de canal combinado en los ADC intercalados en el tiempo". IEEE Transactions on Instrumentation and Measurement . 55 (1): 415–427. Bibcode :2005ITIM...54..415V. CiteSeerX 10.1.1.212.7539 . doi :10.1109/TIM.2004.834046. S2CID 15038020.
- ^ Gabriele Manganaro; David H. Robertson (julio de 2015), Interleaving ADCs: Unraveling the Mysteries, Analog Devices , consultado el 7 de octubre de 2021
- ^ Tutorial MT-028 de Analog Devices: "Convertidores de voltaje a frecuencia" de Walt Kester y James Bryant 2009, aparentemente adaptado de Kester, Walter Allan (2005) Manual de conversión de datos, Newnes, pág. 274, ISBN 0750678410 .
- ^ Microchip AN795 "Convertidor de voltaje a frecuencia / convertidor de frecuencia a voltaje" p. 4: "Convertidor A/D de 13 bits"
- ^ Carr, Joseph J. (1996) Elementos de instrumentación y medición electrónica, Prentice Hall, pág. 402, ISBN 0133416860 .
- ^ "Convertidores analógico-digitales de voltaje a frecuencia". globalspec.com
- ^ Pease, Robert A. (1991) Solución de problemas de circuitos analógicos, Newnes, pág. 130, ISBN 0750694998 .
- ^ Grupo, SAE Media (1 de octubre de 2019). "Cómo utilizar codificadores rotatorios para convertir rápidamente la rotación mecánica en señales digitales". www.techbriefs.com . Consultado el 9 de octubre de 2023 .
{{cite web}}:|last=tiene nombre genérico ( ayuda ) - ^ Jia, Ning (1 de mayo de 2012). "Tecnología de conversión de capacitancia a digital de ADI en aplicaciones sanitarias". Analog Dialogue . Archivado desde el original el 7 de julio de 2023. Consultado el 9 de octubre de 2023 .
- ^ Kasemsadeh, Ben (31 de julio de 2015). "Cómo detectar el movimiento lateral mediante un convertidor de inductancia a digital". Fierce Electronics . Archivado desde el original el 9 de octubre de 2023. Consultado el 9 de octubre de 2023 .
- Knoll, Glenn F. (1989). Detección y medición de la radiación (2.ª ed.). Nueva York: John Wiley & Sons. ISBN 978-0471815044.
- Nicholson, PW (1974). Electrónica nuclear . Nueva York: John Wiley & Sons. págs. 315-316. ISBN. 978-0471636977.
Lectura adicional
- Allen, Phillip E.; Holberg, Douglas R. (2002). Diseño de circuitos analógicos CMOS . ISBN 978-0-19-511644-1.
- Fraden, Jacob (2010). Manual de sensores modernos: física, diseños y aplicaciones . Springer. ISBN 978-1441964656.
- Kester, Walt, ed. (2005). Manual de conversión de datos. Elsevier: Newnes. ISBN 978-0-7506-7841-4.
- Johns, David; Martin, Ken (1997). Diseño de circuitos integrados analógicos . Wiley. ISBN 978-0-471-14448-9.
- Liu, Mingliang (2006). Desmitificando circuitos de condensadores conmutados . Newnes. ISBN 978-0-7506-7907-7.
- Norsworthy, Steven R.; Schreier, Richard; Temes, Gabor C. (1997). Convertidores de datos Delta-Sigma . Prensa IEEE. ISBN 978-0-7803-1045-2.
- Razavi, Behzad (1995). Principios del diseño de sistemas de conversión de datos . Nueva York, NY: IEEE Press. ISBN 978-0-7803-1093-3.
- Ndjountche, Tertulien (24 de mayo de 2011). Circuitos integrados analógicos CMOS: diseño de alta velocidad y bajo consumo de energía . Boca Raton, FL: CRC Press. ISBN 978-1-4398-5491-4.
- Staller, Len (24 de febrero de 2005). "Comprensión de las especificaciones de los convertidores analógicos a digitales". Diseño de sistemas integrados .
- Walden, RH (1999). "Estudio y análisis de convertidores analógicos a digitales". Revista IEEE sobre áreas seleccionadas en comunicaciones . 17 (4): 539–550. CiteSeerX 10.1.1.352.1881 . doi :10.1109/49.761034.
Enlaces externos
- Una introducción a los convertidores Delta Sigma Una muy buena descripción general de la teoría del convertidor Delta-Sigma.
- Análisis dinámico digital de sistemas de conversión A/D mediante software de evaluación basado en análisis FFT/DFT RF Expo East, 1987
- ¿Qué arquitectura de ADC es la adecuada para su aplicación? Artículo de Walt Kester
- Glosario de ADC y DAC en Wayback Machine (archivado el 24 de noviembre de 2009) Define términos técnicos de uso común
- Introducción al ADC en AVR – Conversión analógica a digital con microcontroladores Atmel
- Procesamiento de señales y aspectos del sistema de los ADC entrelazados en el tiempo
- Modelo MATLAB Simulink de un ADC de rampa simple











