Constantes de estabilidad de los complejos
This article provides insufficient context for those unfamiliar with the subject. (February 2015) |
En química de coordinación , una constante de estabilidad (también llamada constante de formación o constante de enlace ) es una constante de equilibrio para la formación de un complejo en solución. Es una medida de la fuerza de la interacción entre los reactivos que se unen para formar el complejo . Hay dos tipos principales de complejos: compuestos formados por la interacción de un ion metálico con un ligando y complejos supramoleculares, como complejos huésped-anfitrión y complejos de aniones. La(s) constante(s) de estabilidad proporciona(n) la(s) información necesaria para calcular la(s) concentración(es) del(de los) complejo(s) en solución. Hay muchas áreas de aplicación en química, biología y medicina.
Historia
Jannik Bjerrum (hijo de Niels Bjerrum ) desarrolló el primer método general para la determinación de las constantes de estabilidad de los complejos de metal-amina en 1941. [1] Beck y Nagypál han resumido las razones por las que esto ocurrió en una fecha tan tardía, casi 50 años después de que Alfred Werner propusiera las estructuras correctas para los complejos de coordinación. [2] La clave del método de Bjerrum fue el uso del electrodo de vidrio y el medidor de pH, desarrollados recientemente en ese momento, para determinar la concentración de iones de hidrógeno en solución. Bjerrum reconoció que la formación de un complejo metálico con un ligando era una especie de equilibrio ácido-base : hay competencia por el ligando, L, entre el ion metálico, M n+ , y el ion hidrógeno, H + . Esto significa que hay dos equilibrios simultáneos que deben considerarse. En lo que sigue, se omiten las cargas eléctricas en aras de la generalidad. Los dos equilibrios son
Por lo tanto, al seguir la concentración de iones de hidrógeno durante una titulación de una mezcla de M y HL con una base y conocer la constante de disociación ácida de HL, se pudo determinar la constante de estabilidad para la formación de ML. Bjerrum procedió a determinar las constantes de estabilidad para sistemas en los que se pueden formar muchos complejos.
En los veinte años siguientes se produjo una auténtica explosión en el número de constantes de estabilidad que se determinaban. Se descubrieron relaciones como la serie de Irving-Williams . Los cálculos se hacían a mano utilizando los llamados métodos gráficos. Las matemáticas que sustentaban los métodos utilizados en este período están resumidas por Rossotti y Rossotti [3] . El siguiente desarrollo clave fue el uso de un programa informático, LETAGROP [4] [5] para realizar los cálculos. Esto permitió el examen de sistemas demasiado complicados para ser evaluados mediante cálculos manuales. Posteriormente, se desarrollaron programas informáticos capaces de manejar equilibrios complejos en general, como SCOGS [6] y MINIQUAD [7], de modo que hoy en día la determinación de constantes de estabilidad se ha convertido casi en una operación "rutinaria". Se pueden encontrar los valores de miles de constantes de estabilidad en dos bases de datos comerciales. [8] [9]
Teoría
La formación de un complejo entre un ion metálico, M, y un ligando, L, es de hecho una reacción de sustitución. Por ejemplo, en soluciones acuosas , los iones metálicos estarán presentes como iones aqua , por lo que la reacción para la formación del primer complejo podría escribirse como
La constante de equilibrio para esta reacción está dada por
[L] debe leerse como "la concentración de L" y lo mismo para los demás términos entre corchetes. La expresión se puede simplificar en gran medida eliminando aquellos términos que son constantes. El número de moléculas de agua unidas a cada ion metálico es constante. En soluciones diluidas, la concentración de agua es efectivamente constante. La expresión se convierte en
Siguiendo esta simplificación se puede dar una definición general para el equilibrio general.
La definición se puede ampliar fácilmente para incluir cualquier número de reactivos. Los reactivos no siempre tienen que ser un metal y un ligando, sino que pueden ser cualquier especie que forme un complejo. Las constantes de estabilidad definidas de esta manera son constantes de asociación . Esto puede generar cierta confusión, ya que los valores de p K a son constantes de disociación . En los programas informáticos de uso general, se acostumbra a definir todas las constantes como constantes de asociación. La relación entre los dos tipos de constantes se da en las constantes de asociación y disociación .
Constantes escalonadas y acumulativas
Una constante acumulativa o global, denominada β , es la constante para la formación de un complejo a partir de reactivos. Por ejemplo, la constante acumulativa para la formación de ML 2 se expresa mediante
- ;
Las constantes escalonadas, K1 y K2 , se refieren a la formación de los complejos paso a paso.
- ;
- ;
Resulta que
Una constante acumulativa siempre se puede expresar como el producto de constantes escalonadas. A la inversa, cualquier constante escalonada se puede expresar como un cociente de dos o más constantes generales. No existe una notación acordada para las constantes escalonadas, aunque se puede utilizar un símbolo como KL
-MlA veces se encuentra en la literatura. Es una buena práctica especificar cada constante de estabilidad explícitamente, como se ilustra arriba.
Productos de hidrólisis
La formación de un complejo hidroxo es un ejemplo típico de una reacción de hidrólisis. Una reacción de hidrólisis es aquella en la que un sustrato reacciona con agua, dividiendo una molécula de agua en iones hidróxido e hidrógeno. En este caso, el ion hidróxido forma un complejo con el sustrato.
- ;
En el agua, la concentración de hidróxido está relacionada con la concentración de iones de hidrógeno por la constante de autoionización , K w .
La expresión para la concentración de hidróxido se sustituye en la expresión de la constante de formación.
En general, para la reacción
En la literatura más antigua, el valor de log K se suele citar para una constante de hidrólisis. El valor de log β * se suele citar para un complejo hidrolizado con la fórmula química genérica M p L q (OH) r .
Complejos ácido-base
Se puede considerar que un ácido de Lewis , A, y una base de Lewis , B, forman un complejo AB.
Hay tres teorías principales relacionadas con la fuerza de los ácidos y bases de Lewis y las interacciones entre ellos.
- Teoría ácido-base dura y blanda ( HSAB ). [10] Se utiliza principalmente con fines cualitativos.
- Drago y Wayland propusieron una ecuación de dos parámetros que predice la entalpía estándar de formación de un gran número de aductos con bastante precisión. −Δ H ⊖ (A − B) = E A E B + C A C B . Los valores de los parámetros E y C están disponibles. [11]
- Números de donantes de Guttmann : para las bases, el número se deriva de la entalpía de reacción de la base con pentacloruro de antimonio en 1,2-dicloroetano como disolvente. Para los ácidos, el número de aceptor se deriva de la entalpía de reacción del ácido con óxido de trifenilfosfina . [12]
Para más detalles, véase: reacción ácido-base , catálisis ácida , extracción (química).
Termodinámica
La termodinámica de la formación de complejos de iones metálicos proporciona mucha información significativa. [13] En particular, es útil para distinguir entre efectos entálpicos y entrópicos . Los efectos entálpicos dependen de la fuerza de los enlaces y los efectos entrópicos tienen que ver con cambios en el orden/desorden de la solución en su conjunto. El efecto quelato, que se muestra a continuación, se explica mejor en términos de termodinámica.
Una constante de equilibrio está relacionada con el cambio de energía libre de Gibbs estándar para la reacción.
R es la constante de los gases y T es la temperatura absoluta . A 25 °C, Δ G ⊖ = (−5,708 kJ mol −1 ) ⋅ log β . La energía libre se compone de un término de entalpía y un término de entropía.
El cambio de entalpía estándar se puede determinar mediante calorimetría o utilizando la ecuación de Van 't Hoff , aunque es preferible el método calorimétrico. Una vez que se han determinado tanto el cambio de entalpía estándar como la constante de estabilidad, el cambio de entropía estándar se calcula fácilmente a partir de la ecuación anterior.
El hecho de que las constantes de formación escalonada de complejos del tipo ML n disminuyan en magnitud a medida que n aumenta puede explicarse en parte en términos del factor de entropía. Tomemos el caso de la formación de complejos octaédricos .
Para el primer paso, m = 6, n = 1 y el ligando puede ir en uno de los 6 sitios. Para el segundo paso, m = 5 y el segundo ligando puede ir en uno de los 5 sitios. Esto significa que hay más aleatoriedad en el primer paso que en el segundo; Δ S ⊖ es más positivo, por lo que Δ G ⊖ es más negativo y . La relación de las constantes de estabilidad escalonada se puede calcular sobre esta base, pero las relaciones experimentales no son exactamente las mismas porque Δ H ⊖ no es necesariamente el mismo para cada paso. [14] Las excepciones a esta regla se analizan a continuación, en #efecto quelato y #Factores geométricos.
Dependencia de la fuerza iónica
La constante de equilibrio termodinámico, K ⊖ , para el equilibrio
se puede definir [15] como
donde {ML} es la actividad de la especie química ML, etc. K ⊖ es adimensional , ya que la actividad es adimensional. Las actividades de los productos se colocan en el numerador, las actividades de los reactivos se colocan en el denominador. Consulte el coeficiente de actividad para obtener una derivación de esta expresión.
Dado que la actividad es el producto de la concentración y el coeficiente de actividad ( γ ), la definición también podría escribirse como
donde [ML] representa la concentración de ML y Γ es un cociente de coeficientes de actividad. Esta expresión se puede generalizar como

Para evitar las complicaciones que implica el uso de actividades, las constantes de estabilidad se determinan , cuando es posible, en un medio que consiste en una solución de un electrolito de fondo a alta fuerza iónica , es decir, en condiciones en las que se puede suponer que Γ es siempre constante. [15] Por ejemplo, el medio podría ser una solución de 0,1 mol dm −3 de nitrato de sodio o 3 mol dm −3 de perclorato de sodio . Cuando Γ es constante, se puede ignorar y se obtiene la expresión general en teoría, anterior.
Todos los valores de constante de estabilidad publicados se refieren al medio iónico específico utilizado en su determinación y se obtienen diferentes valores con diferentes condiciones, como se ilustra para el complejo CuL (L = glicinato ). Además, los valores de la constante de estabilidad dependen del electrolito específico utilizado, ya que el valor de Γ es diferente para diferentes electrolitos, incluso con la misma fuerza iónica . No es necesario que haya ninguna interacción química entre las especies en equilibrio y el electrolito de fondo, pero dichas interacciones pueden ocurrir en casos particulares. Por ejemplo, los fosfatos forman complejos débiles con metales alcalinos , por lo que, al determinar constantes de estabilidad que involucran fosfatos, como ATP , el electrolito de fondo utilizado será, por ejemplo, una sal de tetraalquilamonio . Otro ejemplo involucra al hierro (III) que forma complejos débiles con haluro y otros aniones, pero no con iones de perclorato .
Cuando las constantes publicadas se refieren a una fuerza iónica distinta de la requerida para una aplicación particular, se pueden ajustar mediante la teoría de iones específicos (SIT) y otras teorías. [17]
Dependencia de la temperatura
Todas las constantes de equilibrio varían con la temperatura según la ecuación de Van 't Hoff [18]
Alternativamente
R es la constante de los gases y T es la temperatura termodinámica. Por lo tanto, para las reacciones exotérmicas , donde el cambio de entalpía estándar , Δ H ⊖ , es negativo, K disminuye con la temperatura, pero para las reacciones endotérmicas , donde Δ H ⊖ es positivo, K aumenta con la temperatura.
Factores que afectan las constantes de estabilidad de los complejos
El efecto quelato

Considérense los dos equilibrios, en solución acuosa, entre el ion cobre (II), Cu 2+ y etilendiamina (en) por un lado y la metilamina , MeNH 2 por el otro.
En la primera reacción, el ligando bidentado etilendiamina forma un complejo quelato con el ion cobre. La quelación da como resultado la formación de un anillo de cinco miembros. En la segunda reacción, el ligando bidentado se reemplaza por dos ligandos monodentados de metilamina de aproximadamente el mismo poder donante, lo que significa que la entalpía de formación de enlaces Cu-N es aproximadamente la misma en las dos reacciones. En condiciones de concentraciones iguales de cobre y cuando la concentración de metilamina es el doble de la concentración de etilendiamina, la concentración del complejo bidentado será mayor que la concentración del complejo con 2 ligandos monodentados. El efecto aumenta con el número de anillos quelatos, por lo que la concentración del complejo EDTA , que tiene seis anillos quelatos, es mucho mayor que un complejo correspondiente con dos ligandos monodentados donantes de nitrógeno y cuatro ligandos carboxilato monodentados. Por tanto, el fenómeno del efecto quelato es un hecho empírico firmemente establecido : en condiciones comparables, la concentración de un complejo quelato será mayor que la concentración de un complejo análogo con ligandos monodentados.
El enfoque termodinámico para explicar el efecto quelato considera la constante de equilibrio de la reacción: cuanto mayor sea la constante de equilibrio, mayor será la concentración del complejo.
Cuando la concentración analítica de metilamina es el doble que la de etilendiamina y la concentración de cobre es la misma en ambas reacciones, la concentración [Cu(en)] 2+ es mucho mayor que la concentración [Cu(MeNH 2 ) 2 ] 2+ porque β 11 ≫ β 12 .
La diferencia entre las dos constantes de estabilidad se debe principalmente a la diferencia en el cambio de entropía estándar, Δ S ⊖ . En la reacción con el ligando quelante hay dos partículas a la izquierda y una a la derecha, mientras que en la ecuación con el ligando monodentado hay tres partículas a la izquierda y una a la derecha. Esto significa que se pierde menos entropía de desorden cuando se forma el complejo quelante que cuando se forma el complejo con ligandos monodentados. Este es uno de los factores que contribuyen a la diferencia de entropía. Otros factores incluyen cambios de solvatación y formación de anillos. Algunos datos experimentales para ilustrar el efecto se muestran en la siguiente tabla. [19]
Equilibrio registro β Δ G ⊖ /kJ mol −1 ΔH ⊖ /kJ mol −1 − T Δ S ⊖ /kJ mol −1 Cd2 + + 4MeNH2 ⇌ Cd( MeNH
2)2+
46.55 −37,4 −57,3 19.9 Cd 2+ + 2 en ⇌ Cd(en)2+
210.62 −60,67 −56,48 -4,19

Estos datos muestran que los cambios de entalpía estándar son, de hecho, aproximadamente iguales para las dos reacciones y que la razón principal por la que el complejo quelato es mucho más estable es que el término de entropía estándar es mucho menos desfavorable; de hecho, es favorable en este caso. En general, es difícil explicar con precisión los valores termodinámicos en términos de cambios en la solución a nivel molecular, pero está claro que el efecto quelato es predominantemente un efecto de la entropía. Otras explicaciones, incluida la de Schwarzenbach, [20] se discuten en Greenwood y Earnshaw. [19]

El efecto quelato aumenta a medida que aumenta el número de anillos quelatos. Por ejemplo, el complejo [Ni(dien) 2 )] 2+ es más estable que el complejo [Ni(en) 3 )] 2+ ; ambos complejos son octaédricos con seis átomos de nitrógeno alrededor del ion níquel, pero dien ( dietilentriamina , 1,4,7-triazaheptano) es un ligando tridentado y en es bidentado. El número de anillos quelatos es uno menos que el número de átomos donantes en el ligando. El EDTA (ácido etilendiaminotetraacético) tiene seis átomos donantes, por lo que forma complejos muy fuertes con cinco anillos quelatos. Los ligandos como el DTPA , que tienen ocho átomos donantes, se utilizan para formar complejos con iones metálicos grandes, como iones lantánidos o actínidos , que suelen formar complejos de 8 o 9 coordenadas. Los anillos quelatos de 5 y 6 miembros dan lugar a los complejos más estables. Los anillos de 4 miembros están sujetos a tensión interna debido al pequeño ángulo entre enlaces que tiene el anillo. El efecto quelante también se reduce con anillos de 7 y 8 miembros, porque los anillos más grandes son menos rígidos, por lo que se pierde menos entropía al formarlos.
Desprotonación de grupos alifáticos –OH


La eliminación de un protón de un grupo alifático –OH es difícil de lograr en solución acuosa porque la energía requerida para este proceso es bastante grande. Por lo tanto, la ionización de los grupos alifáticos –OH ocurre en solución acuosa solo en circunstancias especiales. Una de esas circunstancias se encuentra con los compuestos que contienen la subestructura H 2 N–C–C–OH. Por ejemplo, los compuestos que contienen la subestructura 2-aminoetanol pueden formar complejos metal-quelato con la forma desprotonada, H 2 N–C–C–O − . El efecto quelato proporciona la energía adicional necesaria para romper el enlace O–H.
Un ejemplo importante es el de la molécula tris . Esta molécula debe utilizarse con precaución como agente tampón , ya que formará complejos quelantes con iones como Fe 3+ y Cu 2+ .
El efecto macrocíclico
Se encontró que la estabilidad del complejo de cobre (II) con el ligando macrocíclico ciclamo (1,4,8,11-tetraazaciclotetradecano) era mucho mayor de lo esperado en comparación con la estabilidad del complejo con la amina de cadena abierta correspondiente . [21] Este fenómeno se denominó efecto macrocíclico y también se interpretó como un efecto de entropía. Sin embargo, estudios posteriores sugirieron que estaban involucrados tanto los factores de entalpía como de entropía. [22]
Una diferencia importante entre los ligandos macrocíclicos y los ligandos de cadena abierta (quelantes) es que tienen selectividad por los iones metálicos, en función del tamaño de la cavidad en la que se inserta el ion metálico cuando se forma un complejo. Por ejemplo, el éter corona 18-corona-6 forma complejos mucho más fuertes con el ion potasio , K +, que con el ion sodio , más pequeño , Na + . [23]
En la hemoglobina, un ion de hierro(II) se encuentra complejado por un anillo de porfirina macrocíclica. El artículo hemoglobina afirma incorrectamente que la oxihemoglobina contiene hierro(III). Ahora se sabe que el hierro(II) en la hemoglobina es un complejo de bajo espín , mientras que en la oxihemoglobina es un complejo de alto espín. El ion Fe2 + de bajo espín encaja perfectamente en la cavidad del anillo de porfirina, pero el hierro(II) de alto espín es significativamente más grande y el átomo de hierro es forzado a salir del plano del ligando macrocíclico. [24] Este efecto contribuye a la capacidad de la hemoglobina de unirse al oxígeno de forma reversible en condiciones biológicas. En la vitamina B12, un ion de cobalto(II) se encuentra retenido en un anillo de corrina . La clorofila es un complejo macrocíclico de magnesio(II).
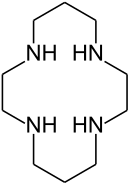 |  |
| Ciclamo | Porfina , la porfirina más simple . |
 |
| Estructuras de éteres corona comunes : 12-corona-4 , 15-corona-5 , 18-corona-6 , dibenzo-18-corona-6 y un éter aza-corona |
Factores geométricos
Las constantes de formación sucesivas por pasos K n en una serie como ML n ( n = 1, 2, ...) suelen disminuir a medida que n aumenta. Las excepciones a esta regla ocurren cuando la geometría de los complejos ML n no es la misma para todos los miembros de la serie. El ejemplo clásico es la formación del complejo de diaminplata(I) [Ag(NH 3 ) 2 ] + en solución acuosa.
En este caso, K 2 > K 1 . La razón de esto es que, en solución acuosa, el ion escrito como Ag + en realidad existe como la especie aqua tetraédrica de cuatro coordenadas [Ag(H 2 O) 4 ] + . El primer paso es entonces una reacción de sustitución que implica el desplazamiento de una molécula de agua ligada por amoníaco formando el complejo tetraédrico [Ag(NH 3 )(H 2 O) 3 ] + . En el segundo paso, todos los ligandos aqua se pierden y se forma un producto lineal de dos coordenadas [H 3 N–Ag–NH 3 ] + . El examen de los datos termodinámicos [25] muestra que la diferencia en el cambio de entropía es el principal contribuyente a la diferencia en las constantes de estabilidad para las dos reacciones de complexación.
| equilibrio | ΔH ⊖ /kJ mol −1 | Δ S ⊖ /J K −1 mol −1 |
|---|---|---|
| Ag ++ NH3⇌ [Ag( NH3 ) ] + | -21,4 | 8.66 |
| [Ag(NH 3 )] + + NH 3 ⇌ [Ag(NH 3 ) 2 ] + | -35,2 | -61,26 |
Existen otros ejemplos en los que el cambio es de octaédrico a tetraédrico, como en la formación de [CoCl 4 ] 2− a partir de [Co(H 2 O) 6 ] 2+ .
Clasificación de los iones metálicos
Ahrland, Chatt y Davies propusieron que los iones metálicos podrían describirse como clase A si formaban complejos más fuertes con ligandos cuyos átomos donantes son nitrógeno , oxígeno o flúor que con ligandos cuyos átomos donantes son fósforo , azufre o cloro y clase B si lo contrario es cierto. [26] Por ejemplo, Ni 2+ forma complejos más fuertes con aminas que con fosfinas , pero Pd 2+ forma complejos más fuertes con fosfinas que con aminas. Más tarde, Pearson propuso la teoría de ácidos y bases duros y blandos (teoría HSAB). [27] En esta clasificación, los metales de clase A son ácidos duros y los metales de clase B son ácidos blandos. Algunos iones, como el cobre (I), se clasifican como limítrofes. Los ácidos duros forman complejos más fuertes con bases duras que con bases blandas. En términos generales, las interacciones duro-duro son predominantemente de naturaleza electrostática, mientras que las interacciones blando-blando son predominantemente de naturaleza covalente. La teoría HSAB, aunque útil, es solo semicuantitativa. [28]
La dureza de un ion metálico aumenta con el estado de oxidación. Un ejemplo de este efecto lo da el hecho de que el Fe 2+ tiende a formar complejos más fuertes con ligandos donadores de N que con ligandos donadores de O , pero lo opuesto es cierto para el Fe 3+ .
Efecto del radio iónico
La serie de Irving-Williams se refiere a iones metálicos divalentes, octaédricos y de alto espín de la primera serie de transición. Coloca las estabilidades de los complejos en el orden
- Mn < Fe < Co < Ni < Cu > Zn
Se encontró que este orden se cumple para una amplia variedad de ligandos. [29] Hay tres vertientes para la explicación de la serie.
- Se espera que el radio iónico disminuya regularmente de Mn 2+ a Zn 2+ . Esta sería la tendencia periódica normal y explicaría el aumento general en la estabilidad.
- La energía de estabilización del campo cristalino (CFSE) aumenta desde cero en el caso del manganeso(II) hasta un máximo en el caso del níquel(II). Esto hace que los complejos sean cada vez más estables. La CFSE vuelve a cero en el caso del zinc(II).
- Aunque el CFSE para el cobre (II) es menor que para el níquel (II), los complejos octaédricos de cobre (II) están sujetos al efecto Jahn-Teller , que da como resultado un complejo con mayor estabilidad.
Otro ejemplo del efecto del radio iónico es el aumento constante de la estabilidad de los complejos con un ligando dado a lo largo de la serie de iones lantánidos trivalentes, un efecto de la conocida contracción de los lantánidos .
Aplicaciones
Los valores constantes de estabilidad se explotan en una amplia variedad de aplicaciones. La terapia de quelación se utiliza en el tratamiento de varias enfermedades relacionadas con metales, como la sobrecarga de hierro en pacientes con β- talasemia que han recibido transfusiones de sangre. El ligando ideal se une al ion metálico objetivo y no a otros, pero este grado de selectividad es muy difícil de lograr. El fármaco sintético deferiprona logra selectividad al tener dos átomos donantes de oxígeno de modo que se une a Fe 3+ con preferencia a cualquiera de los otros iones divalentes que están presentes en el cuerpo humano, como Mg 2+ , Ca 2+ y Zn 2+ . El tratamiento del envenenamiento por iones como Pb 2+ y Cd 2+ es mucho más difícil ya que ambos son iones divalentes y la selectividad es más difícil de lograr. [30] El exceso de cobre en la enfermedad de Wilson se puede eliminar con penicilamina o trietilen tetramina (TETA). La Administración de Alimentos y Medicamentos de Estados Unidos ha aprobado el DTPA para el tratamiento del envenenamiento por plutonio .
El DTPA también se utiliza como agente complejante del gadolinio en la mejora del contraste de la resonancia magnética . El requisito en este caso es que el complejo sea muy fuerte, ya que el Gd 3+ es muy tóxico. La gran constante de estabilidad del ligando octadentado garantiza que la concentración de Gd 3+ libre sea casi insignificante, ciertamente muy por debajo del umbral de toxicidad. [31] Además, el ligando ocupa solo 8 de los 9 sitios de coordinación en el ion de gadolinio. El noveno sitio está ocupado por una molécula de agua que intercambia rápidamente con el fluido que lo rodea y es este mecanismo el que convierte al complejo paramagnético en un reactivo de contraste.
El EDTA forma complejos tan fuertes con la mayoría de los cationes divalentes que tiene muchos usos . Por ejemplo, suele estar presente en el detergente para lavar ropa y actúa como suavizante de agua al secuestrar los iones de calcio y magnesio.
La selectividad de los ligandos macrocíclicos se puede utilizar como base para la construcción de un electrodo selectivo de iones . Por ejemplo, existen electrodos selectivos de potasio que utilizan el antibiótico macrocíclico natural valinomicina .
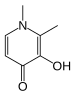 |  |  |  |
| Deferiprona | Penicilamina | trietilentetramina , TETA | Ácido etilendiaminotetraacético , EDTA |
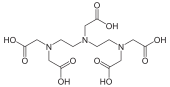 | 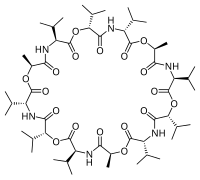 |  | |
| Ácido dietilentriaminopentaacético , DTPA | Valinomicina | Fosfato de tri -n -butilo |
Una resina de intercambio iónico como Chelex 100 , que contiene ligandos quelantes unidos a un polímero , se puede utilizar en ablandadores de agua y en técnicas de separación cromatográfica . En la extracción con disolventes, la formación de complejos eléctricamente neutros permite extraer cationes en disolventes orgánicos. Por ejemplo , en el reprocesamiento de combustible nuclear, el uranio (VI) y el plutonio (VI) se extraen en queroseno como los complejos [MO 2 (TBP) 2 (NO 3 ) 2 ] (TBP = fosfato de tri- n -butilo ). En la catálisis de transferencia de fase , una sustancia que es insoluble en un disolvente orgánico se puede hacer soluble mediante la adición de un ligando adecuado. Por ejemplo, las oxidaciones de permanganato de potasio se pueden lograr añadiendo una cantidad catalítica de un éter corona y una pequeña cantidad de disolvente orgánico a la mezcla de reacción acuosa, de modo que la reacción de oxidación se produzca en la fase orgánica.
En todos estos ejemplos, el ligando se elige en función de las constantes de estabilidad de los complejos formados. Por ejemplo, el TBP se utiliza en el reprocesamiento de combustible nuclear porque (entre otras razones) forma un complejo lo suficientemente fuerte como para que se pueda realizar la extracción con disolvente, pero lo suficientemente débil como para que el complejo pueda destruirse con ácido nítrico para recuperar el catión uranilo en forma de complejos de nitrato , como [UO 2 (NO 3 ) 4 ] 2− en la fase acuosa.
Complejos supramoleculares
Los complejos supramoleculares se mantienen unidos por enlaces de hidrógeno, fuerzas hidrofóbicas, fuerzas de van der Waals, interacciones π-π y efectos electrostáticos, todos los cuales pueden describirse como enlaces no covalentes . Las aplicaciones incluyen reconocimiento molecular , química anfitrión-huésped y sensores de aniones .
Una aplicación típica en el reconocimiento molecular implicó la determinación de constantes de formación para complejos formados entre una molécula de urea sustituida tripodal y varios sacáridos . [32] El estudio se llevó a cabo utilizando un solvente no acuoso y mediciones de desplazamiento químico por RMN . El objetivo era examinar la selectividad con respecto a los sacáridos.
Un ejemplo del uso de complejos supramoleculares en el desarrollo de quimiosensores lo proporciona el uso de conjuntos de metales de transición para detectar ATP . [33]
La formación de complejos aniónicos se puede lograr encapsulando el anión en una jaula adecuada. La selectividad se puede diseñar diseñando la forma de la jaula. Por ejemplo, los aniones dicarboxilato se podrían encapsular en la cavidad elipsoidal en una gran estructura macrocíclica que contenga dos iones metálicos. [34]
Métodos experimentales
El método desarrollado por Bjerrum sigue siendo el principal método en uso hoy en día, aunque la precisión de las mediciones ha aumentado considerablemente. Lo más común es que primero se acidifique una solución que contiene el ion metálico y el ligando en un medio de alta fuerza iónica hasta el punto en que el ligando esté completamente protonado . Luego, esta solución se titula , a menudo por medio de un autotitulador controlado por computadora, con una solución de base libre de CO2 . La concentración o actividad del ion hidrógeno se monitorea por medio de un electrodo de vidrio. El conjunto de datos utilizado para el cálculo tiene tres componentes: una declaración que define la naturaleza de las especies químicas que estarán presentes, llamada modelo del sistema, detalles sobre las concentraciones de los reactivos utilizados en la titulación y, finalmente, las mediciones experimentales en forma de pares de título y pH (o fem ).
Se pueden utilizar otros electrodos selectivos de iones (ISE). Por ejemplo, se puede utilizar un electrodo de fluoruro para determinar complejos de estabilidad de complejos fluorados de un ion metálico.
No siempre es posible utilizar un ISE. Si es así, la titulación se puede controlar mediante otros tipos de medición. La espectroscopia ultravioleta-visible , la espectroscopia de fluorescencia y la espectroscopia de RMN son las alternativas más utilizadas. La práctica actual consiste en tomar mediciones de absorbancia o fluorescencia en un rango de longitudes de onda y ajustar estos datos simultáneamente. También se pueden ajustar varios desplazamientos químicos de RMN .
El modelo químico incluirá valores de las constantes de protonación del ligando, que se habrán determinado en experimentos separados, un valor para log K w y estimaciones de las constantes de estabilidad desconocidas de los complejos formados. Estas estimaciones son necesarias porque el cálculo utiliza un algoritmo de mínimos cuadrados no lineal . Las estimaciones se obtienen generalmente por referencia a un sistema químicamente similar. Las bases de datos de constantes de estabilidad [8] [9] pueden ser muy útiles para encontrar valores de constantes de estabilidad publicados para complejos relacionados.
En algunos casos sencillos, los cálculos se pueden realizar en una hoja de cálculo. [35] De lo contrario, los cálculos se realizan con la ayuda de programas informáticos de uso general. Los programas más utilizados son:
- Datos potenciométricos y/o espectrofotométricos: PSEQUAD [36]
- Datos potenciométricos: HYPERQUAD, [37] BEST, [38] ReactLab pH PRO
- Datos espectrofotométricos: HypSpec, SQUAD, [39] SPECFIT, [40] [41] ReactLab EQUILIBRIA. [42]
- Datos de RMN HypNMR, [43] WINEQNMR2 Archivado el 14 de julio de 2019 en Wayback Machine. [44]
En bioquímica, las constantes de formación de aductos se pueden obtener a partir de mediciones de calorimetría de titulación isotérmica (ITC). Esta técnica proporciona tanto la constante de estabilidad como el cambio de entalpía estándar para el equilibrio. [45] Está limitada principalmente, por la disponibilidad de software, a complejos de estequiometría 1:1.
Datos evaluados críticamente
Las siguientes referencias son revisiones críticas de constantes de estabilidad publicadas para varias clases de ligandos. Todas estas revisiones son publicadas por la IUPAC y el texto completo está disponible, sin cargo, en formato pdf.
- etilendiamina (en) [46]
- Ácido nitrilotriacético (NTA) [47]
- ácidos aminopolicarboxílicos (complexonas) [48]
- Alfahidroxiácidos y otros ácidos hidroxicarboxílicos [49] [50]
- éteres corona [51]
- ácidos fosfónicos [52] [53]
- imidazoles e histaminas [54]
- Aminoácidos con cadenas laterales polares [55]
- nucleótidos [56]
- acetilacetona [57]
- general [58]
- Especiación química de metales pesados de importancia ambiental con ligandos inorgánicos. Parte 1: Hg 2+ –Cl − , OH − , CO2−
3, ENTONCES2−
4, y PO3−
4sistemas. [59] - Especiación química de metales ambientalmente significativos con ligandos inorgánicos Parte 2: Cu 2+ –OH − , Cl − , CO2−
3, ENTONCES2−
4, y PO3−
4sistemas acuosos [60] - Especiación química de metales ambientalmente significativos con ligandos inorgánicos Parte 3: Pb 2+ –OH − , Cl − , CO2−
3, ENTONCES2−
4, y PO3−
4sistemas [61] - Especiación química de metales de importancia ambiental con ligandos inorgánicos. Parte 4: Cd 2+ –OH − , Cl − , CO2−
3, ENTONCES2−
4, y PO3−
4sistemas [62]
Bases de datos
- La base de datos Ki es una base de datos de dominio público de afinidades de unión (Ki) publicadas de medicamentos y compuestos químicos para receptores, transportadores de neurotransmisores, canales iónicos y enzimas.
- BindingDB es una base de datos de dominio público de afinidades de unión medidas, que se centra principalmente en las interacciones de proteínas consideradas objetivos farmacológicos con moléculas pequeñas similares a fármacos.
Referencias
- ^ Bjerrum, J. (1941). "Formación de metal-amina en solución acuosa" . Copenhague: Haase.
- ^ Beck, MT; Nagypál, I. (1990). "Capítulo 1". Química de equilibrios complejos . Horwood. ISBN 0-85312-143-5.
- ^ Rossotti, FJC; Rossotti, H. (1961). La determinación de constantes de estabilidad . McGraw–Hill.
- ^ Dyrssen, D.; Ingri, N.; Sillen, LG (1961). "Mapeo de pozos: un enfoque general para el refinamiento por computadora de las constantes de estabilidad". Acta Chem. Scand . 15 : 694–696. doi : 10.3891/acta.chem.scand.15-0694 .
- ^ Ingri, N.; Sillen, LG (1964). "Computadoras de alta velocidad como complemento a los métodos gráficos, IV. Una versión ALGOL de LETAGROP-VRID". Arkiv para Kemi . 23 : 97-121.
- ^ Sayce, IG (1968). "Cálculos informáticos de las constantes de equilibrio de las especies presentes en mezclas de iones metálicos y reactivos complejantes". Talanta . 15 (12): 1397–1421. doi :10.1016/0039-9140(68)80200-0. PMID 18960446.
- ^ Sabatini, A.; Vacca, A.; Gans, P. (1974). "MINIQUAD - Un programa informático general para el cálculo de constantes de estabilidad". Talanta . 21 (1): 53–77. doi :10.1016/0039-9140(74)80063-9. PMID 18961420.
- ^ ab IUPAC SC-Database Una base de datos completa de datos publicados sobre constantes de equilibrio de complejos metálicos y ligandos
- ^ ab Base de datos de referencia estándar del NIST 46 Constantes de estabilidad críticamente seleccionadas del NIST de complejos metálicos: versión 8.0 (Esta base de datos ha sido descontinuada).
- ^ Pearson, RG (1997). Dureza química: aplicaciones de moléculas a sólidos . Springer-VCH. ISBN 3-527-29482-1.
- ^ Drago, RS; Wong, N.; Bilgrien, C.; Vogel, C. (1987). " Parámetros E y C de las constantes de sustituyentes de Hammett y uso de E y C para comprender las energías de enlace cobalto-carbono". Inorg. Chem . 26 (1): 9–14. doi :10.1021/ic00248a003.
- ^ Gutmann, V. (1978). El enfoque donante-aceptor de las interacciones moleculares . Springer. ISBN 0-306-31064-3.
- ^ Rossotti, FJC (1960). "La termodinámica de la formación de complejos de iones metálicos en solución". En Lewis, J.; RG, Wilkins (eds.). Química de coordinación moderna . Nueva York: Interscience.
- ^ Beck, MT; Nagypál, I. (1990). Química de equilibrios complejos . Horwood. ISBN 0-85312-143-5.Secciones 3.5.1.2, 6.6.1 y 6.6.2
- ^ ab Rossotti, FJC; Rossotti, H. (1961). "Capítulo 2: Cocientes de actividad y concentración". La determinación de constantes de estabilidad . McGraw–Hill.
- ^ Gergely, A.; Nagypál, I.; E., Farkas (1974). "A réz(II)-aminosav törzskomplexek vizes oldatában lejátszodó protoncsere-reakciók kinetikájának NMR-vizsgálata" [Estudio de RMN del proceso de intercambio de protones en soluciones acuosas de complejos parentales de cobre (II)-aminoácido]. Magyar Kémiai Folyóirat . 80 : 545–549.
- ^ "Proyecto: Correcciones de fuerza iónica para constantes de estabilidad". IUPAC . Archivado desde el original el 29 de octubre de 2008. Consultado el 23 de noviembre de 2008 .
- ^ Atkins, PW; De Paula, J. (2006). "Sección 7.4: La respuesta de los equilibrios a la temperatura". Química física . Oxford University Press. ISBN 0-19-870072-5.
- ^ ab Greenwood, Norman N. ; Earnshaw, Alan (1997). Química de los elementos (2.ª ed.). Butterworth-Heinemann . ISBN 978-0-08-037941-8.pág. 910
- ^ Schwarzenbach, G. (1952). "Der Chelateffekt" [El efecto quelato]. Helv. Chim. Acta . 35 (7): 2344–2359. doi :10.1002/hlca.19520350721.
- ^ Cabinness, DK; Margerum, DW (1969). "Efecto macrocíclico sobre la estabilidad de los complejos de tetramina de cobre (II)". J. Am. Chem. Soc . 91 (23): 6540–6541. doi :10.1021/ja01051a091.
- ^ Lindoy, LF (1990). "Capítulo 6: Consideraciones termodinámicas". La química de los complejos de ligandos macrocíclicos . Cambridge University Press. ISBN 0-521-40985-3.
- ^ Pedersen, CJ (1967). "Poliéteres cíclicos y sus complejos con sales metálicas". J. Am. Chem. Soc . 89 (26): 7017–7036. doi :10.1021/ja01002a035.
- ^ Greenwood, Norman N. ; Earnshaw, Alan (1997). Química de los elementos (2.ª ed.). Butterworth-Heinemann . ISBN 978-0-08-037941-8.pág. 1100, Figura 25.7
- ^ Lundeen, M.; Hugus, ZZ (1992). "Un estudio calorimétrico de algunos equilibrios de formación de complejos de iones metálicos". Thermochim. Acta . 196 (1): 93–103. doi :10.1016/0040-6031(92)85009-K.
- ^ Ahrland, S.; Chatt, J.; Davies, NR (1958). "Las afinidades relativas de los átomos de ligando por las moléculas y los iones aceptores". Quart. Rev. 12 ( 3): 265–276. doi :10.1039/QR9581200265.
- ^ Pearson, RG (1963). "Ácidos y bases duros y blandos". J. Am. Chem. Soc . 85 (22): 3533–3539. doi :10.1021/ja00905a001.
- ^ Beck, MT; Nagypál, I. (1990). Química de equilibrios complejos . Horwood. pág. 354. ISBN 0-85312-143-5.
- ^ Irving, HMNH; Williams, RJP (1953). "La estabilidad de los complejos de metales de transición". J. Chem. Soc. : 3192–3210. doi :10.1039/JR9530003192.
- ^ Arena, G.; Contino, A.; Longo, E.; Sciotto, D.; Spoto, G. (2001). "Complejación selectiva de Pb2 + blando y Hg2 + mediante un nuevo calix[4]areno de tioamida funcionalizado con alilo en conformación 1,3-alternativa: una investigación espectroscópica UV-visible y RMN H-1". J. Chem. Soc., Perkin Trans . 2 (12): 2287–2291. doi :10.1039/b107025h.
- ^ Runge, VM; Scott, S. (1998). Imágenes por resonancia magnética clínica con contraste . University Press of Kentucky. ISBN 0-8131-1944-8.
- ^ Vacca, A.; Nativi, C.; Cacciarini, M.; Pergoli, R.; Roelens, S. (2004). "Un nuevo receptor tripodal para el reconocimiento molecular de monosacáridos. Un paradigma para evaluar las afinidades y selectividades de unión de glicósidos mediante espectroscopia de RMN de 1H ". J. Am. Chem. Soc . 126 (50): 16456–16465. doi :10.1021/ja045813s. PMID 15600348.
- ^ Marcotte, N.; Taglietti, A. (2003). "Conjuntos de detección química basados en metales de transición: detección de ATP en condiciones fisiológicas". Supramol. Chem . 15 (7): 617–717. doi :10.1080/10610270310001605205. S2CID 96018200.
- ^ Boiocchi, M.; Bonizzoni, M.; Fabbrizzi, L.; Piovani, G.; Taglietti, A. (2004). "Una jaula dimetálica con una cavidad elipsoidal larga para la detección fluorescente de aniones dicarboxilato en agua". Angew. Chem. Int. Ed . 43 (29): 3847–3852. doi :10.1002/anie.200460036. PMID 15258953.
- ^ Billo, EJ (1997). "Capítulo 22" . Excel para químicos: una guía completa (2.ª ed.). Wiley-VCH. ISBN 0-471-18896-4.
- ^ Zekany, L.; Nagypál, I. (1985). "Capítulo 8: PSEQUAD: Un programa completo para la evaluación de datos de equilibrio potenciométrico y/o espectrofotométrico utilizando derivadas analíticas". En Leggett (ed.). Métodos computacionales para la determinación de constantes de formación . Plenum. ISBN 0-306-41957-2.
- ^ Gans, P.; Sabatini, A.; Vacca, A. (1996). "Investigación de equilibrios en solución. Determinación de constantes de equilibrio con el conjunto de programas HYPERQUAD". Talanta . 43 (10): 1739–1753. doi :10.1016/0039-9140(96)01958-3. PMID 18966661.
- ^ Martell, AE; Motekaitis, RJ (1992). La determinación y el uso de constantes de estabilidad . Wiley-VCH.
- ^ Leggett, D. (1985). "Capítulo 6: SQUAD: Cocientes de estabilidad a partir de datos de absorbancia". En Leggett (ed.). Métodos computacionales para la determinación de constantes de formación . Plenum. ISBN 0-306-41957-2.
- ^ Gampp, M.; Maeder, M.; Mayer, CJ; Zuberbühler, AD (1985). "Cálculo de constantes de equilibrio a partir de datos espectroscópicos de longitud de onda múltiple—I: Consideraciones matemáticas". Talanta . 32 (2): 95–101. doi :10.1016/0039-9140(85)80035-7. PMID 18963802.
- ^ Gampp, M.; Maeder, M.; Mayer, CJ; Zuberbühler, AD (1985). "Cálculo de constantes de equilibrio a partir de datos espectroscópicos de longitud de onda múltiple—II1: Specfit: dos programas fáciles de usar en FORTRAN 77 básico y estándar". Talanta . 32 (4): 251–264. doi :10.1016/0039-9140(85)80077-1. PMID 18963840.
- ^ Jplus Consulting Pty Ltd
- ^ Frassineti, C.; Alderighi, L.; Gans, P.; Sabatini, A.; Vacca, A.; Ghelli, S. (2003). "Determinación de las constantes de protonación de algunas poliaminas fluoradas mediante datos de RMN de 13 C procesados por el nuevo programa informático HypNMR2000. Secuencia de protonación en poliaminas". Anal. Bioanal. Química . 376 (7): 1041–1052. doi :10.1007/s00216-003-2020-0. PMID 12845401. S2CID 14533024.
- ^ Hynes, MJ (1993). "EQNMR: Un programa informático para el cálculo de constantes de estabilidad a partir de datos de desplazamiento químico por resonancia magnética nuclear". J. Chem. Soc., Dalton Trans. (2): 311–312. doi :10.1039/DT9930000311.
- ^ O'Brien, R.; Ladbury, JE; Chowdry, BZ (2000). "Capítulo 10". En Harding, SE; Chowdry, BZ (eds.). Interacciones proteína-ligando: hidrodinámica y calorimetría . Oxford University Press. ISBN 0-19-963749-0.
- ^ Paoletti, P. (1984). "Formación de complejos metálicos con etilendiamina: un estudio crítico de las constantes de equilibrio, valores de entalpía y entropía" (PDF) . Pure Appl. Chem . 56 (4): 491–522. doi :10.1351/pac198456040491. S2CID 5600085.
- ^ Anderegg, G. (1982). "Estudio crítico de las constantes de estabilidad de los complejos NTA" (PDF) . Pure Appl. Chem . 54 (12): 2693–2758. doi :10.1351/pac198254122693. S2CID 44040841.
- ^ Anderegg, G; Arnaud-Neu, F.; Delgado, R.; Felcman, J.; Popov, K. (2003). "Evaluación crítica de las constantes de estabilidad de complejos metálicos de complexonas para aplicaciones biomédicas y ambientales (Informe técnico de la IUPAC)" (PDF) . Pure Appl. Chem . 77 (8): 1445–95. doi :10.1351/pac200577081445. S2CID 94957415.
- ^ Lajunen, LHJ; Portanova, R.; Piispanen, J.; Tolazzi, M. (1997). "Evaluación crítica de las constantes de estabilidad para complejos de ácidos alfa-hidroxicarboxílicos con protones e iones metálicos y los cambios de entalpía que los acompañan. Parte I: Ácidos orto-hidroxicarboxílicos aromáticos (Informe técnico)" (PDF) . Pure Appl. Chem . 69 (2): 329–382. doi :10.1351/pac199769020329. S2CID 100224661.
- ^ Portanova, R; Lajunen, LHJ; Tolazzi, M.; Piispanen, J. (2003). "Evaluación crítica de las constantes de estabilidad para complejos de ácidos alfa-hidroxicarboxílicos con protones e iones metálicos y los cambios de entalpía que los acompañan. Parte II. Ácidos 2-hidroxicarboxílicos alifáticos (Informe técnico de la IUPAC)" (PDF) . Pure Appl. Chem . 75 (4): 495–540. doi :10.1351/pac200375040495. S2CID 97662244.
- ^ Arnaud-Neu, F.; Delgado, R.; Chaves, S. (2003). "Evaluación crítica de las constantes de estabilidad y funciones termodinámicas de complejos metálicos de éteres corona (Informe técnico de la IUPAC)" (PDF) . Pure Appl. Chem . 75 (1): 71–102. doi :10.1351/pac200375010071. S2CID 97549495.
- ^ Popov, K.; Rönkkömäki, H.; Lajunen, LHJ (2001). "Evaluación crítica de las constantes de estabilidad de los ácidos fosfónicos (Informe técnico de la IUPAC)" (PDF) . Pure Appl. Chem . 73 (11): 1641–1677. doi :10.1351/pac200173101641. S2CID 98158286.
- ^ Popov, K.; Rönkkömäki, H.; Lajunen, LHJ (2002). "Erratas" (PDF) . Pura aplicación. química . 74 (11): 2227. doi : 10.1351/pac200274112227. S2CID 195819226.
- ^ Sjöberg, S. (1997). "Evaluación crítica de las constantes de estabilidad de los sistemas metal-imidazol y metal-histamina (Informe técnico)" (PDF) . Pure Appl. Chem . 69 (7): 1549–1570. doi :10.1351/pac199769071549. S2CID 98121760.
- ^ Berthon, G. (1995). "Evaluación crítica de las constantes de estabilidad de complejos metálicos de aminoácidos con cadenas laterales polares (Informe técnico)" (PDF) . Pure Appl. Chem . 67 (7): 1117–1240. doi :10.1351/pac199567071117. S2CID 95757342.
- ^ Smith, RM; Martell, AE; Chen, Y. (1991). "Evaluación crítica de las constantes de estabilidad para complejos de nucleótidos con protones e iones metálicos y los cambios de entalpía que los acompañan" (PDF) . Pure Appl. Chem . 63 (7): 1015–1080. doi :10.1351/pac199163071015. S2CID 97422244.
- ^ Stary, J.; Liljenzin, JO (1982). "Evaluación crítica de las constantes de equilibrio que involucran acetilacetona y sus quelatos metálicos" (PDF) . Pure Appl. Chem . 54 (12): 2557–2592. doi :10.1351/pac198254122557. S2CID 96848983.
- ^ Beck, MT (1977). "Evaluación crítica de las constantes de equilibrio en solución. Constantes de estabilidad de complejos metálicos" (PDF) . Pure Appl. Chem . 49 (1): 127–136. doi :10.1351/pac197749010127. S2CID 39693835.
- ^ Powell, Kipton, J.; Brown, Paul L.; Byrne, Robert H.; Gajda, Tamás; Hefter, Glenn; Sjöberg, Staffan; Wanner, Hans (2005). "Especiación química de metales pesados ambientalmente significativos con ligandos inorgánicos. Parte 1: Los sistemas acuosos Hg2+–Cl−, OH−, CO2−3, SO2−4 y PO3−4" (PDF) . Pure Appl. Chem . 77 (4): 739–800. doi :10.1351/pac200577040739. S2CID 93650787.
{{cite journal}}: CS1 maint: multiple names: authors list (link) - ^ Powell, Kipton J.; Brown, Paul L.; Byrne, Robert H.; Gajda, Tamás; Hefter, Glenn; Sjöberg, Staffan; Wanner, Hans (2007). "Especiación química de metales ambientalmente significativos con ligandos inorgánicos Parte 2: Los sistemas Cu2+–OH−, Cl−, CO2−3, SO2−4 y PO3−4" (PDF) . Pure Appl. Chem . 79 (5): 895–950. doi :10.1351/pac200779050895. S2CID 195819532.
- ^ Powell, Kipton J.; Brown, Paul L.; Byrne, Robert H.; Gajda, Tamás; Hefter, Glenn; Leuz, Ann-Kathrin; Sjöberg, Staffan; Wanner, Hans (2009). "Especiación química de metales ambientalmente significativos con ligandos inorgánicos Parte 3: Los sistemas Pb2+–OH−, Cl−, CO2−3, SO2−4 y PO3−4" (PDF) . Pure Appl. Chem . 81 (12): 2425–2476. doi :10.1351/PAC-REP-09-03-05. S2CID 93738375.
- ^ Powell, Kipton J.; Brown, Paul L.; Byrne, Robert H.; Gajda, Tamás; Hefter, Glenn; Leuz, Ann-Kathrin; Sjöberg, Staffan; Wanner, Hans (2011). "Especiación química de metales ambientalmente significativos con ligandos inorgánicos. Parte 4: Los sistemas Cd2+–OH−, Cl−, CO2−3, SO2−4 y PO3−4" (PDF) . Pure Appl. Chem . 83 (5): 1163–1214. doi :10.1351/PAC-REP-10-08-09. S2CID 195819251.
Lectura adicional
Sigel, Roland KO; Skilandat, Miriam; Sigel, Astrid; Operschall, Bert P.; Sigel, Helmut (2013). "Capítulo 8. Formación compleja de cadmio con residuos de azúcar , nucleobases , fosfatos , nucleótidos y ácidos nucleicos ". En Sigel, Astrid; Sigel, Helmut; Sigel, Roland KO (eds.). Cadmio: de la toxicología a la esencialidad (PDF) . Iones metálicos en las ciencias de la vida. Vol. 11. Springer. págs. 191–274. doi :10.1007/978-94-007-5179-8_8. PMID 23430775.
Sóvágó, Imre; Várnagy, Katalin (2013). "Capítulo 9. Complejos de cadmio(II) de aminoácidos y péptidos". En Sigel, Astrid; Sigel, Helmut; Sigel, Roland KO (eds.). Cadmio: de la toxicología a la esencialidad . Iones metálicos en las ciencias de la vida. Vol. 11. Springer. págs. 275–302. doi :10.1007/978-94-007-5179-8_9. PMID 23430776.
Yatsimirsky, Konstantin Borisovich; Vasilyev, Vladimir Pavlovich (1960). Constantes de inestabilidad de compuestos complejos . Traducido por Patterson, DA OUP.
Enlaces externos
- Sitio web de constantes de estabilidad: contiene información sobre programas de computadora, aplicaciones, bases de datos y hardware para titulaciones experimentales.




![{\displaystyle \mathrm {[M(H_{2}O)} _{n}]+\mathrm {L} \leftrightharpoons \mathrm {[M(H_{2}O)} _{n-1}\mathrm {L} ]+\mathrm {H_{2}O} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/f6c90df793f368a962ab232a4d7445ea67cd553d)
![{\displaystyle \beta ^{'}={\frac {[\mathrm {M(H_{2}O)} _{n-1}\mathrm {L} ][\mathrm {H_{2}O} ] }{[\mathrm {M(H_{2}O)} _{n}][\mathrm {L} ]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cb903e0c6849446ba718798c09f77751851f266c)
![{\displaystyle \beta =\mathrm {\frac {[ML]}{[M][L]}} .}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f6dbc7aecca141447456d84685c3544a3abf8308)

![{\displaystyle \beta _ {pq...}={\frac {[\mathrm {M} _ {p}\mathrm {L} _ {q}...]}{[\mathrm {M} ]^ {p}[\mathrm {L} ]^{q}....}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c9b5cb845f8efec1e7800490f0c4d0e5cd90a76e)

![{\displaystyle \beta _ {1,2}=\mathrm {\frac {[ML_ {2}]}{[M][L]^{2}}} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/cd0600d0b3496515a3e2b2ee1f26e7f6c0c7e0a6)

![{\displaystyle K_{1}=\mathrm {\frac {[ML]}{[M][L]}} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/abf3c8b4381157f0280c84e2286d574f3bf7f0dc)

![{\displaystyle K_{2}=\mathrm {\frac {[ML_{2}]}{[ML][L]}} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/7d69161b913579794614dbb05851b4cc739a3086)


![{\displaystyle K=\mathrm {\frac {[M(OH)]}{[M][OH]}} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/33c23271b9152d2329b562befa69300b63a0124c)
![{\displaystyle K_{w}=\mathrm {[H]} ^{+}\mathrm {[OH]} ^{-}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8dab8030c3e55177ae21c52af1702d35a48e9004)
![{\displaystyle K={\frac {[\mathrm {M} (\mathrm {OH} )]}{[\mathrm {M} ]K_{\mathrm {w} }[\mathrm {H} ]^{- 1}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/15c00635c0c40ce1c98b65ad70c173b71abeedf3)
![{\displaystyle \beta _{1,-1}^{*}=KK_{\mathrm {w} }={\frac {[\mathrm {M} (\mathrm {OH} )]}{[\mathrm { M} ][\mathrm {H} ]^{-1}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7fadb3fd4aca5c5dc7ac61db7e320417f3b128b3)



![{\displaystyle ,K=\mathrm {\frac {[AB]}{[A][B]}} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/47949aaef3e5223551aade26d942897e76d70387)





![{\displaystyle K^{\ominus }=\mathrm {\frac {[ML]}{[M][L]}} \times {\frac {\gamma _{\mathrm {ML} }}{\gamma _ {\mathrm {M} }\gamma _ {\mathrm {L} }}}=\mathrm {\frac {[ML]}{[M][L]}} \times \Gamma }](https://wikimedia.org/api/rest_v1/media/math/render/svg/73bd77587e27db8a47d8bf7dd244d05f84917022)
![{\displaystyle \beta _ {pq...}^{\ominus }={\frac {[\mathrm {M} _ {p}\mathrm {L} _ {q}...]}{[\mathrm {M} ]^{p}[\mathrm {L} ]^{q}...}}\times \Gamma }](https://wikimedia.org/api/rest_v1/media/math/render/svg/07fcbbe22a4e6a23444c531c7ae018239b2f481d)


![{\displaystyle \mathrm {Cu^{2+}+en\rightleftharpoons [Cu(en)]^{2+}} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/537a54fd90a52ed8cba49c5a78741e88fceedbda)
![{\displaystyle Cu^{2+}+2MeNH_{2}\rightleftharpoons [Cu(MeNH_{2})_{2}]^{2+}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6078135f5afd5f03b40d01435a5ea40e9d2dee1d)
![{\displaystyle \mathrm {[Cu(en)]=\beta _ {11}[Cu][en]|} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/e626081c150da6b692dd1bb8e07bec7e42b436c5)
![{\displaystyle \mathrm {[Cu(MeNH_{2})_{2}]=\beta _{12}[Cu][MeNH_{2}]} ^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/547473860966f88d473b83875f9a68480bc65010)
![{\displaystyle \mathrm {Ag^{+}+NH_{3}\rightleftharpoons [Ag(NH_{3})]^{+};K_{1}={\frac {[Ag(NH_{3})] }{[Ag][NH_{3}]}}} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/0dde96e275d8d65b5467ef70aa8c99178407a943)
![{\displaystyle \mathrm {Ag(NH_{3})^{+}+NH_{3}\rightleftharpoons [Ag(NH_{3})_{2}]^{+};K_{2}={\frac {[Ag(NH_{3})_{2}]}{[Ag(NH_{3}][NH_{3}]}}} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/f461e352164a1f5a3ed55eb58b7b415c4b53e261)