Triángulo

Triángulo
Aristas y vértices	3
Símbolo de Schläfli	{3} (para equilátero)
Área	varios métodos; ver más abajo

Un triángulo es un polígono con tres vértices y tres lados, una de las formas básicas de la geometría . Los vértices, también llamados vértices , son puntos de dimensión cero mientras que los lados que los conectan, también llamados aristas , son segmentos de línea unidimensionales . Un triángulo tiene tres ángulos internos , cada uno limitado por un par de aristas adyacentes; la suma de los ángulos de un triángulo siempre es igual a un ángulo recto (180 grados o π radianes). El triángulo es una figura plana y su interior es una región plana . A veces se elige una arista arbitraria para que sea la base , en cuyo caso el vértice opuesto se llama vértice ; el segmento más corto entre la base y el vértice es la altura . El área de un triángulo es igual a la mitad del producto de la altura por la longitud de la base.

En la geometría euclidiana , dos puntos cualesquiera determinan un único segmento de línea situado dentro de una única línea recta , y tres puntos cualesquiera que no se encuentren todos sobre la misma línea recta determinan un único triángulo situado dentro de una única superficie plana . De manera más general, cuatro puntos en el espacio euclidiano tridimensional determinan un tetraedro .

En geometrías no euclidianas , tres segmentos "rectos" (que tienen curvatura cero ) también determinan un triángulo, por ejemplo, un triángulo esférico o un triángulo hiperbólico . Un triángulo geodésico es una región de una superficie bidimensional general encerrada por tres lados que son rectos en relación con la superficie ( geodésicas ).Un triángulo curvilíneo es una figura con tres lados curvos , por ejemplo, un triángulo circular con lados en forma de arco circular . Este artículo trata sobre triángulos de lados rectos en geometría euclidiana, excepto donde se indique lo contrario.

Los triángulos se clasifican en diferentes tipos según sus ángulos y la longitud de sus lados. Las relaciones entre los ángulos y las longitudes de los lados son un tema central de la trigonometría . En particular, las funciones seno, coseno y tangente relacionan las longitudes de los lados y los ángulos en los triángulos rectángulos .

Un triángulo es una figura que consta de tres segmentos de línea, cada uno de cuyos puntos finales están conectados. ^[1] Esto forma un polígono con tres lados y tres ángulos. La terminología para categorizar los triángulos tiene más de dos mil años de antigüedad, habiéndose definido en el Libro Uno de los Elementos de Euclides . ^[2] Los nombres utilizados para la clasificación moderna son una transliteración directa del griego de Euclides o sus traducciones al latín.

Los triángulos tienen muchos tipos basados ​​en la longitud de los lados y los ángulos. Un triángulo cuyos lados tienen todos la misma longitud es un triángulo equilátero , ^[3] un triángulo con dos lados que tienen la misma longitud es un triángulo isósceles , ^{[4] [a]} y un triángulo con tres lados de diferente longitud es un triángulo escaleno . ^[7] Un triángulo en el que uno de los ángulos es un ángulo recto es un triángulo rectángulo , un triángulo en el que todos sus ángulos son menores que ese ángulo es un triángulo acutángulo , y un triángulo en el que uno de sus ángulos es mayor que ese ángulo es un triángulo obtuso . ^[8] Estas definiciones se remontan al menos a Euclides . ^[9]

• 
  Triángulo equilátero
• 
  Triángulo isósceles
• 
  Triángulo escaleno

• 
  Triángulo rectángulo
• 
  Triángulo agudo
• 
  Triángulo obtuso

En la vida real, es habitual encontrar todo tipo de triángulos. En construcciones hechas por el hombre, los triángulos isósceles pueden encontrarse en forma de frontones y frontones , y el triángulo equilátero puede encontrarse en la señal de ceda el paso. ^[10] A veces se considera que las caras de la Gran Pirámide de Giza son equiláteras, pero mediciones más precisas muestran que son isósceles. ^[11] Otras apariciones se dan en símbolos heráldicos como en la bandera de Santa Lucía y la bandera de Filipinas . ^[12]

Los triángulos también aparecen en objetos tridimensionales. Un poliedro es un sólido cuyo límite está cubierto por polígonos planos conocidos como caras, esquinas agudas conocidas como vértices y segmentos de línea conocidos como aristas. Los poliedros en algunos casos se pueden clasificar, a juzgar por la forma de sus caras. Por ejemplo, cuando los poliedros tienen todos los triángulos equiláteros como caras, se conocen como deltaedros . ^[13] Los antiprismas tienen triángulos alternados en sus lados. ^[14] Las pirámides y bipirámides son poliedros con bases poligonales y triángulos como caras laterales; los triángulos son isósceles siempre que sean pirámides y bipirámides rectas. El Kleetope de un poliedro es un nuevo poliedro hecho al reemplazar cada cara del original con una pirámide, por lo que las caras de un Kleetope serán triángulos. ^[15] De manera más general, los triángulos se pueden encontrar en dimensiones superiores, como en la noción generalizada de triángulos conocida como símplex , y los politopos con facetas triangulares conocidos como politopos simpliciales . ^[16]

Cada triángulo tiene muchos puntos especiales en su interior, en sus aristas o asociados de alguna otra forma con él. Se construyen encontrando tres líneas asociadas simétricamente con los tres lados (o vértices) y luego demostrando que las tres líneas se encuentran en un único punto. Una herramienta importante para demostrar la existencia de estos puntos es el teorema de Ceva , que proporciona un criterio para determinar cuándo tres de esas líneas son concurrentes . ^[17] De manera similar, las líneas asociadas con un triángulo a menudo se construyen demostrando que tres puntos construidos simétricamente son colineales ; aquí el teorema de Menelao proporciona un criterio general útil. ^[18] En esta sección, se explican solo algunas de las construcciones más comunes.

Una bisectriz perpendicular de un lado de un triángulo es una línea recta que pasa por el punto medio del lado y es perpendicular a él, formando un ángulo recto con él. ^[19] Las tres bisectrices perpendiculares se encuentran en un solo punto, el circuncentro del triángulo ; este punto es el centro del círculo circunscrito , el círculo que pasa por los tres vértices. ^[20] El teorema de Tales implica que si el circuncentro está ubicado en el lado del triángulo, entonces el ángulo opuesto a ese lado es un ángulo recto. ^[21] Si el circuncentro está ubicado dentro del triángulo, entonces el triángulo es agudo; si el circuncentro está ubicado fuera del triángulo, entonces el triángulo es obtuso. ^[22]

La altura de un triángulo es una línea recta que pasa por un vértice y es perpendicular al lado opuesto. Este lado opuesto se llama base de la altura, y el punto donde la altura interseca la base (o su prolongación) se llama pie de la altura. ^[23] La longitud de la altura es la distancia entre la base y el vértice. Las tres alturas se intersecan en un único punto, llamado ortocentro del triángulo. ^[24] El ortocentro se encuentra dentro del triángulo si y solo si el triángulo es agudo. ^[25]

La bisectriz de un triángulo es una línea recta que pasa por un vértice y corta el ángulo correspondiente por la mitad. Las tres bisectrices de los ángulos se cortan en un único punto, el incentro , que es el centro del círculo inscrito del triángulo . El círculo inscrito es el círculo que se encuentra dentro del triángulo y toca los tres lados. Su radio se llama inradio. Hay otros tres círculos importantes, los excírculos ; se encuentran fuera del triángulo y tocan un lado, así como las extensiones de los otros dos. Los centros de los incírculos y excírculos forman un sistema ortocéntrico . ^{[26] Los puntos medios de los tres lados y los pies de las tres alturas se encuentran todos en un único círculo, el} círculo de nueve puntos del triángulo . ^[27] Los tres puntos restantes por los que recibe el nombre son los puntos medios de la porción de altura entre los vértices y el ortocentro . El radio del círculo de nueve puntos es la mitad del del circuncírculo. Toca el círculo inscrito (en el punto de Feuerbach ) y los tres excírculos . El ortocentro (punto azul), el centro del círculo de nueve puntos (rojo), el baricentro (naranja) y el circuncentro (verde) se encuentran todos en una sola línea, conocida como línea de Euler (línea roja). El centro del círculo de nueve puntos se encuentra en el punto medio entre el ortocentro y el circuncentro, y la distancia entre el baricentro y el circuncentro es la mitad de la que hay entre el baricentro y el ortocentro. ^[27] Generalmente, el centro del círculo inscrito no se encuentra en la línea de Euler. ^{[28] [29]}

La mediana de un triángulo es una línea recta que pasa por un vértice y el punto medio del lado opuesto, y divide el triángulo en dos áreas iguales. Las tres medianas se cortan en un único punto, el baricentro geométrico del triángulo . El baricentro de un objeto triangular rígido (recortado de una lámina delgada de densidad uniforme) es también su centro de masas : el objeto puede equilibrarse sobre su baricentro en un campo gravitatorio uniforme. ^[30] El baricentro corta cada mediana en una proporción de 2:1, es decir, la distancia entre un vértice y el baricentro es el doble de la distancia entre el baricentro y el punto medio del lado opuesto. Si se refleja una mediana en la bisectriz del ángulo que pasa por el mismo vértice, se obtiene una simediana . Las tres simedianas se cortan en un único punto, el punto simediano del triángulo. ^[31]

La suma de las medidas de los ángulos interiores de un triángulo en el espacio euclidiano es siempre 180 grados. ^[32] Este hecho es equivalente al postulado de las paralelas de Euclides . Esto permite determinar la medida del tercer ángulo de cualquier triángulo, dada la medida de dos ángulos. ^[33] Un ángulo exterior de un triángulo es un ángulo que es un par lineal (y por lo tanto suplementario ) de un ángulo interior. La medida de un ángulo exterior de un triángulo es igual a la suma de las medidas de los dos ángulos interiores que no son adyacentes a él; este es el teorema del ángulo exterior . ^[34] La suma de las medidas de los tres ángulos exteriores (uno por cada vértice) de cualquier triángulo es 360 grados, y de hecho, esto es cierto para cualquier polígono convexo, sin importar cuántos lados tenga. ^[35]

Otra relación entre los ángulos internos y los triángulos crea un nuevo concepto de funciones trigonométricas . Las funciones trigonométricas principales son el seno y el coseno , así como las otras funciones. Se pueden definir como la relación entre dos lados cualesquiera de un triángulo rectángulo . ^[36] En un triángulo escaleno, las funciones trigonométricas se pueden utilizar para encontrar la medida desconocida de un lado o de un ángulo interno; los métodos para hacerlo utilizan la ley de los senos y la ley de los cosenos . ^[37]

Tres ángulos cualesquiera que sumen 180° pueden ser los ángulos internos de un triángulo. Una cantidad infinita de triángulos tienen los mismos ángulos, ya que especificar los ángulos de un triángulo no determina su tamaño. (Un triángulo degenerado , cuyos vértices son colineales , tiene ángulos internos de 0° y 180°; si una forma de este tipo cuenta como un triángulo es una cuestión de convención. ^{[ cita requerida ]} ) Las condiciones para que tres ángulos , , y , cada uno de ellos entre 0° y 180°, sean los ángulos de un triángulo también se pueden establecer utilizando funciones trigonométricas. Por ejemplo, un triángulo con ángulos , , y existe si y solo si ^[38]${\estilo de visualización \alpha}$${\estilo de visualización \beta}$${\estilo de visualización \gamma}$${\estilo de visualización \alpha}$${\estilo de visualización \beta}$${\estilo de visualización \gamma}$$${\displaystyle \cos ^{2}\alpha +\cos ^{2}\beta +\cos ^{2}\gamma +2\cos(\alpha )\cos(\beta )\cos(\gamma )= 1.}$$

Se dice que dos triángulos son semejantes si cada ángulo de un triángulo tiene la misma medida que el ángulo correspondiente del otro triángulo. Los lados correspondientes de triángulos semejantes tienen longitudes que están en la misma proporción, y esta propiedad también es suficiente para establecer la semejanza. ^[39]

Algunos teoremas básicos sobre triángulos semejantes son:

• Si y sólo si un par de ángulos internos de dos triángulos tienen la misma medida entre sí, y otro par también tiene la misma medida entre sí, los triángulos son semejantes. ^[40]
• Si y sólo si un par de lados correspondientes de dos triángulos están en la misma proporción que otro par de lados correspondientes, y sus ángulos incluidos tienen la misma medida, entonces los triángulos son semejantes. ^[41] (El ángulo incluido para cualesquiera dos lados de un polígono es el ángulo interno entre esos dos lados).
• Si y sólo si tres pares de lados correspondientes de dos triángulos están todos en la misma proporción, entonces los triángulos son semejantes. ^[b]

Dos triángulos congruentes tienen exactamente el mismo tamaño y forma. Todos los pares de triángulos congruentes son también semejantes, pero no todos los pares de triángulos semejantes son congruentes. Dados dos triángulos congruentes, todos los pares de ángulos interiores correspondientes tienen la misma medida y todos los pares de lados correspondientes tienen la misma longitud. En total, hay seis igualdades, pero tres suelen ser suficientes para demostrar la congruencia. ^[42]

Algunas condiciones individualmente necesarias y suficientes para que un par de triángulos sean congruentes son: ^[43]

• Postulado SAS: Dos lados de un triángulo tienen la misma longitud que dos lados del otro triángulo y los ángulos incluidos tienen la misma medida.
• ASA: Dos ángulos interiores y el lado comprendido entre ellos en un triángulo tienen la misma medida y longitud, respectivamente, que los del otro triángulo. (Esta es la base de la topografía por triangulación ).
• SSS: Cada lado de un triángulo tiene la misma longitud que el lado correspondiente del otro triángulo.
• AAS: Dos ángulos y un lado correspondiente (no incluido) en un triángulo tienen la misma medida y longitud, respectivamente, que los del otro triángulo. (Esto a veces se denomina AAcorrS y luego incluye el ASA mencionado anteriormente).

En el plano euclidiano, el área se define por comparación con un cuadrado de lado ⁠ ⁠${\estilo de visualización 1}$ , que tiene área 1. Hay varias formas de calcular el área de un triángulo arbitrario. Una de las más antiguas y sencillas es tomar la mitad del producto de la longitud de un lado ⁠ ⁠${\estilo de visualización b}$ (la base) por la altura correspondiente ⁠ ⁠${\estilo de visualización h}$ : ^[44]$${\displaystyle T={\tfrac {1}{2}}bh.}$$

Esta fórmula se puede demostrar cortando el triángulo y una copia idéntica en pedazos y reorganizando los pedazos en forma de un rectángulo de base y${\estilo de visualización b}$ altura .${\estilo de visualización h}$

Si se conocen dos lados ⁠ ⁠${\estilo de visualización a}$ y ⁠ ⁠${\estilo de visualización b}$ y su ángulo incluido , entonces la altitud se puede calcular usando trigonometría, ⁠ ⁠ , por lo que el área del triángulo es:${\estilo de visualización \gamma}$${\displaystyle h=a\sin(\gamma )}$$${\displaystyle T={\tfrac {1}{2}}ab\sin \gamma .}$$

La fórmula de Herón , llamada así por Herón de Alejandría , es una fórmula para hallar el área de un triángulo a partir de las longitudes de sus lados , , . Siendo , el semiperímetro , ^[45]${\estilo de visualización a}$${\estilo de visualización b}$${\estilo de visualización c}$${\displaystyle s={\frac {1}{2}}(a+b+c)}$$${\displaystyle T={\sqrt {s(sa)(sb)(sc)}}.}$$

Debido a que las razones entre las áreas de las formas en el mismo plano se conservan mediante transformaciones afines , las áreas relativas de los triángulos en cualquier plano afín se pueden definir sin referencia a una noción de distancia o cuadrados. En cualquier espacio afín (incluidos los planos euclidianos), cada triángulo con la misma base y área orientada tiene su vértice (el tercer vértice) en una línea paralela a la base, y su área común es la mitad de la de un paralelogramo con la misma base cuyo lado opuesto se encuentra en la línea paralela. Este enfoque afín fue desarrollado en el Libro 1 de los Elementos de Euclides . ^[46]

Dadas coordenadas afines (como las coordenadas cartesianas ) ⁠ ⁠${\displaystyle (x_{A},y_{A})}$ , ⁠ ⁠${\displaystyle (x_{B},y_{B})}$ , ⁠ ⁠${\displaystyle (x_{C},y_{C})}$ para los vértices de un triángulo, su área orientada relativa se puede calcular utilizando la fórmula del cordón ,

$${\displaystyle {\begin{aligned}T&={\tfrac {1}{2}}{\begin{vmatrix}x_{A}&x_{B}&x_{C}\\y_{A}&y_{B}&y_ {C}\\1&1&1\end{vmatrix}}={\tfrac {1}{2}}{\begin{vmatrix}x_{A}&x_{B}\\y_{A}&y_{B}\end{ vmatrix}}+{\tfrac {1}{2}}{\begin{vmatrix}x_{B}&x_{C}\\y_{B}&y_{C}\end{vmatrix}}+{\tfrac {1 }{2}}{\begin{vmatrix}x_{C}&x_{A}\\y_{C}&y_{A}\end{vmatrix}}\\&={\tfrac {1}{2}}(x_{A}y_{B}-x_{B}y_{A}+x_{B}y_{C}-x_{C}y_{B}+x_{C}y_{ A}-x_{A}y_{C}),\end{alineado}}}$$

donde es el determinante de la matriz . ^[47]${\estilo de visualización |\cdot |}$

La desigualdad del triángulo establece que la suma de las longitudes de dos lados cualesquiera de un triángulo debe ser mayor o igual que la longitud del tercer lado. ^[48] Por el contrario, existe algún triángulo con tres longitudes de lados positivos dadas si y solo si esas longitudes de lados satisfacen la desigualdad del triángulo. ^[49] La suma de las longitudes de dos lados puede ser igual a la longitud del tercer lado solo en el caso de un triángulo degenerado , uno con vértices colineales.

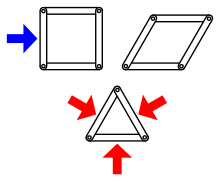
A diferencia de un rectángulo, que puede colapsar y convertirse en un paralelogramo por la presión ejercida sobre uno de sus puntos, ^[50] los triángulos son resistentes porque la especificación de las longitudes de los tres lados determina los ángulos. ^[51] Por lo tanto, un triángulo no cambiará de forma a menos que sus lados se doblen, se extiendan o se rompan, o si sus juntas se rompen; en esencia, cada uno de los tres lados sostiene a los otros dos. Un rectángulo, en cambio, depende más de la resistencia de sus juntas en un sentido estructural.

Los triángulos son fuertes en términos de rigidez, pero, aunque están empaquetados en una disposición teselada , no son tan fuertes como los hexágonos bajo compresión (de ahí la prevalencia de formas hexagonales en la naturaleza ). Sin embargo, los triángulos teselados aún mantienen una resistencia superior para el voladizo , por lo que la ingeniería hace uso de cerchas tetraédricas . ^{[ cita requerida ]}

La triangulación significa la partición de cualquier objeto plano en una colección de triángulos. Por ejemplo, en la triangulación de polígonos , un polígono se subdivide en múltiples triángulos que están unidos borde con borde, con la propiedad de que sus vértices coinciden con el conjunto de vértices del polígono. ^[52] En el caso de un polígono simple con lados, hay triángulos que están separados por diagonales. La triangulación de un polígono simple tiene una relación con la oreja , un vértice conectado por otros dos vértices, cuya diagonal se encuentra completamente dentro del polígono. El teorema de las dos orejas establece que todo polígono simple que no sea en sí mismo un triángulo tiene al menos dos orejas. ^[53]${\estilo de visualización n}$${\estilo de visualización n-2}$${\estilo de visualización n-3}$

Una forma de identificar la ubicación de los puntos dentro (o fuera) de un triángulo es colocar el triángulo en una ubicación y orientación arbitrarias en el plano cartesiano y utilizar coordenadas cartesianas. Si bien este enfoque es conveniente para muchos propósitos, tiene la desventaja de que los valores de las coordenadas de todos los puntos dependen de la ubicación arbitraria en el plano. ^[54]

Dos sistemas evitan esa característica, de modo que las coordenadas de un punto no se ven afectadas al mover el triángulo, rotarlo o reflejarlo como en un espejo, cualquiera de los cuales da un triángulo congruente, o incluso al reescalarlo a un triángulo similar: ^[55]

• Las coordenadas trilineales especifican las distancias relativas de un punto desde los lados, de modo que las coordenadas indican que la relación entre la distancia del punto desde el primer lado y su distancia desde el segundo lado es , etc.${\estilo de visualización x:y:z}$${\estilo de visualización x:y}$
• Las coordenadas baricéntricas de la forma especifican la ubicación del punto mediante los pesos relativos que deberían colocarse en los tres vértices para equilibrar el triángulo, que de otro modo sería ingrávido, en el punto dado.${\displaystyle \alpha :\beta :\gamma }$

Como se ha comentado anteriormente, cada triángulo tiene un único círculo inscrito (incírculo) que es interior al triángulo y tangente a los tres lados. Cada triángulo tiene una única inelipse de Steiner que es interior al triángulo y tangente en los puntos medios de los lados. El teorema de Marden muestra cómo hallar los focos de esta elipse . ^[56] Esta elipse tiene la mayor área de cualquier elipse tangente a los tres lados del triángulo. La inelipse de Mandart de un triángulo es la elipse inscrita en el triángulo tangente a sus lados en los puntos de contacto de sus excírculos. Para cualquier elipse inscrita en un triángulo , sean los focos y , entonces: ^[57]${\estilo de visualización ABC}$${\estilo de visualización P}$${\estilo de visualización Q}$$${\displaystyle {\frac {{\overline {PA}}\cdot {\overline {QA}}}{{\overline {CA}}\cdot {\overline {AB}}}}+{\frac {{\ overline {PB}}\cdot {\overline {QB}}}{{\overline {AB}}\cdot {\overline {BC}}}}+{\frac {{\overline {PC}}\cdot {\ overline {QC}}}{{\overline {BC}}\cdot {\overline {CA}}}}=1.}$$

A partir de un punto interior de un triángulo de referencia, los puntos más próximos de los tres lados sirven como vértices del triángulo pedal de ese punto. Si el punto interior es el circuncentro del triángulo de referencia, los vértices del triángulo pedal son los puntos medios de los lados del triángulo de referencia, por lo que el triángulo pedal se denomina triángulo de punto medio o triángulo medial. El triángulo de punto medio subdivide el triángulo de referencia en cuatro triángulos congruentes que son similares al triángulo de referencia. ^[58]

El triángulo intouch de un triángulo de referencia tiene sus vértices en los tres puntos de tangencia de los lados del triángulo de referencia con su circunferencia inscrita. ^[59] El triángulo extouch de un triángulo de referencia tiene sus vértices en los puntos de tangencia de las circunferencias extraídas del triángulo de referencia con sus lados (no extendidos). ^[60]

Todo triángulo acutángulo tiene tres cuadrados inscritos (cuadrados en su interior de modo que los cuatro vértices de un cuadrado se encuentran en un lado del triángulo, por lo que dos de ellos se encuentran en el mismo lado y, por lo tanto, un lado del cuadrado coincide con parte de un lado del triángulo). En un triángulo rectángulo, dos de los cuadrados coinciden y tienen un vértice en el ángulo recto del triángulo, por lo que un triángulo rectángulo tiene solo dos cuadrados inscritos distintos . Un triángulo obtusángulo tiene solo un cuadrado inscrito, con un lado que coincide con parte del lado más largo del triángulo. Dentro de un triángulo dado, un lado común más largo está asociado con un cuadrado inscrito más pequeño. Si un cuadrado inscrito tiene un lado de longitud y el triángulo tiene un lado de longitud , parte del cual coincide con un lado del cuadrado, entonces , , desde el lado , y el área del triángulo están relacionados de acuerdo con ^[61] La razón más grande posible del área del cuadrado inscrito al área del triángulo es 1/2, lo que ocurre cuando , , y la altura del triángulo desde la base de longitud es igual a . La razón más pequeña posible del lado de un cuadrado inscrito al lado de otro en el mismo triángulo no obtuso es . ^[62] Ambos casos extremos ocurren para el triángulo rectángulo isósceles. ^{[ cita requerida ]}$estilo de visualización q_{a}}$${\estilo de visualización a}$$estilo de visualización q_{a}}$${\estilo de visualización a}$$estilo de visualización h_{a}}$${\estilo de visualización a}$${\estilo de visualización T}$$${\displaystyle q_{a}={\frac {2Ta}{a^{2}+2T}}={\frac {ah_{a}}{a+h_{a}}}.}$$$Estilo de visualización a^{2}=2T$${\displaystyle q=a/2}$${\estilo de visualización a}$${\estilo de visualización a}$${\displaystyle 2{\sqrt {2}}/3}$

El hexágono de Lemoine es un hexágono cíclico cuyos vértices están dados por las seis intersecciones de los lados de un triángulo con las tres líneas que son paralelas a los lados y que pasan por su punto simediano . Tanto en su forma simple como en su forma autointersecante , el hexágono de Lemoine es interior al triángulo con dos vértices en cada lado del triángulo. ^{[ cita requerida ]}

Todo polígono convexo de área puede inscribirse en un triángulo de área como máximo igual a . La igualdad se cumple sólo si el polígono es un paralelogramo . ^[63]${\estilo de visualización T}$${\estilo de visualización 2T}$

El triángulo tangencial de un triángulo de referencia (que no sea un triángulo rectángulo) es el triángulo cuyos lados están en las líneas tangentes al círculo circunscrito del triángulo de referencia en sus vértices. ^[64]

Como se mencionó anteriormente, cada triángulo tiene un circuncírculo único, un círculo que pasa por los tres vértices, cuyo centro es la intersección de las bisectrices perpendiculares de los lados del triángulo. Además, cada triángulo tiene una circunelipse de Steiner única , que pasa por los vértices del triángulo y tiene su centro en el baricentro del triángulo. De todas las elipses que pasan por los vértices del triángulo, es la que tiene el área más pequeña. ^[65]

La hipérbola de Kiepert es una cónica única que pasa por los tres vértices del triángulo, su centroide y su circuncentro. ^[66]

De todos los triángulos contenidos en un polígono convexo dado , se puede encontrar uno con área máxima en tiempo lineal; sus vértices pueden elegirse como tres de los vértices del polígono dado. ^[67]

Un triángulo circular es un triángulo con aristas que forman arcos circulares . Las aristas de un triángulo circular pueden ser convexas (que se curvan hacia afuera) o cóncavas (que se curvan hacia adentro). ^[c] La intersección de tres discos forma un triángulo circular cuyos lados son todos convexos. Un ejemplo de un triángulo circular con tres aristas convexas es un triángulo de Reuleaux , que se puede hacer intersectando tres círculos del mismo tamaño. La construcción se puede realizar solo con un compás sin necesidad de una regla, mediante el teorema de Mohr-Mascheroni . Alternativamente, se puede construir redondeando los lados de un triángulo equilátero. ^[68]

Un caso especial de triángulo circular cóncavo se puede ver en un pseudotriángulo . ^[69] Un pseudotriángulo es un subconjunto simplemente conexo del plano que se encuentra entre tres regiones convexas mutuamente tangentes. Estos lados son tres líneas curvas suavizadas que conectan sus puntos finales llamados puntos de cúspide . Cualquier pseudotriángulo se puede dividir en muchos pseudotriángulos con los límites de discos convexos y líneas bitangentes , un proceso conocido como pseudotriangulación. Para los discos en un pseudotriángulo, la partición da pseudotriángulos y líneas bitangentes. ^[70] La envoltura convexa de cualquier pseudotriángulo es un triángulo. ^[71]${\estilo de visualización n}$${\estilo de visualización 2n-2}$${\estilo de visualización 3n-3}$

Un triángulo no plano es un triángulo que no está incluido en el espacio euclidiano , es decir, un espacio plano. Esto significa que también se pueden encontrar triángulos en varios espacios, como en el espacio hiperbólico y en la geometría esférica . Un triángulo en el espacio hiperbólico se denomina triángulo hiperbólico y se puede obtener dibujando sobre una superficie de curva negativa, como una superficie de silla de montar . Del mismo modo, un triángulo en la geometría esférica se denomina triángulo esférico y se puede obtener dibujando sobre una superficie de curva positiva, como una esfera . ^[72]

Los triángulos en ambos espacios tienen propiedades diferentes a los triángulos en el espacio euclidiano. Por ejemplo, como se mencionó anteriormente, los ángulos internos de un triángulo en el espacio euclidiano siempre suman 180°. Sin embargo, la suma de los ángulos internos de un triángulo hiperbólico es menor que 180°, y para cualquier triángulo esférico, la suma es mayor que 180°. ^[72] En particular, es posible dibujar un triángulo en una esfera tal que la medida de cada uno de sus ángulos internos sea igual a 90°, sumando un total de 270°. Por el teorema de Girard , la suma de los ángulos de un triángulo en una esfera es , donde es la fracción del área de la esfera encerrada por el triángulo. ^{[73] [74]}${\displaystyle 180^{\circ }\times (1+4f)}$${\estilo de visualización f}$

En espacios más generales, existen teoremas de comparación que relacionan las propiedades de un triángulo en el espacio con las propiedades de un triángulo correspondiente en un espacio modelo como el espacio hiperbólico o elíptico. ^[75] Por ejemplo, un espacio CAT(k) se caracteriza por tales comparaciones. ^[76]

Las formas fractales basadas en triángulos incluyen la junta de Sierpiński y el copo de nieve de Koch . ^[77]

Wikimedia Commons tiene medios relacionados con Triángulos .

Busque triangulo en Wikcionario, el diccionario libre.

• Ivanov, AB (2001) [1994]. "Triángulo". Enciclopedia de Matemáticas . EMS Press .
• Clark Kimberling: Enciclopedia de centros de triángulos. Enumera unos 5200 puntos interesantes asociados con cualquier triángulo.