Caída libre

En mecánica clásica , la caída libre es cualquier movimiento de un cuerpo en el que la gravedad es la única fuerza que actúa sobre él. Un objeto que cae libremente no necesariamente cae en dirección vertical . Normalmente, no se considera que un objeto que se mueve hacia arriba esté cayendo, pero si está sujeto únicamente a la fuerza de la gravedad, se dice que está en caída libre. La Luna está, por tanto, en caída libre alrededor de la Tierra , aunque su velocidad orbital la mantiene en una órbita muy alejada de la superficie terrestre .

En un campo gravitatorio aproximadamente uniforme , la gravedad actúa sobre cada parte de un cuerpo de manera aproximadamente igual. Cuando no hay otras fuerzas, como la fuerza normal ejercida entre un cuerpo (por ejemplo, un astronauta en órbita) y los objetos que lo rodean, se producirá la sensación de ingravidez , una condición que también se produce cuando el campo gravitatorio es débil (como cuando se está lejos de cualquier fuente de gravedad).

El término "caída libre" se utiliza a menudo de forma más laxa que en el sentido estricto definido anteriormente. Así, la caída a través de una atmósfera sin un paracaídas desplegado o un dispositivo de elevación también se suele denominar caída libre . Las fuerzas de resistencia aerodinámica en tales situaciones impiden que se produzca una ingravidez total y, por lo tanto, la "caída libre" de un paracaidista después de alcanzar la velocidad terminal produce la sensación de que el peso del cuerpo se apoya sobre un colchón de aire.

En el contexto de la relatividad general , donde la gravitación se reduce a una curvatura del espacio-tiempo , un cuerpo en caída libre no tiene ninguna fuerza actuando sobre él.

En el mundo occidental anterior al siglo XVI, se suponía generalmente que la velocidad de un cuerpo que cae sería proporcional a su peso, es decir, se esperaba que un objeto de 10 kg cayera diez veces más rápido que un objeto idéntico de 1 kg a través del mismo medio. El filósofo griego Aristóteles (384-322 a. C.) analizó la caída de objetos en Física (libro VII), uno de los libros más antiguos sobre mecánica (véase Física aristotélica ). Sin embargo, en el siglo VI, Juan Filópono desafió este argumento y dijo que, por observación, dos bolas de pesos muy diferentes caerán casi a la misma velocidad. ^[1]

En el siglo XII, en Irak, Abu'l-Barakāt al-Baghdādī dio una explicación de la aceleración gravitacional de los cuerpos en caída. Según Shlomo Pines , la teoría del movimiento de al-Baghdādī era "la negación más antigua de la ley dinámica fundamental de Aristóteles [es decir, que una fuerza constante produce un movimiento uniforme], [y es por lo tanto una] anticipación de una manera vaga de la ley fundamental de la mecánica clásica [es decir, que una fuerza aplicada continuamente produce aceleración]". ^[2]

Según un relato que puede ser apócrifo, entre 1589 y 1592 Galileo dejó caer dos objetos de masa desigual desde la Torre Inclinada de Pisa . Dada la velocidad a la que se produciría una caída de este tipo, es dudoso que Galileo pudiera haber extraído mucha información de este experimento. La mayoría de sus observaciones de cuerpos que caían eran en realidad de cuerpos rodando por rampas. Esto ralentizó las cosas lo suficiente como para que pudiera medir los intervalos de tiempo con relojes de agua y su propio pulso (los cronómetros aún no se habían inventado). Repitió esto "cien veces" hasta que logró "una precisión tal que la desviación entre dos observaciones nunca excedió una décima parte de un pulso". Entre 1589 y 1592, Galileo escribió De Motu Antiquiora , un manuscrito inédito sobre el movimiento de los cuerpos que caen. ^{[ cita requerida ]}

Es posible que este artículo contenga una investigación original . Por favor, mejórelo verificando las afirmaciones realizadas y agregando citas en línea . Las afirmaciones que consten únicamente de investigaciones originales deben eliminarse. ( Julio de 2020 ) ( Aprenda cómo y cuándo eliminar este mensaje )

Algunos ejemplos de objetos en caída libre incluyen:

• Una nave espacial (en el espacio) con propulsión desactivada (por ejemplo, en una órbita continua o en una trayectoria suborbital ( balística ) subiendo durante algunos minutos y luego bajando).
• Un objeto que se deja caer en la parte superior de un tubo de caída .
• Un objeto lanzado hacia arriba o una persona que salta del suelo a baja velocidad (es decir, siempre que la resistencia del aire sea insignificante en comparación con el peso).

Técnicamente, un objeto está en caída libre incluso cuando se mueve hacia arriba o se encuentra en reposo instantáneo en el punto más alto de su movimiento. Si la gravedad es la única influencia que actúa, entonces la aceleración ^[3] es siempre hacia abajo y tiene la misma magnitud para todos los cuerpos, comúnmente denotada como .${\displaystyle g}$

Dado que todos los objetos caen a la misma velocidad en ausencia de otras fuerzas, los objetos y las personas experimentarán ingravidez en estas situaciones.

Ejemplos de objetos que no están en caída libre:

• Volar en un avión: también hay una fuerza adicional de sustentación .
• De pie en el suelo: la fuerza de la gravedad es contrarrestada por la fuerza normal del suelo.
• Descender a la Tierra utilizando un paracaídas, que equilibra la fuerza de la gravedad con una fuerza de arrastre aerodinámica (y con algunos paracaídas, una fuerza de sustentación adicional).

El ejemplo de un paracaidista que cae y aún no ha desplegado un paracaídas no se considera caída libre desde una perspectiva física, ya que experimenta una fuerza de arrastre que es igual a su peso una vez que ha alcanzado la velocidad terminal (ver más abajo).

Cerca de la superficie de la Tierra, un objeto en caída libre en el vacío se acelerará aproximadamente a 9,8 m/s2 ^, independientemente de su masa . Con la resistencia del aire actuando sobre un objeto que se ha dejado caer, el objeto eventualmente alcanzará una velocidad terminal, que es de alrededor de 53 m/s (190 km/h o 118 mph ^[4] ) para un paracaidista humano. La velocidad terminal depende de muchos factores, incluidos la masa, el coeficiente de arrastre y el área de superficie relativa, y solo se logrará si la caída se realiza desde una altitud suficiente. Un paracaidista típico en una posición de águila extendida alcanzará la velocidad terminal después de aproximadamente 12 segundos, tiempo durante el cual habrá caído alrededor de 450 m (1500 pies). ^[4]

El astronauta David Scott demostró la caída libre en la Luna el 2 de agosto de 1971. Soltó simultáneamente un martillo y una pluma desde la misma altura sobre la superficie lunar. El martillo y la pluma cayeron a la misma velocidad y tocaron la superficie al mismo tiempo. Esto demostró el descubrimiento de Galileo de que, en ausencia de resistencia del aire, todos los objetos experimentan la misma aceleración debido a la gravedad. Sin embargo, en la Luna, la aceleración gravitatoria es de aproximadamente 1,63 m/s ² , o solo alrededor de ¹ ⁄ ₆  de la de la Tierra.

Este es el caso típico del movimiento vertical de un objeto que cae una pequeña distancia cerca de la superficie de un planeta. Es una buena aproximación en el aire siempre que la fuerza de gravedad sobre el objeto sea mucho mayor que la fuerza de resistencia del aire o, equivalentemente, la velocidad del objeto sea siempre mucho menor que la velocidad terminal (ver más abajo).

${\displaystyle v(t)=v_{0}-gt\,}$

${\displaystyle y(t)=v_{0}t+y_{0}-{\frac {1}{2}}gt^{2}}$

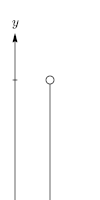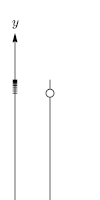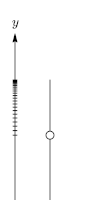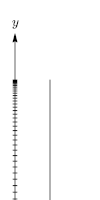
dónde

${\displaystyle v_{0}\,}$es el componente vertical inicial de la velocidad (m/s).

${\displaystyle v(t)\,}$es el componente vertical de la velocidad en (m/s).${\displaystyle t\,}$

${\displaystyle y_{0}\,}$es la altitud inicial (m).

${\displaystyle y(t)\,}$es la altitud en (m).${\displaystyle t\,}$

${\displaystyle t\,}$es el tiempo transcurrido (s).

${\displaystyle g\,}$es la aceleración debida a la gravedad (9,81 m/s ² cerca de la superficie de la tierra).

Si la velocidad inicial es cero, entonces la distancia caída desde la posición inicial crecerá con el cuadrado del tiempo transcurrido. Además, como los números impares suman los cuadrados perfectos , la distancia caída en intervalos de tiempo sucesivos crece con los números impares. Esta descripción del comportamiento de los cuerpos en caída fue dada por Galileo. ^[5]

Este caso, que se aplica a paracaidistas, paracaidistas o cualquier cuerpo de masa, , y área de sección transversal, , con un número de Reynolds muy por encima del número de Reynolds crítico, de modo que la resistencia del aire es proporcional al cuadrado de la velocidad de caída, , tiene una ecuación de movimiento${\displaystyle m}$${\displaystyle A}$${\displaystyle v}$

${\displaystyle m{\frac {\mathrm {d} v}{\mathrm {d} t}}=mg-{\frac {1}{2}}\rho C_{\mathrm {D} }Av^{2}\,,}$

donde es la densidad del aire y es el coeficiente de arrastre , que se supone constante aunque en general dependerá del número de Reynolds.${\displaystyle \rho }$${\displaystyle C_{\mathrm {D} }}$

Suponiendo que un objeto cae desde el reposo y que no hay cambios en la densidad del aire con la altitud, la solución es:

${\displaystyle v(t)=v_{\infty }\tanh \left({\frac {gt}{v_{\infty }}}\right),}$

donde la velocidad terminal viene dada por

${\displaystyle v_{\infty }={\sqrt {\frac {2mg}{\rho C_{D}A}}}\,.}$

La velocidad del objeto en función del tiempo se puede integrar a lo largo del tiempo para encontrar la posición vertical en función del tiempo:

${\displaystyle y=y_{0}-{\frac {v_{\infty }^{2}}{g}}\ln \cosh \left({\frac {gt}{v_{\infty }}}\right).}$

Utilizando la cifra de 56 m/s para la velocidad terminal de un humano, se encuentra que después de 10 segundos habrá caído 348 metros y habrá alcanzado el 94% de la velocidad terminal, y después de 12 segundos habrá caído 455 metros y habrá alcanzado el 97% de la velocidad terminal. Sin embargo, cuando no se puede suponer que la densidad del aire sea constante, como en el caso de los objetos que caen desde gran altitud, la ecuación de movimiento se vuelve mucho más difícil de resolver analíticamente y suele ser necesaria una simulación numérica del movimiento. La figura muestra las fuerzas que actúan sobre los meteoroides que caen a través de la atmósfera superior de la Tierra. Los saltos HALO , incluidos los saltos récord de Joe Kittinger y Felix Baumgartner , también pertenecen a esta categoría. ^[6]

Se puede decir que dos objetos en el espacio que orbitan entre sí en ausencia de otras fuerzas están en caída libre uno alrededor del otro, por ejemplo, que la Luna o un satélite artificial "caen alrededor" de la Tierra, o un planeta "cae alrededor" del Sol. Suponer que los objetos son esféricos significa que la ecuación de movimiento está gobernada por la ley de gravitación universal de Newton , y que las soluciones al problema gravitacional de dos cuerpos son órbitas elípticas que obedecen a las leyes de movimiento planetario de Kepler . Esta conexión entre los objetos que caen cerca de la Tierra y los objetos en órbita se ilustra mejor con el experimento mental de la bala de cañón de Newton .

El movimiento de dos objetos que se desplazan radialmente uno hacia el otro sin momento angular puede considerarse un caso especial de una órbita elíptica de excentricidad e = 1 ( trayectoria elíptica radial ). Esto permite calcular el tiempo de caída libre de dos objetos puntuales en una trayectoria radial. La solución de esta ecuación de movimiento da como resultado el tiempo en función de la separación:

${\displaystyle t(y)={\sqrt {\frac {{y_{0}}^{3}}{2\mu }}}\left({\sqrt {{\frac {y}{y_{0}}}\left(1-{\frac {y}{y_{0}}}\right)}}+\arccos {\sqrt {\frac {y}{y_{0}}}}\right),}$

dónde

${\displaystyle t}$Es el momento después del inicio del otoño.

${\displaystyle y}$es la distancia entre los centros de los cuerpos

${\displaystyle y_{0}}$es el valor inicial de${\displaystyle y}$

${\displaystyle \mu =G(m_{1}+m_{2})}$es el parámetro gravitacional estándar .

Sustituyendo obtenemos el tiempo de caída libre.${\displaystyle y=0}$

${\displaystyle t_{\text{ff}}=\pi {\sqrt {y_{0}^{3}/(8\mu )}}~.}$

La separación puede expresarse explícitamente como una función del tiempo ^[7]

${\displaystyle y(t)=y_{0}~Q\left(1-{\frac {t}{t_{\text{ff}}}};{\frac {3}{2}},{\frac {1}{2}}\right)~,}$

donde es la función cuantil de la distribución Beta , también conocida como la función inversa de la función beta incompleta regularizada .${\displaystyle Q(x;\alpha ,\beta )}$ ${\displaystyle I_{x}(\alpha ,\beta )}$

Esta solución también puede representarse exactamente mediante la serie de potencia analítica

${\displaystyle y(t)=\sum _{n=1}^{\infty }\left[\lim _{r\to 0}\left({\frac {x^{n}}{n!}}{\frac {\mathrm {d} ^{\,n-1}}{\mathrm {d} r^{\,n-1}}}\left[r^{n}\left({\frac {7}{2}}(\arcsin({\sqrt {r}})-{\sqrt {r-r^{2}}})\right)^{-{\frac {2}{3}}n}\right]\right)\right].}$

Evaluando esto obtenemos: ^{[8] [9]}

${\displaystyle y(t)=y_{0}\left(x-{\frac {1}{5}}x^{2}-{\frac {3}{175}}x^{3}-{\frac {23}{7875}}x^{4}-{\frac {1894}{3031875}}x^{5}-{\frac {3293}{21896875}}x^{6}-{\frac {2418092}{62077640625}}x^{7}-\cdots \right)\ ,}$

dónde

${\displaystyle x=\left[{\frac {3}{2}}\left({\frac {\pi }{2}}-t{\sqrt {\frac {2\mu }{{y_{0}}^{3}}}}\right)\right]^{2/3}.}$

En la relatividad general, un objeto en caída libre no está sujeto a ninguna fuerza y ​​es un cuerpo inercial que se mueve a lo largo de una geodésica . Lejos de cualquier fuente de curvatura del espacio-tiempo, donde el espacio-tiempo es plano, la teoría newtoniana de la caída libre concuerda con la relatividad general. De lo contrario, las dos no están de acuerdo; por ejemplo, solo la relatividad general puede explicar la precesión de las órbitas, la descomposición orbital o espiral de las binarias compactas debido a las ondas gravitacionales y la relatividad de la dirección ( precesión geodésica y arrastre de marcos ).

La observación experimental de que todos los objetos en caída libre aceleran al mismo ritmo, como lo señaló Galileo y luego se plasmó en la teoría de Newton como la igualdad de las masas gravitacionales e inerciales, y más tarde se confirmó con gran precisión mediante las formas modernas del experimento de Eötvös , es la base del principio de equivalencia , a partir del cual despegó inicialmente la teoría de la relatividad general de Einstein.

• Ecuaciones para un cuerpo que cae
• Fuerza G
• Paracaidismo militar a gran altitud
• Aeronave de gravedad reducida
• Velocidad terminal
• Ingravidez

• Calculadora de fórmula de caída libre
• La manera en que caen las cosas: un sitio web educativo

Wikimedia Commons alberga una categoría multimedia sobre Caída libre .