Bivector

En matemáticas , un bivector o 2-vector es una cantidad en álgebra exterior o álgebra geométrica que extiende la idea de escalares y vectores . Considerando un escalar como una cantidad de grado cero y un vector como una cantidad de grado uno, un bivector es de grado dos. Los bivectores tienen aplicaciones en muchas áreas de las matemáticas y la física. Están relacionados con los números complejos en dos dimensiones y con los pseudovectores y cuaterniones vectoriales en tres dimensiones. Se pueden utilizar para generar rotaciones en un espacio de cualquier número de dimensiones y son una herramienta útil para clasificar dichas rotaciones.

Geométricamente, un bivector simple puede interpretarse como la caracterización de un segmento de plano dirigido (o segmento de plano orientado ), de forma muy similar a como se puede pensar que los vectores caracterizan segmentos de línea dirigidos . ^[2] El bivector a ∧ b tiene una actitud (o dirección ) del plano abarcado por a y b , tiene un área que es un múltiplo escalar de cualquier segmento de plano de referencia con la misma actitud (y en álgebra geométrica, tiene una magnitud igual al área del paralelogramo con aristas a y b ), y tiene una orientación que es el lado de a en el que b se encuentra dentro del plano abarcado por a y b . ^{[2] [3]} En términos sencillos, cualquier superficie define el mismo bivector si es paralela al mismo plano (misma actitud), tiene la misma área y la misma orientación (véase la figura).

Los bivectores se generan por el producto exterior de los vectores: dados dos vectores a y b , su producto exterior a ∧ b es un bivector, como lo es cualquier suma de bivectores. No todos los bivectores pueden expresarse como un producto exterior sin dicha suma. Más precisamente, un bivector que puede expresarse como un producto exterior se llama simple ; en hasta tres dimensiones todos los bivectores son simples, pero en dimensiones superiores este no es el caso. ^[4] El producto exterior de dos vectores es alterno , por lo que a ∧ a es el bivector cero, y b ∧ a es el negativo del bivector a ∧ b , produciendo la orientación opuesta. Los conceptos directamente relacionados con el bivector son el tensor antisimétrico de rango 2 y la matriz antisimétrica .

El bivector fue definido por primera vez en 1844 por el matemático alemán Hermann Grassmann en álgebra exterior como el resultado del producto exterior de dos vectores. Justo el año anterior, en Irlanda, William Rowan Hamilton había descubierto los cuaterniones . Hamilton acuñó tanto el término vector como el de bivector , este último en sus Lectures on Quaternions (1853) cuando introdujo los bicuaterniones , que tienen bivectores como sus partes vectoriales. No fue hasta que el matemático inglés William Kingdon Clifford en 1888 añadió el producto geométrico al álgebra de Grassmann, incorporando las ideas tanto de Hamilton como de Grassmann, y fundó el álgebra de Clifford , que surgió el bivector de este artículo. Henry Forder utilizó el término bivector para desarrollar el álgebra exterior en 1941. ^[5]

En la década de 1890, Josiah Willard Gibbs y Oliver Heaviside desarrollaron el cálculo vectorial , que incluía productos vectoriales y productos puntuales separados que se derivaban de la multiplicación de cuaterniones. ^{[6] [7] [8]} El éxito del cálculo vectorial y del libro Vector Analysis de Gibbs y Wilson tuvo el efecto de que las ideas de Hamilton y Clifford se pasaran por alto durante mucho tiempo, ya que gran parte de las matemáticas y la física del siglo XX se formularon en términos vectoriales. Gibbs usó vectores para llenar el papel de bivectores en tres dimensiones, y usó bivector en el sentido de Hamilton, un uso que a veces ha sido copiado. ^{[9] [10] [11]} Hoy en día, el bivector se estudia en gran medida como un tema en álgebra geométrica , un álgebra de Clifford sobre espacios vectoriales reales o complejos con una forma cuadrática . Su resurgimiento fue liderado por David Hestenes quien, junto con otros, aplicó el álgebra geométrica a una gama de nuevas aplicaciones en física . ^[12]

En este artículo, el bivector se considerará únicamente en álgebras geométricas reales, que pueden aplicarse en la mayoría de las áreas de la física. Además, a menos que se indique lo contrario, todos los ejemplos tienen una métrica euclidiana y, por lo tanto, una forma cuadrática definida positiva .

El bivector surge de la definición del producto geométrico sobre un espacio vectorial con una forma cuadrática asociada, a veces llamada métrica . Para los vectores a , b y c , el producto geométrico satisface las siguientes propiedades:

Asociatividad

${\displaystyle (\mathbf {ab} )\mathbf {c} =\mathbf {a} (\mathbf {bc} )}$

Distributividad izquierda y derecha

${\displaystyle {\begin{alineado}\mathbf {a} (\mathbf {b} +\mathbf {c} )&=\mathbf {ab} +\mathbf {ac} \\(\mathbf {b} +\mathbf {c} )\mathbf {a} &=\mathbf {ba} +\mathbf {ca} \end{alineado}}}$

Cuadrado escalar

⁠ ⁠${\displaystyle \mathbf {a} ^{2}=Q(\mathbf {a} )}$ , donde Q es la forma cuadrática, que no necesita ser definida positiva .

De la asociatividad, a ( ab ) = a ² b , es un escalar por b . Cuando b no es paralelo a a y, por lo tanto, no es un múltiplo escalar de a , ab no puede ser un escalar. Pero

${\displaystyle {\tfrac {1}{2}}(\mathbf {ab} +\mathbf {ba} )={\tfrac {1}{2}}\left((\mathbf {a} +\mathbf { b} )^{2}-\mathbf {a} ^{2}-\mathbf {b} ^{2}\right)}$

es una suma de escalares y por lo tanto un escalar. De la ley de los cosenos en el triángulo formado por los vectores su valor es | a | | b | cos θ , donde θ es el ángulo entre los vectores. Por lo tanto es idéntico al producto escalar entre dos vectores, y se escribe de la misma manera,

${\displaystyle \mathbf {a} \cdot \mathbf {b} ={\tfrac {1}{2}}(\mathbf {ab} +\mathbf {ba} ).}$

Es simétrico, de valor escalar y se puede utilizar para determinar el ángulo entre dos vectores: en particular, si a y b son ortogonales, el producto es cero.

Así como el producto escalar puede formularse como la parte simétrica del producto geométrico de otra cantidad, el producto exterior (a veces conocido como producto "cuña" o "progresivo") puede formularse como su parte antisimétrica :

${\displaystyle \mathbf {a} \cuña \mathbf {b} ={\frac {1}{2}}(\mathbf {ab} -\mathbf {ba} )}$

Es antisimétrico en a y b

${\displaystyle \mathbf {b} \wedge \mathbf {a} ={\frac {1}{2}}(\mathbf {ba} -\mathbf {ab} )=-{\frac {1}{2}}(\mathbf {ab} -\mathbf {ba} )=-\mathbf {a} \wedge \mathbf {b} }$

y por adición:

${\displaystyle \mathbf {a} \cdot \mathbf {b} +\mathbf {a} \wedge \mathbf {b} ={\frac {1}{2}}(\mathbf {ab} +\mathbf {ba} )+{\frac {1}{2}}(\mathbf {ab} -\mathbf {ba} )=\mathbf {ab} }$

Es decir, el producto geométrico es la suma del producto escalar simétrico y el producto exterior alterno.

Para examinar la naturaleza de a ∧ b , considere la fórmula

${\displaystyle (\mathbf {a} \cdot \mathbf {b} )^{2}-(\mathbf {a} \wedge \mathbf {b} )^{2}=\mathbf {a} ^{2}\mathbf {b} ^{2},}$

que utilizando la identidad trigonométrica pitagórica da el valor de ( a ∧ b ) ²

${\displaystyle (\mathbf {a} \wedge \mathbf {b} )^{2}=(\mathbf {a} \cdot \mathbf {b} )^{2}-\mathbf {a} ^{2} \mathbf {b} ^{2}=\left|\mathbf {a} \right|^{2}\left|\mathbf {b} \right|^{2}(\cos ^{2}\theta - 1)=-\left|\mathbf {a} \right|^{2}\left|\mathbf {b} \right|^{2}\sin ^{2}\theta }$

Con un cuadrado negativo, no puede ser una cantidad escalar o vectorial, por lo que es un nuevo tipo de objeto, un bivector . Tiene magnitud | a | | b | | sen θ | , donde θ es el ángulo entre los vectores y, por lo tanto, es cero para los vectores paralelos.

Para distinguirlos de los vectores, los bivectores se escriben aquí con letras mayúsculas y negrita, por ejemplo:

${\displaystyle \mathbf {A} =\mathbf {a} \cuña \mathbf {b} =-\mathbf {b} \cuña \mathbf {a} \,,}$

aunque se utilizan otras convenciones, en particular porque los vectores y bivectores son ambos elementos del álgebra geométrica.

El álgebra generada por el producto geométrico (es decir, todos los objetos formados al tomar sumas repetidas y productos geométricos de escalares y vectores) es el álgebra geométrica sobre el espacio vectorial. Para un espacio vectorial euclidiano, esta álgebra se escribe o Cl _n ( R ) , donde n es la dimensión del espacio vectorial R ⁿ . Cl _n ( R ) es tanto un espacio vectorial como un álgebra, generada por todos los productos entre vectores en R ⁿ , por lo que contiene todos los vectores y bivectores. Más precisamente, como espacio vectorial contiene los vectores y bivectores como subespacios lineales , aunque no como subálgebras (ya que el producto geométrico de dos vectores no es generalmente otro vector).${\displaystyle {\mathcal {G}}_{n}}$

El espacio de todos los bivectores tiene dimensión ⁠1/2⁠ n ( n − 1) y se escribe ⋀ ² R ⁿ , ^[13] y es la segunda potencia exterior del espacio vectorial original.

La subálgebra generada por los bivectores es la subálgebra par del álgebra geométrica, escrita Cl^[0]
_en( R ) . Esta álgebra resulta de considerar todas las sumas repetidas y productos geométricos de escalares y bivectores. Tiene dimensión 2 ^{n −1} , y contiene ⋀ ² R ⁿ como un subespacio lineal. En dos y tres dimensiones, la subálgebra par contiene solo escalares y bivectores, y cada uno es de particular interés. En dos dimensiones, la subálgebra par es isomorfa a los números complejos , C , mientras que en tres es isomorfa a los cuaterniones , H . La subálgebra par contiene las rotaciones en cualquier dimensión.

Como se señaló en la sección anterior, la magnitud de un bivector simple, es decir, aquel que es el producto exterior de dos vectores a y b , es | a | | b | sen θ , donde θ es el ángulo entre los vectores. Se escribe | B | , donde B es el bivector.

Para los bivectores generales, la magnitud se puede calcular tomando la norma del bivector considerado como un vector en el espacio ⋀ ² R ⁿ . Si la magnitud es cero, entonces todos los componentes del bivector son cero, y el bivector es el bivector cero que, como elemento del álgebra geométrica, es igual al escalar cero.

Un bivector unitario es aquel que tiene una magnitud unitaria. Un bivector de este tipo se puede derivar de cualquier bivector distinto de cero dividiendo el bivector por su magnitud, es decir

${\displaystyle {\frac {\mathbf {B}} {\left\vert \mathbf {B} \right\vert }}.}$

De particular utilidad son los bivectores unitarios formados a partir de los productos de la base estándar del espacio vectorial. Si e _i y e _j son vectores base distintos, entonces el producto e _i ∧ e _j es un bivector. Como e _i y e _j son ortogonales, e _i ∧ e _j = e _i e _j , escrito e _ij , y tiene magnitud unitaria ya que los vectores son vectores unitarios . El conjunto de todos los bivectores producidos a partir de la base de esta manera forman una base para ⋀ ² R ⁿ . Por ejemplo, en cuatro dimensiones la base para ⋀ ² R ⁴ es ( e ₁ e ₂ , e ₁ e ₃ , e ₁ e ₄ , e ₂ e ₃ , e ₂ e ₄ , e ₃ e ₄ ) o ( e ₁₂ , e ₁₃ , e ₁₄ , e ₂₃ , e ₂₄ , e ₃₄ ). ^[14]

El producto exterior de dos vectores es un bivector, pero no todos los bivectores son productos exteriores de dos vectores. Por ejemplo, en cuatro dimensiones el bivector

${\displaystyle \mathbf {B} =\mathbf {e} _{1}\wedge \mathbf {e} _{2}+\mathbf {e} _{3}\wedge \mathbf {e} _{4}=\mathbf {e} _{1}\mathbf {e} _{2}+\mathbf {e} _{3}\mathbf {e} _{4}=\mathbf {e} _{12}+\mathbf {e} _{34}}$

no puede escribirse como el producto exterior de dos vectores. Un bivector que puede escribirse como el producto exterior de dos vectores es simple. En dos y tres dimensiones todos los bivectores son simples, pero no en cuatro o más dimensiones; en cuatro dimensiones cada bivector es la suma de, como máximo, dos productos exteriores. Un bivector tiene un cuadrado real si y solo si es simple, y solo los bivectores simples pueden representarse geométricamente mediante un área plana dirigida. ^[4]

El producto geométrico de dos bivectores, A y B , es

${\displaystyle \mathbf {A} \mathbf {B} =\mathbf {A} \cdot \mathbf {B} +\mathbf {A} \times \mathbf {B} +\mathbf {A} \wedge \mathbf {B} .}$

La cantidad A · B es el producto escalar de valor escalar, mientras que A ∧ B es el producto exterior de grado 4 que surge en cuatro o más dimensiones. La cantidad A × B es el producto conmutador de valor bivectorial , dado por

${\displaystyle \mathbf {A} \times \mathbf {B} ={\tfrac {1}{2}}(\mathbf {AB} -\mathbf {BA} ),}$^[15]

El espacio de bivectores ⋀ ² R ⁿ es un álgebra de Lie sobre R , con el producto conmutador como el corchete de Lie. El producto geométrico completo de bivectores genera la subálgebra par.

De particular interés es el producto de un bivector consigo mismo. Como el producto del conmutador es antisimétrico, el producto se simplifica a

${\displaystyle \mathbf {A} \mathbf {A} =\mathbf {A} \cdot \mathbf {A} +\mathbf {A} \wedge \mathbf {A} .}$

Si el bivector es simple, el último término es cero y el producto es el valor escalar A · A , que puede utilizarse como comprobación de la simplicidad. En particular, el producto exterior de los bivectores solo existe en cuatro o más dimensiones, por lo que todos los bivectores en dos y tres dimensiones son simples. ^[4]

Los bivectores son isomorfos a matrices antisimétricas en cualquier número de dimensiones. Por ejemplo, el bivector general B ₂₃ e ₂₃ + B ₃₁ e ₃₁ + B ₁₂ e ₁₂ en tres dimensiones se asigna a la matriz

${\displaystyle M_{B}={\begin{pmatrix}0&B_{12}&-B_{31}\\-B_{12}&0&B_{23}\\B_{31}&-B_{23}&0\end{pmatrix}}.}$

Esto multiplicado por los vectores de ambos lados da el mismo vector que el producto de un vector y un bivector menos el producto exterior; un ejemplo es el tensor de velocidad angular .

Las matrices antisimétricas generan matrices ortogonales con determinante 1 a través de la función exponencial. En particular, al aplicar la función exponencial a un bivector asociado con una rotación se obtiene una matriz de rotación . La matriz de rotación M _R dada por la matriz antisimétrica anterior es

${\displaystyle M_{R}=\exp {M_{B}}.}$

La rotación descrita por M _R es la misma que la descrita por el rotor R dado por

${\displaystyle R=\exp {{\tfrac {1}{2}}B},}$

y la matriz M _R también se puede calcular directamente a partir del rotor R . En tres dimensiones, esto se da por

${\displaystyle M_{R}={\begin{pmatrix}(R\mathbf {e} _{1}R^{-1})\cdot \mathbf {e} _{1}&(R\mathbf {e} _{2}R^{-1})\cdot \mathbf {e} _{1}&(R\mathbf {e} _{3}R^{-1})\cdot \mathbf {e} _{1}\\(R\mathbf {e} _{1}R^{-1})\cdot \mathbf {e} _{2}&(R\mathbf {e} _{2}R^{-1})\cdot \mathbf {e} _{2}&(R\mathbf {e} _{3}R^{-1})\cdot \mathbf {e} _{2}\\(R\mathbf {e} _{1}R^{-1})\cdot \mathbf {e} _{3}&(R\mathbf {e} _{2}R^{-1})\cdot \mathbf {e} _{3}&(R\mathbf {e} _{3}R^{-1})\cdot \mathbf {e} _{3}\end{pmatrix}}.}$

Los bivectores están relacionados con los valores propios de una matriz de rotación. Dada una matriz de rotación M, los valores propios se pueden calcular resolviendo la ecuación característica para esa matriz 0 = det( M − λI ) . Por el teorema fundamental del álgebra, esto tiene tres raíces (solo una de las cuales es real ya que solo hay un vector propio, es decir, el eje de rotación). Las otras raíces deben ser un par complejo conjugado. Tienen magnitud unitaria, por lo que son logaritmos puramente imaginarios, iguales a la magnitud del bivector asociado con la rotación, que también es el ángulo de rotación. Los vectores propios asociados con los valores propios complejos están en el plano del bivector, por lo que el producto exterior de dos vectores propios no paralelos da como resultado el bivector (o un múltiplo del mismo).

Cuando se trabaja con coordenadas en álgebra geométrica, es habitual escribir los vectores base como ( e ₁ , e ₂ , ...) , una convención que se utilizará aquí.

Un vector en el espacio bidimensional real R ² se puede escribir a = a ₁ e ₁ + a ₂ e ₂ , donde a ₁ y a ₂ son números reales, e ₁ y e ₂ son vectores base ortonormales . El producto geométrico de dos de estos vectores es

${\displaystyle {\begin{aligned}\mathbf {a} \mathbf {b} &=(a_{1}\mathbf {e} _{1}+a_{2}\mathbf {e} _{2})(b_{1}\mathbf {e} _{1}+b_{2}\mathbf {e} _{2})\\&=a_{1}b_{1}\mathbf {e} _{1}\mathbf {e} _{1}+a_{1}b_{2}\mathbf {e} _{1}\mathbf {e} _{2}+a_{2}b_{1}\mathbf {e} _{2}\mathbf {e} _{1}+a_{2}b_{2}\mathbf {e} _{2}\mathbf {e} _{2}\\&=a_{1}b_{1}+a_{2}b_{2}+(a_{1}b_{2}-a_{2}b_{1})\mathbf {e} _{1}\mathbf {e} _{2}.\end{aligned}}}$

Esto se puede dividir en un producto escalar simétrico y un producto exterior bivectorial antisimétrico:

${\displaystyle {\begin{aligned}\mathbf {a} \cdot \mathbf {b} &=a_{1}b_{1}+a_{2}b_{2},\\\mathbf {a} \wedge \mathbf {b} &=(a_{1}b_{2}-a_{2}b_{1})\mathbf {e} _{1}\mathbf {e} _{2}=(a_{1}b_{2}-a_{2}b_{1})\mathbf {e} _{12}.\end{aligned}}}$

Todos los bivectores en dos dimensiones tienen esta forma, es decir, son múltiplos del bivector e ₁ e ₂ , escrito e ₁₂ para enfatizar que es un bivector en lugar de un vector. La magnitud de e ₁₂ es 1 , con

${\displaystyle \mathbf {e} _{12}^{2}=-1,}$

Por eso se le llama bivector unitario . El término bivector unitario se puede utilizar en otras dimensiones, pero solo se define de forma única (hasta un signo) en dos dimensiones y todos los bivectores son múltiplos de e ₁₂ . Como elemento de grado más alto del álgebra, e ₁₂ también es el pseudoescalar al que se le da el símbolo i .

Con las propiedades del cuadrado negativo y la magnitud unitaria, el bivector unitario puede identificarse con la unidad imaginaria de los números complejos . Los bivectores y escalares juntos forman la subálgebra par del álgebra geométrica, que es isomorfa a los números complejos C. La subálgebra par tiene base (1, e ₁₂ ) , el álgebra completa tiene base (1, e ₁ , e ₂ , e ₁₂ ) .

Los números complejos se suelen identificar con los ejes de coordenadas y vectores bidimensionales, lo que significaría asociarlos con los elementos vectoriales del álgebra geométrica. No hay ninguna contradicción en esto, ya que para pasar de un vector general a un número complejo es necesario identificar un eje como el eje real, digamos e ₁ . Esto se multiplica por todos los vectores para generar los elementos de la subálgebra par.

Todas las propiedades de los números complejos se pueden derivar de los bivectores, pero dos son de particular interés. En primer lugar, como en el caso de los números complejos, los productos de los bivectores y, por lo tanto, las subálgebras pares son conmutativas . Esto solo es cierto en dos dimensiones, por lo que las propiedades del bivector en dos dimensiones que dependen de la conmutatividad no suelen generalizarse a dimensiones superiores.

En segundo lugar, se puede escribir un bivector general

${\displaystyle \theta \mathbf {e} _{12}=i\theta ,}$

donde θ es un número real. Al introducir esto en la serie de Taylor para la función exponencial y usar la propiedad e ₁₂ ² = −1 se obtiene una versión bivectorial de la fórmula de Euler ,

${\displaystyle \exp {\theta \mathbf {e} _{12}}=\exp {i\theta }=\cos {\theta }+i\sin {\theta },}$

que al multiplicarse por cualquier vector lo gira un ángulo θ respecto al origen:

${\displaystyle (x'\mathbf {e} _{1}+y'\mathbf {e} _{2})=(x\mathbf {e} _{1}+y\mathbf {e} _{2})\exp {i\theta }.}$

El producto de un vector con un bivector en dos dimensiones es anticonmutativo , por lo que los siguientes productos generan todos la misma rotación

${\displaystyle \mathbf {v} '=\mathbf {v} \exp {i\theta }=\exp(-i\theta )\,\mathbf {v} =\exp({-i\theta }/{2})\,\mathbf {v} \exp({i\theta }/{2}).}$

De estos, el último producto es el que se generaliza a dimensiones superiores. La cantidad necesaria se llama rotor y se le da el símbolo R , por lo que en dos dimensiones un rotor que gira a través del ángulo θ se puede escribir

${\displaystyle R=\exp({-{\tfrac {1}{2}}i\theta })=\exp({-{\tfrac {1}{2}}\theta \mathbf {e} _{12}}),}$

y la rotación que genera es ^[16]

${\displaystyle \mathbf {v} '=R\mathbf {v} R^{-1}.}$

En tres dimensiones el producto geométrico de dos vectores es

${\displaystyle {\begin{aligned}\mathbf {ab} &=(a_{1}\mathbf {e} _{1}+a_{2}\mathbf {e} _{2}+a_{3}\mathbf {e} _{3})(b_{1}\mathbf {e} _{1}+b_{2}\mathbf {e} _{2}+b_{3}\mathbf {e} _{3})\\&=a_{1}b_{1}{\mathbf {e} _{1}}^{2}+a_{2}b_{2}{\mathbf {e} _{2}}^{2}+a_{3}b_{3}{\mathbf {e} _{3}}^{2}+(a_{2}b_{3}-a_{3}b_{2})\mathbf {e} _{2}\mathbf {e} _{3}+(a_{3}b_{1}-a_{1}b_{3})\mathbf {e} _{3}\mathbf {e} _{1}+(a_{1}b_{2}-a_{2}b_{1})\mathbf {e} _{1}\mathbf {e} _{2}.\end{aligned}}}$

Esto se puede dividir en el producto escalar simétrico, de valor escalar, y el producto exterior antisimétrico, de valor bivectorial:

${\displaystyle {\begin{aligned}\mathbf {a} \cdot \mathbf {b} &=a_{1}b_{1}+a_{2}b_{2}+a_{3}b_{3}\\\mathbf {a} \wedge \mathbf {b} &=(a_{2}b_{3}-a_{3}b_{2})\mathbf {e} _{23}+(a_{3}b_{1}-a_{1}b_{3})\mathbf {e} _{31}+(a_{1}b_{2}-a_{2}b_{1})\mathbf {e} _{12}.\end{aligned}}}$

En tres dimensiones todos los bivectores son simples y por tanto el resultado de un producto exterior. Los bivectores unitarios e ₂₃ , e ₃₁ y e ₁₂ forman una base para el espacio de bivectores ⋀ ² R ³ , que es en sí mismo un espacio lineal tridimensional. Por tanto, si un bivector general es:

${\displaystyle \mathbf {A} =A_{23}\mathbf {e} _{23}+A_{31}\mathbf {e} _{31}+A_{12}\mathbf {e} _{12},}$

Se pueden sumar como vectores.

${\displaystyle \mathbf {A} +\mathbf {B} =(A_{23}+B_{23})\mathbf {e} _{23}+(A_{31}+B_{31})\mathbf {e} _{31}+(A_{12}+B_{12})\mathbf {e} _{12}.}$

mientras que al multiplicarse producen lo siguiente

${\displaystyle \mathbf {A} \mathbf {B} =-A_{23}B_{23}-A_{31}B_{31}-A_{12}B_{12}+(A_{12}B_{31}-A_{31}B_{12})\mathbf {e} _{23}+(A_{23}B_{12}-A_{12}B_{23})\mathbf {e} _{31}+(A_{31}B_{23}-A_{23}B_{31})\mathbf {e} _{12}}$

que se puede dividir en partes bivectoriales antisimétricas y escalares simétricas de la siguiente manera

${\displaystyle {\begin{aligned}\mathbf {A} \cdot \mathbf {B} &=-A_{12}B_{12}-A_{31}B_{31}-A_{23}B_{23}\\\mathbf {A} \times \mathbf {B} &=(A_{23}B_{31}-A_{31}B_{23})\mathbf {e} _{12}+(A_{12}B_{23}-A_{23}B_{12})\mathbf {e} _{13}+(A_{31}B_{12}-A_{12}B_{31})\mathbf {e} _{23}.\end{aligned}}}$

El producto exterior de dos bivectores en tres dimensiones es cero.

Un bivector B se puede escribir como el producto de su magnitud y un bivector unitario, por lo que escribiendo β para | B | y usando la serie de Taylor para el mapa exponencial se puede demostrar que

${\displaystyle \exp {\mathbf {B} }=\exp({\beta {\frac {\mathbf {B} }{\beta }}})=\cos {\beta }+{\frac {\mathbf {B} }{\beta }}\sin {\beta }.}$

Esta es otra versión de la fórmula de Euler, pero con un bivector general en tres dimensiones. A diferencia de lo que ocurre en dos dimensiones, los bivectores no son conmutativos, por lo que las propiedades que dependen de la conmutatividad no se aplican en tres dimensiones. Por ejemplo, en general, exp( A + B ) ≠ exp( A ) exp( B ) en tres (o más) dimensiones.

El álgebra geométrica completa en tres dimensiones, Cl ₃ ( R ) , tiene base ( 1 , e ₁ , e ₂ , e ₃ , e ₂₃ , e ₃₁ , e ₁₂ , e ₁₂₃ ). El elemento e ₁₂₃ es un trivector y el pseudoescalar de la geometría. Los bivectores en tres dimensiones a veces se identifican con pseudovectores ^[17] con los que están relacionados, como se analiza a continuación.

Los bivectores no están cerrados bajo el producto geométrico, pero sí lo está la subálgebra par. En tres dimensiones está formada por todos los elementos escalares y bivectoriales del álgebra geométrica, por lo que un elemento general se puede escribir por ejemplo a + A , donde a es la parte escalar y A es la parte bivectorial. Se escribe Cl^[0]
₃y tiene base (1, e ₂₃ , e ₃₁ , e ₁₂ ) . El producto de dos elementos generales del subálgebra par es

${\displaystyle (a+\mathbf {A} )(b+\mathbf {B} )=ab+a\mathbf {B} +b\mathbf {A} +\mathbf {A} \cdot \mathbf {B} +\mathbf {A} \times \mathbf {B} .}$

El subálgebra par, es decir, el álgebra que consta de escalares y bivectores, es isomorfa a los cuaterniones , H. Esto se puede ver comparando la base con la base de cuaterniones, o a partir del producto anterior que es idéntico al producto de cuaterniones, excepto por un cambio de signo que se relaciona con los productos negativos en el producto escalar bivector A · B. Otras propiedades de los cuaterniones pueden estar relacionadas de manera similar con el álgebra geométrica o derivarse de ella.

Esto sugiere que la división habitual de un cuaternión en partes escalares y vectoriales se representaría mejor como una división en partes escalares y bivectoriales; si se hace esto, el producto de cuaterniones es simplemente el producto geométrico. También relaciona los cuaterniones en tres dimensiones con los números complejos en dos, ya que cada uno es isomorfo al subálgebra par para la dimensión, una relación que se generaliza a dimensiones superiores.

El vector de rotación, de la representación eje-ángulo de las rotaciones, es una forma compacta de representar rotaciones en tres dimensiones. En su forma más compacta, consiste en un vector, el producto de un vector unitario ω que es el eje de rotación por el ángulo de rotación (con signo) θ , de modo que la magnitud del vector de rotación general θω es igual al ángulo de rotación (sin signo).

El cuaternión asociado a la rotación es

${\displaystyle q=\left(\cos {{\tfrac {1}{2}}\theta },\omega \sin {{\tfrac {1}{2}}\theta }\right)}$

En álgebra geométrica, la rotación se representa mediante un bivector. Esto se puede ver en su relación con los cuaterniones. Sea Ω un bivector unitario en el plano de rotación y sea θ el ángulo de rotación . Entonces, el bivector de rotación es Ω θ . El cuaternión corresponde estrechamente a la exponencial de la mitad del bivector Ω θ . Es decir, los componentes del cuaternión corresponden a las partes escalar y bivector de la siguiente expresión:$${\displaystyle \exp {{\tfrac {1}{2}}{\boldsymbol {\Omega }}\theta }=\cos {{\tfrac {1}{2}}\theta }+{\boldsymbol {\Omega }}\sin {{\tfrac {1}{2}}\theta }}$$

La exponencial se puede definir en términos de su serie de potencias y evaluarse fácilmente utilizando el hecho de que Ω al cuadrado es −1 .

Por lo tanto, las rotaciones se pueden representar mediante bivectores. Así como los cuaterniones son elementos del álgebra geométrica, están relacionados mediante la función exponencial de esa álgebra.

El bivector Ω θ genera una rotación a través de la función exponencial. Los elementos pares generados rotan un vector general en tres dimensiones de la misma manera que los cuaterniones:$${\displaystyle \mathbf {v} '=\exp(-{\tfrac {1}{2}}{\boldsymbol {\Omega }}\theta )\,\mathbf {v} \exp({\tfrac {1}{2}}{\boldsymbol {\Omega }}\theta ).}$$

Al igual que en dos dimensiones, la cantidad exp(− ⁠1/2⁠ Ω θ ) se llama rotor y se escribe R . La cantidad exp( ⁠1/2⁠ Ω θ ) es entonces R ⁻¹ , y generan rotaciones como$${\displaystyle \mathbf {v} '=R\mathbf {v} R^{-1}.}$$

Esto es idéntico a dos dimensiones, excepto que aquí los rotores son objetos de cuatro dimensiones isomorfos a los cuaterniones. Esto se puede generalizar a todas las dimensiones, con rotores, elementos del subálgebra par con magnitud unitaria, generados por la función exponencial de los bivectores. Forman una doble cobertura sobre el grupo de rotación, por lo que los rotores R y − R representan la misma rotación.

El vector de rotación es un ejemplo de un vector axial . Los vectores axiales, o pseudovectores, son vectores con la característica especial de que sus coordenadas experimentan un cambio de signo en relación con los vectores habituales (también llamados "vectores polares") bajo inversión a través del origen, reflexión en un plano u otra transformación lineal de inversión de orientación. ^[18] Los ejemplos incluyen cantidades como el par , el momento angular y los campos magnéticos vectoriales . Las cantidades que utilizarían vectores axiales en el álgebra vectorial se representan adecuadamente mediante bivectores en el álgebra geométrica. ^[19] Más precisamente, si se elige una orientación subyacente, los vectores axiales se identifican naturalmente con los vectores habituales; el dual de Hodge da entonces el isomorfismo entre vectores axiales y bivectores, por lo que cada vector axial está asociado con un bivector y viceversa; es decir

${\displaystyle \mathbf {A} ={\star }\mathbf {a} \,,\quad \mathbf {a} ={\star }\mathbf {A} }$

donde ⁠ ⁠${\displaystyle {\star }}$ es la estrella de Hodge. Nótese que si la orientación subyacente se invierte por inversión a través del origen, tanto la identificación de los vectores axiales con los vectores usuales como el dual de Hodge cambian de signo, pero los bivectores no se mueven. Alternativamente, usando la unidad pseudoescalar en Cl ₃ ( R ) , i = e ₁ e ₂ e ₃ da

${\displaystyle \mathbf {A} =\mathbf {a} i\,,\quad \mathbf {a} =-\mathbf {A} i.}$

Esto es más fácil de usar ya que el producto es simplemente el producto geométrico. Pero es antisimétrico porque (como en dos dimensiones) la unidad pseudoescalar i se eleva al cuadrado a −1 , por lo que se necesita un negativo en uno de los productos.

Esta relación se extiende a operaciones como el producto vectorial y el producto exterior bivectorial, ya que cuando se escriben como determinantes se calculan de la misma manera:

${\displaystyle \mathbf {a} \times \mathbf {b} ={\begin{vmatrix}\mathbf {e} _{1}&\mathbf {e} _{2}&\mathbf {e} _{3}\\a_{1}&a_{2}&a_{3}\\b_{1}&b_{2}&b_{3}\end{vmatrix}}\,,\quad \mathbf {a} \wedge \mathbf {b} ={\begin{vmatrix}\mathbf {e} _{23}&\mathbf {e} _{31}&\mathbf {e} _{12}\\a_{1}&a_{2}&a_{3}\\b_{1}&b_{2}&b_{3}\end{vmatrix}}\,,}$

Así que están relacionados por el dual de Hodge:

${\displaystyle {\star }(\mathbf {a} \wedge \mathbf {b} )=\mathbf {a\times b} \,,\quad {\star }(\mathbf {a\times b} )=\mathbf {a} \wedge \mathbf {b} \,.}$

Los bivectores tienen varias ventajas sobre los vectores axiales. Permiten desambiguar mejor los vectores axiales y polares, es decir, las cantidades que representan, de modo que resulta más claro qué operaciones se permiten y cuáles son sus resultados. Por ejemplo, el producto interno de un vector polar y un vector axial resultante del producto vectorial en el producto triple debería dar como resultado un pseudoescalar , un resultado que es más obvio si el cálculo se enmarca como el producto externo de un vector y un bivector. Se generalizan a otras dimensiones; en particular, los bivectores se pueden utilizar para describir cantidades como el par y el momento angular en dos y tres dimensiones. Además, se ajustan estrechamente a la intuición geométrica en varios aspectos, como se ve en la siguiente sección. ^[20]

Como sugiere su nombre y el del álgebra, uno de los atractivos de los bivectores es que tienen una interpretación geométrica natural. Esto se puede describir en cualquier dimensión, pero es mejor hacerlo en tres, donde se pueden trazar paralelos con objetos más familiares, antes de aplicarlos a dimensiones superiores. En dos dimensiones, la interpretación geométrica es trivial, ya que el espacio es bidimensional, por lo que solo tiene un plano, y todos los bivectores están asociados a él y difieren solo por un factor de escala.

Todos los bivectores pueden interpretarse como planos o, más precisamente, como segmentos de planos dirigidos. En tres dimensiones, hay tres propiedades de un bivector que pueden interpretarse geométricamente:

• La disposición del plano en el espacio, precisamente la actitud del plano (o alternativamente la rotación , orientación geométrica o pendiente del plano), está asociada con la relación de los componentes del bivector. En particular, los tres bivectores base, e ₂₃ , e ₃₁ y e ₁₂ , o múltiplos escalares de ellos, están asociados con el plano yz , el plano zx y el plano xy respectivamente.
• La magnitud del bivector está asociada al área del segmento del plano. El área no tiene una forma particular, por lo que se puede utilizar cualquier forma. Incluso se puede representar de otras maneras, como por ejemplo mediante una medida angular. Pero si los vectores se interpretan como longitudes, el bivector suele interpretarse como un área con las mismas unidades, de la siguiente manera.
• Al igual que la dirección de un vector, un plano asociado a un bivector tiene una dirección, una circulación o un sentido de rotación en el plano, que toma dos valores vistos como horario y antihorario cuando se observa desde un punto de vista que no está en el plano. Esto está asociado a un cambio de signo en el bivector, es decir, si se invierte la dirección, el bivector se niega. Alternativamente, si dos bivectores tienen la misma actitud y magnitud pero direcciones opuestas, entonces uno es el negativo del otro.
• Si se imagina como un paralelogramo, con el origen de los vectores en 0, entonces el área con signo es el determinante de las coordenadas cartesianas de los vectores ( a _x b _y − b _x a _y ). ^[21]

En tres dimensiones todos los bivectores pueden generarse mediante el producto exterior de dos vectores. Si el bivector B = a ∧ b entonces la magnitud de B es

${\displaystyle |\mathbf {B} |=|\mathbf {a} ||\mathbf {b} |\sin \theta ,}$

donde θ es el ángulo entre los vectores. Esta es el área del paralelogramo con aristas a y b , como se muestra en el diagrama. Una interpretación es que el área es barrida por b a medida que se mueve a lo largo de a . El producto exterior es antisimétrico, por lo que invertir el orden de a y b para hacer un movimiento a lo largo de b da como resultado un bivector con la dirección opuesta que es el negativo del primero. El plano del bivector a ∧ b contiene tanto a como b por lo que ambos son paralelos al plano.

Los bivectores y los vectores axiales están relacionados por el dual de Hodge . En un espacio vectorial real, el dual de Hodge relaciona un subespacio con su complemento ortogonal , por lo que si un bivector está representado por un plano, entonces el vector axial asociado con él es simplemente la normal a la superficie del plano . El plano tiene dos normales, una en cada lado, lo que da las dos orientaciones posibles para el plano y el bivector.

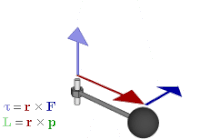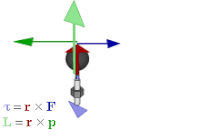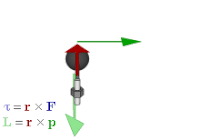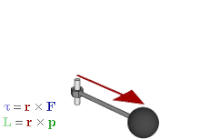
Esto relaciona el producto vectorial con el producto exterior . También se puede utilizar para representar cantidades físicas, como el par y el momento angular . En el álgebra vectorial, suelen representarse mediante vectores, perpendiculares al plano de la fuerza , el momento lineal o el desplazamiento a partir del cual se calculan. Pero si se utiliza un bivector en su lugar, el plano es el plano del bivector, por lo que es una forma más natural de representar las cantidades y la forma en que actúan. Además, a diferencia de la representación vectorial, se generaliza a otras dimensiones.

El producto de dos bivectores tiene una interpretación geométrica. Para los bivectores A y B distintos de cero, el producto se puede dividir en partes simétricas y antisimétricas de la siguiente manera:

${\displaystyle \mathbf {AB} =\mathbf {A} \cdot \mathbf {B} +\mathbf {A} \times \mathbf {B} .}$

Al igual que los vectores, estos tienen magnitudes | A · ​​B | = | A | | B | cos θ y | A × B | = | A | | B | sen θ , donde θ es el ángulo entre los planos. En tres dimensiones es el mismo que el ángulo entre los vectores normales duales a los planos, y se generaliza hasta cierto punto en dimensiones superiores.

Los bivectores se pueden sumar como áreas. Dados dos bivectores B y C distintos de cero en tres dimensiones, siempre es posible encontrar un vector que esté contenido en ambos, por ejemplo, a, por lo que los bivectores se pueden escribir como productos exteriores que involucran a :

${\displaystyle {\begin{aligned}\mathbf {B} &=\mathbf {a} \wedge \mathbf {b} \\\mathbf {C} &=\mathbf {a} \wedge \mathbf {c} \end{aligned}}}$

Esto se puede interpretar geométricamente como se ve en el diagrama: las dos áreas se suman para dar una tercera, y las tres áreas forman las caras de un prisma con a , b , c y b + c como aristas. Esto corresponde a las dos formas de calcular el área utilizando la distributividad del producto exterior:

${\displaystyle {\begin{aligned}\mathbf {B} +\mathbf {C} &=\mathbf {a} \wedge \mathbf {b} +\mathbf {a} \wedge \mathbf {c} \\&=\mathbf {a} \wedge (\mathbf {b} +\mathbf {c} ).\end{aligned}}}$

Esto sólo funciona en tres dimensiones, ya que es la única dimensión en la que debe existir un vector paralelo a ambos bivectores. En dimensiones superiores, los bivectores generalmente no están asociados a un único plano o, si lo están (bivectores simples), dos bivectores pueden no tener ningún vector en común y, por lo tanto, sumar un bivector no simple.

En cuatro dimensiones, los elementos base para el espacio ⋀ ² R ⁴ de bivectores son ( e ₁₂ , e ₁₃ , e ₁₄ , e ₂₃ , e ₂₄ , e ₃₄ ), por lo que un bivector general tiene la forma

${\displaystyle \mathbf {A} =a_{12}\mathbf {e} _{12}+a_{13}\mathbf {e} _{13}+a_{14}\mathbf {e} _{14}+a_{23}\mathbf {e} _{23}+a_{24}\mathbf {e} _{24}+a_{34}\mathbf {e} _{34}.}$

En cuatro dimensiones, el dual de Hodge de un bivector es un bivector, y el espacio ⋀ ² R ⁴ es dual consigo mismo. Los vectores normales no son únicos, sino que cada plano es ortogonal a todos los vectores en su espacio dual de Hodge. Esto se puede utilizar para dividir los bivectores en dos "mitades", de la siguiente manera. Tenemos tres pares de bivectores ortogonales: ( e ₁₂ , e ₃₄ ) , ( e ₁₃ , e ₂₄ ) y ( e ₁₄ , e ₂₃ ) . Hay cuatro formas distintas de elegir un bivector de cada uno de los dos primeros pares, y una vez que se eligen estos dos primeros, su suma da como resultado el tercer bivector del otro par. Por ejemplo, ( e ₁₂ , e ₁₃ , e ₁₄ ) y ( e ₂₃ , e ₂₄ , e ₃₄ ) .

En cuatro dimensiones los bivectores se generan por el producto exterior de los vectores en R ⁴ , pero con una diferencia importante con respecto a R ³ y R ² . En cuatro dimensiones no todos los bivectores son simples. Hay bivectores como e ₁₂ + e ₃₄ que no se pueden generar por el producto exterior de dos vectores. Esto también significa que no tienen un cuadrado real, es decir, escalar. En este caso

${\displaystyle (\mathbf {e} _{12}+\mathbf {e} _{34})^{2}=\mathbf {e} _{12}\mathbf {e} _{12}+\mathbf {e} _{12}\mathbf {e} _{34}+\mathbf {e} _{34}\mathbf {e} _{12}+\mathbf {e} _{34}\mathbf {e} _{34}=-2+2\mathbf {e} _{1234}.}$

El elemento e ₁₂₃₄ es el pseudoescalar en Cl ₄ , distinto del escalar, por lo que el cuadrado no es escalar.

Todos los bivectores en cuatro dimensiones se pueden generar utilizando como máximo dos productos exteriores y cuatro vectores. El bivector anterior se puede escribir como

${\displaystyle \mathbf {e} _{12}+\mathbf {e} _{34}=\mathbf {e} _{1}\wedge \mathbf {e} _{2}+\mathbf {e} _{3}\wedge \mathbf {e} _{4}.}$

De manera similar, cada bivector puede escribirse como la suma de dos bivectores simples. Para ello, resulta útil elegir dos bivectores ortogonales, y esto siempre es posible. Además, para un bivector genérico, la elección de bivectores simples es única, es decir, solo hay una manera de descomponer en bivectores ortogonales; la única excepción es cuando los dos bivectores ortogonales tienen magnitudes iguales (como en el ejemplo anterior): en este caso, la descomposición no es única. ^[4] La descomposición siempre es única en el caso de bivectores simples, con la ventaja adicional de que una de las partes ortogonales es cero.

Como en tres dimensiones, los bivectores en cuatro dimensiones generan rotaciones a través del mapa exponencial, y todas las rotaciones se pueden generar de esta manera. Como en tres dimensiones, si B es un bivector, entonces el rotor R es exp ⁠1/2⁠ B y las rotaciones se generan de la misma manera:

${\displaystyle v'=RvR^{-1}.}$

Las rotaciones generadas son, sin embargo, más complejas. Se pueden clasificar de la siguiente manera:

Las rotaciones simples son aquellas que fijan un plano en 4D y giran en un ángulo "alrededor" de este plano.

Las rotaciones dobles tienen un único punto fijo, el origen, y giran dos ángulos alrededor de dos planos ortogonales. En general, los ángulos son diferentes y los planos están especificados de forma única.

Las rotaciones isoclínicas son rotaciones dobles en las que los ángulos de rotación son iguales. En este caso, los planos sobre los que se produce la rotación no son únicos.

Estos se generan por bivectores de una manera directa. Las rotaciones simples se generan por bivectores simples, con el plano fijo dual u ortogonal al plano del bivector. Se puede decir que la rotación tiene lugar alrededor de ese plano, en el plano del bivector. Todos los demás bivectores generan rotaciones dobles, con los dos ángulos de la rotación iguales a las magnitudes de los dos bivectores simples que componen el bivector no simple. Las rotaciones isoclínicas surgen cuando estas magnitudes son iguales, en cuyo caso la descomposición en dos bivectores simples no es única. ^[22]

Los bivectores en general no conmutan, pero una excepción son los bivectores ortogonales y sus exponentes. Por lo tanto, si se utiliza el bivector B = B ₁ + B ₂ , donde B ₁ y B ₂ son bivectores simples ortogonales, para generar una rotación, se descompone en dos rotaciones simples que conmutan de la siguiente manera:

${\displaystyle R=\exp({\tfrac {1}{2}}(\mathbf {B} _{1}+\mathbf {B} _{2}))=\exp({\tfrac {1}{2}}\mathbf {B} _{1})\,\exp({\tfrac {1}{2}}\mathbf {B} _{2})=\exp({\tfrac {1}{2}}\mathbf {B} _{2})\,\exp({\tfrac {1}{2}}\mathbf {B} _{1})}$

Siempre es posible hacer esto ya que todos los bivectores pueden expresarse como sumas de bivectores ortogonales.

El espacio-tiempo es un modelo matemático para nuestro universo utilizado en la relatividad especial. Consta de tres dimensiones espaciales y una dimensión temporal combinadas en un único espacio de cuatro dimensiones. Se describe naturalmente utilizando álgebra geométrica y bivectores, con la métrica euclidiana reemplazada por una métrica de Minkowski . Esa álgebra es idéntica a la del espacio euclidiano, excepto que se cambia la signatura , por lo que

${\displaystyle \mathbf {e} _{i}^{2}={\begin{cases}1,&i=1,2,3\\-1,&i=4\end{cases}}}$

(Tenga en cuenta que el orden y los índices anteriores no son universales: aquí e ₄ es la dimensión temporal). El álgebra geométrica es Cl _3,1 ( R ) , y el subespacio de bivectores es ⋀ ² R ^3,1 .

Los bivectores simples son de dos tipos. Los bivectores simples e ₂₃ , e ₃₁ y e ₁₂ tienen cuadrados negativos y abarcan los bivectores del subespacio tridimensional correspondiente al espacio euclidiano, R ³ . Estos bivectores generan rotaciones ordinarias en R ³ .

Los bivectores simples e ₁₄ , e ₂₄ y e ₃₄ tienen cuadrados positivos y como planos abarcan una dimensión espacial y la dimensión temporal. Estos también generan rotaciones a través de la función exponencial, pero en lugar de funciones trigonométricas se necesitan funciones hiperbólicas, lo que genera un rotor como el siguiente:

${\displaystyle \exp {{\tfrac {1}{2}}{{\boldsymbol {\Omega }}\theta }}=\cosh {{\tfrac {1}{2}}\theta }+{\boldsymbol {\Omega }}\sinh {{\tfrac {1}{2}}\theta },}$

donde Ω es el bivector ( e ₁₄ , etc.), identificado a través de la métrica con una transformación lineal antisimétrica de R ^3,1 . Se trata de impulsos de Lorentz , expresados ​​de una manera particularmente compacta, utilizando el mismo tipo de álgebra que en R ³ y R ⁴ .

En general todas las rotaciones del espacio-tiempo se generan a partir de bivectores a través del mapa exponencial, es decir, un rotor general generado por el bivector A es de la forma

${\displaystyle R=\exp {{\tfrac {1}{2}}\mathbf {A} }.}$

El conjunto de todas las rotaciones en el espacio-tiempo forman el grupo de Lorentz , y de él se pueden deducir la mayoría de las consecuencias de la relatividad especial. En términos más generales, esto demuestra cómo las transformaciones en el espacio euclidiano y el espacio-tiempo se pueden describir utilizando el mismo tipo de álgebra.

(Nota: en esta sección los 3-vectores tradicionales se indican mediante líneas sobre los símbolos y los vectores espacio-temporales y bivectores mediante símbolos en negrita, con los vectores J y A excepcionalmente en mayúsculas)

Las ecuaciones de Maxwell se utilizan en física para describir la relación entre los campos eléctricos y magnéticos . Normalmente se dan como cuatro ecuaciones diferenciales y tienen una forma particularmente compacta cuando los campos se expresan como un bivector espacio-temporal de ⋀ ² R ^3,1 . Si los campos eléctrico y magnético en R ³ son E y B, entonces el bivector electromagnético es

${\displaystyle \mathbf {F} ={\frac {1}{c}}{\overline {E}}\mathbf {e} _{4}+{\overline {B}}\mathbf {e} _{123},}$

donde e ₄ es nuevamente el vector base para la dimensión temporal y c es la velocidad de la luz . El producto B e ₁₂₃ produce el bivector que es dual de Hodge de B en tres dimensiones, como se discutió anteriormente, mientras que E e ₄ como un producto de vectores ortogonales también tiene un valor bivectorial. En su conjunto, es el tensor electromagnético expresado de manera más compacta como un bivector y se utiliza de la siguiente manera. Primero, se relaciona con la 4-corriente J , una cantidad vectorial dada por

${\displaystyle \mathbf {J} ={\overline {j}}+c\rho \mathbf {e} _{4},}$

donde j es la densidad de corriente y ρ es la densidad de carga . Están relacionadas por un operador diferencial ∂, que es

${\displaystyle \partial =\nabla -\mathbf {e} _{4}{\frac {1}{c}}{\frac {\partial }{\partial t}}.}$

El operador ∇ es un operador diferencial en álgebra geométrica, que actúa sobre las dimensiones del espacio y está dado por ∇ M = ∇· M + ∇∧ M . Cuando se aplica a vectores ∇· M es la divergencia y ∇∧ M es el rizo pero con un resultado bivectorial en lugar de vectorial, que es dual en tres dimensiones con respecto al rizo. Para la cantidad general M actúan como operadores diferenciales de elevación y descenso de pendiente. En particular, si M es un escalar, entonces este operador es simplemente el gradiente , y puede considerarse como un operador del algebraico geométrico.

En conjunto, estos pueden usarse para dar una forma particularmente compacta para las ecuaciones de Maxwell con fuentes:

${\displaystyle \partial \mathbf {F} =\mathbf {J} .}$

Esta ecuación, cuando se descompone según el álgebra geométrica, utilizando productos geométricos que tienen efectos tanto de elevación como de reducción de la pendiente, es equivalente a las cuatro ecuaciones de Maxwell. También está relacionada con el potencial electromagnético 4 , un vector A dado por

${\displaystyle \mathbf {A} ={\overline {A}}+{\frac {1}{c}}V\mathbf {e} _{4},}$

donde A es el potencial magnético vectorial y V es el potencial eléctrico. Está relacionado con el bivector electromagnético de la siguiente manera

${\displaystyle \partial \mathbf {A} =-\mathbf {F} ,}$

utilizando el mismo operador diferencial ∂ . ^[23]

Como se ha sugerido en secciones anteriores, gran parte del álgebra geométrica se generaliza bien a dimensiones superiores. El álgebra geométrica para el espacio real R ⁿ es Cl _n ( R ) , y el subespacio de bivectores es ⋀ ² R ⁿ .

El número de bivectores simples necesarios para formar un bivector general aumenta con la dimensión, por lo que para n impar es ( n − 1) / 2 , para n par es n / 2 . Por lo tanto, para cuatro y cinco dimensiones solo se necesitan dos bivectores simples, pero se requieren tres para seis y siete dimensiones. Por ejemplo, en seis dimensiones con base estándar ( e ₁ , e ₂ , e ₃ , e ₄ , e ₅ , e ₆ ) el bivector

${\displaystyle \mathbf {e} _{12}+\mathbf {e} _{34}+\mathbf {e} _{56}}$

es la suma de tres bivectores simples pero no menos. Como en cuatro dimensiones siempre es posible encontrar bivectores simples ortogonales para esta suma.

Como en tres y cuatro dimensiones los rotores se generan mediante el mapa exponencial, así

${\displaystyle \exp {{\tfrac {1}{2}}\mathbf {B} }}$

es el rotor generado por el bivector B . Las rotaciones simples, que tienen lugar en un plano de rotación alrededor de una pala fija de dimensión ( n − 2 ) son generadas por bivectores simples, mientras que otros bivectores generan rotaciones más complejas que pueden describirse en términos de los bivectores simples de los que son sumas, cada uno relacionado con un plano de rotación. Todos los bivectores pueden expresarse como la suma de bivectores simples ortogonales y conmutativos, por lo que las rotaciones siempre pueden descomponerse en un conjunto de rotaciones conmutativas sobre los planos asociados con estos bivectores. El grupo de los rotores en n dimensiones es el grupo de espín , Spin( n ) .

Una característica notable, relacionada con el número de bivectores simples y, por lo tanto, de planos de rotación, es que en dimensiones impares cada rotación tiene un eje fijo; es engañoso llamarlo eje de rotación, ya que en dimensiones superiores las rotaciones se producen en múltiples planos ortogonales a él. Esto está relacionado con los bivectores, ya que los bivectores en dimensiones impares se descomponen en el mismo número de bivectores que la dimensión par inferior, por lo que tienen el mismo número de planos, pero una dimensión adicional. Como cada plano genera rotaciones en dos dimensiones en dimensiones impares debe haber una dimensión, es decir, un eje, que no se esté rotando. ^[24]

Los bivectores también están relacionados con la matriz de rotación en n dimensiones. Como en tres dimensiones, la ecuación característica de la matriz se puede resolver para encontrar los valores propios . En dimensiones impares, esto tiene una raíz real, con vector propio como eje fijo, y en dimensiones pares no tiene raíces reales, por lo que todas o todas menos una de las raíces son pares conjugados complejos. Cada par está asociado con un componente simple del bivector asociado con la rotación. En particular, el logaritmo de cada par es la magnitud hasta un signo, mientras que los vectores propios generados a partir de las raíces son paralelos a y, por lo tanto, se pueden usar para generar el bivector. En general, los valores propios y los bivectores son únicos, y el conjunto de valores propios da la descomposición completa en bivectores simples; si las raíces se repiten, la descomposición del bivector en bivectores simples no es única.

El álgebra geométrica se puede aplicar a la geometría proyectiva de una manera sencilla. El álgebra geométrica utilizada es Cl _n ( R ), n ≥ 3 , el álgebra del espacio vectorial real R ⁿ . Esto se utiliza para describir objetos en el espacio proyectivo real RP ^{n −1} . Los vectores distintos de cero en Cl _n ( R ) o R ⁿ están asociados con puntos en el espacio proyectivo, por lo que los vectores que difieren solo por un factor de escala, por lo que su producto exterior es cero, se asignan al mismo punto. Los bivectores simples distintos de cero en ⋀ ² R ⁿ representan líneas en RP ^{n −1} , con bivectores que difieren solo por un factor de escala (positivo o negativo) que representa la misma línea.

Se puede construir una descripción de la geometría proyectiva en el álgebra geométrica utilizando operaciones básicas. Por ejemplo, dados dos puntos distintos en RP ^{n −1} representados por los vectores a y b la línea que los contiene está dada por a ∧ b (o b ∧ a ). Dos líneas se cortan en un punto si A ∧ B = 0 para sus bivectores A y B . Este punto está dado por el vector

${\displaystyle \mathbf {p} =\mathbf {A} \lor \mathbf {B} =(\mathbf {A} \times \mathbf {B} )J^{-1}.}$

La operación " ∨ " es el encuentro, que puede definirse como se indicó anteriormente en términos de la unión, J = A ∧ B ^{[ aclaración necesaria ]} para A ∧ B distinto de cero . Utilizando estas operaciones, la geometría proyectiva puede formularse en términos de álgebra geométrica. Por ejemplo, dado un tercer bivector C (distinto de cero), el punto p se encuentra en la línea dada por C si y solo si

${\displaystyle \mathbf {p} \land \mathbf {C} =0.}$

Entonces la condición para que las líneas dadas por A , B y C sean colineales es

${\displaystyle (\mathbf {A} \lor \mathbf {B} )\land \mathbf {C} =0,}$

que en Cl ₃ ( R ) y RP ² se simplifica a

${\displaystyle \langle \mathbf {ABC} \rangle =0,}$

donde los corchetes angulares denotan la parte escalar del producto geométrico. De la misma manera, todas las operaciones del espacio proyectivo pueden escribirse en términos de álgebra geométrica, con bivectores que representan líneas generales en el espacio proyectivo, por lo que toda la geometría puede desarrollarse utilizando álgebra geométrica. ^[15]

Como se señaló anteriormente, un bivector se puede escribir como una matriz antisimétrica, que a través del mapa exponencial genera una matriz de rotación que describe la misma rotación que el rotor, también generada por el mapa exponencial pero aplicada al vector. Pero también se utiliza con otros bivectores como el tensor de velocidad angular y el tensor electromagnético , respectivamente una matriz o tensor antisimétrico de 3×3 y 4×4.

Los bivectores reales en ⋀ ² R ⁿ son isomorfos a matrices antisimétricas n × n o , alternativamente, a tensores antisimétricos de grado 2 en R ⁿ . Si bien los bivectores son isomorfos a los vectores (a través del dual) en tres dimensiones, pueden representarse mediante matrices antisimétricas en cualquier dimensión. Esto es útil para relacionar los bivectores con problemas descritos por matrices, de modo que se puedan reformular en términos de bivectores, dada una interpretación geométrica, y luego, a menudo, resolverse más fácilmente o relacionarse geométricamente con otros problemas de bivectores. ^[25]

En términos más generales, toda álgebra geométrica real es isomorfa a un álgebra matricial . Estas contienen bivectores como subespacio, aunque a menudo de una manera que no es especialmente útil. Estas matrices son de interés principalmente como una forma de clasificar las álgebras de Clifford. ^[26]

Busque bivector en Wikcionario, el diccionario libre.

• Diádicas
• Multivector
• Álgebra multilineal

• Dorst, Leo; Fontijne, Daniel; Mann, Stephen (2009). "§ 2.3.3 Visualización de bivectores". Álgebra geométrica para la informática: un enfoque orientado a objetos para la geometría (2.ª ed.). Morgan Kaufmann. pág. 31 y siguientes . ISBN 978-0-12-374942-0.
• Whitney, Hassler (1957). Teoría de la integración geométrica . Princeton: Princeton University Press . ISBN 978-0-486-44583-0.
• Lounesto, Pertti (2001). Álgebras y espinores de Clifford. Cambridge: Cambridge University Press . ISBN 978-0-521-00551-7.^{[ enlace muerto permanente ]}
• Chris Doran y Anthony Lasenby (2003). "§ 1.6 El producto externo". Álgebra geométrica para físicos . Cambridge: Cambridge University Press . pág. 11 y siguientes . ISBN . 978-0-521-71595-9.