Simetría rotacional

Propiedad de los objetos que parecen inalterados después de una rotación parcial

La simetría rotacional , también conocida como simetría radial en geometría , es la propiedad que tiene una forma cuando se ve igual después de una rotación parcial. El grado de simetría rotacional de un objeto es la cantidad de orientaciones distintas en las que se ve exactamente igual en cada rotación.

Ciertos objetos geométricos son parcialmente simétricos cuando se rotan en ciertos ángulos, como los cuadrados rotados 90°, sin embargo, los únicos objetos geométricos que son completamente simétricos rotacionalmente en cualquier ángulo son las esferas, los círculos y otros esferoides . ^[1]^[2]

Tratamiento formal

Formalmente, la simetría rotacional es la simetría con respecto a algunas o todas las rotaciones en el espacio euclidiano de dimensión $m$ . Las rotaciones son isometrías directas , es decir, isometrías que conservan la orientación . Por lo tanto, un grupo de simetría de simetría rotacional es un subgrupo de $E$ $+$ $($ $m$ $)$ (véase grupo euclidiano ).

La simetría con respecto a todas las rotaciones sobre todos los puntos implica simetría traslacional con respecto a todas las traslaciones, por lo que el espacio es homogéneo y el grupo de simetría es todo $E (m)$ . Con la noción modificada de simetría para campos vectoriales, el grupo de simetría también puede ser $E + (m)$ .

Para la simetría con respecto a las rotaciones sobre un punto podemos tomar ese punto como origen. Estas rotaciones forman el grupo ortogonal especial $SO(m)$ , el grupo de matrices ortogonales $m \times m$ con determinante 1. Para $m$ $= 3$ este es el grupo de rotación $SO(3)$ .

En otra definición de la palabra, el grupo de rotación de un objeto es el grupo de simetría dentro de $E + (n)$ , el grupo de isometrías directas ; en otras palabras, la intersección del grupo de simetría completa y el grupo de isometrías directas. Para los objetos quirales es lo mismo que el grupo de simetría completa.

Las leyes de la física son SO(3)-invariantes si no distinguen direcciones diferentes en el espacio. Debido al teorema de Noether , la simetría rotacional de un sistema físico es equivalente a la ley de conservación del momento angular .

Simetría rotacional discreta

La simetría rotacional de orden $n$ , también llamada simetría rotacional $de n$ pliegues o simetría rotacional discreta de orden $n$ , con respecto a un punto particular (en 2D) o eje (en 3D) significa que la rotación en un ángulo de ⁠ ⁠ ${\tfrac {360^{\circ }}{n}}$ (180°, 120°, 90°, 72°, 60°, 51 3 ⁄ 7 °, etc.) no cambia el objeto. Una simetría de "1 pliegue" no es simetría (todos los objetos se ven iguales después de una rotación de 360°).

La notación para la simetría $n$ -fold es $C n$ o simplemente $n$ . El grupo de simetría real se especifica por el punto o eje de simetría, junto con $n$ . Para cada punto o eje de simetría, el tipo de grupo abstracto es grupo cíclico de orden $n$ , $Z n$ . Aunque para este último también se utiliza la notación $C n$ $, el C n$ geométrico y abstracto deben distinguirse: hay otros grupos de simetría del mismo tipo de grupo abstracto que son geométricamente diferentes, ver grupos de simetría cíclica en 3D .

El dominio fundamental es un sector de ⁠ ⁠ ${\tfrac {360^{\circ }}{n}}.$

Ejemplos sin simetría de reflexión adicional :

$n = 2$ , 180°: la díada ; las letras Z, N, S; los contornos, aunque no los colores, delsímbolo del yin y el yang ; la bandera de la Unión (dividida a lo largo de la diagonal de la bandera y rotada sobre el punto central de la bandera)
$n = 3$ , 120°: tríada , trisquel , anillos borromeos ; a veces se utilizael término simetría trilateral ;
$n = 4$ , 90°: tétrada , esvástica
$n = 6$ , 60°: hexad , estrella de David (esta tiene simetría de reflexión adicional )
$n = 8$ , 45°: octad , muqarnas octogonales , generados por computadora (CG), techo

$C n$ es el grupo de rotación de un polígono regular $de n$ lados en 2D y de una pirámide regular $de n$ lados en 3D.

Si existe, por ejemplo, simetría rotacional con respecto a un ángulo de 100°, entonces también con respecto a uno de 20°, el máximo común divisor de 100° y 360°.

Un objeto 3D típico con simetría rotacional (posiblemente también con ejes perpendiculares) pero sin simetría especular es una hélice .

Ejemplos

$C 2$ (más)	$C 3$ (más)	$C 4$ (más)	$C 5$ (más)	$C 6$ (más)
Fractal de doble péndulo	Señal de tráfico de rotonda		Estrella del Bicentenario de Estados Unidos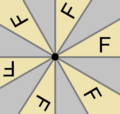
La posición inicial en el shogi	Diseño de cuernos para beber entrelazados de Snoldelev Stone

Múltiples ejes de simetría que pasan por el mismo punto

Para simetría discreta con múltiples ejes de simetría que pasan por el mismo punto, existen las siguientes posibilidades:

Además de un eje $de n pliegues,$ $n$ ejes de 2 pliegues perpendiculares: los grupos diedros $D n$ de orden $2 n$ ( $n \geq 2$ ). Este es el grupo de rotación de un prisma regular o bipirámide regular . Aunque se utiliza la misma notación, se debe distinguir entre el $D n$ geométrico y el abstracto : existen otros grupos de simetría del mismo tipo de grupo abstracto que son geométricamente diferentes, véase grupos de simetría diedros en 3D .
Ejes 4×3 y 3×2: el grupo de rotación $T$ de orden 12 de un tetraedro regular . El grupo es isomorfo al grupo alternante $A 4$ .
Ejes 3×4, 4×3 y 6×2: el grupo de rotación O de orden 24 de un cubo y un octaedro regular . El grupo es isomorfo al grupo simétrico $S 4$ .
Ejes de 6×5, 10×3 y 15×2: el grupo de rotación $I$ de orden 60 de un dodecaedro y un icosaedro . El grupo es $isomorfo$ al grupo alternante $A5$ . El grupo contiene 10 versiones de $D3$ y 6 versiones de $D5$ $($ simetrías rotacionales como prismas y antiprismas) $.$

En el caso de los sólidos platónicos , los ejes de 2 pliegues pasan por los puntos medios de las aristas opuestas, y el número de ellos es la mitad del número de aristas. Los demás ejes pasan por vértices opuestos y por centros de caras opuestas, excepto en el caso del tetraedro, donde los ejes de 3 pliegues pasan cada uno por un vértice y el centro de una cara.

Simetría rotacional con respecto a cualquier ángulo

La simetría rotacional respecto de cualquier ángulo es, en dos dimensiones, simetría circular . El dominio fundamental es una semirrecta .

En tres dimensiones podemos distinguir simetría cilíndrica y simetría esférica (sin cambios al rotar sobre un eje, o para cualquier rotación). Es decir, no hay dependencia del ángulo usando coordenadas cilíndricas y no hay dependencia de ninguno de los ángulos usando coordenadas esféricas . El dominio fundamental es un semiplano a través del eje, y una semilínea radial, respectivamente. Axisimétrico y axisimétrico son adjetivos que se refieren a un objeto que tiene simetría cilíndrica, o axisimetría (es decir, simetría rotacional con respecto a un eje central) como un donut ( toro ). Un ejemplo de simetría esférica aproximada es la Tierra (con respecto a la densidad y otras propiedades físicas y químicas).

En 4D, la simetría rotacional continua o discreta sobre un plano corresponde a la simetría rotacional 2D correspondiente en cada plano perpendicular, sobre el punto de intersección. Un objeto también puede tener simetría rotacional sobre dos planos perpendiculares, por ejemplo, si es el producto cartesiano de dos figuras 2D con simetría rotacional, como en el caso, por ejemplo, del duocilindro y de varios duoprismas regulares .

Simetría rotacional con simetría traslacional

Disposición dentro de una célula primitiva de rotocentros de 2 y 4 pliegues. Un dominio fundamental se indica en amarillo.	Disposición dentro de una celda primitiva de rotocentros de 2, 3 y 6 pliegues, solos o en combinación (considere el símbolo de 6 pliegues como una combinación de un símbolo de 2 y 3 pliegues); en el caso de simetría de 2 pliegues solamente, la forma del paralelogramo puede ser diferente. Para el caso p6, un dominio fundamental se indica en amarillo.

La simetría rotacional doble junto con la simetría traslacional simple es uno de los grupos Frieze . Un rotocentro es el punto fijo o invariante de una rotación. ^[3] Hay dos rotocentros por celda primitiva .

Junto con la doble simetría traslacional, los grupos de rotación son los siguientes grupos de papel tapiz , con ejes por celda primitiva:

p2 (2222): grupo de rotación de 4×2 pliegues de una red paralela , rectangular y rómbica .
p3 (333): 3×3-fold; no es el grupo de rotación de ninguna red (todas las redes son iguales al revés, pero eso no se aplica a esta simetría); es, por ejemplo, el grupo de rotación del mosaico triangular regular con los triángulos equiláteros coloreados alternativamente.
p4 (442): 2×4-plegado, 2×2-plegado; grupo de rotación de una red cuadrada .
p6 (632): 1×6-plegado, 2×3-plegado, 3×2-plegado; grupo de rotación de una red hexagonal .
Los rotocentros de 2 pliegues (incluidos los posibles de 4 y 6 pliegues), si los hay, forman la traslación de una red igual a la red traslacional, escalada por un factor 1/2. En el caso de la simetría traslacional en una dimensión, se aplica una propiedad similar, aunque el término "red" no se aplica.
Los rotocentros triples (incluidos los posibles de seis), si están presentes, forman una red hexagonal regular igual a la red traslacional, rotada 30° (o equivalentemente 90°) y escalada por un factor ${\tfrac {1}{3}}{\sqrt {3}}$
Los rotocentros cuádruples, si están presentes, forman una red cuadrada regular igual a la red traslacional, rotada 45° y escalada por un factor ${\tfrac {1}{2}}{\sqrt {2}}$
Los rotocentros séxtuples, si están presentes, forman una red hexagonal regular que es la traducción de la red traslacional.

La escala de una red divide el número de puntos por unidad de área por el cuadrado del factor de escala. Por lo tanto, el número de rotocentros de 2, 3, 4 y 6 pliegues por celda primitiva es 4, 3, 2 y 1, respectivamente, incluyendo nuevamente el cuádruple como un caso especial del doble pliegue, etc.

La simetría rotacional triple en un punto y doble en otro (o lo mismo en 3D con respecto a ejes paralelos) implica un grupo de rotación p6, es decir, simetría traslacional doble y simetría rotacional séxtuple en algún punto (o, en 3D, eje paralelo). La distancia de traslación para la simetría generada por un par de rotocentros de este tipo es multiplicada por su distancia. $2{\sqrt {3}}$

Plano euclidiano	Plano hiperbólico
Mosaico triangular hexakis , un ejemplo de p6, [6,3] ⁺ , (632) (con colores) y p6m, [6,3], (*632) (sin colores); las líneas son ejes de reflexión si se ignoran los colores, y un tipo especial de eje de simetría si no se ignoran los colores: la reflexión invierte los colores. Se pueden distinguir cuadrículas de líneas rectangulares en tres orientaciones.	Kisrombille de orden 3-7 , un ejemplo de simetría [7,3] ^{+ (732) y [7,3], (*732) (sin colores)}

Véase también

Referencias

^ Simetría rotacional de esferas de Weingarten en variedades tridimensionales homogéneas. Por José A. Gálvez, Pablo Mira
^ Estados ligados topológicos en el continuo en matrices de esferas dieléctricas. Por Dmitrii N. Maksimov, Instituto de Física LV Kirensky, Krasnoyarsk, Rusia
^ Loeb, AL (1971). Color y simetría , Wiley-Interscience, Nueva York, pág. 2. ISBN 9780471543350 , OCLC 163904

Weyl, Hermann (1982) [1952]. Simetría . Princeton: Princeton University Press. ISBN 0-691-02374-3.

Enlaces externos

Medios relacionados con Simetría rotacional en Wikimedia Commons
Ejemplos de simetría rotacional de Math Is Fun

[1] Simetría rotacional de esferas de Weingarten en variedades tridimensionales homogéneas. Por José A. Gálvez, Pablo Mira

[2] Estados ligados topológicos en el continuo en matrices de esferas dieléctricas. Por Dmitrii N. Maksimov, Instituto de Física LV Kirensky, Krasnoyarsk, Rusia

[3] Loeb, AL (1971). Color y simetría , Wiley-Interscience, Nueva York, pág. 2. ISBN 9780471543350 , OCLC 163904