Autoenergía

En la teoría cuántica de campos , la energía que tiene una partícula como resultado de los cambios que provoca en su entorno define la autoenergía , y representa la contribución a la energía de la partícula , o masa efectiva , debido a las interacciones entre la partícula y su entorno. En electrostática , la energía requerida para ensamblar la distribución de carga toma la forma de autoenergía al traer las cargas constituyentes desde el infinito, donde la fuerza eléctrica tiende a cero. En un contexto de materia condensada , la autoenergía se utiliza para describir la renormalización inducida por la interacción de la masa de las cuasipartículas ( dispersiones ) y la vida útil. La autoenergía se utiliza especialmente para describir las interacciones electrón-electrón en los líquidos de Fermi . Otro ejemplo de autoenergía se encuentra en el contexto del ablandamiento de fonones debido al acoplamiento electrón-fonón. ${\estilo de visualización \Sigma}$

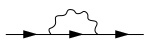
Matemáticamente, esta energía es igual al llamado valor de capa de masa del operador de autoenergía propio (u operador de masa propio ) en la representación momento-energía (más precisamente, a multiplicado por este valor). En esta u otras representaciones (como la representación espacio-temporal), la autoenergía se representa gráficamente (y económicamente) por medio de diagramas de Feynman , como el que se muestra a continuación. En este diagrama en particular, las tres líneas rectas con flechas representan partículas, o propagadores de partículas , y la línea ondulada una interacción partícula-partícula; eliminando (o amputando ) las líneas rectas más a la izquierda y más a la derecha en el diagrama que se muestra a continuación (estas llamadas líneas externas corresponden a valores prescritos para, por ejemplo, momento y energía, o cuatro momentos ), se conserva una contribución al operador de autoenergía (en, por ejemplo, la representación momento-energía). Usando un pequeño número de reglas simples, cada diagrama de Feynman se puede expresar fácilmente en su forma algebraica correspondiente.${\estilo de visualización \hbar}$

En general, el valor en la capa de masa del operador de autoenergía en la representación de momento-energía es complejo . En tales casos, es la parte real de esta autoenergía la que se identifica con la autoenergía física (denominada anteriormente "autoenergía" de la partícula); la inversa de la parte imaginaria es una medida de la vida útil de la partícula en investigación. Para mayor claridad, las excitaciones elementales, o partículas revestidas (ver cuasipartícula ), en sistemas en interacción son distintas de las partículas estables en el vacío; sus funciones de estado consisten en superposiciones complicadas de los estados propios del sistema subyacente de muchas partículas, que solo momentáneamente, si es que lo hacen, se comportan como los específicos de las partículas aisladas; la vida útil mencionada anteriormente es el tiempo durante el cual una partícula revestida se comporta como si fuera una sola partícula con momento y energía bien definidos.

El operador de autoenergía (a menudo denotado por , y con menor frecuencia por ) está relacionado con los propagadores desnudos y vestidos (a menudo denotados por y respectivamente) a través de la ecuación de Dyson (nombrada en honor a Freeman Dyson ):${\displaystyle \Sigma _{}^{}}$$Estilo de visualización M_{}^{}}$$Estilo de visualización G_{0}^{}}$$estilo de visualización G_{}^{}}$

${\displaystyle G=G_{0}^{}+G_{0}\Sigma G.}$

Multiplicando a la izquierda por el inverso del operador y a la derecha por obtenemos$Estilo de visualización G_{0}^{-1}}$$Estilo de visualización G_{0}$$Estilo de visualización G-1$

${\displaystyle \Sigma =G_{0}^{-1}-G^{-1}.}$

El fotón y el gluón no obtienen masa mediante la renormalización porque la simetría de calibración los protege de ello. Esto es una consecuencia de la identidad de Ward . El bosón W y el bosón Z obtienen sus masas mediante el mecanismo de Higgs ; experimentan una renormalización de masa mediante la renormalización de la teoría electrodébil .

Las partículas neutras con números cuánticos internos pueden mezclarse entre sí mediante la producción de pares virtuales . El principal ejemplo de este fenómeno es la mezcla de kaones neutros . Con supuestos simplificadores adecuados, esto puede describirse sin la teoría cuántica de campos .

En química , la energía propia o energía de Born de un ion es la energía asociada con el campo del propio ion. ^{[ cita requerida ]}

En la física del estado sólido y de la materia condensada, las autoenergías y una miríada de propiedades relacionadas de las cuasipartículas se calculan mediante los métodos de la función de Green y la función de Green (teoría de muchos cuerpos) de excitaciones de baja energía en interacción sobre la base de cálculos de la estructura de bandas electrónicas . Las autoenergías también encuentran una amplia aplicación en el cálculo del transporte de partículas a través de sistemas cuánticos abiertos y la incrustación de subregiones en sistemas más grandes (por ejemplo, la superficie de un cristal semiinfinito). ^{[ cita requerida ]}

• Teoría cuántica de campos
• Vacío QED
• Renormalización
• Fuerza propia
• Aproximación de GW
• Teoría de absorción de Wheeler-Feynman

• AL Fetter y JD Walecka, Teoría cuántica de sistemas de muchas partículas (McGraw-Hill, Nueva York, 1971); (Dover, Nueva York, 2003)
• J. W. Negele y H. Orland, Sistemas cuánticos de muchas partículas (Westview Press, Boulder, 1998)
• AA Abrikosov, LP Gorkov e IE Dzyaloshinski (1963): Métodos de la teoría cuántica de campos en física estadística Englewood Cliffs: Prentice-Hall.
• Alexei M. Tsvelik (2007). Teoría cuántica de campos en física de la materia condensada (2.ª ed.). Cambridge University Press. ISBN 978-0-521-52980-8.
• AN Vasil'ev El grupo de renormalización teórica de campos en la teoría crítica del comportamiento y la dinámica estocástica (Routledge Chapman & Hall 2004); ISBN 0-415-31002-4 ; ISBN 978-0-415-31002-4  
• John E. Inglesfield (2015). El método de incrustación para la estructura electrónica . IOP Publishing. ISBN 978-0-7503-1042-0.