Álgebra exterior
En matemáticas, el álgebra exterior o álgebra de Grassmann de un espacio vectorial es un álgebra asociativa que contiene que tiene un producto, llamado producto exterior o producto cuña y denotado con , tal que para cada vector en El álgebra exterior lleva el nombre de Hermann Grassmann , [3] y los nombres del producto provienen del símbolo "cuña" y del hecho de que el producto de dos elementos de es "exterior"
El producto de cuña de vectores se llama cuchilla de grado o cuchilla - . El producto de cuña se introdujo originalmente como una construcción algebraica utilizada en geometría para estudiar áreas , volúmenes y sus análogos de dimensiones superiores: La magnitud de una cuchilla 2 es el área del paralelogramo definido por y y, de manera más general, la magnitud de una cuchilla - es el (hiper)volumen del paralelotopo definido por los vectores constituyentes. La propiedad alternante que implica una propiedad antisimétrica que y de manera más general, cualquier cuchilla cambia de signo siempre que se intercambian dos de sus vectores constituyentes, lo que corresponde a un paralelotopo de orientación opuesta.
El álgebra exterior completa contiene objetos que no son en sí mismos cuchillas, sino combinaciones lineales de cuchillas; una suma de cuchillas de grado homogéneo se llama k - vector , mientras que una suma más general de cuchillas de grado arbitrario se llama multivector . [4] El espacio lineal de las -cuchillas se llama -ésima potencia exterior de El álgebra exterior es la suma directa de las -ésimas potencias exteriores de y esto hace que el álgebra exterior sea un álgebra graduada .
El álgebra exterior es universal en el sentido de que toda ecuación que relaciona elementos de en el álgebra exterior también es válida en toda álgebra asociativa que contiene y en la que el cuadrado de cada elemento de es cero.
La definición del álgebra exterior puede extenderse para espacios construidos a partir de espacios vectoriales, como cuerpos vectoriales y funciones cuyo dominio es un espacio vectorial. Además, el cuerpo de escalares puede ser cualquier cuerpo (sin embargo, para cuerpos de característica dos, la condición anterior debe reemplazarse por que sea equivalente en otras características). De manera más general, el álgebra exterior puede definirse para módulos sobre un anillo conmutativo . En particular, el álgebra de formas diferenciales en variables es un álgebra exterior sobre el anillo de las funciones suaves en variables.
Ejemplos motivadores
Áreas en el plano

El espacio vectorial euclidiano bidimensional es un espacio vectorial real dotado de una base formada por un par de vectores unitarios ortogonales.
Supongamos que
son un par de vectores dados en , escritos en componentes. Existe un paralelogramo único que tiene y como dos de sus lados. El área de este paralelogramo está dada por la fórmula del determinante estándar:
Consideremos ahora el producto exterior de y :
donde el primer paso utiliza la ley distributiva para el producto exterior, y el último utiliza el hecho de que el producto exterior es una función alternada , y en particular (El hecho de que el producto exterior sea una función alternada también obliga a ) Nótese que el coeficiente en esta última expresión es precisamente el determinante de la matriz [ v w ] . El hecho de que esto pueda ser positivo o negativo tiene el significado intuitivo de que v y w pueden estar orientados en sentido antihorario o horario como los vértices del paralelogramo que definen. Tal área se llama área con signo del paralelogramo: el valor absoluto del área con signo es el área ordinaria, y el signo determina su orientación.
El hecho de que este coeficiente sea el área con signo no es casual. De hecho, es relativamente fácil ver que el producto exterior debería estar relacionado con el área con signo si uno intenta axiomatizar esta área como una construcción algebraica. En detalle, si A( v , w ) denota el área con signo del paralelogramo del cual el par de vectores v y w forman dos lados adyacentes, entonces A debe satisfacer las siguientes propiedades:
- A( r v , s w ) = rs A( v , w ) para cualquier número real r y s , ya que al reescalar cualquiera de los lados se reescala el área en la misma cantidad (y al invertir la dirección de uno de los lados se invierte la orientación del paralelogramo).
- A( v , v ) = 0 , ya que el área del paralelogramo degenerado determinado por v (es decir, un segmento de línea ) es cero.
- A( w , v ) = −A( v , w ) , ya que intercambiar los roles de v y w invierte la orientación del paralelogramo.
- A( v + r w , w ) = A( v , w ) para cualquier número real r , ya que sumar un múltiplo de w a v no afecta ni a la base ni a la altura del paralelogramo y en consecuencia preserva su área.
- A( e 1 , e 2 ) = 1 , ya que el área del cuadrado unitario es uno.

Con excepción de la última propiedad, el producto exterior de dos vectores satisface las mismas propiedades que el área. En cierto sentido, el producto exterior generaliza la propiedad final al permitir que el área de un paralelogramo se compare con la de cualquier paralelogramo elegido en un plano paralelo (aquí, el de lados e 1 y e 2 ). En otras palabras, el producto exterior proporciona una formulación del área independiente de la base . [5]
Productos cruzados y triples

Para los vectores en R 3 , el álgebra exterior está estrechamente relacionada con el producto vectorial y el producto triple . Utilizando la base estándar { e 1 , e 2 , e 3 } , el producto exterior de un par de vectores
y
es
donde { e 1 ∧ e 2 , e 3 ∧ e 1 , e 2 ∧ e 3 } es la base del espacio tridimensional ⋀ 2 ( R 3 ). Los coeficientes anteriores son los mismos que los de la definición habitual del producto vectorial de vectores en tres dimensiones, con la única diferencia de que el producto exterior no es un vector ordinario, sino un bivector .
Incorporando un tercer vector
El producto exterior de tres vectores es
donde e 1 ∧ e 2 ∧ e 3 es el vector base del espacio unidimensional ⋀ 3 ( R 3 ). El coeficiente escalar es el triple producto de los tres vectores.
El producto vectorial y el producto triple en tres dimensiones admiten interpretaciones tanto geométricas como algebraicas. El producto vectorial u × v puede interpretarse como un vector que es perpendicular tanto a u como a v y cuya magnitud es igual al área del paralelogramo determinado por los dos vectores. También puede interpretarse como el vector que consiste en los menores de la matriz con columnas u y v . El producto triple de u , v y w es geométricamente un volumen (con signo). Algebraicamente, es el determinante de la matriz con columnas u , v y w . El producto exterior en tres dimensiones permite interpretaciones similares. De hecho, en presencia de una base ortonormal orientada positivamente , el producto exterior generaliza estas nociones a dimensiones superiores.
Definición formal
El álgebra exterior de un espacio vectorial sobre un cuerpo se define como el álgebra cociente del álgebra tensorial por el ideal bilateral generado por todos los elementos de la forma tales que . [6] Simbólicamente,
El producto exterior de dos elementos de se define por
Propiedades algebraicas
Producto alterno
El producto exterior es por construcción alternante en elementos de , lo que significa que para todo por la construcción anterior. Se deduce que el producto también es anticonmutativo en elementos de , pues suponiendo que ,
por eso
De manera más general, si es una permutación de los números enteros , y , , ..., son elementos de , se deduce que
donde es la firma de la permutación . [7]
En particular, si para algún , entonces también se cumple la siguiente generalización de la propiedad alterna:
Junto con la propiedad distributiva del producto exterior, una generalización adicional es que una condición necesaria y suficiente para que un conjunto de vectores sea linealmente dependiente es que
Energía exterior
La k -ésima potencia exterior de , denotada , es el subespacio vectorial de generado por elementos de la forma
Si , entonces se dice que es un k -vector . Si, además, se puede expresar como un producto exterior de elementos de , entonces se dice que es descomponible (o simple , por algunos autores; o una cuchilla , por otros). Aunque los -vectores descomponibles abarcan , no todos los elementos de son descomponibles. Por ejemplo, dado con una base , el siguiente 2-vector no es descomponible:
Base y dimensión
Si la dimensión de es y es una base para , entonces el conjunto
es una base para . La razón es la siguiente: dado cualquier producto exterior de la forma
cada vector puede escribirse como una combinación lineal de los vectores base ; utilizando la bilinealidad del producto exterior, esto puede expandirse a una combinación lineal de productos exteriores de esos vectores base. Cualquier producto exterior en el que el mismo vector base aparezca más de una vez es cero; cualquier producto exterior en el que los vectores base no aparezcan en el orden adecuado puede reordenarse, cambiando el signo siempre que dos vectores base cambien de lugar. En general, los coeficientes resultantes de los k -vectores base pueden calcularse como los menores de la matriz que describe los vectores en términos de la base .
Contando los elementos base, la dimensión de es igual a un coeficiente binomial :
donde es la dimensión de los vectores , y es el número de vectores en el producto. El coeficiente binomial produce el resultado correcto, incluso para casos excepcionales; en particular, para .
Cualquier elemento del álgebra exterior puede escribirse como una suma de k -vectores . Por lo tanto, como espacio vectorial, el álgebra exterior es una suma directa.
(donde, por convención, , el campo subyacente , y ), y por lo tanto su dimensión es igual a la suma de los coeficientes binomiales, que es .
Rango de una-vector
Si , entonces es posible expresar como una combinación lineal de k -vectores descomponibles :
donde cada uno es descomponible, digamos
El rango del k -vector es el número mínimo de k -vectores descomponibles en dicha expansión de . Esto es similar a la noción de rango tensorial .
El rango es particularmente importante en el estudio de 2-vectores (Sternberg 1964, §III.6) (Bryant et al. 1991). El rango de un 2-vector puede identificarse con la mitad del rango de la matriz de coeficientes de en una base. Por lo tanto, si es una base para , entonces puede expresarse de forma única como
donde (la matriz de coeficientes es antisimétrica ). Por lo tanto, el rango de la matriz es par y es el doble del rango de la forma .
En la característica 0, el 2-vector tiene rango si y sólo si
- y
Estructura graduada
El producto exterior de un vector k con un vector p es un vector , lo que nuevamente invoca la bilinealidad. En consecuencia, la descomposición de suma directa de la sección anterior
da al álgebra exterior la estructura adicional de un álgebra graduada , es decir
Además, si K es el campo base, tenemos
- y
El producto exterior es anticonmutativo graduado, lo que significa que si y , entonces
Además de estudiar la estructura graduada en el álgebra exterior, Bourbaki (1989) estudia estructuras graduadas adicionales en álgebras exteriores, como aquellas del álgebra exterior de un módulo graduado (un módulo que ya tiene su propia gradación).
Propiedad universal
Sea V un espacio vectorial sobre el cuerpo K . De manera informal, la multiplicación en se realiza manipulando símbolos e imponiendo una ley distributiva , una ley asociativa y usando la identidad para v ∈ V . Formalmente, es el álgebra "más general" en la que se cumplen estas reglas para la multiplicación, en el sentido de que cualquier K -álgebra asociativa unital que contenga V con multiplicación alternada en V debe contener una imagen homomórfica de . En otras palabras, el álgebra exterior tiene la siguiente propiedad universal : [8]
Dada cualquier K -álgebra asociativa unitaria A y cualquier K - mapa lineal tal que para cada v en V , entonces existe precisamente un homomorfismo de álgebra unitaria tal que j ( v ) = f ( i ( v )) para todo v en V (aquí i es la inclusión natural de V en , ver arriba).
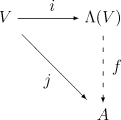
Para construir el álgebra más general que contiene a V y cuya multiplicación es alternada en V , es natural comenzar con el álgebra asociativa más general que contiene a V , el álgebra tensorial T ( V ) , y luego hacer cumplir la propiedad alternada tomando un cociente adecuado. Por lo tanto, tomamos el ideal bilateral I en T ( V ) generado por todos los elementos de la forma v ⊗ v para v en V , y definimos como el cociente
(y use ∧ como símbolo de multiplicación en ). Entonces es sencillo demostrar que contiene V y satisface la propiedad universal anterior.
Como consecuencia de esta construcción, la operación de asignar a un espacio vectorial V su álgebra exterior es un funtor de la categoría de espacios vectoriales a la categoría de álgebras.
En lugar de definir primero y luego identificar las potencias externas como ciertos subespacios, se pueden definir alternativamente los espacios primero y luego combinarlos para formar el álgebra . Este enfoque se utiliza a menudo en geometría diferencial y se describe en la siguiente sección.
Generalizaciones
Dado un anillo conmutativo y un módulo - , podemos definir el álgebra exterior tal como se indicó anteriormente, como un cociente adecuado del álgebra tensorial . Satisfará la propiedad universal análoga. Muchas de las propiedades de también requieren que sea un módulo proyectivo . Cuando se utiliza dimensionalidad finita, las propiedades requieren además que sea finitamente generada y proyectiva. Se pueden encontrar generalizaciones para las situaciones más comunes en Bourbaki (1989).
Las álgebras exteriores de fibrados vectoriales se consideran con frecuencia en geometría y topología. No existen diferencias esenciales entre las propiedades algebraicas del álgebra exterior de fibrados vectoriales de dimensión finita y las del álgebra exterior de módulos proyectivos finitamente generados, según el teorema de Serre-Swan . Se pueden definir álgebras exteriores más generales para haces de módulos.
Álgebra tensorial alternada
Para un cuerpo de característica distinta de 2, [9] el álgebra exterior de un espacio vectorial sobre puede identificarse canónicamente con el subespacio vectorial de que consiste en tensores antisimétricos . Para característica 0 (o mayor que ), el espacio vectorial de tensores antisimétricos -lineales es transversal al ideal , por lo tanto, una buena opción para representar el cociente. Pero para característica distinta de cero, el espacio vectorial de tensores antisimétricos -lineales podría no ser transversal al ideal (en realidad, para , el espacio vectorial de tensores antisimétricos -lineales está contenido en ); Sin embargo, transversal o no, se puede definir un producto en este espacio de modo que el álgebra resultante sea isomorfa al álgebra exterior: en el primer caso la elección natural para el producto es simplemente el producto cociente (usando la proyección disponible), en el segundo caso, este producto debe modificarse ligeramente como se indica a continuación (según la configuración de Arnold), pero de modo que el álgebra permanezca isomorfa con el álgebra exterior, es decir, el cociente de por el ideal generado por elementos de la forma . Por supuesto, para la característica (o mayor que la dimensión del espacio vectorial), se podría usar una u otra definición del producto, ya que las dos álgebras son isomorfas (ver VI Arnold o Kobayashi-Nomizu).
Sea el espacio de tensores homogéneos de grado . Éste está abarcado por tensores descomponibles
La antisimetrización (o a veces la simetrización sesgada ) de un tensor descomponible se define por
y, cuando (para un campo característico distinto de cero podría ser 0):
donde la suma se toma sobre el grupo simétrico de permutaciones en los símbolos . Esto se extiende por linealidad y homogeneidad a una operación, también denotada por y , en el álgebra tensorial completa .
Tenga en cuenta que
De modo que, cuando se define, es la proyección para el álgebra exterior (cociente) sobre el subespacio tensorial alterno homogéneo r. Por otra parte, la imagen es siempre el subespacio tensorial alterno graduado (aún no un álgebra, ya que el producto aún no está definido), denotado . Este es un subespacio vectorial de , y hereda la estructura de un espacio vectorial graduado de aquel en . Además, el núcleo de es precisamente , el subconjunto homogéneo del ideal , o el núcleo de es . Cuando se define, lleva un producto graduado asociativo definido por (el mismo que el producto de cuña)
Suponiendo que tiene característica 0, ya que es un suplemento de en , con el producto dado anteriormente, existe un isomorfismo canónico
Cuando la característica del campo no es cero, se hará lo mismo que antes, pero el producto no se puede definir como se indica más arriba. En tal caso, el isomorfismo sigue siendo válido, a pesar de no ser un complemento del ideal , pero entonces, el producto se debe modificar como se indica a continuación ( producto, configuración de Arnold).
Finalmente, siempre obtenemos isomorfo con , pero el producto podría (o debería) elegirse de dos maneras (o solo una). En realidad, el producto podría elegirse de muchas maneras, reescalándolo en espacios homogéneos como para una secuencia arbitraria en el cuerpo, siempre que la división tenga sentido (esto es tal que el producto redefinido también es asociativo, es decir, define un álgebra en ). También tenga en cuenta que la definición del producto interior debe cambiarse en consecuencia, para mantener su propiedad de derivación sesgada.
Notación de índice
Supóngase que V tiene dimensión finita n , y que se da una base e 1 , ..., e n de V. Entonces cualquier tensor alterno t ∈ A r ( V ) ⊂ T r ( V ) se puede escribir en notación de índice con la convención de suma de Einstein como
donde t i 1 ⋅⋅⋅ i r es completamente antisimétrico en sus índices.
El producto exterior de dos tensores alternos t y s de rangos r y p está dado por
Los componentes de este tensor son precisamente la parte sesgada de los componentes del producto tensorial s ⊗ t , denotados por corchetes en los índices:
El producto interior también puede describirse en notación de índice de la siguiente manera. Sea un tensor antisimétrico de rango . Entonces, para α ∈ V ∗ , es un tensor alterno de rango , dado por
donde n es la dimensión de V .
Dualidad
Operadores alternantes
Dados dos espacios vectoriales V y X y un número natural k , un operador alterno de V k a X es una función multilineal
de manera que siempre que v 1 , ..., v k sean vectores linealmente dependientes en V , entonces
El mapa
que se asocia a vectores de su producto exterior, es decir, su -vector correspondiente, también es alternante. De hecho, esta función es el operador alternante "más general" definido en dado cualquier otro operador alternante existe una única función lineal con Esta propiedad universal caracteriza el espacio de operadores alternantes en y puede servir como su definición.
Formas multilineales alternas

La discusión anterior se especializa en el caso cuando , el campo base. En este caso, una función multilineal alternada
se llama forma multilineal alternada . El conjunto de todas las formas multilineales alternadas es un espacio vectorial, ya que la suma de dos de tales mapas, o el producto de tal mapa con un escalar, es nuevamente alternada. Por la propiedad universal de la potencia exterior, el espacio de formas alternadas de grado en es naturalmente isomorfo con el espacio vectorial dual . Si es de dimensión finita, entonces este último es naturalmente isomorfo [ aclaración necesaria ] a . En particular, si es -dimensional, la dimensión del espacio de mapas alternados de a es el coeficiente binomial .
En virtud de esta identificación, el producto exterior toma una forma concreta: produce una nueva función antisimétrica a partir de dos funciones dadas. Supóngase que ω : V k → K y η : V m → K son dos funciones antisimétricas. Como en el caso de los productos tensoriales de funciones multilineales, el número de variables de su producto exterior es la suma del número de sus variables. Dependiendo de la elección de la identificación de elementos de potencia exterior con formas multilineales, el producto exterior se define como
o como
donde, si la característica del campo base es 0, la alternancia Alt de un mapa multilineal se define como el promedio de los valores ajustados por signo sobre todas las permutaciones de sus variables:
Cuando el campo tiene característica finita , una versión equivalente de la segunda expresión sin ningún factorial ni ninguna constante está bien definida:
donde aquí Sh k , m ⊂ S k + m es el subconjunto de ( k , m ) baraja : permutaciones σ del conjunto {1, 2, ..., k + m } tales que σ (1) < σ (2) < ⋯ < σ ( k ) , y σ ( k + 1) < σ ( k + 2) < ... < σ ( k + m ) . Como esto puede parecer muy específico y ajustado, una versión cruda equivalente es sumar en la fórmula anterior sobre permutaciones en clases laterales izquierdas de S k + m / ( S k × S m ) .
Producto interior
Supongamos que es de dimensión finita. Si denota el espacio dual al espacio vectorial , entonces para cada , es posible definir una antiderivación en el álgebra ,
Esta derivación se llama producto interior con , o a veces operador de inserción , o contracción por .
Supóngase que . Entonces es una aplicación multilineal de a , por lo que se define por sus valores en el producto cartesiano k -fold . Si u 1 , u 2 , ..., u k −1 son elementos de , entonces defina
Además, sea siempre que sea un escalar puro (es decir, perteneciente a ).
Caracterización axiomática y propiedades
El producto interior satisface las siguientes propiedades:
- Para cada y cada (donde por convención ),
- Si es un elemento de ( ), entonces es el emparejamiento dual entre elementos de y elementos de .
- Para cada , es una derivación graduada de grado −1:
Estas tres propiedades son suficientes para caracterizar el producto interior así como definirlo en el caso general de dimensión infinita.
Otras propiedades del producto interior incluyen:
Dualidad de Hodge
Supongamos que tiene dimensión finita . Entonces el producto interior induce un isomorfismo canónico de espacios vectoriales
por la definición recursiva
En el contexto geométrico, un elemento distinto de cero de la potencia exterior superior (que es un espacio vectorial unidimensional) a veces se denomina forma de volumen (o forma de orientación , aunque este término a veces puede generar ambigüedad). El nombre forma de orientación proviene del hecho de que la elección del elemento superior preferido determina una orientación de todo el álgebra exterior, ya que equivale a fijar una base ordenada del espacio vectorial. En relación con la forma de volumen preferida , el isomorfismo se da explícitamente por
Si, además de una forma de volumen, el espacio vectorial V está equipado con un producto interno que se identifica con , entonces el isomorfismo resultante se llama operador de estrella de Hodge , que asigna un elemento a su dual de Hodge :
La composición de consigo misma se aplica a y es siempre un múltiplo escalar de la función identidad. En la mayoría de las aplicaciones, la forma de volumen es compatible con el producto interno en el sentido de que es un producto externo de una base ortonormal de . En este caso,
donde id es la asignación de identidad y el producto interno tiene firma métrica ( p , q ) : p más y q menos.
Producto interior
Para un espacio de dimensión finita, un producto interno (o un producto interno pseudoeuclidiano ) en define un isomorfismo de con , y por lo tanto también un isomorfismo de con . El emparejamiento entre estos dos espacios también toma la forma de un producto interno. En los -vectores descomponibles,
el determinante de la matriz de productos internos. En el caso especial v i = w i , el producto interno es la norma cuadrada del k -vector, dada por el determinante de la matriz de Gram (⟨ v i , v j ⟩) . Esto se extiende luego bilinealmente (o sesquilinealmente en el caso complejo) a un producto interno no degenerado en Si e i , i = 1, 2, ..., n , forman una base ortonormal de , entonces los vectores de la forma
constituyen una base ortonormal para , un enunciado equivalente a la fórmula de Cauchy–Binet .
Con respecto al producto interno, la multiplicación externa y el producto interno son mutuamente adjuntos. Específicamente, para , , y ,
donde x ♭ ∈ V ∗ es el isomorfismo musical , el funcional lineal definido por
para todos . Esta propiedad caracteriza completamente el producto interno en el álgebra externa.
De hecho, de manera más general para , , y , la iteración de las propiedades adjuntas anteriores da
¿Dónde está ahora el dual -vector definido por
para todos .
Estructura de biálgebra
Existe una correspondencia entre el dual graduado del álgebra graduada y las formas multilineales alternas en . El álgebra exterior (así como el álgebra simétrica ) hereda una estructura de biálgebra y, de hecho, una estructura de álgebra de Hopf , del álgebra tensorial . Consulte el artículo sobre álgebras tensoriales para un tratamiento detallado del tema.
El producto exterior de las formas multilineales definidas anteriormente es dual de un coproducto definido en , dando la estructura de una coalgebra . El coproducto es una función lineal , que está dada por
sobre elementos . El símbolo representa el elemento unitario del campo . Recordemos que , de modo que lo anterior realmente se encuentra en . Esta definición del coproducto se eleva al espacio completo mediante el homomorfismo (lineal). La forma correcta de este homomorfismo no es la que uno podría escribir ingenuamente, sino que tiene que ser la que se define cuidadosamente en el artículo sobre la coalgebra . En este caso, se obtiene
Ampliando esto en detalle, se obtiene la siguiente expresión sobre elementos descomponibles:
donde la segunda suma se toma sobre todos los ( p , k − p ) -shuffles . Por convención, se toma que Sh( k, 0) y Sh(0, k ) es igual a {id: {1, ..., k } → {1, ..., k }}. También es conveniente tomar los productos de cuña puros y para que sean iguales a 1 para p = 0 y p = k , respectivamente (el producto vacío en ). El shuffle se sigue directamente del primer axioma de un co-álgebra: el orden relativo de los elementos se conserva en el shuffle riffle: el shuffle riffle simplemente divide la secuencia ordenada en dos secuencias ordenadas, una a la izquierda y otra a la derecha.
Obsérvese que el coproducto conserva la gradación del álgebra. Extendiendo al espacio completo se tiene
El símbolo tensorial ⊗ usado en esta sección debe entenderse con cierta cautela: no es el mismo símbolo tensorial que el que se usa en la definición del producto alternado. Intuitivamente, es quizás más fácil pensarlo como otro producto tensorial, pero diferente: sigue siendo (bi)lineal, como deberían ser los productos tensoriales, pero es el producto apropiado para la definición de una biálgebra, es decir, para crear el objeto . Cualquier duda persistente puede ser sacudida ponderando las igualdades (1 ⊗ v ) ∧ (1 ⊗ w ) = 1 ⊗ ( v ∧ w ) y ( v ⊗ 1) ∧ (1 ⊗ w ) = v ⊗ w , que se siguen de la definición de la coalgebra, en oposición a manipulaciones ingenuas que involucran los símbolos tensoriales y de cuña. Esta distinción se desarrolla con mayor detalle en el artículo sobre álgebras tensoriales . Aquí, hay mucho menos problema, ya que el producto alternado corresponde claramente a la multiplicación en el álgebra exterior, dejando el símbolo libre para su uso en la definición de la biálgebra. En la práctica, esto no presenta ningún problema particular, siempre que se evite la trampa fatal de reemplazar sumas alternadas de por el símbolo de cuña, con una excepción. Se puede construir un producto alternado de , con el entendimiento de que funciona en un espacio diferente. Inmediatamente debajo, se da un ejemplo: el producto alternado para el espacio dual se puede dar en términos del coproducto. La construcción de la biálgebra aquí es casi exactamente paralela a la construcción en el artículo de álgebra tensorial , excepto por la necesidad de rastrear correctamente los signos alternados para el álgebra exterior.
En términos del coproducto, el producto exterior en el espacio dual es simplemente el dual graduado del coproducto:
donde el producto tensorial en el lado derecho es de mapas lineales multilineales (extendido por cero en elementos de grado homogéneo incompatible: más precisamente, α ∧ β = ε ∘ ( α ⊗ β ) ∘ Δ , donde es la counit, como se define actualmente).
El counit es el homomorfismo que devuelve el componente de grado 0 de su argumento. El coproducto y el counit, junto con el producto exterior, definen la estructura de una biálgebra en el álgebra exterior.
Con un antípoda definido en elementos homogéneos por , el álgebra exterior es además un álgebra de Hopf . [12]
Funcionalidad
Supóngase que y son un par de espacios vectoriales y es una función lineal . Entonces, por la propiedad universal, existe un homomorfismo único de álgebras graduadas
de tal manera que
En particular, conserva el grado homogéneo. Los componentes k -graduados de se dan en elementos descomponibles por
Dejar
Los componentes de la transformación relativa a una base de y es la matriz de menores de . En particular, si y es de dimensión finita , entonces es una aplicación de un espacio vectorial unidimensional a sí mismo, y por lo tanto está dada por un escalar: el determinante de .
Exactitud
Si es una secuencia corta y exacta de espacios vectoriales, entonces
es una secuencia exacta de espacios vectoriales graduados, [13] como es
- [14]
Sumas directas
En particular, el álgebra exterior de una suma directa es isomorfa al producto tensorial de las álgebras exteriores:
Este es un isomorfismo graduado, es decir,
En términos más generales, para una secuencia corta y exacta de espacios vectoriales existe una filtración natural.
donde for está abarcado por elementos de la forma for y Los cocientes correspondientes admiten un isomorfismo natural
- dado por
En particular, si U es unidimensional entonces
es exacta, y si W es unidimensional entonces
es exacto. [15]
Aplicaciones
Volumen orientado en el espacio afín
El contexto natural para el volumen -dimensional (orientado) y el álgebra exterior es el espacio afín . Esta es también la conexión íntima entre el álgebra exterior y las formas diferenciales , ya que para integrar necesitamos un objeto 'diferencial' para medir el volumen infinitesimal. Si es un espacio afín sobre el espacio vectorial , y una colección ( símplex ) de puntos ordenados , podemos definir su volumen -dimensional orientado como el producto exterior de vectores (usando la concatenación para significar el vector de desplazamiento del punto a ); si se cambia el orden de los puntos, el volumen orientado cambia en un signo, de acuerdo con la paridad de la permutación. En el espacio -dimensional , el volumen de cualquier símplex -dimensional es un múltiplo escalar de cualquier otro.
La suma de las áreas orientadas -dimensionales de los símplex de contorno de un símplex -dimensional es cero, al igual que la suma de los vectores alrededor de un triángulo o los triángulos orientados que delimitan el tetraedro en la sección anterior.
La estructura del espacio vectorial generaliza la adición de vectores en : tenemos y de manera similar, una k -cuchilla es lineal en cada factor.
Álgebra lineal
En aplicaciones al álgebra lineal , el producto exterior proporciona una manera algebraica abstracta de describir el determinante y los menores de una matriz . Por ejemplo, es bien sabido que el determinante de una matriz cuadrada es igual al volumen del paraleletopo cuyos lados son las columnas de la matriz (con un signo para rastrear la orientación). Esto sugiere que el determinante puede definirse en términos del producto exterior de los vectores columna. Del mismo modo, los k × k menores de una matriz pueden definirse observando los productos exteriores de los vectores columna elegidos k a la vez. Estas ideas pueden extenderse no solo a las matrices sino también a las transformaciones lineales : el determinante de una transformación lineal es el factor por el cual escala el volumen orientado de cualquier paraleletopo de referencia dado. Por lo tanto, el determinante de una transformación lineal puede definirse en términos de lo que la transformación hace a la potencia exterior superior. La acción de una transformación sobre las potencias exteriores menores proporciona una manera independiente de la base para hablar sobre los menores de la transformación.
Física
En física, muchas magnitudes se representan de forma natural mediante operadores alternantes. Por ejemplo, si el movimiento de una partícula cargada se describe mediante vectores de velocidad y aceleración en el espacio-tiempo de cuatro dimensiones, entonces la normalización del vector de velocidad requiere que la fuerza electromagnética sea un operador alternante sobre la velocidad. Sus seis grados de libertad se identifican con los campos eléctrico y magnético.
Campo electromagnético
En las teorías de la relatividad de Einstein , el campo electromagnético se da generalmente como una forma diferencial 2 en un espacio 4 o como el campo tensorial alterno equivalente, el tensor electromagnético . Entonces o la identidad de Bianchi equivalente Nada de esto requiere una métrica.
La adición de la métrica de Lorentz y una orientación proporciona el operador de estrella de Hodge y, por lo tanto, permite definir la divergencia tensorial equivalente donde
Geometría lineal
Los k -vectores descomponibles tienen interpretaciones geométricas: el bivector representa el plano abarcado por los vectores, "ponderado" con un número, dado por el área del paralelogramo orientado con lados y . Análogamente, el 3-vector representa el 3-espacio abarcado ponderado por el volumen del paralelepípedo orientado con aristas , , y .
Geometría proyectiva
Los k -vectores descomponibles en corresponden a subespacios lineales k -dimensionales ponderados de . En particular, el Grassmanniano de subespacios k -dimensionales de , denotado , puede identificarse naturalmente con una subvariedad algebraica del espacio proyectivo . Esto se llama incrustación de Plücker , y la imagen de la incrustación puede caracterizarse por las relaciones de Plücker .
Geometría diferencial
El álgebra exterior tiene aplicaciones notables en geometría diferencial , donde se utiliza para definir formas diferenciales . [16] Las formas diferenciales son objetos matemáticos que evalúan la longitud de vectores, áreas de paralelogramos y volúmenes de cuerpos de dimensiones superiores , por lo que pueden integrarse sobre curvas, superficies y variedades de dimensiones superiores de una manera que generaliza las integrales de línea y las integrales de superficie del cálculo. Una forma diferencial en un punto de una variedad diferenciable es una forma multilineal alternada en el espacio tangente en el punto. Equivalentemente, una forma diferencial de grado k es un funcional lineal en la k -ésima potencia exterior del espacio tangente. Como consecuencia, el producto exterior de las formas multilineales define un producto exterior natural para las formas diferenciales. Las formas diferenciales juegan un papel importante en diversas áreas de la geometría diferencial.
Un enfoque alternativo define las formas diferenciales en términos de gérmenes de funciones .
En particular, la derivada exterior da al álgebra exterior de formas diferenciales en una variedad la estructura de un álgebra diferencial graduada . La derivada exterior conmuta con pullback a lo largo de aplicaciones suaves entre variedades y, por lo tanto, es un operador diferencial natural . El álgebra exterior de formas diferenciales, equipada con la derivada exterior, es un complejo de cocadena cuya cohomología se denomina cohomología de De Rham de la variedad subyacente y desempeña un papel vital en la topología algebraica de las variedades diferenciables.
Teoría de la representación
En teoría de representaciones , el álgebra exterior es uno de los dos funtores de Schur fundamentales en la categoría de espacios vectoriales, siendo el otro el álgebra simétrica . Juntas, estas construcciones se utilizan para generar las representaciones irreducibles del grupo lineal general (véase Representación fundamental ).
Superespacio
El álgebra exterior sobre los números complejos es el ejemplo arquetípico de una superálgebra , que desempeña un papel fundamental en las teorías físicas relativas a los fermiones y la supersimetría . Un solo elemento del álgebra exterior se denomina supernúmero [17] o número de Grassmann . El álgebra exterior en sí misma es entonces simplemente un superespacio unidimensional : es simplemente el conjunto de todos los puntos en el álgebra exterior. La topología en este espacio es esencialmente la topología débil , siendo los conjuntos abiertos los conjuntos cilíndricos . Un superespacio n -dimensional es simplemente el producto -fold de álgebras exteriores.
Homología del álgebra de Lie
Sea un álgebra de Lie sobre un cuerpo , entonces es posible definir la estructura de un complejo de cadenas sobre el álgebra exterior de . Esta es una aplicación -lineal
definido en elementos descomponibles por
La identidad de Jacobi se cumple si y solo si , por lo que esta es una condición necesaria y suficiente para que un álgebra no asociativa anticonmutativa sea un álgebra de Lie. Además, en ese caso es un complejo de cadena con operador de frontera . La homología asociada a este complejo es la homología del álgebra de Lie .
Álgebra homológica
El álgebra exterior es el ingrediente principal en la construcción del complejo de Koszul , un objeto fundamental en el álgebra homológica .
Historia
El álgebra exterior fue introducida por primera vez por Hermann Grassmann en 1844 bajo el término general de Ausdehnungslehre o teoría de la extensión . [18] Esto se refería de manera más general a una teoría algebraica (o axiomática) de cantidades extendidas y fue uno de los primeros precursores de la noción moderna de espacio vectorial . Saint-Venant también publicó ideas similares de cálculo exterior para las que reivindicó la prioridad sobre Grassmann. [19]
El álgebra en sí se construyó a partir de un conjunto de reglas, o axiomas, que capturaban los aspectos formales de la teoría de multivectores de Cayley y Sylvester. Por lo tanto, era un cálculo , muy parecido al cálculo proposicional , excepto que se centraba exclusivamente en la tarea de razonamiento formal en términos geométricos. [20] En particular, este nuevo desarrollo permitió una caracterización axiomática de la dimensión, una propiedad que anteriormente solo se había examinado desde el punto de vista de las coordenadas.
La importancia de esta nueva teoría de vectores y multivectores se perdió para los matemáticos de mediados del siglo XIX, [21] hasta que fue examinada exhaustivamente por Giuseppe Peano en 1888. El trabajo de Peano también permaneció algo oscuro hasta el cambio de siglo, cuando el tema fue unificado por miembros de la escuela de geometría francesa (notablemente Henri Poincaré , Élie Cartan y Gaston Darboux ) quienes aplicaron las ideas de Grassmann al cálculo de formas diferenciales .
Poco después, Alfred North Whitehead , tomando prestadas las ideas de Peano y Grassmann, introdujo su álgebra universal , que allanó el camino para los desarrollos del álgebra abstracta del siglo XX al colocar la noción axiomática de un sistema algebraico sobre una base lógica firme.
Véase también
- Álgebra alternada
- Identidades de cálculo exterior
- Álgebra de Clifford , una generalización del álgebra exterior a una forma cuadrática distinta de cero
- Álgebra geométrica
- Complejo Koszul
- Álgebra multilineal
- Álgebra simétrica , el análogo simétrico
- Álgebra tensorial
- Álgebra de Weyl , una deformación cuántica del álgebra simétrica mediante una forma simpléctica
Notas
- ^ ab Penrose, R. (2007). El camino hacia la realidad . Libros antiguos. ISBN 978-0-679-77631-4.
- ^ Wheeler, Misner y Thorne 1973, pág. 83
- ^ Grassmann (1844) las introdujo como álgebras extendidas (cf. Clifford 1878).
- ^ El término k-vector no es equivalente y no debe confundirse con términos similares como 4-vector , que en un contexto diferente podría significar un elemento de un espacio vectorial de 4 dimensiones. Una minoría de autores utiliza el término -multivector en lugar de -vector, lo que evita esta confusión.
- ^ Esta axiomatización de áreas se debe a Leopold Kronecker y Karl Weierstrass ; véase Bourbaki (1989b, Historical Note). Para un tratamiento moderno, véase Mac Lane y Birkhoff (1999, Theorem IX.2.2). Para un tratamiento elemental, véase Strang (1993, Capítulo 5).
- ^ Esta definición es estándar. Véase, por ejemplo, Mac Lane y Birkhoff (1999).
- ^ Una prueba de esto se puede encontrar con mayor generalidad en Bourbaki (1989).
- ^ Véase Bourbaki (1989, §III.7.1) y Mac Lane & Birkhoff (1999, Teorema XVI.6.8). Se pueden encontrar más detalles sobre las propiedades universales en general en Mac Lane & Birkhoff (1999, Capítulo VI) y en toda la obra de Bourbaki.
- ^ Véase Bourbaki (1989, §III.7.5) para generalizaciones.
- ^ Nota : Las orientaciones que se muestran aquí no son correctas; el diagrama simplemente da la sensación de que se define una orientación para cada forma k .
- ^ Wheeler, JA; Misner, C.; Thorne, KS (1973). Gravitación . WH Freeman & Co. págs. 58-60, 83, 100-9, 115-9. ISBN 0-7167-0344-0.
- ^ De hecho, el álgebra exterior de es el álgebra envolvente de la estructura de la superálgebra de Lie abeliana en .
- ^ Esta parte del enunciado también se cumple con mayor generalidad si y son módulos sobre un anillo conmutativo: Esto convierte los epimorfismos en epimorfismos. Véase Bourbaki (1989, Proposición 3, §III.7.2).
- ^ Esta afirmación se generaliza únicamente al caso en que V y W son módulos proyectivos sobre un anillo conmutativo. De lo contrario, no suele ser el caso que convierte monomorfismos en monomorfismos. Véase Bourbaki (1989, Corolario a la Proposición 12, §III.7.9).
- ^ Esta filtración también es válida para los fibrados vectoriales y los módulos proyectivos sobre un anillo conmutativo. Por lo tanto, es más general que el resultado citado anteriormente para las sumas directas, ya que no todas las secuencias cortas exactas se dividen en otras categorías abelianas .
- ^ James, AT (1983). "Sobre el producto Wedge". En Karlin, Samuel; Amemiya, Takeshi; Goodman, Leo A. (eds.). Estudios en econometría, series temporales y estadísticas multivariadas . Academic Press. págs. 455–464. ISBN 0-12-398750-4.
- ^ DeWitt, Bryce (1984). "Capítulo 1". Supermanifolds . Cambridge University Press. pág. 1. ISBN 0-521-42377-5.
- ^ Kannenberg (2000) publicó una traducción del trabajo de Grassmann en inglés; tradujo Ausdehnungslehre como Teoría de extensión .
- ^ J Itard, Biografía en Diccionario de biografía científica (Nueva York 1970–1990).
- ^ En el pasado, los autores se han referido a este cálculo de diversas formas: como cálculo de extensión (Whitehead 1898; Forder 1941), álgebra extensiva (Clifford 1878) y, recientemente, álgebra vectorial extendida (Browne 2007).
- ^ Bourbaki 1989, pág. 661.
Referencias
Referencias matemáticas
- Bishop, R. ; Goldberg, SI (1980), Análisis tensorial en variedades , Dover, ISBN 0-486-64039-6
- Incluye un tratamiento de tensores alternados y formas alternadas, así como una discusión detallada de la dualidad de Hodge desde la perspectiva adoptada en este artículo.
- Bourbaki, Nicolas (1989), Elementos de matemáticas, Álgebra I , Springer-Verlag, ISBN 3-540-64243-9
- Esta es la principal referencia matemática del artículo. Presenta el álgebra exterior de un módulo sobre un anillo conmutativo (aunque este artículo se especializa principalmente en el caso en el que el anillo es un cuerpo), e incluye un análisis de la propiedad universal, la funtorialidad, la dualidad y la estructura de biálgebra. Véase §III.7 y §III.11.
- Bryant, RL ; Chern, SS ; Gardner, RB; Goldschmidt, HL; Griffiths, PA (1991), Sistemas diferenciales exteriores , Springer-Verlag
- Este libro contiene aplicaciones de álgebras exteriores a problemas de ecuaciones diferenciales parciales . En los primeros capítulos se desarrollan los conceptos de rango y relacionados.
- Mac Lane, S.; Birkhoff , G. (1999), Álgebra , AMS Chelsea, ISBN 0-8218-1646-2
- Las secciones 6 a 10 del capítulo XVI ofrecen una explicación más elemental del álgebra exterior, incluyendo la dualidad, los determinantes y los menores, y las formas alternas.
- Sternberg, Shlomo (1964), Conferencias sobre geometría diferencial , Prentice Hall
- Contiene un tratamiento clásico del álgebra exterior como tensores alternados y aplicaciones a la geometría diferencial.
Referencias históricas
- Bourbaki (1989, Nota histórica sobre los capítulos II y III)
- Clifford, W. (1878), "Aplicaciones del álgebra extensiva de Grassmann", American Journal of Mathematics , 1 (4), The Johns Hopkins University Press: 350–358, doi :10.2307/2369379, JSTOR 2369379
- Forder, HG (1941), El cálculo de la extensión, Internet Archive
- Grassmann, Hermann (1844), Die Lineale Ausdehnungslehre – Ein neuer Zweig der Mathematik (en alemán)(La teoría de la extensión lineal: una nueva rama de las matemáticas) referencia alternativa
- Kannenberg, Lloyd (2000), Teoría de la extensión (traducción de la Ausdehnungslehre de Grassmann ) , American Mathematical Society, ISBN 0-8218-2031-1
- Peano, Giuseppe (1888), Calcolo Geométrico segundo el Ausdehnungslehre di H. Grassmann preceduto dalle Operazioni della Logica Deduttiva; Kannenberg, Lloyd (1999), Cálculo geométrico: según el Ausdehnungslehre de H. Grassmann , Birkhäuser, ISBN 978-0-8176-4126-9.
- Whitehead, Alfred North (1898), "Un tratado sobre álgebra universal, con aplicaciones", Nature , 58 (1504), Cambridge: 385, Bibcode :1898Natur..58..385G, doi :10.1038/058385a0, S2CID 3985954
Otras referencias y lecturas complementarias
- Browne, JM (2007), Álgebra de Grassmann: exploración de aplicaciones del álgebra vectorial extendida con Mathematica, archivado desde el original el 19 de febrero de 2009 , consultado el 9 de mayo de 2007
- Introducción al álgebra exterior y al álgebra geométrica , con especial atención a las aplicaciones. También incluye una sección de historia y una bibliografía.
- Spivak, Michael (1965), Cálculo en variedades , Addison-Wesley, ISBN 978-0-8053-9021-6
- Incluye aplicaciones del álgebra exterior a las formas diferenciales, específicamente centradas en la integración y el teorema de Stokes . La notación en este texto se utiliza para indicar el espacio de k -formas alternadas en V ; es decir, para Spivak es lo que este artículo llamaría Spivak analiza esto en el Anexo 4.
- Strang, G. (1993), Introducción al álgebra lineal , Wellesley-Cambridge Press, ISBN 978-0-9614088-5-5
- Incluye un tratamiento elemental de la axiomatización de determinantes como áreas con signo, volúmenes y volúmenes de dimensiones superiores.
- Onishchik, AL (2001) [1994], "Álgebra exterior", Enciclopedia de Matemáticas , EMS Press
- Wendell, Fleming (2012) [1977], "7. Álgebra exterior y cálculo diferencial", Funciones de varias variables (2.ª ed.), Springer, págs. 275–320, ISBN 978-1-4684-9461-7
- Este libro de texto de cálculo multivariado introduce el álgebra exterior de formas diferenciales hábilmente en la secuencia de cálculo para universidades.
- Shafarevich, IR ; Remizov, AO (2012). Álgebra lineal y geometría. Springer . ISBN 978-3-642-30993-9.
- Capítulo 10: El producto exterior y las álgebras exteriores
- "El método Grassmann en geometría proyectiva" Una recopilación de traducciones al inglés de tres notas de Cesare Burali-Forti sobre la aplicación del álgebra exterior a la geometría proyectiva
- C. Burali-Forti, "Introducción a la geometría diferencial, siguiendo el método de H. Grassmann". Traducción al inglés de un libro temprano sobre las aplicaciones geométricas de las álgebras exteriores.
- "Mecánica, según los principios de la teoría de la extensión" Una traducción al inglés de un artículo de Grassmann sobre las aplicaciones del álgebra exterior







































![{\displaystyle [1,\puntos ,k]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/60710fea4ba764d784a1cfee13f73f633e65e8e3)


















































































![{\displaystyle (t~{\widehat {\otimes }}~s)^{i_{1}\cdots i_{r+p}}=t^{[i_{1}\cdots i_{r}}s^{i_{r+1}\cdots i_{r+p}]}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d3a6e1f0d329e0d2883efe13d67dc45065142bba)
























































































































![{\displaystyle F_{ij}=A_{[i,j]}=A_{[i;j]},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4158dbf3e9425d402c1c7350c68a73ac96a0176f)

![{\displaystyle F_{[ij,k]}=F_{[ij;k]}=0.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/39498c21115979961e612d1ea550016064bc6659)










![{\displaystyle \partial(x_{1}\wedge \cdots \wedge x_{p+1})={\frac {1}{p+1}}\sum _{j<\ell }(-1)^{j+\ell +1}[x_{j},x_{\ell }]\wedge x_{1}\wedge \cdots \wedge {\hat {x}}_{j}\wedge \cdots \wedge {\hat {x}}_{\ell }\wedge \cdots \wedge x_{p+1}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/78a74a56321a71b4e71d78158149d5c833f7a56e)





