Nonograma

Los nonogramas , también conocidos como Hanjie , Paint by Numbers , Picross , Griddlers y Pic-a-Pix , son juegos de lógica con imágenes en los que las celdas de una cuadrícula deben colorearse o dejarse en blanco según los números que aparecen en los bordes de la cuadrícula para revelar una imagen oculta. En este juego, los números son una forma de tomografía discreta que mide cuántas líneas continuas de cuadrados llenos hay en una fila o columna determinada. Por ejemplo, una pista de "4 8 3" significaría que hay conjuntos de cuatro, ocho y tres cuadrados llenos, en ese orden, con al menos un cuadrado en blanco entre conjuntos sucesivos.

Estos rompecabezas suelen ser en blanco y negro (describen una imagen binaria ), pero también pueden ser de color. Si están coloreados, las pistas numéricas también están coloreadas para indicar el color de los cuadrados. Dos números de diferente color pueden tener o no un espacio entre ellos. Por ejemplo, un cuatro negro seguido de un dos rojo podría significar cuatro casillas negras, algunos espacios vacíos y dos casillas rojas, o podría significar simplemente cuatro casillas negras seguidas inmediatamente de dos rojas. Los nonogramas no tienen límites teóricos de tamaño y no están restringidos a diseños de cuadrados.

Los nonogramas reciben su nombre en honor a Non Ishida, uno de los dos inventores del rompecabezas.

Los nonogramas también se conocen por muchos otros nombres, entre ellos, rompecabezas Hanjie, Paint by Numbers, ^[1] Crosspix, ^[1] Griddlers, ^[1] Pic-a-Pix, ^[1] Picross, ^[1] Picma, PrismaPixels, Pixel Puzzles, Crucipixel, Edel, FigurePic, Hanjie, HeroGlyphix, Illust-Logic, Crucigramas japoneses, Rompecabezas japoneses, ^[2] Kare Karala!, Logic Art, Logic Square, Logicolor, Logik-Puzzles, Logimage, Oekaki Logic, ^[1] Paint Logic, Picture Logic, Tsunamii, Paint by Sudoku, Rompecabezas de lógica formadores de imágenes, ^[2] y Binary Coloring Books.

En 1987, Non Ishida, una editora de gráficos japonesa, ganó un concurso en Tokio al diseñar imágenes en cuadrícula utilizando luces de rascacielos que se encendían o apagaban. Esto la llevó a la idea de un rompecabezas basado en completar ciertos cuadrados en una cuadrícula. Casualmente, un profesional japonés de los rompecabezas llamado Tetsuya Nishio inventó los mismos rompecabezas de forma independiente y los publicó en otra revista. En esa época, los nonogramas también se llamaban rompecabezas lógicos de formación de imágenes. ^{[2] [1]}

En 1988, Non Ishida publicó tres rompecabezas de cuadrícula de imágenes en Japón bajo el nombre de "Window Art Puzzles". En 1990, James Dalgety en el Reino Unido inventó el nombre Nonograms en honor a Non Ishida, ^{[ cita requerida ]} y The Sunday Telegraph comenzó a publicarlos semanalmente. ^[1] En 1993, Non Ishida publicó el primer libro de nonogramas en Japón. The Sunday Telegraph publicó un libro de rompecabezas dedicado titulado "Book of Nonograms". Los nonogramas también se publicaron en Suecia, Estados Unidos (originalmente por la revista Games ^[3] ), Sudáfrica y otros países. The Sunday Telegraph organizó un concurso en 1998 para elegir un nuevo nombre para sus rompecabezas. Griddlers fue el nombre ganador que eligieron los lectores. En 1993, Ishida publicó el "Book of Nonograms". ^[2]

Los rompecabezas de pintar por números se implementaron en 1995 en juguetes electrónicos portátiles como Game Boy y en otros juguetes de rompecabezas de plástico. Nintendo se sumó a esta moda de los rompecabezas y lanzó dos títulos de " Picross " (crucigramas con imágenes) para Game Boy y nueve para Super Famicom (ocho de los cuales se lanzaron en intervalos de dos meses para Nintendo Power Super Famicom Cartridge Writer como la serie NP ) en Japón. Solo uno de ellos, Mario's Picross para Game Boy, se lanzó fuera de Japón. Desde entonces, uno de los desarrolladores de juegos Picross más prolíficos ha sido Jupiter Corporation , que lanzó Picross DS para Nintendo DS en 2007, 8 títulos de la serie Picross e para Nintendo 3DS eShop (junto con 5 títulos específicos de personajes, incluidos algunos con personajes de Pokémon , Zelda y Sanrio ) y 9 títulos de la serie Picross S para Nintendo Switch (junto con dos títulos específicos de personajes con Kemono Friends y Overlord respectivamente, y otro con propiedades intelectuales de Master System y Genesis de Sega ).

La creciente popularidad en Japón impulsó a nuevos editores y para entonces ya existían varias revistas mensuales, algunas de las cuales contenían hasta 100 rompecabezas. El juego arcade japonés Logic Pro fue lanzado por Deniam Corp en 1996, con una secuela lanzada al año siguiente. El desarrollador de juegos del Reino Unido Jagex lanzó un rompecabezas de nonograma en 2011 como parte de su evento anual de Halloween para su juego de rol , Runescape . En 2013, Casual Labs lanzó una versión móvil de estos rompecabezas llamada Paint it Back con el tema de restaurar una galería de arte. Lanzado a principios de 2017, Pictopix ha sido presentado como un digno heredero de Picross en PC por Rock, Paper, Shotgun. ^[4] En particular, el juego permite a los jugadores compartir sus creaciones.

Pintar por números ha sido publicado por Sanoma Uitgevers en los Países Bajos, Puzzler Media (anteriormente British European Associated Publishers) en el Reino Unido y Nikui Rosh Puzzles en Israel. Se publican revistas con rompecabezas de nonogramas en los EE. UU., el Reino Unido, Alemania, los Países Bajos, Italia, Hungría, Finlandia, la República Checa, Eslovaquia, Rusia, Ucrania y muchos otros países.

Esta sección tiene varios problemas. Ayúdanos a mejorarla o a discutir estos problemas en la página de discusión . ( Aprende cómo y cuándo eliminar estos mensajes ) Esta sección contiene instrucciones, consejos o contenido instructivo .Por favor, ayude a reescribir el contenido para que sea más enciclopédico o muévalo a Wikiversidad, Wikilibros o Wikivoyage. ( Enero 2014 ) Esta sección no cita ninguna fuente .Por favor, ayude a mejorar esta sección añadiendo citas de fuentes confiables . El material sin fuentes puede ser cuestionado y eliminado . ( Enero de 2018 )( Aprenda cómo y cuándo eliminar este mensaje ) ( Aprenda cómo y cuándo eliminar este mensaje )

Para resolver un rompecabezas, es necesario determinar qué celdas serán casillas y cuáles estarán vacías. Los solucionadores suelen utilizar un punto o una cruz para marcar las celdas que están seguros de que son espacios. Las celdas que se pueden determinar mediante la lógica deben llenarse. Si se utiliza la adivinación, un solo error puede extenderse por todo el campo y arruinar por completo la solución. A veces, un error sale a la superficie solo después de un tiempo, cuando es muy difícil corregir el rompecabezas. La imagen oculta puede ayudar a localizar y eliminar un error, pero de lo contrario juega un papel pequeño en el proceso de resolución, ya que puede confundir.

Muchos acertijos se pueden resolver razonando sobre una sola fila o columna a la vez, luego probando con otra fila o columna y repitiendo hasta completar el acertijo. Los acertijos más difíciles también pueden requerir varios tipos de razonamiento del tipo "¿qué pasaría si...?" que incluyan más de una fila (o columna). Esto funciona para buscar contradicciones, por ejemplo, cuando una celda no puede ser un recuadro porque alguna otra celda produciría un error, debe ser un espacio.

Al principio de la solución, se puede utilizar un método sencillo para determinar la mayor cantidad posible de casillas. Este método utiliza conjunciones de posibles lugares para cada bloque de casillas. Por ejemplo, en una fila de diez celdas con una sola pista de 8 , el bloque ligado que consta de 8 casillas podría extenderse desde

• el borde derecho, dejando dos espacios a la izquierda;
• el borde izquierdo, dejando dos espacios a la derecha;
• o algún punto intermedio.

Como resultado, el bloque debe extenderse a través de las seis celdas más centrales de la fila.

Lo mismo se aplica cuando hay más pistas en la fila. Por ejemplo, en una fila de diez celdas con pistas de 4 y 3 , los bloques de casillas enlazadas podrían ser

• apiñados a la izquierda, uno al lado del otro, dejando dos espacios a la derecha;
• apiñados a la derecha, uno al lado del otro, dejando dos espacios a la izquierda;
• o algo intermedio.

En consecuencia, el primer bloque de cuatro casillas incluye definitivamente la tercera y cuarta celdas, mientras que el segundo bloque de tres casillas incluye definitivamente la octava celda. Por lo tanto, se pueden colocar casillas en las celdas tercera, cuarta y octava. Al determinar las casillas de esta manera, solo se pueden colocar casillas en celdas cuando el mismo bloque se superpone; en este ejemplo, hay superposición en la sexta celda, pero es de bloques diferentes y, por lo tanto, aún no se puede decir si la sexta celda contendrá o no una casilla.

Este método consiste en determinar espacios buscando celdas que estén fuera del rango de cualquier bloque de casillas posible. Por ejemplo, considerando una fila de diez celdas con casillas en la cuarta y novena celda y con pistas de 3 y 1 , el bloque ligado a la pista 3 se extenderá por la cuarta celda y la pista 1 estará en la novena celda.

Primero, la pista 1 está completa y habrá un espacio a cada lado del bloque delimitado.

En segundo lugar, la pista 3 sólo puede extenderse en algún lugar entre la segunda celda y la sexta celda, porque siempre tiene que incluir la cuarta celda; sin embargo, esto puede dejar celdas que en ningún caso pueden ser casillas, es decir, la primera y la séptima.

Nota: En este ejemplo se tienen en cuenta todos los bloques, pero no siempre es así. El jugador debe tener cuidado porque puede haber pistas o bloques que aún no estén unidos entre sí.

En este método se mostrará la importancia de los espacios. Un espacio colocado en algún lugar en el medio de una fila incompleta puede forzar un bloque grande hacia un lado o hacia el otro. Además, un espacio que sea demasiado pequeño para cualquier bloque posible puede llenarse con espacios.

Por ejemplo, considerando una fila de diez celdas con espacios en la quinta y séptima celda y con pistas de 3 y 2 :

• La pista del 3 quedaría forzada a la izquierda, porque no podría caber en ningún otro lugar.
• El espacio vacío en la sexta celda es demasiado pequeño para acomodar pistas como 2 o 3 y puede llenarse con espacios.
• Finalmente, la pista del 2 se propagará a través de la novena celda según el método de Cajas Simples anterior.

A veces, hay un cuadro cerca del borde que no está más lejos del borde que la longitud de la primera pista. En este caso, la primera pista se extenderá a través de ese cuadro y se verá forzada a salir del borde. En el caso más simple, siempre que haya un cuadro en la primera o última celda de una fila o columna, la primera o última pista debe estar alineada con el borde de esa fila o columna.

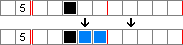
Considerando una fila de diez celdas con un recuadro en la tercera celda y con una pista de 5 , la pista de 5 siempre abarcará desde la tercera hasta la quinta celda (pero no necesariamente hasta la segunda o la sexta). Por lo tanto, es posible marcar la tercera, cuarta y quinta celda como pertenecientes al 5 .

Nota: Este método también puede funcionar en el medio de una fila, más lejos de los bordes.

• Un espacio puede actuar como un borde, si la primera pista se coloca a la derecha de ese espacio.
• La primera pista también puede estar precedida por otras pistas, si todas las pistas ya están ligadas a la izquierda del espacio de forzamiento.

Las casillas que están más cerca unas de otras pueden estar unidas en un bloque o divididas por un espacio en varios bloques. Cuando hay dos bloques con una celda vacía entre ellos, esta celda será:

• Un espacio si uniendo los dos bloques mediante un cuadro se produciría un bloque demasiado grande
• Una caja si se dividen los dos bloques por un espacio produciría un bloque demasiado pequeño que no tiene suficientes celdas libres restantes

Por ejemplo, considerando una fila de quince celdas con casillas en la tercera, cuarta, sexta, séptima, undécima y decimotercera celda y con pistas de 5 , 2 y 2 :

• La pista del 5 unirá los dos primeros bloques mediante una casilla en un bloque grande, porque un espacio produciría un bloque de solo 4 casillas que no es suficiente allí.
• Las pistas del 2 dividirán los dos últimos bloques por un espacio, porque una casilla produciría un bloque de 3 casillas continuas, lo cual no está permitido allí.

Nota: La imagen ilustrativa también muestra cómo se completan las pistas del 2. Sin embargo, esto no forma parte de la técnica de unión y separación , sino de la técnica de pegado descrita anteriormente.

Para resolver el rompecabezas, también suele ser muy importante encerrar inmediatamente cada bloque de casillas completo o delimitado mediante espacios de separación, como se describe en el método de espacios simples . La puntuación precisa suele generar más fuerza y ​​puede ser vital para terminar el rompecabezas. Nota: Los ejemplos anteriores no hicieron eso solo para mantener la simplicidad.

El mercurio es un caso especial de la técnica de espacios simples . Su nombre proviene de la forma en que el mercurio se retrae de los lados de un recipiente.

Si hay una casilla en una fila que está a la misma distancia del borde que la longitud de la primera pista, la primera celda será un espacio. Esto se debe a que la primera pista no cabría a la izquierda de la casilla. Tendrá que extenderse por esa casilla, dejando atrás la primera celda. Además, cuando la casilla es en realidad un bloque de más casillas a la derecha, habrá más espacios al principio de la fila, lo que se determina utilizando este método varias veces.

Algunos acertijos más difíciles también pueden requerir un razonamiento avanzado. Cuando se hayan agotado todos los métodos simples anteriores, puede resultar útil buscar contradicciones . Es recomendable utilizar un lápiz (u otro color) para facilitar las correcciones. El procedimiento incluye:

1. Intentando convertir una celda vacía en un cuadro (o luego en un espacio).
2. Utilizando todos los métodos disponibles para resolver lo máximo posible.
3. Si se encuentra un error, la celda que se ha intentado introducir no será un cuadro con seguridad, sino un espacio (o un cuadro, si se ha intentado introducir un espacio).

En este ejemplo, se prueba con un cuadro en la primera fila, lo que genera un espacio al principio de esa fila. El espacio fuerza entonces a que haya un cuadro en la primera columna, que se adhiere a un bloque de tres cuadros en la cuarta fila. Sin embargo, esto es incorrecto porque la tercera columna no permite ningún cuadro allí, lo que lleva a la conclusión de que la celda que se intenta colocar no debe ser un cuadro, por lo que debe ser un espacio.

El problema de este método es que no hay una manera rápida de saber qué celda vacía probar primero. Por lo general, solo unas pocas celdas dan lugar a algún progreso y las demás celdas conducen a callejones sin salida. Las celdas con las que más vale la pena empezar pueden ser:

• celdas que tienen muchos vecinos no vacíos;
• celdas que están próximas a los bordes o próximas a los bloques de espacios;
• celdas que están dentro de filas que constan de más celdas no vacías.

Es posible comenzar a resolver un rompecabezas utilizando una técnica matemática para completar bloques de filas o columnas independientemente de otras filas o columnas. Este es un buen "primer paso" y es un atajo matemático a las técnicas descritas anteriormente. El proceso es el siguiente:

1. Sume las pistas, más 1 por cada "espacio" que haya entre ellas. Por ejemplo, si la pista es 6 2 3, este paso produce la suma 6 + 1 + 2 + 1 + 3 = 13.
2. Resta este número del total disponible en la fila (normalmente el ancho o la altura del rompecabezas). Por ejemplo, si la pista del paso 1 está en una fila de 15 celdas de ancho, la diferencia es 15 - 13 = 2. Nota: Si se pueden utilizar espacios en los bordes izquierdo o derecho (superior o inferior), esto "reduce" el área disponible. Si se sabe que la celda más a la derecha es un espacio, la diferencia es 14 - 13 = 1.
3. Cualquier pista que sea mayor que el número del paso 2 tendrá algunos bloques llenos. En el ejemplo, esto se aplica a las pistas 6 y 3, pero no a la 2.
4. Para cada pista del paso 3, reste el número del paso 2 para determinar la cantidad de bloques que se pueden completar. Por ejemplo, la pista 6 tendrá (6 - 2 =) 4 bloques completados y la pista 3 tendrá (3 - 2 =) 1. Nota: si aplica el mismo procedimiento a una pista que "falló" en el paso 3, se obtendrá un número no positivo, lo que indica que no se completarán bloques para esta pista. La pista 2 produce el número (2 - 2 =) 0; si hubiera una pista 1, produciría el número (1 - 2 =) -1.
5. Para completar los bloques, suponga que todos los bloques están empujados hacia un lado, cuente desde ese lado "a través" de los bloques y vuelva a llenar la cantidad adecuada de bloques. Esto se puede hacer desde cualquier dirección. Por ejemplo, la pista 6 se puede hacer de dos maneras, como se indica a continuación:
   1. Desde la izquierda: dado que el 6 es el primer número, cuente 6 bloques desde el borde izquierdo, hasta el bloque 6. Ahora, "rellene" 4 bloques (la cantidad obtenida en el paso 4), de modo que las celdas 3 a 6 estén completas.
   2. Desde la derecha: comenzando desde la derecha, se deben tener en cuenta las pistas que están a la derecha de la pista 6. Comenzando desde la celda 15, cuente 3 celdas para la pista 3 (hasta la celda 13), luego un espacio (12), luego la pista 2 (10), luego un espacio (9), luego la pista 6 (3). Desde la celda 3, "rellene" 4 bloques, llenando las celdas 3 a 6. Los resultados son los mismos que si lo hiciera desde la izquierda en el paso anterior.
6. Repita el paso 5 para todas las pistas identificadas en el paso 3.

En la ilustración, la fila 1 muestra las celdas que se rellenan con este procedimiento, las filas 2 y 4 muestran cómo se empujan los bloques hacia un lado en el paso 5, y las filas 3 y 5 muestran las celdas que se rellenan en el paso 5.

El uso de esta técnica para todas las filas y columnas al comienzo del rompecabezas produce una buena ventaja para completarlo. Nota: Algunas filas o columnas no arrojarán ningún resultado inicialmente. Por ejemplo, una fila de 20 celdas con una pista de 1 4 2 5 arrojará 1 + 1 + 4 + 1 + 2 + 1 + 5 = 15. 20 - 15 = 5. Ninguna de las pistas es mayor que 5. Además, esta técnica se puede utilizar en una escala más pequeña. Si hay espacios disponibles en el centro o en cualquiera de los lados, incluso si ya se descubrieron ciertas pistas, este método se puede utilizar con las pistas restantes y los espacios disponibles.

Algunos acertijos pueden requerir que se busquen más a fondo las contradicciones. Sin embargo, esto no es posible simplemente con un bolígrafo y un lápiz, debido a las muchas posibilidades que se deben buscar. Este método es práctico para utilizarlo con un ordenador.

En algunos casos, el razonamiento sobre un conjunto de filas también puede llevar al siguiente paso de la solución incluso sin contradicciones ni recursión más profunda. Sin embargo, encontrar dichos conjuntos suele ser tan difícil como encontrar contradicciones.

La resolución de rompecabezas de nonogramas es un problema NP-completo . ^{[5] [6] [7]} Esto significa que no existe un algoritmo de tiempo polinomial que resuelva todos los rompecabezas de nonogramas a menos que P = NP .

Sin embargo, ciertas clases de rompecabezas, como aquellos en los que cada fila o columna tiene solo un bloque de celdas y todas las celdas están conectadas, pueden resolverse en tiempo polinomial transformando el problema en una instancia de 2-satisfacibilidad . ^[8]

En el sitio WebPBN (Web Paint-By-Number) se puede encontrar una extensa comparación y discusión de algoritmos de resolución de nonogramas. ^[9] Un solucionador de nonogramas escrito en C++ y publicado en la revista Pattern Recognition resuelve líneas en tiempo cuadrático como máximo. ^[10]

Nintendo ha publicado varios videojuegos de nonogramas con el nombre "Picross" (ピクロス, Pikurosu ) . El juego de Game Boy Mario's Picross se lanzó inicialmente en Japón el 14 de marzo de 1995 con un éxito decente. Sin embargo, el juego no logró convertirse en un éxito en el mercado estadounidense, a pesar de una fuerte campaña publicitaria por parte de Nintendo. El juego tiene una dificultad creciente, con niveles de rompecabezas sucesivos que contienen rompecabezas más grandes. Cada rompecabezas tiene una cantidad limitada de tiempo para ser resuelto. Se pueden solicitar pistas (límites de línea) con una penalización de tiempo, y los errores cometidos también generan penalizaciones de tiempo (la cantidad aumenta con cada error). Picross 2 fue lanzado más tarde para Game Boy y Mario's Super Picross para Super Famicom, ninguno de los cuales fue traducido para el mercado estadounidense ( Mario's Super Picross , sin embargo, fue lanzado más tarde en el servicio PAL de la Consola Virtual de Wii el 14 de septiembre de 2007, como parte de su Festival Hanabi , así como en el servicio Nintendo Switch Online en todo el mundo el 23 de septiembre de 2020 ^[11] ). Ambos juegos también introdujeron Wario's Picross , con el némesis de Mario en el papel. Estas rondas varían al eliminar la función de pista y los errores no se penalizan, al precio de que los errores ni siquiera se revelan. Estas rondas solo se pueden superar cuando se marcan todas las casillas correctas, sin errores. También se eliminó el límite de tiempo. Nintendo también lanzó ocho volúmenes de Picross en el periférico japonés Nintendo Power en Japón, llamado NP Picross , cada uno con un nuevo conjunto de rompecabezas, incluidos rompecabezas basados ​​​​en varios personajes de Nintendo, como Mario , The Legend of Zelda y Pokémon .

Nintendo lanzó Picross DS para la consola portátil Nintendo DS en 2007. Contiene varias etapas de dificultad variable, desde cuadrículas de 5x5 hasta cuadrículas de 25x20. El modo normal le dice a los jugadores si cometieron un error (con una penalización de tiempo) y el modo libre no. Hay una pista disponible antes de comenzar el rompecabezas en todos los modos; el juego revela una fila y columna completas al azar. Rompecabezas adicionales estaban disponibles a través de la Conexión Wi-Fi de Nintendo; algunos de los rompecabezas originales de Mario Picross estaban disponibles. Sin embargo, el servicio se cerró el 20 de mayo de 2014. Nintendo hizo que los nuevos lanzamientos estuvieran disponibles quincenalmente. Picross DS se lanzó en Europa y Australia el 11 de mayo de 2007 y en los Estados Unidos el 30 de julio de 2007 y ha sido bien recibido por los críticos, incluidos Craig Harris, ^[12] Jessica Wadleigh ^[13] y Dave McCarthy ^[14] etiquetando el juego como "adictivo". ^{[15] [16]} Una versión 3D del juego, titulada Picross 3D , también fue lanzada para la DS en Japón en 2009 e internacionalmente en 2010. Una secuela, Picross 3D: Round 2 , fue lanzada para Nintendo 3DS en 2015. ^[17] Otra versión descargable del juego fue lanzada para Nintendo eShop de Nintendo 3DS, llamada Picross e , Picross e2 y Picross e3 lanzada en 2013, con Picross e4 lanzado en 2014. Nintendo también lanzó un spin-off de Pokémon el 7 de diciembre de 2015 en forma del juego freemium de Pokémon Picross para Nintendo 3DS. My Nintendo Picross The Legend of Zelda: Twilight Princess fue lanzado para Nintendo 3DS el 31 de marzo de 2016, exclusivamente como una recompensa premium para My Nintendo .

Otras compañías también han lanzado videojuegos de nonogramas, como Falcross ^[18] en iOS , Across-Stitch de Knitwit Studios en Microsoft Windows y Apple macOS , y la serie de juegos Color Cross de Little Worlds Studio en Nintendo DS, Microsoft Windows e iOS . Además, los rompecabezas de nonogramas han aparecido en juegos de rompecabezas que no son de picross, como en la quinta entrega de Deadly Rooms of Death , The Second Sky . En él, los rompecabezas de nonogramas (de nuevo llamados rompecabezas "Picross") que representan objetos del juego son rompecabezas opcionales y desbloqueables al final del juego que se pueden jugar en el nivel "La estación central", y resolverlos desbloquea niveles de bonificación en el juego. En 2018, Konami lanzó un juego titulado Pixel Puzzle Collection , o Picross Puzzle (ピクロジパズル), con personajes y sprites clásicos de Konami.

Esta sección necesita citas adicionales para su verificación . Por favor, ayude a mejorar este artículo añadiendo citas de fuentes confiables en esta sección. El material sin fuentes puede ser cuestionado y eliminado. ( Enero de 2018 ) ( Aprenda cómo y cuándo eliminar este mensaje )

Pintar por números con pentominós es una variante en la que las doce figuras de pentominós deben colocarse en la cuadrícula, sin que se toquen entre sí (ni siquiera en diagonal).

Los Triddlers ^[19] son ​​una rama que utiliza formas triangulares en lugar de cuadrados.

El juego de pintar por pares o Link-a-Pix consiste en una cuadrícula con números que llenan algunos cuadrados; los pares de números deben ubicarse correctamente y conectarse con una línea que llene un total de cuadrados igual a ese número. Solo hay una forma única de unir todos los cuadrados en un rompecabezas correctamente construido. Cuando se completa, los cuadrados que tienen líneas están llenos; el contraste con los cuadrados en blanco revela la imagen. (Como se mencionó anteriormente, existen versiones en color que implican unir números del mismo color).

Fill-a-Pix también utiliza una cuadrícula con números dentro. En este formato, cada número indica cuántos de los cuadrados que lo rodean y cuántos de ellos se rellenarán. Por ejemplo, un cuadrado marcado con un "9" tendrá los ocho cuadrados que lo rodean y también él mismo rellenados. Si está marcado con un "0", todos esos cuadrados estarán en blanco.

Maze-a-Pix utiliza un laberinto en una cuadrícula estándar. Cuando se encuentra la única ruta correcta desde el principio hasta el final, se rellena cada "casilla" de la solución (o se rellenan todas las casillas que no son soluciones) para crear la imagen.

Tile Paint es otro tipo de rompecabezas de lógica con imágenes de Nikoli. Funciona como los nonogramas normales, excepto que solo especifica la cantidad total de cuadrados que se rellenarán en cada fila o columna y las secciones irregulares dentro de la cuadrícula tienen bordes a su alrededor que indican que, si uno de los cuadrados dentro de ella está lleno, todos deben rellenarse.

• Acorazado (rompecabezas)