Icositetragón
| Icositetragon regular | |
|---|---|
 Un icositetragón regular | |
| Tipo | Polígono regular |
| Aristas y vértices | 24 |
| Símbolo de Schläfli | {24}, t{12}, tt{6}, ttt{3} |
| Diagramas de Coxeter-Dynkin |        |
| Grupo de simetría | Diédrico (D 24 ), orden 2×24 |
| Angulo interno ( grados ) | 165° |
| Propiedades | Convexo , cíclico , equilátero , isogonal , isotoxal |
| Polígono dual | Ser |
En geometría , un icositetragono (o icosikaitetragono ) o 24-gono es un polígono de veinticuatro lados . La suma de los ángulos interiores de cualquier icositetragono es 3960 grados.
Icositetragon regular
El icositetragono regular se representa mediante el símbolo de Schläfli {24} y también se puede construir como un dodecágono truncado , t{12}, o un hexágono dos veces truncado , tt{6}, o un triángulo tres veces truncado, ttt{3}.
Un ángulo interior en un icositetragono regular es 165°, lo que significa que un ángulo exterior sería 15°.
El área de un icositetragono regular es: (con t = longitud del borde)
El icositetragono apareció en la aproximación poligonal de Arquímedes de pi , junto con el hexágono (6-gono), el dodecágono (12-gono), el tetracontaoctágono (48-gono) y el eneacontahexágono (96-gono).
Construcción
Como 24 = 2 3 × 3, un icositetragono regular se puede construir utilizando un trisector de ángulos . [1] Como un dodecágono truncado , se puede construir mediante una bisección de arista de un dodecágono regular.
Simetría

El icositetragón regular tiene simetría Dih 24 , orden 48. Hay 7 simetrías diédricas de subgrupo: (Dih 12 , Dih 6 , Dih 3 ) y (Dih 8 , Dih 4 , Dih 2 Dih 1 ) y 8 simetrías de grupo cíclicas : ( Z24 , Z12 , Z6 , Z3 ) , y (Z8 , Z4 , Z2 , Z1 ) .
Estas 16 simetrías se pueden ver en 22 simetrías distintas en el icositetragono. John Conway las etiqueta con una letra y un orden de grupo. [2] La simetría completa de la forma regular es r48 y ninguna simetría está etiquetada como a1 . Las simetrías diedras se dividen dependiendo de si pasan por vértices ( d para diagonales) o aristas ( p para perpendiculares), e i cuando las líneas de reflexión pasan por aristas y vértices. Las simetrías cíclicas en la columna del medio están etiquetadas como g para sus órdenes de giro centrales.
Cada simetría de subgrupo permite uno o más grados de libertad para formas irregulares. Solo el subgrupo g24 no tiene grados de libertad pero puede verse como aristas dirigidas .
Disección
 regular |  Isotoxal |
Coxeter afirma que cada zonógono (un 2 m -gono cuyos lados opuestos son paralelos y de igual longitud) puede diseccionarse en m ( m -1)/2 paralelogramos. [3] En particular, esto es cierto para polígonos regulares con un número uniforme de lados, en cuyo caso los paralelogramos son todos rombos. Para el icositetragono regular , m = 12, y puede dividirse en 66: 6 cuadrados y 5 conjuntos de 12 rombos. Esta descomposición se basa en una proyección de polígono de Petrie de un cubo de 12 .
 12 cubos |  |  |  | 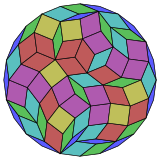 |
Polígonos relacionados

Un triángulo regular, un octágono y un icositetragono pueden llenar completamente un vértice plano.
Un icositetragrama es un polígono estrellado de 24 lados . Existen 3 formas regulares dadas por los símbolos de Schläfli : {24/5}, {24/7} y {24/11}. También existen 7 figuras estelares regulares que utilizan la misma disposición de vértices : 2{12}, 3{8}, 4{6}, 6{4}, 8{3}, 3{8/3} y 2{12/5}.
| Icositetragramas como polígonos estelares y figuras estelares | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Forma | Polígono convexo | Compuestos | Polígono estrellado | Compuesto | |||||||
| Imagen |  {24/1}={24} |  {24/2}=2{12} |  {24/3}=3{8} |  {24/4}=4{6} |  {24/5} |  {24/6}=6{4} | |||||
| Angulo interior | 165° | 150° | 135° | 120° | 105° | 90° | |||||
| Forma | Polígono estrellado | Compuestos | Polígono estrellado | Compuesto | |||||||
| Imagen |  {24 horas al día, 7 días a la semana} |  {24/8}=8{3} |  {24/9}=3{8/3} |  {24/10}=2{12/5} |  {24/11} |  {24/12}=12{2} | |||||
| Angulo interior | 75° | 60° | 45° | 30° | 15° | 0° | |||||
También existen icositetragramas isogonales construidos como truncamientos más profundos del dodecágono regular {12} y del dodecagrama {12/5}. Estos también generan dos cuasitruncamientos: t{12/11}={24/11} y t{12/7}={24/7}. [4]
| Truncamientos isogonales de dodecágonos y dodecagramas regulares | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Cuasiregular | Isogonal | Cuasiregular | |||||||||
 t{12}={24} |  |  |  |  |  |  t{12/11}={24/11} | |||||
 t{12/5}={24/5} |  |  |  |  |  |  t{12/7}={24/7} | |||||
Icositetragon sesgado
Un icositetragono oblicuo es un polígono oblicuo con 24 vértices y aristas pero que no se encuentran en el mismo plano. El interior de un icositetragono de este tipo no suele estar definido. Un icositetragono oblicuo en zigzag tiene vértices que se alternan entre dos planos paralelos.
Un icositetragono oblicuo regular es transitivo en vértices con longitudes de aristas iguales. En 3 dimensiones será un icositetragono oblicuo en zigzag y se puede ver en los vértices y aristas laterales de un antiprisma dodecagonal con la misma simetría D 12d , [2 + ,24], orden 48. El antiprisma dodecagrámico, s{2,24/5} y el antiprisma dodecagrámico cruzado, s{2,24/7} también tienen dodecágonos oblicuos regulares.
Polígonos de Petrie
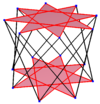
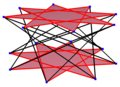
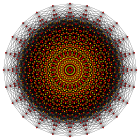
El icositetragono regular es el polígono de Petrie para muchos politopos de dimensiones superiores, vistos como proyecciones ortogonales en planos de Coxeter , incluidos:
| 2º piso 4 | ||
|---|---|---|
 Bittruncadas de 24 celdas |  Runcinado de 24 celdas |  Omnitruncado de 24 celdas |
| E8 | ||
|---|---|---|
 4 21 |  2 41 | 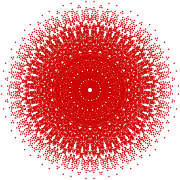 1 42 |
Referencias
- ^ Polígono construible
- ^ John H. Conway , Heidi Burgiel, Chaim Goodman-Strauss , (2008) Las simetrías de las cosas, ISBN 978-1-56881-220-5 (Capítulo 20, Símbolos generalizados de Schaefli, Tipos de simetría de un polígono, págs. 275-278)
- ^ Coxeter , Recreaciones matemáticas y ensayos, decimotercera edición, pág. 141
- ^ El lado más luminoso de las matemáticas: Actas de la Conferencia en memoria de Eugène Strens sobre matemáticas recreativas y su historia (1994), Metamorfosis de polígonos , Branko Grünbaum
- Weisstein, Eric W. "Icositetragon". MundoMatemático .
- Nombramiento de polígonos y poliedros
- Polígono (simple)
- icosatetragón