Viscosidad

Viscosidad
Simulación de líquidos con diferentes viscosidades. El líquido de la izquierda tiene una viscosidad menor que el de la derecha.
Símbolos comunes	η , μ
Derivaciones de otras magnitudes	μ = G · t
Dimensión	${\displaystyle {\mathsf {M}}{\mathsf {L}}^{-1}{\mathsf {T}}^{-1}}$

Parte de una serie sobre
Mecánica de medios continuos
${\displaystyle J=-D{\frac {d\varphi }{dx}}}$ Leyes de difusión de Fick
Leyes Conservaciones Masa Impulso Energía Desigualdades Clausius-Duhem (entropía)
Mecánica de sólidos Deformación Elasticidad lineal Plasticidad Ley de Hooke Estrés Cepa Deformación finita Deformación infinitesimal Compatibilidad Doblado Mecánica de contacto friccional Teoría de la falla del material Mecánica de fracturas
Mecánica de fluidos Fluidos Estática  · Dinámica Archimedes' principle · Bernoulli's principle Navier–Stokes equations Poiseuille equation · Pascal's law Viscosity (Newtonian · non-Newtonian) Buoyancy · Mixing · Pressure Liquids Adhesion Capillary action Chromatography Cohesion (chemistry) Surface tension Gases Atmosphere Boyle's law Charles's law Combined gas law Fick's law Gay-Lussac's law Graham's law Plasma
Rheology Viscoelasticity Rheometry Rheometer Smart fluids Electrorheological Magnetorheological Ferrofluids
Scientists Bernoulli Boyle Cauchy Charles Euler Fick Gay-Lussac Graham Hooke Newton Navier Noll Pascal Stokes Truesdell
v t e

La viscosidad de un fluido es una medida de su resistencia a la deformación a una velocidad determinada. ^[1] En el caso de los líquidos, corresponde al concepto informal de "espesor": por ejemplo, el jarabe tiene una viscosidad mayor que el agua . ^[2] La viscosidad se define científicamente como una fuerza multiplicada por un tiempo dividido por un área. Por lo tanto, sus unidades del SI son newton-segundos por metro cuadrado o pascal-segundos. ^[1]

La viscosidad cuantifica la fuerza de fricción interna entre capas adyacentes de fluido que están en movimiento relativo. ^[1] Por ejemplo, cuando un fluido viscoso se fuerza a pasar a través de un tubo, fluye más rápidamente cerca de la línea central del tubo que cerca de sus paredes. ^[3] Los experimentos muestran que se necesita cierta tensión (como una diferencia de presión entre los dos extremos del tubo) para mantener el flujo. Esto se debe a que se requiere una fuerza para superar la fricción entre las capas del fluido que están en movimiento relativo. Para un tubo con una tasa de flujo constante, la intensidad de la fuerza compensatoria es proporcional a la viscosidad del fluido.

En general, la viscosidad depende del estado del fluido, como su temperatura, presión y velocidad de deformación. Sin embargo, la dependencia de algunas de estas propiedades es insignificante en ciertos casos. Por ejemplo, la viscosidad de un fluido newtoniano no varía significativamente con la velocidad de deformación.

La viscosidad cero (sin resistencia al esfuerzo cortante ) se observa solo a temperaturas muy bajas en los superfluidos ; de lo contrario, la segunda ley de la termodinámica requiere que todos los fluidos tengan una viscosidad positiva. ^{[4] [5]} Un fluido que tiene viscosidad cero (no viscoso) se denomina ideal o no viscoso .

Para la viscosidad de los fluidos no newtonianos , existen flujos pseudoplásticos , plásticos y dilatantes que son independientes del tiempo, y hay flujos tixotrópicos y reopécticos que son dependientes del tiempo.

La palabra "viscosidad" se deriva del latín viscum (" muérdago "). Viscum también se refería a un pegamento viscoso derivado de las bayas de muérdago. ^[6]

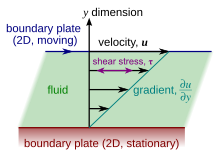
En la ciencia y la ingeniería de materiales , suele haber interés en comprender las fuerzas o tensiones implicadas en la deformación de un material. Por ejemplo, si el material fuera un simple resorte, la respuesta la daría la ley de Hooke , que dice que la fuerza experimentada por un resorte es proporcional a la distancia desplazada desde el equilibrio. Las tensiones que se pueden atribuir a la deformación de un material a partir de un estado de reposo se denominan tensiones elásticas . En otros materiales, existen tensiones que se pueden atribuir a la tasa de deformación a lo largo del tiempo . Estas se denominan tensiones viscosas. Por ejemplo, en un fluido como el agua, las tensiones que surgen del cizallamiento del fluido no dependen de la distancia que se ha cortado el fluido; más bien, dependen de la rapidez con la que se produce el cizallamiento.

La viscosidad es la propiedad del material que relaciona las tensiones viscosas en un material con la tasa de cambio de una deformación (la tasa de deformación). Aunque se aplica a flujos generales, es fácil de visualizar y definir en un flujo de corte simple, como un flujo de Couette plano .

En el flujo de Couette, un fluido está atrapado entre dos placas infinitamente grandes, una fija y otra en movimiento paralelo a velocidad constante (ver ilustración a la derecha). Si la velocidad de la placa superior es lo suficientemente baja (para evitar turbulencias), entonces en estado estacionario las partículas de fluido se mueven paralelas a ella, y su velocidad varía desde abajo hasta arriba. ^[7] Cada capa de fluido se mueve más rápido que la que está justo debajo de ella, y la fricción entre ellas da lugar a una fuerza que resiste su movimiento relativo. En particular, el fluido aplica sobre la placa superior una fuerza en la dirección opuesta a su movimiento, y una fuerza igual pero opuesta sobre la placa inferior. Por lo tanto, se requiere una fuerza externa para mantener la placa superior en movimiento a velocidad constante.${\displaystyle u}$${\displaystyle 0}$${\displaystyle u}$

En muchos fluidos, se observa que la velocidad de flujo varía linealmente desde cero en la parte inferior hasta la parte superior. Además, se ha descubierto que la magnitud de la fuerza, , que actúa sobre la placa superior es proporcional a la velocidad y al área de cada placa, e inversamente proporcional a su separación : ${\displaystyle u}$${\displaystyle F}$${\displaystyle u}$${\displaystyle A}$${\displaystyle y}$

${\displaystyle F=\mu A{\frac {u}{y}}.}$

El factor de proporcionalidad es la viscosidad dinámica del fluido, a menudo denominada simplemente viscosidad . Se denota con la letra griega mu ( μ ). La viscosidad dinámica tiene las dimensiones , por lo que se expresa en unidades del SI y en unidades derivadas :${\displaystyle \mathrm {(mass/length)/time} }$

${\displaystyle [\mu ]={\frac {\rm {kg}}{\rm {m{\cdot }s}}}={\frac {\rm {N}}{\rm {m^{2}}}}{\cdot }{\rm {s}}={\rm {Pa{\cdot }s}}=}$ presión multiplicada por el tiempo energía por unidad de volumen multiplicada por el tiempo.${\displaystyle =}$

La razón antes mencionada se denomina tasa de deformación por corte o velocidad de corte y es la derivada de la velocidad del fluido en la dirección paralela al vector normal de las placas (ver ilustraciones a la derecha). Si la velocidad no varía linealmente con , entonces la generalización apropiada es:${\displaystyle u/y}$${\displaystyle y}$

${\displaystyle \tau =\mu {\frac {\partial u}{\partial y}},}$

donde , y es la velocidad de corte local. Esta expresión se conoce como la ley de viscosidad de Newton . En flujos de corte con simetría plana, es lo que define . Es un caso especial de la definición general de viscosidad (ver más abajo), que se puede expresar en forma libre de coordenadas.${\displaystyle \tau =F/A}$${\displaystyle \partial u/\partial y}$ ${\displaystyle \mu }$

El uso de la letra griega mu ( ) para la viscosidad dinámica (a veces también llamada viscosidad absoluta ) es común entre los ingenieros mecánicos y químicos , así como entre los matemáticos y los físicos. ^{[8] [9] [10]} Sin embargo, la letra griega eta ( ) también es utilizada por químicos, físicos y la IUPAC . ^[11] La viscosidad a veces también se denomina viscosidad de cizallamiento . Sin embargo, al menos un autor desaconseja el uso de esta terminología, señalando que puede aparecer en flujos sin cizallamiento además de en flujos con cizallamiento. ^[12]${\displaystyle \mu }$${\displaystyle \eta }$${\displaystyle \mu }$${\displaystyle \mu }$

En dinámica de fluidos, a veces es más apropiado trabajar en términos de viscosidad cinemática (a veces también llamada difusividad del momento ), definida como la relación entre la viscosidad dinámica ( μ ) y la densidad del fluido ( ρ ). Generalmente se denota con la letra griega nu ( ν ):

${\displaystyle \nu ={\frac {\mu }{\rho }},}$

y tiene las dimensiones , por lo que da como resultado las unidades SI y las unidades derivadas :${\displaystyle \mathrm {(length)^{2}/time} }$

${\displaystyle [\nu ]=\mathrm {\frac {m^{2}}{s}} =\mathrm {{\frac {N{\cdot }m}{kg}}{\cdot }s} =\mathrm {{\frac {J}{kg}}{\cdot }s} =}$ energía específica multiplicada por el tiempo energía por unidad de masa multiplicada por el tiempo.${\displaystyle =}$

En términos muy generales, las tensiones viscosas en un fluido se definen como aquellas resultantes de la velocidad relativa de diferentes partículas del fluido. Como tal, las tensiones viscosas deben depender de gradientes espaciales de la velocidad del flujo. Si los gradientes de velocidad son pequeños, entonces, en una primera aproximación, las tensiones viscosas dependen solo de las primeras derivadas de la velocidad. ^[13] (Para fluidos newtonianos, esto también es una dependencia lineal). En coordenadas cartesianas, la relación general puede escribirse como

${\displaystyle \tau _{ij}=\sum _{k}\sum _{\ell }\mu _{ijk\ell }{\frac {\partial v_{k}}{\partial r_{\ell }}},}$

donde es un tensor de viscosidad que mapea el tensor de gradiente de velocidad sobre el tensor de tensión viscosa . ^[14] Dado que los índices en esta expresión pueden variar de 1 a 3, hay 81 "coeficientes de viscosidad" en total. Sin embargo, suponiendo que el tensor de viscosidad de rango 2 es isotrópico, estos 81 coeficientes se reducen a tres parámetros independientes , , :${\displaystyle \mu _{ijk\ell }}$${\displaystyle \partial v_{k}/\partial r_{\ell }}$${\displaystyle \tau _{ij}}$${\displaystyle \mu _{ijkl}}$${\displaystyle \alpha }$${\displaystyle \beta }$${\displaystyle \gamma }$

${\displaystyle \mu _{ijk\ell }=\alpha \delta _{ij}\delta _{k\ell }+\beta \delta _{ik}\delta _{j\ell }+\gamma \delta _{i\ell }\delta _{jk},}$

y además, se supone que no pueden surgir fuerzas viscosas cuando el fluido está experimentando una rotación simple de cuerpo rígido, por lo que , dejando solo dos parámetros independientes. ^[13] La descomposición más habitual es en términos de la viscosidad estándar (escalar) y la viscosidad volumétrica tal que y . En notación vectorial esto aparece como:${\displaystyle \beta =\gamma }$${\displaystyle \mu }$ ${\displaystyle \kappa }$${\displaystyle \alpha =\kappa -{\tfrac {2}{3}}\mu }$${\displaystyle \beta =\gamma =\mu }$

${\displaystyle {\boldsymbol {\tau }}=\mu \left[\nabla \mathbf {v} +(\nabla \mathbf {v} )^{\mathrm {T} }\right]-\left({\frac {2}{3}}\mu -\kappa \right)(\nabla \cdot \mathbf {v} )\mathbf {\delta } ,}$

donde es el tensor unitario. ^{[12] [15]} Esta ecuación puede considerarse como una forma generalizada de la ley de viscosidad de Newton.${\displaystyle \mathbf {\delta } }$

La viscosidad volumétrica (también llamada viscosidad en masa) expresa un tipo de fricción interna que resiste la compresión o expansión sin cizallamiento de un fluido. El conocimiento de con frecuencia no es necesario en problemas de dinámica de fluidos. Por ejemplo, un fluido incompresible satisface y, por lo tanto, el término que contiene se elimina. Además, a menudo se supone que es insignificante para los gases, ya que está en un gas ideal monatómico . ^[12] Una situación en la que puede ser importante es el cálculo de la pérdida de energía en ondas de sonido y de choque , descritas por la ley de atenuación del sonido de Stokes , ya que estos fenómenos involucran expansiones y compresiones rápidas.${\displaystyle \kappa }$${\displaystyle \nabla \cdot \mathbf {v} =0}$${\displaystyle \kappa }$${\displaystyle \kappa }$${\displaystyle 0}$ ${\displaystyle \kappa }$

Las ecuaciones que definen la viscosidad no son leyes fundamentales de la naturaleza, por lo que su utilidad, así como los métodos para medirla o calcularla, deben establecerse utilizando medios separados. Un problema potencial es que la viscosidad depende, en principio, del estado microscópico completo del fluido, que abarca las posiciones y los momentos de cada partícula en el sistema. ^[16] Esta información altamente detallada normalmente no está disponible en sistemas realistas. Sin embargo, en ciertas condiciones se puede demostrar que la mayor parte de esta información es insignificante. En particular, para fluidos newtonianos cerca del equilibrio y lejos de los límites (estado en masa), la viscosidad depende solo de campos macroscópicos dependientes del espacio y el tiempo (como la temperatura y la densidad) que definen el equilibrio local. ^{[16] [17]}

Sin embargo, la viscosidad puede tener una dependencia no despreciable de varias propiedades del sistema, como la temperatura, la presión y la amplitud y frecuencia de cualquier fuerza externa. Por lo tanto, las mediciones precisas de la viscosidad solo se definen con respecto a un estado de fluido específico. ^[18] Para estandarizar las comparaciones entre experimentos y modelos teóricos, los datos de viscosidad a veces se extrapolan a casos límite ideales, como el límite de cizallamiento cero o (para gases) el límite de densidad cero .

La teoría del transporte proporciona una interpretación alternativa de la viscosidad en términos de transporte de momento: la viscosidad es la propiedad material que caracteriza el transporte de momento dentro de un fluido, así como la conductividad térmica caracteriza el transporte de calor y la difusividad (de masa) caracteriza el transporte de masa. ^[19] Esta perspectiva está implícita en la ley de viscosidad de Newton, , porque la tensión cortante tiene unidades equivalentes a un flujo de momento , es decir, momento por unidad de tiempo por unidad de área. Por lo tanto, puede interpretarse como la especificación del flujo de momento en la dirección de una capa de fluido a la siguiente. Según la ley de viscosidad de Newton, este flujo de momento ocurre a través de un gradiente de velocidad, y la magnitud del flujo de momento correspondiente está determinada por la viscosidad.${\displaystyle \tau =\mu (\partial u/\partial y)}$${\displaystyle \tau }$${\displaystyle \tau }$${\displaystyle y}$

La analogía con la transferencia de calor y masa se puede hacer explícita. Así como el calor fluye de alta temperatura a baja temperatura y la masa fluye de alta densidad a baja densidad, el momento fluye de alta velocidad a baja velocidad. Todos estos comportamientos se describen mediante expresiones compactas, llamadas relaciones constitutivas , cuyas formas unidimensionales se dan aquí:

${\displaystyle {\begin{aligned}\mathbf {J} &=-D{\frac {\partial \rho }{\partial x}}&&{\text{(Fick's law of diffusion)}}\\[5pt]\mathbf {q} &=-k_{t}{\frac {\partial T}{\partial x}}&&{\text{(Fourier's law of heat conduction)}}\\[5pt]\tau &=\mu {\frac {\partial u}{\partial y}}&&{\text{(Newton's law of viscosity)}}\end{aligned}}}$

donde es la densidad, y son los flujos de masa y calor, y y son la difusividad de masa y la conductividad térmica. ^[20] El hecho de que el transporte de masa, momento y energía (calor) se encuentren entre los procesos más relevantes en la mecánica del medio continuo no es una coincidencia: se encuentran entre las pocas cantidades físicas que se conservan a nivel microscópico en las colisiones entre partículas. Por lo tanto, en lugar de estar dictadas por la rápida y compleja escala de tiempo de interacción microscópica, su dinámica ocurre en escalas de tiempo macroscópicas, como se describe en las diversas ecuaciones de la teoría del transporte y la hidrodinámica.${\displaystyle \rho }$${\displaystyle \mathbf {J} }$${\displaystyle \mathbf {q} }$${\displaystyle D}$${\displaystyle k_{t}}$

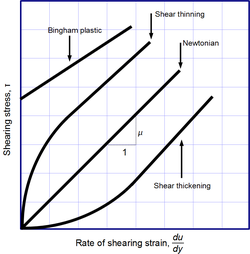
La ley de viscosidad de Newton no es una ley fundamental de la naturaleza, sino más bien una ecuación constitutiva (como la ley de Hooke , la ley de Fick y la ley de Ohm ) que sirve para definir la viscosidad . Su forma está motivada por experimentos que muestran que para una amplia gama de fluidos, es independiente de la velocidad de deformación. Dichos fluidos se denominan newtonianos . Los gases , el agua y muchos líquidos comunes pueden considerarse newtonianos en condiciones y contextos ordinarios. Sin embargo, hay muchos fluidos no newtonianos que se desvían significativamente de este comportamiento. Por ejemplo:${\displaystyle \mu }$${\displaystyle \mu }$

• Líquidos espesantes por cizallamiento (dilatantes), cuya viscosidad aumenta con la velocidad de la deformación por cizallamiento.
• Líquidos pseudoplásticos , cuya viscosidad disminuye con la velocidad de la deformación por cizallamiento.
• Líquidos tixotrópicos , que se vuelven menos viscosos con el tiempo cuando se agitan, se sacuden o se someten a alguna otra tensión.
• Líquidos reopécticos que se vuelven más viscosos con el tiempo cuando se agitan, se sacuden o se someten a alguna otra tensión.
• Plásticos de Bingham que se comportan como un sólido bajo tensiones bajas pero fluyen como un fluido viscoso bajo tensiones altas.

El coeficiente de Trouton es la relación entre la viscosidad extensional y la viscosidad de cizallamiento . Para un fluido newtoniano, el coeficiente de Trouton es 3. ^{[21] [22]} Los líquidos pseudoplásticos se describen muy comúnmente, pero de manera engañosa, como tixotrópicos. ^[23]

La viscosidad también puede depender del estado físico del fluido (temperatura y presión) y de otros factores externos . En el caso de los gases y otros fluidos compresibles , depende de la temperatura y varía muy lentamente con la presión. La viscosidad de algunos fluidos puede depender de otros factores. Un fluido magnetorreológico , por ejemplo, se vuelve más espeso cuando se lo somete a un campo magnético , posiblemente hasta el punto de comportarse como un sólido.

Las fuerzas viscosas que surgen durante el flujo de un fluido son distintas de las fuerzas elásticas que se producen en un sólido en respuesta a tensiones de corte, compresión o extensión. Mientras que en estas últimas la tensión es proporcional a la cantidad de deformación por corte, en un fluido es proporcional a la velocidad de deformación a lo largo del tiempo. Por esta razón, James Clerk Maxwell utilizó el término elasticidad fugitiva para la viscosidad del fluido.

Sin embargo, muchos líquidos (incluida el agua) reaccionarán brevemente como sólidos elásticos cuando se los somete a una tensión repentina. Por el contrario, muchos "sólidos" (incluso el granito ) fluirán como líquidos, aunque muy lentamente, incluso bajo una tensión arbitrariamente pequeña. ^[24] Estos materiales se describen mejor como viscoelásticos , es decir, que poseen tanto elasticidad (reacción a la deformación) como viscosidad (reacción a la velocidad de deformación).

Los sólidos viscoelásticos pueden presentar tanto viscosidad de cizallamiento como viscosidad volumétrica. La viscosidad extensional es una combinación lineal de las viscosidades de cizallamiento y volumétrica que describe la reacción de un material elástico sólido a la elongación. Se utiliza ampliamente para caracterizar polímeros.

En geología , los materiales terrestres que presentan una deformación viscosa al menos tres órdenes de magnitud mayor que su deformación elástica a veces se denominan reidas . ^[25]

La viscosidad se mide con distintos tipos de viscosímetros y reómetros . El control estricto de la temperatura del fluido es esencial para obtener mediciones precisas, en particular en materiales como los lubricantes, cuya viscosidad puede duplicarse con un cambio de tan solo 5 °C. Un reómetro se utiliza para fluidos que no se pueden definir con un único valor de viscosidad y, por lo tanto, requieren que se establezcan y midan más parámetros que en el caso de un viscosímetro. ^[26]

En algunos fluidos, la viscosidad es constante en un amplio rango de velocidades de corte ( fluidos newtonianos ). Los fluidos sin una viscosidad constante ( fluidos no newtonianos ) no pueden describirse con un solo número. Los fluidos no newtonianos presentan una variedad de correlaciones diferentes entre la tensión de corte y la velocidad de corte.

Uno de los instrumentos más comunes para medir la viscosidad cinemática es el viscosímetro capilar de vidrio.

En las industrias de recubrimiento , la viscosidad se puede medir con una copa en la que se mide el tiempo de eflujo . Existen varios tipos de copas, como la copa Zahn y la copa de viscosidad Ford , y el uso de cada tipo varía principalmente según la industria.

El viscosímetro Stormer , que también se utiliza en recubrimientos, emplea una rotación basada en la carga para determinar la viscosidad. La viscosidad se expresa en unidades Krebs (KU), que son exclusivas de los viscosímetros Stormer.

Los viscosímetros vibratorios también se pueden utilizar para medir la viscosidad. Los viscosímetros resonantes o vibracionales funcionan creando ondas de corte dentro del líquido. En este método, el sensor se sumerge en el líquido y se hace resonar a una frecuencia específica. A medida que la superficie del sensor atraviesa el líquido, se pierde energía debido a su viscosidad. Esta energía disipada se mide y se convierte en una lectura de viscosidad. Una viscosidad más alta provoca una mayor pérdida de energía. ^{[ cita requerida ]}

La viscosidad extensional se puede medir con varios reómetros que aplican tensión extensional .

La viscosidad volumétrica se puede medir con un reómetro acústico .

La viscosidad aparente es un cálculo derivado de pruebas realizadas en el fluido de perforación utilizado en el desarrollo de pozos de petróleo o gas. Estos cálculos y pruebas ayudan a los ingenieros a desarrollar y mantener las propiedades del fluido de perforación según las especificaciones requeridas.

La nanoviscosidad (viscosidad detectada por nanosondas) se puede medir mediante espectroscopia de correlación de fluorescencia . ^[27]

La unidad SI de viscosidad dinámica es el newton -segundo por metro cuadrado (N·s/m ² ), también expresado frecuentemente en las formas equivalentes pascal - segundo (Pa·s), kilogramo por metro por segundo (kg·m ⁻¹ ·s ⁻¹ ) y poiseuille (Pl). La unidad CGS es el poise (P, o g·cm ⁻¹ ·s ⁻¹ = 0,1 Pa·s), ^[28] llamado así por Jean Léonard Marie Poiseuille . Se expresa comúnmente, particularmente en las normas ASTM , como centipoise (cP). El centipoise es conveniente porque la viscosidad del agua a 20 °C es de aproximadamente 1 cP, y un centipoise es igual al milipascal segundo SI (mPa·s).

La unidad SI de viscosidad cinemática es el metro cuadrado por segundo (m ² /s), mientras que la unidad CGS para la viscosidad cinemática es el stokes (St, o cm ² ·s ⁻¹ = 0,0001 m ² ·s ⁻¹ ), llamado así por Sir George Gabriel Stokes . ^[29] En el uso estadounidense, stoke se utiliza a veces como forma singular. El submúltiplo centistokes (cSt) se utiliza a menudo en su lugar, 1 cSt = 1 mm ² ·s ⁻¹  = 10 ⁻⁶  m ² ·s ⁻¹ . 1 cSt es 1 cP dividido por 1000 kg/m^3, cerca de la densidad del agua. La viscosidad cinemática del agua a 20 °C es de aproximadamente 1 cSt.

Los sistemas de unidades habituales de EE. UU., o Imperial , que se utilizan con más frecuencia son el sistema gravitacional británico (BG) y el sistema de ingeniería inglés (EE). En el sistema BG, la viscosidad dinámica tiene unidades de libras -segundos por pie cuadrado (lb·s/ft ² ), y en el sistema EE tiene unidades de libras-fuerza -segundos por pie cuadrado (lbf·s/ft ² ). La libra y la libra-fuerza son equivalentes; los dos sistemas difieren solo en cómo se definen la fuerza y ​​la masa. En el sistema BG, la libra es una unidad básica a partir de la cual la unidad de masa (el slug ) se define mediante la Segunda Ley de Newton , mientras que en el sistema EE las unidades de fuerza y ​​masa (la libra-fuerza y ​​la libra-masa respectivamente) se definen independientemente a través de la Segunda Ley utilizando la constante de proporcionalidad g _c .

La viscosidad cinemática tiene unidades de pies cuadrados por segundo (ft ² /s) en los sistemas BG y EE.

Las unidades no estándar incluyen el reyn (lbf·s/in ² ), una unidad británica de viscosidad dinámica. ^[30] En la industria automotriz, el índice de viscosidad se utiliza para describir el cambio de viscosidad con la temperatura.

El recíproco de la viscosidad es la fluidez , que suele simbolizarse con o , según la convención utilizada, medida en poises recíprocos (P ⁻¹ , o cm · s · g ⁻¹ ), a veces llamado rhe . La fluidez rara vez se utiliza en la práctica de la ingeniería . ^{[ cita requerida ]}${\displaystyle \phi =1/\mu }$${\displaystyle F=1/\mu }$

En un tiempo, la industria petrolera dependía de la medición de la viscosidad cinemática por medio del viscosímetro Saybolt y de la expresión de la viscosidad cinemática en unidades de segundos universales Saybolt (SUS). ^[31] A veces se utilizan otras abreviaturas como SSU ( segundos universales Saybolt ) o SUV ( viscosidad universal Saybolt ). La viscosidad cinemática en centistokes se puede convertir desde SUS según la aritmética y la tabla de referencia proporcionada en ASTM D 2161.

El transporte de momento en los gases está mediado por colisiones moleculares discretas, y en los líquidos por fuerzas de atracción que unen a las moléculas. ^[19] Debido a esto, las viscosidades dinámicas de los líquidos suelen ser mucho mayores que las de los gases. Además, la viscosidad tiende a aumentar con la temperatura en los gases y a disminuir con la temperatura en los líquidos.

Por encima del punto crítico líquido-gas , las fases líquida y gaseosa son reemplazadas por una única fase supercrítica . En este régimen, los mecanismos de transporte de momento se interpolan entre el comportamiento similar al líquido y al gas. Por ejemplo, a lo largo de una isobara supercrítica (superficie de presión constante), la viscosidad cinemática disminuye a baja temperatura y aumenta a alta temperatura, con un mínimo entre ambas. ^{[32] [33]} Una estimación aproximada del valor en el mínimo es

${\displaystyle \nu _{\text{min}}={\frac {1}{4\pi }}{\frac {\hbar }{\sqrt {m_{\text{e}}m}}}}$

donde es la constante de Planck , es la masa del electrón y es la masa molecular. ^[33]${\displaystyle \hbar }$${\displaystyle m_{\text{e}}}$${\displaystyle m}$

En general, sin embargo, la viscosidad de un sistema depende en detalle de cómo interactúan las moléculas que constituyen el sistema, y ​​no hay fórmulas simples pero correctas para ello. Las expresiones exactas más simples son las relaciones de Green-Kubo para la viscosidad de corte lineal o las expresiones de la función de correlación temporal transitoria derivadas por Evans y Morriss en 1988. ^[34] Aunque estas expresiones son exactas, calcular la viscosidad de un fluido denso utilizando estas relaciones actualmente requiere el uso de simulaciones informáticas de dinámica molecular . Se puede lograr un progreso algo mayor para un gas diluido, ya que las suposiciones elementales sobre cómo se mueven e interactúan las moléculas de gas conducen a una comprensión básica de los orígenes moleculares de la viscosidad. Se pueden construir tratamientos más sofisticados mediante el granulado grueso sistemático de las ecuaciones de movimiento de las moléculas de gas. Un ejemplo de dicho tratamiento es la teoría de Chapman-Enskog , que deriva expresiones para la viscosidad de un gas diluido a partir de la ecuación de Boltzmann . ^[17]

Cálculo elemental de la viscosidad de un gas diluido

Consideremos un gas diluido que se mueve en paralelo al eje y con una velocidad que depende únicamente de la coordenada. Para simplificar el análisis, se supone que el gas tiene una temperatura y una densidad uniformes.${\displaystyle x}$${\displaystyle u(y)}$${\displaystyle y}$ Según estos supuestos, la velocidad de una molécula que pasa a través de ella es igual a la velocidad que tenía esa molécula cuando comenzó su recorrido libre medio. Como suele ser pequeña en comparación con las escalas macroscópicas, la velocidad media de una molécula de este tipo tiene la forma${\displaystyle x}$${\displaystyle y=0}$${\displaystyle \lambda }$${\displaystyle \lambda }$${\displaystyle x}$ ${\displaystyle u(0)\pm \alpha \lambda {\frac {du}{dy}}(0),}$ donde es una constante numérica del orden de . (Algunos autores estiman ; [19] [35] por otro lado, un cálculo más cuidadoso para esferas elásticas rígidas da .) A continuación, debido a que la mitad de las moléculas de cada lado se mueven hacia , y lo hacen en promedio con la mitad de la velocidad molecular promedio , el flujo de momento de cada lado es${\displaystyle \alpha }$${\displaystyle 1}$${\displaystyle \alpha =2/3}$${\displaystyle \alpha \simeq 0.998}$${\displaystyle y=0}$ ${\displaystyle (8k_{\text{B}}T/\pi m)^{1/2}}$ ${\displaystyle {\frac {1}{4}}\rho \cdot {\sqrt {\frac {8k_{\text{B}}T}{\pi m}}}\cdot \left(u(0)\pm \alpha \lambda {\frac {du}{dy}}(0)\right).}$ El flujo de momento neto en es la diferencia de los dos:${\displaystyle y=0}$ ${\displaystyle -{\frac {1}{2}}\rho \cdot {\sqrt {\frac {8k_{\text{B}}T}{\pi m}}}\cdot \alpha \lambda {\frac {du}{dy}}(0).}$ Según la definición de viscosidad, este flujo de momento debe ser igual a , lo que conduce a${\displaystyle -\mu {\frac {du}{dy}}(0)}$ ${\displaystyle \mu =\alpha \rho \lambda {\sqrt {\frac {2k_{\text{B}}T}{\pi m}}}.}$

La viscosidad de los gases surge principalmente de la difusión molecular que transporta el momento entre capas de flujo. Un cálculo elemental para un gas diluido a temperatura y densidad da${\displaystyle T}$${\displaystyle \rho }$

${\displaystyle \mu =\alpha \rho \lambda {\sqrt {\frac {2k_{\text{B}}T}{\pi m}}},}$

donde es la constante de Boltzmann , la masa molecular y una constante numérica del orden de . La cantidad , el camino libre medio , mide la distancia promedio que recorre una molécula entre colisiones. Incluso sin conocimiento a priori de , esta expresión tiene implicaciones no triviales. En particular, dado que es típicamente inversamente proporcional a la densidad y aumenta con la temperatura, debería aumentar con la temperatura y ser independiente de la densidad a temperatura fija. De hecho, ambas predicciones persisten en tratamientos más sofisticados y describen con precisión las observaciones experimentales. Por el contrario, la viscosidad del líquido típicamente disminuye con la temperatura. ^{[19] [35]}${\displaystyle k_{\text{B}}}$${\displaystyle m}$${\displaystyle \alpha }$${\displaystyle 1}$${\displaystyle \lambda }$${\displaystyle \alpha }$${\displaystyle \lambda }$${\displaystyle \mu }$

Para esferas elásticas rígidas de diámetro , se puede calcular, obteniéndose${\displaystyle \sigma }$${\displaystyle \lambda }$

${\displaystyle \mu ={\frac {\alpha }{\pi ^{3/2}}}{\frac {\sqrt {k_{\text{B}}mT}}{\sigma ^{2}}}.}$

En este caso es independiente de la temperatura, por lo que . Sin embargo, para modelos moleculares más complicados, depende de la temperatura de una manera no trivial, y los argumentos cinéticos simples como los que se utilizan aquí son inadecuados. Más fundamentalmente, la noción de un camino libre medio se vuelve imprecisa para partículas que interactúan en un rango finito, lo que limita la utilidad del concepto para describir gases del mundo real. ^[36]${\displaystyle \lambda }$${\displaystyle \mu \propto T^{1/2}}$${\displaystyle \lambda }$

Una técnica desarrollada por Sydney Chapman y David Enskog a principios de la década de 1900 permite un cálculo más refinado de . ^[17] Se basa en la ecuación de Boltzmann , que proporciona una descripción estadística de un gas diluido en términos de interacciones intermoleculares. ^[37] La ​​técnica permite un cálculo preciso de para modelos moleculares que son más realistas que las esferas elásticas rígidas, como los que incorporan atracciones intermoleculares. Hacerlo es necesario para reproducir la dependencia de temperatura correcta de , que los experimentos muestran que aumenta más rápidamente que la tendencia predicha para esferas elásticas rígidas. ^[19] De hecho, el análisis de Chapman-Enskog muestra que la dependencia de temperatura predicha se puede ajustar variando los parámetros en varios modelos moleculares. Un ejemplo simple es el modelo de Sutherland, ^[a] que describe esferas elásticas rígidas con atracción mutua débil . En tal caso, la fuerza de atracción se puede tratar de forma perturbativa , lo que conduce a una expresión simple para :${\displaystyle \mu }$${\displaystyle \mu }$${\displaystyle \mu }$${\displaystyle T^{1/2}}$${\displaystyle \mu }$

${\displaystyle \mu ={\frac {5}{16\sigma ^{2}}}\left({\frac {k_{\text{B}}mT}{\pi }}\right)^{\!\!1/2}\ \left(1+{\frac {S}{T}}\right)^{\!\!-1},}$

donde es independiente de la temperatura, estando determinada únicamente por los parámetros de la atracción intermolecular. Para conectar con el experimento, es conveniente reescribir como${\displaystyle S}$

${\displaystyle \mu =\mu _{0}\left({\frac {T}{T_{0}}}\right)^{\!\!3/2}\ {\frac {T_{0}+S}{T+S}},}$

donde es la viscosidad a temperatura . Esta expresión se denomina habitualmente fórmula de Sutherland. ^[38] Si se conoce a partir de experimentos a y al menos otra temperatura, entonces se puede calcular. Las expresiones para obtenidas de esta manera son cualitativamente precisas para varios gases simples. Modelos ligeramente más sofisticados, como el potencial de Lennard-Jones , o el potencial de Mie más flexible , pueden proporcionar una mejor concordancia con los experimentos, pero solo a costa de una dependencia más opaca de la temperatura. Una ventaja adicional de estos potenciales de interacción más complejos es que se pueden utilizar para desarrollar modelos precisos para una amplia variedad de propiedades utilizando los mismos parámetros potenciales. En situaciones en las que hay pocos datos experimentales disponibles, esto hace posible obtener parámetros del modelo a partir del ajuste a propiedades como equilibrios de vapor-líquido de fluido puro , antes de utilizar los parámetros así obtenidos para predecir las viscosidades de interés con una precisión razonable.${\displaystyle \mu _{0}}$${\displaystyle T_{0}}$${\displaystyle \mu }$${\displaystyle T=T_{0}}$${\displaystyle S}$${\displaystyle \mu }$

En algunos sistemas, se debe abandonar el supuesto de simetría esférica , como es el caso de los vapores con moléculas altamente polares como el H ₂ O . En estos casos, el análisis de Chapman-Enskog es significativamente más complicado. ^{[39] [40]}

En el panorama cinético-molecular, una viscosidad volumétrica distinta de cero surge en los gases siempre que existan escalas de tiempo de relajación no despreciables que rijan el intercambio de energía entre la energía traslacional de las moléculas y su energía interna, por ejemplo, rotacional y vibracional . Como tal, la viscosidad volumétrica es para un gas ideal monatómico, en el que la energía interna de las moléculas es despreciable, pero es distinta de cero para un gas como el dióxido de carbono , cuyas moléculas poseen energía tanto rotacional como vibracional. ^{[41] [42]}${\displaystyle 0}$

A diferencia de lo que ocurre con los gases, no existe una imagen simple pero precisa de los orígenes moleculares de la viscosidad en los líquidos.

En el nivel de descripción más simple, el movimiento relativo de las capas adyacentes en un líquido se opone principalmente a las fuerzas moleculares atractivas que actúan a través del límite de las capas. En esta imagen, uno espera (correctamente) que la viscosidad disminuya con el aumento de la temperatura. Esto se debe a que el aumento de la temperatura aumenta el movimiento térmico aleatorio de las moléculas, lo que les hace más fácil superar sus interacciones atractivas. ^[43]

Partiendo de esta visualización, se puede construir una teoría sencilla en analogía con la estructura discreta de un sólido: los grupos de moléculas en un líquido se visualizan como formando "jaulas" que rodean y encierran moléculas individuales. ^[44] Estas jaulas pueden estar ocupadas o desocupadas, y una atracción molecular más fuerte corresponde a jaulas más fuertes. Debido al movimiento térmico aleatorio, una molécula "salta" entre jaulas a una velocidad que varía inversamente con la fuerza de las atracciones moleculares. En equilibrio , estos "saltos" no están sesgados en ninguna dirección. Por otro lado, para que dos capas adyacentes se muevan una con respecto a la otra, los "saltos" deben estar sesgados en la dirección del movimiento relativo. La fuerza necesaria para sostener este movimiento dirigido se puede estimar para una velocidad de corte dada, lo que lleva a

${\displaystyle \mu \approx {\frac {N_{\text{A}}h}{V}}\operatorname {exp} \left(3.8{\frac {T_{\text{b}}}{T}}\right),}$

( 1 )

donde es la constante de Avogadro , es la constante de Planck , es el volumen de un mol de líquido y es el punto de ebullición normal . Este resultado tiene la misma forma que la conocida relación empírica${\displaystyle N_{\text{A}}}$${\displaystyle h}$${\displaystyle V}$${\displaystyle T_{\text{b}}}$

${\displaystyle \mu =Ae^{B/T},}$

( 2 )

donde y son constantes ajustadas a partir de los datos. ^{[44] [45]} Por otra parte, varios autores expresan cautela con respecto a este modelo. Se pueden encontrar errores de hasta un 30% utilizando la ecuación ( 1 ), en comparación con el ajuste de la ecuación ( 2 ) a los datos experimentales. ^[44] Más fundamentalmente, se han criticado los supuestos físicos subyacentes a la ecuación ( 1 ). ^[46] También se ha argumentado que la dependencia exponencial en la ecuación ( 1 ) no necesariamente describe las observaciones experimentales con mayor precisión que las expresiones más simples, no exponenciales. ^{[47] [48]}${\displaystyle A}$${\displaystyle B}$

En vista de estas deficiencias, el desarrollo de un modelo menos ad hoc es una cuestión de interés práctico. Dejando de lado la simplicidad en favor de la precisión, es posible escribir expresiones rigurosas para la viscosidad a partir de las ecuaciones fundamentales del movimiento de las moléculas. Un ejemplo clásico de este enfoque es la teoría de Irving-Kirkwood. ^[49] Por otra parte, dichas expresiones se dan como promedios sobre funciones de correlación de múltiples partículas y, por lo tanto, son difíciles de aplicar en la práctica.

En general, las expresiones derivadas empíricamente (basadas en mediciones de viscosidad existentes) parecen ser el único medio consistentemente confiable para calcular la viscosidad en líquidos. ^[50]

Se ha descubierto que los cambios locales en la estructura atómica observados en líquidos subenfriados al enfriarse por debajo de la temperatura de fusión de equilibrio, ya sea en términos de la función de distribución radial g ( r ) ^[51] o del factor de estructura S ( Q ) ^[52], son directamente responsables de la fragilidad del líquido: desviación de la dependencia de la temperatura de la viscosidad del líquido subenfriado de la ecuación de Arrhenius (2) a través de la modificación de la energía de activación para el flujo viscoso. Al mismo tiempo, los líquidos en equilibrio siguen la ecuación de Arrhenius.

La misma imagen cinético-molecular de un gas monocomponente también se puede aplicar a una mezcla gaseosa. Por ejemplo, en el enfoque de Chapman-Enskog , la viscosidad de una mezcla binaria de gases se puede expresar en términos de las viscosidades de los componentes individuales , sus respectivas fracciones de volumen y las interacciones intermoleculares. ^[17]${\displaystyle \mu _{\text{mix}}}$${\displaystyle \mu _{1,2}}$

En cuanto al gas de un solo componente, la dependencia de los parámetros de las interacciones intermoleculares entra a través de varias integrales de colisión que pueden no ser expresables en forma cerrada . Para obtener expresiones utilizables para las que coincidan razonablemente con los datos experimentales, las integrales de colisión se pueden calcular numéricamente o a partir de correlaciones. ^[53] En algunos casos, las integrales de colisión se consideran parámetros de ajuste y se ajustan directamente a los datos experimentales. ^[54] Este es un enfoque común en el desarrollo de ecuaciones de referencia para viscosidades en fase gaseosa. Un ejemplo de dicho procedimiento es el enfoque de Sutherland para el gas de un solo componente, analizado anteriormente.${\displaystyle \mu _{\text{mix}}}$${\displaystyle \mu _{\text{mix}}}$

Se ha demostrado que para mezclas de gases que consisten en moléculas simples, la teoría revisada de Enskog representa con precisión la dependencia de la viscosidad tanto de la densidad como de la temperatura en un amplio rango de condiciones. ^{[55] [53]}

En el caso de los líquidos puros, la viscosidad de una mezcla de líquidos es difícil de predecir a partir de principios moleculares. Un método consiste en extender la teoría de la "jaula" molecular presentada anteriormente a un líquido puro. Esto se puede hacer con distintos niveles de sofisticación. Una expresión resultante de dicho análisis es la ecuación de Lederer-Roegiers para una mezcla binaria:

${\displaystyle \ln \mu _{\text{blend}}={\frac {x_{1}}{x_{1}+\alpha x_{2}}}\ln \mu _{1}+{\frac {\alpha x_{2}}{x_{1}+\alpha x_{2}}}\ln \mu _{2},}$

donde es un parámetro empírico, y y son las respectivas fracciones molares y viscosidades de los líquidos componentes. ^[56]${\displaystyle \alpha }$${\displaystyle x_{1,2}}$${\displaystyle \mu _{1,2}}$

Dado que la mezcla es un proceso importante en las industrias de lubricantes y aceites, existe una variedad de ecuaciones empíricas y patentadas para predecir la viscosidad de una mezcla. ^[56]

Según el soluto y el rango de concentración, una solución acuosa de electrolitos puede tener una viscosidad mayor o menor que la del agua pura a la misma temperatura y presión. Por ejemplo, una solución salina ( cloruro de sodio ) al 20 % tiene una viscosidad 1,5 veces superior a la del agua pura, mientras que una solución de yoduro de potasio al 20 % tiene una viscosidad aproximadamente 0,91 veces superior a la del agua pura.

Un modelo idealizado de soluciones electrolíticas diluidas conduce a la siguiente predicción para la viscosidad de una solución: ^[57]${\displaystyle \mu _{s}}$

${\displaystyle {\frac {\mu _{s}}{\mu _{0}}}=1+A{\sqrt {c}},}$

donde es la viscosidad del disolvente, es la concentración y es una constante positiva que depende tanto de las propiedades del disolvente como del soluto. Sin embargo, esta expresión solo es válida para soluciones muy diluidas, que tengan menos de 0,1 mol/L. ^[58] Para concentraciones más altas, son necesarios términos adicionales que tengan en cuenta correlaciones moleculares de orden superior:${\displaystyle \mu _{0}}$${\displaystyle c}$${\displaystyle A}$${\displaystyle c}$

${\displaystyle {\frac {\mu _{s}}{\mu _{0}}}=1+A{\sqrt {c}}+Bc+Cc^{2},}$

donde y se ajustan a partir de los datos. En particular, un valor negativo de puede explicar la disminución de la viscosidad observada en algunas soluciones. Los valores estimados de estas constantes se muestran a continuación para el cloruro de sodio y el yoduro de potasio a una temperatura de 25 °C (mol = mol , L = litro ). ^[57]${\displaystyle B}$${\displaystyle C}$${\displaystyle B}$

Sustancia disoluta	${\displaystyle A}$(mol -1/2 L 1/2 )	${\displaystyle B}$(mol -1 L)	${\displaystyle C}$(mol -2 L 2 )
Cloruro de sodio (NaCl)	0,0062	0,0793	0,0080
Yoduro de potasio (KI)	0,0047	-0,0755	0.0000

En una suspensión de partículas sólidas (por ejemplo, esferas de tamaño micrométrico suspendidas en aceite), una viscosidad efectiva se puede definir en términos de componentes de tensión y deformación que se promedian sobre un volumen grande en comparación con la distancia entre las partículas suspendidas, pero pequeño con respecto a las dimensiones macroscópicas. ^[59] Tales suspensiones generalmente exhiben un comportamiento no newtoniano. Sin embargo, para sistemas diluidos en flujos constantes, el comportamiento es newtoniano y las expresiones para se pueden derivar directamente de la dinámica de partículas. En un sistema muy diluido, con fracción de volumen , se pueden ignorar las interacciones entre las partículas suspendidas. En tal caso, se puede calcular explícitamente el campo de flujo alrededor de cada partícula de forma independiente y combinar los resultados para obtener . Para las esferas, esto da como resultado la fórmula de viscosidad efectiva de Einstein:${\displaystyle \mu _{\text{eff}}}$${\displaystyle \mu _{\text{eff}}}$${\displaystyle \phi \lesssim 0.02}$${\displaystyle \mu _{\text{eff}}}$

${\displaystyle \mu _{\text{eff}}=\mu _{0}\left(1+{\frac {5}{2}}\phi \right),}$

donde es la viscosidad del líquido en suspensión. La dependencia lineal de es una consecuencia de descuidar las interacciones entre partículas. Para sistemas diluidos en general, se espera que tome la forma${\displaystyle \mu _{0}}$${\displaystyle \phi }$${\displaystyle \mu _{\text{eff}}}$

${\displaystyle \mu _{\text{eff}}=\mu _{0}\left(1+B\phi \right),}$

donde el coeficiente puede depender de la forma de la partícula (por ejemplo, esferas, varillas, discos). ^[60] Sin embargo, la determinación experimental del valor preciso de es difícil: incluso la predicción para esferas no ha sido validada de manera concluyente, y varios experimentos han encontrado valores en el rango . Esta deficiencia se ha atribuido a la dificultad de controlar las condiciones experimentales. ^[61]${\displaystyle B}$${\displaystyle B}$${\displaystyle B=5/2}$${\displaystyle 1.5\lesssim B\lesssim 5}$

En suspensiones más densas, adquiere una dependencia no lineal de , lo que indica la importancia de las interacciones entre partículas. Existen varios esquemas analíticos y semiempíricos para capturar este régimen. En el nivel más básico, se agrega un término cuadrático en a :${\displaystyle \mu _{\text{eff}}}$${\displaystyle \phi }$${\displaystyle \phi }$${\displaystyle \mu _{\text{eff}}}$

${\displaystyle \mu _{\text{eff}}=\mu _{0}\left(1+B\phi +B_{1}\phi ^{2}\right),}$

y el coeficiente se ajusta a partir de datos experimentales o se aproxima a partir de la teoría microscópica. Sin embargo, algunos autores recomiendan cautela al aplicar fórmulas tan simples, ya que el comportamiento no newtoniano aparece en suspensiones densas ( para esferas), ^[61] o en suspensiones de partículas alargadas o flexibles. ^[59]${\displaystyle B_{1}}$${\displaystyle \phi \gtrsim 0.25}$

Existe una distinción entre una suspensión de partículas sólidas, descrita anteriormente, y una emulsión . Esta última es una suspensión de gotitas diminutas, que pueden presentar circulación interna. La presencia de circulación interna puede disminuir la viscosidad efectiva observada, y se deben utilizar diferentes modelos teóricos o semiempíricos. ^[62]

En los límites de temperatura alta y baja, el flujo viscoso en materiales amorfos (por ejemplo, en vidrios y masas fundidas) ^{[64] [65] [66]} tiene la forma de Arrhenius :

${\displaystyle \mu =Ae^{Q/(RT)},}$

donde Q es una energía de activación relevante , dada en términos de parámetros moleculares; T es la temperatura; R es la constante molar de los gases ; y A es aproximadamente una constante. La energía de activación Q toma un valor diferente dependiendo de si se considera el límite de temperatura alto o bajo: cambia de un valor alto Q _H a bajas temperaturas (en el estado vítreo) a un valor bajo Q _L a altas temperaturas (en el estado líquido).

Para temperaturas intermedias, varía de manera no trivial con la temperatura y la fórmula simple de Arrhenius falla. Por otra parte, la ecuación de dos exponentes${\displaystyle Q}$

${\displaystyle \mu =AT\exp \left({\frac {B}{RT}}\right)\left[1+C\exp \left({\frac {D}{RT}}\right)\right],}$

donde , , , son todas constantes, proporciona un buen ajuste a los datos experimentales en todo el rango de temperaturas, mientras que al mismo tiempo se reduce a la forma correcta de Arrhenius en los límites de temperatura baja y alta. Esta expresión, también conocida como modelo de Duouglas-Doremus-Ojovan ^[67] , puede motivarse a partir de varios modelos teóricos de materiales amorfos a nivel atómico. ^[65]${\displaystyle A}$${\displaystyle B}$${\displaystyle C}$${\displaystyle D}$

Se puede derivar una ecuación de dos exponentes para la viscosidad dentro del modelo de empuje de Dyre de líquidos superenfriados, donde la barrera de energía de Arrhenius se identifica con el módulo de corte de alta frecuencia multiplicado por un volumen de empuje característico. ^{[68] [69]} Al especificar la dependencia de la temperatura del módulo de corte a través de la expansión térmica y a través de la parte repulsiva del potencial intermolecular, se recupera otra ecuación de dos exponentes: ^[70]

${\displaystyle \mu =\exp {\left\{{\frac {V_{c}C_{G}}{k_{B}T}}\exp {\left[(2+\lambda )\alpha _{T}T_{g}\left(1-{\frac {T}{T_{g}}}\right)\right]}\right\}}}$

donde denota el módulo de corte de alta frecuencia del material evaluado a una temperatura igual a la temperatura de transición vítrea , es el llamado volumen de empuje, es decir, es el volumen característico del grupo de átomos involucrados en el evento de empuje por el cual un átomo/molécula escapa de la jaula de vecinos más cercanos, típicamente del orden del volumen ocupado por unos pocos átomos. Además, es el coeficiente de expansión térmica del material, es un parámetro que mide la inclinación del ascenso de la ley de potencia del flanco ascendente del primer pico de la función de distribución radial , y está cuantitativamente relacionado con la parte repulsiva del potencial interatómico . ^[70] Finalmente, denota la constante de Boltzmann .${\displaystyle C_{G}}$${\displaystyle T_{g}}$${\displaystyle V_{c}}$${\displaystyle \alpha _{T}}$${\displaystyle \lambda }$${\displaystyle k_{B}}$

En el estudio de la turbulencia en fluidos , una estrategia práctica común es ignorar los vórtices de pequeña escala (o remolinos ) en el movimiento y calcular un movimiento a gran escala con una viscosidad efectiva , llamada "viscosidad de remolino", que caracteriza el transporte y la disipación de energía en el flujo de escala más pequeña (ver simulación de remolinos grandes ). ^{[71] [72]} En contraste con la viscosidad del fluido en sí, que debe ser positiva por la segunda ley de la termodinámica , la viscosidad de remolino puede ser negativa. ^{[73] [74]}

Como la viscosidad depende continuamente de la temperatura y la presión, no se puede caracterizar completamente mediante un número finito de mediciones experimentales. Las fórmulas predictivas se hacen necesarias si no se dispone de valores experimentales a las temperaturas y presiones de interés. Esta capacidad es importante para las simulaciones termofísicas, en las que la temperatura y la presión de un fluido pueden variar continuamente con el espacio y el tiempo. Una situación similar se da en las mezclas de fluidos puros, donde la viscosidad depende continuamente de las relaciones de concentración de los fluidos constituyentes.

Para los fluidos más simples, como los gases monoatómicos diluidos y sus mezclas, los cálculos mecánicos cuánticos ab initio pueden predecir con precisión la viscosidad en términos de constantes atómicas fundamentales, es decir, sin referencia a las mediciones de viscosidad existentes. ^[75] Para el caso especial del helio diluido, las incertidumbres en la viscosidad calculada ab initio son dos órdenes de magnitudes menores que las incertidumbres en los valores experimentales. ^[76]

Para fluidos y mezclas ligeramente más complejos a densidades moderadas (es decir, densidades subcríticas ), la teoría de Enskog revisada se puede utilizar para predecir viscosidades con cierta precisión. ^[53] La teoría de Enskog revisada es predictiva en el sentido de que se pueden obtener predicciones de viscosidad utilizando parámetros ajustados a otras propiedades termodinámicas de fluidos puros o propiedades de transporte , por lo que no se requieren mediciones de viscosidad experimentales a priori .

Para la mayoría de los fluidos, los cálculos de alta precisión y de primeros principios no son factibles. En cambio, las expresiones teóricas o empíricas deben ajustarse a las mediciones de viscosidad existentes. Si dicha expresión se ajusta a datos de alta fidelidad en un amplio rango de temperaturas y presiones, entonces se denomina "correlación de referencia" para ese fluido. Se han publicado correlaciones de referencia para muchos fluidos puros; algunos ejemplos son agua , dióxido de carbono , amoníaco , benceno y xenón . ^{[77] [78 ] [79] [80] [81]} Muchas de estas cubren rangos de temperatura y presión que abarcan fases gaseosas, líquidas y supercríticas .

El software de modelado termofísico a menudo se basa en correlaciones de referencia para predecir la viscosidad a la temperatura y presión especificadas por el usuario. Estas correlaciones pueden ser exclusivas . Algunos ejemplos son REFPROP ^[82] (exclusiva) y CoolProp ^[83] (código abierto).

La viscosidad también se puede calcular utilizando fórmulas que la expresan en términos de las estadísticas de las trayectorias de partículas individuales. Estas fórmulas incluyen las relaciones de Green-Kubo para la viscosidad de corte lineal y las expresiones de la función de correlación de tiempo transitorio derivadas por Evans y Morriss en 1988. ^{[84] [34]} La ventaja de estas expresiones es que son formalmente exactas y válidas para sistemas generales. La desventaja es que requieren un conocimiento detallado de las trayectorias de las partículas, disponible solo en simulaciones computacionalmente costosas como la dinámica molecular . También se requiere un modelo preciso para las interacciones entre partículas, que puede ser difícil de obtener para moléculas complejas. ^[85]

Los valores observados de viscosidad varían en varios órdenes de magnitud, incluso para sustancias comunes (véase la tabla de órdenes de magnitud a continuación). Por ejemplo, una solución de sacarosa (azúcar) al 70% tiene una viscosidad 400 veces superior a la del agua y 26.000 veces superior a la del aire. ^[87] Más dramáticamente, se ha estimado que la brea tiene una viscosidad 230 mil millones de veces superior a la del agua. ^[86]

La viscosidad dinámica del agua es de aproximadamente 0,89 mPa·s a temperatura ambiente (25 °C). Como función de la temperatura en grados Kelvin , la viscosidad se puede estimar utilizando la ecuación semiempírica de Vogel-Fulcher-Tammann :${\displaystyle \mu }$

${\displaystyle \mu =A\exp \left({\frac {B}{T-C}}\right)}$

donde A = 0,02939 mPa·s, B = 507,88 K y C = 149,3 K. ^[88] Los valores de viscosidad determinados experimentalmente también se dan en la tabla siguiente. Los valores a 20 °C son una referencia útil: allí, la viscosidad dinámica es de aproximadamente 1 cP y la viscosidad cinemática es de aproximadamente 1 cSt.

En condiciones atmosféricas estándar (25 °C y presión de 1 bar), la viscosidad dinámica del aire es de 18,5 μPa·s, aproximadamente 50 veces menor que la viscosidad del agua a la misma temperatura. Excepto a presiones muy altas, la viscosidad del aire depende principalmente de la temperatura. Entre las muchas fórmulas aproximadas posibles para la dependencia de la temperatura (véase Dependencia de la viscosidad con la temperatura ), una es: ^[89]

${\displaystyle \eta _{\text{air}}=2.791\times 10^{-7}\times T^{0.7355}}$

que es precisa en el rango de -20 °C a 400 °C. Para que esta fórmula sea válida, la temperatura debe expresarse en kelvins ; entonces corresponde a la viscosidad en Pa·s.${\displaystyle \eta _{\text{air}}}$

Sustancia	Viscosidad (mPa·s)	Temperatura (°C)	Árbitro.
Benceno	0,604	25	[87]
Agua	1.0016	20
Mercurio	1.526	25
Leche entera	2.12	20	[90]
Cerveza oscura	2.53	20
Aceite de oliva	56.2	26	[90]
Miel	${\displaystyle \approx }$2.000–10.000	20	[91]
Salsa de tomate [b]	${\displaystyle \approx }$5.000–20.000	25	[92]
Mantequilla de maní [b]	${\displaystyle \approx }$10 4 –10 6		[93]
Paso	2,3 × 10 11	10–30 (variable)	[86]

La siguiente tabla ilustra el rango de valores de viscosidad observados en sustancias comunes. A menos que se indique lo contrario, se supone una temperatura de 25 °C y una presión de 1 atmósfera.

Los valores enumerados son solo estimaciones representativas, ya que no tienen en cuenta las incertidumbres de medición, la variabilidad en las definiciones de materiales o el comportamiento no newtoniano.

Busque viscosidad en Wikcionario, el diccionario libre.

Wikisource tiene el texto del artículo " Viscosidad de los líquidos " de The New Student's Reference Work .

Wikiquote tiene citas relacionadas con Viscosidad .

• Viscosidad - Las conferencias de Feynman sobre física
• Propiedades de fluidos: cálculo de alta precisión de la viscosidad para líquidos y gases puros que se encuentran con frecuencia
• Cuadro de características de fluidos: una tabla de viscosidades y presiones de vapor para varios fluidos
• Caja de herramientas de dinámica de gases: cálculo del coeficiente de viscosidad para mezclas de gases
• Medición de la viscosidad del vidrio: medición de la viscosidad, unidades de viscosidad y puntos fijos, cálculo de la viscosidad del vidrio
• Viscosidad cinemática: conversión entre viscosidad cinemática y dinámica
• Características físicas del agua: tabla de la viscosidad del agua en función de la temperatura
• Cálculo de viscosidades dinámicas dependientes de la temperatura para algunos componentes comunes
• Viscosidad artificial
• Viscosidad del aire, dinámica y cinemática, Engineers Edge