Velocidad

Velocidad
A medida que se produce un cambio de dirección mientras los coches de carreras giran en la pista curva, su velocidad no es constante aunque su rapidez sí lo sea.
Símbolos comunes	v , v , v → , v
Otras unidades	mph , pies/s
En unidades base del SI	EM​​
Dimensión	L T -1

Parte de una serie sobre
Mecánica clásica
${\displaystyle {\textbf {F}}={\frac {d\mathbf {p} }{dt}}}$ Segunda ley del movimiento
Historia Cronología Libros de texto
Sucursales Aplicado Celestial Continuo Dinámica Cinemática Cinética Estática Mecánica estadística
Fundamentos Aceleración Momento angular Pareja Principio de D'Alembert Energía cinético potencial Fuerza Marco de referencia Marco de referencia inercial Impulso Inercia  / Momento de inercia Masa Potencia mecánica Trabajo mecánico Momento Impulso Espacio Velocidad Tiempo Esfuerzo de torsión Velocidad Trabajo virtual
Formulaciones Leyes del movimiento de Newton Mecánica analítica Mecánica lagrangiana Mecánica hamiltoniana Mecánica de Routh Ecuación de Hamilton-Jacobi Ecuación de movimiento de Appell Mecánica de Koopman-von Neumann
Temas centrales Mojadura Desplazamiento Ecuaciones de movimiento Leyes del movimiento de Euler Fuerza ficticia Fricción Oscilador armónico Marco de referencia inercial  / no inercial Mecánica del movimiento de partículas planas Movimiento  ( lineal ) Ley de gravitación universal de Newton Leyes del movimiento de Newton Velocidad relativa Cuerpo rígido dinámica Ecuaciones de Euler Movimiento armónico simple Vibración
Rotación Movimiento circular Marco de referencia giratorio Fuerza centrípeta Fuerza centrífuga reactivo Fuerza de Coriolis Péndulo Velocidad tangencial Frecuencia rotacional Angular acceleration / displacement / frequency / velocity
Scientists Kepler Galileo Huygens Newton Horrocks Halley Maupertuis Daniel Bernoulli Johann Bernoulli Euler d'Alembert Clairaut Lagrange Laplace Poisson Hamilton Jacobi Cauchy Routh Liouville Appell Gibbs Koopman von Neumann
Physics portal  Category
v t e

La velocidad es la rapidez en combinación con la dirección del movimiento de un objeto . La velocidad es un concepto fundamental en la cinemática , la rama de la mecánica clásica que describe el movimiento de los cuerpos.

La velocidad es una cantidad vectorial física : se necesitan tanto la magnitud como la dirección para definirla. El valor absoluto escalar ( magnitud ) de la velocidad se denomina rapidez , siendo una unidad derivada coherente cuya cantidad se mide en el SI ( sistema métrico ) en metros por segundo (m/s o m⋅s ⁻¹ ). Por ejemplo, "5 metros por segundo" es un escalar, mientras que "5 metros por segundo al este" es un vector. Si hay un cambio en la velocidad, la dirección o ambas, se dice que el objeto está experimentando una aceleración .

La velocidad media de un objeto durante un período de tiempo es su cambio de posición , , dividido por la duración del período, , dado matemáticamente como ^[1]${\displaystyle \Delta s}$${\displaystyle \Delta t}$$${\displaystyle {\bar {v}}={\frac {\Delta s}{\Delta t}}.}$$

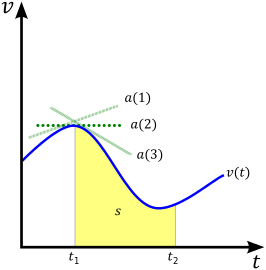
La velocidad instantánea de un objeto es la velocidad media límite a medida que el intervalo de tiempo se acerca a cero. En cualquier momento particular t , se puede calcular como la derivada de la posición con respecto al tiempo: ^[2]$${\displaystyle {\boldsymbol {v}}=\lim _{{\Delta t}\to 0}{\frac {\Delta {\boldsymbol {s}}}{\Delta t}}={\frac {d{\boldsymbol {s}}}{dt}}.}$$

A partir de esta ecuación derivada, en el caso unidimensional se puede ver que el área bajo una gráfica de velocidad vs. tiempo ( v vs. t ) es el desplazamiento, s . En términos de cálculo, la integral de la función de velocidad v ( t ) es la función de desplazamiento s ( t ) . En la figura, esto corresponde al área amarilla bajo la curva. s = ∫ v d t . {\displaystyle {\boldsymbol {s}}=\int {\boldsymbol {v}}\ dt.}

Aunque el concepto de velocidad instantánea puede parecer contraintuitivo a primera vista, puede considerarse como la velocidad a la que el objeto continuaría viajando si dejara de acelerar en ese momento.

Si bien los términos rapidez y velocidad se usan a menudo de manera indistinta para indicar la velocidad a la que se mueve un objeto, en términos científicos son diferentes. La rapidez, la magnitud escalar de un vector de velocidad, indica únicamente la velocidad a la que se mueve un objeto, mientras que la velocidad indica tanto la velocidad como la dirección del objeto. ^{[3] [4] [5]}

Para que un objeto tenga una velocidad constante , debe tener una rapidez constante en una dirección constante. La dirección constante obliga al objeto a moverse en una trayectoria recta, por lo que una velocidad constante significa movimiento en línea recta a una rapidez constante.

Por ejemplo, un automóvil que se desplaza a una velocidad constante de 20 kilómetros por hora en una trayectoria circular tiene una rapidez constante, pero no una velocidad constante porque su dirección cambia. Por lo tanto, se considera que el automóvil está experimentando una aceleración.

Como la derivada de la posición con respecto al tiempo da el cambio en la posición (en metros ) dividido por el cambio en el tiempo (en segundos ), la velocidad se mide en metros por segundo (m/s).

La velocidad se define como la tasa de cambio de posición con respecto al tiempo, que también puede denominarse velocidad instantánea para enfatizar la distinción con la velocidad promedio. En algunas aplicaciones, puede ser necesaria la velocidad promedio de un objeto, es decir, la velocidad constante que proporcionaría el mismo desplazamiento resultante que una velocidad variable en el mismo intervalo de tiempo, v ( t ) , durante un período de tiempo Δ t . La velocidad promedio se puede calcular como: ^{[6] [7]}

v ¯ = Δ x Δ t = ∫ t 0 t 1 v ( t ) d t t 1 − t 0 . {\displaystyle \mathbf {\bar {v}} ={\frac {\Delta \mathbf {x} }{\Delta t}}={\frac {\int _{t_{0}}^{t_{1}}\mathbf {v} (t)dt}{t_{1}-t_{0}}}.}

La velocidad media siempre es menor o igual que la rapidez media de un objeto. Esto se puede comprobar si tenemos en cuenta que, si bien la distancia siempre aumenta estrictamente, el desplazamiento puede aumentar o disminuir en magnitud, así como cambiar de dirección.

En términos de un gráfico de desplazamiento-tiempo ( x vs. t ), la velocidad instantánea (o, simplemente, velocidad) puede considerarse como la pendiente de la línea tangente a la curva en cualquier punto , y la velocidad promedio como la pendiente de la línea secante entre dos puntos con coordenadas t iguales a los límites del período de tiempo para la velocidad promedio.

• Cuando una partícula se mueve con diferentes velocidades uniformes v ₁ , v ₂ , v ₃ , ..., v _n en diferentes intervalos de tiempo t ₁ , t ₂ , t ₃ , ..., t _n respectivamente, entonces la velocidad promedio durante el tiempo total del viaje se da como$${\displaystyle {\bar {v}}={v_{1}t_{1}+v_{2}t_{2}+v_{3}t_{3}+\dots +v_{n}t_{n} \over t_{1}+t_{2}+t_{3}+\dots +t_{n}}}$$

Si t ₁ = t ₂ = t ₃ = ... = t , entonces la velocidad promedio está dada por la media aritmética de las velocidades.$${\displaystyle {\bar {v}}={v_{1}+v_{2}+v_{3}+\dots +v_{n} \over n}={\frac {1}{n}}\sum _{i=1}^{n}{v_{i}}}$$

• Cuando una partícula se mueve diferentes distancias s ₁ , s ₂ , s ₃ ,..., s _n con velocidades v ₁ , v ₂ , v ₃ ,..., v _n respectivamente, entonces la velocidad promedio de la partícula sobre la distancia total se da como ^[8]

$${\displaystyle {\bar {v}}={s_{1}+s_{2}+s_{3}+\dots +s_{n} \over t_{1}+t_{2}+t_{3}+\dots +t_{n}}={{s_{1}+s_{2}+s_{3}+\dots +s_{n}} \over {{s_{1} \over v_{1}}+{s_{2} \over v_{2}}+{s_{3} \over v_{3}}+\dots +{s_{n} \over v_{n}}}}}$$Si s ₁ = s ₂ = s ₃ = ... = s , entonces la velocidad promedio está dada por la media armónica de las velocidades ^[8]$${\displaystyle {\bar {v}}=n\left({1 \over v_{1}}+{1 \over v_{2}}+{1 \over v_{3}}+\dots +{1 \over v_{n}}\right)^{-1}=n\left(\sum _{i=1}^{n}{\frac {1}{v_{i}}}\right)^{-1}.}$$

Aunque la velocidad se define como la tasa de cambio de posición, a menudo es común comenzar con una expresión para la aceleración de un objeto . Como se ve por las tres líneas tangentes verdes en la figura, la aceleración instantánea de un objeto en un punto en el tiempo es la pendiente de la línea tangente a la curva de un gráfico v ( t ) en ese punto. En otras palabras, la aceleración instantánea se define como la derivada de la velocidad con respecto al tiempo: ^[9] a = d v d t . {\displaystyle {\boldsymbol {a}}={\frac {d{\boldsymbol {v}}}{dt}}.}

A partir de ahí, la velocidad se expresa como el área bajo un gráfico de aceleración a ( t ) en función del tiempo. Como se indicó anteriormente, esto se hace utilizando el concepto de integral:

$${\displaystyle {\boldsymbol {v}}=\int {\boldsymbol {a}}\ dt.}$$

En el caso especial de aceleración constante, la velocidad puede estudiarse utilizando las ecuaciones de Suvat . Al considerar a como igual a algún vector constante arbitrario, esto muestra que v es la velocidad en el tiempo t y u es la velocidad en el tiempo t = 0. Al combinar esta ecuación con la ecuación de Suvat x = u t + a t ² /2 , es posible relacionar el desplazamiento y la velocidad promedio mediante También es posible derivar una expresión para la velocidad independiente del tiempo, conocida como la ecuación de Torricelli , como sigue: donde v = | v | etc.$${\displaystyle {\boldsymbol {v}}={\boldsymbol {u}}+{\boldsymbol {a}}t}$$$${\displaystyle {\boldsymbol {x}}={\frac {({\boldsymbol {u}}+{\boldsymbol {v}})}{2}}t={\boldsymbol {\bar {v}}}t.}$$$${\displaystyle v^{2}={\boldsymbol {v}}\cdot {\boldsymbol {v}}=({\boldsymbol {u}}+{\boldsymbol {a}}t)\cdot ({\boldsymbol {u}}+{\boldsymbol {a}}t)=u^{2}+2t({\boldsymbol {a}}\cdot {\boldsymbol {u}})+a^{2}t^{2}}$$$${\displaystyle (2{\boldsymbol {a}})\cdot {\boldsymbol {x}}=(2{\boldsymbol {a}})\cdot ({\boldsymbol {u}}t+{\tfrac {1}{2}}{\boldsymbol {a}}t^{2})=2t({\boldsymbol {a}}\cdot {\boldsymbol {u}})+a^{2}t^{2}=v^{2}-u^{2}}$$$${\displaystyle \therefore v^{2}=u^{2}+2({\boldsymbol {a}}\cdot {\boldsymbol {x}})}$$

Las ecuaciones anteriores son válidas tanto para la mecánica newtoniana como para la relatividad especial . La mecánica newtoniana y la relatividad especial difieren en cómo diferentes observadores describirían la misma situación. En particular, en la mecánica newtoniana, todos los observadores están de acuerdo en el valor de t y las reglas de transformación para la posición crean una situación en la que todos los observadores que no aceleran describirían la aceleración de un objeto con los mismos valores. Ninguna de las dos cosas es cierta para la relatividad especial. En otras palabras, solo se puede calcular la velocidad relativa.

En mecánica clásica, la segunda ley de Newton define el momento , p, como un vector que es el producto de la masa y la velocidad de un objeto, dada matemáticamente como p = m v {\displaystyle {\boldsymbol {p}}=m{\boldsymbol {v}}} donde m es la masa del objeto.

La energía cinética de un objeto en movimiento depende de su velocidad y está dada por la ecuación ^[10] E k = 1 2 m v 2 {\displaystyle E_{\text{k}}={\tfrac {1}{2}}mv^{2}} donde E _k es la energía cinética. La energía cinética es una cantidad escalar ya que depende del cuadrado de la velocidad.

En dinámica de fluidos , la resistencia es una fuerza que actúa en sentido opuesto al movimiento relativo de cualquier objeto que se mueve con respecto a un fluido circundante. La fuerza de resistencia, , depende del cuadrado de la velocidad y se expresa como F D = 1 2 ρ v 2 C D A {\displaystyle F_{D}\,=\,{\tfrac {1}{2}}\,\rho \,v^{2}\,C_{D}\,A} donde${\displaystyle F_{D}}$

• ${\displaystyle \rho }$es la densidad del fluido, ^[11]
• ${\displaystyle v}$es la velocidad del objeto en relación con el fluido,
• ${\displaystyle A}$es el área de la sección transversal , y
• ${\displaystyle C_{D}}$es el coeficiente de arrastre , un número adimensional .

La velocidad de escape es la velocidad mínima que necesita un objeto balístico para escapar de un cuerpo masivo como la Tierra. Representa la energía cinética que, cuando se suma a la energía potencial gravitatoria del objeto (que siempre es negativa), es igual a cero. La fórmula general para la velocidad de escape de un objeto a una distancia r del centro de un planeta con masa M es ^[12] donde G es la constante gravitatoria y g es la aceleración gravitatoria . La velocidad de escape desde la superficie de la Tierra es de aproximadamente 11 200 m/s, y es independiente de la dirección del objeto. Esto hace que "velocidad de escape" sea un nombre poco apropiado, ya que el término más correcto sería "velocidad de escape": cualquier objeto que alcance una velocidad de esa magnitud, independientemente de la atmósfera, abandonará las proximidades del cuerpo base siempre que no se cruce con algo en su camino.$${\displaystyle v_{\text{e}}={\sqrt {\frac {2GM}{r}}}={\sqrt {2gr}},}$$

En relatividad especial , el factor de Lorentz adimensional aparece con frecuencia y está dado por ^[13] γ = 1 1 − v 2 c 2 {\displaystyle \gamma ={\frac {1}{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}} donde γ es el factor de Lorentz y c es la velocidad de la luz.

La velocidad relativa es una medida de la velocidad entre dos objetos determinada en un único sistema de coordenadas. La velocidad relativa es fundamental tanto en la física clásica como en la moderna, ya que muchos sistemas de la física se ocupan del movimiento relativo de dos o más partículas.

Consideremos un objeto A que se mueve con un vector de velocidad v y un objeto B con un vector de velocidad w ; estas velocidades absolutas se expresan típicamente en el mismo marco de referencia inercial . Entonces, la velocidad del objeto A con respecto al objeto B se define como la diferencia de los dos vectores de velocidad: De manera similar, la velocidad relativa del objeto B que se mueve con una velocidad w , con respecto al objeto A que se mueve con una velocidad v es: Por lo general, el marco inercial elegido es aquel en el que el último de los dos objetos mencionados está en reposo.$${\displaystyle {\boldsymbol {v}}_{A{\text{ relative to }}B}={\boldsymbol {v}}-{\boldsymbol {w}}}$$$${\displaystyle {\boldsymbol {v}}_{B{\text{ relative to }}A}={\boldsymbol {w}}-{\boldsymbol {v}}}$$

En la mecánica newtoniana, la velocidad relativa es independiente del sistema de referencia inercial elegido. Esto ya no es así en la relatividad especial , en la que las velocidades dependen del sistema de referencia elegido.

En el caso unidimensional, ^[14] las velocidades son escalares y la ecuación es: si los dos objetos se mueven en direcciones opuestas, o: si los dos objetos se mueven en la misma dirección.$${\displaystyle v_{\text{rel}}=v-(-w),}$$$${\displaystyle v_{\text{rel}}=v-(+w),}$$

En sistemas de coordenadas cartesianas multidimensionales , la velocidad se divide en componentes que corresponden a cada eje dimensional del sistema de coordenadas. En un sistema bidimensional, donde hay un eje x y un eje y, los componentes de velocidad correspondientes se definen como ^[15]

$${\displaystyle v_{x}=dx/dt,}$$

$${\displaystyle v_{y}=dy/dt.}$$

El vector de velocidad bidimensional se define entonces como . La magnitud de este vector representa la velocidad y se obtiene mediante la fórmula de la distancia como${\displaystyle {\textbf {v}}=<v_{x},v_{y}>}$

$${\displaystyle |v|={\sqrt {v_{x}^{2}+v_{y}^{2}}}.}$$

En sistemas tridimensionales donde hay un eje z adicional, el componente de velocidad correspondiente se define como

$${\displaystyle v_{z}=dz/dt.}$$

El vector de velocidad tridimensional se define como, con su magnitud, que también representa la velocidad y está determinado por${\displaystyle {\textbf {v}}=<v_{x},v_{y},v_{z}>}$

$${\displaystyle |v|={\sqrt {v_{x}^{2}+v_{y}^{2}+v_{z}^{2}}}.}$$

Mientras que algunos libros de texto utilizan la notación de subíndice para definir los componentes cartesianos de la velocidad, otros utilizan , , y para los ejes -, - y - respectivamente. ^[16]${\displaystyle u}$${\displaystyle v}$${\displaystyle w}$${\displaystyle x}$${\displaystyle y}$${\displaystyle z}$

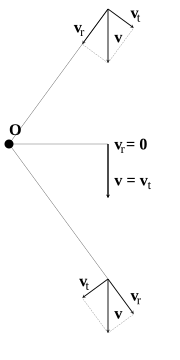
En coordenadas polares , una velocidad bidimensional se describe mediante una velocidad radial , definida como el componente de la velocidad que se aleja o se acerca al origen, y una velocidad transversal , perpendicular a la radial. ^{[17] [18]} Ambas surgen de la velocidad angular , que es la tasa de rotación alrededor del origen (con cantidades positivas que representan la rotación en sentido antihorario y cantidades negativas que representan la rotación en el sentido horario, en un sistema de coordenadas diestro).

Las velocidades radial y transversal se pueden derivar de los vectores de velocidad y desplazamiento cartesianos descomponiendo el vector de velocidad en componentes radial y transversal. La velocidad transversal es el componente de la velocidad a lo largo de un círculo centrado en el origen. donde$${\displaystyle {\boldsymbol {v}}={\boldsymbol {v}}_{T}+{\boldsymbol {v}}_{R}}$$

• ${\displaystyle {\boldsymbol {v}}_{T}}$es la velocidad transversal
• ${\displaystyle {\boldsymbol {v}}_{R}}$es la velocidad radial.

La velocidad radial (o magnitud de la velocidad radial) es el producto escalar del vector velocidad y el vector unitario en la dirección radial. donde es la posición y es la dirección radial.$${\displaystyle v_{R}={\frac {{\boldsymbol {v}}\cdot {\boldsymbol {r}}}{\left|{\boldsymbol {r}}\right|}}={\boldsymbol {v}}\cdot {\hat {\boldsymbol {r}}}}$$${\displaystyle {\boldsymbol {r}}}$${\displaystyle {\hat {\boldsymbol {r}}}}$

La velocidad transversal (o magnitud de la velocidad transversal) es la magnitud del producto vectorial del vector unitario en la dirección radial y el vector de velocidad. También es el producto escalar de la velocidad y la dirección transversal, o el producto de la velocidad angular y el radio (la magnitud de la posición). de modo que${\displaystyle \omega }$$${\displaystyle v_{T}={\frac {|{\boldsymbol {r}}\times {\boldsymbol {v}}|}{|{\boldsymbol {r}}|}}={\boldsymbol {v}}\cdot {\hat {\boldsymbol {t}}}=\omega |{\boldsymbol {r}}|}$$$${\displaystyle \omega ={\frac {|{\boldsymbol {r}}\times {\boldsymbol {v}}|}{|{\boldsymbol {r}}|^{2}}}.}$$

El momento angular en forma escalar es la masa multiplicada por la distancia al origen multiplicada por la velocidad transversal, o, equivalentemente, la masa multiplicada por la distancia al cuadrado multiplicada por la velocidad angular. La convención de signos para el momento angular es la misma que para la velocidad angular .$${\displaystyle L=mrv_{T}=mr^{2}\omega }$$

• ${\displaystyle m}$es masa
• ${\displaystyle r=|{\boldsymbol {r}}|.}$

La expresión se conoce como momento de inercia . Si las fuerzas están en la dirección radial solo con una dependencia inversa del cuadrado, como en el caso de una órbita gravitacional , el momento angular es constante y la velocidad transversal es inversamente proporcional a la distancia, la velocidad angular es inversamente proporcional a la distancia al cuadrado y la velocidad a la que se barre el área es constante. Estas relaciones se conocen como leyes de Kepler del movimiento planetario .${\displaystyle mr^{2}}$

• Robert Resnick y Jearl Walker, Fundamentals of Physics , Wiley; 7ª subedición (16 de junio de 2004). ISBN  0-471-23231-9 .

Wikimedia Commons tiene medios relacionados con Velocidad .

• Velocidad y aceleración
• Introducción a los mecanismos ( Universidad Carnegie Mellon )