Vértice universal

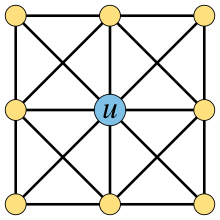
En teoría de grafos , un vértice universal es un vértice de un grafo no dirigido que es adyacente a todos los demás vértices del grafo. También se lo puede llamar vértice dominante , ya que forma un conjunto dominante de un elemento en el grafo. Un grafo que contiene un vértice universal puede llamarse cono , y su vértice universal puede llamarse el vértice del cono. ^[1] Esta terminología debe distinguirse del uso no relacionado de estas palabras para cuantificadores universales en la lógica de grafos y para grafos de vértice .

Los grafos que contienen un vértice universal incluyen las estrellas , los grafos trivialmente perfectos y los grafos de amistad . En el caso de los grafos de rueda (los grafos de las pirámides ) y los grafos de politopos piramidales de dimensiones superiores , el vértice en el vértice de la pirámide es universal. Cuando un grafo contiene un vértice universal, es un grafo de cop-win , y casi todos los grafos de cop-win contienen un vértice universal.

El número de grafos etiquetados que contienen un vértice universal se puede contar por inclusión-exclusión , lo que muestra que hay un número impar de tales grafos en cualquier número par de vértices. Esto, a su vez, se puede utilizar para mostrar que la propiedad de tener un grafo universal es evasiva : probar esta propiedad puede requerir verificar la adyacencia de todos los pares de vértices. Sin embargo, un vértice universal se puede reconocer inmediatamente a partir de su grado : en un grafo -vértice, tiene grado . Los vértices universales se pueden describir mediante una fórmula lógica corta, que se ha utilizado en algoritmos de grafos para propiedades relacionadas.${\displaystyle n}$${\displaystyle n-1}$

Las estrellas son exactamente los árboles que tienen un vértice universal, y pueden construirse añadiendo un vértice universal a un conjunto independiente . Los grafos de rueda pueden formarse añadiendo un vértice universal a un grafo de ciclo . ^[2] Los grafos trivialmente perfectos se obtienen a partir de árboles con raíz añadiendo una arista que conecta cada par ancestro-descendiente en el árbol. Estos siempre contienen un vértice universal, la raíz del árbol. Más fuertemente pueden caracterizarse como los grafos finitos en los que cada subgrafo inducido conexo contiene un vértice universal. ^{[3] Los} grafos de umbral conexos forman una subclase de los grafos trivialmente perfectos, por lo que también contienen un vértice universal. Pueden definirse como los grafos que pueden formarse mediante la adición repetida de un vértice universal o un vértice aislado (uno sin aristas incidentes). ^[4]

En geometría, las pirámides tridimensionales tienen como esqueletos gráficos de rueda [ 5 ^] y, de manera más general, una pirámide de dimensión superior es un politopo cuyas caras de todas las dimensiones conectan un vértice con todas las caras de una base de dimensión inferior, incluidos todos los vértices de la base. Se dice que el politopo es piramidal en su vértice y puede tener más de un vértice. Sin embargo, la existencia de politopos vecinos significa que el gráfico de un politopo puede tener un vértice universal, o todos los vértices universales, sin que el politopo en sí sea una pirámide ^[6] .

El teorema de la amistad establece que, si cada dos vértices de un grafo finito tienen exactamente un vecino compartido, entonces el grafo contiene un vértice universal. Los grafos descritos por este teorema son los grafos de la amistad , formados por sistemas de triángulos conectados entre sí en un vértice compartido común, el vértice universal. ^[7] La ​​suposición de que el grafo es finito es importante; existen grafos infinitos en los que cada dos vértices tienen un vecino compartido, pero sin ningún vértice universal. ^[8]

Todo grafo finito con un vértice universal es un grafo desmantelable , lo que significa que puede reducirse a un único vértice eliminando repetidamente un vértice cuyo vecindario cerrado es un subconjunto del vecindario cerrado de otro vértice. En un grafo con un vértice universal, cualquier secuencia de eliminación que deje el vértice universal en su lugar, eliminando todos los demás vértices, se ajusta a esta definición. Casi todos los grafos desmantelables tienen un vértice universal, en el sentido de que la fracción de grafos desmantelables con -vértice que tienen un vértice universal tiende a uno en el límite cuando tiende a infinito. Los grafos desmantelables también se denominan grafos de policía-ganador, porque el bando que juega a policía gana un determinado juego de policía y ladrón definido en estos grafos. ^[9]${\displaystyle n}$${\displaystyle n}$

Cuando un grafo tiene un vértice universal, el conjunto de vértices que consiste únicamente en ese vértice es un conjunto dominante , un conjunto que incluye o es adyacente a cada vértice. Por esta razón, en el contexto de problemas de conjuntos dominantes, un vértice universal también puede llamarse vértice dominante . ^[10] Para el producto fuerte de grafos , los números dominantes y obedecen las desigualdades Esto implica que un producto fuerte tiene un vértice dominante si y solo si ambos de sus factores lo hacen; en este caso, el límite superior de su número dominante es uno, y en cualquier otro caso el límite inferior es mayor que uno. ^[11]${\displaystyle G\boxtimes H}$${\displaystyle \gamma (G)}$${\displaystyle \gamma (H)}$$${\displaystyle \max\{\gamma (G),\gamma (H)\}\leq \gamma (G\boxtimes H)\leq \gamma (G)\gamma (H).}$$

La cantidad de grafos etiquetados con vértices, al menos uno de los cuales es universal (o equivalentemente aislado, en el grafo de complemento ) se puede contar mediante el principio de inclusión-exclusión , en el que se cuentan los grafos en los que un vértice elegido es universal, luego se corrige el recuento excesivo restando los recuentos de los grafos con dos vértices universales elegidos, luego sumando los recuentos de los grafos con tres vértices universales elegidos, etc. Esto produce la fórmula${\displaystyle n}$

${\displaystyle \displaystyle \sum _{k=1}^{n}(-1)^{k+1}{\binom {n}{k}}2^{\tbinom {n-k}{2}}.}$

En cada término de la suma, es el número de vértices elegidos para ser universales, y es el número de maneras de hacer esta elección. es el número de pares de vértices que no incluyen un vértice universal elegido, y tomando este número como el exponente de una potencia de dos se cuenta el número de grafos con los vértices elegidos como universales. ^[12]${\displaystyle k}$${\displaystyle {\tbinom {n}{k}}}$${\displaystyle {\tbinom {n-k}{2}}}$

A partir de , estos números de gráficos son:${\displaystyle n=1}$

Para , estos números son impares cuando es par, y viceversa. ^[12] La versión sin etiquetar de este problema de enumeración de grafos es trivial, en el sentido de que el número de grafos sin etiquetar de -vértice con un vértice universal es el mismo que el número de grafos de -vértice. ^[13]${\displaystyle n>1}$${\displaystyle n}$${\displaystyle n}$${\displaystyle (n-1)}$

En un gráfico con vértices, un vértice universal es un vértice cuyo grado es exactamente . ^[10]${\displaystyle n}$${\displaystyle n-1}$

La propiedad de tener un vértice universal se puede expresar mediante una fórmula en la lógica de primer orden de grafos . Utilizando para indicar la relación de adyacencia en un grafo, un grafo tiene un vértice universal si y solo si modela la fórmula La existencia de esta fórmula, y su pequeño número de alternancias entre cuantificadores universales y existenciales , se puede utilizar en un algoritmo manejable con parámetros fijos para probar si se puede hacer que todos los componentes de un grafo tengan vértices universales mediante pasos de eliminación de un vértice de cada componente. ^[14]${\displaystyle \sim }$${\displaystyle G}$$${\displaystyle \exists u\forall v{\bigl (}(u\neq v)\Rightarrow (u\sim v){\bigr )}.}$$${\displaystyle k}$

La propiedad de tener un vértice universal (o equivalentemente un vértice aislado) se ha considerado con respecto a la conjetura de Aanderaa–Karp–Rosenberg sobre cuántas consultas (llamadas a subrutinas) se necesitan para probar si un grafo etiquetado tiene una propiedad, dado acceso al grafo solo a través de una subrutina que puede probar si dos vértices dados son adyacentes. En un grafo con vértices, uno puede determinar el grafo completo y probar cualquier propiedad, utilizando consultas. Una propiedad de grafo es evasiva si ningún algoritmo puede probar la propiedad garantizando menos consultas. Probar la existencia de un vértice universal es evasivo, en grafos con un número par de vértices. Hay un número impar de estos grafos que tienen un vértice universal. Un algoritmo de prueba puede verse obligado a consultar todos los pares de vértices mediante una subrutina de adyacencia que siempre responde de tal manera que deja un número impar de grafos restantes que tienen un vértice universal. Hasta que se prueben todos los bordes, el número total de gráficos restantes será par, por lo que el algoritmo no podrá determinar si el gráfico que está consultando tiene un vértice universal. ^[12]${\displaystyle n}$${\displaystyle {\tbinom {n}{2}}}$