Desigualdad triangular

En matemáticas , la desigualdad del triángulo establece que para cualquier triángulo , la suma de las longitudes de dos lados cualesquiera debe ser mayor o igual que la longitud del lado restante. ^{[1] [2]} Esta afirmación permite la inclusión de triángulos degenerados , pero algunos autores, especialmente aquellos que escriben sobre geometría elemental, excluirán esta posibilidad, dejando así fuera la posibilidad de igualdad. ^[3] Si a , b y c son las longitudes de los lados de un triángulo, entonces la desigualdad del triángulo establece que

${\displaystyle c\leq a+b,}$

con igualdad sólo en el caso degenerado de un triángulo con área cero.

En la geometría euclidiana y algunas otras geometrías, la desigualdad del triángulo es un teorema sobre vectores y longitudes de vectores ( normas ):

${\displaystyle \|\mathbf {u} +\mathbf {v} \|\leq \|\mathbf {u} \|+\|\mathbf {v} \|,}$

donde la longitud del tercer lado ha sido reemplazada por la longitud de la suma vectorial u + v . Cuando u y v son números reales , pueden verse como vectores en , y la desigualdad triangular expresa una relación entre valores absolutos .${\displaystyle \mathbb {R} ^{1}}$

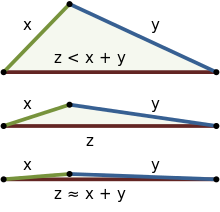
En la geometría euclidiana, para los triángulos rectángulos la desigualdad triangular es una consecuencia del teorema de Pitágoras y, para los triángulos generales, una consecuencia de la ley de los cosenos , aunque puede demostrarse sin estos teoremas. La desigualdad puede verse intuitivamente en o . La figura de la derecha muestra tres ejemplos que comienzan con una desigualdad clara (arriba) y se aproximan a la igualdad (abajo). En el caso euclidiano, la igualdad solo ocurre si el triángulo tiene un ángulo de 180° y dos ángulos de 0° , lo que hace que los tres vértices sean colineales , como se muestra en el ejemplo inferior. Por lo tanto, en la geometría euclidiana, la distancia más corta entre dos puntos es una línea recta.${\displaystyle \mathbb {R} ^{2}}$${\displaystyle \mathbb {R} ^{3}}$

En geometría esférica , la distancia más corta entre dos puntos es un arco de un círculo máximo , pero la desigualdad del triángulo se cumple siempre que se haga la restricción de que la distancia entre dos puntos de una esfera sea la longitud de un segmento de línea esférica menor (es decir, uno con ángulo central en [0, π ] ) con esos puntos finales. ^{[4] [5]}

La desigualdad triangular es una propiedad definitoria de las normas y medidas de distancia . Esta propiedad debe establecerse como teorema para cualquier función propuesta a tales efectos para cada espacio particular: por ejemplo, espacios como los números reales , los espacios euclidianos , los espacios L ^p ( p ≥ 1 ) y los espacios de producto interno .

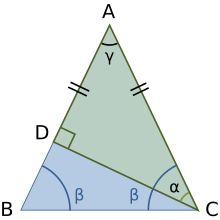
Euclides demostró la desigualdad del triángulo para las distancias en geometría plana usando la construcción de la figura. ^[6] Comenzando con el triángulo ABC , se construye un triángulo isósceles con un lado tomado como BC y el otro cateto igual BD a lo largo de la extensión del lado AB . Luego se argumenta que el ángulo β tiene una medida mayor que el ángulo α , por lo que el lado AD es más largo que el lado AC . Sin embargo:

${\displaystyle {\overline {AD}}={\overline {AB}}+{\overline {BD}}={\overline {AB}}+{\overline {BC}},}$

Por lo tanto, la suma de las longitudes de los lados AB y BC es mayor que la longitud de AC . Esta prueba aparece en los Elementos de Euclides , Libro 1, Proposición 20. ^[7]

Para un triángulo propio, la desigualdad del triángulo, tal como se enuncia en palabras, se traduce literalmente en tres desigualdades (dado que un triángulo propio tiene longitudes de lados a , b , c que son todas positivas y excluye el caso degenerado de área cero):

${\displaystyle a+b>c,\quad b+c>a,\quad c+a>b.}$

Se puede demostrar que una forma más sucinta de este sistema de desigualdad es

${\displaystyle |ab|<c<a+b.}$

Otra forma de decirlo es

${\displaystyle \max(a,b,c)<a+b+c-\max(a,b,c)}$

reticente

${\displaystyle 2\max(a,b,c)<a+b+c}$

y por lo tanto la longitud del lado más largo es menor que el semiperímetro .

Una formulación matemáticamente equivalente es que el área de un triángulo con lados a , b , c debe ser un número real mayor que cero. La fórmula de Heron para el área es

${\displaystyle {\begin{aligned}4\cdot {\text{área}}&={\sqrt {(a+b+c)(-a+b+c)(a-b+c)(a+bc)}}\\&={\sqrt {-a^{4}-b^{4}-c^{4}+2a^{2}b^{2}+2a^{2}c^{2}+2b^{2}c^{2}}}.\end{aligned}}}$

En términos de cualquiera de las expresiones del área, la desigualdad triangular impuesta en todos los lados es equivalente a la condición de que la expresión bajo el signo de raíz cuadrada sea real y mayor que cero (por lo que la expresión del área es real y mayor que cero).

La desigualdad triangular proporciona dos restricciones más interesantes para los triángulos cuyos lados son a , b , c , donde a ≥ b ≥ c y es la proporción áurea , como${\estilo de visualización \phi}$

${\displaystyle 1<{\frac {a+c}{b}}<3}$

${\displaystyle 1\leq \min \left({\frac {a}{b}},{\frac {b}{c}}\right)<\phi .}$^[8]

En el caso de los triángulos rectángulos, la desigualdad triangular se especializa en la afirmación de que la hipotenusa es mayor que cualquiera de los dos lados y menor que su suma. ^[9]

La segunda parte de este teorema ya se estableció anteriormente para cualquier lado de cualquier triángulo. La primera parte se establece utilizando la figura inferior. En la figura, considere el triángulo rectángulo ADC . Se construye un triángulo isósceles ABC con lados iguales AB = AC . A partir del postulado del triángulo , los ángulos en el triángulo rectángulo ADC satisfacen:

${\displaystyle \alpha +\gamma =\pi /2\ .}$

Asimismo, en el triángulo isósceles ABC , los ángulos satisfacen:

${\displaystyle 2\beta +\gamma =\pi \ .}$

Por lo tanto,

${\displaystyle \alpha =\pi /2-\gamma ,\ \mathrm {while} \ \beta =\pi /2-\gamma /2\ ,}$

y así, en particular,

${\displaystyle \alpha <\beta \ .}$

Esto significa que el lado AD , que es opuesto al ángulo α , es más corto que el lado AB , que es opuesto al ángulo mayor β . Pero AB = AC . Por lo tanto:

${\displaystyle {\overline {AC}}>{\overline {AD}}\ .}$

Una construcción similar muestra que AC > DC , lo que establece el teorema.

Una prueba alternativa (también basada en el postulado del triángulo) procede considerando tres posiciones para el punto B : ^[10] (i) como se representa (lo cual debe demostrarse), o (ii) B coincidente con D (lo que significaría que el triángulo isósceles tenía dos ángulos rectos como ángulos base más el ángulo del vértice γ , lo que violaría el postulado del triángulo ), o por último, (iii) B interior al triángulo rectángulo entre los puntos A y D (en cuyo caso el ángulo ABC es un ángulo exterior de un triángulo rectángulo BDC y por lo tanto mayor que π /2 , lo que significa que el otro ángulo base del triángulo isósceles también es mayor que π /2 y su suma excede a π en violación del postulado del triángulo).

Este teorema que establece desigualdades se agudiza con el teorema de Pitágoras hasta la igualdad de que el cuadrado de la longitud de la hipotenusa es igual a la suma de los cuadrados de los otros dos lados.

Consideremos un triángulo cuyos lados están en progresión aritmética y sean los lados a , a + d , a + 2 d . Entonces la desigualdad del triángulo requiere que

${\displaystyle {\begin{array}{rcccl}0&<&a&<&2a+3d,\\0&<&a+d&<&2a+2d,\\0&<&a+2d&<&2a+d.\end{array}}}$

Para satisfacer todas estas desigualdades se requiere

${\displaystyle a>0{\text{ and }}-{\frac {a}{3}}<d<a.}$^[11]

Cuando se elige d tal que d = a /3 , se genera un triángulo rectángulo que siempre es similar al triple pitagórico con lados 3 , 4 , 5 .

Ahora considere un triángulo cuyos lados están en una progresión geométrica y sean los lados a , ar , ar ² . Entonces la desigualdad del triángulo requiere que

${\displaystyle {\begin{array}{rcccl}0&<&a&<&ar+ar^{2},\\0&<&ar&<&a+ar^{2},\\0&<&\!ar^{2}&<&a+ar.\end{array}}}$

La primera desigualdad requiere a > 0 ; por lo tanto, se puede dividir y eliminar. Con a > 0 , la desigualdad del medio solo requiere r > 0 . Esto deja ahora la primera y tercera desigualdades que necesitan satisfacer

${\displaystyle {\begin{aligned}r^{2}+r-1&{}>0\\r^{2}-r-1&{}<0.\end{aligned}}}$

La primera de estas desigualdades cuadráticas requiere que r se encuentre en la región más allá del valor de la raíz positiva de la ecuación cuadrática r ² + r − 1 = 0 , es decir r > φ − 1 donde φ es la proporción áurea . La segunda desigualdad cuadrática requiere que r se encuentre entre 0 y la raíz positiva de la ecuación cuadrática r ² − r − 1 = 0 , es decir 0 < r < φ . Los requisitos combinados dan como resultado que r esté confinado al rango

${\displaystyle \varphi -1<r<\varphi \,{\text{ and }}a>0.}$^[12]

Cuando se elige la razón común r tal que r = √ φ se genera un triángulo rectángulo que siempre es similar al triángulo de Kepler .

La desigualdad del triángulo se puede extender por inducción matemática a trayectorias poligonales arbitrarias, mostrando que la longitud total de una trayectoria de ese tipo no es menor que la longitud de la línea recta entre sus extremos. En consecuencia, la longitud de cualquier lado del polígono es siempre menor que la suma de las longitudes de los otros lados del polígono.

Consideremos un cuadrilátero cuyos lados están en progresión geométrica y sean los lados a , ar , ar ² , ar ³ . Entonces la desigualdad poligonal generalizada requiere que

${\displaystyle {\begin{array}{rcccl}0&<&a&<&ar+ar^{2}+ar^{3}\\0&<&ar&<&a+ar^{2}+ar^{3}\\0&<&ar^{2}&<&a+ar+ar^{3}\\0&<&ar^{3}&<&a+ar+ar^{2}.\end{array}}}$

Estas desigualdades para a > 0 se reducen a lo siguiente

${\displaystyle r^{3}+r^{2}+r-1>0}$

${\displaystyle r^{3}-r^{2}-r-1<0.}$^[13]

Los polinomios del lado izquierdo de estas dos desigualdades tienen raíces que son la constante de Tribonacci y su recíproca. En consecuencia, r está limitada al rango 1/ t < r < t donde t es la constante de Tribonacci.

Esta generalización se puede utilizar para demostrar que la curva más corta entre dos puntos en la geometría euclidiana es una línea recta.

Ningún camino poligonal entre dos puntos es más corto que la línea que los une. Esto implica que ninguna curva puede tener una longitud de arco menor que la distancia entre sus puntos finales. Por definición, la longitud del arco de una curva es el límite superior mínimo de las longitudes de todas las aproximaciones poligonales de la curva. El resultado para los caminos poligonales muestra que la línea recta entre los puntos finales es la más corta de todas las aproximaciones poligonales. Debido a que la longitud del arco de la curva es mayor o igual que la longitud de cada aproximación poligonal, la curva en sí no puede ser más corta que el camino en línea recta. ^[14]

El recíproco del teorema de desigualdad del triángulo también es cierto: si tres números reales son tales que cada uno es menor que la suma de los otros, entonces existe un triángulo con estos números como longitudes de sus lados y con área positiva; y si un número es igual a la suma de los otros dos, existe un triángulo degenerado (es decir, con área cero) con estos números como longitudes de sus lados.

En cualquier caso, si las longitudes de los lados son a , b , c, podemos intentar colocar un triángulo en el plano euclidiano como se muestra en el diagrama. Necesitamos demostrar que existe un número real h consistente con los valores a , b y c , en cuyo caso existe este triángulo.

Por el teorema de Pitágoras tenemos b ² = h ² + d ² y a ² = h ² + ( c − d ) ² según la figura de la derecha. Restando estos valores obtenemos a ² − b ² = c ² − 2 cd . Esta ecuación nos permite expresar d en términos de los lados del triángulo:

${\displaystyle d={\frac {-a^{2}+b^{2}+c^{2}}{2c}}.}$

Para la altura del triángulo tenemos que h ² = b ² − d ² . Reemplazando d por la fórmula dada anteriormente, tenemos

${\displaystyle h^{2}=b^{2}-\left({\frac {-a^{2}+b^{2}+c^{2}}{2c}}\right)^{2}.}$

Para que un número real h satisfaga esto, h ² debe ser no negativo:

${\displaystyle {\begin{aligned}0&\leq b^{2}-\left({\frac {-a^{2}+b^{2}+c^{2}}{2c}}\right)^{2}\\[4pt]0&\leq \left(b-{\frac {-a^{2}+b^{2}+c^{2}}{2c}}\right)\left(b+{\frac {-a^{2}+b^{2}+c^{2}}{2c}}\right)\\[4pt]0&\leq \left(a^{2}-(b-c)^{2})((b+c)^{2}-a^{2}\right)\\[6pt]0&\leq (a+b-c)(a-b+c)(b+c+a)(b+c-a)\\[6pt]0&\leq (a+b-c)(a+c-b)(b+c-a)\end{aligned}}}$

que se cumple si la desigualdad del triángulo se cumple para todos los lados. Por lo tanto, existe un número real consistente con los lados , y el triángulo existe. Si cada desigualdad del triángulo se cumple estrictamente , y el triángulo no es degenerado (tiene área positiva); pero si una de las desigualdades se cumple con igualdad, entonces , el triángulo es degenerado.${\displaystyle h}$${\displaystyle a,b,c}$${\displaystyle h>0}$${\displaystyle h=0}$

This section does not cite any sources. Please help improve this section by adding citations to reliable sources. Unsourced material may be challenged and removed. (October 2021) (Learn how and when to remove this message)

El área de una cara triangular de un tetraedro es menor o igual a la suma de las áreas de las otras tres caras triangulares. De manera más general, en el espacio euclidiano, el hipervolumen de una faceta (n − 1) de un símplex n es menor o igual a la suma de los hipervolúmenes de las otras n facetas.

Así como la desigualdad triangular se generaliza a una desigualdad poligonal, la desigualdad de un símplex de cualquier dimensión se generaliza a un politopo de cualquier dimensión: el hipervolumen de cualquier faceta de un politopo es menor o igual a la suma de los hipervolúmenes de las facetas restantes.

En algunos casos, la desigualdad tetraédrica es más fuerte que varias aplicaciones de la desigualdad triangular. Por ejemplo, la desigualdad triangular parece permitir la posibilidad de cuatro puntos A , B , C y Z en el espacio euclidiano tales que las distancias

AB = BC = CA = 26

y

A-Z = B-Z = C-Z = 14 .

Sin embargo, no pueden existir puntos con tales distancias: el área del triángulo equilátero ABC 26–26–26 es , que es mayor que tres veces , el área de un triángulo isósceles 26–14–14 (todo por la fórmula de Herón ), y por lo tanto la disposición está prohibida por la desigualdad tetraédrica.${\textstyle 169{\sqrt {3}}}$${\textstyle 39{\sqrt {3}}}$

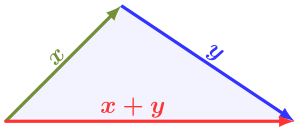
En un espacio vectorial normado V , una de las propiedades definitorias de la norma es la desigualdad triangular:

${\displaystyle \|\mathbf {u} +\mathbf {v} \|\leq \|\mathbf {u} \|+\|\mathbf {v} \|\quad \forall \,\mathbf {u} ,\mathbf {v} \in V}$

Es decir, la norma de la suma de dos vectores es, como máximo, tan grande como la suma de las normas de los dos vectores. Esto también se conoce como subaditividad . Para que cualquier función propuesta se comporte como una norma, debe satisfacer este requisito. ^[15]

Si el espacio normado es euclidiano o, más generalmente, estrictamente convexo , entonces si y solo si el triángulo formado por u , v y u + v es degenerado, es decir, u y v están en el mismo rayo, es decir, u = 0 o v = 0 o u = α v para algún α > 0. Esta propiedad caracteriza a los espacios normados estrictamente convexos, como los espacios ℓ _p con 1 < p < ∞ . Sin embargo, hay espacios normados en los que esto no es cierto. Por ejemplo, considere el plano con la norma ℓ ₁ (la distancia de Manhattan ) y denote u = (1, 0) y v = (0, 1) . Entonces, el triángulo formado por u , v y u + v no es degenerado pero${\displaystyle \|\mathbf {u} +\mathbf {v} \|=\|\mathbf {u} \|+\|\mathbf {v} \|}$

${\displaystyle \|\mathbf {u} +\mathbf {v} \|=\|(1,1)\|=|1|+|1|=2=\|\mathbf {u} \|+\|\mathbf {v} \|.}$

El valor absoluto es una norma para la línea real ; como se requiere, el valor absoluto satisface la desigualdad triangular para cualquier número real u y v . Si u y v tienen el mismo signo o cualquiera de ellos es cero, entonces Si u y v tienen signos opuestos, entonces sin pérdida de generalidad suponga Entonces Combinando estos casos: ^[16]${\displaystyle |u+v|=|u|+|v|.}$${\displaystyle |u|>|v|.}$${\displaystyle |u+v|=|u|-|v|<|u|+|v|.}$

$${\displaystyle |u+v|\leq |u|+|v|.}$$

La desigualdad triangular es útil en el análisis matemático para determinar la mejor estimación superior del tamaño de la suma de dos números, en términos de los tamaños de los números individuales. También existe una estimación inferior, que se puede encontrar utilizando la desigualdad triangular inversa que establece que para cualquier número real u y v ,${\displaystyle |u-v|\geq {\bigl |}|u|-|v|{\bigr |}.}$

La norma del taxi o 1-norma es una generalización del valor absoluto a dimensiones superiores. Para encontrar la norma de un vector, basta con sumar el valor absoluto de cada componente por separado.${\displaystyle v=(v_{1},v_{2},\ldots v_{n}),}$$${\displaystyle \|v\|_{1}=|v_{1}|+|v_{2}|+\dotsb +|v_{n}|.}$$

La norma euclidiana o norma 2 define la longitud de los vectores de traslación en un espacio euclidiano n -dimensional en términos de un sistema de coordenadas cartesianas . Para un vector, su longitud se define utilizando el teorema de Pitágoras n -dimensional :${\displaystyle v=(v_{1},v_{2},\ldots v_{n}),}$$${\displaystyle \|v\|_{2}={\sqrt {|v_{1}|^{2}+|v_{2}|^{2}+\dotsb +|v_{n}|^{2}}}.}$$

El producto interno es la norma en cualquier espacio de producto interno , una generalización de los espacios vectoriales euclidianos que incluye ejemplos de dimensión infinita. La desigualdad triangular se deduce de la desigualdad de Cauchy-Schwarz de la siguiente manera: Dados los vectores y , y denotando el producto interno como : ^[17]${\displaystyle u}$${\displaystyle v}$${\displaystyle \langle u,v\rangle }$

${\displaystyle \|u+v\|^{2}}$	${\displaystyle =\langle u+v,u+v\rangle }$
	${\displaystyle =\|u\|^{2}+\langle u,v\rangle +\langle v,u\rangle +\|v\|^{2}}$
	${\displaystyle \leq \|u\|^{2}+2|\langle u,v\rangle |+\|v\|^{2}}$
	${\displaystyle \leq \|u\|^{2}+2\|u\|\|v\|+\|v\|^{2}}$(por la desigualdad de Cauchy-Schwarz)
	${\displaystyle =\left(\|u\|+\|v\|\right)^{2}}$.

La desigualdad de Cauchy-Schwarz se convierte en una igualdad si y solo si u y v son linealmente dependientes. La desigualdad se convierte en una igualdad para y si uno de los vectores u o v es un escalar no negativo del otro. Al tomar la raíz cuadrada del resultado final se obtiene la desigualdad triangular.${\displaystyle \langle u,v\rangle +\langle v,u\rangle \leq 2\left|\left\langle u,v\right\rangle \right|}$${\displaystyle u}$${\displaystyle v}$

La p -norma es una generalización de las normas de taxi y euclidiana, utilizando un exponente entero positivo arbitrario, donde v _i son los componentes del vector v .$${\displaystyle \|v\|_{p}={\bigl (}|v_{1}|^{p}+|v_{2}|^{p}+\dotsb +|v_{n}|^{p}{\bigr )}^{1/p},}$$

Excepto en el caso p = 2 , la p -norma no es una norma de producto interno, porque no satisface la ley del paralelogramo . La desigualdad triangular para valores generales de p se denomina desigualdad de Minkowski . ^[18] Tiene la forma:$${\displaystyle \|u+v\|_{p}\leq \|u\|_{p}+\|v\|_{p}\ .}$$

En un espacio métrico M con métrica d , la desigualdad triangular es un requisito sobre la distancia :

${\displaystyle d(A,\ C)\leq d(A,\ B)+d(B,\ C)\ ,}$

para todos los puntos A , B y C en M. Es decir, la distancia de A a C es como máximo tan grande como la suma de la distancia de A a B y la distancia de B a C.

La desigualdad triangular es responsable de la mayor parte de la estructura interesante en un espacio métrico, es decir, la convergencia. Esto se debe a que los requisitos restantes para una métrica son bastante simplistas en comparación. Por ejemplo, el hecho de que cualquier secuencia convergente en un espacio métrico sea una secuencia de Cauchy es una consecuencia directa de la desigualdad triangular, porque si elegimos cualquier x _n y x _m tal que d ( x _n , x ) < ε /2 y d ( x _m , x ) < ε /2 , donde ε > 0 está dado y es arbitrario (como en la definición de un límite en un espacio métrico), entonces por la desigualdad triangular, d ( x _n , x _m ) ≤ d ( x _n , x ) + d ( x _m , x ) < ε /2 + ε /2 = ε , de modo que la secuencia { x _n } es una secuencia de Cauchy, por definición.

Esta versión de la desigualdad triangular se reduce a la enunciada anteriormente en el caso de espacios vectoriales normados donde se induce una métrica mediante d ( u , v ) ≔ ‖ u − v ‖ , siendo u − v el vector que apunta del punto v al punto u .

La desigualdad triangular inversa es una formulación alternativa lógicamente equivalente de la desigualdad triangular que proporciona límites inferiores en lugar de límites superiores. Para la geometría plana, el enunciado es: ^[19]

Cualquier lado de un triángulo es mayor o igual a la diferencia entre los otros dos lados .

En el caso de un espacio vectorial normado, la afirmación es:

${\displaystyle {\big |}\|u\|-\|v\|{\big |}\leq \|u-v\|,}$

o para espacios métricos, . Esto implica que tanto la norma como la función de distancia son Lipschitz continuas con constante de Lipschitz 1 , y por lo tanto son en particular uniformemente continuas .${\displaystyle |d(A,C)-d(B,C)|\leq d(A,B)}$${\displaystyle \|\cdot \|}$${\displaystyle z}$${\displaystyle d(z,\cdot )}$

La prueba de la desigualdad del triángulo inverso se obtiene a partir de la ecuación habitual :${\displaystyle \|v-u\|=\|{-}1(u-v)\|=|{-}1|\cdot \|u-v\|=\|u-v\|}$

${\displaystyle \|u\|=\|(u-v)+v\|\leq \|u-v\|+\|v\|\Rightarrow \|u\|-\|v\|\leq \|u-v\|,}$

${\displaystyle \|v\|=\|(v-u)+u\|\leq \|v-u\|+\|u\|\Rightarrow \|u\|-\|v\|\geq -\|u-v\|,}$

Combinando estas dos afirmaciones obtenemos:

${\displaystyle -\|u-v\|\leq \|u\|-\|v\|\leq \|u-v\|\Rightarrow {\big |}\|u\|-\|v\|{\big |}\leq \|u-v\|.}$

A la inversa, la prueba de la desigualdad triangular a partir de la desigualdad triangular inversa funciona en dos casos:

Si entonces por la desigualdad del triángulo inverso, ,${\displaystyle \|u+v\|-\|u\|\geq 0,}$${\displaystyle \|u+v\|-\|u\|={\big |}\|u+v\|-\|u\|{\big |}\leq \|(u+v)-u\|=\|v\|\Rightarrow \|u+v\|\leq \|u\|+\|v\|}$

y si entonces trivialmente por la no negatividad de la norma. ${\displaystyle \|u+v\|-\|u\|<0,}$${\displaystyle \|u\|+\|v\|\geq \|u\|>\|u+v\|}$

Así, en ambos casos, encontramos que .${\displaystyle \|u\|+\|v\|\geq \|u+v\|}$

Para espacios métricos, la prueba de la desigualdad del triángulo inverso se encuentra de manera similar:

${\displaystyle d(A,B)+d(B,C)\geq d(A,C)\Rightarrow d(A,B)\geq d(A,C)-d(B,C)}$

${\displaystyle d(C,A)+d(A,B)\geq d(C,B)\Rightarrow d(A,B)\geq d(B,C)-d(A,C)}$

Juntando estas ecuaciones encontramos:

${\displaystyle d(A,B)\geq |d(A,C)-d(B,C)|}$

Y a la inversa, partiendo de la desigualdad del triángulo inverso, podemos volver a utilizar dos casos:

Si , entonces ,${\displaystyle d(A,C)-d(B,C)\geq 0}$${\displaystyle d(A,B)\geq |d(A,C)-d(B,C)|=d(A,C)-d(B,C)\Rightarrow d(A,B)+d(B,C)\geq d(A,C)}$

y si entonces de nuevo por la no negatividad de la métrica. ${\displaystyle d(A,C)-d(B,C)<0,}$${\displaystyle d(A,B)+d(B,C)\geq d(B,C)>d(A,C)}$

Así, en ambos casos, encontramos que .${\displaystyle d(A,B)+d(B,C)\geq d(A,C)}$

Aplicando la función coseno a la desigualdad triangular y a la desigualdad triangular inversa para longitudes de arco y empleando las fórmulas de suma y resta de ángulos para cosenos, se deduce inmediatamente que

$${\displaystyle \operatorname {sim} (u,w)\geq \operatorname {sim} (u,v)\cdot \operatorname {sim} (v,w)-{\sqrt {\left(1-\operatorname {sim} (u,v)^{2}\right)\cdot \left(1-\operatorname {sim} (v,w)^{2}\right)}}}$$

y

$${\displaystyle \operatorname {sim} (u,w)\leq \operatorname {sim} (u,v)\cdot \operatorname {sim} (v,w)+{\sqrt {\left(1-\operatorname {sim} (u,v)^{2}\right)\cdot \left(1-\operatorname {sim} (v,w)^{2}\right)}}\,.}$$

Con estas fórmulas, es necesario calcular una raíz cuadrada para cada triple de vectores { u , v , w } que se examina en lugar de arccos(sim( u , v )) para cada par de vectores { u , v } examinado, y podría ser una mejora del rendimiento cuando el número de triples examinados es menor que el número de pares examinados.

La métrica del espacio de Minkowski no es definida positivamente, lo que significa que puede tener cualquier signo o anularse, incluso si el vector u no es cero. Además, si u y v son ambos vectores temporales que se encuentran en el cono de luz futuro, la desigualdad triangular se invierte:${\displaystyle \eta _{\mu \nu }}$${\displaystyle \|u\|^{2}=\eta _{\mu \nu }u^{\mu }u^{\nu }}$

${\displaystyle \|u+v\|\geq \|u\|+\|v\|.}$

Un ejemplo físico de esta desigualdad es la paradoja de los gemelos en la relatividad especial . La misma forma inversa de la desigualdad se cumple si ambos vectores se encuentran en el cono de luz pasado y si uno o ambos son vectores nulos. El resultado se cumple en dimensiones para cualquier . Si el plano definido por y es similar al espacio (y, por lo tanto, un subespacio euclidiano), entonces se cumple la desigualdad triangular habitual.${\displaystyle n+1}$${\displaystyle n\geq 1}$${\displaystyle u}$${\displaystyle v}$

• Subaditividad
• Desigualdad de Minkowski
• La desigualdad de Ptolomeo

• Pedoe, Daniel (1988). Geometría: un curso completo . Dover. ISBN 0-486-65812-0.
• Rudin, Walter (1976). Principios del análisis matemático . Nueva York: McGraw-Hill . ISBN. 0-07-054235-X.

• Desigualdad triangular en ProofWiki