Maximización de beneficios

Proceso para determinar las mayores utilidades de una empresa

{\displaystyle Q^{*}} — Un ejemplo de diagrama de maximización de beneficios: En el gráfico de oferta y demanda, la producción de es el punto de intersección de (Ingreso marginal) y (Coste marginal), donde . Se dice que la empresa que produce a este nivel de producción maximiza los beneficios. Si la producción producida es menor que la cantidad de equilibrio ( ), como se muestra en la parte roja, entonces es mayor que ( ), y el beneficio no se maximiza. La empresa tiene interés en aumentar su nivel de producción para maximizar los beneficios, porque el ingreso obtenido será mayor que el costo a pagar. Sin embargo, si el nivel de producción es mayor que ( ), como se muestra en la parte azul, el beneficio total de la empresa disminuirá porque la unidad adicional producida aumentará el costo total. Aquí también el beneficio no se maximiza y la empresa tiene que reducir su nivel de producción para maximizar los beneficios. $Q^{*}$ ${\text{MR}}$ ${\text{MC}}$ ${\text{MR}}={\text{MC}}$ $Q^{*}$ ${\text{MR}}$ ${\text{MC}}$ ${\text{MR}}>{\text{MC}}$ $Q^{*}$ ${\text{MR}}<{\text{MC}}$

En economía , la maximización de beneficios es el proceso a corto o largo plazo mediante el cual una empresa puede determinar los niveles de precios , insumos y producción que conducirán a la mayor ganancia total posible (o simplemente ganancia, en pocas palabras). En la economía neoclásica , que actualmente es el enfoque dominante en la microeconomía , se supone que la empresa es un " agente racional " (ya sea que opere en un mercado perfectamente competitivo o no) que desea maximizar su beneficio total, que es la diferencia entre sus ingresos totales y su costo total.

Medir el costo total y el ingreso total es a menudo poco práctico, ya que las empresas no tienen la información confiable necesaria para determinar los costos en todos los niveles de producción. En cambio, adoptan un enfoque más práctico al examinar cómo pequeños cambios en la producción influyen en los ingresos y los costos. Cuando una empresa produce una unidad adicional de producto, el ingreso adicional obtenido por su venta se denomina ingreso marginal ( ), y el costo adicional para producir esa unidad se denomina costo marginal ( ). Cuando el nivel de producción es tal que el ingreso marginal es igual al costo marginal ( ), entonces se dice que la ganancia total de la empresa se maximiza. Si el ingreso marginal es mayor que el costo marginal ( ), entonces su ganancia total no se maximiza, porque la empresa puede producir unidades adicionales para obtener una ganancia adicional. En otras palabras, en este caso, es en el interés "racional" de la empresa aumentar su nivel de producción hasta que su ganancia total se maximice. Por otra parte, si el ingreso marginal es menor que el costo marginal ( ), entonces tampoco se maximiza su beneficio total, porque producir una unidad menos reducirá el costo total más que el ingreso total obtenido, lo que le dará a la empresa un mayor beneficio total. En este caso, una empresa "racional" tiene un incentivo para reducir su nivel de producción hasta maximizar su beneficio total. ^[1] ${\text{MR}}$ ${\text{MC}}$ ${\text{MR}}={\text{MC}}$ ${\text{MR}}>{\text{MC}}$ ${\text{MR}}<{\text{MC}}$

Existen varias perspectivas que se pueden adoptar para maximizar las ganancias. En primer lugar, dado que las ganancias son iguales a los ingresos menos los costos , se pueden representar gráficamente cada una de las variables ingresos y costos como funciones del nivel de producción y encontrar el nivel de producción que maximiza la diferencia (o esto se puede hacer con una tabla de valores en lugar de un gráfico). En segundo lugar, si se conocen formas funcionales específicas para los ingresos y los costos en términos de producción, se puede utilizar el cálculo para maximizar las ganancias con respecto al nivel de producción. En tercer lugar, dado que la condición de primer orden para la optimización iguala los ingresos marginales y los costos marginales , si las funciones de ingresos marginales ( ) y costos marginales ( ) en términos de producción están directamente disponibles, se pueden igualar, utilizando ecuaciones o un gráfico. En cuarto lugar, en lugar de una función que dé el costo de producir cada nivel de producción potencial, la empresa puede tener funciones de costo de insumos que den el costo de adquirir cualquier cantidad de cada insumo, junto con una función de producción que muestre cuánta producción resulta de usar cualquier combinación de cantidades de insumos. En este caso, se puede utilizar el cálculo para maximizar las ganancias con respecto a los niveles de uso de insumos, sujeto a las funciones de costo de insumos y la función de producción. La condición de primer orden para cada insumo iguala el producto del ingreso marginal del insumo (el incremento en los ingresos por la venta del producto causado por un incremento en la cantidad del insumo utilizado) al costo marginal del insumo. ${\text{MR}}$ ${\text{MC}}$

Para una empresa en un mercado perfectamente competitivo para su producción, la función de ingresos será simplemente igual al precio de mercado multiplicado por la cantidad producida y vendida, mientras que para un monopolista , que elige su nivel de producción simultáneamente con su precio de venta. En el caso del monopolio, la empresa producirá más productos porque todavía puede obtener beneficios normales. Para obtener el máximo beneficio, es necesario fijar precios más altos y cantidades más bajas que en el mercado competitivo. Sin embargo, la función de ingresos tiene en cuenta el hecho de que unos niveles más altos de producción requieren un precio más bajo para poder venderse. Una característica análoga se aplica a los mercados de insumos: en un mercado de insumos perfectamente competitivo, el coste del insumo de la empresa es simplemente la cantidad comprada para su uso en la producción multiplicada por el coste unitario del insumo determinado por el mercado, mientras que el precio del insumo por unidad de un monopsonista es más alto para cantidades mayores del insumo comprado.

La principal diferencia entre la maximización de beneficios a corto y largo plazo es que en el largo plazo las cantidades de todos los insumos, incluido el capital físico , son variables de elección, mientras que en el corto plazo la cantidad de capital está predeterminada por decisiones de inversión anteriores . En ambos casos, hay insumos de trabajo y materias primas .

Definiciones básicas

Los costos en los que incurre una empresa pueden clasificarse en dos grupos: costos fijos y costos variables . Los costos fijos, que ocurren solo en el corto plazo, son los que incurre la empresa en cualquier nivel de producción, incluida la producción cero. Estos pueden incluir el mantenimiento del equipo, el alquiler, los salarios de los empleados cuyo número no se puede aumentar o disminuir en el corto plazo y el mantenimiento general. Los costos variables cambian con el nivel de producción y aumentan a medida que se genera más producto. Los materiales consumidos durante la producción a menudo tienen el mayor impacto en esta categoría, que también incluye los salarios de los empleados que pueden ser contratados y despedidos en el corto plazo del período de tiempo considerado. El costo fijo y el costo variable, combinados, equivalen al costo total .

Los ingresos son la cantidad de dinero que una empresa recibe de sus actividades comerciales normales, generalmente de la venta de bienes y servicios (a diferencia del dinero proveniente de la venta de valores como acciones o emisiones de deuda).

La fórmula de las cinco formas consiste en aumentar los clientes potenciales, las tasas de conversación, las ventas promedio en dólares, el número promedio de ventas y la ganancia promedio del producto. Las ganancias pueden aumentar hasta en un 1000 por ciento, esto es importante para los comerciantes individuales y las pequeñas empresas, por no hablar de las grandes empresas, pero no obstante, la maximización de las ganancias es una cuestión de cada etapa de la empresa y de mayores retornos por participación en las ganancias, por lo tanto, salarios más altos y motivación. ^[2]^{[ cita completa requerida ]}

El costo marginal y el ingreso marginal , dependiendo de si se adopta o no el enfoque del cálculo , se definen como el cambio en el costo o el ingreso a medida que se produce cada unidad adicional o como la derivada del costo o el ingreso con respecto a la cantidad de producción. Por ejemplo, tomando la primera definición, si a una empresa le cuesta $400 producir 5 unidades y $480 producir 6, el costo marginal de la sexta unidad es 80 dólares. Por el contrario, el ingreso marginal de la producción de 6 unidades es el ingreso de la producción de 6 unidades menos el ingreso de la producción de 5 unidades (el último elemento menos el elemento anterior).

Perspectiva de ingresos totales y costos totales

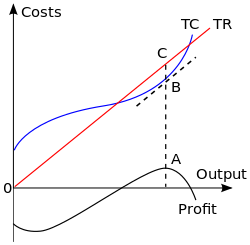
Para obtener la cantidad de producción que maximiza las ganancias, comenzamos por reconocer que las ganancias son iguales a los ingresos totales ( ) menos los costos totales ( ). Dada una tabla de costos e ingresos en cada cantidad, podemos calcular ecuaciones o representar los datos directamente en un gráfico. La producción que maximiza las ganancias es aquella en la que esta diferencia alcanza su máximo. ${\text{TR}}$ ${\text{TC}}$

En el diagrama adjunto, la curva de ingreso total lineal representa el caso en el que la empresa es un competidor perfecto en el mercado de bienes y, por lo tanto, no puede fijar su propio precio de venta. El nivel de producción que maximiza los beneficios se representa como aquel en el que el ingreso total es la altura de y el coste total es la altura de ; el beneficio máximo se mide como la longitud del segmento . Este nivel de producción es también aquel en el que la curva de beneficio total está en su máximo. ${\text{C}}$ ${\text{B}}$ ${\overline {\text{CB}}}$

Si, contrariamente a lo que se supone en el gráfico, la empresa no es un competidor perfecto en el mercado de producción, el precio al que se vende el producto puede leerse en la curva de demanda en la cantidad óptima de producción de la empresa. Esta cantidad óptima de producción es la cantidad en la que el ingreso marginal es igual al costo marginal .

Perspectiva de los ingresos marginales y los costes marginales

Una perspectiva equivalente se basa en la relación de que, por cada unidad vendida, la ganancia marginal ( ) es igual al ingreso marginal ( ) menos el costo marginal ( ). Entonces, si el ingreso marginal es mayor que el costo marginal en algún nivel de producción, la ganancia marginal es positiva y, por lo tanto, se debe producir una mayor cantidad, y si el ingreso marginal es menor que el costo marginal, la ganancia marginal es negativa y se debe producir una menor cantidad. En el nivel de producción en el que el ingreso marginal es igual al costo marginal, la ganancia marginal es cero y esta cantidad es la que maximiza la ganancia. ^[3] Dado que la ganancia total aumenta cuando la ganancia marginal es positiva y la ganancia total disminuye cuando la ganancia marginal es negativa, debe alcanzar un máximo donde la ganancia marginal sea cero (donde el costo marginal sea igual al ingreso marginal) y donde los niveles de producción más bajos o más altos den niveles de ganancia más bajos. ^[3] En términos de cálculo, el requisito de que la producción óptima tenga una ganancia mayor que los niveles de producción adyacentes es que: ^[3] ${\text{M}}\pi$ ${\text{MR}}$ ${\text{MC}}$

{\frac {\operatorname {d} ^{2}R}{{\operatorname {d} Q}^{2}}}<{\frac {\operatorname {d} ^{2}C}{{\operatorname {d} Q}^{2}}}.

La intersección de y se muestra en el siguiente diagrama como el punto . Si la industria es perfectamente competitiva (como se supone en el diagrama), la empresa enfrenta una curva de demanda ( ) que es idéntica a su curva de ingreso marginal ( ), y esta es una línea horizontal a un precio determinado por la oferta y la demanda de la industria. Los costos totales promedio están representados por la curva . La ganancia económica total está representada por el área del rectángulo . La cantidad óptima ( ) es la misma que la cantidad óptima en el primer diagrama. ${\text{MR}}$ ${\text{MC}}$ ${\text{A}}$ ${\text{D}}$ ${\text{MR}}$ ${\text{ATC}}$ ${\overline {\text{PABC}}}$ ${\estilo de visualización Q}$

Si la empresa es monopolista , la curva de ingreso marginal tendría una pendiente negativa, como se muestra en el siguiente gráfico, porque se basaría en la curva de demanda del mercado con pendiente negativa. La producción óptima, que se muestra en el gráfico como , es el nivel de producción en el que el costo marginal es igual al ingreso marginal. El precio que induce esa cantidad de producción es la altura de la curva de demanda en esa cantidad (indicada como ). $Q_{m}$ $Estilo de visualización P_{m}$

Una derivación genérica del nivel de maximización de beneficios de la producción se obtiene mediante los siguientes pasos. En primer lugar, supongamos que una empresa representativa tiene información perfecta sobre sus beneficios, dada por: ${\estilo de visualización i}$

\pi _{i}={\text{TR}}_{i}-{\text{TC}}_{i}

donde denota los ingresos totales y denota los costos totales. La expresión anterior se puede reescribir como: ${\text{TR}}$ ${\text{TC}}$

\pi _{i}=p_{i}\cdot q_{i}-c_{i}\cdot q_{i}

donde denota precio (ingreso marginal), cantidad y costo marginal. La empresa maximiza su beneficio con respecto a la cantidad para alcanzar el nivel de maximización de beneficios de la producción: ${\estilo de visualización p}$ ${\estilo de visualización q}$ ${\estilo de visualización c}$

{\frac {\left(\pi _{i}\right)}{\left(\q_{i}\right)}}=p_{i}-c_{i}=0

Como tal, el nivel de maximización de ganancias de la producción es el ingreso marginal equivalente al costo marginal . $estilo de visualización p_{i}}$ $Estilo de visualización c_{i}}$

En un entorno competitivo pero no perfectamente competitivo, las soluciones de maximización de beneficios más complicadas implican el uso de la teoría de juegos .

Caso en el que maximizar los ingresos es equivalente

En algunos casos, las condiciones de demanda y de costes de una empresa son tales que los beneficios marginales son mayores que cero para todos los niveles de producción hasta un determinado máximo. ^[4] En este caso, el beneficio marginal cae a cero inmediatamente después de que se alcanza ese máximo; por lo tanto, la regla implica que la producción debe producirse al nivel máximo, que también resulta ser el nivel que maximiza los ingresos. ^[4] En otras palabras, la cantidad y el precio que maximizan los beneficios pueden determinarse fijando el ingreso marginal en cero, lo que ocurre en el nivel máximo de producción. El ingreso marginal es igual a cero cuando la curva de ingresos totales ha alcanzado su valor máximo. Un ejemplo sería un vuelo regular de una aerolínea. Los costes marginales de llevar a un pasajero más en el vuelo son insignificantes hasta que se ocupen todos los asientos. La aerolínea maximizaría los beneficios al ocupar todos los asientos. ${\text{M}}\pi = 0$

Maximizar ganancias en el mundo real

En el mundo real, no es fácil maximizar las ganancias. La empresa debe conocer con precisión el ingreso marginal y el costo marginal del último producto vendido debido a MR .

La elasticidad precio de la demanda de bienes depende de la respuesta de las demás empresas. Cuando es la única empresa que sube los precios, la demanda será elástica. Si una familia sube los precios y las demás la siguen, la demanda puede ser inelástica.

Las empresas pueden intentar maximizar sus beneficios mediante la estimación. Cuando el aumento de precio provoca una pequeña caída de la demanda, la empresa puede aumentar el precio tanto como sea posible antes de que la demanda se vuelva elástica. Por lo general, es difícil modificar el impacto del precio en función de la demanda, ya que esta puede producirse debido a muchos otros factores además del precio.

La empresa también puede tener otros objetivos y consideraciones. Por ejemplo, las empresas pueden optar por obtener menos del beneficio máximo en pos de una mayor participación de mercado . Debido a que los aumentos de precios maximizan los beneficios a corto plazo, atraerán a más empresas para que entren en el mercado.

Muchas empresas intentan minimizar los costos trasladando la producción a lugares extranjeros con mano de obra barata (por ejemplo, Nike, Inc. ). Sin embargo, trasladar la línea de producción a un lugar extranjero puede ocasionar costos de transporte innecesarios. Las ubicaciones cercanas al mercado para producir y vender productos pueden mejorar la optimización de la demanda, pero cuando el costo de producción es mucho más alto, no es una buena opción.

Herramientas

Análisis de beneficios: Registrar y analizar habitualmente los costos comerciales de todos los productos o servicios vendidos. Hay muchos elementos diversos en el costo, como mano de obra, materiales, transporte, publicidad, almacenamiento, etc. relacionados con cualquier bien o servicio vendido, que se convierten en gastos.
Herramientas de inteligencia empresarial: Puede ser necesario integrar toda la información financiera para registrar informes de gastos para que la empresa pueda comprender claramente todos los costos relacionados con las operaciones y su precisión.
Planificación y ejecución real: Al implementar una solución hipotética para ayudar en el proceso de planificación de ventas y operaciones, es útil estar familiarizado con las operaciones de la empresa, incluida la cadena de suministro, la gestión de inventario y el proceso de ventas. Se requieren restricciones para evitar que los planes corporativos se vuelvan inviables.

Cambios en los costos totales y maximización de ganancias

Una empresa maximiza sus ganancias operando en un punto en el que el ingreso marginal es igual al costo marginal. Esto se estipula en la teoría neoclásica, en la que una empresa maximiza sus ganancias para determinar un nivel de producción e insumos que proporcione la condición de precio igual al costo marginal. ^[5]^{[ cita completa requerida ]} En el corto plazo, un cambio en los costos fijos no tiene efecto en la producción o el precio que maximizan las ganancias. ^[6] La empresa simplemente trata los costos fijos de corto plazo como costos hundidos y continúa operando como antes. ^[7] Esto se puede confirmar gráficamente. Usando el diagrama que ilustra la perspectiva de costo total-ingreso total, la empresa maximiza sus ganancias en el punto en el que las pendientes de la línea de costo total y la línea de ingreso total son iguales. ^[4] Un aumento en el costo fijo haría que la curva de costo total se desplazara hacia arriba rígidamente por la cantidad del cambio. ^[4] No habría ningún efecto en la curva de ingreso total o en la forma de la curva de costo total. En consecuencia, la producción que maximiza las ganancias permanecería igual. Este punto también se puede ilustrar usando el diagrama para la perspectiva de ingreso marginal-costo marginal. Un cambio en el costo fijo no tendría efecto en la posición o forma de estas curvas. ^[4] En términos simples, aunque la ganancia está relacionada con el costo total, , la empresa puede maximizar la ganancia produciendo hasta la máxima ganancia (el valor máximo de ) para maximizar la ganancia. Pero cuando el costo total aumenta, no significa que la maximización de la ganancia cambiará, porque el aumento en el costo total no cambia necesariamente el costo marginal. Si el costo marginal permanece igual, la empresa aún puede producir hasta la unidad de ( ) para maximizar la ganancia. En el largo plazo, una empresa teóricamente tendrá cero ganancias esperadas bajo el equilibrio competitivo. El mercado debería ajustarse para eliminar cualquier ganancia si hay competencia perfecta. En situaciones donde hay ganancias distintas de cero, deberíamos esperar ver alguna forma de desequilibrio de largo plazo o condiciones no competitivas, como barreras de entrada, donde no hay competencia perfecta entre empresas. ^[5]^[^{cita completa requerida}^] ${\text{Ganancia}}={\text{TR}}-{\text{TC}}$ ${\text{TR}}-{\text{TC}}$ ${\text{IM}}={\text{CM}}={\text{Precio}}$

Precios de margen

Además de utilizar métodos para determinar el nivel óptimo de producción de una empresa, una empresa que no es perfectamente competitiva puede fijar el precio de manera equivalente para maximizar las ganancias (ya que fijar el precio a lo largo de una curva de demanda dada implica elegir un punto preferido en esa curva, lo que equivale a elegir una cantidad preferida para producir y vender). Las condiciones de maximización de las ganancias se pueden expresar en una forma o regla empírica "más fácilmente aplicable" que la que utilizan las perspectivas anteriores. ^[8]^{[ cita completa requerida ]} El primer paso es reescribir la expresión para el ingreso marginal como

${\begin{aligned}{\text{MR}}=&{\frac {\Delta {\text{TR}}}{\Delta Q}}\\=&{\frac {P\Delta Q+Q\Delta P}{\Delta Q}}\\=&P+{\frac {Q\Delta P}{\Delta Q}}\\\end{aligned}}$

, donde y se refieren a los puntos medios entre los valores antiguos y nuevos de precio y cantidad respectivamente. ^[8] El ingreso marginal de una unidad incremental de producción tiene dos partes: primero, el ingreso que la empresa obtiene al vender las unidades adicionales o, dando el término . Las unidades adicionales se denominan unidades marginales. ^[9]^[^{cita completa requerida}^] Producir una unidad adicional y venderla al precio genera un ingreso de . Además, uno debe considerar "el ingreso que la empresa pierde en las unidades que podría haber vendido al precio más alto" ^[9] —es decir, si el precio de todas las unidades no se hubiera reducido por el esfuerzo de vender más unidades. Estas unidades que han perdido ingresos se denominan unidades inframarginales. ^[9] Es decir, vender la unidad adicional da como resultado una pequeña caída en el precio que reduce el ingreso por todas las unidades vendidas en la cantidad . Por lo tanto, , donde es la elasticidad precio de la demanda que caracteriza la curva de demanda de los clientes de las empresas, que es negativa. Luego, al establecer se obtiene así y . Por lo tanto, la regla de margen óptimo es: ${\estilo de visualización P}$ ${\estilo de visualización Q}$ $Estilo de visualización P Delta Q$ ${\estilo de visualización P}$ ${\estilo de visualización P}$ $Q\cdot \left({\frac {\Delta P}{\Delta Q}}\right)$ ${\text{MR}}=P+Q\cdot {\frac {\Delta P}{\Delta Q}}=P+P\cdot {\frac {Q}{P}}\cdot {\frac {\Delta P}{\Delta Q}}=P+{\frac {P}{\text{PED}}}$ ${\text{PED}}$ ${\text{MC}}={\text{MR}}$ ${\text{MC}}=P+{\frac {P}{\text{PED}}}$ ${\frac {P-{\text{MC}}}{P}}={\frac {-1}{\text{PED}}}$ $P={\frac {MC}{1+\left({\frac {1}{\text{PED}}}\right)}}$

{\frac {\left(P-{\text{MC}}\right)}{P}}={\frac {1}{\left(-{\text{PED}}\right)}}

o equivalentemente

P={\frac {\text{PED}}{1+{\text{PED}}}}\cdot {\text{MC}}

. ^[10]^[11]^{[ cita completa necesaria ]}

En otras palabras, la regla es que el tamaño del margen de precio sobre el costo marginal es inversamente proporcional al valor absoluto de la elasticidad precio de la demanda del bien. ^[10]

La regla del margen óptimo también implica que una empresa no competitiva producirá en la región elástica de su curva de demanda de mercado. El coste marginal es positivo. El término sería positivo solo si está entre y (es decir, si la demanda es elástica en ese nivel de producción). ^[12]^[^{cita completa necesaria}^] La intuición detrás de este resultado es que, si la demanda es inelástica en algún valor , entonces una disminución en aumentaría más que proporcionalmente, aumentando así los ingresos ; dado que una disminución también conduciría a un menor coste total, la ganancia aumentaría debido a la combinación de mayores ingresos y menores costes. Por lo tanto, no da la mayor ganancia posible. ${\frac {PED}{1+{\text{PED}}}}$ $P>0$ ${\text{PED}}$ $-1$ $-\infty$ $Q_{1}$ $Q$ $P$ $P\cdot Q$ $Q$ $Q_{1}$

Producto marginal del trabajo, producto marginal del ingreso del trabajo y maximización de las ganancias

La regla general es que la empresa maximiza sus ganancias produciendo la cantidad de producción en la que el ingreso marginal es igual al costo marginal . La cuestión de la maximización de las ganancias también puede abordarse desde el lado de los insumos. Es decir, ¿cuál es el uso que maximiza las ganancias del insumo variable? ^[13] Para maximizar las ganancias, la empresa debe aumentar el uso del insumo "hasta el punto en que el producto del ingreso marginal del insumo sea igual a sus costos marginales". ^[14] Matemáticamente, la regla de maximización de las ganancias es , donde el subíndice se refiere al insumo variable comúnmente asumido, el trabajo. ${\text{MRP}}_{L}={\text{MC}}_{L}$ $_{L}$

El producto de ingreso marginal es el cambio en el ingreso total por unidad de cambio en la entrada variable, es decir, . ${\text{MRP}}_{L}={\frac {\Delta {\text{TR}}}{\Delta L}}$

${\text{MRP}}_{L}$ es el producto del ingreso marginal y el producto marginal del trabajo o . ${\text{MRP}}_{L}={\text{MR}}\cdot {\text{MP}}_{L}$

Crítica

La maximización del excedente del productor puede en algunos casos reducir el excedente del consumidor . ^[15] Algunas formas de maximización de las ganancias del productor se consideran prácticas anticompetitivas y están reguladas por la ley de competencia . ^[15] La maximización de las ganancias del productor a corto plazo puede reducir las ganancias del productor a largo plazo, lo que puede ser explotado mediante precios predatorios como el dumping . ^[16]

Regulación gubernamental

Las cuotas de mercado reflejan el poder de una empresa en el mercado; es muy común que una empresa domine un mercado y, a menudo, un exceso de poder se convierte en el motivo de un comportamiento no Hong Kong. La fijación de precios predatorios , la vinculación , la especulación con los precios y otras conductas reflejan la crisis del poder excesivo de los monopolistas en el mercado. En un intento por evitar que las empresas abusen de su poder para maximizar sus propias ganancias, los gobiernos suelen intervenir para detenerlas. Un ejemplo importante de esto es la regulación antimonopolio que, en la práctica, prohíbe la mayoría de los monopolios industriales . A través de esta regulación, los consumidores disfrutan de una mejor relación con las empresas que los atienden, aunque la propia empresa pueda sufrir, financieramente hablando.

Véase también

Notas

^ Karl E. Case; Ray C. Fair; Sharon M. Oster (2012), Principios de economía (10.ª ed.), Prentice Hall, págs. 180-181
^ empresario.com
^ abc Lipsey (1975). págs. 245–47.
^ abcde Samuelson, W y Marks, S (2003). pág. 47.
^ por Desai, M (2017).
^ Samuelson, W y Marks, S (2003). pág. 52.
^ Landsburg, S (2002).
^ ab Pindyck, R y Rubinfeld, D (2001) pág. 333.
^ abc Besanko, D. y Beautigam, R, (2001) pág. 408.
^ ab Samuelson, W y Marks, S (2003). págs. 103–05.
^ Pindyck, R y Rubinfeld, D (2001) pág. 341.
^ Besanko y Braeutigam (2005) pág. 419.
^ Samuelson, W y Marks, S (2003). pág. 230.
^ Samuelson, W y Marks, S (2003). pág. 23.
^ ab Pittman, Russell W. (17 de diciembre de 2007). "El excedente del consumidor como estándar apropiado para la aplicación de las leyes antimonopolio". Búsqueda en eLibrary . Consultado el 24 de agosto de 2024 .
^ Cheng, Ho Fung Griffith (1 de septiembre de 2020). «Una perspectiva económica sobre la plausibilidad inherente y la frecuencia de los precios predatorios: argumentos a favor de una regulación más agresiva». Revista Europea de Competencia . 16 (2–3): 343–367. doi :10.1080/17441056.2020.1770478. ISSN 1744-1056.

Referencias

Landsburg, S. (2002). Teoría de precios y aplicaciones (quinta ed.). Suroeste.
- Landsburg, S. (2013). Teoría de precios y aplicaciones (PDF) (novena edición). Suroeste. ISBN 978-1-285-42352-4.
Lipsey, Richard G. (1975). Introducción a la economía positiva (cuarta edición). Weidenfeld y Nicolson. Págs. 214-217. ISBN 0-297-76899-9.
Samuelson, W.; Marks, S. (2003). Economía gerencial (cuarta edición). Wiley. ISBN 0470000449.

Enlaces externos

Maximización de ganancias en competencia perfecta por Fiona Maclachlan, Wolfram Demonstrations Project .
Maximización de ganancias: la guía completa de Richard Gulle, Proyecto Techfunnel.
Maximización de beneficios por Tejvan Pettinger.
Tres pasos para dominar la maximización prescriptiva de ganancias por Riverlogic.

[1] Karl E. Case; Ray C. Fair; Sharon M. Oster (2012), Principios de economía (10.ª ed.), Prentice Hall, págs. 180-181

[2] resario.com

[lipsey-3] Lipsey (1975). págs. 245–47.

[samuelson-4] Samuelson, W y Marks, S (2003). pág. 47.

[Desai,_M_2017-5] r Desai, M (2017).

[6] Samuelson, W y Marks, S (2003). pág. 52.

[7] Landsburg, S (2002).

[pindyck-8] Pindyck, R y Rubinfeld, D (2001) pág. 333.

[besanko-9] Besanko, D. y Beautigam, R, (2001) pág. 408.

[samuelson103-10] Samuelson, W y Marks, S (2003). págs. 103–05.

[11] Pindyck, R y Rubinfeld, D (2001) pág. 341.

[12] Besanko y Braeutigam (2005) pág. 419.

[samuelson230-13] Samuelson, W y Marks, S (2003). pág. 230.

[14] Samuelson, W y Marks, S (2003). pág. 23.

[f307-15] Pittman, Russell W. (17 de diciembre de 2007). "El excedente del consumidor como estándar apropiado para la aplicación de las leyes antimonopolio". Búsqueda en eLibrary . Consultado el 24 de agosto de 2024 .

[j276-16] Cheng, Ho Fung Griffith (1 de septiembre de 2020). «Una perspectiva económica sobre la plausibilidad inherente y la frecuencia de los precios predatorios: argumentos a favor de una regulación más agresiva». Revista Europea de Competencia . 16 (2–3): 343–367. doi :10.1080/17441056.2020.1770478. ISSN 1744-1056.